JBCS

INTRODUÇÃO

Um desafio central que permeia diversas vertentes da química é alcançar níveis elevados de eficiência em reações ou processos químicos. Por consequência do avanço tecnológico, os métodos para extração de substâncias de fontes vegetais, animais e minerais, ou para a síntese destes e outros compostos químicos, passaram por transformações significativas ao longo da história. As técnicas usadas para obtenção dessas substâncias, assim como os próprios alvos desejados, têm evoluído de maneira profunda ao longo do tempo. Neste contexto, o pesquisador que atua no que hoje denominamos como área de síntese orgânica associa o conceito de eficiência à necessidade de preparar moléculas orgânicas, seja para aprimorar o entendimento das propriedades moleculares, ou viabilizar alternativas mais acessíveis e economicamente viáveis de se obter certos produtos naturais ou sintéticos como é o caso de compostos bioativos, muitas vezes produzidos por microrganismos como é o caso dos antibióticos. No entanto, a síntese de moléculas complexas é uma tarefa desafiadora, onde cada átomo deve ser posicionado com precisão. Orientados pela lógica de síntese de Corey¹ apoiada pela compreensão mecanística das reações orgânicas, e mais recentemente, com a evolução dos conceitos de eficiência (ou idealidade)^2,3 e sustentabilidade^4,5 em processos químicos, podemos confiar nesses princípios para realizar a difícil tarefa de construir moléculas funcionais que possam trazer benefícios para a nossa sociedade. Pautados por estes novos princípios, temos um cenário de enormes oportunidades para o desenvolvimento científico para os neófitos em síntese orgânica, que ainda hoje tem sido considerada ao mesmo tempo como ciência e arte.⁶

O marco inaugural da Química Orgânica é associado à preparação do primeiro composto orgânico sintético, a ureia, por Wöhler⁷ em 1828. Posteriormente, surge o conceito de quiralidade molecular, marcado pela separação física de cristais enantioméricos de um sal de tartarato realizada por Pasteur⁸ em 1848. A quiralidade, caracterizada pela existência de formas não sobreponíveis e que são imagens especulares entre si, é evidente tanto em nível molecular quanto macroscópico, assemelhando-se à distinção entre as mãos esquerda e direita (Figura 1). Porém, a base molecular da quiralidade só foi estabelecida mais de 25 anos depois, quando Le Bel⁹ e van't Hoff,¹⁰ de forma independente, estabeleceram o átomo de carbono tetraédrico com quatro substituintes diferentes como um centro estereogênico, que apresenta um arranjo espacial que não é sobreponível em sua imagem especular. Ainda no século XIX, um feito extraordinário alcançado por Fischer¹¹ em 1890 foi a síntese da (+)-glicose que incluiu pela primeira vez o controle de elementos estereoquímicos em uma molécula orgânica, introduzindo o conceito de síntese assimétrica.

 

 

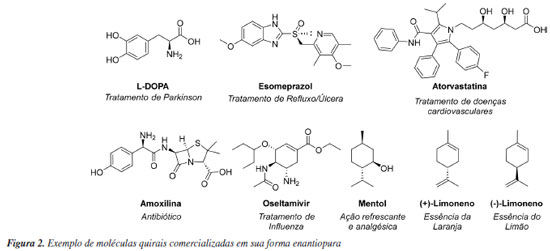
Pesquisas relacionadas à obtenção de moléculas de maneira enantiosseletiva tem se destacado nas atuais linhas de pesquisa em síntese orgânica. O faturamento de produtos químicos quirais em 2023 foi de U$ 71,4 bilhões de dólares, e estima-se que em 10 anos este mercado quase triplique.¹² Alguns exemplos de produtos sintéticos enantiopuros amplamente comercializados estão ilustrados na Figura 2. O interesse na obtenção e comercialização de moléculas enantiopuras se deve ao fato de que os diferentes enantiômeros de uma determinada molécula podem exibir atividades dramaticamente diferentes em organismos vivos, impactando no processo de produção de matérias primas empregadas na indústria de fármacos, agroquímicos, fragrâncias e materiais. Esse fenômeno está relacionado ao conceito de homoquiralidade, que se refere à predominância de aminoácidos na configuração l e açúcares na configuração d na natureza, uma característica considerada uma assinatura fundamental da vida (Figura 2).¹³ Portanto, estes blocos de construção de biopolímeros os tornam intrinsecamente quirais e passíveis de reconhecer de maneira distinta os enantiômeros de uma determinada substância química. Essa discriminação estereosseletiva deve-se as interações tridimensionalmente distintas entre os enantiômeros de uma molécula e os receptores biológicos, que de maneira bastante simplificada pode ser sumarizada pela teoria dos três pontos.¹⁴

 

 

A síntese de moléculas quirais, na ausência de uma força direcionadora quiral, resulta em uma mistura equimolar (racêmica) de enantiômeros. Por meio de técnicas de resolução quiral, baseadas tanto em cromatografia quiral, na formação de sais diastereoisoméricos ou em técnicas de cocristalização, bem como biocatálise, inúmeras moléculas de interesse industrial podem ser separadas em seus enantiômeros puros.¹⁵ Entretanto, essas técnicas não são capazes de separar qualquer racemato, e frequentemente apresentam limitações na eficiência de recuperação do material utilizado na separação, resultando em perdas significativas de massa e tornando o processo economicamente inviável. É crucial destacar que, devido à escassez de técnicas sintéticas enantiosseletivas até a década de 60, a síntese enantiopura de moléculas foi historicamente negligenciada pela comunidade científica, um fato exemplificado pelo caso notório da talidomida.¹⁶ Uma exceção a esse cenário é a semissíntese de substâncias partindo de matérias-primas naturais que apresentavam um certo grau de complexidade, a exemplo da preparação de antibióticos, alguns quimioterápicos e hormônios esteroidais. De todo modo, o cenário mundial mudou drasticamente com novas regulações de agências como FDA (Food and Drug Administration)¹⁷ dos Estados Unidos em 1992, e EMA (European Medicines Agency),¹⁸ que dificultaram a aprovação de novas drogas em sua forma racêmica. Soma-se a este fato a prática das indústrias farmacêuticas denominada de chiral switch (ou troca quiral) iniciada no final da década de 1990 e início dos anos 2000,¹⁹ caracterizada pela substituição de um medicamento quiral racêmico com patente próxima de expirar, por seu enantiômero puro, visando aprimoramento da eficiência, redução de efeitos adversos, e reposicionamento de mercado. Todo este cenário impulsiona o que hoje denominamos como síntese assimétrica, que é hoje a fronteira mais proeminente da química orgânica sintética.

Existem várias estratégias para obter o controle da assimetria de uma molécula, e recomendamos como material introdutório uma revisão desta mesma revista, feita por Pinheiro e Ferreira²⁰ que busca familiarizar a evolução destas abordagens, desde o uso de substratos quirais (chiral approach) até o uso de auxiliares quirais, reagentes quirais e o uso de catálise assimétrica para substratos pró-quirais. Formas alternativas de controle de assimetria foram resumidas por Feringa e van Delden,²¹ incluindo o uso de forças físicas, luz polarizada, amplificação de quiralidade, dentre outros.

Dentre os diversos métodos contemporâneos de controle estereoquímico, a catálise enantiosseletiva se destaca de maneira notável. Avanços iniciais nessa área eram centrados no uso de complexos metálicos contendo ligantes quirais, com posterior desenvolvimento da bio- e organocatálise enantiosseletiva. É notável que num intervalo de apenas 20 anos, dois Prêmios Nobel em Química relacionados a catálise enantiosseletiva tenham sido concedidos: em 2001, a Knowles, Sharpless e Noyori pelo desenvolvimento de métodos assimétricos de hidrogenação, epoxidação e di-hidroxilação; e em 2021, aos pesquisadores List e MacMillan pelo desenvolvimento da organocatálise assimétrica. Neste último caso, embora o conceito de organocatálise tenha sido introduzido formalmente por volta dos anos 2000, relatos do uso de moléculas orgânicas pequenas como catalisadores de reações são encontrados desde 1859.²² Apesar de a disseminação destas moléculas orgânicas quirais como catalisadores ser algo recente, seu uso já está estabelecido como um pilar importante para o desenvolvimento contínuo da síntese orgânica, inclusive no contexto dos princípios fundamentais de Sustentabilidade e Química Verde.^23,24

Ainda nos dias de hoje, o desenvolvimento de catalisadores continua a depender principalmente de observações empíricas, o que exige um grande número de experimentos para atingir níveis significativos de eficiência.²⁵ Apesar dos extraordinários avanços nas aplicações sintéticas envolvendo organocatálise enantiosseletiva, persistem várias lacunas metodológicas que impedem sua adoção generalizada em termos de métodos e aplicações. A capacidade de projetar organocatalisadores de forma sistemática para uma ampla gama de substratos, visando alcançar seletividades e/ou rendimentos mais elevados, é limitada pela dificuldade em identificar prontamente as características estruturais necessárias para um desempenho ideal. Para facilitar esse processo, a previsão de reatividade usando química computacional tem sido um recurso valioso no desenvolvimento de processos catalíticos.²⁶

Uma vez que a organocatálise assimétrica surge no início dos anos 2000, o uso de métodos computacionais foi presente no desenvolvimento inicial da área de modo a suportar descrições mecanísticas e de seletividade.²⁷ Esses trabalhos iniciais foram fundamentais para definir as variações estruturais dos primeiros organocatalisadores quirais, servindo como base para avanços subsequentes em termos de modificações estruturais. Isso possibilitou a expansão para novas classes de catalisadores e para o desenvolvimento de novas reações químicas.

Para além das aplicações iniciais de mecânica quântica, utilizadas em um primeiro momento como ferramenta de apoio, novos métodos in silico provaram-se um caminho importante para a previsão do comportamento catalítico. Portanto, o designin silico de catalisadores tornou-se uma área de grande interesse dentro do campo da química computacional, sendo considerada o novo "Santo Graal" da catálise.^28,29 Nestes últimos 20 anos, novas e efetivas abordagens computacionais foram desenvolvidas para obter um organocatalisador ótimo, capaz de alcançar altos níveis de seletividade.

Esta revisão pretende abordar os avanços da organocatálise aliada à química computacional ao longo dos anos, apresentando exemplos seminais e trabalhos relevantes da área com destaque ao método teórico utilizado para solução de problemas. Adicionalmente, busca inspirar pesquisadores a utilizarem essas ferramentas, muitas das quais desenvolvidas para um público não especialista em química computacional, em seus estágios iniciais de desenvolvimento sintético.

 

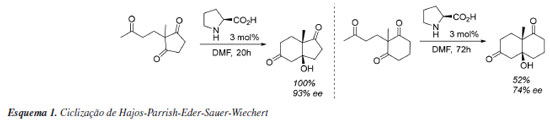
O RENASCIMENTO DA ORGANOCATÁLISE

A primeira síntese assimétrica organocatalisada foi descrita por Bredig envolvendo a preparação de ciano-hidrinas catalisada por alcaloides, mas com uma modesta enantiosseletividade.³⁰ Porém, a primeira com alta seletividade ocorreu dentro do âmbito da indústria farmacêutica em 1973, reação que hoje é conhecida como Hajos-Parrish-Eder-Sauer-Wiechert,³¹ a qual focava na síntese de um esteroide a partir da reação de anelação de Robinson, na qual foi utilizado como organocatalisador a (S)-prolina (Esquema 1). Cabe ressaltar que o termo organocatálise não foi introduzido por esse trabalho, mas consiste no relato seminal de organocatálise via intermediários do tipo enamina, posteriormente explorado por Barbas e List.³²

 

 

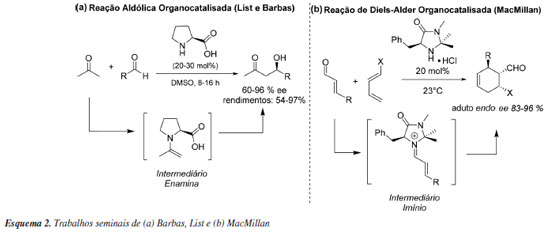
Ainda que a temática tenha sido explorada antes dos anos 2000 por alguns grupos como o de Denmark,³³ fazendo uso de cetonas enantiomericamente puras na epoxidação de alcenos, e por Jacobsen e Sigman,³⁴ ao demonstrar a catálise por ligação de hidrogênio utilizando bases de Shiff na reação assimétrica de Strecker, ainda não havia uma área específica para denominar esses processos dentro da química orgânica sintética. Isso foi concretizado apenas no início dos anos 2000, através da publicação dos trabalhos de Benjamin List, Richard Lerner e Carlos Barbas³² que exploraram reações aldólicas assimétricas via enamina, e por David MacMillan e colaboradores³⁵ em reações de Diels-Alder assimétricas com o desenvolvimento da catálise via íon imínio (Esquema 2). Ambos os organocatalisadores utilizados são derivados diretos de aminoácidos simples.

 

 

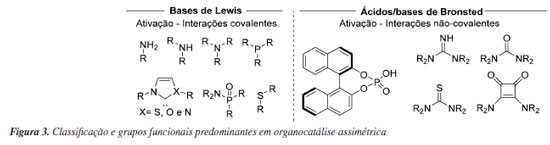
Nas décadas seguintes ocorreu então o renascimento da organocatálise, onde os conceitos fundamentais da área foram desenvolvidos a partir de diversos trabalhos pioneiros em explorar diferentes organocatalisadores e seus respectivos modos de ativação em catálise enantiosseletiva. Esses estudos demonstraram que essas transformações podem passar por mecanismos capazes de produzir estados de transição bem organizados, responsáveis pela ativação e seletividade nessas reações. Dessa forma, os organocatalisadores passaram a ser classificados a partir dos seguintes critérios: (i) mecanismo de ativação baseado em transferência de próton envolvendo ácidos e bases de Bronsted e ligações de hidrogênio, em que o catalisador quiral não se liga quimicamente ao substrato; (ii) mecanismo de formação de intermediários reativos, tal como enaminas e íons imínio, onde o organocatalisador forma um intermediário quimicamente ligado ao substrato, sendo regenerado no final do ciclo catalítico; (iii) mecanismos de transferência de fase em que o catalisador quiral forma um complexo com o substrato e se desloca entre as fases da reação; (iv) mecanismo de cavidade-molecular-acelerada, nos quais o catalisador é capaz de selecionar, de acordo com tamanho e estruturas, substratos competitivos.³⁶ Alguns dos exemplos mais representativos de catalisadores assimétricos e sua respectiva classificação podem ser vistos na Figura 3, sendo algumas destas classes exploradas nos exemplos subsequentes desta revisão, e recentemente analisada de forma abrangente e detalhada em revisões subsequentes.^37-39

 

 

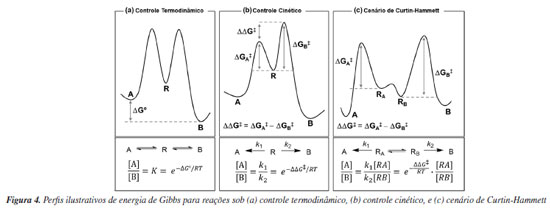
CALCULANDO SELETIVIDADES SOB CONTROLE CINÉTICO OU TERMODINÂMICO

Vários trabalhos utilizam a química computacional como ferramenta na racionalização de fenômenos químicos, com o intuito de validar ou explicar descobertas experimentais e estudos mecanísticos, de modo que os estudos teóricos são integrados aos resultados experimentais de forma colaborativa, normalmente ao final da concretização do trabalho, e não fornecem nenhuma informação preditiva de resultados ou de auxílio no design de catalisadores. A proporção de um certo produto reacional de interesse em relação aos demais possíveis produtos é uma medida de seletividade de uma reação química. Essa proporção pode estar relacionada principalmente à estabilidade termodinâmica dos produtos ou às barreiras de ativação das etapas elementares do processo. Comumente, esses cenários são denominados controle termodinâmico e controle cinético, respectivamente. Para processos reversíveis, que ocorrem em equilíbrio, o controle termodinâmico é o cenário em que a proporção dos produtos é definida por suas estabilidades termodinâmicas relativas (Figura 4a). Nesse caso, a proporção de produtos dependerá da constante de equilíbrio K, que por sua vez está relacionada à energia livre de Gibbs (ΔG⁰) da reação. O controle cinético, por outro lado, é a situação na qual a proporção dos produtos é determinada pelas energias livres de ativação (ΔG^‡) das etapas em que esses produtos são formados (Figura 4b). Assim, essa proporção está relacionada com a razão entre as velocidades de reação k₁ e k₂, que por sua vez dependem da diferença de energia livre (ΔG^‡) entre os estados de transição de cada caminho competitivo. A investigação da enantiosseletividade é restrita às reações sob controle cinético, uma vez que enantiômeros são isoenergéticos. Transformações sintéticas relevantes frequentemente ocorrem em múltiplas etapas reacionais. Quando a formação irreversível do produto é precedida pela rápida interconversão dos reagentes, tem-se um cenário descrito pelo princípio de Curtin-Hammett (Figura 4c). Uma importante implicação desse princípio é que a formação do produto majoritário não envolve, necessariamente, o intermediário termodinamicamente mais estável, mas depende principalmente de qual dos possíveis caminhos reacionais tem menor energia de ativação. A seletividade e eficiência se associam aos conceitos de estado de transição (ET), barreira de ativação e superfície de energia potencial (PES), os quais podem ser investigados computacionalmente.

 

 

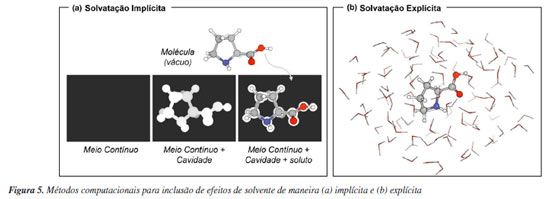
MODELOS QUÍMICOS BASEADOS EM MECANISMOS

Algumas reflexões sobre métodos computacionais e histórico

Os cálculos de química computacional podem ser executados por meio de uma variedade de programas. Estes podem ser obtidos mediante pagamento de licenças, como é o caso do Gaussian,⁴⁰ do Turbomole⁴¹ e do Q-Chem.⁴² Dos que são gratuitos para uso acadêmico, destaca-se o ORCA.^43,44 Existem também os programas de código aberto e gratuitos, como o PySCF,^45,46 PSi4⁴⁷ e xTB.⁴⁸ Apesar de alguns métodos computacionais, em particular os mais recentes, só estarem disponíveis em certos programas, a maioria apresenta as principais implementações que são utilizadas rotineiramente. Apesar de não ser uma regra, é comum executar as etapas de um projeto de química computacional empregando um único programa, em especial aquelas que envolvem cálculos de mecânica quântica. Todos esses programas têm documentações detalhadas, as quais tratam desde a instalação até conceitos teóricos dos métodos disponíveis. Alguns dispõem de fóruns de discussão onde usuários podem interagir entre si e com os desenvolvedores para solução de dúvidas ou problemas técnicos. Esse cenário contribui sobremaneira para disseminar o acesso e o uso de química computacional aos que não são teóricos ou especializados em computação. Evidentemente, um usuário especializado é necessário para questões que são mais complexas. Contudo, apesar dessa conveniência, é inerente à química a descrição de fenômenos na forma de modelos e a química computacional não é exceção. É típico o uso da separação de Born-Oppenheimer, que é quando a parte eletrônica de uma molécula é separada da parte nuclear, para representar tais sistemas. Neste contexto, se faz necessário escolher uma descrição teórica para a estrutura eletrônica. Diferentes componentes podem ser incluídos nessa descrição para que o modelo in silico se aproxime tanto quanto possível da realidade. Modelos mais simples ignoram a existência dos elétrons, e tratam a molécula como um sistema de massas e molas, no que se conhece por mecânica molecular (MM). Essa solução é particularmente relevante para o estudo da evolução temporal de moléculas ou grupos de moléculas, distribuição conformacional, estrutura de proteínas e outras biomoléculas, entre outras aplicações. Isso porque a inclusão de interações eletrônicas, e de mecânica quântica de forma geral, na descrição do sistema, impõe um custo computacional crescente ao modelo. Uma maneira de aproveitar o menor custo computacional de métodos parametrizados e, simultaneamente, incluir a descrição eletrônica é utilizar os métodos quânticos semiempíricos. Nesses modelos, algumas das complexas expressões de mecânica quântica que surgem são substituídas por expressões mais simples, sendo que certos parâmetros são introduzidos para reproduzir dados experimentais nos cálculos. Dessa maneira, o trabalho realizado pelo computador é reduzido e se obtém uma descrição superior ao que seria possível com mecânica molecular. Mais refinados são os métodos ab initio, os quais visam, idealmente, descrever moléculas partindo apenas de constantes fundamentais. O método de Hartree-Fock (HF) é o mais simples dentre os ab initio. Este método permite descrever sistemas contendo N elétrons em termos de N sistemas contendo um único elétron. Um ponto importante é que é exata a energia de troca, que é uma consequência do Princípio de Exclusão de Pauli, calculada por meio desse método. Esse fato é utilizado por muitos métodos que foram desenvolvidos posteriormente. Um ponto importante sobre o método HF é que a correlação entre os elétrons é aproximada por meio de um campo médio. Um cenário no qual essa correlação é importante é na descrição de interações não-covalentes. Assim, métodos eletrônicos que descrevam explicitamente a correlação eletrônica são necessários. Dentre eles, existem os que são baseados em funções de onda (WFT, do inglês wave function theory) e os que são baseados em density functional theory (DFT).

Além de optar por um método de estrutura eletrônica, frequentemente é necessário considerar fatores externos, em particular o uso de solventes. Interações entre solvente e soluto podem impactar diretamente nas propriedades calculadas das moléculas e estados de transição, afetando energia, geometria, conformação, entre outros. Como via de regra, devemos nos preocupar com o efeito do solvente quando uma determinada reação química for conduzida em solventes polares e envolver intermediários ou estados de transição carregados ou polarizados. Para considerar esses efeitos duas estratégias são utilizadas em cálculos computacionais: modelos de solvatação implícita e solvatação explícita. Na solvatação implícita, as moléculas de solvente não são incluídas diretamente no cálculo. Na realidade, o solvente é representado como um meio contínuo com uma constante dielétrica fixada e o soluto ocupa uma cavidade criada nesse meio contínuo. O solvente é polarizado pelo potencial eletrostático gerado pelo soluto, e esta polarização do solvente pode ser representada por cargas na superfície da cavidade, que interagem com o soluto (Figura 5a). Apesar de inicialmente parecer uma abordagem um tanto restrita, a facilidade de uso e disponibilidade desses modelos os tornaram os métodos mais populares. Esse tipo de modelo tem menor custo computacional que a solvatação explícita, mas não é representativo para casos em que o solvente participa ativamente da reação a partir de interações intermoleculares específicas, por exemplo. Os modelos de solvatação explícita consistem em inserir moléculas individuais de solvente em torno do soluto, e realizar os cálculos desejados (Figura 5b). Normalmente esta estratégia se faz necessária quando o solvente/soluto exercem entre si interações intermoleculares fortes, como por exemplo ligações de hidrogênio, determinando um arranjo molecular distinto quando comparado ao soluto isolado. Ao se adotar esta estratégia, deve-se ter em mente que haverá um aumento do custo computacional, não só pelo aumento do número de elétrons no sistema, mas também porque o espaço conformacional torna-se ainda mais complexo de ser explorado. Uma condição de compromisso entre esses dois modelos gerais de solvatação é utilizar apenas algumas moléculas do solvente ao redor do soluto juntamente com o solvente implícito. Essa abordagem é conhecida por micro-solvatação, ou solvatação discreta-contínua, cluster-contínua, implícita-explícita, dentre outras denominações.⁴⁹ É importante frisar que a escolha do local onde serão incluídas as moléculas explícitas de solvente não é trivial. Felizmente, têm crescido o número de programas que permitem automatizar esse processo.⁵⁰ Destacamos uma revisão desta mesma revista pelo professor Pliego Jr.,⁵¹ que discute as bases teóricas destes tipos de modelos.

 

 

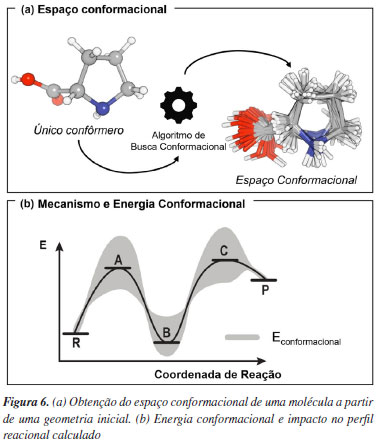
Para exemplificar o uso de modelos implícitos, temos o trabalho de Rankin et al.⁵² que descreveram um estudo mecanístico envolvendo a reação aldólica entre acetona e acetaldeído, demonstrando o papel crucial do efeito do solvente (DMSO) em reduzir as barreiras energéticas dos estados de transição da reação. Um exemplo onde o uso da solvatação explicita foi necessária foi relatado por Zhu e colaboradores,⁵³ onde a consideração explicita do ânion CF₃CO₂^- e de uma molécula de H₂O estabilizaram os estados de transição da epoxidação catalítica por meio de ligação de hidrogênio, sendo este efeito necessário para computar a atividade e enantiosseletividade da epoxidação catalítica de enonas cíclicas catalisada por diaminas quirais.

É interessante notar que enquanto Barton e Hassel foram laureados, em 1969, com o prêmio Nobel em Química por seu trabalho sobre análise conformacional,⁵⁴ hoje esse tipo de estudo é uma etapa fundamental e indispensável em trabalhos de química computacional. Em termos práticos, modelos computacionais envolvendo moléculas orgânicas são, idealmente, iniciados justamente pela exploração do espaço conformacional de reagentes, possíveis intermediários e estados de transição (Figura 6). Cálculos baseados em mecânica molecular ou em métodos semiempíricos são tipicamente empregados nessa etapa. Isso porquê em reações com aplicação prática, em oposição à modelos simplificados, as moléculas costumam apresentar um número significativo de ligações rotacionáveis. Consequentemente, o número de estruturas a serem descritas é grande, e dessa forma o uso de métodos de baixo custo computacional se torna imperativo. Atualmente, programas modernos como o Macromodel^55,56 e o Crest,⁵⁷ permitem obter confôrmeros de moléculas orgânicas de maneira quase automatizada. Em muitos casos, por consequência de limitações impostas pela natureza dos métodos computacionais mais simples, tais como a mecânica molecular e os semiempíricos, é necessário refinar as estruturas obtidas na etapa de análise conformacional. De forma geral, se busca melhorar as geometrias e as energias obtidas utilizando para isso métodos eletrônicos robustos como os baseados em DFT.

 

 

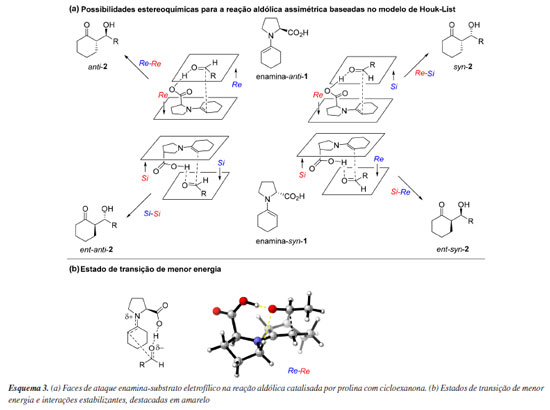
Dentro de uma mesma família de métodos, como os já mencionados semiempíricos, DFT e WFT, existem implementações distintas. Apesar de exata, a DFT não descreve o que seria o verdadeiro funcional da densidade eletrônica. Consequentemente, os funcionais existentes são resultados de uma série de aproximações. Uma delas se refere ao tratamento da interação de troca. Os funcionais híbridos incluem frações variáveis da energia de troca calculada por HF na composição da energia final. Adicionalmente, podem incluir também termos como o gradiente da densidade eletrônica, a densidade de energia cinética ou também contribuições dos orbitais vazios, entre outros. Já os funcionais "puros" são aqueles em que não se utiliza a energia de troca de HF. Enquanto alguns incorporam um número variável de parâmetros empíricos ajustados a dados experimentais (como B3LYP, famílias M05 e M06, B88, B97X-D, entre outros), outros baseiam-se unicamente em parâmetros derivados de princípios gerais da mecânica quântica (como PBE, LDA, TPSS e TPSSh). Uma forma comum de classificação dos funcionais DFT é a "Escada de Jacó", proposta por Perdew.⁵⁸ Do ponto de vista prático, essa variedade de métodos e aproximações faz com que alguns funcionais sejam mais adequados para cálculo de energias de reação, outros para energias de ativação ou ainda que sejam eficientes na obtenção de boas geometrias ou espectros. Muitas das vezes, se faz necessário calcular algumas dessas propriedades simultaneamente e com um mesmo método.

Dessa forma, encontrar uma condição de compromisso entre o método computacional adequado e custo computacional costuma ser uma decisão difícil. Um complicador adicional é que, para grande parte dos métodos computacionais, é necessário escolher uma aproximação para descrever os orbitais atômicos. Essa aproximação é denominada conjunto de funções de base e, assim como existem diferentes métodos de estrutura eletrônica, existem também diversos tipos de conjuntos de funções de base. Esses conjuntos, "a grosso modo", diferem na quantidade de funções de base que são atribuídas a cada átomo. Quanto maior o número de funções, melhor é a descrição molecular. Em contrapartida, o aumento do número de funções implica no aumento da quantidade de operações matemáticas e, consequentemente, do tempo requerido para finalizar um cálculo de química computacional. Uma forma de agregar diversos métodos computacionais numa mesma métrica é por meio de estudos de benchmark. Nestes, uma biblioteca de estruturas moleculares é proposta e para ela são definidos valores de referência, os quais podem ser obtidos por meio de medidas experimentais ou via cálculos computacionais de alta qualidade. Diversos métodos são então aplicados à biblioteca, fornecendo assim respostas que podem ser comparadas às referências e, dessa forma, classificá-los.^59-64

É comum o uso do termo "nível de teoria" para se referir a alguma combinação entre um método de estrutura eletrônica e um conjunto de funções de base. Certos níveis de teoria são mais utilizados do que outros. No entanto, a popularidade não significa que um certo método seja o mais adequado ou eficiente. Na realidade, existe um consenso por parte da comunidade de química teórica de que novos métodos computacionais tendem a ser lentamente adotados por usuários, e de que muitos métodos considerados obsoletos continuam a ser utilizados, conforme discutido por Goerigk et al.⁶¹ Um exemplo notório é o caso do funcional híbrido B3LYP. O uso desse funcional associado ao conjunto de funções de base 6-31G(d) é uma combinação amplamente reportada na literatura, em muitos casos para descrever seletividades em reações orgânicas.⁶⁵ Em retrospecto, a notável e inesperada eficiência deste nível de teoria em inúmeros trabalhos na literatura pode ser atribuída ao cancelamento de erros proveniente da comparação de estruturas quimicamente semelhantes. Em particular, a investigação de reações estereosseletivas se beneficia significativamente desse cancelamento. Atualmente, são claras as limitações do funcional B3LYP, as quais o tornam impreciso quando são avaliados sistemas onde interações dispersivas são importantes.⁶⁶ Por esse motivo, o uso do B3LYP em sua forma canônica, isto é, sem correção para efeitos dispersivos, é desencorajado. Ainda assim, é importante salientar que mesmo os modelos de dispersão mais modernos nem sempre são suficientes para se obter uma acurácia adequada. De forma geral, o uso de estudos de benchmark, utilizados para encontrar o método eletrônico mais adequado, são recomendados. É possível incluir correções para efeitos de dispersão por meio de modelos empíricos, muitos desses já implementados nos principais programas. Alguns funcionais, inclusive, incluem o tratamento de interações de dispersão diretamente em sua parametrização. Outros são formulados especificamente para o uso conjunto de um modelo empírico, como é o caso do funcional ωB97X-V, que utiliza o modelo VV10 e variantes desse método como o ωB97X-D4 que utiliza o modelo de correção empírica DFT-D4.^67,68 Esses funcionais, em conjunto com funções de base triplo-ζ, tem demonstrado um excelente desempenho a um custo computacional baixo, e podem ser a escolha inicial de trabalho para a maioria das investigações computacionais.

Para explorar as origens da estereosseletividade em reações organocatalisadas assimétricas, trabalhos iniciais que utilizaram a química computacional buscaram descrever as estruturas de estados de transição competitivos e de intermediários reacionais relevantes. Por meio desses estudos, valores teóricos de seletividade foram obtidos. No entanto, é importante ressaltar que os métodos computacionais utilizados nesses trabalhos eram limitados, consequentemente seletividades experimentais e efeitos cinéticos isotópicos foram, muitas vezes, utilizados para conciliar a teoria com a experimentação. Com o aumento na disponibilidade de recursos computacionais e o desenvolvimento de métodos melhores, tornou-se frequente o uso de uma estratégia composta. Inicialmente, geometrias, energias e correções termoquímicas para estados de transição e intermediários são obtidas por meio de métodos de custo computacional menor. Em seguida, a energia eletrônica de cada estrutura é refinada por meio de um método computacional mais preciso.⁶⁹ No trabalho seminal de Houk e colaboradores⁷⁰ em 2003, responsável por estabelecer o mecanismo e o senso de indução assimétrica das reações aldólicas, e de reações organocatalisadas correlatas, usando derivados de prolina, foi adotado o nível de teoria B3LYP/6-31G(d). Este estudo teórico concentrou-se principalmente na etapa de formação da ligação carbono-carbono, envolvendo estados de transição e produtos calculados em fase gasosa no nível de teoria B3LYP/6-31G(d), seguido por cálculos de energia de ponto único usando um modelo de solvatação CPCM (polarizable continuum model) e solvente DMSO (Esquema 3). A partir de enaminas (1) derivadas da cicloexanona, foram avaliadas as possíveis orientações com o ácido, em relação as faces proquirais Re e Si dos aldeídos e enaminas, levando a formação de 4 possíveis produtos estereoisoméricos (2). Considerando ambas as conformações de meia-cadeira no anel do cicloexeno são 24 os potenciais estados de transição, dos quais 8 foram considerados os mais relevantes após análise de um sistema simplificado. O estudo concluiu que os estados de transição que envolvem o ataque facial Re na enamina anti apresentam menor energia, sendo mais favoráveis do que os estados de transição para ataque Si na enamina syn (Esquema 3a). A geometria destes estados de transição de menor energia apresentou conformação meia-cadeira para o anel cicloexanona e uma ligação de hidrogênio entre o carboxilato e o aldeído (destacada em amarelo no Esquema 3b), levando ao produto anti-2. Outra importante interação estabilizante de natureza eletrostática envolveu o hidrogênio do carbono adjacente ao nitrogênio da prolina e o alcóxido em formação (destacada em amarelo no Esquema 3b). Essa interação pode ser afetada pela conformação envelope do anel pirrolidínico, a qual pode variar dependendo do substituinte presente, o que, por sua vez, influencia na estereosseletividade do processo. Todas estas descobertas demonstram a grande importância de um tratamento adequado do espaço conformacional de sistemas complexos.

 

 

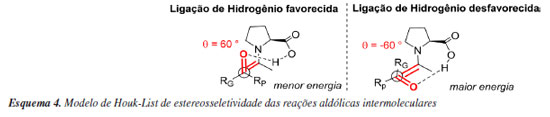
Essas informações, obtidas pelo estudo computacional do mecanismo, contribuíram significativamente para estabelecer o assim nomeado Modelo de Houk-List de estereosseletividade das reações aldólicas intermoleculares. Esse modelo, fundamentado através dos cálculos de energia de diferentes combinações de estado de transição, mostra que é necessário que o sistema atinja conformações com ângulo diedro específico de 60º, onde a enamina e carbonila estejam alinhadas, para assim participar da doação de ligação de hidrogênio envolvida no estado de transição, mantendo o grupo R_G (grande) voltado para a posição mais desimpedida do anel formado no estado de transição de menor energia (Esquema 4).

 

 

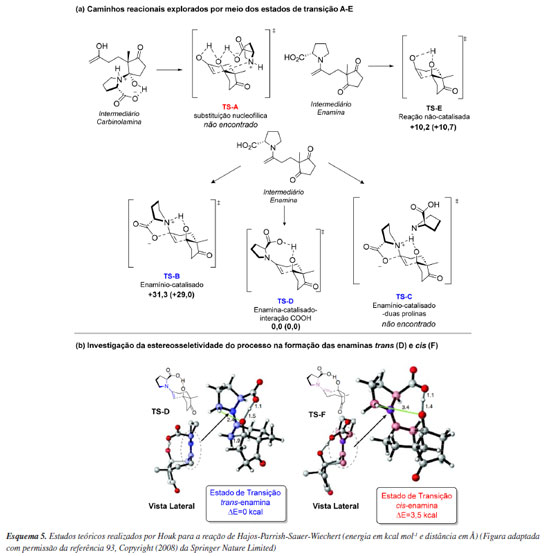
Trabalhos subsequentes reforçaram a proposta de mecanismo sumarizada pelo modelo de Houk e List. Um exemplo é o trabalho de Rzepa e colaboradores,⁷¹ que revisitaram essa reação com métodos computacionais mais modernos e reforçaram o papel determinante da ligação de hidrogênio na estereoquímica da formação da ligação C-C. O efeito de outras etapas do ciclo catalítico na determinação da velocidade, conversão e excesso enantiomérico da reação aldólica foi estudado por Coote e colaboradores.⁷² Por meio de um modelo cinético computacional, demonstraram que a etapa de formação de enamina pode envolver a participação de duas moléculas de prolina, que a velocidade de formação de enaminas syn e anti não importa uma vez que se interconvertem rapidamente e que reações paralelas, como a desativação do catalisador por formação de heterociclos, tem um impacto muito baixo na conversão e excesso enantiomérico.

Testando hipóteses e construindo modelos

Uma das grandes vantagens da aplicação da química computacional está na capacidade de testar caminhos reacionais plausíveis, avaliando a viabilidade desses do ponto de vista cinético e termodinâmico. Isso permite, por exemplo, acelerar o entendimento de um processo estereosseletivo. Esta potencialidade foi prontamente explorada no contexto da organocatálise assimétrica em 2004 por Clemente e Houk⁷³ no contexto da reação de Hajos-Parrish-Sauer-Wiechert que teve como proposta inicial alguns mecanismos que diferiram no Modelo de Houk-List. Os autores exploraram computacionalmente 5 caminhos reacionais distintos por meio dos estados de transição A-E (Esquema 5a), onde todas as geometrias foram otimizadas utilizando o nível de teoria B3LYP/6-31G(d) e as energias obtidas em B3LYP/6-31+G(d,p). No Esquema 5a, destaca-se que o mecanismo via enamina catalisado por ácido carboxílico (D - referente ao modelo de Houk-List) emerge como o mais favorável energeticamente, com uma redução de energia de mais de 10 kcal mol^-1 em comparação ao processo não catalisado (E). No artigo original, Hajos e Parrish³¹ propuseram os mecanismos A e B. Os cálculos computacionais não conseguiram localizar o estado de transição A, baseado num processo de substituição nucleofílica e que requer a formação de um intermediário carbinolamina altamente energético. Particularmente, este caminho reacional foi inspirado pela não incorporação de ¹⁸O a partir de experimentos de Hajos e Parrish com água marcada isotopicamente, resultados estes refutados posteriormente por List e colaboradores.⁷⁴ Por outro lado, foi identificado o estado de transição B como desfavorecido em cerca de 30 kcal mol^-1, algo particularmente esperado pois o intermediário enamínio leva a uma significativa redução de nucleofilicidade da dupla ligação. O estado de transição C não foi encontrado por meio dos cálculos computacionais, sendo ele análogo ao B, se diferenciando pela presença de uma segunda molécula de prolina. A proposta de C foi feita por meio de evidências experimentais de efeitos cinéticos não linerares³¹ onde a segunda molécula de enamina auxiliaria na transferência de próton, fato este posteriormente refutado por List e colaboradores.⁷⁴ Por fim, o trabalho permitiu que fosse investigado a razão da estereosseletividade observada, mostrando que o estado de transição trans-enamina (D) possui menor energia, o que está em acordo com os resultados experimentais de excesso enantiomérico apresentados no trabalho original, revelando neste caso uma interação eletrostática mais forte e estabilizante entre um hidrogênio do anel pirrolidínico e o oxigênio do alcóxido (Esquema 5b). É possível observar que esse intermediário é mais estável e menos distorcido quando comparado a cis-enamina (F), com uma diferença na energia relativa de 3,5 kcal mol^-1.

 

 

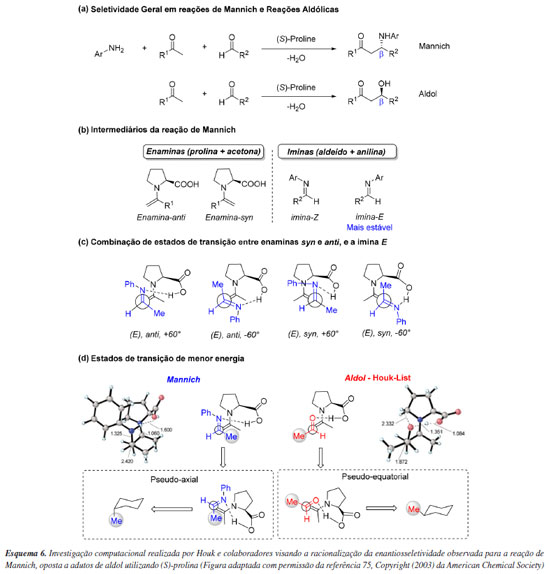
O grupo de Houk⁷⁵ também foi pioneiro em avaliar a seletividade de reação de Mannich (Esquema 6a). Notadamente, essas reações formam b-amino cetonas com estereoquímica oposta àquela das b-hidroxi cetonas encontradas na reação aldólica catalisada por (S)-prolina segundo o Modelo Houk-List. Para tentar compreender este fenômeno, o trabalho consistiu no cálculo de otimização dos estados de transição em B3LYP/6-31G, onde foram consideradas apenas estruturas em que havia ligação de hidrogênio entre a porção carboxílica da enamina e a imina, em um cenário de Curtin-Hammett de controle cinético (Esquema 6b). Neste sentido, 4 estados de transição principais foram avaliados, considerando a imina paralela (+60º) ou anti-paralela (-60º) à enamina (Esquema 6c). Como resultado, enquanto que para reações aldólicas o aldeído assume um arranjo pseudoequatorial do seu substituinte R², em reações de Mannich a (E)-imina mais estável mantém seu grupo Ar em uma posição mais afastada do anel prolínico, o que força uma posição pseudoaxial para R², ou seja, a face dos eletrófilos são opostas para cada uma das diferentes reações (Esquema 6d). Estas diferenças explicam a reversão da seletividade ao comparar esses dois tipos de transformação.

 

 

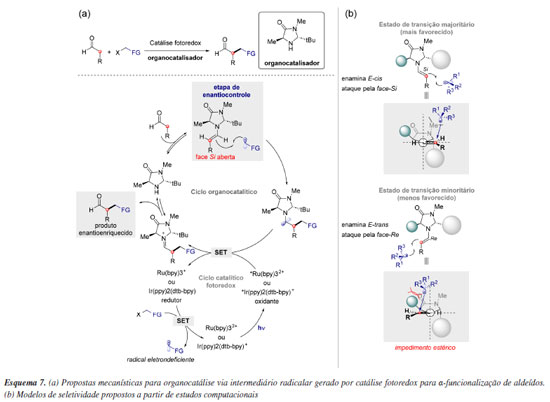
A importância na criação de modelos de indução reside no fato de se manterem consistentes em relação à estereosseletividade, mesmo diante de variações na natureza da espécie reativa. Nesse contexto, a combinação do fotocatalisador Ru(bpy)₃Cl₂, responsável por gerar fotoquicamente espécies radicalares,³⁸ com um organocatalisador do tipo imidazolidinona, descrita por MacMillan e colaboradores, permitiu uma série de α-funcionalizações altamente enantiosseletivas de aldeídos envolvendo intermediários radicalares via catálise, representando um marco na organocatálise fotoredox (Esquema 7a). Cheng e colaboradores⁷⁶ demonstraram a partir de modelos computacionais que a estereosseletividade é controlada, principalmente, por dois estados de transição competitivos: o ataque do radical à face superior (face Si) da E-cis-enamina, levando ao produto majoritário, e o ataque à face superior (face Re) da E-trans-enamina, resultando no produto minoritário (Esquema 7b). Dessa forma, a enantiosseletividade nessas adições radicalares é determinada, em grande parte, por efeitos estéricos, baseados na disposição pseudo-C₂-simétrica dos grupos metil e t-butil presentes no catalisador.

 

 

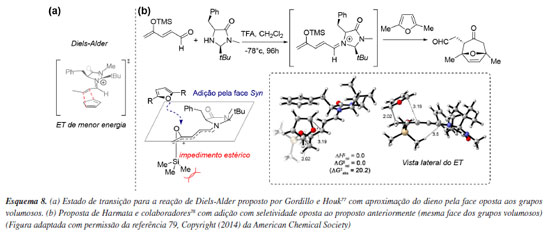
Aplicações computacionais frequentemente permitem a revisão de modelos de seletividade previamente estabelecidos, evidenciando como pequenas modificações no substrato podem levar à inversão na seletividade. O modelo de seletividade de MacMillan,³⁵ baseado na catálise por íon imínio em sistemas α,β-insaturados utilizando imidazolidinonas quirais, prevê a aproximação de nucleófilos pela face oposta aos grupos volumosos do catalisador, fato posteriormente comprovado computacionalmente por Gordillo e Houk⁷⁷ ao serem calculados os estados de transição competitivos (Esquema 8a). Por outro lado, Harmata e colaboradores,⁷⁸ ao investigarem a cicloadição assimétrica (4 + 3) catalisada por imidazolidinonas, observaram uma seletividade oposta. Estudos computacionais indicaram que o local de adição se encontra distante demais do catalisador para que os substituintes anteriormente citados bloqueiem a aproximação do dieno. Os cálculos dos estados de transição revelaram que o grupo OSi(CH₃)₃ transmite a informação quiral por meio do deslocamento do grupo Si(CH₃)₃ para fora do plano, acomodando a aproximação do dieno pela face oposta (Esquema 8b).

 

 

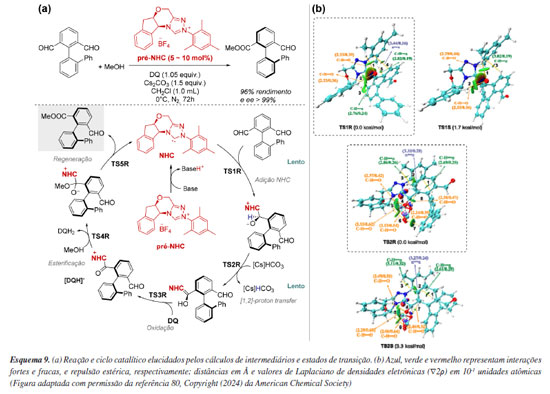
Um uso bastante relevante da química computacional está na quantificação de interações não covalentes menos intuitivas, que podem ser evidenciadas por meio da análise de estados de transição competitivos. Em um estudo liderado por Hou e Wei,⁷⁹ foi investigada computacionalmente a reação de desimetrização catalisada por carbeno N-heterocíclico (NHC) em esqueletos biarílicos para a síntese de aldeídos axialmente quirais.^80,81 A partir do cálculo de intermediários e estados de transição competitivos relevantes ao mecanismo, seguido da análise das barreiras de energia, os processos de dessimetrização (TS1) e formação do intermediário de Breslow (TS2) foram identificados como as etapas determinantes da estereosseletividade e da velocidade da reação (Esquema 9a). O ataque do NHC ocorre preferencialmente à face Si do grupo aldeído de R¹, através do estado de transição de menor energia TS1R. A transferência protônica estereosseletiva assistida por [Cs]HCO₃ ocorre pelo estado de transição de menor energia TS2R, formando o intermediário de Breslow, que corresponde ao caminho energeticamente mais favorável. As últimas etapas se mostraram mais rápidas, e envolvem a oxidação do intermediário de Breslow por DQ, esterificação e a regeneração do catalisador carbeno (Esquema 9a). Adicionalmente, ferramentas como a análise NCI (non-covalent interaction)⁸² e AIM (atoms in molecules),⁸³ demonstraram que as interações estabilizantes fracas C−H···O e C−H···π são mais numerosas nos estados de transição R, portanto, seriam supostamente responsáveis pela estabilização das etapas chave TS1 e TS2 (Esquema 9b). Vale destacar que enquanto a NCI é um índice de visualização baseado na densidade eletrônica (ρ) e no gradiente reduzido de densidade (s), colorido por uma escala de intensidade, a AIM analisa a topologia da densidade eletrônica, identificando pontos críticos e a natureza das ligações químicas.

 

 

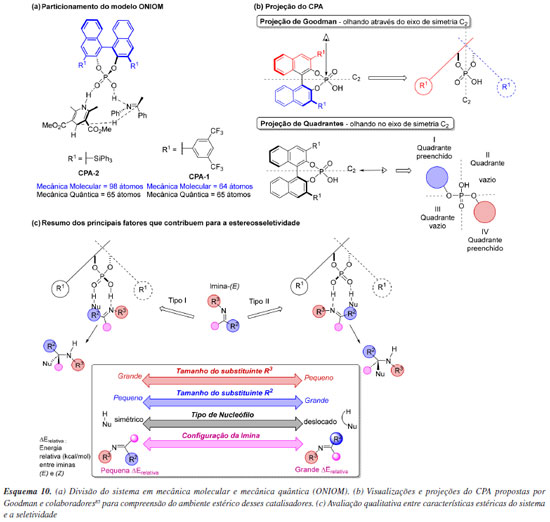
Apesar da organocatálise ter se estabelecido a partir do uso de pequenas moléculas orgânicas, novas classes de catalisadores de tamanho molecular significativamente maior foram prontamente identificadas. Como consequência do aumento do número de átomos nesses novos catalisadores, muitos cálculos computacionais se tornaram proibitivos. Além da disponibilidade de recursos computacionais como núcleos de processamento e dispositivos de armazenamento, um fator que influencia de maneira significativa no custo de um cálculo computacional é a quantidade de elétrons e, consequentemente, o número de funções de base necessárias para descrever o sistema. O método HF, um cálculo elementar de estrutura eletrônica, apresenta um custo computacional que cresce em N⁴, onde N é o número de funções de base utilizadas. Isso significa, por exemplo, que para um sistema que apresente o dobro de funções de base que outro, o número de operações é 2⁴ vezes maior, e consequentemente nos mesmos recursos computacionais haverá um crescimento exponencial do tempo necessário para completar um cálculo de energia. Outros métodos de estrutura eletrônica podem apresentar escalas ainda mais desfavoráveis, como é o caso do método MP4 que apresenta uma escala de N⁷. Uma das formas de contornar esse custo computacional crescente é por meio da utilização de métodos híbridos que consistem em particionar uma molécula em fragmentos menores e em cada fragmento aplicar diferentes níveis de teoria. Um destes modelos híbridos que são encontradas prontamente em vários pacotes computacionais é o ONIOM (our own N-layered integrated molecular orbital and molecular mechanics) desenvolvido por Morokuma e colaboradores,⁸⁴ e que pode ser usado para otimização e frequências de moléculas em seu estado fundamental e em estados de transição.

Um importante trabalho que demonstra o uso desta estratégia em organocatálise foi descrito por Goodman e colaboradores,⁸⁵ que relata a criação de um modelo de indução de ácido fosfórico quirais (CPA-chiral phosphoric acid) derivados de BINOL (1,1'-bi-2-naftol), utilizados em reações de indução assimétrica nas reações de Strecker, Friedel-Crafts e Mannich. Em geral, nesses mecanismos o CPA é capaz de ativar tanto o eletrófilo (imina) quanto o nucleófilo, por meio de ligações de hidrogênio envolvendo a hidroxila e o grupo P=O do ácido fosfórico, respectivamente. Ou seja, o catalisador mantém os substratos em um ambiente quiral gerado pelos substituintes nas posições 3 e 3' da porção binaftol. Por meio de cálculos computacionais, os pesquisadores exploraram estados de transição descritos por um modelo ONIOM (B3LYP/6-31G(d):UFF). Nesse modelo, o binaftol e seus substituintes foram calculados com mecânica molecular, enquanto o ácido fosfórico e os outros reagentes foram descritos utilizando mecânica quântica. Esse particionamento é razoável, uma vez que a região descrita com MM é pouco flexível e interage principalmente por efeitos estéricos com os demais componentes da reação. O método ONIOM foi aplicado nesse trabalho principalmente para reduzir o custo das otimizações de geometria. Quanto à escolha do campo de força para os cálculos de MM, o uso do universal force field foi justificado por sua capacidade em descrever corretamente a barreira rotacional do BINOL (Esquema 10a). Os autores categorizaram o sítio reativo dos catalisadores em quadrantes, utilizando um eixo de simetria dos CPAs, e avaliaram os quadrantes desimpedidos onde poderia ocorrer aproximação dos parceiros reacionais (Esquema 10b). Para racionalizar a seletividade dessas reações, nos cálculos de estado de transição foram considerados as características de substituintes e dos catalisadores, sendo estes classificados como tipo I, com substituinte do N direcionado para longe da posição 3,3' do CPA, e do tipo II, com substituinte do N em direção ao 3,3' do CPA (Esquema 10c). Com base nas seletividades teóricas validada por resultados da literatura foi possível sumarizar os principais fatores que contribuem para a estereosseletividade das reações estudadas. As demandas estéricas (tamanho dos substituintes R² e R³), configuração do substrato imina e o tipo de nucleófilo (simétrico ou deslocado) determinam como ocorre a interação na cavidade quiral (ou quadrante) e em qual face o ataque do nucleófilo será favorecido.

 

 

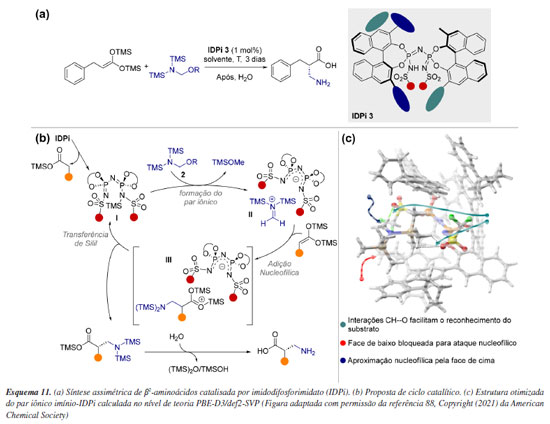
Uma alternativa para contornar a dificuldade de amostragem de estados de transição é explorar apenas o espaço conformacional de espécies reativas. Essa abordagem é viável em sistemas capazes de acomodação, ou seja, suficientemente grandes para formar bolsões de reatividade com ambiente quiral, evidenciando aproximações favoráveis do substrato. Um exemplo desse tipo de catálise é o modo de ativação via contra-íon, em que um catalisador iônico quiral, juntamente com um reagente ou substrato quiral, permanece associado por interações eletrostáticas.⁸⁶ Computacionalmente, os principais desafios desse mecanismo estão relacionados a modelagem precisa dessa interação, além do espaço conformacional envolvido que geralmente é extenso, além das dificuldades associadas à descrição precisa da solvatação. List e colaboradores⁸⁷ descreveram a síntese assimétrica de β²-aminoácidos catalisada por imidodifosforimidato (IDPi), utilizando bis-silil ceteno acetais e um éter aminometílico sililado (Esquema 11a). A etapa de indução de quiralidade ocorre após a reação do α-aminometil éter 2 com o catalisador I, gerando o par iônico metileno-imínio/ânion IDPi II (Esquema 11b). Subsequentemente, o bis-SKA 1 reage com o cátion metileno-imínio no ambiente aniônico do catalisador, formando o par iônico III. Para confirmar a importância do par iônico II, foi realizada uma busca conformacional detalhada seguida de otimização das geometrias usando o nível de teoria PBE-D3/def2-SVP. A partir disso, propôs-se um modelo de seletividade baseado em impedimento estérico, no qual a adição pela face Re do bis-SKA 1 ao par iônico metileno-imínio/IDPi II conduz ao enantiômero observado (Esquema 11c).

 

 

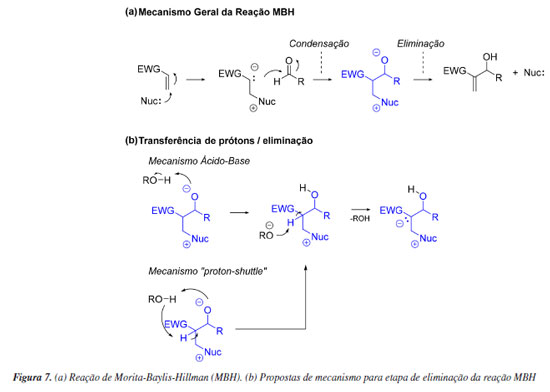
Finalmente, deve ser enfatizada a importância das evidências experimentais para limitar o escopo de mecanismos de reação possíveis e também para estabelecer condições de contorno que devem ser respeitadas por modelos computacionais. Esse último ponto é discutido por Plata e Singleton⁸⁸ no contexto de estudos experimentais e teóricos do mecanismo da reação de Morita Baylis-Hillman (MBH). A reação MBH clássica envolve a formação de uma ligação C-C por meio da condensação catalisada por aminas entre um alceno substituído e um aldeído. O mecanismo dessa transformação envolve um ataque nucleofílico do catalisador ao alceno, gerando um intermediário reativo, que por sua vez ataca o aldeído - um processo semelhante a uma reação aldólica. O produto é então formado via reação de eliminação (Figura 7). Surgem controvérsias sobre esse mecanismo quando são reportados estudos experimentais que divergem sobre a etapa determinante da reação e sobre a natureza da formação da ligação C-C e é nesse contexto que diversos estudos computacionais são realizados. Plata e Singleton determinaram de maneira engenhosa diversos parâmetros cinéticos dessa reação e os compararam a alguns desses estudos. Eles verificaram que métodos computacionais populares à época eram inadequados para explicar observações experimentais triviais, que um mecanismo plausível para a etapa de eliminação envolve transferências de prótons via mecanismo ácido-base (em oposição a mecanismo tipo "proton shuttle") e que a etapa determinante do processo depende da temperatura reacional. Os autores sumarizaram o desempenho dos modelos computacionais avaliados com a célebre citação atribuída à Wolfgang Ernst Pauli de que esses modelos nem sequer estão errados.⁸⁹ Não deixa de ser irônico o fato de que esse mesmo trabalho foi questionado anos depois por Sunoj e colaboradores.⁹⁰ Eles demonstraram que utilizando métodos computacionais adequados - não necessariamente aqueles que são mais populares, a reação MBH é descrita adequadamente. Mesmo assim, não deixa de ser pertinente o fato de que reações como essa, em que efeitos importantes de solvatação e entropia estão presentes, estão entre as mais desafiadoras para os estudos mecanísticos computacionais.^90,91

 

 

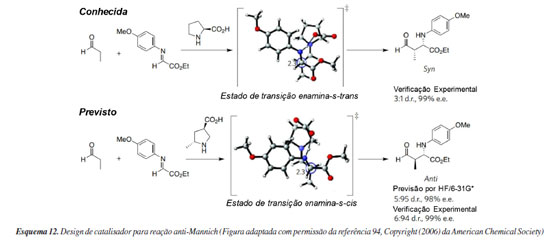
Do computador para a bancada: redesenhando catalisadores

Atualmente, um esforço considerável é investido na descoberta e refinamento de novos catalisadores assimétricos. Tradicionalmente, abordagens de tentativa e erro têm sido utilizadas, incorporando insights mecanísticos por meio da química computacional ao fim do estudo. O percurso lógico para o encurtamento deste caminho é por meio do uso da química computacional para guiar a descoberta de novas classes de organocatalisadores assimétricos, mas este objetivo ainda não foi demonstrado. Isso porque é muito difícil, senão impossível, modelar de maneira acurada uma reação, considerando todos os seus componentes (reagentes, solventes, catalisadores e aditivos), a participação de possíveis reações paralelas, mudanças de mecanismo de reação e outras variáveis. Ou seja, é imprescindível, por exemplo, ter evidências experimentais de que a natureza explícita de um solvente, ou a necessidade de considerar um aditivo ao modelar um estado de transição se faz (ou não) necessária ao predizer enantiosseletividades via cálculos de estados de transição competitivos.

Conforme já mencionado, desde os primeiros anos da organocatálise alguns trabalhos foram descritos se concentrando na modificação computacional de catalisadores ou estruturas de ligantes existentes, possibilitando o ajuste da reatividade para certas reações. Com isso, a química computacional aplicada no design de novos catalisadores tem focado principalmente em seletividades já bem estabelecidas.⁹² Um exemplo bem-sucedido e posteriormente validado experimentalmente resultou do trabalho seminal e colaborativo entre os grupos de Houk e Barbas⁹³ (Esquema 12). Eles se concentraram no desenvolvimento de um derivado da (S)-prolina para catalisar as reações de Mannich gerando diastereosseletividades opostas à prolina natural. A mudança de seletividade de syn para anti foi projetada fixando a conformação da enamina. No organocatalisador recém-projetado, um grupo metil foi introduzido na posição 5 e o ácido carboxílico foi movido para a posição 3, com os dois substituintes pirrolidina na posição trans. Semelhante à prolina, a seletividade facial é controlada por meio de ligação de hidrogênio, enquanto as interações estéricas, devido a presença do grupo metila, forçam a enamina a reagir a partir da face oposta. Os quatro estados de transição concorrentes foram considerados no nível teórico HF/6-31G(d). Foi previsto para essa transformação uma diastereosseletividade 95:5 anti:syn e excesso enantiomérico de 98%, resultando em valores muito próximos aos resultados experimentais posteriormente obtidos. É importante destacar que nesse trabalho a base teórica utilizada foi derivada do modelo computacional estabelecido no contexto do estudo das reações aldólicas catalisadas por (S)-prolina. Dessa forma, foi utilizado um nível de teoria muito simples com o objetivo de se obter em pouco tempo estimativas para a seletividade teórica da reação.

 

 

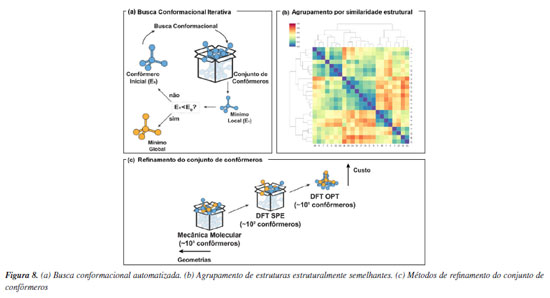
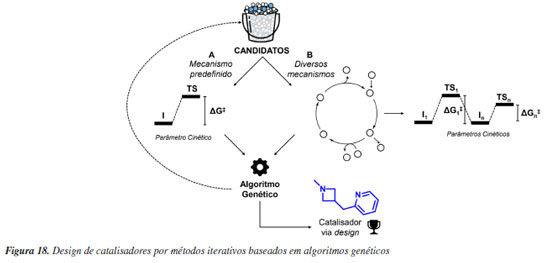
Da simulação automatizada à triagem virtual de alto rendimento de catalisadores

Do ponto de vista computacional, apresentamos anteriormente que a enantiosseletividade de reações organocatalisadas em sistemas sob o controle de Curtin-Hammett pode ser atribuída a partir da diferença nas energias livres entre os estados de transição que levam aos produtos estereoisoméricos em maior e menor proporção. No entanto, na maioria das reações catalíticas a grande variabilidade conformacional de substratos e catalisadores tornam acessíveis múltiplas conformações e configurações de estados de transição para uma etapa elementar única. Com isso, determinar de maneira confiável seletividades a partir de métodos quânticos torna-se um processo exaustivo de busca de estados de transição de menor energia.⁹⁴ Devido à variedade de orientações relativas entre substratos e catalisadores flexíveis (assim como aqueles com substituintes rotacionáveis, como OEt e Et), pode haver um número enorme de conformações acessíveis termodinamicamente, o que pode causar problemas para uma busca conformacional adequada.

Para aumentar a automação e facilitar a amostragem de estados de transição foram desenvolvidos na última década diversos programas, como o ACE (asymmetric catalyst evaluation)⁹⁵ e o CatVS (catalyst virtual screening),⁹⁶ que implementam métodos específicos para otimização de estados de transição e o AARON (automated reaction optimiser for new catalysts),⁹⁷ e o autodE,⁹⁸ que são interfaces para programas tradicionais de química quântica. Essas ferramentas permitem a aceleração da descoberta de catalisadores através de métodos como a triagem virtual de alto rendimento, reduzindo o tempo necessário em comparação com experimentos de laboratório, aprimorado a compreensão mecanística e promovendo avanços significativos na área. A ideia central destes programas é oferecer a possibilidade de automação para o estudo de mecanismos de reação com ferramentas computacionais a partir de uma linguagem acessível para usuários não especializados. É interessante que nesses programas o uso de métodos de baixo custo permite lidar com a amostragem de confôrmeros para muitos catalisadores. O uso de métodos de mecânica molecular usando campos de força reativos,⁹⁶ ou métodos semiempíricos fornecem a velocidade necessária para gerar conformações de maneira automatizada e rápida, mas no geral de menor qualidade do ponto de vista energético (Figura 8a). Consequentemente, nesse processo é realizada uma filtragem por meio de agrupamento e seleção (Figura 8b), com o uso de uma hierarquia de níveis de teorias visando o uso de métodos mais sofisticados apenas para uma pequena parcela daquelas geometrias selecionadas (Figura 8c). Aqui cabe destacar que os desafios técnicos dos programas estão em conseguir otimizar de maneira consistente as conformações geradas para a estrutura de estado de transição. Por fim, a maior limitação do uso destas técnicas está na necessidade de se postular hipóteses mecanísticas prévias, o que impede a aplicação destas ferramentas em estágios iniciais de desenvolvimento de novas reações químicas.

 

 

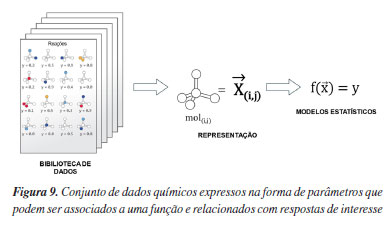
MODELOS QUÍMICOS BASEADOS EM ESTATÍSTICA

Motivação

Enquanto ferramenta utilizada nos estudos de mecanismos reacionais, a Química Computacional permite compreender aspectos de reatividade a nível molecular. Esses estudos permitem intervir numa certa transformação para que se modifique alguma resposta, como a seletividade. No entanto, obter mecanismos completos via cálculos computacionais, especialmente para reações que envolvem muitos intermediários e estados estacionários off-cycle, pode rapidamente se tornar um problema irresolvível por consequência dos fatores que discutimos, de forma que nesses casos o uso de experimentos se torna uma alternativa muito mais conveniente para obtenção de informações. Quando a seletividade, ou outra resposta de interesse, pode ser expressa como função de parâmetros moleculares, o uso de modelos computacionais baseados nesses parâmetros é uma poderosa alternativa aos tradicionais cálculos de mecanismos quando a aplicação destes é proibitiva (Figura 9). No campo da quimioinformática, o uso desse tipo de modelo é bem estabelecido, especialmente nas relações de estrutura-atividade de pequenas moléculas orgânicas e suas propriedades biológicas. Dessa forma, havia precedentes relevantes quando, na última década, modelos estatísticos passaram a ser propostos no contexto de reações orgânicas envolvendo catálise assimétrica. Inclusive, o uso de múltiplos parâmetros em um mesmo modelo aprimorou a relação estrutura-atividade interativa, levando ao desenvolvimento de diversos descritores moleculares fisicamente significativos para o estudo de reatividade química.⁹⁹ De maneira concreta, as relações de seletividade podem ser construídas a partir de propriedades dos reagentes ou catalisadores no seu estado fundamental, o que do ponto de vista computacional representa uma enorme economia de tempo e recursos. No contexto da catálise, esses conceitos podem ser expandidos para avaliar reatividade e seletividade de um catalisador com suas possíveis modificações estruturais, correlacionando quantitativamente a estrutura com o impacto na sua atividade/reatividade. Sendo assim, o uso de modelos estatísticos representa significativa economia de recursos, precisão e compreensão de aspectos mecanísticos, sendo que estas abordagens serão apropriadamente discutidas a seguir.

 

 

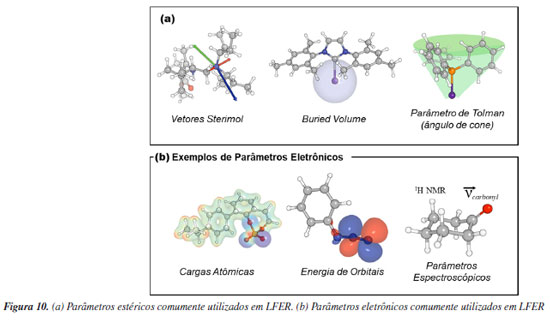
Modelos parametrizados

O uso de modelos parametrizados não se trata de um conceito novo, já que por várias décadas os químicos têm utilizado a regressão linear para estudar os impactos dos efeitos eletrônicos e estéricos nos resultados das reações, para compreender mecanismos e prever transformações químicas. A relação de Hammett é um exemplo notório de linear free energy relationship (LFER) em química orgânica.¹⁰⁰ Proposta em 1937, essa relação deu os passos iniciais na investigação da influência eletrônica de reagentes, seguido por Taft,¹⁰¹ Charton,¹⁰² e outros, que introduziram termos estéricos. Com os avanços nesse campo, ao longo do tempo as LFER passaram a utilizar múltiplos descritores estéricos e eletrônicos para modelar o impacto nos resultados das reações, considerando diversos componentes. O uso de parâmetros surge da necessidade de transformar a representação química, tradicionalmente feita na forma gráfica, para uma representação numérica. A partir dessa representação quantitativa é possível utilizar a regressão linear, e diversos outros métodos desenvolvidos no campo da aprendizagem estatística, para propor uma relação quantitativa entre molécula ou sistema e alguma resposta de interesse. A Química Computacional é utilizada na obtenção de parâmetros devido a sua capacidade em definir estruturas moleculares, a partir das quais se pode obter quantitativos estéricos e eletrônicos.

Os efeitos estéricos têm papel fundamental na determinação da enantiosseletividade de transformações assimétricas. Descritores estéricos, portanto, permitem parametrizar a orientação espacial dos reagentes envolvidos em etapas estéreo-determinantes. Tais parâmetros podem ser otimizados para que obtenha reações mais seletivas. No contexto das reações assimétricas organocatalisadas, parâmetros estéricos tais como valores de Taft, Charton, Sterimol, volume ocupado, ângulo de cone de Tolman, ângulos de torção, comprimentos de ligação e ângulos de mordida foram utilizados para representar a relação entre tamanho molecular e seletividade. Para parametrização de propriedades eletrônicas, os descritores utilizados incluem o parâmetro de Hammet, parâmetros de infravermelho (IV) e de ressonância magnética nuclear (RMN), cargas atômicas, energias de orbitais, densidades eletrônicas e parâmetros de interação não-covalente (NCI) (Figura 10).^103-108

 

 

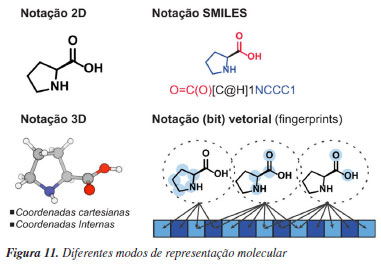
Além da representação molecular por parâmetros derivados de suas propriedades, a própria estrutura molecular pode ser descrita computacionalmente. A maneira tradicional de se obter essa descrição é por meio das coordenadas cartesianas de seus núcleos atômicos. Em contrapartida, a notação SMILES (simplified molecular input line entry system) é uma representação linear baseada em texto. Notações vetoriais denominadas fingerprints¹⁰⁹ permitem descrever a molécula utilizando sequências numéricas (Figura 11). Algoritmos de aprendizagem estatística requerem descritores em formatos específicos, de forma que todas essas diferentes representações moleculares, baseadas em propriedades ou em estruturas, podem ser usadas individualmente ou combinadas e podem ser transformadas a posteriori para atender os requisitos de algum algoritmo em particular.

 

 

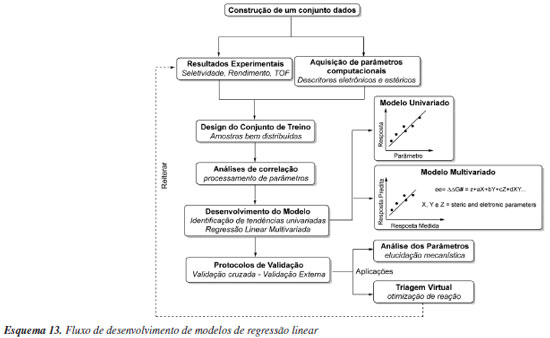
Diferentes respostas podem ser utilizadas como objetivo para elaboração de modelos. São muito explorados os modelos baseados em constantes de equilíbrio (K) ou constantes de velocidade (k). Outras respostas incluem diferentes tipos de seletividade, rendimentos, conversões ou propriedades moleculares. Para algumas respostas, a construção de modelos tende a ser mais difícil do que para outras. A predição de rendimentos de reações químicas é um desses casos difíceis, devido a influência não apenas das variáveis da reação em questão, mas também de todas as reações secundárias possíveis.¹¹⁰

Um dos pontos críticos na construção de modelos preditivos se refere a qualidade e estruturação dos dados, onde seu tamanho e qualidade determinarão a capacidade preditiva do modelo. Portanto, é crucial ter um conjunto de dados que represente amplamente o espaço químico do problema. Isso deve incluir tanto a diversidade química das moléculas, quanto a variedade de resultados envolvendo respostas baixas, médias e altas. As previsões fora do domínio de aplicabilidade, ou seja, pouco representadas nos dados de treinamento, são menos confiáveis.

Um outro problema comum na construção de um conjunto de dados está no viés de resultados publicados, ou seja, muitos pesquisadores escolhem publicar apenas as condições e/ou catalisadores que apresentam bons resultados. Modelos preditivos gerados nestas circunstâncias são limitados pois não são suficientemente treinados para reconhecer padrões moleculares e/ou condições reacionais associados a resultados inferiores. Por este motivo, cada vez mais tem-se buscado a criação de conjunto de dados com espaço químico previamente definido de acordo com objetivos específicos, e se evitado a composição de um conjunto de dados advindos de referências múltiplas. Nesse contexto, técnicas de experimentação de alto rendimento (HTE, high throughput experimentation) têm se popularizado recentemente na Química. Largamente utilizadas em diversas indústrias farmacêuticas,¹¹¹ essas técnicas permitem executar muitos experimentos simultâneos e, consequentemente, explorar uma variedade de combinações de catalisadores, reagentes e condições reacionais com uso eficiente de tempo e recursos. O ganho de produtividade pelo uso de HTE se dá, entre outros fatores, pelo agrupamento e redução do número de operações a serem realizadas. A adoção dessas técnicas em laboratórios acadêmicos de Química é crescente, mas lenta quando comparada a outras áreas nas quais seu uso é rotineiro. Isso porquê a variedade de condições experimentais para reações químicas é amplo e envolve diversos regimes cinéticos, solventes, muitos dos quais são voláteis, condições com atmosferas inertes, uso de reagentes sólidos, entre outros fatores. Além da questão experimental, o uso e desenvolvimento de novas técnicas analíticas de alto rendimento são fundamentais para gerar dados a partir desses muitos experimentos. Soluções para essas e outras dificuldades têm sido discutidas na literatura,^112,113 e o uso desse tipo de experimentação é considerado fundamental para a aplicação de métodos de aprendizagem estatística em Química.

Exemplos de modelos reatividade/seletividade

Como demonstrado em sistemas mais complexos, o uso de um único (ou poucos) parâmetro de resposta pode não ser eficiente em capturar características que impulsionem a seletividade no sistema de interesse. Neste sentido, o uso de multiparâmetros capazes de capturar diferentes características independentes do sistema (substratos, catalisadores ou condições reacionais), tem sido recentemente explorado no contexto de modelos preditivos de reatividade ou seletividade de reações. Os modelos multiparâmetros podem ser construídos por abordagem estatística conhecida como regressão linear multivariada (MLR, multivariate linear regression) e os parâmetros necessários podem ser obtidos por cálculos computacionais ou derivados de dados experimentais. Um exemplo de fluxograma geral para execução de estudos de regressão linear multivariada está apresentado no Esquema 13. Vale ressaltar que tanto em modelos multivariados ou univariados, derivados das LFER's, muitas vezes o termo QSPR (quantitative structure-property relationship) é utilizado para classificar esse tipo de modelagem.

 

 

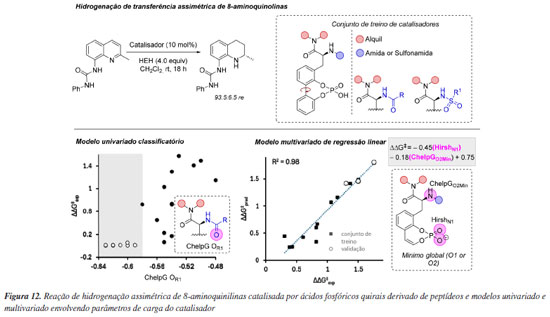
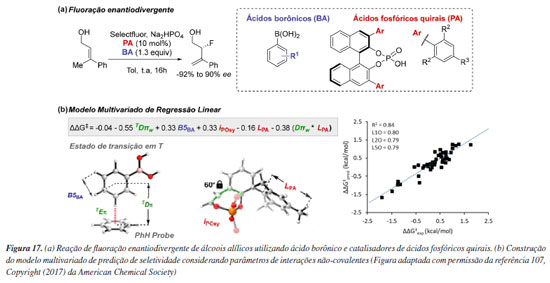
Propriedades simples, como cargas atômicas, podem ser utilizadas para criação de modelos estatísticos em química orgânica. Especificamente, em organocatálise esse tipo de modelagem vem sendo empregada de diversas formas para predição de reatividade ou seletividade, desde modelos mais simplista, como modelos classificatórios, até modelos multivariados de regressão linear que fornecem uma visão completa de um determinado sistema. Neste âmbito Toste e colaboradores¹⁰⁸ utilizaram ferramentas de ciência de dados para otimizar novos ácidos fosfóricos quirais do tipo BINOL (CPAs), focando em parâmetros eletrônicos essenciais para seletividade em reações específicas (Figura 12). Inspirados em catalisadores derivados de peptídeos e utilizando a reação de hidrogenação de transferência da 8-aminoquinolina, foi possível construir um conjunto de catalisadores com ampla variação de enantiosseletividade. Então, descritores moleculares, obtidos a partir de ensembles conformacionais, foram usados em uma árvore de decisão, que identificou a carga parcial no oxigênio da amida/sulfonamida como classificadora da seletividade do catalisador. Para obter mais informações a respeito dos fatores que governam a seletividade, um modelo de regressão linear multivariada, com base em dois parâmetros eletrônicos - a carga de Hirshfeld no nitrogênio e a carga ChelpG no oxigênio do fosfato - revelou que uma carga negativa maior no nitrogênio aumentava a enantiosseletividade, enquanto uma carga negativa no oxigênio do fosfato correlacionava-se inversamente. Esse comportamento sugere que a acidez do ácido fosfórico é modulada pela estabilização da base conjugada por meio de ligações de hidrogênio intramoleculares. Cálculos de DFT confirmaram a influência dessas interações intramoleculares na transmissão de informação quiral, validando o modelo. A metodologia previu com precisão um catalisador altamente seletivo, com potencial de aplicação em outras reações, mostrando-se promissora para o desenvolvimento de ligantes privilegiados.

 

 

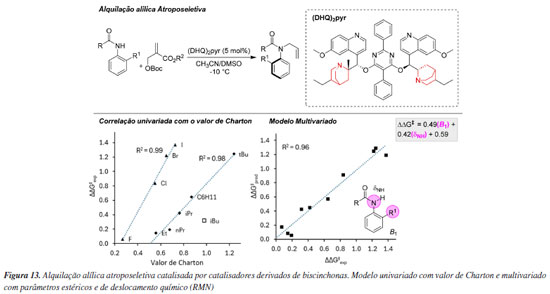
Em outro exemplo, utilizando organocatalisadores de biscinchonas ((DHQ)₂PYR), Li e colaboradores¹¹⁴ desenvolveram uma metodologia de alquilação alílica assimétrica para a síntese de anilidas quirais (Figura 13). Foi observado que a presença de grupos amídicos com elevado impedimento estérico no anel aromático influenciava de maneira significativa a estereosseletividade da reação. Análises revelaram uma correlação isolada entre substratos halogenados e alquilados e seus respectivos valores de Charton, indicando que os efeitos estéricos desempenhavam um papel central no direcionamento da seletividade. No entanto, os valores de Charton, por si só, mostraram-se insuficientes para explicar completamente o comportamento observado, uma vez que também foram identificados efeitos eletrônicos que impactavam a seletividade da reação. Para melhor compreender esses fatores, o termo B₁ (parâmetro sterimol) foi utilizado para quantificar a influência estérica, enquanto o deslocamento químico d_NH (parâmetro de ressonância magnética nuclear) foi empregado para integrar tanto os efeitos estéricos quanto eletrônicos. Essa combinação de parâmetros ressaltou a importância do grupo volumoso na posição orto do anel aromático, que exerce influência significativa na conformação e, consequentemente, na indução quiral do sistema catalítico. Assim, a integração de efeitos estéricos e eletrônicos foi essencial para explicar os mecanismos de seletividade observados nesse sistema.

 

 

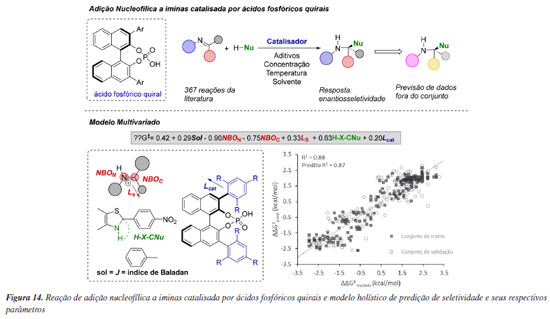
Em um trabalho pioneiro, Reid e Sigman¹¹⁵ propuseram a criação de modelos estatísticos holísticos que fossem capazes de prever resultados de reações orgânicas de forma mais generalizada em sistemas complexos. Para esse objetivo, os autores investigaram uma série de adições nucleofílicas a iminas organocatalisadas por uma classe de ácidos fosfóricos quirais. Assim, uma biblioteca composta por diferentes substratos e valores experimentais de enantiosseletividade foi construída com 367 reações da literatura. A parametrização desses dados foi realizada com parâmetros de todos os componentes da reação e modelos de regressão linear multivariada foram construídos. No modelo mais representativo obtido, parâmetros do solvente (índice de Balaban, em preto), das iminas (cargas orbitais de ligação natural (NBO) do nitrogênio e do carbono da imina, sterimol L_s representando o menor substituinte da imina, em vermelho), do nucleófilo (medida do ângulo H-X-CNu, em verde), e do catalisador (L_cat para o comprimento do catalisador ao nucleófilo, em azul) foram considerados como maiores contribuintes para a enantiosseletividade em 17 tipos de reação presentes no conjunto de dados (Figura 14). O parâmetro de maior coeficiente neste modelo se refere aos parâmetros NBO da imina, demostrando que o substrato tem um importante papel na enantiosseletividade dessas reações, uma vez que a formação dos produtos enantioméricos é uma consequência da configuração E ou Z da imina.

 

 

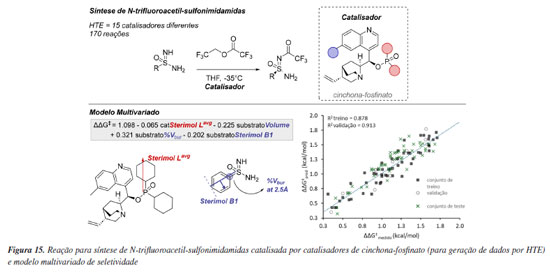
Mais recentemente, Miller e colaboradores¹⁰⁴ empregaram modelagem holística na acilação enantiosseletiva de sulfonimidamidas por meio da desimetrização catalisada por alcalóides de cinchona (Figura 15). Especificamente, concentraram-se em sulfonimidamidas não protegidas, utilizando um catalisador de cinchona-fosfinato para sintetizar N-trifluoroacetil-sulfonimidamidas por meio de experimentação de alto rendimento (HTE). Foi construído um conjunto de dados com 170 reações, abrangendo uma ampla gama de seletividades. O modelo inicial se mostrou insatisfatório, pois alguns catalisadores podem atuar por um modo de ativação diferente, uma conclusão alcançada após estudos mecanísticos envolvendo cinética e cálculos de estado de transição. Após a exclusão desses catalisadores, foi criado um modelo final, utilizando parâmetros das sulfonimidamidas que descrevem a natureza dos substratos no sítio catalítico. O modelo indicou que o substrato deve possuir volume estérico suficiente para assegurar a conformação necessária à enantiosseletividade.

 

 

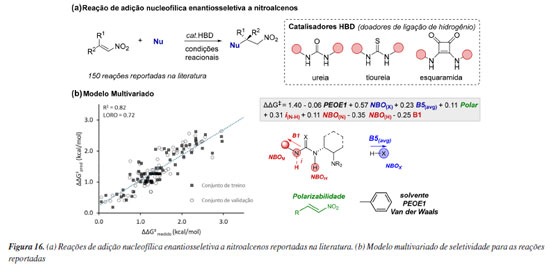
Ainda no âmbito de modelos holísticos, outro importante trabalho reportado por Werth e Sigman¹¹⁶ explorou diferentes tipos de catalisadores bifuncionais doadores de ligação de hidrogênio (HBD, hydrogen bond donor) para criar modelos preditivos a partir da parametrização de multireações. Essa classe de catalisadores é capaz de ativar simultaneamente nucleófilo e eletrófilo através de interações não-covalentes, tipicamente promovidas por um sítio básico de amina terciária e HBD baseados em ureia, tioureia ou esquaramidas. Os autores investigaram correlações entre diferentes tipos de organocatalisadores dessas classes, utilizando dados experimentais de 150 reações reportadas na literatura para adição enantiosseletiva de nucleófilos à nitroalcenos (Figura 16a). No conjunto de treinamento, que incluiu 39 catalisadores, 51 eletrófilos, 21 nucleófilos e 11 solventes, foram calculados parâmetros estéricos e eletrônicos focados em capturar as interações não-covalentes que pudessem ser responsáveis pela enantiosseletividade, tal como sterimol, deslocamentos químicos de RMN, NBO, comprimentos de ligação e frequências/vibrações IR, criando assim um conjunto de dados para construção de um modelo de regressão linear multivariada. O melhor modelo obtido conta com uma predominância de parâmetros do orgacatalisador, demonstrando sua grande influência na seletividade das reações catalogadas. Especificamente, os valores de carga NBO do hidrogênio (NBO_H) e nitrogênio (NBO_N) foram usados para reconhecer diferenças estéricas e eletrônicas sutis da porção quiral do catalisador, bem como diferenciar a classe do catalisador HBD (ureia/tioureia/esquaramida). Já os parâmetros de intensidade de estiramento IR(i_N-H) e sterimol (B₁) representam a influência da porção aquiral destes. No que se refere aos nucleófilos, dois parâmetros se mostraram relevantes para enantiosseletivade B_5(avg) e NBO_X, que representam o átomo do nucleófilo que sofrerá a ativação/desprotonação pelo catalisador. Os eletrófilos são representados por apenas um parâmetro que caracteriza a polarizabilidade (polar), necessário para descrever o caráter/tamanho geral da substituição e potenciais interações não-covalentes. Por fim, foi também incluído um descritor topológico (PEOE1) que descreve interações de van der Waals em relação ao solvente (Figura 16b). Como resultado, além da unificação de catalisadores HBD bifuncionais, o modelo desenvolvido forneceu uma plataforma de previsão para resultados de reação envolvendo novas combinações de catalisador e substratos, sendo expandido com sucesso para outras reações fora do conjunto de dados, utilizando outras classes de catalisadores e novos eletrófilos.

 

 

Para além de parâmetros descrevendo componentes da reação, diferentes trabalhos na literatura abordam descritores de interações não-covalentes (NCI, non-covalent interactions) em modelos de reatividade ou seletividade. Em geral, tanto interações covalentes como não-covalentes são cruciais nos mecanismos e nas energias de estado de transição de determinadas reações, em especial, uma vasta gama de organocatalisadores têm sua reatividade atrelada a essas interações, como por exemplo com ligações de hidrogênio. Neste contexto, os catalisadores de ácidos fosfóricos quirais foram extensamente explorados com parâmetros que pudessem capturar interações não-covalentes cruciais em diferentes mecanismos de ativação, transpondo a necessidade de se conhecer o mecanismo previamente. Notoriamente, Sigman e colaboradores¹⁰⁶ demonstraram o uso de parâmetros computacionais para descrever interações π-stacking e CH-π em modelos MLR aplicados a reações seletivas. Os autores introduziram energias e distâncias de interação (Eπ e Dπ), além de parâmetros ponderados (Eπw e Dπw) para lidar com diferentes confôrmeros utilizando probes de benzeno para representar interações π. Como prova de conceito, utilizaram a resolução cinética de álcoois benzílicos quirais, onde as interações π-stacking foram identificadas como determinantes no estado de transição (Figura 17). A correlação entre os parâmetros de distância (SDπw) e a energia de ativação relativa (ΔΔG^‡) validou a presença dessas interações. Em seguida, os autores aplicaram esses parâmetros à fluoração enantiodivergente de álcoois alílicos catalisada por ácidos fosfóricos na presença de ácidos borônicos, propondo um novo modelo que incorpora uma interação π em forma de T entre ácido borônico e o ácido fosfórico, utilizando a distância π em forma de T (TDπw) e efeitos estéricos dos catalisadores. Neste modelo os parâmetros incluem ^TDπw, que considera os requisitos geométricos da possibilidade de uma interação π em formato de T; B_5,BA e L_PA, que descrevem os efeitos estéricos do ácido borônico e do catalisador, respectivamente; e i_POsy, a intensidade do estiramento simétrico da porção fosfórica do catalisador, que pode indicar o potencial de cada porção do ânion fosfato para participar de interações de ligação de hidrogênio e eletrostáticas. A validação do modelo foi confirmada por cálculos de estado de transição via DFT, que corroboraram a presença das NCIs observadas no modelo computacional. Além disso, inspirados por este trabalho, os autores investigaram a mesma estratégia em reações de fluoração de álcoois homoalílicos racêmicas também catalisadas por ácidos fosfóricos, investigando quais NCIs seriam relevantes se baseando nas interações π em T propostas pelo modelo anterior.¹⁰⁷

 

 

Os trabalhos apresentados até o momento, baseados em modelos estatísticos de regressão linear, de modo geral, contam com conjuntos de dados relativamente pequenos, tendo em vista a dependência por dados experimentais. Com o avanço de técnicas de categorização de estruturas, grandes bibliotecas vêm sendo construídas, aumentando a necessidade da adoção de novas abordagens, capazes de lidar com grandes volumes de dados. Neste contexto, outros protocolos computacionais têm sido aplicados com eficiência no contexto da organocatálise assimétrica. Em especial, técnicas de aprendizado de máquina (ML, machine learning) têm se destacado em solucionar problemas complexos em diversos campos da química orgânica,¹¹⁷ como síntese de produtos naturais,^118,119 análises retrossintéticas,¹²⁰ descobrimento de fármacos¹²¹ e também na organocatálise.^122-124 Para o desenvolvimento desses trabalhos, técnicas de ML são aplicadas a conjuntos de dados de interesse para a criação de modelos de seletividade, reatividade e design de novas estruturas. Os modelos multivariados de regressão linear, citados nos exemplos anteriores, são considerados algoritmos de aprendizado de máquina, por relacionarem uma variável de interesse a uma combinação linear de parâmetros. Cabe destacar os métodos baseados em árvores de decisão (DT, decision tree), um tipo de aprendizado de máquina hierárquico que pode ser utilizado para classificação e regressão. Algoritmos de floresta aleatória (RF, random forest) utilizam combinações de várias DTs, permitindo obter melhor ajuste aos dados, e são frequentemente utilizados. Outros algoritmos, como k-vizinhos mais próximos (KNN, k-nearest neighbours) e support vector machines (SVM) são métodos capazes de predizer novos pontos a partir da semelhança destes com sua vizinhança, sendo extremamente relevantes para predição de reatividade de materiais de partida, por exemplo.¹²⁵ Esses diferentes algoritmos e outros podem ser utilizados para investigar diversas variáveis em síntese orgânica.

No contexto da reação de MBH (Figura 7), Jensen e colaboradores¹²⁶ propuseram um algoritmo para otimização de novo de um catalisador para essa reação. Enquanto DABCO, uma amina terciária, é um catalisador tipicamente utilizado nessa transformação, os resultados obtidos pelos autores levaram à síntese de uma azetidina, uma classe de moléculas até então não explorada, que apresentou atividade oito vezes maior para a mesma transformação quando catalisada por DABCO. Chama atenção nesse trabalho que os autores utilizaram uma abordagem iterativa baseada em cálculos de mecanismo. Como alternativa aos custosos cálculos DFT, foi utilizado o método semiempírico GFN2-xTB. Dessa forma, os autores calcularam parâmetros cinéticos para diversos candidatos à catalisador, e um algoritmo de ML genético foi utilizado para filtrar somente os melhores candidatos por diversos ciclos e propor variações nessas moléculas selecionadas para ampliar o escopo de estruturas avaliadas. Um pressuposto fundamental desse trabalho é que essa reação apresenta um mecanismo simples e bem estabelecido. Assim, essa proposta de design via algoritmo genética foi estendida posteriormente para incluir não somente a otimização do catalisador, mas a própria exploração de possíveis mecanismos por meios automatizados (Figura 18).¹²⁷

 

 

Uma classe de catalisadores interessante para estudos de design são os derivados de cinchonas, muito utilizados no contexto da catálise por transferência de fase. Ainda em 1984, Dolling et al.¹²⁸ demonstram a síntese da (+)-indacrinona utilizando um desses catalisadores. O estudo do mecanismo de indução assimétrica para essa transformação resultou no modelo de Dolling-Grabowski, no qual a seletividade é explicada pela formação de um par-iônico entre um enolato e o íon cinchônio, os quais interagem via ligação de hidrogênio e via π-stacking. Alternativamente, Pliego Jr. e Freitas¹²⁹ propuseram um novo modelo para indução assimétrica nessa transformação. Baseados em cálculos DFT, os autores demonstraram que a formação da interação π-stacking não é favorecida. Na realidade, além da ligação de hidrogênio um efeito importante é a estabilização eletrostática do grupo de saída Cl^-. É interessante notar que alguns dos cálculos computacionais realizados nesse trabalho foram revisitados por Houk e colaboradores.¹³⁰ Utilizando modelos teóricos distintos, os autores chegaram a conclusões semelhantes, de que a posição do cloreto com relação ao nitrogênio quinuclidínico é importante e que esse grupo de saída é estabilizado por interações com ligações C-H polarizadas.

Sherer e colaboradores,¹³¹ utilizaram a técnica de floresta aleatória (RF) para aperfeiçoar a rota de síntese do medicamento letermovir (antiviral) a partir do estudo da etapa chave de adição conjugada assimétrica promovida por catalisadores de transferência de fase derivados de cinchonas (Esquema 14a). Em resumo, na técnica de floresta aleatória um algoritmo utiliza uma partição recursiva de um grande conjunto de dados para criar uma "árvore de decisão" em que cada nó do fluxograma resultante é uma condição (variável) e se verificada, o fluxo que seguirá por ela, assim sucessivamente até obter uma predição final. Neste trabalho, essa estratégia foi empregada para otimização de condições reacionais e predição de novos catalisadores com eficiência superior aos anteriormente reportados. Desse modo, um conjunto de dados inicial foi utilizado em cinco rodadas de otimização do aprendizado de máquina, ao final das rodadas foi identificado um aumento da enantiosseletividade dos produtos com catalisadores mais seletivos (Esquema 14b). Assim, um dos melhores catalisadores de transferência de fase identificados pelo processo de aprendizado de máquina, o Rnd4_8, foi aplicado para catalisar a penúltima etapa da síntese do letermovir, resultando no intermediário desejado com 89% ee e conversão completa. Este resultado representa um aumento de 13% na enantiosseletividade com melhor rendimento (melhoria geral de 6,5%) em relação ao processo original. Além disso, ao longo das rodadas, dados experimentais obtidos por experimentação de alto rendimento foram utilizados para implementar o modelo, mostrando como a combinação das duas técnicas pode resultar estratégias poderosas no design de catalisadores.

 

 

Estratégias de aprendizado de máquina atomístico para predizer o excesso enantiomérico de reações de propargilação de aldeídos organocatalisada por bases de Lewis derivadas de N,N'-dióxido piridinas quirais foram descritas (Esquema 15a).¹²⁴ Nessa abordagem, os autores criaram o modelo baseando-se em estruturas dos intermediários do ciclo catalítico estudado. Para isso, pares de intermediários de reação foram utilizados para treinar o modelo de aprendizado de máquina, essas estruturas foram otimizadas em DFT (B97-D/TZV(2p,2d)) e as informações contidas nas estruturas 3D foram transformadas em representações moleculares de SLATM (spectral london and Axilrod-Teller-Muto). Adicionalmente, para os valores alvos, as representações de input foram realizadas utilizando KRR (kernel ridge regression), que consiste em utilizar funções de Kernel para mapear dados em um espaço com maior dimensionalidade, para capturar relações não-lineares dos dados e então foram utilizados gráficos de dissimilaridade medindo a distância euclidiana entre duas representações estruturais e uma propriedade alvo, no caso a energia de ativação desses intermediários. Por fim, uma etapa de otimização de hiperparâmetros e validação cruzada foi realizada. Uma descrição geral do workflow aplicado neste trabalho está representada no Esquema 15b. O modelo construído por aprendizado de máquina pôde predizer acuradamente a enantiosseletividade dos produtos álcoois homopropargílicos computada por DFT, mostrando que predições semiquantitativas de excesso enantiomérico em catálise assimétrica podem ser computadas por valores de energia de ativação. Com isso, foi possível concluir que modelos atomísticos de aprendizado de máquina, com os descritores moleculares adequados, podem ser alternativas viáveis aos cálculos clássicos de energia utilizando mecânica quântica que muitas vezes podem ser onerosos.

 

 

CONCLUSÕES

Em resumo, a participação complementar de estudos computacionais em trabalhos sobre síntese de compostos orgânicos, organocatálise e estudos de mecanismos de reação é crescente e bem estabelecida. Parte significativa dessa popularização surge da colaboração crescente entre grupos teóricos e experimentais, do desenvolvimento de métodos computacionais mais eficientes e com o aumento da oferta de programas de Química Computacional que são acessíveis à um público não especializado em computação. Com o avanço da digitalização das publicações científicas e com o aumento de recursos computacionais disponíveis, o uso de computação passou a ser protagonista em estudos de reatividade. No entanto, a complexidade das transformações químicas, que surge devido a fatores estruturais dos reagentes envolvidos, condições reacionais e da ação de fatores externos, limita em muitos casos a aplicação de métodos computacionais avançados. Discutimos algumas alternativas para esses cenários, como o uso de modelos compostos QM/MM (ONIOM), no contexto da organocatálise. O uso de modelos estatísticos baseados em parâmetros moleculares e seletividade de reações tem se mostrado como um caminho promissor para a otimização de organocatalisadores. Esses modelos permitem trabalhar em uma escala que não é acessível para estudos computacionais tradicionais. Discutimos aqui diversos exemplos nos quais catalisadores mais seletivos foram selecionados por meio de modelos. Por fim, é certo que há substancial volume de informação disponível em publicações científicas e que muito esforço para catalogar e padronizar esses dados é empenhado pelos repositórios científicos. Contudo, é comum que exemplos negativos - casos onde dada transformação não se comporta conforme esperado - não sejam reportados. Esse cenário fomenta a necessidade de se elaborar conjuntos de dados voltados especificamente para alimentar modelos estatísticos. Discutimos alguns caminhos para produção dessas bibliotecas, por exemplo via HTE. Buscamos destacar trabalhos que têm sido executados por diversos grupos de pesquisa acadêmicos e industriais nesse sentido. Acreditamos que a adoção de todas essas ferramentas computacionais no contexto da Química Orgânica, e não apenas na área de organocatálise, permite acelerar de forma geral o desenvolvimento de métodos sintéticos e, por meio da associação entre o conhecimento da reatividade de compostos orgânicos e ferramentas computacionais, expandir a área de atuação do químico orgânico.

 

AGRADECIMENTOS

Agradecemos ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, 306516/2022-5 e 140710/2022-1), e a Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP, 20/10246-0, 22/11314-5, 21/12394-0, 22/14197-0, 24/00752-7, e 20/13563-7) pelo apoio financeiro. Este estudo foi financiado em parte pela Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, Brasil (CAPES, código financeiro 001).

 

REFERÊNCIAS

1. Corey, E. J.; Cheng, X. M.; Logic of Chemical Synthesis, New ed.; Wiley: New York, 1995.

2. Gaich, T.; Baran, P. S.; J. Org. Chem. 2010, 75, 4657. [Crossref]

3. Wender, P. A.; Nat. Prod. Rep. 2014, 31, 433. [Crossref]

4. Li, C. J.; Trost, B. M.; Proc. Natl. Acad. Sci.U. S. A. 2008, 105, 13197. [Crossref]

5. Varma, R. S.; ACS Sustainable Chem. Eng. 2016, 4, 5866. [Crossref]

6. Nicolaou, K. C.; Vourloumis, D.; Winssinger, N.; Baran, P. S.; Angew. Chem., Int. Ed. 2000, 39, 44. [Crossref]

7. Wöhler, F.; Ann. Phys. 1828, 88, 253. [Crossref]

8. Pasteur, L.; Ann. Chim. Phys. 1848, 26, 535.

9. Le Bel, J. A.; Bull. Soc. Chim. Fr. 1874, 22, 337.

10. van't Hoff, J. H.; Voorstel tot Uitbreiding der Tegenwoordig in de Scheikunde Gebruikte Structuur-Formules in de Ruimte: Benevents een Daarmeê Samenhangende Opmerking Omtrent het Verband Tusschen Optisch Actief Vermogen en Chemische Constitutie van Organische Verbindingen; J. Greven: Utrecht, 1874.

11. Fischer, E.; Ber. Dtsch. Chem. Ges. 1890, 23, 799. [Crossref]

12. Fact.MR, Chiral Chemicals Market, https://www.factmr.com/report/5397/chiral-chemicals-market, acessado em Março 2025.

13. Blackmond, D. G.; Cold Spring Harbor Perspect. Biol. 2019, 11, a032540. [Crossref]

14. Easson, L. H.; Stedman, E.; Biochem. J. 1933, 27, 1257. [Crossref]

15. Kaviani, R.; Jouyban, A.; Shayanfar, A.; CrystEngComm 2023, 25, 6120. [Crossref]

16. Fabro, S.; Smith, R. L.; Williams, R. T.; Nature 1967, 215, 296. [Crossref]

17. U. S. Food and Drug Administration (FDA), Development of New Stereoisomeric Drugs, https://www.fda.gov/regulatory-information/search-fda-guidance-documents/development-new-stereoisomeric-drugs, acessado em Março 2025.

18. European Medicines Agency; Investigation of Chiral Active Substances, 1994. [Link] acessado em Março 2025

19. Hancu, G.; Modroiu, A.; Pharmaceuticals 2022, 15, 240. [Crossref]

20. Pinheiro, S.; Ferreira, V. F.; Quim. Nova 1998, 21, 312. [Crossref]

21. Feringa, B. L.; van Delden, R. A.; Angew. Chem., Int. Ed. 1999, 38, 3418. [Crossref]

22. List, B.; Chem. Rev. 2007, 107, 5413. [Crossref]

23. Dondoni, A.; Massi, A.; Angew. Chem., Int. Ed. 2008, 47, 4638. [Crossref]

24. MacMillan, D. W. C.; Nature 2008, 455, 304. [Crossref]

25. Knowles, W. S.; Acc. Chem. Res. 1983, 16, 106. [Crossref]

26. Peng, Q.; Duarte, F.; Paton, R. S.; Chem. Soc. Rev. 2016, 45, 6093. [Crossref]

27. Cheong, P. H. Y.; Houk, K. N.; Warrier, J. S.; Hanessian, S.; Adv. Synth. Catal. 2004, 346, 1111. [Crossref]

28. Houk, K. N.; Liu, F.; Acc. Chem. Res. 2017, 50, 539. [Crossref]

29. Poree, C.; Schoenebeck, F.; Acc. Chem. Res. 2017, 50, 605. [Crossref]

30. Langenbeck, W.; Justus Liebigs Ann. Chem. 1929, 469, 16. [Crossref]

31. Hajos, Z. G.; Parrish, D. R.; J. Org. Chem. 1974, 39, 1615. [Crossref]

32. List, B.; Lerner, R. A.; Barbas, C. F.; J. Am. Chem. Soc. 2000, 122, 2395. [Crossref]

33. Denmark, S. E.; Wu, Z.; Crudden, C. M.; Matsuhashi, H.; J. Org. Chem. 1997, 62, 8288. [Crossref]

34. Sigman, M. S.; Jacobsen, E. N.; J. Am. Chem. Soc. 1998, 120, 4901. [Crossref]

35. Ahrendt, K. A.; Borths, C. J.; MacMillan, D. W. C.; J. Am. Chem. Soc. 2000, 122, 4243. [Crossref]

36. Dalko, P. I.; Moisan, L.; Angew. Chem., Int. Ed. 2001, 40, 3726. [Crossref]

37. Finelli, F.; Santos, B.; Frota, L.; Quim. Nova 2019, 42, 425. [Crossref]

38. Yao, W.; Bazan-Bergamino, E. A.; Ngai, M. Y.; ChemCatChem 2022, 14, e202101292. [Crossref]

39. Brière, J. F.; Oudeyer, S.; Dalla, V.; Levacher, V.; Chem. Soc. Rev. 2012, 41, 1696. [Crossref]

40. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Petersson, G. A.; Nakatsuji, H.; Li, X.; Caricato, M.; Marenich, A. V.; Bloino, J.; Janesko, B. G.; Gomperts, R.; Mennucci, B.; Hratchian, H. P.; Ortiz, J. V.; Izmaylov, A. F.; Sonnenberg, J. L.; Williams-Young, D.; Ding, F.; Lipparini, F.; Egidi, F.; Goings, J.; Peng, B.; Petrone, A.; Henderson, T.; Ranasinghe, D.; Zakrzewski, V. G.; Gao, J.; Rega, N.; Zheng, G.; Liang, W.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Throssell, K.; Montgomery Jr., J. A.; Peralta, J. E.; Ogliaro, F.; Bearpark, M. J.; Heyd, J. J.; Brothers, E. N.; Kudin, K. N.; Staroverov, V. N.; Keith, T. A.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A. P.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Millam, J. M.; Klene, M.; Adamo, C.; Cammi, R.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Farkas, O.; Foresman, J. B.; Fox, D. J.; Gaussian 16, Revision C.01; Gaussian, Inc., Wallingford CT, 2016.

41. Franzke, Y. J.; Holzer, C.; Andersen, J. H.; Begušić, T.; Bruder, F.; Coriani, S.; Della Sala, F.; Fabiano, E.; Fedotov, D. A.; Fürst, S.; Gillhuber, S.; Grotjahn, R.; Kaupp, M.; Kehry, M.; Krstić, M.; Mack, F.; Majumdar, S.; Nguyen, B. D.; Parker, S. M.; Pauly, F.; Pausch, A.; Perlt, E.; Phun, G. S.; Rajabi, A.; Rappoport, D.; Samal, B.; Schrader, T.; Sharma, M.; Tapavicza, E.; Treß, R. S.; Voora, V.; Wodyński, A.; Yu, J. M.; Zerulla, B.; Furche, F.; Hättig, C.; Sierka, M.; Tew, D. P.; Weigend, F.; J. Chem. Theory Comput. 2023, 19, 6859. [Crossref]

42. Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A. T. B.; Wormit, M.; Kussmann, J.; Lange, A. W.; Behn, A.; Deng, J.; Feng, X.; Ghosh, D.; Goldey, M.; Horn, P. R.; Jacobson, L. D.; Kaliman, I.; Khaliullin, R. Z.; Kuś, T.; Landau, A.; Liu, J.; Proynov, E. I.; Rhee, Y. M.; Richard, R. M.; Rohrdanz, M. A.; Steele, R. P.; Sundstrom, E. J.; Woodcock III, H. L.; Zimmerman, P. M.; Zuev, D.; Albrecht, B.; Alguire, E.; Austin, B.; Beran, G. J. O.; Bernard, Y. A.; Berquist, E.; Brandhorst, K.; Bravaya, K. B.; Brown, S. T.; Casanova, D.; Chang, C. M.; Chen, Y.; Chien, S. H.; Closser, K. D.; Crittenden, D. L.; Diedenhofen, M.; DiStasio Jr., R. A.; Do, H.; Dutoi, A. D.; Edgar, R. G.; Fatehi, S.; Fusti-Molnar, L.; Ghysels, A.; Golubeva-Zadorozhnaya, A.; Gomes, J.; Hanson-Heine, M. W. D.; Harbach, P. H. P.; Hauser, A. W.; Hohenstein, E. G.; Holden, Z. C.; Jagau, T. C.; Ji, H.; Kaduk, B.; Khistyaev, K.; Kim, J.; Kim, J.; King, R. A.; Klunzinger, P.; Kosenkov, D.; Kowalczyk, T.; Krauter, C. M.; Lao, K. U.; Laurent, A. D.; Lawler, K. V.; Levchenko, S. V.; Lin, C. Y.; Liu, F.; Livshits, E.; Lochan, R. C.; Luenser, A.; Manohar, P.; Manzer, S. F.; Mao, S. P.; Mardirossian, N.; Marenich, A. V.; Maurer, S. A.; Mayhall, N. J.; Neuscamman, E.; Oana, C. M.; Olivares-Amaya, R.; O'Neill, D. P.; Parkhill, J. A.; Perrine, T. M.; Peverati, R.; Prociuk, A.; Rehn, D. R.; Rosta, E.; Russ, N. J.; Sharada, S. M.; Sharma, S.; Small, D. W.; Sodt, A.; Stein, T.; Stück, D.; Su, Y. C.; Thom, A. J. W.; Tsuchimochi, T.; Vanovschi, V.; Vogt, L.; Vydrov, O.; Wang, T.; Watson, M. A.; Wenzel, J.; White, A.; Williams, C. F.; Yang, J.; Yeganeh, S.; Yost, S. R.; You, Z. Q.; Zhang, I. Y.; Zhang, X.; Zhao, Y.; Brooks, B. R.; Chan, G. K. L.; Chipman, D. M.; Cramer, C. J.; Goddard III, W. A.; Gordon, M. S.; Hehre, W. J.; Klamt, A.; Schaefer III, H. F.; Schmidt, M. W.; Sherrill, C. D.; Truhlar, D. G.; Warshel, A.; Xu, X.; Aspuru-Guzik, A.; Baer, R.; Bell, A. T.; Besley, N. A.; Chai, J. D.; Dreuw, A.; Dunietz, B. D.; Furlani, T. R.; Gwaltney, S. R.; Hsu, C. P.; Jung, Y.; Kong, J.; Lambrecht, D. S.; Liang, W.; Ochsenfeld, C.; Rassolov, V. A.; Slipchenko, L. V.; Subotnik, J. E.; Van Voorhis, T.; Herbert, J. M.; Krylov, A. I.; Gill, P. M. W.; Head-Gordon, M.; Mol. Phys. 2015, 113, 184. [Crossref]

43. Neese, F.; WIREs Comput. Mol. Sci. 2012, 2, 73. [Crossref]

44. Neese, F.; WIREs Comput. Mol. Sci. 2022, 12, e1606. [Crossref]

45. Sun, Q.; Berkelbach, T. C.; Blunt, N. S.; Booth, G. H.; Guo, S.; Li, Z.; Liu, J.; McClain, J. D.; Sayfutyarova, E. R.; Sharma, S.; Wouters, S.; Chan, G. K. L.; WIREs Comput. Mol. Sci. 2018, 8, e1340. [Crossref]

46. Sun, Q.; Zhang, X.; Banerjee, S.; Bao, P.; Barbry, M.; Blunt, N. S.; Bogdanov, N. A.; Booth, G. H.; Chen, J.; Cui, Z. H.; Eriksen, J. J.; Gao, Y.; Guo, S.; Hermann, J.; Hermes, M. R.; Koh, K.; Koval, P.; Lehtola, S.; Li, Z.; Liu, J.; Mardirossian, N.; McClain, J. D.; Motta, M.; Mussard, B.; Pham, H. Q.; Pulkin, A.; Purwanto, W.; Robinson, P. J.; Ronca, E.; Sayfutyarova, E. R.; Scheurer, M.; Schurkus, H. F.; Smith, J. E. T.; Sun, C.; Sun, S. N.; Upadhyay, S.; Wagner, L. K.; Wang, X.; White, A.; Whitfield, J. D.; Williamson, M. J.; Wouters, S.; Yang, J.; Yu, J. M.; Zhu, T.; Berkelbach, T. C.; Sharma, S.; Sokolov, A. Y.; Chan, G. K. L.; J. Chem. Phys. 2020, 153, 024109. [Crossref]

47. Smith, D. G. A.; Burns, L. A.; Simmonett, A. C.; Parrish, R. M.; Schieber, M. C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; James, A. M.; Lehtola, S.; Misiewicz, J. P.; Scheurer, M.; Shaw, R. A.; Schriber, J. B.; Xie, Y.; Glick, Z. L.; Sirianni, D. A.; O'Brien, J. S.; Waldrop, J. M.; Kumar, A.; Hohenstein, E. G.; Pritchard, B. P.; Brooks, B. R.; Schaefer III, H. F.; Sokolov, A. Y.; Patkowski, K.; DePrince III, A. E.; Bozkaya, U.; King, R. A.; Evangelista, F. A.; Turney, J. M.; Crawford, T. D.; Sherrill, C. D.; J. Chem. Phys. 2020, 152, 184108. [Crossref]

48. Bannwarth, C.; Caldeweyher, E.; Ehlert, S.; Hansen, A.; Pracht, P.; Seibert, J.; Spicher, S.; Grimme, S.; WIREs Comput. Mol. Sci. 2021, 11, e1493. [Crossref]

49. Pliego Jr., J. R.; Riveros, J. M.; WIREs Comput. Mol. Sci. 2020, 10, e1440. [Crossref]

50. Spicher, S.; Plett, C.; Pracht, P.; Hansen, A.; Grimme, S.; J. Chem. Theory Comput. 2022, 18, 3174. [Crossref]

51. Pliego Jr., J. R.; Quim. Nova 2006, 29, 535. [Crossref]

52. Rankin, K. N.; Gauld, J. W.; Boyd, R. J.; J. Phys. Chem. A 2002, 106, 5155. [Crossref]

53. Lv, P. L.; Zhu, R. X.; Zhang, D. J.; Duan, C. G.; Liu, C. B.; J. Phys. Chem. A 2012, 116, 1251. [Crossref]

54. The Nobel Prize, https://www.nobelprize.org/prizes/chemistry/1969/summary/, acessado em Março 2025.

55. Mohamadi, F.; Richards, N. G. J.; Guida, W. C.; Liskamp, R.; Lipton, M.; Caufield, C.; Chang, G.; Hendrickson, T.; Still, W. C.; J. Comput. Chem. 1990, 11, 440. [Crossref]

56. Watts, K. S.; Dalal, P.; Tebben, A. J.; Cheney, D. L.; Shelley, J. C.; J. Chem. Inf. Model. 2014, 54, 2680. [Crossref]

57. Grimme, S.; J. Chem. Theory Comput. 2019, 15, 2847. [Crossref]

58. Perdew, J. P.; Ruzsinszky, A.; Constantin, L. A.; Sun, J.; Csonka, G. I.; J. Chem. Theory Comput. 2009, 5, 902. [Crossref]

59. Goerigk, L.; Grimme, S.; Phys. Chem. Chem. Phys. 2011, 13, 6670. [Crossref]

60. Mardirossian, N.; Head-Gordon, M.; J. Chem. Theory Comput. 2016, 12, 4303. [Crossref]

61. Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S.; Phys. Chem. Chem. Phys. 2017, 19, 32184. [Crossref]

62. Mardirossian, N.; Head-Gordon, M.; Mol. Phys. 2017, 115, 2315. [Crossref]

63. McAnanama-Brereton, S.; Waller, M. P.; J. Chem. Inf. Model. 2018, 58, 61. [Crossref]

64. Bursch, M.; Mewes, J. M.; Hansen, A.; Grimme, S.; Angew. Chem., Int. Ed. 2022, 61, e202205735. [Crossref]

65. Lam, Y.; Grayson, M. N.; Holland, M. C.; Simon, A.; Houk, K. N.; Acc. Chem. Res. 2016, 49, 750. [Crossref]

66. Kruse, H.; Goerigk, L.; Grimme, S.; J. Org. Chem. 2012, 77, 10824. [Crossref]

67. Mardirossian, N.; Head-Gordon, M.; Phys. Chem. Chem. Phys. 2014, 16, 9904. [Crossref]

68. Najibi, A.; Goerigk, L.; J. Comput. Chem. 2020, 41, 2562. [Crossref]

69. Schenker, S.; Schneider, C.; Tsogoeva, S. B.; Clark, T.; J. Chem. Theory Comput. 2011, 7, 3586. [Crossref]

70. Bahmanyar, S.; Houk, K. N.; Martin, H. J.; List, B.; J. Am. Chem. Soc. 2003, 125, 2475. [Crossref]

71. Armstrong, A.; Boto, R. A.; Dingwall, P.; Contreras-García, J.; Harvey, M. J.; Mason, N. J.; Rzepa, H. S.; Chem. Sci. 2014, 5, 2057. [Crossref]

72. Yu, L. J.; Blyth, M. T.; Coote, M. L.; Top. Catal. 2022, 65, 354. [Crossref]

73. Clemente, F. R.; Houk, K. N.; Angew. Chem., Int. Ed. 2004, 43, 5766. [Crossref]

74. List, B.; Hoang, L.; Martin, H. J.; Proc. Natl. Acad. Sci. U. S. A. 2004, 101, 5839. [Crossref]

75. Bahmanyar, S.; Houk, K. N.; Org. Lett. 2003, 5, 1249. [Crossref]

76. Li, M.; Sang, Y.; Xue, X. S.; Cheng, J. P.; J. Org. Chem. 2018, 83, 3333. [Crossref]

77. Gordillo, R.; Houk, K. N.; J. Am. Chem. Soc. 2006, 128, 3543. [Crossref]

78. Krenske, E. H.; Houk, K. N.; Harmata, M.; J. Org. Chem. 2015, 80, 744. [Crossref]

79. Hou, X. X.; Wei, D.; J. Org. Chem. 2024, 89, 3133. [Crossref]

80. Zhao, W.; Liu, J.; He, X.; Jiang, H.; Lu, L.; Xiao, W.; Chin. J. Org. Chem. 2022, 42, 2504. [Crossref]

81. Wu, Y.; Li, M.; Sun, J.; Zheng, G.; Zhang, Q.; Angew. Chem., Int. Ed. 2022, 61, e202117340. [Crossref]

82. Johnson, E. R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A. J.; Yang, W.; J. Am. Chem. Soc. 2010, 132, 6498. [Crossref]

83. Bader, R. F. W.; Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, 1990.

84. Chung, L. W.; Sameera, W. M. C.; Ramozzi, R.; Page, A. J.; Hatanaka, M.; Petrova, G. P.; Harris, T. V.; Li, X.; Ke, Z.; Liu, F.; Li, H. B.; Ding, L.; Morokuma, K.; Chem. Rev. 2015, 115, 5678. [Crossref]

85. Reid, J. P.; Simón, L.; Goodman, J. M.; Acc. Chem. Res. 2016, 49, 1029. [Crossref]

86. Mahlau, M.; List, B.; Angew. Chem., Int. Ed. 2013, 52, 518. [Crossref]

87. Zhu, C.; Mandrelli, F.; Zhou, H.; Maji, R.; List, B.; J. Am. Chem. Soc. 2021, 143, 3312. [Crossref]

88. Plata, R. E.; Singleton, D. A.; J. Am. Chem. Soc. 2015, 137, 3811. [Crossref]

89. Peierls, R. E.; Biogr. Mem. Fellows R. Soc. 1997, 5, 174. [Crossref]

90. Liu, Z.; Patel, C.; Harvey, J. N.; Sunoj, R. B.; Phys. Chem. Chem. Phys. 2017, 19, 30647. [Crossref]

91. Besora, M.; Vidossich, P.; Lledós, A.; Ujaque, G.; Maseras, F.; J. Phys. Chem. A 2018, 122, 1392. [Crossref]

92. Houk, K. N.; Cheong, P. H. Y.; Nature 2008, 455, 309. [Crossref]

93. Mitsumori, S.; Zhang, H.; Ha-Yeon, P. C.; Houk, K. N.; Tanaka, F.; Barbas, C. F.; J. Am. Chem. Soc. 2006, 128, 1040. [Crossref]

94. Seeman, J. I.; Chem. Rev. 1983, 83, 83. [Crossref]

95. Weill, N.; Corbeil, C. R.; De Schutter, J. W.; Moitessier, N.; J. Comput. Chem. 2011, 32, 2878. [Crossref]

96. Rosales, A. R.; Wahlers, J.; Limé, E.; Meadows, R. E.; Leslie, K. W.; Savin, R.; Bell, F.; Hansen, E.; Helquist, P.; Munday, R. H.; Wiest, O.; Norrby, P. O.; Nat. Catal. 2019, 2, 41. [Crossref]

97. Guan, Y.; Ingman, V. M.; Rooks, B. J.; Wheeler, S. E.; J. Chem. Theory Comput. 2018, 14, 5249. [Crossref]

98. Young, T. A.; Silcock, J. J.; Sterling, A. J.; Duarte, F.; Angew. Chem., Int. Ed. 2021, 60, 4266. [Crossref]

99. Williams, W. L.; Zeng, L.; Gensch, T.; Sigman, M. S.; Doyle, A. G.; Anslyn, E. V.; ACS Cent. Sci. 2021, 7, 1622. [Crossref]

100. Hammett, L. P.; J. Am. Chem. Soc. 1937, 59, 96. [Crossref]

101. Taft Jr., R. W.; J. Am. Chem. Soc. 1952, 74, 2729. [Crossref]

102. Charton, M.; J. Am. Chem. Soc. 1975, 97, 1552. [Crossref]

103. Wang, Y.; Zhou, H.; Yang, K.; You, C.; Zhang, L.; Luo, S.; Org. Lett. 2019, 21, 407. [Crossref]

104. Haas, B. C.; Lim, N. K.; Jermaks, J.; Gaster, E.; Guo, M. C.; Malig, T. C.; Werth, J.; Zhang, H.; Toste, F. D.; Gosselin, F.; Miller, S. J.; Sigman, M. S.; J. Am. Chem. Soc. 2024, 146, 8536. [Crossref]

105. Li, J.; Grosslight, S.; Miller, S. J.; Sigman, M. S.; Toste, F. D.; ACS Catal. 2019, 9, 9794. [Crossref]

106. Orlandi, M.; Coelho, J. A. S.; Hilton, M. J.; Toste, F. D.; Sigman, M. S.; J. Am. Chem. Soc. 2017, 139, 6803. [Crossref]

107. Coelho, J. A. S.; Matsumoto, A.; Orlandi, M.; Hilton, M. J.; Sigman, M. S.; Toste, F. D.; Chem. Sci. 2018, 9, 7153. [Crossref]

108. Liles, J. P.; Rouget-Virbel, C.; Wahlman, J. L. H.; Rahimoff, R.; Crawford, J. M.; Medlin, A.; O'Connor, V. S.; Li, J.; Roytman, V. A.; Toste, F. D.; Sigman, M. S.; Chem 2023, 9, 1518. [Crossref]

109. Rogers, D.; Hahn, M.; J. Chem. Inf. Model. 2010, 50, 742. [Crossref]

110. Saebi, M.; Nan, B.; Herr, J. E.; Wahlers, J.; Guo, Z.; Zurański, A. M.; Kogej, T.; Norrby, P. O.; Doyle, A. G.; Chawla, N. V.; Wiest, O.; Chem. Sci. 2023, 14, 4997. [Crossref]

111. Mennen, S. M.; Alhambra, C.; Allen, C. L.; Barberis, M.; Berritt, S.; Brandt, T. A.; Campbell, A. D.; Castañón, J.; Cherney, A. H.; Christensen, M.; Damon, D. B.; de Diego, J. E.; García-Cerrada, S.; García-Losada, P.; Haro, R.; Janey, J.; Leitch, D. C.; Li, L.; Liu, F.; Lobben, P. C.; MacMillan, D. W. C.; Magano, J.; McInturff, E.; Monfette, S.; Post, R. J.; Schultz, D.; Sitter, B. J.; Stevens, J. M.; Strambeanu, I. I.; Twilton, J.; Wang, K.; Zajac, M. A.; Org. Process Res. Dev. 2019, 23, 1213. [Crossref]

112. Shevlin, M.; ACS Med. Chem. Lett. 2017, 8, 601. [Crossref]

113. Krska, S. W.; DiRocco, D. A.; Dreher, S. D.; Shevlin, M.; Acc. Chem. Res. 2017, 50, 2976. [Crossref]

114. Li, S. L.; Yang, C.; Wu, Q.; Zheng, H. L.; Li, X.; Cheng, J. P.; J. Am. Chem. Soc. 2018, 140, 12836. [Crossref]

115. Reid, J. P.; Sigman, M. S.; Nature 2019, 571, 343. [Crossref]

116. Werth, J.; Sigman, M. S.; J. Am. Chem. Soc. 2020, 142, 16382. [Crossref]

117. Joshi, P. B.; Artificial Intelligence Review 2023, 56, 9089. [Crossref]

118. Tantillo, D. J.; Chem. Soc. Rev. 2018, 47, 7845. [Crossref]

119. Marth, C. J.; Gallego, G. M.; Lee, J. C.; Lebold, T. P.; Kulyk, S.; Kou, K. G. M.; Qin, J.; Lilien, R.; Sarpong, R.; Nature 2015, 528, 493. [Crossref]

120. Parrot, M.; Tajmouati, H.; da Silva, V. B. R.; Atwood, B. R.; Fourcade, R.; Gaston-Mathé, Y.; Do Huu, N.; Perron, Q.; J. Cheminf. 2023, 15, 83. [Crossref]

121. Ahmed, F.; Lee, J. W.; Samantasinghar, A.; Kim, Y. S.; Kim, K. H.; Kang, I. S.; Memon, F. H.; Lim, J. H.; Choi, K. H.; Frontiers Public Health 2022, 10, 902123. [Crossref]

122. Ahneman, D. T.; Estrada, J. G.; Lin, S.; Dreher, S. D.; Doyle, A. G.; Science 2018, 360, 186. [Crossref]

123. Kondo, M.; Wathsala, H. D. P.; Sako, M.; Hanatani, Y.; Ishikawa, K.; Hara, S.; Takaai, T.; Washio, T.; Takizawa, S.; Sasai, H.; Chem. Commun. 2020, 56, 1259. [Crossref]

124. Gallarati, S.; Fabregat, R.; Laplaza, R.; Bhattacharjee, S.; Wodrich, M. D.; Corminboeuf, C.; Chem. Sci. 2021, 12, 6879. [Crossref]

125. Strieth-Kalthoff, F.; Sandfort, F.; Segler, M. H. S.; Glorius, F.; Chem. Soc. Rev. 2020, 49, 6154. [Crossref]

126. Seumer, J.; Hansen, J. K. S.; Nielsen, M. B.; Jensen, J. H.; Angew. Chem., Int. Ed. 2023, 62, e202218565. [Crossref]

127. Rasmussen, M. H.; Seumer, J.; Jensen, J. H.; Angew. Chem., Int. Ed. 2023, 62, e202310580. [Crossref]

128. Dolling, U. H.; Davis, P.; Grabowski, E. J. J.; J. Am. Chem. Soc. 1984, 106, 446. [Crossref]

129. Martins, E. F.; Pliego Jr., J. R.; ACS Catal. 2013, 3, 613. [Crossref]

130. He, C. Q.; Simon, A.; Lam, Y.; Brunskill, A. P. J.; Yasuda, N.; Tan, J.; Hyde, A. M.; Sherer, E. C.; Houk, K. N.; J. Org. Chem. 2017, 82, 8645. [Crossref]

131. Lexa, K. W.; Belyk, K. M.; Henle, J.; Xiang, B.; Sheridan, R. P.; Denmark, S. E.; Ruck, R. T.; Sherer, E. C.; Org. Process Res. Dev. 2022, 26, 670. [Crossref]

 

Editor Associado responsável pelo artigo: Giovanni W. Amarante