JBCS

INTRODUÇÃO

O espectro de absorção ultravioleta-visível (UV-Vis) tem sido largamente empregado em vários campos da ciência molecular e tecnológica.^1-4 Ele, por exemplo, fornece informações úteis sobre a estrutura eletrônica e auxilia na identificação de moléculas. No entanto, a interpretação dos espectros eletrônicos experimentais raramente é direta, pois envolve a interação de diversos efeitos que influenciam seu perfil, tornando sua análise complexa e ambígua.^1,5-11 Em um cenário tão complexo, os estudos de química computacional podem ser úteis em três níveis diferentes: (i) apoiar e complementar os resultados experimentais para determinar a estrutura e as propriedades eletrônicas do sistema alvo, a partir de suas propriedades espectrais; (ii) identificar e avaliar o papel dos diferentes efeitos físico-químicos que afetam as propriedades espectroscópicas observadas e (iii) prever as propriedades espectroscópicas esperadas para uma determinada espécie química.

Por apresentarem um bom compromisso entre precisão química e custo computacional, cálculos baseados na teoria do funcional da densidade (DFT) e TD-DFT (DFT dependente do tempo)^4,5,12-16 são os métodos mais empregados no entendimento e interpretação dos espectros de absorção UV-Vis experimentais.^17-20 No entanto, o uso destes métodos deve ser realizado com cautela porque, além de terem desempenho dependente do sistema, estados eletrônicos degenerados e quase degenerados podem estar presentes fazendo com que esses métodos baseados em uma única referência não sejam os mais apropriados.^21-23 Mesmo com essas limitações, é necessário reconhecer os inúmeros avanços que a área de fotoquímica e fotofísica orgânica e inorgânica tiveram com a aplicação dessas abordagens.^24-29 Em particular, fornecendo visões qualitativas e iniciais sobre a forma dos espectros e a natureza das transições envolvidas.^30-33

Como os métodos DFT (e TD-DFT) são amplamente usados na pesquisa sendo ferramentas úteis no auxílio ao estudo experimental, é interessante um guia que possa auxiliar estudiosos de diferentes áreas da química e outras relacionadas em suas utilizações práticas. Nesse contexto, o presente trabalho traz, de forma conceitual e metodológica, como os cálculos DFT e TD-DFT podem ser usados para investigar propriedades estruturais e eletrônicas em sistemas contrastantes - trans-azobenzeno (trans-AB) e 3-ferrocenil-trans-azobenzeno (3-FCAB), Figura 1 - reforçando o caráter dependente-de-sistema da escolha do funcional de densidade. Por consequência, se explora como os espectros de absorção UV-Vis podem ser obtidos e interpretados. Embora estudos com conjuntos extensos de dados e análises estatisticamente robustas sejam possíveis e altamente desejáveis,^34-39 este trabalho também se mostra relevante por realizar uma escolha cuidadosa do modelo computacional - incluindo o funcional de densidade, o conjunto de bases e o modelo de solvatação - um aspecto crítico em qualquer estudo baseado em química quântica.

 

 

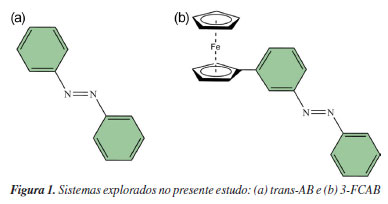
O azobenzeno (Figura 1a), em particular, é uma molécula que se destaca devido a sua versatilidade, podendo ser explorado como memórias e/ou interruptores moleculares, por exemplo.^40,41 A descoberta do ferroceno e sua posterior caracterização estrutural impeliu um renascimento da química organometálica.^42,43 As propriedades eletrônicas e estruturais do ferroceno permitem aplicações em vários campos, como: aditivos de combustível para melhoramento de desempenho e redução de emissões; sensores eletroquímicos; catalisadores em diversas reações orgânicas; desenvolvimento de medicamentos anticancerígenos, antivirais e antimicrobianos, dentre outros.^42,44

A associação do azobenzeno com complexos metálicos, no presente caso o 3-FCAB, Figura 1b, permite compor sistemas com funcionalidades que combinam as propriedades redox, ópticas e magnéticas dos complexos metálicos com a fotoisomerização do grupamento azobenzeno, possibilitando a criação de materiais responsivos à luz, viabilizando aplicações inovadoras, como dispositivos fotossensíveis, armazenamento óptico de informações, sistemas de liberação controlada de fármacos e materiais inteligentes, nos quais mudanças estruturais e de propriedades podem ser induzidas e revertidas de forma controlada por irradiação luminosa.^41,45,46

Do ponto de vista didático, trans-AB e 3-FCAB são interessantes para um estudo teórico comparativo, pois ambos possuem dados consolidados de cristalografia e espectros de absorção UV-Vis em diferentes meios e condições.^47-50 Adicionalmente, o fato de ambos compartilharem o azobenzeno como unidade estrutural, permite evidenciar as semelhanças e diferenças metodológicas que surgem ao longo de um estudo computacional baseado em cálculos DFT e TD-DFT.

 

METODOLOGIA

O procedimento que será descrito a seguir representa um compromisso entre precisão química e custo computacional e envolve duas tarefas principais: (i) obtenção da geometria e propriedades do estado eletrônico fundamental (estado eletrônico de mais baixa energia) e (ii) cálculos das energias dos estados eletrônicos excitados para obtenção dos espectros de absorção UV-Vis. Embora o texto esteja centrado nos sistemas trans-AB e 3-FCAB, Figura 1, a abordagem aqui apresentada permite que outros tipos de sistemas moleculares, contendo essa mesma ordem de grandeza e propriedades químicas semelhantes (mesmos tipos de átomos e ligações, mesmas classes de ligantes e íon metálico) sejam também explorados, desde que a escolha do funcional também seja adequadamente feita.

Os cálculos de estrutura eletrônica de sistemas moleculares, normalmente, requerem duas aproximações principais, o "método" - que pode envolver a expansão da função de onda ou a escolha do funcional de troca e correlação - e o "conjunto de bases" - a expansão das funções de um elétron para descrição dos orbitais atômicos e moleculares do sistema. A seleção apropriada do nível de teoria, método e base, é central, uma vez que determina a precisão e o custo dos resultados.

Para o tratamento da estrutura eletrônica de diferentes sistemas químicos, metodologias diversas foram desenvolvidas.^16,22,51-53 Dentre elas, destacam-se a teoria do funcional da densidade (DFT)^54,55 e sua abordagem dependente do tempo, a TD-DFT, amplamente empregadas na descrição do estado eletrônico fundamental e dos estados excitados, respectivamente, devido ao seu equilíbrio entre custo computacional e precisão.^{1,33-36,38,56-61} No entanto, é também conhecido que a investigação da estrutura eletrônica de sistemas fortemente correlacionados (como é o caso de muitos complexos de metais de transição) pode demandar métodos multirreferenciais e multiconfiguracionais,^21,37,61-71 como o CASSCF (complete active space self-consistent field),^72,73 o CASPT2 (complete active space second-order perturbation theory),^74,75 NEVPT2 (n-electron valence state second-order perturbation theory),^76-78 ou o MC­PDFT (multicon-guration pair-density functional theory),^79-81 por exemplo.

Devido à disponibilidade de mais de 500 funcionais de densidade^82-84 e ao fato de que eles nem sempre seguem a acurácia sugerida pela posição na escada de Jacó,⁸⁵ a escolha do funcional mais adequado não é trivial.^{21,36,82-84,86,87} Portanto, a realização de uma investigação prévia com base em dados de referência experimentais ou teóricos de alto nível é sempre recomendada.

Estado eletrônico fundamental: testes de funcionais e geometrias moleculares

Para se obter a geometria molecular de equilíbrio do estado eletrônico de mais baixa energia, um cálculo de otimização da geometria deve ser feito (tarefa (i)). Essa geometria pode ser comparada com a estrutura experimental de raios-X, quando disponível, e constitui o ponto de partida para uma caracterização molecular subsequente: a maioria dos demais cálculos de estrutura eletrônica que descrevem propriedades do estado fundamental são baseados nessa geometria.

Para a molécula de azobenzeno, somente a forma trans foi considerada porque esse é o isômero termodinamicamente mais estável.⁸⁸ As geometrias de partida foram obtidas pelo Cambridge Crystallographic Data Centre (CCDC), a partir dos arquivos .CIF disponibilizados para o trans-AB ⁸⁹ e para o 3-FCAB.⁴⁷ As estruturas de raios-X foram analisadas e convertidas em arquivos .XYZ, usando o software Avogadro, versão 12.0.⁹⁰ Todos os cálculos, descritos a seguir, foram feitos no Orca, versão 5.0.4.^91,92 Informações sobre capacidade das máquinas utilizadas, condições e tempo médio dos cálculos são descritos no Material Suplementar.

A fim de selecionar o funcional mais adequado, otimizações de geometria, empregando um mesmo grupo de funcionais populares para ambas as classes de sistemas,^93-96 foram realizadas: BP86­D3(BJ) (generalized gradient approximation, GGA),^97,98 PBE­D3(BJ) (GGA),⁹⁹ MN15-L (meta-GGA),¹⁰⁰ M06-L (meta­GGA),¹⁰¹ B3LYP/G­D3(BJ) (híbrido GGA),^102,103 PBE0­D3(BJ) (híbrido GGA)¹⁰⁴ e ωB97X-D3(BJ) (híbrido com correção de longo alcance).¹⁰⁵ Em que, a categoria a qual cada funcional pertence é mostrada entre parênteses. Para evitar flutuações indesejadas nos valores de energia e nas propriedades moleculares, o defgrid3 foi escolhido para os cálculos com os funcionais de Minnesota (MN15-L e M06-L), uma vez que são sensíveis ao grid de integração.^106-109 Na notação utilizada, D3(BJ) se refere aos casos em que a correção de dispersão D3 de Grimme com a variante proposta por Becke-Johnson foi utilizada.^110,111

A escolha do conjunto de bases determina a precisão do cálculo dentro dos limites do método teórico associado. Para cálculos de correlação eletrônica é interessante usar funções de base balanceadas, com funções de momento angular alto e que apresentem convergência para o limite de base completa (CBS, complete basis set). Além disso, é necessário que elas sejam capazes de descrever a densidade eletrônica em regiões espaciais que determinam as propriedades moleculares de interesse. A família de base def2, de Ahlrichs e colaboradores,^112,113 cobre grande parte da tabela periódica e são boas escolhas para cálculos DFT. As bases def2-TZVP, def2­TZVPP e def2-QZVP^113,114 foram testadas e, para átomos pesados, são convenientes porque elas possuem um pseudo-potencial (ECP, effective core potentials). Resumidamente, esse potencial é uma função de energia potencial adicionada a um cálculo de estrutura eletrônica para substituir o tratamento explícito dos elétrons mais internos. Os ECPs têm três grandes vantagens em cálculos de química quântica:¹¹⁵ (i) reduzem o custo dos cálculos, diminuindo o tamanho do conjunto de bases que é necessário para se obter uma determinada precisão; (ii) com um ECP relativístico (RECP) é possível a inclusão de correções relativísticas no tamanho e forma dos orbitais mais internos sem usar um tratamento totalmente relativístico da função de onda; (iii) o uso de ECPs reduz erros de superposição de conjuntos de bases (BSSE, basis set superposition errors). No entanto, ECPs não foram empregados neste trabalho, uma vez que para elementos até o quarto período da tabela periódica (Z < 36), os efeitos relativísticos podem ser considerados desprezíveis.^116,117

Para verificar as discrepâncias entre a geometria experimental e as obtidas por DFT, uma comparação entre cada uma das geometrias DFT geradas e a experimental foi feita usando as seguintes análises de erro:

• Root mean square error (RMSE), sobre a diferença entre os dois conjuntos de coordenadas, Equação 1.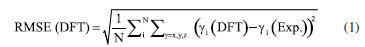

onde γ_i: coordenadas Cartesianas obtidas via DFT e experimentalmente, respectivamente.

• Mean unsigned error (MUE) e mean signed error (MSE), a partir da comparação entre as distâncias interatômicas de duas estruturas, Equações 2 e 3, respectivamente.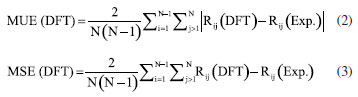

onde R_ij: distâncias internucleares entre pares de átomos ij.

O RMSE é calculado comparando as coordenadas cartesianas dos conjuntos de dados DFT e de raios-X. O MUE e o MSE são derivados da avaliação de todas as distâncias interatômicas entre esses dois tipos de dados, fornecendo assim uma investigação sistemática sobre o comprimento da ligação e complementando a análise RMSE. Os dados do MSE, por exemplo, dizem sobre o quanto os dados teóricos superestimam ou subestimam os comprimentos de ligação nas estruturas experimentais.

Dependendo do tipo de sistema de metal de transição e do funcional de densidade empregado, RMSEs com valores acima de 1,0 Å podem ser encontrados.^36,118 Para sistemas orgânicos, no entanto, os valores de RMSE são geralmente menores, variando entre 0,1 e 0,5 Å. Por exemplo, para moléculas orgânicas pequenas e médias, como o benzeno e seus derivados, RMSEs na faixa de 0,1 a 0,3 Å são comumente reportados.^119,120 Já para sistemas orgânicos maiores e mais flexíveis, como o trans-AB, valores de RMSE podem se aproximar de 0,5 Å, especialmente, quando há desafios na descrição de ligações duplas conjugadas e interações não covalentes.¹²¹

Ao final, o nível de teoria (funcional de densidade e conjunto de bases) mais adequado para descrever o estado eletrônico fundamental será aquele que fornece a melhor geometria com custo computacional que seja praticável. Um exemplo de input Orca para otimização de geometria é fornecido no Material Suplementar (Figura 1S). As geometrias otimizadas (arquivos xyz gerados ao final dos cálculos pelo programa Orca) foram visualizadas no Jmol, versão 14.30¹²² e a ausência de frequências vibracionais imaginárias confirmaram a obtenção de estruturas moleculares de mínimo. Todas as geometrias obtidas se encontram, em um arquivo de formato .XYZ, no Material Suplementar.

Absorção no UV-Vis: avaliação de funcionais de densidade, obtenção e atribuição de espectros

Uma vez determinada a geometria otimizada do sistema no estado eletrônico fundamental, a tarefa seguinte envolve o cálculo TD-DFT dos estados eletrônicos excitados e a obtenção das energias de absorção (tarefa (ii)).

Como os espectros de absorção UV-Vis dos sistemas selecionados são feitos em solução de um certo solvente, é interessante analisar esse efeito na geometria do estado eletrônico fundamental. Há duas maneiras principais de incluir a influência do solvente:^123-125 a solvatação implícita e a solvatação explícita. Em um modelo de solvatação implícito, o solvente é tratado como um meio contínuo dielétrico e as moléculas não são consideradas individualmente e espacialmente, ao contrário da aproximação explícita. Dessa forma, na modelagem implícita, a exploração das configurações das moléculas do solvente ao redor da espécie solvatada é eliminada, o que reduz significativamente o custo computacional em comparação com os modelos de solvatação explícita. Diferentes modelos de solvatação implícitos têm sido adotados^123,126,127 e, nesse estudo, as geometrias solvatadas foram obtidas usando a abordagem C-PCM (conductor-like polarizable continuum model),¹²⁶ conforme implementado no programa Orca. Para as otimizações com o solvente implícito, a geometria otimizada, obtida na etapa anterior com o melhor funcional/base, foi considerada como ponto de partida.

Tal como o estudo realizado para o estado fundamental, diferentes funcionais devem ser testados nos cálculos TD-DFT. Nesse caso, os espectros de absorção UV-Vis constituem bons dados de referência. Assim, o objetivo é simular um espectro de absorção UV-Vis TD­DFT que seja o mais próximo possível do experimental, a um custo computacional factível e que possibilite interpretações confiáveis. Para essa tarefa (ii), perfis teóricos de absorção UV-Vis foram calculados usando o conjunto de bases selecionado pelos cálculos de otimização de geometria e os seguintes funcionais: PBE (GGA),⁹⁹ M06-L (meta-GGA),¹⁰¹ O3LYP (híbrido GGA),¹²⁸ B3LYP/G (híbrido GGA),^102,103 PBE0 (híbrido GGA),¹⁰⁴ CAM-B3LYP (híbrido om correção de longo alcance)¹²⁹ e ωB97X (híbrido com correção de longo alcance).¹⁰⁵ Os dados espectrais experimentais do trans-AB¹³⁰ e do 3-FCAB¹³¹ foram utilizados para selecionar o melhor protocolo TD-DFT.

A maneira mais simples de obter as energias de absorção, é assumir que a geometria dos estados eletrônicos excitados (EEEs) não difere substancialmente da geometria do estado eletrônico fundamental (EEF) e, então, obter as propriedades dos estados eletrônicos excitados a partir da geometria do estado fundamental. A otimização de geometria de vários estados eletrônicos excitados é muito cara do ponto de vista computacional. As energias de absorção obtidas dessa maneira são chamadas de energias verticais de absorção (E^vert-abs).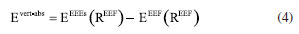

em que R^EEF indica as coordenadas dos átomos na geometria do estado eletrônico fundamental.

Para evidenciar a influência que o solvente exerce nessas energias, sempre no sentido de aproximar os dados teóricos dos valores experimentais e a um custo computacional factível, quatro diferentes protocolos TD-DFT foram explorados:

ou seja, os protocolos I e II são cálculos pontuais de energia com TD­DFT feitos em fase gasosa e solvente, respectivamente, mas sempre tendo a geometria otimizada do EEF em gás (gas) como ponto de partida, enquanto os protocolos TD-DFT III e IV, seguem a mesma ideia, porém partindo da geometria do estado eletrônico fundamental obtida na presença do solvente (solv). Essas quatro possibilidades permitem verificar o "ponto Pauling": uma situação em que o cancelamento de erros produz um modelo fisicamente equilibrado.¹³² Além de tal ponto, qualquer refinamento adicional diminui, em vez de aumentar, a precisão dos resultados. Assim, podemos verificar o mínimo de esforço computacional necessário para aproximar os dados teóricos dos experimentais, propondo protocolos baseados em DFT mais rápidos, ainda sim, confiáveis para estudos futuros. Utilizando a geometria do estado eletrônico fundamental (seja em gás ou solvente), os espectros de absorção UV-Vis foram obtidos empregando até trinta (30) estados eletrônicos singletos de menor energia.

Mesmo que o espectro TD-DFT corresponda ao experimento, o cálculo ainda não reproduz exatamente o que acontece durante a absorção de luz, uma vez que os cálculos teóricos fornecem picos discretos, enquanto os espectros experimentais exibem larguras de linha finita. Dentre os muitos fatores que contribuem para o alargamento das bandas observadas em um espectro de absorção UV-Vis (efeito Doppler térmico, colisões, resolução do espectrômetro e tempo de vida finito dos estados eletrônicos excitados),^133-135 pode-se citar os efeitos vibrônicos:¹³⁶ embora a maioria dos espectros experimentais não sejam resolvidos vibracionalmente, cada transição eletrônica é acompanhada por uma série de transições vibracionais.

A maneira mais simples de simular o formato da banda é assumir o princípio de Franck-Condon (basicamente, descreve que a probabilidade de uma transição eletrônica ocorre sem alterações significativas na separação nuclear), calcular as transições eletrônicas verticais e usar uma função de alargamento (gaussiana ou lorentziana, por exemplo) para obter um perfil para o "formato" da banda. Nesse caso, a largura da banda é escolhida empiricamente.^137,138 Por sua simplicidade e acessibilidade, esse foi o procedimento realizado nesse estudo: os espectros UV-Vis para cada um dos sistemas foi construído usando uma função de alargamento gaussiana, com o utilitário orca_mapspc do pacote Orca, aplicando o alargamento padrão de 1000 cm^-1.

Além de obter os espectros de absorção, é fundamental interpretar e compreender o tipo de transição eletrônica descrita em cada região espectral, ou seja, fazer a atribuição das bandas do espectro. Um procedimento computacional particularmente conveniente para essa tarefa é o uso dos orbitais naturais de transição (natural transition orbitals, NTOs).^139,140 Essa abordagem proporciona uma interpretação mais clara e intuitiva das transições eletrônicas, em comparação com a análise baseada exclusivamente nos orbitais moleculares canônicos, por exemplo. Os NTOs são orbitais derivados da decomposição da matriz de densidade de transição que descreve as alterações na densidade eletrônica durante uma transição entre o estado fundamental e um estado excitado. Eles conseguem empregar um número reduzido de pares de orbitais que contribuem para a transição. Na maioria dos casos, um único par de NTO - constituído de um orbital ocupado e um orbital virtual - é suficiente para descrever a maior parte da densidade de transição.^139-144 Além de simplificar a atribuição das transições eletrônicas, os NTOs proporcionam insights detalhados sobre a natureza das excitações, auxiliando na identificação de fenômenos como transferência de carga, localizações eletrônicas e interações entre fragmentos moleculares.

Os orbitais moleculares canônicos, comumente utilizados, são definidos como soluções que diagonalizam a matriz de Fock, conferindo energias bem definidas ao sistema. Contudo, eles tendem ser amplamente deslocalizados, o que dificulta a identificação de regiões específicas onde as alterações eletrônicas ocorrem. Essa deslocalização pode mascarar características importantes, como transferências de carga localizadas ou interações π→π*, tornando a interpretação química mais desafiadora. Em termos práticos, analisar transições eletrônicas com base nos orbitais canônicos, frequentemente, resulta em um cenário confuso, porque as transições eletrônicas podem envolver combinações de elétrons que "saem" de múltiplos orbitais ocupados e "vão" para diferentes orbitais virtuais.^143,145 Logo, neste trabalho, os NTOs foram empregados.

O cálculo dos NTOs foi realizado conjuntamente com os cálculos TD-DFT. Para auxiliar na reprodução dos espectros teóricos, um exemplo de input Orca para a obtenção dos espectros de absorção é fornecido no material suplementar (Figura 2S). Os perfis espectrais foram gerados utilizando o Gnuplot, versão 6.0 (Williams, T.; Kelley, C.; EUA, 2023), enquanto a visualização e análise dos NTOs foram realizadas com o PyMOL.¹⁴⁶

 

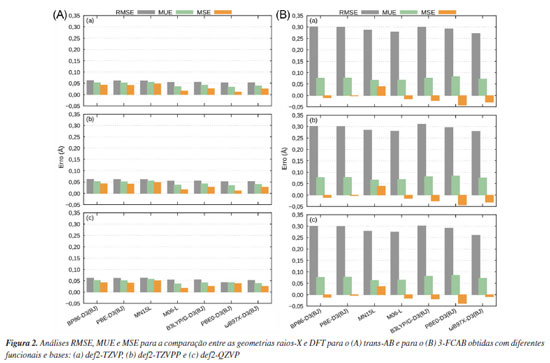
RESULTADOS E DISCUSSÃO

Análises das geometrias do estado eletrônico fundamental

Comparação das geometrias experimentais com DFT

Antes de iniciar a discussão, alguns comentários sobre a comparação entre geometrias otimizadas DFT de moléculas isoladas e estruturas obtidas a partir de experimentos de difração de raios-X de cristais devem ser feitos:

(i) é bem conhecido que a densidade de elétrons de átomos e moléculas espalha raios-X e o poder de espalhamento de um elemento depende de seu número atômico Z. A amplitude de espalhamento dos raios-X é proporcional a Z, quando espalhada em pequenos ângulos e proporcional a ca. Z^1/2 para ângulos relativamente maiores. Portanto, costuma ser difícil determinar a posição de elementos leves (Z pequeno) na presença de átomos pesados (Z grande). Sendo assim, na comparação entre estrutura experimental e DFT, uma melhor análise é feita quando os átomos de H são desconsiderados, porque reduz as incertezas nas comparações e ajuda a selecionar, da melhor forma possível, o funcional de densidade mais apropriado. Primeiro, otimiza-se via DFT (nesse caso) a geometria dos sistemas com todos os hidrogênios presentes e, posteriormente, os átomos de hidrogênio são removidos da geometria otimizada para realizar a comparação. Do contrário, durante o cálculo computacional de otimização, os átomos fariam ligações não esperadas, tentando completar sua valência devido a remoção dos hidrogênios.

(ii) parâmetros de geometria, em particular aqueles que envolvem um centro de metal de transição, são modificados pela influência das moléculas circundantes na estrutura cristalina do sólido. Tal situação se difere dos cálculos DFT que são executados para uma molécula isolada em fase gasosa. Em geral, a diferença entre o sistema real e o modelo usado na teoria, gera desvios cuja magnitude representa a principal fonte de incerteza durante a comparação. As variações observadas para as distâncias de ligação metal-ligante são, tipicamente, da ordem de 0,01-0,02 Å, comparado com aqueles observados em moléculas orgânicas, ≤ 0,01 Å.^36,38,147 Portanto, espera-se antecipadamente que desvios sejam introduzidos pelo funcional de densidade escolhido e pelo uso de uma estrutura molecular "isolada" durante os cálculos, que difere da obtida a partir de experimentos de difração de raios-X.

As otimizações de geometria do trans-AB e do 3-FCAB foram realizadas no estado eletrônico fundamental singleto (ambas as moléculas têm a mesma multiplicidade no estado fundamental), sem efeito do solvente, carga nula, utilizando os funcionais e conjunto de bases descritos. Os dados para análise comparativa entre os resultados de DFT e o experimento de raios-X são apresentados na Figura 2.

 

 

Observa-se que os erros são menores e menos dispersos para o trans-AB, Figura 2A. Isso reforça estudos anteriores^148-151 que indicam que os funcionais DFT têm maior facilidade em descrever geometrias de sistemas orgânicos relativamente simples. Em contraste, para o 3-FCAB (Figura 2B), os erros são mais pronunciados devido à presença do grupo ferroceno. A inclusão de um átomo metálico aumenta significativamente a complexidade estrutural e eletrônica do sistema, tornando sua descrição mais desafiadora. Os metais de transição possuem um maior número de elétrons, estados eletrônicos degenerados ou quase degenerados e contribuições significativas de orbitais d. Esses fatores impõem dificuldades para os cálculos de estrutura eletrônica que podem não capturar adequadamente os efeitos de correlação eletrônica e de transferência de carga envolvendo o metal. Uma alternativa para mitigar essas limitações é a aplicação de métodos multiconfiguracionais e/ou multirreferenciais, como citado anteriormente, pois conseguem capturar melhor os efeitos de correlação eletrônica estática e os processos de transferência de carga envolvendo o centro metálico.^21,37,61-71

Conforme mostrado na Figura 2A, para o trans-AB, os funcionais BP86-D3(BJ), PBE-D3(BJ) e MN15-L apresentaram os maiores valores de RMSE, MUE e MSE, indicando um desempenho limitado na descrição da geometria dessa molécula em comparação com os demais funcionais testados. Em particular, esses três funcionais exibiram RMSE em torno de 0,062 Å, MUE entre 0,052 e 0,055 Å e MSE variando de 0,041 a 0,051 Å, dependendo da base utilizada. Por outro lado, os funcionais B3LYP/G-D3(BJ) e ωB97X-D3(BJ) apresentaram erros intermediários em relação aos demais, com RMSE de 0,055 e 0,053 Å, MUE de 0,041 e 0,039 Å e MSE de 0,027 e 0,026 Å, respectivamente, mantendo uma constância entre as diferentes bases. Já o funcional PBE0-D3(BJ) obteve valores de RMSE inferiores aos demais, porém a expansão da base resultou em um aumento nos valores de MUE e MSE, atingindo, por exemplo, um MSE de 0,038 Å com a base def2-QZVP, revelando certa inconsistência. O funcional M06-L, por sua vez, apresentou um desempenho satisfatório e estável, com RMSE próximo a 0,054 Å e MUE de aproximadamente 0,017 Å, mantendo um comportamento regular entre as diferentes bases. Esses dados sugerem que o M06-L é o mais adequado para descrever o trans-AB, justificando sua escolha para os cálculos subsequentes. Dessa forma, a escolha final do método DFT/def2-TZVP/M06-L se justifica por sua robustez, elevada acurácia e desempenho nos testes realizados.

Para o 3-FCAB, Figura 2B, os valores de RMSE, MUE e MSE permanecem constantes com o aumento da base em praticamente todos os funcionais. Logo, a expansão da base não apresentou melhoras significativas que justifiquem seu uso, sendo a def2-TZVP suficiente. Os funcionais M06-L e ωB97X-D3(BJ) apresentaram os menores valores de RMSE entre os funcionais testados, 0,278 e 0,271 Å, respectivamente, utilizando a base def2-TZVP. O funcional ωB97X-D3(BJ) se destacou particularmente nessa métrica com a base def2-QZVP, para a qual o RMSE foi de 0,260 Å, o menor valor obtido entre os níveis de teoria testados. Por outro lado, os valores de MUE foram mais baixos para o funcional M06-L, 0,068, 0,069 e 0,065 Å, enquanto o funcional ωB97X-D3(BJ) apresentou valores ligeiramente superiores: 0,072, 0,075 e 0,072 Å, respectivamente, para as bases def2-TZVP, def2-TZVPP e def2-QZVP. Em relação ao MSE, os melhores resultados foram obtidos para o M06-L com as bases def2-TZVP e def2-TZVPP (-0,015 Å em ambos os casos), enquanto o ωB97X-D3(BJ) apresentou o menor MSE com a base def2-QZVP (-0,009 Å). Esses resultados indicam que ambos os funcionais fornecem descrições adequadas para a molécula.

Comparando os funcionais ωB97X-D3(BJ) e M06-L para o sistema 3-FCAB, o M06-L é o que apresenta, teoricamente, menor custo computacional. Contudo a parametrização flexível, voltada para a reprodução de propriedades específicas do M06-L pode gerar superfícies de energia potencial menos suaves,^22,152-154 aumentando a probabilidade de problemas de convergência,¹⁵⁵ especialmente, em sistemas contendo metais de transição, como no caso do 3-FCAB.^156,157 Esses problemas de convergência podem demandar cálculos extras para correção, aumentando o custo computacional final. Por outro lado, o funcional ωB97X-D3(BJ) tende a produzir superfícies de energia mais suaves, permitindo a obtenção dos mínimos da superfície de energia de forma mais eficiente.^108,158 Assim, o funcional ωB97X­D3(BJ) foi escolhido para dar sequência às demais análises deste estudo. O nível de teoria DFT/def2-TZVP/ωB97X-D3(BJ) se tornou uma escolha eficiente para o sistema 3-FCAB, equilibrando precisão e economia de recursos computacionais.

Em resumo, os resultados indicam que a abordagem DFT/def2­TZVP/M06-L apresentou desempenho satisfatório para ambos os sistemas. No trans-AB, o funcional M06-L demonstrou boa precisão e eficiência computacional, justificando sua escolha final. Já para o 3-FCAB problemas de convergência com o M06-L tornaram o ωB97X-D3(BJ) mais adequado. Isso reforça a importância de ajustar a escolha metodológica conforme a complexidade estrutural e eletrônica de cada sistema e o tipo de propriedade investigada.

Efeito do solvente nas geometrias do estado eletrônico fundamental

Após a seleção do melhor nível de teoria para as otimizações DFT, realizou-se a análise do efeito do solvente, uma vez que os espectros UV-Vis desses compostos foram obtidos em solução. A quantificação prévia da influência do solvente nas geometrias do estado fundamental orienta os cálculos dos estados eletrônicos excitados de forma eficiente. Na Figura 3 são apresentadas as sobreposições estruturais - geradas com o software PyMOL - entre as geometrias otimizadas em fase gasosa e em solvente. Para o trans-AB, utilizou-se n-hexano, enquanto para o 3-FCAB, optou-se pela acetonitrila. Essas escolhas foram basedas nas condições experimentais empregadas na obtenção dos respectivos espectros de absorção UV-Vis.^130,131

 

 

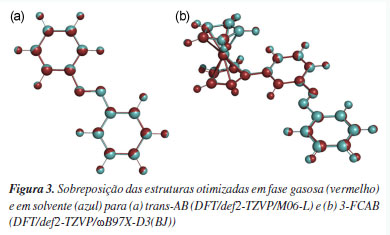
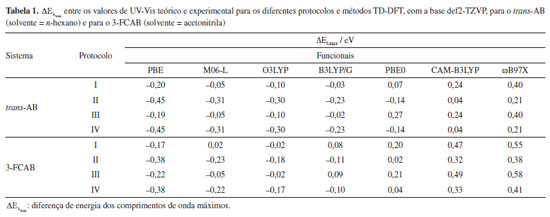
De acordo com as sobreposições, o solvente exerce menor influência na estrutura do trans-AB (Figura 3a) do que no composto de coordenação 3-FCAB (Figura 3b). Para o 3-FCAB, as maiores diferenças estão, especialmente, na posição dos átomos de hidrogênio dos anéis do ferroceno e nos átomos do segundo anel do azobenzeno.

Em sistemas orgânicos simples, como o trans-AB, a solvatação implícita, geralmente, tem pouco impacto na geometria molecular.¹²⁴ Isso ocorre porque as interações solvente-soluto, predominantemente eletrostáticas, não alteram significativamente as ligações covalentes ou a estrutura geral da molécula. Por outro lado, a presença de átomos metálicos e de grupos coordenados, que possuem maior polarizabilidade e cargas parciais mais elevadas, pode produzir interações mais intensas com o meio.^159,160 A solvatação pode influenciar a geometria ao redor do metal, bem como as ligações metal-ligante. Além disso, o efeito do solvente pode se refletir na reorganização de fragmentos menos rígidos, como os átomos de hidrogênio nos anéis do ferroceno, como observado nos resultados obtidos. A magnitude desse efeito depende da natureza do metal, dos ligantes e do solvente.¹⁶⁰

Para verificar se as diferenças observadas nas geometrias moleculares poderiam ser atribuídas à polaridade do solvente, foram realizados testes adicionais com o trans-AB em acetonitrila e com o 3-FCAB em n-hexano. Como o arranjo espacial dos átomos nos compostos-alvo se manteve praticamente inalterado, independentemente do solvente empregado, reforça-se a hipótese de que as diferenças observadas decorrem predominantemente da complexidade estrutural, e não da polaridade do meio, pelo menos nos dois sistemas avaliados.

Espectros de absorção UV-Vis

Obtenção das energias eletrônicas de transição

Cálculos baseados em funções de onda, que empregam métodos altamente correlacionados para a obtenção de energias de excitação, geralmente alcançam uma acurácia elevada, na ordem de 0,1­0,2 eV.¹⁶¹ Entretanto, exibem maior custo computacional, o que acaba inviabilizando cálculos de sistemas químicos maiores, diferentemente da abordagem TD-DFT.¹⁶² Assim, após a otimização das geometrias do estado eletrônico fundamental em fase gasosa e em solvente, cálculos TD-DFT foram realizados para obter as energias de transição eletrônica dos sistemas trans-AB e 3-FCAB. Para isso, foram aplicados os quatro protocolos descritos na seção "Metodologia". Esses protocolos permitiram avaliar a influência do solvente (e alterações na geometria decorrentes da consideração do solvente) nas energias de transição, comparar o desempenho de diferentes funcionais (PBE, M06-L, O3LYP, B3LYP/G, PBE0, CAM-B3LYP e ωB97X) na descrição dos espectros UV-Vis e identificar o "ponto Pauling". As energias verticais de absorção, após trabalhadas, permitiram a comparação com os dados experimentais e a seleção do método TD-DFT mais adequado para cada sistema. A seguir, são apresentadas as métricas utilizadas na comparação.

Uma primeira e simples métrica que pode ser usada para averiguar a adequação de um protocolo TD-DFT para cálculo de espectros de absorção UV-Vis é a avaliação do quão próximo o comprimento de onda máximo teórico (λ_teo) está do máximo experimental (λ_exp). Cada um dos comprimentos de onda máximos tem uma energia correspondente (E_λ) e, portanto, podemos fazer essa diferença em termos de energia:

O valor de λ_exp (e, portanto, a respectiva energia) é prontamente identificado no espectro experimental, um máximo na banda de absorção em uma dada região. Já para se obter λ_teo, é necessário analisar a transição de maior força do oscilador (f_osc), a linha de maior intensidade (em uma dada região). Um gráfico obtido a partir do arquivo .stk do Orca, um dos arquivos de saída do utilitário orca_mapspc, permite a confirmação visual das transições mais intensas. A comparação entre esses valores foi realizada dentro de uma mesma região do espectro de absorção, permitindo verificar a consistência entre os resultados teóricos e experimentais. Especificamente, para ambos os sistemas analisados, utilizamos o máximo entre 300-350 nm para o cálculo de . Os resultados obtidos para as comparações dos máximos de energia estão apresentados na Tabela 1.

 

 

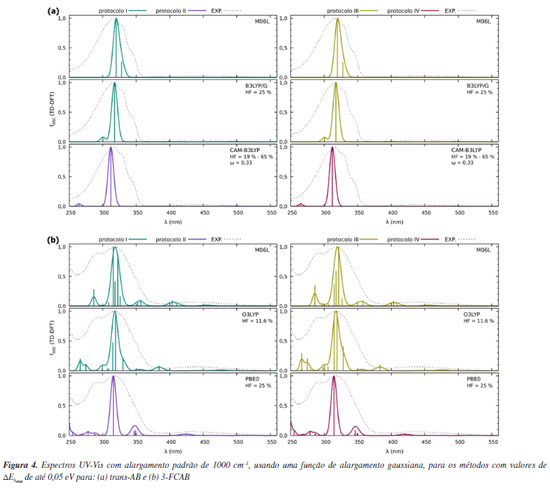
Para o trans-AB, o funcional B3LYP/G apresenta os melhores resultados nos protocolos I e III. Entre eles, o protocolo III se destaca, com uma diferença de 0,02 eV entre os valores teóricos e experimentais. Assim, considerando a métrica de comparação de máximos, o protocolo III com o funcional B3LYP/G é o mais consistente em relação aos dados experimentais. Além deste, os funcionais CAM-B3LYP nos protocolos II e IV e M06-L nos protocolos I e III também se mostraram interessantes, com diferenças de até 0,05 eV em relação aos máximos experimentais. Cabe ressaltar que, embora a inclusão de solvente na otimização geométrica do estado eletrônico fundamental aumente o custo computacional, para este sistema orgânico, o tempo de cálculo permaneceu na ordem de minutos. Isso viabiliza a escolha de protocolos mais precisos, como o protocolo III, para futuras análises. No entanto, para determinar o método e protocolo ideais se faz ainda necessário uma avaliação complementar dos perfis de absorção.

No caso do 3-FCAB, o menor valor absoluto na comparação dos máximos de banda foi de 0,02 eV. Esse resultado foi alcançado com os seguintes funcionais e protocolos: M06-L e O3LYP no protocolo I, PBE0 no protocolo II e O3LYP no protocolo III. Para sistemas contendo átomos metálicos e ligantes coordenados, como o 3-FCAB, é importante destacar que o uso de funcionais adequados e a consideração dos efeitos de solvatação podem ser cruciais em determinadas condições. Nesse caso, o protocolo I apresentou um bom equilíbrio entre precisão e custo computacional, justificando sua seleção para análises subsequentes. Contudo, como diferentes combinações de funcionais e protocolos apresentaram discrepâncias similares, a análise dos máximos isoladamente não é suficiente para determinar o método ideal. Análises adicionais, como reprodução do perfil e atribuição de bandas, sobre o espectro também devem ser consideradas. Por isso, na sequência, o método (funcional) e protocolo selecionados para cada composto foram explorados para verificar se reproduzem o perfil geral dos espectros de absorção.

O perfil dos espectros de absorção UV-Vis

Além de avaliar a concordância entre os máximos de absorção, é interessante analisar o perfil geral do espectro calculado, ou seja, como podemos construir o formato das bandas que compõem o espectro de absorção UV-Vis? Até o momento, havíamos calculado as energias das transições eletrônicas, ou seja, a posição de uma banda. Agora, queremos também, simular o formato geral das bandas do espectro.

Os espectros obtidos para os funcionais e protocolos com valores de até 0,05 eV nas análises de máximos são apresentados na Figura 4. A análise do perfil geral dos espectros complementa a análise inicial envolvendo apenas as "posições" esperadas para uma banda e, portanto, permite identificar o método e o protocolo que melhor descrevem cada sistema. Os espectros de absorção UV-Vis obtidos para todos os métodos descritos na Tabela 1 podem ser visualizados nas Figuras 3S e 4S, presentes no Material Suplementar.

 

 

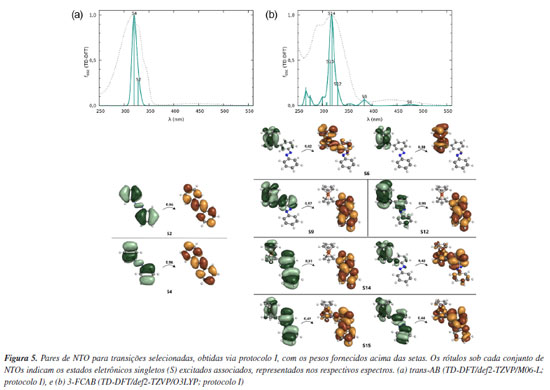
Os perfis espectrais para o trans-AB (Figura 4a) revelam que o espectro experimental exibe uma banda com máximo de absorção em 315,5 nm, acompanhada de dois ombros subsequentes na região de 320 a 350 nm. Entre os perfis teóricos apresentados, o funcional M06-L é o que melhor reproduz essa região espectral. Como os espectros obtidos com os protocolos I e III são similares, optou-se pelo protocolo I para a continuidade das análises, uma vez que proporciona uma redução no custo computacional sem comprometer a qualidade da descrição espectral.

Para o 3-FCAB (Figura 4b), o espectro experimental é um pouco mais complexo e notamos um máximo próximo de 320 nm. Essa banda apresenta, além do máximo de absorção, um ombro na região de 290 nm e outra em torno de 250 nm. A análise dos perfis teóricos indica que o funcional O3LYP é o que melhor descreve o comportamento geral observado experimentalmente. Além disso, quando combinado com o protocolo I, ele proporciona uma descrição mais clara em comparação ao protocolo III, pois consegue representar o espectro com um número menor de estados eletrônicos, reduzindo a complexidade da análise e sem comprometer a precisão dos resultados.

A superioridade do protocolo I pode ser interpretada à luz do conceito do "ponto Pauling", que sugere que um equilíbrio entre simplificações computacionais pode levar a um modelo fisicamente consistente. Nesse caso, o uso da geometria otimizada em fase gasosa como ponto de partida para cálculos TD-DFT (também realizados em fase gasosa) parece atingir um equilíbrio ideal entre esforço computacional e precisão. Refinamentos adicionais, como a inclusão de efeitos de solvente na otimização geométrica (protocolos III e IV) ou nos cálculos TD-DFT (protocolo II), não melhoraram significativamente a concordância com os dados experimentais, indicando que o "ponto Pauling" foi alcançado. Além desse ponto, qualquer aumento na complexidade do modelo tende a introduzir erros sistemáticos ou a demandar recursos computacionais desnecessários, sem ganhos proporcionalmente significativos em precisão. Portanto, o protocolo I representa um compromisso eficiente entre custo computacional e confiabilidade, sendo um bom ponto de partida para estudos futuros de espectroscopia UV-Vis em sistemas orgânicos e de coordenação quimicamente semelhantes aos abordados neste trabalho.

Considerando a comparação entre as posições dos máximos de absorção (Tabela 1) e o perfil geral dos espectros (Figura 4) obtidos via TD-DFT, o protocolo I se destaca por apresentar a melhor concordância com os dados experimentais, tanto para o trans-AB quanto para o 3-FCAB. Esse protocolo fornece uma descrição confiável das características espectrais, tornando-se a escolha mais adequada para a análise subsequente: a atribuição das bandas usando NTOs.

Atribuições das bandas

Para interpretar as transições obtidas nos espectros teóricos e permitir a comparação com as atribuições experimentais, NTOs (Figura 5) foram calculados dentro do protocolo I.

 

 

O trans-AB é caracterizado por uma banda experimental com máximo em 315,5 nm, atribuída como do tipo π→π*.¹³⁰ O espectro teórico obtido reproduz essa região de absorção por meio das excitações S0→S2 e S0→S4, em que S é usado para designar excitações singleto e S0, o estado eletrônico fundamental, Figura 5a. A análise visual dos NTOs associados a essas transições confirma que os resultados teóricos são consistentes com a atribuição experimental, evidenciando que o método empregado descreve adequadamente a natureza dessa banda.

O 3-FCAB apresenta um espectro experimental caracterizado por uma banda de absorção com máximo na região próxima a 320 nm atribuída como π→π*; na região de 444 nm é visto uma banda do tipo MLCT (metal-to-ligand charge transfer).¹³¹ A interpretação desse espectro envolve múltiplas transições eletrônicas, como pode ser observado na Figura 5b. Na região espectral caracterizada experimentalmente como MLCT, a análise visual dos NTOs para a transição S0→S6 indica que a excitação envolve uma porção predominantemente dentro do fragmento ferroceno, sem uma contribuição expressiva do azobenzeno. As transições S0→S9 e S0→S12 representam excitações do tipo MLCT, envolvendo orbitais d do ferro (fragmento ferroceno) e orbitais π* do fragmento azobenzeno. Esse tipo de transição é característico de sistemas híbridos orgânico-metálicos e desempenha um papel crucial na modulação das propriedades eletrônicas e espectroscópicas da molécula. As transições S0→S14 e S0→S15 apresentam uma mistura de π→π*, esperada para essa região do espectro,¹³¹ e MLCT (envolvendo o metal e os anéis do ferroceno).

De modo geral, os espectros obtidos via TD-DFT (desde que o funcional seja adequadamente selecionado) são boas escolhas iniciais para a reprodução de espectros de absorção UV-Vis experimentais e para a obtenção de NTOs na atribuição das bandas. Apesar das limitações inerentes ao método, os resultados reforçam a capacidade do TD-DFT, aliado à análise de NTOs, de fornecer uma interpretação confiável para as transições eletrônicas, contribuindo para a compreensão dos espectros de absorção dos sistemas selecionados e de outros análogos.

 

CONCLUSÕES

Neste estudo, foi avaliado o comportamento de diferentes funcionais e conjuntos de bases para descrever a geometria do estado eletrônico fundamental e os espectros de absorção UV-Vis para o trans-AB e para o 3-FCAB. Os resultados de otimização de geometria indicam que o funcional M06-L foi robusto para o trans­AB, enquanto o ωB97X-D3(BJ), o mais adequado na descrição do 3-FCAB. Para ambos os sistemas, a base def2-TZVP se apresentou eficiente e suficiente. A inclusão do solvente, via modelo implícito C-PCM e em detrimento do observado no 3-FCAB, revelou pouca influência na geometria do trans-AB.

Na análise dos espectros de absorção UV-Vis, a avaliação dos máximos de absorção e dos perfis espectrais reforçou a adequação do funcional M06-L para o sistema orgânico, enquanto o O3LYP forneceu melhores resultados para o composto de coordenação. Esses funcionais descreveram os espectros teóricos de forma consistente com os experimentais, proporcionando interpretações confiáveis das bandas de absorção. Além disso, a aplicação do protocolo I - ausência de solvente na descrição dos estados fundamental e excitado - foi eficiente na abordagem de ambos os sistemas. Esse resultado está em consonância com o conceito do "ponto Pauling", que sugere que um equilíbrio entre simplificações computacionais pode levar a um modelo fisicamente consistente. No uso do protocolo I, a geometria otimizada em fase gasosa e cálculos TD-DFT também em fase gasosa, geraram um equilíbrio ideal, e refinamentos adicionais, como a inclusão de solvente, não trouxeram melhorias significativas na obtenção dos resultados. Adicionalmente, o uso de NTOs dentro do protocolo I possibilitou uma interpretação mais clara das transições eletrônicas, destacando as características das bandas espectrais.

O presente trabalho reforça que a escolha do método DFT depende intrinsecamente das particularidades do sistema e das propriedades alvo. Destaca a importância de testes preliminares para a escolha do nível DFT/TD-DFT na obtenção de resultados confiáveis e viáveis. Espera-se que este estudo seja um guia e um bom ponto de partida para a investigação de sistemas quimicamente parecidos.

 

MATERIAL SUPLEMENTAR

Detalhes dos cálculos, exemplos de inputs para: obtenção das geometrias (Figura 1S) e realização dos cálculos TD-DFT com os NTOs (Figura 2S), espectros de absorção eletrônica obtidos para o trans-AB (Figura 3S) e espectros de absorção eletrônica obtidos para o 3-FCAB (Figura 4S) (em formato PDF). Coordenadas xyz obtidas pelos cálculos de otimização descritos neste trabalho, para ambos os sistemas (em formato .XYZ) também são disponibilizados. Esse material está disponível em http://quimicanova.sbq.org.br/, com acesso livre.

 

DECLARAÇÃO DE DISPONIBILIDADE DE DADOS

Todos os dados estão disponíveis no texto e no Material Suplementar.

 

AGRADECIMENTOS

Os autores agradecem à Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP, processos: 2021/00675-4, 2022/12043-5, 2024/01971­4 e 2024/21701-1), à Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) - código de financiamento 001 e ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq).

 

REFERÊNCIAS

1. Brahim, H.; J. Lumin. 2019, 210, 96. [Crossref]

2. Zederkof, D. B.; Møller, K. B.; Nielsen, M. M.; Haldrup, K.; González, L.; Mai, S.; J. Am. Chem. Soc. 2022, 144, 12861. [Crossref]

3. Malme, J. T.; Clendening, R. A.; Ash, R.; Curry, T.; Ren, T.; Vura-Weis, J.; J. Am. Chem. Soc. 2023, 145, 6029. [Crossref]

4. Badran, H. M.; Eid, K. M.; Al-Nadary, H. O.; Ammar, H. Y.; Comput. Theor. Chem. 2023, 1226, 114215. [Crossref]

5. Mai, S.; González, L.; Angew. Chemie., Int. Ed. 2020, 59, 16832. [Crossref]

6. Daniel, C.; Coord. Chem. Rev. 2015, 282, 19. [Crossref]

7. Matute, R. A.; Contreras, R.; González, L.; J. Phys. Chem. Lett. 2010, 1, 796. [Crossref]

8. Huber, F. L.; Wernbacher, A. M.; Perleth, D.; Nauroozi, D.; González, L.; Rau, S.; Inorg. Chem. 2021, 60, 13299. [Crossref]

9. Wernbacher, A. M.; González, L.; Phys. Chem. Chem. Phys. 2021, 23, 17724. [Crossref]

10. Zobel, J. P.; Heindl, M.; Nogueira, J. J.; González, L.; J. Chem. Theory Comput. 2018, 14, 3205. [Crossref]

11. Mai, S.; Ashwood, B.; Marquetand, P.; Crespo-Hernández, C. E.; González, L.; J. Phys. Chem. B 2017, 121, 5187. [Crossref]

12. Penfold, T.; Rankine, C.; Eng, J. Em Comprehensive Inorganic Chemistry III; Reedijk, J.; Poeppelmeier, K. R., orgs.; Elsevier: Oxford, 2023, cap. 8.16.

13. Garino, C.; Salassa, L.; Philos. Trans. R. Soc., A 2013, 371, 20120134. [Crossref]

14. Herbert, J. M.; Phys. Chem. Chem. Phys. 2023, 26, 3755. [Crossref]

15. Zobel, J. P.; González, L.; JACS Au 2021, 1, 1116. [Crossref]

16. Custodio, R.; Morgon, N. H.; Quim. Nova 1995, 18, 44. [Link] acessado em junho 2025

17. Avagliano, D.; Skreta, M.; Arellano-Rubach, S.; Aspuru-Guzik, A.; Chem. Sci. 2024, 15, 4489. [Crossref]

18. Garino, C.; Terenzi, A.; Barone, G.; Salassa, L.; J. Chem. Educ. 2016, 93, 292. [Crossref]

19. Souza, J. R.; Curutchet, C.; Aoto, Y. A.; Homem-de-Mello, P.; J. Mol. Graphics Modell. 2023, 122, 108460. [Crossref]

20. Corrêa, R. L. G. Q.; de Moraes, M. M. F.; de Oliveira, K. T.; Aoto, Y. A.; Coutinho-Neto, M. D.; Homem-de-Mello, P.; J. Mol. Model. 2023, 29, 166. [Crossref]

21. Aoto, Y. A.; Batista, A. P. L.; Köhn, A.; de Oliveira Filho, A. G. S.; J. Chem. Theory Comput. 2017, 13, 5291. [Crossref]

22. Bursch, M.; Mewes, J.; Hansen, A.; Grimme, S.; Angew. Chem. 2022, 134, e202205735. [Crossref]

23. de Araújo, A. V. S.; Marques, L. R.; Borin, A. C.; Ando, R. A.; Phys. Chem. Chem. Phys. 2022, 24, 28522. [Crossref]

24. Dias, L. C.; Custodio, R.; Pessine, F. B. T.; Int. J. Quantum Chem. 2006, 106, 2624. [Crossref]

25. de Souza, K. F.; Martins, J. A.; Pessine, F. B. T.; Custodio, R.; Spectrochim. Acta, Part A 2010, 75, 901. [Crossref]

26. Fonseca, S.; dos Santos, N. S. S.; Georg, H. C.; Fonseca, T. L.; Provasi, P. F.; Coutinho, K.; Canuto, S.; da Cunha, A. R.; Gester, R.; ACS Omega 2024, 9, 40583. [Crossref]

27. Queiroz, M. H.; Santos, S. A.; Sampaio, B. S.; Alves, T. V.; Rivelino, R.; Spectrochim. Acta, Part A 2024, 320, 124637. [Crossref]

28. Das, D.; Roy, A.; Souza, C. P.; Mondal, S.; Sutradhar, S.; Sarkar, P.; Fantuzzi, F.; Ghosh, B. N.; J. Photochem. Photobiol., A 2025, 461, 116154. [Crossref]

29. Yilmaz, Y.; Mack, J.; Şener, M. K.; Sönmez, M.; Nyokong, T.; J. Photochem. Photobiol., A 2014, 277, 102. [Crossref]

30. Cooke, M. V.; Malvacio, I.; Peláez, W. J.; Pepino, A. J.; Mazzieri, M. R.; Argüello, G. A.; RSC Adv. 2015, 5, 26255. [Crossref]

31. Maschietto, F.; Campetella, M.; Sanz García, J.; Adamo, C.; Ciofini, I.; J. Chem. Phys. 2021, 154, 204102. [Crossref]

32. Jacquemin, D.; Mennucci, B.; Adamo, C.; Phys. Chem. Chem. Phys. 2011, 13, 16987. [Crossref]

33. Jacquemin, D.; Wathelet, V.; Perpète, E. A.; Adamo, C.; J. Chem. Theory Comput. 2009, 5, 2420. [Crossref]

34. Iron, M. A.; Janes, T.; J. Phys. Chem. A 2019, 123, 3761. [Crossref]

35. Wappett, D. A.; Goerigk, L.; J. Chem. Theory Comput. 2023, 19, 8365. [Crossref]

36. Zhao, C.; Wu, R.; Zhang, S.; Hong, X.; J. Phys. Chem. A 2023, 127, 6791. [Crossref]

37. Di Grande, S.; Barone, V.; J. Phys. Chem. A 2024, 128, 4886. [Crossref]

38. Minenkov, Y.; Singstad, Å.; Occhipinti, G.; Jensen, V. R.; Dalton Trans. 2012, 41, 5526. [Crossref]

39. Jacobsen, H.; Cavallo, L. Em Handbook of Computational Chemistry, 2^nd ed.; Springer International Publishing: Cham, 2017.

40. Fedele, C.; Ruoko, T. P.; Kuntze, K.; Virkki, M.; Priimagi, A.; Photochem. Photobiol. Sci. 2022, 21, 1719. [Crossref]

41. Jerca, F. A.; Jerca, V. V.; Hoogenboom, R.; Nat. Rev. Chem. 2022, 6, 51. [Crossref]

42. Rauf, U.; Shabir, G.; Bukhari, S.; Albericio, F.; Saeed, A.; Molecules 2023, 28, 5765. [Crossref]

43. Štěpnička, P.; Dalton Trans. 2022, 51, 8085. [Crossref]

44. Heinze, K.; Lang, H.; Organometallics 2013, 32, 5623. [Crossref]

45. Rölz, M.; Butschke, B.; Breit, B.; J. Am. Chem. Soc. 2024, 146, 13210. [Crossref]

46. Tylkowski, B.; Trojanowska, A.; Marturano, V.; Nowak, M.; Marciniak, L.; Giamberini, M.; Ambrogi, V.; Cerruti, P.; Coord. Chem. Rev. 2017, 351, 205. [Crossref]

47. Sakamoto, A.; Hirooka, A.; Namiki, K.; Kurihara, M.; Murata, M.; Sugimoto, M.; Nishihara, H.; Inorg. Chem. 2005, 44, 7547. [Crossref]

48. Sun, S.; Liang, S.; Xu, W. C.; Xu, G.; Wu, S.; Polym. Chem. 2019, 10, 4389. [Crossref]

49. Tagg, T.; Jamali, S. A. M.; Salleh, H.; Hegde, G.; Mol. Cryst. Liq. Cryst. 2014, 604, 142. [Crossref]

50. Li, G. L.; Liu, J. Q.; Zhao, B. D.; Wang, T.; Spectrochim. Acta, Part A 2013, 104, 287. [Crossref]

51. Custodio, R.; Quim. Nova 2015, 38, 995. [Crossref]

52. McArdle, S.; Endo, S.; Aspuru-Guzik, A.; Benjamin, S. C.; Yuan, X.; Rev. Mod. Phys. 2020, 92, 015003. [Crossref]

53. Fernández, I.; Cossío, F. P.; Chem. Soc. Rev. 2014, 43, 4906. [Crossref]

54. Hohenberg, P.; Kohn, W.; Phys. Rev. 1964, 136, B864. [Crossref]

55. Kohn, W.; Sham, L. J.; Phys. Rev. 1965, 140, A1133. [Crossref]

56. Mendes, R. A.; Haiduke, R. L. A.; Theor. Chem. Acc. 2021, 140, 146. [Crossref]

57. Fehér, P. P.; Stirling, A.; Chem.: Methods 2025, e202400071. [Crossref]

58. Petit, L.; Maldivi, P.; Adamo, C.; J. Chem. Theory Comput. 2005, 1, 953. [Crossref]

59. Latouche, C.; Skouteris, D.; Palazzetti, F.; Barone, V.; J. Chem. Theory Comput. 2015, 11, 3281. [Crossref]

60. Atkins, A. J.; Talotta, F.; Freitag, L.; Boggio-Pasqua, M.; González, L.; J. Chem. Theory Comput. 2017, 13, 4123. [Crossref]

61. Knepp, Z. J.; Repa, G. M.; Fredin, L. A.; Chem. Phys. Rev. 2025, 6, 021304. [Crossref]

62. Nagy, P. R.; Chem. Sci. 2024, 15, 14556. [Crossref]

63. Radoń, M.; Drabik, G.; Hodorowicz, M.; Szklarzewicz, J.; Chem. Sci. 2024, 15, 20189. [Crossref]

64. Batista, A. P. L.; de Oliveira Filho, A. G. S.; Galembeck, S. E.; Phys. Chem. Chem. Phys. 2017, 19, 13860. [Crossref]

65. Heil, A.; Kleinschmidt, M.; Marian, C. M.; J. Chem. Phys. 2018, 149, 164106. [Crossref]

66. Heil, A.; Kleinschmidt, M.; Marian, C. M.; J. Chem. Phys. 2019, 150, 164106. [Crossref]

67. Ferré, N.; Filatov, M.; Huix-Rotllant, M.; Density-Functional Methods for Excited States, 1^st ed.; Springer International Publishing: Cham, 2015.

68. González, L.; Escudero, D.; Serrano - Andrés, L.; ChemPhysChem 2012, 13, 28. [Crossref]

69. Lischka, H.; Nachtigallová, D.; Aquino, A. J. A.; Szalay, P. G.; Plasser, F.; Machado, F. B. C.; Barbatti, M.; Chem. Rev. 2018, 118, 7293. [Crossref]

70. Radoń, M.; Phys. Chem. Chem. Phys. 2023, 25, 30800. [Crossref]

71. Neugebauer, H.; Vuong, H. T.; Weber, J. L.; Friesner, R. A.; Shee, J.; Hansen, A.; J. Chem. Theory Comput. 2023, 19, 6208. [Crossref]

72. Knowles, P. J.; Werner, H. J.; Chem. Phys. Lett. 1985, 115, 259. [Crossref]

73. Werner, H. J.; Knowles, P. J.; J. Chem. Phys. 1985, 82, 5053. [Crossref]

74. Andersson, K.; Malmqvist, P. A.; Roos, B. O.; Sadlej, A. J.; Wolinski, K.; J. Phys. Chem. 1990, 94, 5483. [Crossref]

75. Andersson, K.; Malmqvist, P. A.; Roos, B. O.; J. Chem. Phys. 1992, 96, 1218. [Crossref]

76. Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J. P.; J. Chem. Phys. 2001, 114, 10252. [Crossref]

77. Angeli, C.; Cimiraglia, R.; Malrieu, J. P.; J. Chem. Phys. 2002, 117, 9138. [Crossref]

78. Pastore, M.; Angeli, C.; Cimiraglia, R.; Theor. Chem. Acc. 2007, 118, 35. [Crossref]

79. Li Manni, G.; Carlson, R. K.; Luo, S.; Ma, D.; Olsen, J.; Truhlar, D. G.; Gagliardi, L.; J. Chem. Theory Comput. 2014, 10, 3669. [Crossref]

80. Li Manni, G.; Carlson, R. K.; Luo, S.; Ma, D.; Olsen, J.; Truhlar, D. G.; Gagliardi, L.; J. Chem. Theory Comput. 2016, 12, 458. [Crossref]

81. Gagliardi, L.; Truhlar, D. G.; Li Manni, G.; Carlson, R. K.; Hoyer, C. E.; Bao, J. L.; Acc. Chem. Res. 2017, 50, 66. [Crossref]

82. Marques, M. A. L.; Oliveira, M. J. T.; Burnus, T.; Comput. Phys. Commun. 2012, 183, 2272. [Crossref]

83. Lehtola, S.; Steigemann, C.; Oliveira, M. J. T.; Marques, M. A. L.; SoftwareX 2018, 7, 1. [Crossref]

84. Jax_xc, https://jax-xc.readthedocs.io/en/latest/, acessado em julho 2025.

85. Perdew, J. P.; Schimidt, K.; AIP Conf. Proc. 2001, 577, 1. [Crossref]

86. Suo, B.; Shen, K.; Li, Z.; Liu, W.; J. Phys. Chem. A 2017, 121, 3929. [Crossref]

87. Li, J.; Lopez, S. A. Em Comprehensive Computational Chemistry; Yáñez, M.; Boyd, R. J., orgs.; Elsevier: Oxford, 2024, p. 658.

88. Vetráková, Ľ.; Ladányi, V.; Al Anshori, J.; Dvořák, P.; Wirz, J.; Heger, D.; Photochem. Photobiol. Sci. 2017, 16, 1749. [Crossref]

89. Brown, C. J.; Acta Crystallogr. 1966, 21, 146. [Crossref]

90. Hanwell, M. D.; Curtis, D. E.; Lonie, D. C.; Vandermeersch, T.; Zurek, E.; Hutchison, G. R.; J. Cheminf. 2012, 4, 17. [Crossref]

91. Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C.; J. Chem. Phys. 2020, 152, 224108. [Crossref]

92. Neese, F.; Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2022, 12, e1606. [Crossref]

93. Brémond, E.; Savarese, M.; Su, N. Q.; Pérez-Jiménez, A. J.; Xu, X.; Sancho-García, J. C.; Adamo, C.; J. Chem. Theory Comput. 2016, 12, 459. [Crossref]

94. Korth, M.; Grimme, S.; J. Chem. Theory Comput. 2009, 5, 993. [Crossref]

95. Quintal, M. M.; Karton, A.; Iron, M. A.; Boese, A. D.; Martin, J. M. L.; J. Phys. Chem. A 2006, 110, 709. [Crossref]

96. Havenridge, S.; Liu, C.; J. Phys. Chem. A 2024, 128, 3947. [Crossref]

97. Perdew, J. P.; Phys. Rev. B 1986, 33, 8822. [Crossref]

98. Becke, A. D.; Phys. Rev. A 1988, 38, 3098. [Crossref]

99. Ernzerhof, M.; Scuseria, G. E.; J. Chem. Phys. 1999, 110, 5029. [Crossref]

100. Yu, H. S.; He, X.; Truhlar, D. G.; J. Chem. Theory Comput. 2016, 12, 1280. [Crossref]

101. Zhao, Y.; Truhlar, D. G.; J. Chem. Phys. 2006, 125, 194101. [Crossref]

102. Becke, A. D.; J. Chem. Phys. 1993, 98, 5648. [Crossref]

103. Lee, C.; Yang, W.; Parr, R. G.; Phys. Rev. B 1988, 37, 785. [Crossref]

104. Adamo, C.; Barone, V.; J. Chem. Phys. 1999, 110, 6158. [Crossref]

105. Chai, J. D.; Head-Gordon, M.; J. Chem. Phys. 2008, 128, 084106. [Crossref]

106. Mardirossian, N.; Head-Gordon, M.; J. Chem. Theory Comput. 2013, 9, 4453. [Crossref]

107. Morgante, P.; Peverati, R.; Int. J. Quantum Chem. 2020, 120, e26332. [Crossref]

108. Mardirossian, N.; Head-Gordon, M.; Mol. Phys. 2017, 115, 2315. [Crossref]

109. Mardirossian, N.; Head-Gordon, M.; J. Chem. Theory Comput. 2016, 12, 4303. [Crossref]

110. Tran, F.; Hutter, J.; J. Chem. Phys. 2013, 138, 204103. [Crossref]

111. Grimme, S.; Ehrlich, S.; Goerigk, L.; J. Comput. Chem. 2011, 32, 1456. [Crossref]

112. Weigend, F.; Furche, F.; Ahlrichs, R.; J. Chem. Phys. 2003, 119, 12753. [Crossref]

113. Weigend, F.; Ahlrichs, R.; Phys. Chem. Chem. Phys. 2005, 7, 3297. [Crossref]

114. Weigend, F.; Phys. Chem. Chem. Phys. 2006, 8, 1057. [Crossref]

115. Xu, X.; Truhlar, D. G.; J. Chem. Theory Comput. 2011, 7, 2766. [Crossref]

116. Autschbach, J.; J. Chem. Phys. 2012, 136, 150902. [Crossref]

117. Brakestad, A.; Jensen, S. R.; Tantardini, C.; Pitteloud, Q.; Wind, P.; Užulis, J.; Gulans, A.; Hopmann, K. H.; Frediani, L.; J. Chem. Theory Comput. 2024, 20, 728. [Crossref]

118. Boychuk, B. T. A.; Wetmore, S. D.; J. Chem. Theory Comput. 2023, 19, 5273. [Crossref]

119. Yeo, C.; Nguyen, M.; Wang, L. P.; J. Phys. Chem. A 2022, 126, 7566. [Crossref]

120. Li, C.; Xie, H. B.; Chen, J.; Yang, X.; Zhang, Y.; Qiao, X.; Environ. Sci. Technol. 2014, 48, 13808. [Crossref]

121. Modee, R.; Laghuvarapu, S.; Priyakumar, U. D.; J. Comput. Chem. 2022, 43, 308. [Crossref]

122. Herráez, A.; Hanson, R. M.; Glasser, L.; J. Chem. Educ. 2009, 86, 566. [Crossref]

123. Marenich, A. V.; Cramer, C. J.; Truhlar, D. G.; J. Phys. Chem. B 2009, 113, 6378. [Crossref]

124. Zhang, J.; Zhang, H.; Wu, T.; Wang, Q.; Van Der Spoel, D.; J. Chem. Theory Comput. 2017, 13, 1034. [Crossref]

125. Tomasi, J.; Mennucci, B.; Cammi, R.; Chem. Rev. 2005, 105, 2999. [Crossref]

126. Barone, V.; Cossi, M.; J. Phys. Chem. A 1998, 102, 1995. [Crossref]

127. Gerlach, T.; Müller, S.; de Castilla, A. G.; Smirnova, I.; Fluid Phase Equilib. 2022, 560, 113472. [Crossref]

128. Handy, N. C.; Cohen, A. J.; Mol. Phys. 2001, 99, 403. [Crossref]

129. Yanai, T.; Tew, D. P.; Handy, N. C.; Chem. Phys. Lett. 2004, 393, 51. [Crossref]

130. Lednev, I. K.; Ye, T. Q.; Hester, R. E.; Moore, J. N.; J. Phys. Chem. 1996, 100, 13338. [Crossref]

131. Kurihara, M.; Hirooka, A.; Kume, S.; Sugimoto, M.; Nishihara, H.; J. Am. Chem. Soc. 2002, 124, 8800. [Crossref]

132. Olsen, S.; J. Phys. Chem. A 2012, 116, 1486. [Crossref]

133. Manian, A.; Russo, S. P.; Sci. Rep. 2022, 12, 21481. [Crossref]

134. Li, S. L.; Truhlar, D. G.; J. Chem. Theory Comput. 2017, 13, 2823. [Crossref]

135. Roy, P. P.; Kundu, S.; Makri, N.; Fleming, G. R.; J. Phys. Chem. Lett. 2022, 13, 7413. [Crossref]

136. Kundu, S.; Roy, P. P.; Fleming, G. R.; Makri, N.; J. Phys. Chem. B 2022, 126, 2899. [Crossref]

137. Herbert, J. M. Em Theoretical and Computational Photochemistry: Fundamentals, Methods, Applications and Synergy with Experimental Approaches; García-Iriepa, C.; Marazzi, M., orgs.; Elsevier: Amsterdã, Holanda, 2023, cap. 3.

138. Cuéllar-Zuquin, J.; Giussani, A.; Segarra-Martí, J. Em Theoretical and Computational Photochemistry: Fundamentals, Methods, Applications and Synergy with Experimental Approaches; García-Iriepa, C.; Marazzi, M., orgs.; Elsevier: Amsterdã, Holanda, 2023, cap. 17.

139. Martin, R. L.; J. Chem. Phys. 2003, 118, 4775. [Crossref]

140. Mayer, I.; Chem. Phys. Lett. 2007, 437, 284. [Crossref]

141. Plasser, F.; Wormit, M.; Dreuw, A.; J. Chem. Phys. 2014, 141, 024106. [Crossref]

142. Plasser, F.; Thomitzni, B.; Bäppler, S. A.; Wenzel, J.; Rehn, D. R.; Wormit, M.; Dreuw, A.; J. Comput. Chem. 2015, 36, 1609. [Crossref]

143. Höfener, S.; Klopper, W.; Chem. Phys. Lett. 2017, 679, 52. [Crossref]

144. Kasper, J. M.; Li, X.; J. Comput. Chem. 2020, 41, 1557. [Crossref]

145. Pederson, M. R.; Lin, C. C.; J. Chem. Phys. 1988, 88, 1807. [Crossref]

146. The PyMOL Molecular Graphics System, version 2.5.0; Schrödinger, LLC, New York, USA, 2021.

147. Bühl, M.; Kabrede, H.; J. Chem. Theory Comput. 2006, 2, 1282. [Crossref]

148. Goli, M.; Shahbazian, S.; J. Chem. Phys. 2022, 156, 044104. [Crossref]

149. Winter, N. O. C.; Graf, N. K.; Leutwyler, S.; Hättig, C.; Phys. Chem. Chem. Phys. 2013, 15, 6623. [Crossref]

150. van de Streek, J.; Neumann, M. A.; Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2014, 70, 1020. [Crossref]

151. Huenerbein, R.; Schirmer, B.; Moellmann, J.; Grimme, S.; Phys. Chem. Chem. Phys. 2010, 12, 6940. [Crossref]

152. Zhao, Y.; Truhlar, D. G.; Theor. Chem. Acc. 2008, 120, 215. [Crossref]

153. Zhao, Y.; Truhlar, D. G.; Theor. Chem. Acc. 2008, 119, 525. [Crossref]

154. Peverati, R.; Truhlar, D. G.; Phys. Chem. Chem. Phys. 2012, 14, 16187. [Crossref]

155. Goerigk, L.; Grimme, S.; Phys. Chem. Chem. Phys. 2011, 13, 6670. [Crossref]

156. Dohm, S.; Hansen, A.; Steinmetz, M.; Grimme, S.; Checinski, M. P.; J. Chem. Theory Comput. 2018, 14, 2596. [Crossref]

157. Maurer, L. R.; Bursch, M.; Grimme, S.; Hansen, A.; J. Chem. Theory Comput. 2021, 17, 6134. [Crossref]

158. Chai, J. D.; Head-Gordon, M.; Phys. Chem. Chem. Phys. 2008, 10, 6615. [Crossref]

159. Elmi, A.; Cockroft, S. L.; Acc. Chem. Res. 2021, 54, 92. [Crossref]

160. Sorenson, B. A.; Hong, S. S.; Herbol, H. C.; Clancy, P.; Comput. Mater. Sci. 2019, 170, 109138. [Crossref]

161. Lee, J.; Small, D. W.; Head-Gordon, M.; J. Chem. Phys. 2019, 151, 214103. [Crossref]

162. Plasser, F.; Ruckenbauer, M.; Mai, S.; Oppel, M.; Marquetand, P.; González, L.; J. Chem. Theory Comput. 2016, 12, 1207. [Crossref]

 

Editor responsável pelo artigo: Nelson H. Morgon