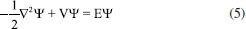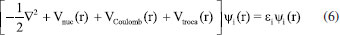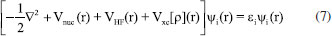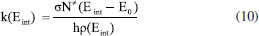Assuntos Gerais
|
|
| Desvendando reações e colisões: como a química quântica computacional assiste no entendimento das fragmentações na espectrometria de massas tandem por colisão Unveiling reactions and collisions: how computational quantum chemistry supports the understanding of collision-induced dissociation in tandem mass spectrometry |
|
Vinicius Kuchenbecker Instituto de Química, Universidade Estadual de Campinas, 13083-970 Campinas - SP, Brasil Recebido: 24/08/2025 *e-mail: vinicius.kuchenbecker@gmail.com; nhmorgon@unicamp.br Editora Associada responsável pelo artigo: Lucia Mascaro Tandem mass spectrometry (MS/MS) occupies a central position in experimental and analytical sciences, with collision-induced dissociation (CID) standing out as a fundamental technique for investigating molecular structures. In this process, molecular ions collide with a neutral gas, generating fragments that enable the elucidation of dissociation mechanisms. However, achieving a rational understanding of the collision phenomenon and its physicochemical implications - particularly the fragmentation channels and mechanisms - remains a theoretical challenge, especially when comparing models with experimental data obtained as a function of collision energy, as in energy-resolved mass spectrometry (ERMS). In this context, theories such as the transition state theory (TST) and the Rice-Ramsperger-Kassel-Marcus (RRKM) model have become well established for providing robust descriptions of the physicochemical processes involved in CID. The foundation of their success lies in the application of quantum mechanics, particularly computational quantum chemistry. This integration makes it possible to predict spectra, estimate energy-dependent intensities, and, above all, model dissociation channels and mechanisms and determine reaction rate constants. Thus, this work presents a synthesis of the contributions of quantum chemistry to the theory applied to CID, highlighting its essential role in advancing understanding and consolidating theoretical foundations for mass spectrometry. INTRODUÇÃO A espectrometria de massas é uma técnica analítica química que opera sob o princípio que moléculas eletricamente carregadas (íons) podem ser aceleradas em um campo eletromagnético. Diferentes moléculas com razão massa-carga terão diferentes tempo de voo ou desvio espacial na trajetória, por isso a técnica visa distinguir entre moléculas iônicas e seus fragmentos iônicos.1 Os primeiros espectrômetros de massas criados utilizavam um feixe de elétrons para colidir com a molécula analito de interesse e, dessa forma, ionizá-la e fragmentá-la. Esta técnica clássica é amplamente empregada para moléculas apolares e voláteis, sendo a espectrometria de massas por impacto de elétrons frequentemente acoplada à cromatografia gasosa. Todavia, outras formas de ionização surgiram e novas fontes foram projetadas, distanciando-se da padronizada fonte de impacto de elétrons. Enquanto a última é considerada uma técnica de ionização "forte", novas fontes de ionização "suave" são utilizadas principalmente para análise de moléculas polares e maiores, como carboidratos, peptídeos e proteínas, metabólitos, etc.1 Há uma pletora de fontes de ionização e uma das mais conhecidas é a interface de ionização por eletrospray (ESI, electrospray interface, no inglês). Também há diferentes formas de fragmentar o íon precursor na célula de fragmentação, desde colisão explícita com outras moléculas neutras ou reativas, colisão com superfície, fragmentação via fotodissociação ou infravermelho, captura ou transferência de elétrons, dentre outros.1 Uma das mais conhecidas é a dissociação induzida por colisão (CID).1-3 Na CID, o equipamento isola o íon precursor desejado na célula de colisão, fragmenta-o e analisa o espectro dos íons fragmentos. O design varia com o tipo de equipamento, como nos triplo-quadrupólos (QqQ) e Orbitraps.4,5 Esta técnica de dois estágios (geração e isolamento de íon precursor seguido de fragmentação) é chamada de espectrometria de massas tandem (EMT).3 Doravante, sempre que CID é mencionado implica em uma técnica EMT. A colisão do íon precursor com o gás neutro tem como foco reduzir sua energia cinética e aumentar a energia interna. Existem casos em que os íons são acelerados com energias da ordem de quiloelétron-volt (KeV), chamado de CID de alta energia, enquanto CID de baixa energia as colisões envolvem, no máximo, 100 eV de energia cinética. Em laboratórios de química, o último caso é mais comum do que CID de alta energia, geralmente usado somente em equipamentos de setor magnético.1 Além de gerar espectros de massa-carga, a EMT pode ser usada de forma a variar a energia de colisão (EC) e monitorar a intensidade de ambos íons moleculares e fragmentos. Esta técnica visa obter informação dinâmica da fragmentação em função da energia e é chamada de espectrometria de massas de energia resolvida (EMER).6,7 Aliado aos resultados da EMER, para obter-se informações importantes e confiáveis sobre a dinâmica reacional de fragmentação, é necessário o uso de físico-química teórica para modelar e predizer o comportamento reacional em uma célula de colisão.4 As teorias mais amplamente utilizadas para explicar as reações de dissociação são ambas fundamentadas na termodinâmica estatística: teoria do estado de transição (TET) e teoria de Rice-Ramsperger-Kassel-Marcus (RRKM).1,3 A primeira utiliza-se da modelagem de uma superfície de energia potencial (SEP), enfatizando a relação termodinâmica entre reagentes, produtos e a reação, enquanto a última utiliza-se do conceito de densidade de estados em função da energia interna e sua distribuição. Ambas são pautadas no fundamento do quasi-equilíbrio. Outras formas de modelar e entender fenômenos observados na CID são baseados em métodos não estatísticos, como dinâmica molecular.8 Em todas elas, a mecânica quântica, sobretudo o ramo chamado química quântica e também a química computacional desempenham papel central e fundamental. Comumente, a união de ambas é chamada de química quântica computacional (QQC). A mecânica quântica passou por anos e etapas de desenvolvimento de seu formalismo e rigor como teoria, especialmente dentro do contexto de interesse dos físicos no início do século XX em entender os átomos e moléculas, seus constituintes e comportamento destas entidades.9-11 Embora aplicada a vários sistemas, - como movimento de uma partícula em uma dimensão (partícula na caixa), osciladores harmônicos e não-harmônicos, partícula em movimento de anel, casca e rotor rígido, por fim chegando a descrição do átomo de hidrogênio - a equação de Schrödinger possui resolução analítica somente para sistemas monoeletrônicos. Para além de sistemas monoeletrônicos, Douglas R. Hartree12 foi um dos principais contribuintes para iniciar o desenvolvimento de métodos quânticos para sistemas multieletrônicos, introduzindo aproximações que ainda foram refinadas em formalismo e acurácia por Vladimir A. Fock,13 nos anos 1930, e estruturadas de forma que possibilitou sua excelente aplicação a diversos sistemas. Seu uso com computadores foi possível notoriamente devido às contribuições de Clemens C. J. Roothaan,14 nos anos 1950. Com isso, o primeiro método quântico usado na química (para moléculas) foi de Hartree-Fock-Roothaan, conhecido como HFR ou HF.10 Nesse contexto, a energia obtida ainda é consideravelmente afastada da energia exata, principalmente devido à negligência da correlação eletrônica, o que pode ser menos significativo em alguns resultados atômicos, mas costuma ser muito relevante em moléculas, especialmente porque essa diferença pode chegar à diferença energética de uma ligação química.11 Por isso, novos métodos foram sendo desenvolvidos a partir do método HF, chamados de pós-HF, com propósito de obter cada vez maior acurácia e menor custo computacional, que é elevado quanto maior o sistema em estudo. Estes métodos de estrutura eletrônica também são chamados de ab initio, ou primeiros princípios em Latim.11 Exemplos de métodos ab initio incluem teoria de perturbação Moller-Plesset de segunda ordem (MP2), método de configuração de interação (CI, do inglês), teoria de aglomerados acoplados, ou comumente conhecida em inglês como coupled cluster (CC), dentre outras. Estes métodos são comumente utilizados como referências teóricas de cálculos de propriedades de estrutura eletrônica, a depender do sistema. A maior contribuição destes é a recuperação da perda de energia de correlação eletrônica que ocorre nas aproximações impostas no método HF, e por isso são chamados de pós-HF. Todavia, são métodos que rapidamente escalam em custo computacional em função do tamanho do sistema estudado. Dentro desse escopo, a teoria do funcional de densidade (DFT, em inglês) foi desenvolvida. Tendo fatores comuns ao método HF, a diferença principal é o uso de funcionais para descrever aproximadamente interações eletrônicas e melhorar a descrição energética. Embora conceitualmente a DFT seja tão antiga quanto o desenvolvimento do método HF, a forma de Kohn-Sham,15 majoritariamente usada hoje, foi cunhada em meados de 1965, já no período do uso de computadores.9,16 A DFT pode ser descrita como uma teoria entre os métodos ab initio e os métodos semi-empíricos. Sua vantagem é trazer elementos formais da química quântica mantendo um custo-benefício computacional, de tal forma que a mesma se disseminou na química como um método "black-box" aplicado por muitos químicos em muitos problemas diversos.17 Todavia, a DFT requer um cuidado especial uma vez que sua formulação teórica depende da escolha da forma de um funcional de energia. Existe uma diversidade de funcionais de energia de correlação-troca disponíveis que podem ser utilizados. Os funcionais podem ser classificados em níveis de acordo com sua exatidão e rigor formal, como os chamados generalized-gradient-approximations (GGA), meta-GGA (mGGA), hybrids e double-hybrids. Os termos são mantidos em inglês devido a sua comum difusão na comunidade científica. A classificação em ordem supracitada ajuda a ter uma estimativa de nível de exatidão. Por exemplo, funcionais GGA e mGGA, como PBE e R2SCAN, não incluem nenhum termo de troca de Hartree-Fock, enquanto hybrids e double-hybrids, como B3LYP e ωB97X-D, possuem alguma porcentagem de termo de troca HF, o que contribui em muitos casos para melhor descrição da energia do sistema devido a introdução de termos de troca mais explícitos, i.e., não locais.17 O resultado disso é que se espera maior exatidão e precisão nos cálculos de B3LYP se comparado ao PBE, por exemplo. Apesar das classificações e tentativas de organizar os funcionais, na prática a performance pode variar dependendo dos sistemas estudados, mesmo dentro do mesmo nível de funcionais. A exemplo, embora o funcional ωB97X-D seja considerado bom para cálculos de energias e propriedades de ligação e espectroscopia, versões como ωB97XM-V, ωB97X-D4, ωB97X-V, etc., já foram propostas para obter maior custo-benefício e exatidão para certos sistemas, especialmente tratando-se de barreiras energéticas.17,18 Além da escolha de métodos DFT apropriados, a escolha do conjunto de funções de base utilizado para representar a função de onda do sistema (tanto em métodos ab initio como DFT) pode levar a impactos significativos nos resultados finais. Por exemplo, funcionais double-hybrids mencionados como bons para cálculo de propriedades, como frequência, na verdade não apresentam uma performance tão boa utilizando-se de uma base pequena, como as de duplo-ζ, se comparado ao mesmo método usando uma base triplo-ζ e isso pode ainda variar mais significativamente dependendo exatamente do sistema molecular estudado, com estruturas mais complexas ou não. Outros efeitos, como relativístico para átomos pesados (Z > 36) ou multi-referência para estruturas com espaçamento entre orbital ocupado de maior energia (HOMO, do inglês) e orbital não-ocupado de menor energia (LUMO, do inglês) também pode ser importantes e são considerados com mais detalhes em outros trabalhos.17-19 Utilização de parâmetros empíricos para melhor escrever interações de longa distância, como efeito de dispersão também existem e impactam significativamente para moléculas maiores. Para isso, correções como as de D3 e D4 de Grimme também são utilizadas junto aos métodos DFT, se necessárias.20,21 Por isso, grande parte da química computacional quântica está relacionada ao desenvolvimento de funcionais para o DFT, conjunto de funções de bases e outras correções visando criar métodos mais universais possíveis e com melhor relação custo-benefício computacional. No entanto, comumente trabalhos de modelagem molecular e QQC aplicam algum tipo de validação dos resultados de energia quando usam DFT, especialmente comparando-se com os resultados com os dos métodos pós-HF de maior nível, i.e., ab initio, que embora sejam computacionalmente muito caros, apresentam os resultados teóricos mais exatos.10,11 A química quântica empenha-se centralmente em modelar, i.e., descrever, e entender sistemas químicos usando o formalismo da teoria quântica, como propriedades de sistemas e, especialmente, mecanismos de reações e energias envolvidas nestes fenômenos. Devido ao tamanho dos sistemas de interesse químico, a dependência de métodos computacionais foi inevitável, levando ao surgimento da QQC. Por isso, no ano que se comemora o centésimo aniversário do desenvolvimento da Mecânica Quântica, este trabalho objetiva sumarizar de forma não exaustiva, mas conceitualmente didática as contribuições da QQC para o estudo teórico de reações que ocorrem via CID na espectrometria de massas, sobretudo no contexto da modelagem e cálculos envolvendo a elucidação dos mecanismos de reação. Um trabalho de referência, publicado por Vessecchi et al.,22 apresentou e discutiu de forma abrangente a aplicação da química quântica computacional aos processos químicos envolvidos na espectrometria de massas. Em continuidade a essa abordagem, o presente estudo tem como objetivo enfatizar o papel da química quântica computacional especificamente no contexto das teorias mais amplamente empregadas para descrever os mecanismos de fragmentação induzida por colisão - em particular, a teoria do estado de transição (TET) e a teoria de Rice-Ramsperger-Kassel-Marcus (RRKM) - além de incluir breves considerações sobre outros métodos teóricos correlatos. Apesar das revisões recentes23-26 abordarem o uso de métodos teóricos em espectrometria de massas, nenhuma examina sistematicamente a interseção entre a teoria da transição de elétrons (TET) e a teoria de Rice-Ramsperger-Kassel-Marcus (RRKM) como pilares conceituais fundamentados na química quântica aplicada à CID. Este artigo propõe uma abordagem integrativa, direcionada a não especialistas, que realça a conexão entre a modelagem teórica e os resultados experimentais em CID, com ênfase na união da química quântica com a compreensão teórica das reações de dissociação. Apesar do grande foco em predições de espectros na química analítica de forma prática, este estudo complementa a literatura existente ao estabelecer uma ponte explicativa entre duas teorias cruciais em estudos de dissociação, detalhando sua implementação com base em cálculos de química quântica e exemplificando suas aplicações em comparação aos métodos experimentais de energia resolvida. Para auxiliar na leitura do texto extensamente dependente de abreviações e significados, a Tabela 1 apresenta um sumário destas com explicações em contexto. Os detalhes quanto a cada item são providos ao longo do texto e algumas siglas que surgem com significado muito pontual no texto não foram incluídas.
ESPECTROMETRIA DE MASSAS TANDEM DE DISSOCIAÇÃO INDUZIDA POR COLISÃO O design de um equipamento de ionização soft tem como objetivo que, na interface/fonte, as moléculas sejam apenas ionizadas, permitindo, em seguida, sua aceleração e separação em um campo eletromagnético, de modo a determinar diferentes picos de razão massa-carga, denominados picos do íon precursor. Diferentemente da ionização por impacto de elétrons, não se espera que ocorra fragmentação do íon precursor na interface de ionização.1 A Figura 1 apresenta, de forma esquemática, o funcionamento geral de um equipamento de EMT.

Tipicamente, na CID, o precursor colide com um gás considerado inerte e de menor massa que a molécula, como argônio ou nitrogênio.1-3,27 Quando o íon deixa o acelerador (quadrupolo) e entra na célula de colisão, menos de 1% possui energia suficiente para fragmentar no tempo de análise, sendo denominados íons metaestáveis. Para aumentar tanto a quantidade de íons fragmentados quanto o número de canais de fragmentação, emprega-se a colisão com o gás neutro. Existem três principais modos de dissociação induzida por colisão (CID) de baixa energia: beam-type, trap-type e o mais recente, dissociação colisional de maior energia (higher-energy collisional dissociation, HCD). Este último, característico dos analisadores Orbitrap, combina elementos dos dois anteriores - é formalmente um sistema trap-type, mas opera com energia cinética semelhante à dos dispositivos beam-type.1 Essas variações estruturais refletem diferentes formas de deposição de energia e, consequentemente, distintos mecanismos de fragmentação. No modo beam-type, o íon precursor é acelerado por uma diferença de potencial elétrico e direcionado como um feixe contra o gás neutro da célula de colisão (geralmente argônio ou nitrogênio). Como não há aprisionamento do íon, a colisão ocorre em trajetória livre, resultando em fragmentação de maior energia. Nessa configuração, os fragmentos não passam por múltiplas colisões de resfriamento e podem continuar a se dissociar devido à energia interna remanescente. Por isso, o beam-type tende a gerar espectros mais ricos em fragmentos, envolvendo rotas de dissociação múltiplas, e não apenas a quebra das ligações mais fracas. Exemplos típicos de instrumentos beam-type incluem o triplo quadrupolo (QqQ) e o quadrupolo time-of-flight (qTOF).2 Em contraste, no modo trap-type, o íon precursor é primeiramente aprisionado na célula de colisão, onde sofre múltiplas colisões sucessivas com o gás neutro. Esse processo de "aquecimento e resfriamento" é controlado por excitação ressonante de radiofrequência (RF), cuja rampa crescente promove aumento gradual da energia interna média dos íons.1 A CID ocorre, portanto, de forma estatística e controlada, com redistribuição equilibrada de energia vibracional e, por consequência, fragmentação preferencial das ligações mais fracas. Diferentemente do beam-type, não é necessária uma diferença de potencial elevada, pois o ganho de energia cinética decorre da oscilação da RF na célula. O modo HCD, por sua vez, combina as vantagens dos dois anteriores: utiliza um sistema de retenção de íons semelhante ao trap-type, mas permite colisões de maior energia, comparáveis às do beam-type. Essa abordagem produz espectros mais extensos e detalhados, mantendo o controle energético característico das armadilhas de íons.4,28,29 Teoria de colisão, dissociação e a físico-química teórica da CID-BE Alguns equipamentos fornecem diretamente a energia cinética de colisão que está sendo empregada no experimento, chamado de energia cinética em regime de laboratório (ELab). Outros equipamentos fornecem o valor da diferença de potencial do acelerador, em volts, que pode ser convertido em energia cinética sabendo-se a carga do precursor e utilizando-se a relação ELab = qU, sendo U o potencial e q a carga.1 Pode-se calcular a energia máxima que pode ser convertida em energia interna em uma única colisão, chamada também de energia de centro de massa (ECdM) conforme a Equação 1, onde mg é a massa molar do gás de colisão, mp é a massa molar do íon precursor.
Levando-se em conta que mais de uma colisão pode acontecer, espera-se que a cada colisão uma quantidade discreta de energia cinética seja perdida. Além disso, nem toda energia cinética é convertida em energia interna quando o íon precursor colide com o gás neutro. Na verdade, alguns fatores como a inelasticidade (η) da colisão e mesmo a massa do gás neutro influenciam a colisão, e.g., hélio ou nitrogênio.2 A ECdM é amplamente utilizada em espectrometria de massas de energia resolvida (EMER) para obter-se curvas de rendimento de sobrevivência (do inglês, survival yield, SY), que em um primeiro momento servem para visualizar o comportamento das intensidades dos íons em função da energia de colisão (EC) de forma qualitativa, ou pseudo-quantitativa, como quando compara-se qual o valor de EC para reduzir 50% da intensidade de diferentes estruturas moleculares de íons precursores, chamado também de EC50. Por isso, em alguns trabalhos, utiliza-se intercambiavelmente ECdM e EC50, ainda que conceitualmente ambas não sejam exatamente a mesma.27 Especificamente, o SY é a forma mais adequada de estudar a relação da energia de colisão com as reações de dissociação que ocorrem em experimentos do tipo CID, sem necessitar modificar a estrutura física do equipamento. A Equação 2 define o SY em função das intensidades. Estas, por sua vez, dependem diretamente da energia de colisão, como realçado. Ip+(E) é a intensidade do íon precursor e If+(E) a intensidade do íon fragmento.
A Figura 2 mostra um exemplo genérico do formato de um gráfico de SY em função da CE.
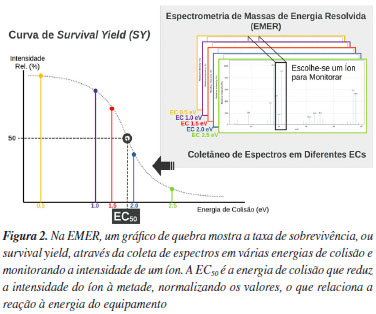
A energia interna real de íon precursor depende de outras variáveis e os modelos podem ficar tão complexos quanto necessário. Mais importante, porém, é notar que as descrições para o processo de CID requerem um tratamento estatístico, i.e., consideração da população de íons precursores que fragmentam. Por isso, parâmetros como tamanho da célula de colisão e tempo de ativação do íon podem influenciar significativamente o resultado de SY, i.e., equipamentos com células de colisão de diferentes tamanhos e tempo de permanência do íon irão impor condições energéticas de fragmentação diferentes e os valores de SY e EC50 serão diferentes mesmo para a mesma substância.1,27,30 Um estudo4 mostra que mesmo entre trap-type e HCD há uma diferença significativa da importância do tempo de ativação, uma vez que no trap-type o mesmo muda o espectro consideravelmente, enquanto no HCD não. Uma das principais explicações está no fato que o HCD não depende de um aumento gradual da energia cinética do precursor via ressonância, como ocorre na CID trap-type. Dado que energia e tempo de reação são fatores importantes para reações de dissociação, cada rota (ou canal) de reação de fragmentação tem uma constante de reação k associada. Especificamente, essa constante comumente é descrita em função da energia k(E) interna. Por isso, entender o processo físico-químico de reação de dissociação é importante. Ainda assim, também é necessário entender os aspectos físicos das colisões para obter-se modelos adequados para predizer espectros e quantidades características deles, como SY. A Equação 3, apresentada no trabalho de Kuki et al.,27 é um exemplo de modelo que prediz o SYi em função tanto de parâmetros físicos, como tempo de ativação τi para cada colisão i, da constante de reação dependente da energia interna k(Eint), uma propriedade intrínseca da reação unimolecular.
Quando o íon precursor colide com o gás, dois processos ocorrem, conforme sumarizado na Equação 4, em que AB+ é o íon precursor, N o gás de colisão, A a perda neutra, B+ o íon fragmento e [AB+] o complexo ativado. O primeiro e mais rápido de todos é a colisão direta (etapa 1), em que parte da energia cinética é transformada em energia interna, promovendo uma excitação do precursor, i.e., [AB+] e tem uma constante k1(E) associada. Essa etapa ocorre num regime de tempo de 10-14 a 10-16 segundos.2 A etapa 2 é a dissociação unimolecular do íon precursor ativado e o rendimento dessa reação de dissociação depende da natureza probabilística de dissociação do íon ativado, também tendo uma constante de reação k2(E) associada. O mecanismo desse processo de dois estágios está diretamente relacionado com as duas constantes de reação para cada etapa.1,2
Especialmente em trap-type, a suposição de que o equilíbrio ocorre, mostra-se coerente com os dados teóricos e empíricos. Uma das explicações é o modo de excitação dos íons precursores nesse tipo: multi colisões devido a radiofrequência. Todavia, no caso de beam-type e HCD, geralmente há um espectro rico em mais fragmentos. Diante do pressuposto do equilíbrio interno, a explicação é que maior energia cinética inicial favorece maior energia interna em menos tempo, possibilitando que rotas de fragmentação com barreiras energéticas maiores sejam acessadas antes da conclusão da análise. Porém, alguns sugerem que beam-type e HCD possam também gerar resultados fora do tratamento em equilíbrio energético. Assim, tanto a modelagem explícita das colisões como estatística da distribuição de energia e consequências reacionais são pontos importantes no entendimento teórico do processo de CID. Notoriamente, o ponto de partida teórico mais utilizado para dissociações unimoleculares incorpora conceitos intrínsecos da mecânica quântica.
MÉTODOS DE QUÍMICA QUÂNTICA APLICADOS A CID Cálculos ab initio e DFT em química reacional A Equação 5 é a equação de Schrödinger independente do tempo apresentada com seu hamiltoniano cinético e potencial em unidades atômicas, em que ψ é a função de onda dada em qualquer sistema de coordenadas necessários,
Para além dos sistemas monoeletrônicos, a equação de HF (Equação 6) é utilizada. Neste caso, ψi(r) é geralmente representada com um conjunto de bases combinadas linearmente, como por exemplo, funções gaussianas. Os termos Vnuc(r), VCoulomb(r) e Vtroca(r) são os potenciais de atração elétron-núcleo, repulsão elétron-elétron e de troca eletrônica, respectivamente.
Seguindo a mesma base teórica da Equação 6, a Equação 7 é conhecida como Equação de Kohn-Sham (KS). Nela, além do potencial que advém da equação de HF, VHF(r), um potencial dependente da densidade é adicionado, chamado de funcional de densidade, Vxc[ρ] (r). Esta é a equação base dos métodos de DFT, sendo que existem vários tipos de funcionais disponíveis.
Assim, quaisquer cálculos de química quântica envolvem, em linhas gerais e simplificadas, as equações de HF e KS, este último para a DFT. Implícito está o fato que todas foram derivadas a partir da equação de Schrödinger e esta, por sua vez, descreve a energia usando um hamiltoniano, advindo da mecânica hamiltoniana clássica.11 Isso significa que o uso da química quântica assume que, dentro das aproximações utilizadas, os métodos são cunhados visando englobar todas possíveis variações de energia (cinética e potencial), o que torna a QQC particularmente útil para casos onde o fenômeno é bem explicado em termos de variações de energia, como ocorre na CID em espectrometria de massas. Teoria do estado de transição (TET) A TET é discutivelmente a teoria quasi-equilíbrio mais importante em estudos de reações químicas, especialmente no contexto da cinética e mecanismo de reação. Pode ser vista como uma descrição estatística da dinâmica de reações químicas e comumente está associada a uma SEP. Foi introduzida na década de 1935 por Eyring, Evans e Polanyi pioneiramente como uma das primeiras tentativas de derivar a constante absoluta de reação k do ponto de vista térmico e, posteriormente, foi atrelada com a dinâmica do sistema por Wigner, que entendeu que a mesma descreve de forma estatística a dinâmica da reação química.31 Um princípio básico da TET é que reagentes estão em equilíbrio termodinâmico com o estado de transição. Para isso, também assume-se separação entre a descrição da dinâmica eletrônica e nuclear, em semelhança à aproximação de Born-Oppenheimer na mecânica quântica, e os estados são distribuídos de acordo com Maxwell-Boltzmann.31 A formulação da TET é mediante uso de coeficientes de partição, conforme Equação 8, mas pode ser formulada de forma termodinâmica, conforme Equação 9, visando facilitar sua aplicação. Na Equação 8, kb é a constante de Boltzmann, T a temperatura em Kelvin, Q#, QA e QB os coeficientes de partição do estado de transição, espécie A e B, respectivamente, h a constante de Planck e -E0 a energia de dissociação/crítica. Na Equação 9, ΔG#0 é a variação de energia de Gibbs de dissociação/crítica e ΔH#0 e ΔS#0 são a entalpia e entropia de dissociação, respectivamente.
Diretamente, não existe uma formulação da TET na mecânica quântica devido à incerteza da trajetória e momento, como prevê a incerteza descrita por Werner Heisenberg. Antes, o uso da mecânica quântica com TET está em sua acurácia e precisão para calcular entalpia ΔH#0, entropia ΔS#0 e energia de Gibbs ΔG#0, quantidades termodinâmicas que são utilizadas para calcular constantes de acordo com a TET.31 Qualitativamente, embora os coeficientes de partição translacionais, rotacionais e vibracionais não estejam explícitos na Equação 9, cálculos ab initio e de DFT podem ser consideravelmente exatos para prever informações termodinâmicas/energéticas sobre esses modos e, por isso, são usados comumente para aplicar a TET a sistemas de foram teórica. Embora dados termodinâmicos absolutos não possam ser derivados com precisão por este modelo, o uso da QQC permite modelar barreiras energéticas relativas entre reagentes, estado de transição e produtos, bem como a coordenada intrínseca de reação (CIR). A Figura 3 apresenta um gráfico de exemplo de corte transversal da SEP e mostra o "caminho" de reagentes para produtos passando pelo estado de transição, como pressuposto na TET. Assim, é possível comparar diferentes reações e estruturas do estado de transição de forma relativa, especialmente para reações de dissociação do tipo AB+ → A + B+, como ocorre em fragmentação CID.
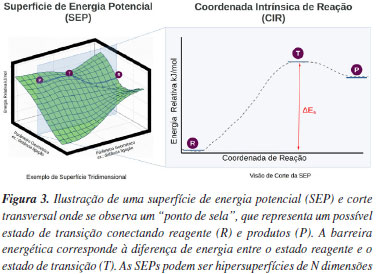
Existem trabalhos32-37 que têm explorado o uso da QQC, especialmente a DFT para modelar a SEP e, com isso, determinar quais são as barreiras energéticas, a CIR e, assim, propor teoricamente quais são os canais de fragmentação mais factíveis para as massas observadas em espectros experimentais de CID. O estudo apresentado por Cautereels et al.32 visou contribuir com a racionalização de uma controversa quanto ao mecanismo de formação do íon b2 do peptídeo Gln-His-Ser. Partindo das possibilidades de protonação de ligação amídica ou formação de íon b2 envolvendo reação entre histidina e cadeia lateral de imidazol num mecanismo de interação entre cadeias laterais, a investigação do mecanismo de reação levou à conclusão que o fragmento referente à m/z 266 é uma mistura de estruturas lactama e oxazolona formadas a partir da protonação do nitrogênio da amida, mostrando a utilidade de se modelar o mecanismo de reação em conjunto com dado experimental de CID. Utilizaram-se de DFT a nível B3LYP/6-311+G*. O trabalho de Mendonça et al.33 apresenta resultados empíricos de CID para o hormônio Juvenil III junto com uso de DFT M06-2X/6-311++G(d,p) para calcular energias de Gibbs para protômeros possíveis e propor canais de fragmentação com mecanismo provável, levando à conclusão que mesmo fragmentações na fonte podem ocorrer com este íon precursor. Ritacco et al.34 utilizaram B3LYP com conjunto de bases LANL2DZ para estudar os mecanismos e barreiras energéticas de fragmentação de complexos formados a base de carnosina-oxaliplatina protonada submetida a CID, racionalizando as menores barreiras e, assim, supondo os principais fragmentos formados. Mais recentemente, em 2025, Takayama et al.35 estudaram o mecanismo de reações de rearranjo de McLafferty em valerato de metila utilizando-se de cálculos teóricos, visando o que chamam de mapeamento global das rotas de reação. Embora os rearranjos de McLafferty sejam classicamente citados como um tipo de reação que ocorre na CID, utilizando-se de busca de estado de transição com HF/STO-3G, seguido de otimização das estruturas em equilíbrio com DFT restrito e irrestrito a nível M06-2X/6-31+G(d), os autores demonstraram que, levando-se em consideração os tempos de cada possível etapa de reação, é possível de forma teórica identificar um estado de transição não previamente reportado que potencialmente suporta que exista um rearranjo em duas etapas com a última etapa sendo a mais lenta, como pressuposto em outros trabalhos. Intrigantemente, outra rota identificada é uma reação totalmente concertada e sem estado de transição, evidenciando que ainda há lacunas no entendimento do mecanismo de reação deste clássico rearranjo, mas que os cálculos de química quântica apresentam-se essenciais na modelagem e compreensão desta reação. Os resultados foram comparados com dados experimentais de CID usando interface de ionização eletrospray. Outro estudo em 2024, publicado por Nguan et al.,36 interessantemente utilizou de dados experimentais de CID e cálculos teóricos para estudar diferentes mecanismos de anomerização de α e β-L-fucose cationizado com sódio. O protocolo inicia com escolha dos confórmeros mais relevantes, passando por otimização geométrica dos estados estacionários, busca de estados de transição usando o método nudge-elastic band (NEB) e otimização dos mesmos com final cálculo de coordenada intrínseca de reação. Os autores utilizam DFT tight binding de terceira ordem (DFTB3) a nível de teoria M06-2X/6-311+(d,p). Ao notarem a ordem de intensidade dos picos gerados pela fragmentação CID tanto para espécies α e β, comparando-se com os cálculos e modelagem teórica, os autores observaram que o perfil pode ser racionalizado por reações de desidratação e abertura de anel, sendo que a ligação entre O1-O2 é um dos principais fatores para a primeira reação, enquanto número de grupos -OH perto do O1 é essencial para entender a última. Essa racionalização permitiu traçar uma explicação na diferença de perfil de fragmentação experimental, observando-se que a barreira para desidratação da espécie α-fucose é menor do que para espécie β, por exemplo. Inspirados pela técnica de dissociação por ativação de elétron, Fabijanczuk et al.,37 reportaram não somente uma forma de caracterizar glicanos por CID, mas também um estudo de mecanismo de reação de dissociação induzida por radical. Experimentalmente utilizaram-se de rotulação isotópica de carbono. Todos cálculos de energia foram feitos a nível PBE0/def2-TZVPP e PW6B95/def2-TZVPP com correções de dispersão B3-BJ de Grimme. Os resultados indicam que existe uma cascata de reações radicalares envolvidas, incluindo abstração de hidrogênio, β-eliminação, migração de radical e abstração de hidreto. Todavia, a maior parte dos resultados pode ser explicada com uma etapa inicial e limitante de abstração de hidrogênio, o que foi corroborado pelos cálculos teóricos. A despeito destes exemplos, alguns dos trabalhos vão para além da TET e utilizam seus dados para cálculos cinéticos, empregando, por exemplo, a teoria RRKM, descrita na próxima seção. Os parâmetros termodinâmicos derivados da TET (servindo de base para o cálculo de ΔG e constantes kT) são diretamente utilizados como insumos para a formulação micro-canônica da RRKM, onde as densidades e somas de estados são computadas a partir dos modos vibracionais obtidos pelos cálculos ab initio. Teoria de Rice-Ramsperger-Kassel-Marcus (RRKM) Uma das teorias mais bem-sucedidas e empregadas para descrever e explicar a dissociação unimolecular em espectrometria de massas é a teoria de Rice-Ramsperger-Kassel-Marcus (RRKM) através do cálculo da constante de dissociação unimolecular (Equação 10), assumindo um regime quasi-equilíbrio, de tal forma que a mesma é associada a espectrometria de massas em via de definição oficial pela União de Química Pura e Aplicada (IUPAC, no inglês).
Na Equação 10, σ é a degenerência da coordenada de reação, N#(Eint - E0) é o total de estados do estado de transiçãoo, E0 é a energia crítica de dissociação, ρ(Eint) é a densidade de estados do reagente e, h a constante de Planck. A base da teoria RRKM é que a energia interna é distribuída na molécula de acordo com os modos internos vibracionais. Ou seja, a molécula toda é tratada como um conjunto de osciladores harmônicos. Algumas informações e aproximações chaves para esta teoria são:1,31 (i) Quanto maior a molécula, maiores as quantidades de modos normais/níveis de energias em que a energia pode ser distribuída. Portanto, o rendimento da colisão reduz quanto maior a molécula. (ii) A dissociação ocorre em um regime de tempo muito maior se comparado com a etapa de redistribuição da energia nos modos normais. (iii) A teoria é estatística: não se leva em conta que existam modos específicos de colisão de forma que haja diferentes constantes de reação. (iv) Os fragmentos gerados são produtos de uma série de reações competitivas e consecutivas. (v) Translação, rotação, vibração e movimentos eletrônicos são independentes. Assumindo estes princípios, a CID é considerada um processo ergódico de dissociação, em que a constante de reação depende somente da energia depositada mediante colisão enquanto a energia distribui-se de forma igualitária por todos os modos e as ligações mais fracas - de um ponto de vista que as ligações sejam descritas como um oscilador - são as que rompem. É importante notar como a teoria de RRKM é cunhada de forma clássica segundo os pressupostos da termodinâmica estatística para sistema micro-canônico. Todavia, Marcus incorporou aspectos da mecânica quântica ao introduzir os estados como conjunto de níveis de energia quantizados, como descrito pela mecânica quântica para um oscilador harmônico. Como o equilíbrio é assumido, neste modo as ligações rompidas são as mais fracas. Isto é, a energia interna vai aumentando e, de acordo com a teoria de RRKM, ocupando níveis de energia vibracional até que um nível seja suficiente para dissociação daquela ligação. O resultado é um espectro menos rico em fragmentos, e estes sendo geralmente oriundos da fragmentação das ligações mais fracas.1,3,31 Em outras palavras, pode-se explicar o espectro considerando-se as barreiras energéticas para todas possíveis reações de dissociação das ligações mais fracas (níveis de energia mais acessíveis). As menores barreiras são as reações favorecidas. Enquanto a formulação da TET é em termos de coeficiente de partição e, portanto, do equilíbrio térmico, a teoria RRKM é formulada no âmbito da distribuição de energia interna, centralizada da densidade de estados.1,31 Mais especificamente, enquanto a TET é uma teoria canônica (NVT), RRKM é a versão micro-canônica da TET que considera a energia distribuída fora do equilíbrio térmico. Por isso é mais amplamente referida para estudos de caráter quantitativo para CID. Porém, não são teorias competitivas. Antes, para obter-se valores para cálculos de constante via RRKM, invariavelmente é necessário propor e validar possíveis rotas de fragmentação e quais estados de transição envolvidos, o que é majoritariamente o foco da aplicação da TET em reações usando QQC. É por meio do cálculo das propriedades termodinâmicas, como energia de dissociação e as frequências de vibração obtidas pelas matrizes hessianas geradas nos cálculos de química quântica computacional, tanto para os estados estacionários como no ponto do estado de transição, que a constante de reação via teoria RRKM pode ser calculada. De fato, informações como densidades de estados do estado de transição só podem ser fornecidos por meio da apropriada modelagem via TET anterior a qualquer cálculo de constante reacional via RRKM. Colocando de outra forma, modelar erroneamente a coordenada intrínseca de reação, i.e., obter o estado de transição incorreto ou, mesmo que qualitativamente correto, utilizar-se de cálculos de barreira energética não apropriados podem levar a interpretações qualitativas de quais são os canais reacionais de forma muito diferente.38 Portanto, trabalhos teóricos com a teoria de RRKM são possíveis somente com coordenadas intrínsecas de reação, cálculos de barreira energética e frequências adequadamente calculadas, o que é essencialmente o núcleo da química quântica teórica no escopo da TET. Nos últimos anos, trabalhos foram publicados demonstrando como RRKM é utilizado para modelagem teórica de CID, de acordo com a filosofia já explicada anteriormente. Importante ressaltar que, embora para muitos exemplos a DFT tenha equivalentemente produzido bons resultados se comparado a métodos computacionalmente mais caros como em ab initio, no que concerne a RRKM, a DFT pode produzir resultados insatisfatórios se alguns pontos não forem considerados.39 Como a energia calculada em sistemas químicos quânticos pode muitas vezes ser extremamente dependente de correlação dinâmica e até estática - no último caso se for um sistema multi-referência - a escolha de um funcional/base apropriado exige cautela.10,17,18 De todos aspectos a serem considerados, o mais importante deve ser a performance do método para cálculo de energia. No caso da teoria RRKM, não basta apenas descrever apropriadamente os produtos e reagentes, que devem ser encontrados em um mínimo local na superfície de energia potencial, mas igualmente o estado de transição no ponto de sela, o que impacta diretamente o cálculo da barreira energética.38,40 Como reportado em outros trabalhos,18,38,40 especialmente para sistemas mais elaborados, a exatidão química exige incorporação apropriada de correlação dinâmica. Neste sentido, funcionais com algum mínimo de energia de troca explícita (HF) devem ser considerados, o que torna os hybrids e range separated double-hybrids fortemente recomendados. A exemplo já validado para muitos casos de estudos envolvendo energias com exatidão de barreiras energéticas são os funcionais ωB97M-V ou ωB97X-V.18 Não obstante, se o estado de transição tiver caráter multi-referência, mesmo os melhores funcionais levarão a resultados incorretos e métodos mais avançados devem ser necessários. Como as frequências são calculadas a partir da matriz hessiana, um método adequado para descrever energia deve implicar em aceitável exatidão nas frequências e outras propriedades oriundas da mesma, por consequência. Os trabalhos de Kuki et al.27,41 apresentam um estudo empírico e teórico usando teoria RRKM para avaliar a estabilidade de alguns poliéteres mediante CID, derivando-se a relação entre o aumento de graus de liberdade do sistema com a energia necessária para promover um perfil específico de SY.41 Utilizando-se o peptídeo leucina encefalina, uma molécula comumente usada para modelos teóricos em CID, criaram um modelo descritivo consideravelmente exato para calcular teoricamente a SY dos poliéteres com graus de liberdade semelhantes ao do peptídeo. Também compararam variações energéticas teóricas e empíricas entre trap-type e HCD.27 O trabalho de Ichou et al.4 também empregou uso de modelagem explícita do processo de CID com a teoria RRKM para comparar o comportamento de três peptídeos conhecidos como íons termômetros para estudos teóricos (massas 69, 228 e 420 m/z). Utilizaram-se dos dados obtidos da EMER, especialmente SY, tanto para trap-type quanto HCD para modelar e explicar o comportamento físico nos diferentes regimes de colisão/fragmentação. Já o trabalho de Asakawa et al.39 estudou a eficiência de fragmentação de fenetilaminas com fonte de ionização de eletrospray em CID usando-se a teoria de RRKM para calcular SY teórico. Este trabalho enfatiza o trabalho teórico necessário usando cálculos de DFT e ab initio para obter-se dados utilizáveis nos cálculos de RRKM. Primeiro utilizaram-se do método pós-Hartre-Fock (pós-HF) CCSD(T) com base cc-pVTZ e MP2(full) com base 6-311++G(d,p), junto com estes dados teóricos e experimentais compararam com alguns métodos de DFT, obtendo particularmente resultados considerados bons usando funcionais ωB97-XD, M06-2X-3D e funcionais duplo-híbridos recém desenvolvidos como PBE0 DH, DSD-PEBP86-D3(J) e PBE-QIDH. Enfatizou-se como os métodos pós-HF produziram os melhores resultados teóricos de SY, comparando-se com o experimental. O trabalho de Paizs e Suhai42 parte de resultados experimentais de CID para o peptídeo GGG protonado e mostra como teoricamente a isomerização cis-trans é possível, de forma que esse processo e sua barreira energética impactam como parte da energia recebida pelo íon precursor no processo de fragmentação é utilizada para este rearranjo molecular. Notoriamente, utilizaram de método HF/3-21G para vários escaneamentos de posição para determinar várias estruturas que depois foram otimizadas usando funcional B3LYP/6-31G(d), enfatizando a não necessidade do uso de métodos computacionalmente mais caros para obtenção de resultados aceitáveis, desde que dentro de um contexto de estudo dirigido com foco específico. Não foram calculados SY teóricos, por isso métodos teóricos mais simples foram considerados satisfatórios para demonstrar que as barreiras energéticas de isomerização são relevantes e não desprezíveis no mecanismo de dissociação. Martín-Sómer et al.43 realizaram exclusivamente um estudo exaustivo de quais eram os melhores funcionais para estudar a dissociação de formamida-M2+ (M = Ca, Sr) via CID utilizando-se da teoria de RRKM. Além das constantes de reação de acordo com a Equação 5, o trabalho também construiu um modelo para calcular a constante de reação considerando rotações externas via quase simetria de topo, mantendo as condições adiabáticas necessárias para utilização de RRKM. Reportaram que o funcional/base G96LYP/6-31G(d) é o que melhor reproduz a SEP e cinética obtida de métodos de alto nível (pós-HF). Observaram tendências semelhantes para ambos cátions, com mecanismo de explosão Coulômbica sendo um dos principais fatores para a dissociação dos duplo-cátions. O trabalho de Zima et al.44 apresentou um estudo da clivagem de anel de ribose em radicais catiônicos de adenosina e 2'-desoxiadenosina. Por meio de resultados de CID e fotodissociação por ultravioleta-visível (UV-Vis), reações de migração radicalar competitiva foram identificadas e modeladas. Através da identificação de estruturas de estado de transição usando CCSD(T)/6-311++G(3d,2p) e M06-2X/aug-cc-pVTZ, observou-se como a transferência de hidrogênio envolve primordialmente o 3'-H e nenhuma contribuição de 4'-H, isto é, não reativo. Usando cálculo de cinética de reação via RRKM, observou-se que a transferência de hidrogênio para o radical acetoxila é a etapa limitante da reação, enquanto a abertura dos anéis é rápida. Comparando-se ambas riboses, a 2'-desoxirribose apresentou barreira energética menor para clivagem do anel. Chalet et al.45 abordam um tema importante da EMT que é o uso de complexos não covalentes para analisar quiralidade usando espectrometria de massas, baseado no fato de que distinções enantioméricas podem ser realizadas devido a diferentes constantes de reação com cobre quaternário. Os dados são apresentados com cálculos a nível B3LYP/6-31G(d,p) e teoria RRKM. Ao realizarem EMER e compararem com a modelagem de reação de redução e de clivagem em baixo e alta energia de colisão, observaram que enantiosseletividade não é causada pela pronunciada redução nos complexos homoquirais, mas sim pela clivagem sendo favorecida nos complexos heteroquirais. Mais recentemente, Radnoff et al.46 realizaram um estudo do mecanismo de reação de dissociação via CID de espécies polifluor alquiladas. O trabalho utilizou de nível de teoria M06/6-311+G(d,p) e teoria RRKM. Os autores realizaram experimentos de EMER e modelaram as curvas SY para os íons mais abundantes. Todas moléculas polifluoradas apresentaram reações de perda de CO2, HF e CH2O. Qualitativamente, os resultados de SY estão de acordo com o esperado teoricamente via cálculos. Observaram que o maior número de hidrogênios presentes em espécies maiores levou a caminhos de reação competitivos. Como os resultados foram semelhantes aos já reportados para degradação térmica, os autores prospectam que estudos via CID podem ser úteis para entender a degradação térmica dessas moléculas altamente resistentes à degradação no meio ambiente. Outros trabalhos42,43,47-50 que envolvem o protocolo supracitado de modelagem molecular via TET seguido de cálculo de constante de reação por RRKM usando cálculos ab initio e DFT foram publicados e o leitor é convidado a buscá-los para verificar as diferentes conclusões. Porém, todos partem do fundamental uso da QQC para obter resultados comparáveis com dados experimentais até então não racionalizados, sobretudo de um ponto de vista cinético-químico. Todos estes trabalhos encaixam-se como exemplos de uso da TET para estudar mecanismos de fragmentação oriundos da CID usando QQC. Todavia, separamos especificamente estes para enfatizar o passo além da modelagem da SEP dentro do âmbito da cinética química teórica usando RRKM. Para além da ergodicidade: estudos não adiabáticos e dinâmica molecular ab initio (DMAI) Como explicado anteriormente, a ergodicidade da teoria RRKM assume que o equilíbrio de energia interna sempre é atingido antes da dissociação e que o modo que a colisão ocorre não tem significância no resultado final de canais de dissociação. Porém, alguns resultados mostram como o tratamento puramente estatístico em equilíbrio tanto na TET como RRKM podem falhar em descrever o resultado da fragmentação. Nestes casos, é necessário dar um passo além de cálculos teóricos e incluir simulações de colisão explícita, via dinâmica molecular. Como os modos vibracionais e eletrônicos continuam sendo importantes, a dinâmica molecular deve ser realizada também utilizando-se de cálculos de QQC. Partindo-se da separação do movimento nuclear e eletrônico (Born-Oppenheimer) é possível realizar estudos de dinâmica molecular ab initio (DMAI) ou também conhecida como dinâmicas Born-Oppenheimer.8,31,50 Simulação explícita de colisão é um tópico que, por si só, traz aspectos teóricos e computacionais próprios que merecem ser tratados em um texto à parte. No entanto, por envolver uso da QQC, seguem-se algumas menções sobre estudos de CID usando-se DMAI. É importante ressaltar a diferença de filosofia do uso, sendo que DMAI tem sido mais amplamente estudada como uma ferramenta in silico para predizer espectros, e menos para entender aspectos físico-químicos das reações.50 O trabalho já supracitado de Martín-Sómer et al.43 conclui que, utilizando-se TET e RRKM, incluindo termos adicionais como rotação externa, não foi possível explicar a relação entre algumas espécies, particularmente porque o produto [Sr(NH2)+]/[HCO]+ não aparece no espectro, embora predito pela teoria e concluem que teorias não-estatísticas são necessárias para entender a dinâmica de reação dos espectros dos duplo-cátions estudados. Utilizando não somente dados de CID, mas também de dissociação por incidência de multifótons de infravermelho e ressonância magnética nuclear, Ortiz et al.51 realizaram um estudo via DMAI com DFT para entender quais eram as estruturas dos fragmentos gerados e o mecanismo para eles. Com isso, identificaram que N-formilalanilamida fragmenta em íons b1, y1, a1 e imônio sob o mecanismo de mobilidade de próton, confirmando observações empíricas e teóricas prévias. Recentemente, Lee et al.8 publicaram um estudo detalhado usando DMAI e DFT para simular as colisões e reações de fragmentação, concluindo uma aceitável acurácia para moléculas menores, de forma que o aumento do tamanho do sistema levou a perda de acurácia. Já o programa QCxMS (anteriormente chamado QCEIMS) criado por Grimme e colaboradores50,52,53 tornou-se um exemplo importante de programa de predição e comparação de espectros de CID via DMAI. Uma versão nova chamada QCxMS254 foi recém-publicada, porém focada em uso de TET sem dinâmica molecular específica. Assim, a primeira versão permanece como uma referência exemplar de proposta de uso de DMAI. Utiliza-se de amostragem de várias posições e velocidades iniciais diferentes de colisão. Sua limitação também reside no tamanho do sistema, bem como na composição do mesmo: átomos muito pesados para além da segunda fileira da tabela periódica podem gerar resultados insatisfatórios. A viabilidade e as limitações desse programa têm sido evidenciadas à medida que novos estudos vêm sendo publicados com seu uso.
PERSPECTIVAS FUTURAS: SISTEMATIZAÇÃO, GENERALIZAÇÃO E INTELIGÊNCIA ARTIFICIAL Um dos desafios na aplicação do valor de EC50 obtido da EMER reside na não comparabilidade direta entre dados gerados por equipamentos distintos e configurações variadas.30 Conforme amplamente discutido em trabalhos anteriores,29,30,55 a implementação de técnicas de pré-processamento para mitigar vieses e variações é crucial. A padronização desses valores para futuras bibliotecas pode ser essencial para a consolidação da EMT em equipamentos comerciais, visando o entendimento da dinâmica energética das dissociações. Uma abordagem de pré-processamento para espectrometria é a construção de indicadores ou valores derivados de informações espectrais.55 Nesse sentido, a integração de cálculos teóricos com os resultados experimentais de EMER pode, futuramente, gerar novas informações mais diretamente comparáveis entre diferentes sistemas experimentais. Por exemplo, a identificação de características estruturais e energéticas comuns entre dados experimentais e teóricos pode fundamentar a criação de pseudo-taxonomias. Estas, por sua vez, auxiliariam na compreensão da relação entre o perfil energético obtido na EMER e o conjunto de características moleculares reais. Para tal, o papel das redes neurais artificiais e do machine learning será indispensável, dada a expectativa de grande volume de dados e a necessidade de identificação de padrões.55,56 Esta premissa torna-se cada vez mais plausível com o avanço dos computadores e algoritmos, que têm aprimorado a precisão dos cálculos e tornado a computação mais rotineira, mantendo um rigor teórico crescente. Assim, é expectável que o futuro reserve estudos focados na criação de vastas relações entre dados experimentais e teóricos de espectrometria de massas de colisão no âmbito energético, como no caso da EMER. Uma das principais barreiras a serem superadas nos estudos de EMER via CID, com o auxílio de cálculos teóricos, é a comparação direta entre a constante de dissociação em função da energia calculada via SY (derivada de dados experimentais) e a energia calculada via teoria. Fatores ainda não total e sistematicamente incorporados aos modelos e teorias, e que variam significativamente entre equipamentos, impedem um cálculo direto da energia de ligação a partir dos dados de dissociação via EMER. Portanto, a construção de bibliotecas de dados de dissociação, empregando teorias bem-sucedidas na área da CID, como a teoria RRKM, em conjunto com a inteligência artificial, pode representar um passo fundamental para o desenvolvimento de modelos e teorias modernas mais refinadas. Isso proporcionaria uma ponte mais sólida entre os dados de EMER e as reais energias de dissociação molecular esperadas. Assim, espera-se que os avanços recentes em machine learning, redes neurais artificiais e outros algoritmos, bem como os progressos no hardware e nas otimizações de cálculos de química quântica, sejam exaustiva e sistematicamente utilizados. O objetivo é o desenvolvimento de novos modelos e o aprimoramento das teorias vigentes, como TET e RRKM, para que a EMT se consolide, no futuro, como uma técnica confiável, acessível e padronizada para o cálculo e o entendimento das reações de dissociação em fase gasosa em função da energia.
CONCLUSÕES Este artigo oferece uma visão geral de como a dissociação induzida por colisão (CID), um processo crucial na espectrometria de massas tandem, pode ser investigada com o auxílio fundamental da química teórica e quântica computacional. Embora a espectrometria de massas de energia resolvida forneça informações relevantes sobre a dinâmica energética das reações de dissociação, a relação absoluta entre a energia de colisão medida em laboratório e as barreiras energéticas das reações químicas permanece um desafio contemporâneo. Teorias como a do estado de transição (TET) e a de Rice-Ramsperger-Kassel-Marcus (RRKM) são as abordagens teóricas predominantes e amplamente difundidas para o estudo da CID, ambas dependentes de cálculos de química quântica computacional (QQC). Conforme os resultados apresentados, tanto os métodos ab initio quanto os DFT são extensivamente empregados, com destaque para o último. Aspectos importantes da química quântica são essenciais para modelar e compreender as reações de CID, tais como a seleção de métodos e funções de base apropriados. Apesar do histórico de trabalhos dedicados a este tema, o desafio de correlacionar mecanismos teóricos de reação e dados experimentais de energia de dissociação ainda depende de novos avanços que, com o crescente aumento de ferramentas de inteligência artificial (IA), podem receber contribuições significativas no futuro. Novos pré-processamentos de dados experimentais de energia resolvida na CID e a criação sistemática de bibliotecas de dados reacionais teóricos baseados na química quântica, integrados por algoritmos de IA, podem impulsionar o avanço desejado na medição precisa e confiável das energias de dissociação químicas via espectrometria de massas, auxiliando a comunidade química a aprofundar a compreensão das reações químicas.
DECLARAÇÃO DE DISPONIBILIDADE DE DADOS Todos os dados utilizados estão disponíveis neste texto ou nas referências mencionadas.
AGRADECIMENTOS Agradecemos muito ao Instituto de Química da Unicamp e a Chemyunion Ltda. pelo direto suporte e encorajamento para o desenvolvimento deste trabalho, especialmente os pesquisadores desta última por acreditarem no potencial da união entre teoria e experimentação.
REFERÊNCIAS 1. de Hoffmann, E.; Mass Spectrometry: Principles and Applications, 3rd ed.; John Wiley & Sons: New York, 2013. 2. HÅkansson, K.; Klassen, J. S. Em Ion Activation Methods for Tandem Mass Spectrometry; Cole, R. B., ed.; John Wiley & Sons: Hoboken, 2010, cap. 16. [Crossref] 3. Sleno, L.; Volmer, D. A.; J. Mass Spectrom. 2004, 39, 1091. [Crossref] 4. Ichou, F.; Schwarzenberg, A.; Lesage, D.; Alves, S.; Junot, C.; Machuron-Mandard, X.; Tabet, J. C.; J. Mass Spectrom. 2014, 49, 498. [Crossref] 5. Crotti, A. E. M.; Vessecchi, R.; Lopes, J. L. C.; Lopes, N. P.; Quim. Nova 2006, 29, 287. [Crossref] 6. Carlo, M. J.; Nanney, A. L. M.; Patrick, A. L.; J. Am. Soc. Mass Spectrom. 2024, 35, 2631. [Crossref] 7. Maroto, A.; Dit Fouque, D. J.; Memboeuf, A.; J. Mass Spectrom. 2020, 55, e4478. [Crossref] 8. Lee, J.; Tantillo, D. J.; Wang, L. P.; Fiehn, O.; J. Chem. Inf. Model. 2024, 64, 7470. [Crossref] 9. Custodio, R.; Gomes, A. S.; Martins, L. R.; Revista Chemkeys 2018, 3, 1. [Crossref] 10. Castro, M. A.; Canuto, S. Em Métodos de Química Teórica e Modelagem Molecular; Morgon, N. H.; Coutinho, K., eds.; LF Editorial: São Paulo, 2007, cap. 1. 11. McQuarrie, D. A.; Simon, J. D.; Physical Chemistry: A Molecular Approach; University Science Books: Sausalito, 1997. 12. Hartree, D. R.; Math. Proc. Cambridge Philos. Soc. 1928, 24, 89. [Crossref] 13. Fock, V.; Z. Med. Phys. 1930, 61, 126. [Crossref] 14. Roothaan, C. C. J.; Rev. Mod. Phys. 1951, 23, 69. [Crossref] 15. Kohn, W.; Sham, L. J.; Phys. Rev. 1965, 140, A1133. [Crossref] 16. Morgon, N. H.; Quim. Nova 2001, 24, 676. [Crossref] 17. Bursch, M.; Mewes, J.; Hansen, A.; Grimme, S.; Angew. Chem. 2022, 134, e202205735. [Crossref] 18. Liu, X.; Spiekermann, K. A.; Menon, A.; Green, W. H.; Head-Gordon, M.; Phys. Chem. Chem. Phys. 2025, 27, 13326. [Crossref] 19. Jakubowska, K.; Pecul, M.; Ruud, K.; J. Phys. Chem. A 2021, 125, 10315. [Crossref] 20. Grimme, S.; Hansen, A.; Brandenburg, J. G.; Bannwarth, C.; Chem. Rev. 2016, 116, 5105. [Crossref] 21. Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S.; J. Chem. Phys. 2019, 150, 154122. [Crossref] 22. Vessecchi, R.; Galembeck, S. E.; Lopes, N. P.; Nascimento, P. G. B. D.; Crotti, A. E. M.; Quim. Nova 2008, 31, 840. [Crossref] 23. Wang, S.; Kind, T.; Tantillo, D. J.; Fiehn, O.; J. Cheminf. 2020, 12, 63. [Crossref] 24. Chakraborty, P.; Pradeep, T.; NPG Asia Mater. 2019, 11, 48. [Crossref] 25. Geue, N.; Winpenny, R. E. P.; Barran, P. E.; J. Am. Chem. Soc. 2024, 146, 8800. [Crossref] 26. Hecht, H.; Rojas, W. Y.; Ahmad, Z.; Křenek, A.; Klánová, J.; Price, E. J.; Anal. Chem. 2024, 96, 13652. [Crossref] 27. Kuki, A.; Shemirani, G.; Nagy, L.; Antal, B.; Zsuga, M.; Kéki, S.; J. Am. Soc. Mass Spectrom. 2013, 24, 1064. [Crossref] 28. Olsen, J. V.; Macek, B.; Lange, O.; Makarov, A.; Horning, S.; Mann, M.; Nat. Methods 2007, 4, 709. [Crossref] 29. Jora, M.; Burns, A. P.; Ross, R. L.; Lobue, P. A.; Zhao, R.; Palumbo, C. M.; Beal, P. A.; Addepalli, B.; Limbach, P. A.; J. Am. Soc. Mass Spectrom. 2018, 29, 1745. [Crossref] 30. Kertesz, T. M.; Hall, L. H.; Hill, D. W.; Grant, D. F.; J. Am. Soc. Mass Spectrom. 2009, 20, 1759. [Crossref] 31. Steinfeld, J. I.; Francisco, J. S.; Hase, W. L.; Chemical Kinetics and Dynamics; Prentice Hall: Upper Saddle River, 1999. 32. Cautereels, J.; Giribaldi, J.; Enjalbal, C.; Blockhuys, F.; Rapid Commun. Mass Spectrom. 2020, 34, e8778. [Crossref] 33. Mendonça, J.; Jabor, V.; Arini, G.; da Silva, R.; Vessecchi, R.; do Nascimento, F.; Lopes, N.; Quim. Nova 2024, 47, e-20230091. [Crossref] 34. Ritacco, I.; Moustafa, E. M.; Sicilia, E.; Russo, N.; Shoeib, T.; Dalton Trans. 2015, 44, 4455. [Crossref] 35. Takayama, M.; Hashimoto, M.; Ohshimo, K.; Misaizu, F.; Ubukata, M.; Nagatomo, K.; Phys. Chem. Chem. Phys. 2025, 27, 261. [Crossref] 36. Nguan, H. S.; Chen, J. L.; Ni, C. K.; J. Phys. Chem. A 2024, 128, 3812. [Crossref] 37. Fabijanczuk, K.; Yu, Z. J.; Bakestani, R. M.; Murtada, R.; Denton, N.; Gaspar, K.; Otegui, T.; Acosta, J.; Kenttämaa, H. I.; Eshuis, H.; Gao, J.; Anal. Chem. 2023, 95, 2932. [Crossref] 38. Shojaei, S. H. R.; Shiroudi, A.; Abdel-Rahman, M. A.; Heliyon 2022, 8, e11274. [Crossref] 39. Asakawa, D.; Sugiyama, E.; Mizuno, H.; Todoroki, K.; J. Am. Soc. Mass Spectrom. 2021, 32, 2144. [Crossref] 40. Huang, C.; Zhou, Z.; Yang, B.; Zhang, F.; Combust. Flame 2022, 242, 112189. [Crossref] 41. Kuki, A.; Nagy, L.; Shemirani, G.; Memboeuf, A.; Drahos, L.; Vékey, K.; Zsuga, M.; Kéki, S.; Rapid Commun. Mass Spectrom. 2012, 26, 304. [Crossref] 42. Paizs, B.; Suhai, S.; Rapid Commun. Mass Spectrom. 2001, 15, 2307. [Crossref] 43. Martín-Sómer, A.; Gaigeot, M. P.; Yáñez, M.; Spezia, R.; Phys. Chem. Chem. Phys. 2014, 16, 14813. [Crossref] 44. Zima, V.; Marek, A.; Tureček, F.; J. Phys. Chem. A 2024, 128, 1109. [Crossref] 45. Chalet, C.; Lesage, D.; Darii, E.; Perret, A.; Alves, S.; Gimbert, Y.; Tabet, J. C.; J. Am. Soc. Mass Spectrom. 2024, 35, 456. [Crossref] 46. Radnoff, A. S.; Charpentier‐St‐Pierre, S.; Mayer, P. M.; J. Mass Spectrom. 2025, 60, e5175. [Crossref] 47. Csonka, I. P.; Paizs, B.; Lendvay, G.; Suhai, S.; Rapid Commun. Mass Spectrom. 2001, 15, 1457. [Crossref] 48. Korany, M.; Ritacco, I.; Dabbish, E.; Sicilia, E.; Shoeib, T.; J. Chem. Inf. Model. 2022, 62, 4411. [Crossref] 49. Rezaee, M.; McNary, C. P.; Armentrout, P. B.; J. Chem. Phys. 2017, 147, 164308. [Crossref] 50. Koopman, J.; Grimme, S.; J. Am. Soc. Mass Spectrom. 2021, 32, 1735. [Crossref] 51. Ortiz, D.; Martin-Gago, P.; Riera, A.; Song, K.; Salpin, J. Y.; Spezia, R.; Int. J. Mass Spectrom. 2013, 335, 33. [Crossref] 52. Koopman, J.; Grimme, S.; ACS Omega 2019, 4, 15120. [Crossref] 53. Bauer, C. A.; Grimme, S.; J. Phys. Chem. A 2016, 120, 3755. [Crossref] 54. Gorges, J.; Grimme, S.; Phys. Chem. Chem. Phys. 2025, 27, 6899. [Crossref] 55. Beck, A. G.; Muhoberac, M.; Randolph, C. E.; Beveridge, C. H.; Wijewardhane, P. R.; Kenttämaa, H. I.; Chopra, G.; ACS Meas. Sci. Au 2024, 4, 233. [Crossref] 56. Chen, B.; Li, H.; Huang, R.; Tang, Y.; Li, F.; Nat. Commun. 2024, 15, 8396. [Crossref] |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access









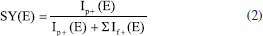

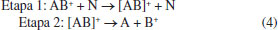
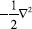 é o operador de energia cinética, sendo ∇ o operador laplaciano, V é o operador de energia potencial e E é a energia do sistema, o autovalor da equação. Para sistemas atômicos como hidrogênio, ψ é função de coordenadas polares ψ(r, θ, φ), podendo também ser representada por coordenadas cartesianas ψ (x, y, z). Além disso, pode-se mais rigorosamente incluir coordenadas de spin.
é o operador de energia cinética, sendo ∇ o operador laplaciano, V é o operador de energia potencial e E é a energia do sistema, o autovalor da equação. Para sistemas atômicos como hidrogênio, ψ é função de coordenadas polares ψ(r, θ, φ), podendo também ser representada por coordenadas cartesianas ψ (x, y, z). Além disso, pode-se mais rigorosamente incluir coordenadas de spin.