JBCS

INTRODUCTION

Oligothiophenes have been a prominent model for conducting polymers, all-organic field-effect transistor materials, and light-emitting devices because of their chemical/thermal stability, synthetic tailorability, solubility, processability, and relatively large carrier mobility.^1-9 However, the synthesis, reactivity as dienes in Diels-Alder reactions, and photochemical and electrochemical behavior of other thiophene-related molecules such as thiophene S,S-dioxide, and thiophene S-oxide have also been investigated.^10-20 The orbital energies and electrochemical properties of thiophene S-oxide monomers have been studied theoretically using MP2/6-31G^*.²¹ The bridging of thiophene derivatives to modulate the electronic band gaps has attracted interest of researchers at both experimental and theoretical levels.^22-32 More recently, in one of our research works the bridging phenomenon was extended to the study of structure, electronic, and thermodynamics properties of dithiophene S-oxide with X (X= S, S=O, O, SiH₂, and BH₂) as a bridge.³³

In this paper, the structural and electronic properties of α,α-ditert-butyl-4H-cyclopenta[2,1-b,3;4-b']dithiophene (DBDT) and α,α-ditert-butyl-4H-cyclopenta[2,1-b,3;4-b'] dithiophene S-oxide (DBDTO) derivatives were compared using a density functional theory method. The bridges used in this work are C=O, C=S, and CH_2, since it has been shown that the transport properties of the oligothiophene skeletons are highly sensitive to the nature of the skeletal functionalization.^34,35

COMPUTATIONAL METHOD

The equilibrium geometries of α,α-ditert-butyl-4H-cyclopenta [2,1-b,3;4-b']dithiophene and α,α-ditert-butyl-4H-cyclopenta[2,1-b,3;4-b']dithiophene S-oxide derivatives were fully optimized at DFT level of theory with a standard 6-311G^* basis set. The DFT calculations were carried out with a three-parameter B3LYP density functional, which includes Becke's gradient exchange correction and the Lee, Yang, Parr correlation functions.^36,37 The absorption transitions were calculated from the optimized geometry in the ground S₀ state by TD-DFT/6-311G^* theory. The solvation energy was calculated using the SM5.4 model based on semi-empirical wave functions.³⁸ The solvation energy is a sum of two terms: the energy required to create a "cavity" in the solvent (water) and the energy of electrostatic interactions between solvent and solute once the solute/molecule is "placed" in the cavity. The equilibrium geometries as well as spectra and any properties derived from the wave function are unaffected by the SM5.4 model for salvation energy calculations.³⁹ All calculations were performed by a Spartan 06 program implemented on an Intel Pentium M 2.0 GHz Computer.⁴⁰

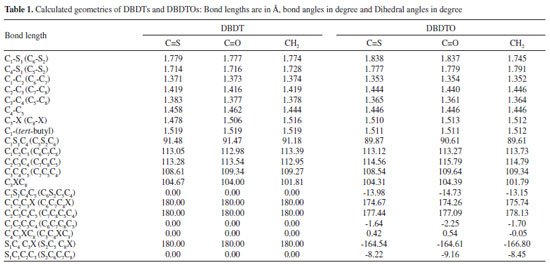
RESULTS AND DISCUSSION

Geometries

The selected geometries of the studied molecules shown in Figure 1 are listed in Table 1. The calculated bond lengths for DBDTs and DBDTOs are slightly different. For instance, the average C₁-S₁ (C₄-S₁) bond lengths are 1.765 Å and 1.807 Å for DBDT and DBDTO respectively; thus, C₁-S₁ (C₄-S₁) bond lengths in DBDTs are shorter by 0.042 Å. However, C₁-C₂ bonds are shorter in DBDTOs by ≈ 0.02 Å. Therefore, the shortening of terminal C₁=C₂ and C₆=C₇ bonds in the ϖ-center of DBDTO compared to DBDT analogues should lead to a higher vibrational frequency of terminal C=C bonds in DBDTO.^32,33

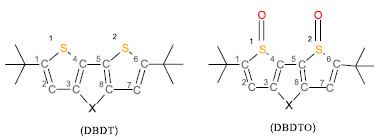Figure 1. The structure and atomic numbering of α,α-ditert-butyl-4H-cyclopenta[2,1-b,3;4-b']dithiophene (DBDT) and α,α-ditert-butyl-4H-cyclopenta[2,1-b,3;4-b']dithiophene S-oxide (DBDTO) ; X=CH2, C=S and
C=O

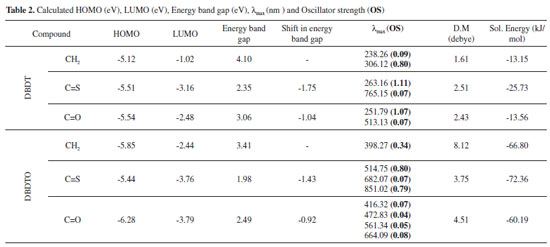
Considering the DBDT series, C₁-S₁ (C₄-S₁) bond lengths are 1.779 Å (1.714 Å) for C=S bridged, 1.777 Å (1.716 Å) for C=O bridged, and 1.774 Å (1.728 Å) for CH₂ bridged, but in DBDTOs they are 1.838 Å (1.777 Å) for C=S bridged, 1.837 Å (1.779 Å) for C=O bridged, and 1.745 Å (1.791 Å) for CH₂ bridged. Furthermore, C₃-X bond lengths are 1.478 Å, 1.506 Å, and 1.516 Å for DBDT with C=S, C=O, and CH₂ bridges, respectively. In DBDTO, C₃-X bond lengths are 1.510 Å, 1.513 Å, and 1.512 Å for C=S, C=O, and CH₂ bridges, respectively. The bond angles and torsion angles are less affected by the bridged groups in each series (Table 1).

The bond angles calculated for both series are similar. The only significant difference is in the C₂C₃C₄ and C-S-C bond angles. The molecular structures of DBDTs are more planar than the corresponding DBDTOs, as revealed by dihedral angles, and this is caused by the out of plane projection of the two sulphoxide oxygen atoms.

Frontier molecular orbitals

The HOMO, LUMO, and band gaps are listed in Table 2. DBDT and DBDTO with a C=S bridge presented the lowest band gap. There is destabilization of both the HOMO and LUMO, which leads to a reduction in the band gap in DBDTs and DBDTOs with C=S and C=O bridges. The HOMOs in DBDTs with C=S and C=O bridges are destabilized by 1.75 eV and 1.04 eV, and 1.43 eV and 0.92 eV for DBDTOs, respectively, compared to CH₂ bridges. The band gaps for DBDTs are 2.35, 3.06, and 4.10 eV with C=S, C=O, and CH₂ bridges, respectively. For DBDTOs, the band gaps are 1.98, 2.49, and 3.41 eV with C=S, C=O, and CH₂ bridges, respectively. Generally, the HOMOs of C=C units are π-bonding and have an alternating phase with respect to their neighboring C=C units; the LUMOs of C=C units are π-antibonding in both the DBDT and DBDTO series. The bridged group, C1/C6 carbon atoms, and sulfur atoms contributed to the LUMO map in DBDTs, but in DBDTOs, the oxygen atom of sulphoxide, not sulfur, contributed to the LUMO maps (Figure 2). The contribution of the bridged group is pronounced in molecules with C=O and C=S bridges. Thus, C=O and C=S groups have the ability to withdraw electrons from thiophene/thiophene oxide rings, which brings about destabilization of both the HOMO and LUMO.

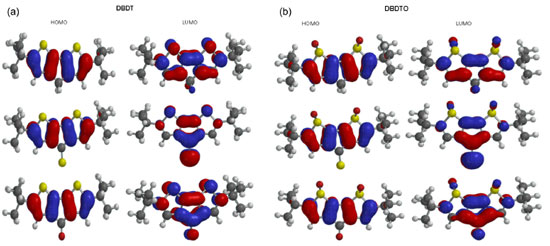Figure 2. (a) The contour plots of HOMO and LUMO orbitals of DBDT series. (b) The contour plots of HOMO and LUMO orbitals of DBDTO series

To gain insight into the molecular energy levels of the studied molecules, the molecular orbital energy levels of DBDTs and DBDTOs, which each consist of seven HOMOs and seven LUMOs, are displayed in Figure 3. In DBDT for a C=S bridge, the HOMO-4, HOMO-5, and HOMO-6 energies are very close, i.e., -8.99 eV, -9.09 eV, and -9.11 eV, respectively. For the C=O bridge, HOMO-5 and HOMO-6 are -9.10 eV and -9.11 eV, respectively. However, for a CH₂ bridge, these are two sets of HOMO energies that are very close, HOMO-1 and HOMO-2 with -6.65 eV and -6.81 eV and HOMO-4 and HOMO-5 with -8.77 eV and -8.78 eV, respectively. Also, LUMO+3 and LUMO+4 energies are very close in CH₂ bridged molecules.

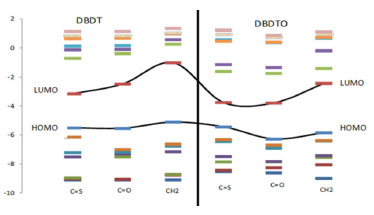Figure 3. Partial molecular orbital energy diagram for DBDT and DBDTO series as calculated with the B3LYP/6-311G^* method

In the DBDTO series, HOMO-5, HOMO-6, LUMO+3, and LUMO+4 are -8.45 eV, -8.56 eV, 0.95 eV, and 0.96 eV, respectively, for C=S bridges. HOMO-3, HOMO-4, LUMO+3, and LUMO+4 are -7.84 eV, -7.88 eV, 0.36 eV, and 0.40 eV for C=O bridges, respectively. For CH₂ bridges, HOMO-1, HOMO-2, HOMO-3, and HOMO-4 are -6.40 eV, -6.44 eV, -7.44 eV, and -7.57 eV, respectively. The LUMO+5 and LUMO+6 energies are close in CH₂ bridges. Since the molecular orbital spacings are not similar, different levels of electronic interactions are expected in the molecules. Therefore, DBDTOs could have more complex electronic interactions because of the presence of more atoms with lone pairs of electrons. This is in agreement with the UV-visible absorption spectra of C=S and C=O bridged molecules that have three absorption peaks (Table 2). The dipole moment and solvation energy of a molecule are also important properties when considering the interactions of molecules in solvents. The higher the value of the dipole moment and solvation energy, the stronger the intermolecular interactions should be. Thus, DBDTOs are expected to have stronger solvent-solute interactions than the corresponding DBDTs, but the orientation of the dipole moment vector is also an important parameter to be considered in solute-solvent interactions.

The UV-visible absorptions calculated at TD-DFT/6-311G^* show two absorption peaks for all the molecules except C=S and C=O bridged DBDTO, which have three and four absorption peaks, respectively. The absorption λ_max for CH₂ bridged are 238.26 nm and 306.12 nm for DBDT and 398.27 nm for DBDTO. In DBDT, the absorption λ_max are 263.16 nm and 765.15 nm for C=S bridged and 251.79 nm and 513.13 nm for C=O bridged. However, in DBDTO the absorption λ_max for C=S bridged are 514.75, 682.07, and 851.02 nm, and 416.32, 472.83, 561.24, and 664.09 nm for C=O bridged. In each series, there is a bathochromic (red) shift for C=O and C=S bridges, which is attributed to the electron-withdrawing effect of the bridged groups compared to a CH₂ bridge. Oscillation strength values, which present the probability of electron transitions as a function of the fraction of negative charges (electrons), accomplish the transition in question (oscillate) and revealed that the probability of electron transition would be higher in DBDTs than DBDTOs (Table 2).

In general, the DBDTO presented lower band gaps and longer wavelengths than the corresponding DBDT. In each series, molecules with a C=S bridge could be potential candidates as materials for opto-electronic applications in terms of band gap and wavelength.

Selected vibrational frequencies for DBDT and DBDTO derivatives

Vibrational spectroscopy is a powerful method extensively used in organic chemistry to identify functional groups of organic compounds, and it has been used to distinguish molecular conformers, tautomers, and isomers.⁴¹ Comparison of the experimental and theoretical vibration modes with proper assignments is helpful for understanding a fairly complex system. However in the absence of experimental data, calculated vibrational frequencies could be used with a reasonable degree of accuracy to understand the properties of molecules and to study the effect of functional groups on molecules. The accuracy of calculated vibrational frequencies is improved by using a scale factor. Therefore, scale factors have been recommended for more accurate predictions, and 0.9682 was used as a scale factor in this work.^42,43 The C=C vibrational frequencies and simulated spectra calculated at B3LYP/6-311G^* are presented in Table 3 and Figure 4, respectively, to study the effect of bridged groups on both DBDT and DBDTO. The prominent DBDT terminal C=C stretching bands (i.e., C₁ = C₂/C₆ = C₇) are 1554 and 1548 cm^-1 for C=O bridge, 1554 and 1546 cm^-1 for C=S bridge, and 1564 and 1558 cm^-1 for CH₂ bridge. These stretching bands experienced an up-shift in the DBDTO analogues. The terminal C=C stretching modes for the rings in the dithiophene derivatives and Raman-active (C=C) stretch mode in the oligoene were used to establish a structure-property relationship for the compounds.^32,33,44 In this paper, it was found that the terminal C=C stretching modes of both DBDT and DBDTO molecules correlated with the λ_max in the UV-visible absorption spectrum. The higher the terminal stretch mode, the lower the value of λ_max, i.e., 1586 cm^-1 (C=S, λ_max = 851.02 nm) → 1598 cm^-1 (C=O, λ_max = 664.08 nm) → 1614 cm^-1 (CH₂, λ_max = 398.27 nm) in DBDTO and 1546 cm^-1 (C=S, λ_max = 765.15 nm) → 1548 cm^-1 (C=O, λ_max = 513.13 nm) → 1558 cm^-1 (CH₂, λ_max = 306.12 nm) in DBDT.

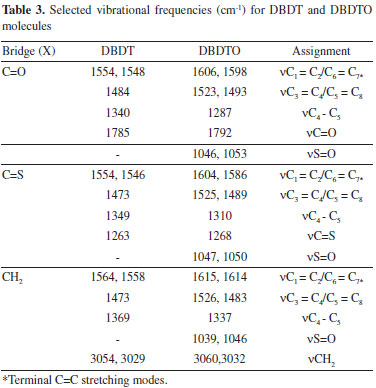
Figure 4. Simulated IR spectra for DBDT and DBDTO derivatives at B3LYP/6-31G^* level

The C₃ = C₄/C₅ = C₈ stretching bands are 1484, 1472, and 1473 cm^-1 for C=O, C=S, and CH₂ bridges, respectively, in DBDT. These bands are up-shifted and split into two components in DBDTO derivatives at 1523 and 1493 cm^-1 for C=O bridges, 1525 and 1489 cm^-1 for C=S bridges, and 1526 and 1483 cm^-1 for CH₂ bridges (Table 3). This has been attributed to a typical indicator of the attainment of a heteroquinonoid-like pattern for the ϖ-conjugated path.⁴⁵ The C₄-C₅ stretching bands are 1340, 1349, and 1369 cm^-1 for C=O, C=S, and CH₂ bridges, respectively, in DBDT. In DBDTO, these bands are 1287, 1310, and 1337 cm^-1 for C=O, C=S, and CH₂ bridges, respectively. Therefore, C₄-C₅ stretching bands experienced a down-shift in DBDTO derivatives. The stretching vibrations of C=O and C=S bridge groups are 1785 and 1263 cm^-1 in DBDT and 1792 and 1268 cm^-1 in DBDTO, respectively. For CH₂ bridges, they are 3054 and 3029 cm^-1 in DBDT and 3060 and 3032 cm^-1 in DBDTO.

Molecular electrostatic potential (MEP)

The electrostatic potential V(r) shows static distributions of charge on a molecule. This has been a very useful property for analyzing and predicting molecular reactive behavior to indicate sites or regions of a molecule where an approaching electrophile/nucleophile is initially attracted. It has also been successfully used to explain the three-dimensional orientation of molecules in a crystal. The MEP was calculated at a B3LYP/6-311G^* optimized geometry to predict reactive sites for electrophilic and nucleophilic attack for the DBDTs and DBTOs studied. The positive regions (blue) of MEP are related to nucleophilic reactivity and the negative regions (red) to electrophilic reactivity, shown in Figure 5. The MEP of DBDT and DBDTO with CH₂ bridges is displayed in Figures 5a and 5b, respectively, as a representation of both the DBDT and DBDTO series. The MEP values for DBDT-CH₂ are ranged from + 80.277 to -84.228 kJ/mol, and the negative regions are on the rings' surface. Therefore, the π-π stacking arrangement of DBDT-CH₂ molecules would be perpendicular (≈ 90º) to the main planes of the adjacent molecule. The MEP values for DBDTO-CH₂ are in the range of + 136.143 to -233.807 kJ/mol, and the negative regions are on the two oxygen atoms of sulphoxide in the bridged thiophene S oxide. This suggests that the π-π stacking arrangement of DBDTO-CH₂ should tend towards 0º. The distortions of π-π stacking from perpendicular in DBDT and lateral in DBDTO molecules are expected because of steric hindrance from the t-butyl substituent. The out of plane projection of two oxygen atoms of sulphoxides in DBDTO may further affect the intermolecular π-π stacking through the space between neighboring molecules.

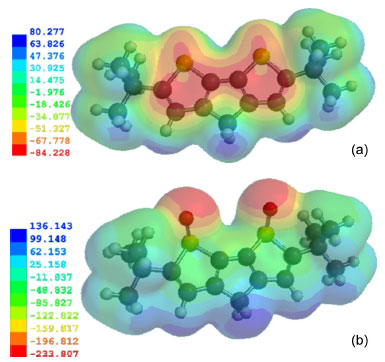Figure 5. Molecular electrostatic potential energy (kJ/mol) map calculated at B3LYP/6-311G^* level: (a) = DBDT-CH₂ and (b) = DBDTO-CH₂

Thermodynamic properties

The standard heats of formation (Hº_f) calculated at 298 K and 1 atm using PM3 method are 82.33, 13.35, and 36.51 kcal/mol for DBDT with C=S, C=O, and CH₂ bridges, respectively. However, this calculated values for DBDTO are 56.18, -13.14, and 5.66 kcal/mol with C=S, C=O, and CH₂ bridges, respectively. The standard enthalpy (H_mº), Gibb's free energy (G_mº), and entropy (S_mº) calculated at 298 K and 1 atm using B3LYP/6-311G^* for DBDT and DBDTO with a C=S bridge are 217.30 kcal/mol, 147.98 kcal/mol, and 173.17 J/mol for DBDT and 222.47 kcal/mol, 163.54 kcal/mol, and 173.70 J/mol for DBDTO, respectively.

CONCLUSION

B3LYP/6-311G^* has been used to study the geometries and electronic properties of α,α-ditert-butyl-4H-cyclopenta[2,1-b,3;4-b']dithiophene and α,α-ditert-butyl-4H-cyclopenta[2,1-b,3;4-b']dithiophene S-oxide with CH₂, C=S, and C=O bridges. The results reveal that the bond angles calculated for both DBDT and DBDTO series are similar except for the C₂C₃C₄ and C-S-C bond angles, which are larger and smaller, respectively, in the DBDTO series. The electron-withdrawing bridge (C=S and C=O) destabilized the HOMO and LUMO levels, which lead to a lowering of the band gap. In each series, molecules with a C=S bridge presented the lowest band gaps and longest wavelengths, and they were better candidates for optoelectronic applications. The DBDTOs are expected to have stronger solvent-solute interactions than the corresponding DBDT series.

REFERENCES

1. Tourillon, G. In Handbook of Conducting Polymers, vol. 1; Skotheim, T.A., ed.; Dekker, Inc.: New York, 1986, p. 293; Baeuerle, P. In The Oligomeric Approach; Wegner, G. Muellen, K., eds.; Wiley-VCH, Weinheim, 1998, p. 105.

2. Garnier, F.; Horowitz, G.; Fichou, D.; Yassar, A.; Synth. Met. 1996, 81, 163.

3. Li, X.-C.; Siringhaus, H.; Garnier, F.; Holmes, A. B.; Moratti, S. C.; Feeder, N.; Clegg, W.; Teat, S. J.; Friend R. H.; J. Am. Chem. Soc. 1998, 120, 2206.

4. Geiger, F.; Stoldt, M.; Baeuerle, P.; Scheizer, H. Umbach, E.; Adv. Mater. 1993, 5, 922.

5. Gill, R.E.; Malliaras, G.G.; Wildeman, J.; Hadziioannou, G.; Adv. Mater. 1994, 6, 132.

6. Mushrush, M.; Facchetti, A.; Lefenfeld, M.; Katz, H. E.; Marks, T. J.; J. Am. Chem. Soc. 2003, 125, 9414.

7. Lovinger, A. J.; Davis, D. D.; Dodabalapur, A.; Katz, H. E. Chem. Mater. 1996, 8, 2836.

8. Facchetti, A.; Mushrush, M.; Yoon, M.-H.; Hutchison, G. R.; Ratner, M. A.; Marks, T. J.; J. Am. Chem. Soc. 2004, 126, 13859.

9. Rozen, S.; Bareket, Y.; J. Org. Chem. 1997, 62, 1457.

10. Oliva, M. M.; Casado, J.; Navarrete, J. T. L.; Patchokovskii, S.; Goodson III, T.; Harpham, M. R.; de Melo, S. S.; Amir, E.; Rozen, S.; J. Am. Chem. Soc. 2010, 132, 6231.

11. Zhang, C.; Nguyen, T. H.; Sun, J.; Li, R.; Black, S.; Bonner, C. E.; Sun, S.-S.; Macromolecules 2009, 42, 663.

12. King, S. M.; Perepichka, I. I.; Perepichka, I. F.; Dias, F. B.; Bryce, M. R.; Monkman, A. P.; Adv. Funct. Mater. 2009, 19, 586.

13. Barbarella, G.; Favaretto, L.; Zambianchi, M.; Pudova, O.; Arbizzani, C.; Bongini, A.; Mastragostino, M.; Adv. Mater. 1998, 10, 551.

14. Melucci, M.; Frere, P.; Allain, M.; Levillain, E.; Barbarella, G.; Roncali, J.; Tetrahedron 2007, 63, 9774.

15. Camaioni, N.; Ridolfi, G.; Fattori, V.; Favaretto, L.; Barbarella, G.; Appl. Phys. Lett. 2004, 84, 1901.

16. Barbarella, G.; Favaretto, L.; Sotgiu, G.; Zambianchi, M.; Fattori, V.; Cocchi, M.; Cacialli, F.; Gigli, G.; Cingolani, R.; Adv. Mater. 1999, 11, 1375.

17. Amir, E.; Sivanadan, K.; Cochran, J. E.; Cowart, J. J.; Ku, S. -Y.; Seo, J. H.; Chabinyc, M. L.; Hawker, C. J.; J. Polym. Sci., Part A: Polym. Chem. 2011, 49, 1933.

18. Lukevics, E.; Arsenyan, P.; Belyakov, S.; Pudova, O.; Chem. Heterocycl. Compd. 2002, 38, 632.

19. Thiemann, T.; Walton, D. J.; Brett, A. O.; Iniesta, J.; Marken, F.; Li, Y. Q.; ARKIVOC 2003, 6, 96.

20. Thiemann, T.; Ohira, D.; Arima, K.; Sawada, T.; Mataka, S.; Marken, F.; Compton, R. G.; Bull, S. D.; Davies, S. G.; J. Phys. Org. Chem. 2000, 13, 648.

21. Bongini, A.; Barbarella, G.; Zambainchi, M.; Arbizzani, C.; Mastragostino, M.; Chem. Commun. 2000, 439

22. Casado, J.; Katz, H. E.; Hernández, V.; López Navarrete, J.T.; J. Phys. Chem B. 2002, 106, 2488.

23. Lee, U. R.; Lee, T. W.; Hoang, M. H.; Kang, N. S.; Yu, J. W.; Kim, K. H.; Lim, K.-G.; Lee, T. -O.; Jin, J. -I.; Choi D. H.; Org. Electron. 2011, 12, 269.

24. Aydogan, B.; Gundogan, A. S.; Ozturk, T.; Yagci Y.; Macromolecules 2008, 41, 3468.

25. Kim, O.-K.; Lee, K.-S.; Huang, Z.; Heuer, W.B.; Paik-Sung C.S.; Opt. Mater. 2002, 21, 559.

26. Kim, O.-K.; Woo, H. Y.; Kim, J.-K.; Heuer, W.B.; Lee, K.-S.; Kim, C.-Y.; Chem. Phys. Lett. 2002, 364, 432.

27. Bouzzine, S. M.; Bouzakraoui, S.; Bouachrine, M.; Hamidi, M.; J. Mol. Struct. THEOCHEM 2005, 726, 271.

28. Rubio, M.; Merchan, M.; Ortı, E.; J. Chem Phys. 1995, 102, 3580.

29. Bouzzine, S. M.; Hamidi, M.; Bouachrine, M.; Orbital 2009, 1, 203.

30. Aouchiche, H. A.; Djennane, S.; Boucekkine, A.; Synth. Met. 2004, 140, 127.

31. Amazonas, J. G.; Guimaraes, J. R.; Santos Costa, S. C.; Laks, B.; Nero J. D.; J. Mol. Struct. THEOCHEM 2006, 759, 87.

32. Oliva, M. M.; Gonzalez, S. R.; Casado, J.; Navarrete, J. T. L.; Seixas de Melo, J. S.; Rojen, S.; Port. Electrochim. Acta 2009, 27, 531

33. Semire, B.; Odunola, O. A.; Adejoro, I. A.; J. Mol. Model. 2012, 18, 2755.

34. Fichou, D.; J. Mater. Chem. 2000, 10, 571.

35. Horowitz, G.; Hajlaoui, M. E.; Adv. Mater. 2000, 12, 1046.

36. Becke, A. D.; J. Chem. Phys. 1993, 98, 5648.

37. Lee, C.; Yang, W.; Parr, R. G.; Phys. Rev. B: Condens. Matter 1988, 37, 785.

38. Chambers, C. C.; Hawkins, G. D.; Cramer, C. J.; Truhlar, D. G.; J. Chem. Phys. 1996, 100, 16385.

39. Hehre, W. J.; A Guide to Molecular Mechanics and Quantum Chemical Calculations. Wavefunction, Inc.: USA, 2003, p. 50.

40. Spartan 06, wavefunction, INC, Irvine CA 92612, USA .

41. Silverstein, M.; Basseler, G. C.; Morill, C.; Spectrometric Identification of Organic compounds. Wiley: New York, 1981.

42. Zhang, R.; Dub, B.; Sun, G.; Sun, Y.; Spectrochim. Acta 2010, 75A, 1115.

43. Jeffery P. M.; Moran M.; Radom L.; J. Phys. Chem. A 2007, 111, 11683

44. Liu G.; Yu J.; J. Mol. Struct. THEOCHEM 2005, 717, 15.

45. Casado, J.; Hernandez, V.; Hotta, S.; Navarrete, J. T. L.; Adv. Mater. 1998, 10, 1258; Casado, J.; Hernández, V.; Kim, O.-K.; Lehn, J. M.; Navarrete, J. T. L.; Ledesma, S. D.; Ortiz, R. P.; Delgado M. C. R.; Vida, Y.; Pérez-Inestrosa, E.; Chem. Eur. J. 2004, 10, 3805; Semire, B.; Oyebamiji, B.; Ahmad , M.; Pak. J. Chem. 2012, 2, 166.