Artigo
|
|
| Propriedades estruturais e eletrônicas de nanofilmes de TiO2 anatase: cálculos B3LYP-D* em sistemas periódicos bidimensionais Structural and electronic properties of anatase TiO2 thin films: periodic B3LYP-D* calculations in 2D systems |
|
Anderson R. AlbuquerqueI,II,III; Iêda M. G. SantosII; Júlio R. SambranoI,*
IDepartamento de Matemática, Universidade Estadual Paulista, 17033-360 Bauru - SP, Brasil Recebido em 23/01/2014 *e-mail: sambrano@fc.unesp.br Structural and electronic properties of titanium dioxide (TiO2) thin films, in anatase phase, were investigated using periodic 2D calculations at density functional theory (DFT) level with B3LYP hybrid functional. The Grimme dispersion correction (DFT/B3LYP-D*) was included to better reproduce structural features. The electronic properties were discussed based on the band gap energy, and proved dependent on surface termination. Surface energies ranged from 0.80 to 2.07 J/m2, with the stability orders: (101) > (100) > (112) > (110) ~ (103) > (001) >> (111), and crystal shape by Wulff construction in accordance with experimental data. INTRODUÇAO O dióxido de titânio (TiO2) é um material cerâmico que tem despertado um crescente interesse por apresentar inúmeras possibilidades de aplicaçoes, dentre as quais catálise, fotocatálise, sensor químico de gás, células solares, dispositivos eletrônicos e pigmentos.1-4 Uma das mais importantes propriedades do TiO2 é sua atividade (foto)catalítica. Entre os polimorfos do TiO2, as formas mais encontradas na natureza e obtidas em sínteses convencionais sao: anatase (tetragonal), rutilo (tetragonal) e brookita (ortorrômbico). No que diz respeito à nanotecnologia, nanomateriais à base de TiO2 vem sendo utilizados com sucesso para conversao catalítica de uma variedade de poluentes orgânicos (hidrocarbonetos, hidrocarbonetos clorados, fenóis, surfactantes, pesticidas e corantes orgânicos) e gases,1 além de mostrar-se eficiente na destruiçao de microorganismos como bactérias, fungos e vírus.5-8 Para aplicaçoes em catálise, a fase anatase do TiO2 é a mais importante por ser dominante em cristais nanométricos9 e possuir um maior tempo de recombinaçao elétron-buraco quando comparado com a fase rutilo,10 permitindo melhor desempenho em processos de transferência eletrônica em reaçoes redox nas suas superfícies. Neste sentido, fica claro que um dos aspectos importantes e primordiais nos estudos de reaçoes sobre superfícies é o de inicialmente compreender a fundo como estas se formam e quais suas propriedades eletrônicas, estruturais e sua ordem de estabilidade. A ordem de estabilidade das superfícies depende da direçao e da exposiçao dos átomos superficiais. A determinaçao experimental das energias de formaçao e respectiva ordem de estabilidade de superfícies de óxidos nao é um trabalho trivial. Sua estabilidade pode ser inferida medindo-se a área superficial dos monocristais por técnicas de microscopia.11 Durante o processo de crescimento de monocristais sob controle termodinâmico, as faces com menor energia de formaçao sao preferencialmente expostas de modo a diminuir a energia livre total de superfície da partícula. Tipicamente, monocristais de TiO2 anatase sao dominados pelas faces {101}, termodinamicamente mais estáveis.12 A produçao de cristais com exposiçao de faces de alta energia obtidas por reaçoes sob controle cinético é um desafio, e materiais desse tipo vêm sendo obtidos, por exemplo, via funcionalizaçao temporária de superfícies com halogenetos.13 Do ponto de vista teórico, a modelagem e simulaçao computacional aplicada a modelos periódicos bidimensionais permitem compreender as propriedades estruturais e eletrônica de superfícies deste óxido, bem como determinar a energia para formaçao de suas facetas.14-16 Esse conhecimento permite ainda modelar superfícies (limpas ou funcionalizadas/dopadas) e prever a forma microscópica do cristal segundo a regra de Wulff-Gibbs.17-19 Resultados mais recentes, segundo a teoria do Funcional da Densidade (DFT) com o funcional híbrido PBE0 aplicado a sistemas periódicos nos dao uma estimativa para a estabilidade relativa das superfícies do TiO2 anatase: (110) > (103) > (001) > (112) > (100) > (101).20 Sabe-se que interaçoes de London sao um fenômeno intrínseco em todos os sistemas eletrônicos como resultado das correlaçoes dinâmicas entre as distribuiçoes flutuantes de cargas, e devem ser levadas em consideraçao na simulaçao de sistemas periódicos com certo grau de covalência. Em trabalhos recentes, incluímos a contribuiçao da energia de dispersao na descriçao do cristal (bulk) da fase anatase do TiO2.21 Neste trabalho obtivemos resultados com uma melhor aproximaçao com respeito aos valores experimentais de parâmetros de rede, entre outras propriedades eletrônicas e estruturais. Entretanto, até o presente momento nenhum trabalho foi encontrado incluindo a energia de dispersao para a determinaçao das energias superficiais e a respectiva ordem de estabilidade das superfícies da anatase. Nesse sentido, o presente trabalho tem como objetivos determinar as energias de superfície do TiO2 anatase por meio de cálculos DFT utilizando modelos periódicos bidimensionais (slabs) com o funcional híbrido B3LYP, acrescido com a correçao de Grimme22 (B3LYP-D*) para a energia de dispersao do cristal, e descrever sua estrutura eletrônica por meio de diagramas de estrutura de bandas e densidade de estados.
MODELOS E MÉTODOS COMPUTACIONAIS Modelo estrutural O TiO2 anatase possui estrutura tetragonal com grupo espacial
I41/amd, definida por dois parâmetros de rede (a = 3,7842 Å e c = 9,5146 Å)23 e um parâmetro interno u = 0,2081 (u =
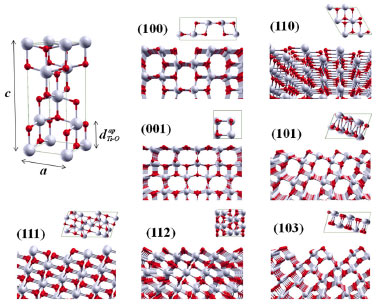 Figura 1. Célula unitária convencional da anatase e suas superfícies nao relaxadas (100), (110), (001), (101), (111), (112) e (103) do TiO2 anatase. Os insets mostram a vista superior das células unitárias 2D. Os átomos de Ti e O sao mostrados como esferas claras e escuras, respectivamente
Para a construçao de superfícies da anatase, foram considerados nesse trabalho sete planos cristalográficos com baixo índices (hkl) de Miller: (100), (110), (001), (101), (111), (112) e (103), como mostrado na Figura 1. Computacionalmente, o procedimento consiste em seccionar o bulk perpendicularmente ao vetor da direçao desejada, formando uma estrutura periódica em duas dimensoes (x e y), mas com espessura finita (direçao z). As superficies sao definidas por dois vetores ortogonais à direçao [hkl] escolhida. Do ponto de vista experimental, o modelo destas superficies pode ser comparado a um filme fino. As informaçoes decorrentes da simulaçao podem auxiliar na interpretaçao experimental ou e até mesmo ajudar a racionalizar experimentos. Um problema de natureza química torna necessária a definiçao das camadas atômicas inicial e terminal do slab, bem como da sua espessura, uma vez que nem todas as terminaçoes sao estáveis, podendo nao existir ou sofrerem rapidamente uma reconstruçao (rearranjo estrutural com mudança nas coordenaçoes dos átomos). Fisicamente, a assimetria vertical do slab pode gerar um momento de dipolo intrínseco nao nulo perpendicular à superfície. Superfícies desse tipo, quando iônicas, geralmente sao instáveis e necessitam de um campo eletromagnético externo ou um adsorbato para estabilizaçao da energia. Outra condiçao a ser observada na contruçao de modelos de superfícies é que a espessura do slab seja larga o bastante para que as interaçoes entre as terminaçoes superior e inferior sejam desprezíveis. Esse procedimento é realizado construindo uma série de modelos com espessuras crescentes até alcançar uma convergencia da energia superficial com relaçao à espessura do modelo, isto é, ate que relaçao entre espessura e energia superficial seja constante. A energia de uma superfície, Es (hkl), pode ser definida como sendo a energia livre de excesso da superfície (hkl) por unidade de área. Esta grandeza é fundamental para a compreençao da forma e direçao de crescimento de cristais em equilíbrio termodinâmico. Em T = 0, Es (hkl) é dado pela Eq.1:
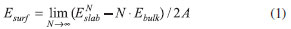
na qual ENslab é a energia total do slab, N é o número de unidades de TiO2, Ebulk é a energia total do bulk por unidades de TiO2, e A é a área da célula unitária 2D. O fator ½ advém da existência de duas faces limitantes no slab. Es (hkl) é intrinsecamente uma grandeza positiva, e a medida que mais camadas sao adicionadas (N → ∞), a energia converge para a energia de formaçao por unidade de área. Método computacional A simulaçao computacional foi feita por meio do programa CRYSTAL versao 09.24,25 O código CRYSTAL realiza cálculos ab initio e DFT em sistemas periódicos 3D, (bulk), 2D (slabs), 1D (polímeros, nanotubos e hélices) e 0D (átomos e moléculas) usando a aproximaçao da Combinaçao Linear de Orbitais Atômicos (LCAO). Para tanto, orbitais cristalinos Ψi(
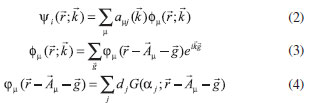
Nas Equaçoes 2-4, Além da simetria translacional, o programa CRYSTAL explora a simetria interna da célula unitária, reduzindo proporcionalmente o custo computacional. As funçoes de base all electron 6-21G(d31) e 6-31G(d) foram utilizadas para a descriçao dos átomos de titânio e oxigênio, respectivamente. O limite de convergência considerado foi 10-7 hartree para os cálculos de otimizaçao. O funcional híbrido B3LYP26,27 foi utilizado em todos os cálculos. As superfícies do TiO2 na fase anatase foram modeladas a partir dos parâmetros de rede e coordenada interna u do bulk pré-otimizado com a correçao para dispersao de Grimme22 parametrizado especificamente para a anatase.21,28 A forma geral da energia total com a correçao na energia de dispersao (EDFT-D) pelo método DFT-D2 de Grimme é dado pela Equaçao 5.22
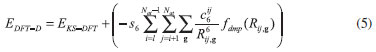
onde EKS-DFT é a energia usual de Kohn-Sham calculada para um determinado funcional e o segundo termo da equaçao é o potencial de dispersao, cujo somatório estende-se sobre todos os pares atômicos Rij e vetores de rede g (exceto para i = j, g =
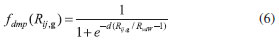
Nesse trabalho, adotamos os raios RvdW(Ti) = 1.4214 Å e RvdW(O) = 1.3420 Å, recentemente parametrizados para o bulk do TiO2 anatase com o funcional B3LYP, e denominado B3LYP-D*.21 Esse procedimento garante uma excelente descriçao estrutural deste óxido (a = 3.7875 Å, c = 9.5146 Å and u = 0.2082), com desvios menores que 0,1% com relaçao aos parâmetros de rede e parâmetros internos, e uma boa descriçao eletrônica, com energia de band gap (Egap) igual a 3.55 eV contra 3.42 eV experimentalmente reportados para monocristais de anatase à 4K.29 A análise da estrutura eletrônica do TiO2 foi discutida com base nas estruturas de banda e mapas de densidade de estados, que sao equivalentes aos diagramas de energias dos orbitais de Kohn-Sham para moléculas isoladas. As estruturas de bandas foram obtidas interpolando-se pontos de alta simetria na primeira zona de Brillouin. A densidade de estados (DOS) também foi projetada sobre os átomos das camadas (PDOS) mais externas das superfícies a fim de determinar sua contribuiçao nas bandas de valência (VB) e banda de conduçao (CB).
RESULTADOS E DISCUSSAO Na Figura 2 sao mostradas as energias de superfícies para as sete superficies selecionadas em funçao da espessura do filme. A ordem de estabilidade das superfícies é (101) > (100) > (112) > (110) ~ (103) > (001) >> (111). Observa-se que para distâncias intrafaciais maiores que 10 Å as energias permanecem praticamente constantes para todos os slabs. Na metodologia utilizada, todas as posiçoes atomicas sao relaxadas durante o processo de otimizaçao, mantendo-se fixos os parâmetros de rede com relaçao ao bulk otimizado. Este procedimento permite uma rápida convergência com relaçao à espessura do slab. Uma metodologia alternativa, consiste na otimizaçao total (posiçoes atômicas em conjunto com os parâmetros de rede) do slab. Esta é equivalente à primeira quando dface-dface é de aproximadamente 50 Å no TiO2 anatase, de modo que os parâmetros de rede do slab convergem para os valores do bulk truncado e Es converge para os mesmos valores obtidos com a primeira metodologia.
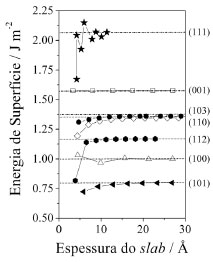 Figura 2. Energia das surperfícies (Es) em funçao das espessuras dos filmes de TiO2 anatase
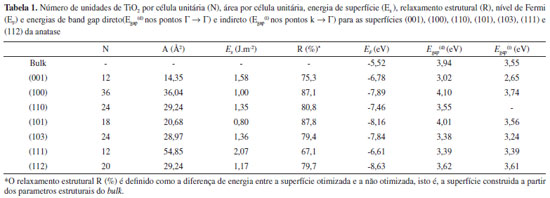
A energia de uma determinada superfície [hkl] pode ser considerada como sendo a energia de clivagem (forma pela qual o cristal se fragmenta em planos bem definidos) do bulk na direçao pela qual passa o vetor [hkl] normal ao plano seccionado mais a energia de relaxamento da superfícies, cuja contribuiçao é dada principalmente pelos átomos da primeira e última camadas. Os atomos das camadas mais externas sao os que tem maior mobilidade (relaxaçao) de modo a minimizar as coordenaçoes reduzidas. Facetas com um grande número de átomos e com baixa coordenaçao tendem a se reconstruir, a menos que estabilizada quimicamente por algum agente de recobrimento ou mesmo eletrostaticamente pela mudança de solvente em reaçoes soft como os métodos hidrotermais e solvotermais, estrategicamente utilizados em sínteses de nanocristais de anatase.11 Na Tabela 1 sao mostradas as energias de superfícies e energias de relaxamento estrutural para os slabs da anatase com espessura suficiente para que a interaçao face-face seja desprezível. O relaxamento estrutural R (%) é definido como a diferença de energia entre a superfície otimizada e a nao otimizada, isto é, a superfície construída a partir dos parâmetros estruturais do bulk.
A ordem de estabilidade das superfícies pode ser melhor compreendida observando-se os átomos de baixa coordenaçao formados quando da clivagem no plano (hkl). Na Figura 3 sao mostradas as superfícies otimizadas. A superfície mais estável, a (101), contém ambos titânios com coordenaçao seis, Ti(6c), e cinco Ti(5c). Situaçao similar ocorre na superfície (100), segunda mais estável. Ambas as superfícies sofreram um relaxamento superior a 87%, obtido comparando-se as energias das superfícies truncadas do bulk e relaxadas. Xu et al. (2013)30 obtiveram nanocristais monocristalinos de anatase com 95% de superfícies {100} e 2 nm de espessura, apresentando elevada atividade fotocatalítica na reduçao de CO2 a CH4, e H2O a H2.
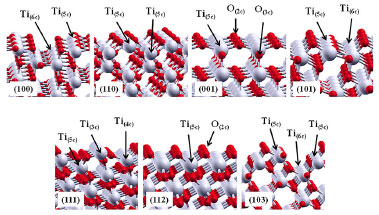 Figura 3. Superfícies relaxadas do TiO2 anatase. As flechas indicam a coordenaçao de Ti e O nas camadas mais externas
Na superfície (112), somente Ti(5c) e oxigenios com coordenaçao dois, O(2c), sao expostos. Nesta superficie observa-se que os octaédros [TiO5] apresentam uma pequena rotaçao, distinta de outras superfícies, como a (001), menos estável de todas. Com energias muito próximas, a (110) e (103) também expoem Ti(5c) e sofrem um relaxamento da ordem de 80%. Conjuntamente com a (101), a (103) é da série de planos (10l), com l = 1,2,3..., de modo que o aumento de l tende a expor mais titânios de baixa coordenaçao pela formaçao de steps mais longos, necessitando em alguns casos da utilizaçao de supercélulas para permitir a reconstruçao nas camadas mais externas. A otimizaçao da superfície (001) apresentou energia cerca de duas vezes maior que a superfície mais estável (101). Essa superfície é formada pela clivagem dos octaédros [TiO6] do bulk ao longo da ligaçao Ti-O apical, formando no topo do filme apenas poliedros de [TiO5] que compartilham vértices entre si por oxigênios O(3c) e O(2c). Tal característica confere à (001) uma alta acidez e reatividade, facilmente hidroxilável ou recoberta por bases fracas como o íon fluoreto (F-).13 A elevada energia da superfície (111) pode ser explicada com base na baixa coordenaçao dos átomos de titânios expostos (Ti(5c), Ti(4c), Ti(3c)). Experimentalmente, essa terminaçao estaria fadada à reconstruçao estrutural ou necessitaria de estabilizaçao pela ligaçao com espécies básicas para crescer no cristal. Recentemente, Xu et al. (2013)31 conseguiram obter monocristais com elevada exposiçao de superfícies {111} utilizando fluoreto e amônia como agentes capeantes e verificaram sua atividade fotocatalítica como sendo 5, 9, e 13 vezes maior que a de monocristais de anatase com as faces dominantes {010}, {101} e {001}, respectivamente. Sob o ponto de vista termodinâmico, a morfologia teórica de um monocristal em enquilíbrio é determinado pelas energias de suas superfícies e pode ser descrita seguindo a regra clássica da construçao de Wulff, expressa pela Equaçao 7,32
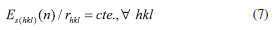
em que a relaçao entre a energia da superficie (hkl) (Es(hkl)) e a distância (rhkl) do centro do cristal ao primeiro plano normal à superfície (hkl) é constante (cte.) para toda e qualquer superfície (hlk). Desta forma, a partir da equaçao 7 foi possivel construir o solido de Wulff que está contido no sólido resultate de todas as intersecçoes dos planos hkl. A Figura 4 ilustra o sólido de Wulff gerado antes e após o relaxamento estrutural das respectivas superfícies. A figura foi feita com o auxílio do programa Vesta.33
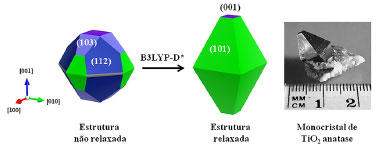 Figura 4. Forma dos nanocristais de TiO2 anatase obtidos a partir das energias das superfícies nao-relaxadas e relaxada em nível B3LYP-D*. A bipirâmide truncada expondo ~ 3% de (001) e 97% de (101) é condizente com a forma do monocristal de anatase encontrado na natureza, retirada de Diebold et al.,34 com permissao da Elsevier
Experimentalmente, o caminho inverso pode ser realizado e, conhecendo-se a porcentagem relativa de cada superfície exposta em um monocristal por técnicas de microscopia eletrônica, podendo-se inferir acerca das energias de superfícies.35 Outros fatores como a cínetica de formaçao do cristal e a tensao superficial nas arestas e vértices das facetas também contribuem para a morfologia cristalina, tendo sido incluídos em modelos mais extendidos.36 Antes da otimizaçao, o cristal possui uma forma quase esférica, expondo em sua maior parte as superfícies (112), (101), (103) e (001), e uma pequena quantidade de (111). Após o relaxamento estrutural, o cristal toma uma forma de bipirâmide de base quadrada truncada, com ~ 3% da superfície (001) e 97% de (101), perfeitamente de acordo com a forma do monocristal de TiO2 anatase encontrado na natureza, ou obtidos por sínteses convencionais sem uso de agente capeante.37 Esta é mais uma evidencia de que em procedimentos teóricos para a modelagem de superfícies a otimizaçao total é um fator determinante para uma completa descriçao estrutural e eletrônica. Nas reaçoes de fotocatálise, a estrutura eletrônica das superfícies do catalisador é um dos fatores que determinam a faixa do espectro na qual o material pode absorver os fótons para formaçao do par eléctron (e/) - buraco (h•), via excitaçao para banda de conduçao (TiO2 + hv → h•(BV) + e/(BC)). Na Tabela 1 sao mostradas as energias de band gap direto e indireto para cada superfície, e na Figura 5 sao mostradas suas estruturas de banda e densidade de estados. A ordem crescente de energia do band gap das superfícies é (001) < (103) < (111) < (110) = bulk < (101) < (112) < (100).
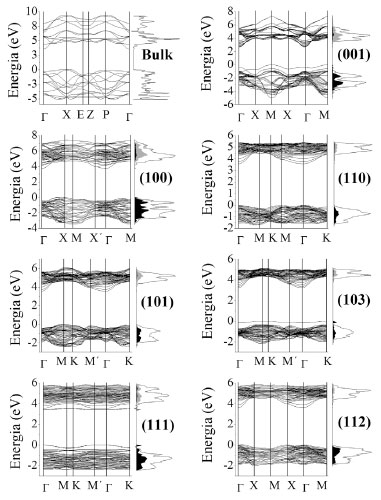 Figura 5. Estrutura de bandas do bulk e das superfícies do TiO2 anatase. O DOS projetado sobre os átomos de Ti e O das camadas mais externas dos slabs sao representados à direita nas cores cinza e preto, respectivamente
A superfície com menor valor de Egap foi a (001), o que faz com que essa face do cristal absorva mais radiaçao na faixa do UV-Visível que as demais superfícies, aumentando a probabilidade de excitaçao eletrônica, mesmo que com reduzida área de exposiçao nos cristais de anatase. Por outro lado, a fácil recombinaçao elétron-buraco na (001) pode diminuir sua atividade catalítica. Entretanto, filmes de (001) crescidos em suportes condutores podem ter sua atividade fotocatalítica aumentada pela transferência eletrônica óxido-metal, diminuindo a recombinaçao e'-h•. Experimentalmente também atribui-se à superfície (103) uma elevada atividade catalítica.15 Cristais com essa terminaçao sao de difícil obtençao, mas podem ser sintetizados mediante utilizaçao de agentes capeantes seletivos que reduzam sua energia de formaçao em detrimento de outras superfícies. Recentemente, Oropeza et al. (2013)38 obtiveram filmes finos de anatase com elevada exposiçao de faces {101} e {103} quando suportados em SrTiO3 [001]. Assim como no bulk, nas superfícies da anatase o topo da banda de valência é formada principalmente por bandas compostas de orbitais de Khon-Sham do tipo O 2p, enquanto que as bandas eletrônicas desocupadas de menor energia sao compostas principalmente por orbitais Ti 3d. Como consequência, a excitaçao eletrônica resulta na formaçao de níveis intermediários no band gap ocupados por elétrons trapeados nos Ti4+, reduzindo-os a Ti3+ (3d1). Analogamente, a formaçao de buracos na camada de valência leva à oxidaçao de O2- a O-. Geralmente, a formaçao desses defeitos ocorre de forma mais fácil nas superfícies com relaçao ao bulk. Sao nessas interfaces com Ti de baixa coordenaçao que ocorrem os processos de adsorçao e equilíbrio para oxidaçao e reduçao do material via difusao de O2. Na Figura 6 sao mostrados os mapas de densidade de carga obtidos pela diferença entre a densidade eletrônica do cristal relaxado e a densidade eletrônica dos átomos Ti e O isolados na matriz.
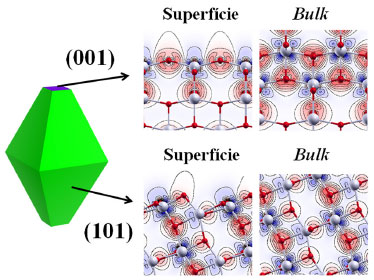 Figura 6. Mapa diferencial da densidade de carga para as superficies (101) e (001), mostrando uma variaçao de carga superficial com relaçao ao bulk em ambas as direçoes. As cores azul e vermelho indicam as diferenças de cargas em torno dos cátions Ti4+ e ânions O2-, respectivamente, no intervalo das isolínieas (-0.05 a 0.05 |e|.Å-1)
Analisando os mapas de diferença de densidade ilustrados na Figura 6, observam-se a formaçao dos cátions e ânions. Com relaçao ao bulk, uma baixa variaçao de carga (ΔQ Mulliken ~ 0.1|e|) é observada nas superfícies, dada pelas baixas coordenaçoes dos Ti(5c) e O(2c). Além dos defeitos nativos presentes em superfícies da anatase obtidas em condiçoes de atmosfera redutora, como vacâncias de oxigênio e titânio intersticiais, sabe-se que a atividade (foto)catalítica de monocristais nanométricos de anatase é dependente da natureza da superfície exposta, sendo a terminaçao {001} uma das mais reativa frente à reaçoes de fotocatálise de moléculas orgânicas.39 Trabalhos recentes de Di Valentin40 mostraram, por meio de cálculos computacionais em sistemas periódicos 2D, a importância da formaçao do exciton em processos fotocatalíticos na anatase, em que o par elétron-buraco migra em direçao às camadas mais externas das superfícies, sendo trapeados por Ti4+ e O2-, respectivamente, ou ocasionalmente trapeados por hidroxilas (agentes capeantes oriundos de síntese em meio básico) ou por adsorbatos, propagando o processo radicalar de fotodegradaçao.
CONCLUSOES Estudos aplicando a modelagem e simulaçoes computacionais baseados na Teoria do Funcional da Densidade podem ser importantes para elucidar e reproduzir propriedades eletrônicas e estruturais de materiais na forma de bulk e/ou superfícies. O conhecimento da estrutura eletrônica para cada face de um cristal e sua estabilidade relativa está relacionada também à sua atividade catalítica e, como efeito, deve auxiliar (e estimular) na busca pela síntese de materiais mais seletivos e específicos de acordo com a exposiçao desejada de faces {hkl}. As conclusoes decorrentes deste estudo podem ser sumarizadas a seguir: (i) os modelos periódicos em conjunçao com o funcional híbrido B3LYP acrescido com a correçao de Grimme (B3LYP-D*) demonstram ser importantes nos estudo teóricos onde a reproduçao de parâmetros eletrônicos e estruturais apresentam certos desvios quando tratados por métodos convencionais; (ii) a analise da estrutura eletrônica do cristal de TiO2 na fase anatase mostra um band gap indireto de 3,55 eV, em excelente concordância se comparados a resultados teóricos e experimentais disponíveis na literatura; (iii) o processo de otimizaçao das superfícies demonstra uma tendência de um descolamento ascendente dos átomos de Ti da camada mais externa enquanto que os átomos de oxigênio tendem a se deslocar para o interior do material; (iv) os átomos das três primeiras camadas sao os que mais sofrem modificaçoes estruturais enquanto que os átomos das camadas mais internas tendem a permanecer na posiçao original do cristal; (v) o cálculo do band gap apresenta a seguinte sequencia crescente, (001) < (103) < (111) < (110) = bulk < (101) < (112) < (100). As superfícies menos estáveis apresentaram band gap menores que o bulk, permitindo absorver uma maior radiaçao, resultando em uma maior probabilidade de excitaçao eletrônica se comparada às demais superfícies, o que explicaria, em parte, a atividade fotocatalítica superior de monocristais crescidos com faces expostas {001}, {103} e {111}. A análise da densidade de estados indica que o topo da Banda de Valencia é formado prioritariamente por orbitais 2p dos átomos de O, enquanto que a BC é formada principalmente por orbitais Ti 3d. Os cálculos das energias de superfícies para os sete modelos selecionados em funçao da espessura demonstraram a seguinte ordem de estabilidade decrescente: (101) > (100) > (112) > (110) ~ (103) > (001) >> (111). A analise morfológica segundo a construçao de Wulff está em perfeita concordância com resultados experimentais. Fica também evidenciada a importância do processo de otimizaçao total dos modelos de superfícies, pois um processo com a ausência da otimizaçao (estrutura nao relaxada) nos levaria a uma análise equivocada da morfologia. Neste caso a forma do cristal seria praticamente esférica, contrariando as observaçoes experimentais com cristais crescidos em equilíbrio termodinâmico. Esta técnica teórica permite reproduzir fielmente a forma de um cristal, confirmando os resultados obtidos com o uso de técnicas experimentais avançadas, tais como a microscopia eletrônica de varredura e transmissao.
AGRADECIMENTOS Os autores agradecem ao CNPq pelas bolsas de pesquisa concedidas, à FAPESP/CEPID e ao INCTMN pelo fomento, e ao Laboratorio de Modelagem e Simulaçao Molecular da Unesp, Centro de Computaçao Científica da Universidade do Estado de Sao Paulo (GRID-Unesp) pelo suporte computacional. Gostaríamos de agradecer ao Me. Jefferson Maul (Lacom-UFPB; LSM-Unesp) pelo instrutivo auxílio nas construçoes de Wulff.
REFERENCIAS 1. Diebold, U.; Surf. Sci. Rep. 2003, 48, 53. 2. Hoffmann, M. R.; Martin, S. T.; Choi, W. Y.; Bahnemann, D. W.; Chem. Rev. 1995, 95, 69. 3. Linsebigler, A. L.; Lu, G. Q.; Yates, J. T.; Chem. Rev. 1995, 95, 735. 4. Oregan, B.; Gratzel, M.; Nature 1991, 353, 737. 5. Saito, T.; Iwase, T.; Horie, J.; Morioka, T.; J. Photochem. Photobiol., B 1992, 14, 369. 6. Wei, C.; Lin, W. Y.; Zainal, Z.; Williams, N. E.; Zhu, K.; Kruzic, A. P.; Smith, R. L.; Rajeshwar, K.; Environ. Sci. Technol. 1994, 28, 934. 7. Yu, J. C.; Ho, W. K.; Yu, J. G.; Yip, H.; Wong, P. K.; Zhao, J. C.; Environ. Sci. Technol. 2005, 39, 1175. 8. Longo, V. M.; Picon, F. C.; Zamperini, C.; Albuquerque, A. R.; Sambrano, J. R.; Vergani, C. E.; Machado, A. L.; Andrés, J.; Hernandes, A. C.; Varela, J. A.; Longo, E.; Chem. Phys. Lett. 2013, 577, 114. 9. Chen, B.; Zhang, H.; Dunphy, K. A.; Spagnoli, D.; Kruger, M. B.; Muthu, D. V. S.; Kunz, M.; Fakra, S.; Hu, J. Z.; Guo, Q. Z.; Banfield, J. F.; Phys. Rev. B 2009, 79, 125406. 10. Yamada, Y.; Kanemitsu, Y.; Appl. Phys. Lett. 2012, 101, 133907. 11. Kuang, Q.; Wang, X.; Jiang, Z.; Xie, Z.; Zheng, L.; Acc. Chem. Res. 2014, 47, 308. 12. Selloni, A.; Nature Materials 2008, 7, 613. 13. Liu, S. W.; Yu, J. G.; Jaroniec, M.; Chem. Mat. 2011, 23, 4085. 14. Lazaro, S.; Penteado, R. F.; Tebcherani, S. M.; Berger, D.; Varela, J. A.; Kubaski, E. T.; Quim. Nova 2012, 35, 920. 15. Sambrano, J. R. ; Vasconcellos, L. A. S.; Martins, J. B. L.; Santos, M. R. C.; Longo, E.; Beltran, A.; J. Mol. Struct. 2003, 629, 307. 16. Beltran, A.; Sambrano, J. R.; Calatayud, M.; Sensato, F. R.; Andres, J.; Surf. Sci. 2001, 490, 116. 17. Linsebigler, A. L.; Lu, G. Q.; Yates, J. T.; Chem. Rev. 1995, 95, 735. 18. Oregan, B.; Gratzel, M.; Nature 1991, 353, 737. 19. Simons, P. Y.; Dachille, F.; Acta Crystallogr. 1967, 23, 334. 20. Mino, L.; Ferrari, A. M.; Lacivita, V.; Spoto, G.; Bordiga, S.; Zecchina, A.; J. Phys. Chem. C 2011, 115, 7694. 21. Albuquerque, A. R.; Garzim, M. L.; Santos, I. M. G.; Longo, V.; Longo, E.; Sambrano, J. R.; J. Phys. Chem. A 2012, 116, 11731. 22. Grimme, S.; J. Comput. Chem. 2006, 27, 1787. 23. Horn, M.; Schwerdt, Cf; Meagher, E. P.; Z. Kristallogr. 1972, 136, 273. 24. Dovesi, R.; Saunders, V. R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C. M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N. M.; Bush, I. J.; D'Arco, P.; Llunell, M.; CRYSTAL09 User's Manual (University of Torino, Torino, 2009). 25. Dovesi, R.; Orlando, R.; Civalleri, B.; Roetti, C.; Saunders, V. R.; Zicovich-Wilson, C. M.; Z. Kristallogr. 2005, 220, 571. 26. Becke, A. D.; J. Chem. Phys. 1993, 98, 5648. 27. Lee, C. T.; Yang, W. T.; Parr, R. G.; Phys. Rev. B 1988, 37, 785. 28. Albuquerque, A. R.; Maul, J.; Longo, E.; Santos, I. M. G.; Sambrano, J. R.; J. Phys. Chem. C 2013, 117, 7050. 29. Tang, H.; Levy, F.; Berger, H.; Schmid, P. E.; Phys. Rev. B 1995, 52, 7771. 30. Xu, H.; Ouyang, S.; Li, P.; Kako, T.; Ye, J.; Appl. Mater. Interfaces 2013, 5, 1348. 31. Xu, H.; Reunchan, P.; Ouyang, S.; Tong, H.; Umezawa, N.; Kako, T.; Ye, J.; Chem. Mater. 2013, 25, 405. 32. Wulff, G.; Z. Kristallogr. 1901, 34, 449. 33. Momma, K.; Izumi, F.; J. Appl. Crystallogr. 2011, 44, 1272. 34. Diebold, U.; Ruzycki, N.; Herman, G. S.; Selloni, A.; Catal. Today 2003, 85, 93. 35. Zasada, F.; Piskorz, W.; Stelmachowski, P.; Kotarba, A.; Paul, J.; Pzocinski, T.; Kurzydzowski, K. J.; Sojka, Z.; J. Phys. Chem. C 2011, 115, 6423. 36. Ringe, E.; Van Duyne, R. P; Marks, L. D.; Nano Lett. 2011, 11, 3399. 37. Barnard, A. S.; Curtiss, L. A.; Nano Lett. 2005, 5, 1261. 38. Oropeza, F. E.; Zhang, K. H. L.; Regoutz, A.; Lazarov, V. K.; Wermeille, D.; Poll, C. G.; Egdell, R. G.; Cryst. Growth Des. 2013, 13, 1438. 39. Liu, S.; Yu, J.; Jaroniec, M.; Chem. Mater. 2011, 23, 4085. 40. Di Valentin, C.; Selloni, A.; J. Phys. Chem. Lett. 2011, 2, 2223. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






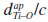 , onde
, onde 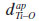 é o comprimento da ligaçao Ti-O apical, na direçao [001]). A célula unitária convencional do TiO2 anatase é mostrada na Figura 1. Essa estrutura pode ser descrita em termos de: (i) octaedros [TiO6] dispostos por arestas compartilhadas, em um total de quatro [TiO6] por célula unitária convencional; (ii) quatro octaedros intersticiais de O6; ou (iii) 16 tetraedros vazios de O4. Os octaedros centrados no Ti sao distorcidos e possuem diferentes comprimentos de ligaçao Ti-O apical (
é o comprimento da ligaçao Ti-O apical, na direçao [001]). A célula unitária convencional do TiO2 anatase é mostrada na Figura 1. Essa estrutura pode ser descrita em termos de: (i) octaedros [TiO6] dispostos por arestas compartilhadas, em um total de quatro [TiO6] por célula unitária convencional; (ii) quatro octaedros intersticiais de O6; ou (iii) 16 tetraedros vazios de O4. Os octaedros centrados no Ti sao distorcidos e possuem diferentes comprimentos de ligaçao Ti-O apical (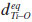 ), com
), com 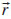 ,
,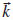 ) (Eq. 2) sao tratados com uma combinaçao linear de funçoes de Bloch Фµ(
) (Eq. 2) sao tratados com uma combinaçao linear de funçoes de Bloch Фµ(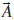 µ -
µ - 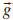 )(Eq. 4) centradas em A, com coeficientes dj e expoentes αj.
)(Eq. 4) centradas em A, com coeficientes dj e expoentes αj.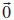 ). O fator de escala s6 é um valor pré-definido e dependente do funcional (1,05 para o funcional B3LYP), c6ij é o coeficiente de dispersao para o par ij calculado usando a média geométrica dos coeficientes individuais, e Rij,g é a distância interatômica entre os átomos i na célula de referência e os átomos j nas células vizinhas à uma distância de ||g||. A funçao de amortecimento (fdmp) é usada para evitar singularidades às pequenas distâncias Rij,g e é dada pela Equaçao 6, em que d = 20 é uma constante que determina o decaimento da funçao e RvdW é a soma dos raios de corte (aqui tratados como raios de van der Waals) do Ti e do O.
). O fator de escala s6 é um valor pré-definido e dependente do funcional (1,05 para o funcional B3LYP), c6ij é o coeficiente de dispersao para o par ij calculado usando a média geométrica dos coeficientes individuais, e Rij,g é a distância interatômica entre os átomos i na célula de referência e os átomos j nas células vizinhas à uma distância de ||g||. A funçao de amortecimento (fdmp) é usada para evitar singularidades às pequenas distâncias Rij,g e é dada pela Equaçao 6, em que d = 20 é uma constante que determina o decaimento da funçao e RvdW é a soma dos raios de corte (aqui tratados como raios de van der Waals) do Ti e do O.