Educação
|
|
| Simulação de sinais de RMN através das equações de Bloch Simulation of NMR signals through the Bloch equations |
|
Tiago Bueno MoraesI,*; Luiz Alberto ColnagoII
IInstituto de Física de São Carlos, Universidade de São Paulo, Av. Trabalhador São-carlense 400, 13560-970 São Carlos - SP, Brasil Recebido em 17/12/2013 *e-mail: tiagobuemoraes@gmail.com The aim of this paper was to present a simple and fast way of simulating Nuclear Magnetic Resonance signals using the Bloch equations. These phenomenological equations describe the classical behavior of macroscopic magnetization and are easily simulated using rotation matrices. Many NMR pulse sequences can be simulated with this formalism, allowing a quantitative description of the influence of many experimental parameters. Finally, the paper presents simulations of conventional sequences such as Single Pulse, Inversion Recovery, Spin Echo and CPMG. INTRODUÇAO A espectroscopia de ressonância magnética nuclear (RMN) é hoje uma ferramenta indispensável em praticamente todos os campos de aplicaçao das análises químicas.1 A primeira aplicaçao da RMN em química foi com o uso dos parâmetros espectrais como deslocamento químico, acoplamento spin-spin, etc, que permitem a determinaçao da estrutura de moléculas orgânicas naturais e sintéticas. Essa aplicaçao foi dominante até final da década de 1970. No entanto, desde o início da década de 1980, a RMN no Brasil, como em todo o mundo, passou a ser uma técnica com importantes aplicaçoes em bioquímica, com a análise da estrutura tridimensional de proteínas, análises in vivo, metabolômica; em materiais com a determinaçao de estrutura e dinâmica de materiais inorgânicos, polímeros orgânicos (estado sólido e soluçao); na análise qualitativa e quantitativa de produtos farmacêuticos, agrícolas, petróleo e derivados, entre muitas outras aplicaçoes. Além disso, a RMN em baixo campo passou a ser largamente usada no controle de qualidade de produtos das indústrias de alimentos, petróleo, polímeros e dentífricos. Desde a década de 1990, a tomografia por RMN, conhecida como ressonância magnética, passou a ser um método padrao de diagnóstico por imagens, em medicina. Entretanto, a RMN ainda é ensinada nos cursos de graduaçao e em alguns cursos de pós-graduaçao apenas como um método de determinaçao de estrutura de moléculas orgânicas, nao levando em conta a grande potencialidade da técnica nas outras aplicaçoes científicas e tecnológicas. Assim, o objetivo desse artigo é apresentar de maneira simples, rápida e quantitativa os fenômenos básicos da RMN, para que os estudantes possam entender a maioria das aplicaçoes da RMN em alto campo, baixo campo e imagens. Para isso serao usados diagramas vetoriais e as respectivas simulaçoes computacionais, utilizando as equaçoes de fenomenológicas de Bloch. Essas equaçoes descrevem de maneira clássica o comportamento da magnetizaçao macroscópica, sendo facilmente simuladas utilizando matrizes de rotaçao.2 Essa descriçao nao depende de conhecimento de mecânica quântica3-4 e permite uma descriçao quantitativa de diversos parâmetros espectrais como o ângulo de rotaçao da magnetizaçao, relaxaçao spin-rede, longitudinal ou T1, relaxaçao spin-spin, transversal ou T2 entre outros. Além disso, pode-se demonstrar quantitativamente a evoluçao temporal de vários experimentos de RMN pulsado, como as sequências de pulsos usadas na inversao recuperaçao, eco de spin, eco estimulado e Carr-Purcell-Meiboom-Gill, entre outras sequências. A descriçao quantitativa será inicialmente realizada passo a passo e em seguida serao simulados experimentos mais complexos, utilizando o algoritmo que está descrito e comentado no artigo. Descriçao clássica do fenômeno de RMN A base moderna da espectroscopia por RMN surgiu em 1946, quando dois grupos de pesquisa independentes conseguiram observar os efeitos da ressonância magnética nuclear em amostras líquidas e sólidas (matéria condensada) e nao mais em feixes de partículas como nos experimentos anteriores.5 O grupo de Harvard (Purcell, Torrey, Pound)6 entendia o experimento de RMN em termos das transiçoes entre os estados quânticos, enquanto o grupo de Stanford (Bloch, Hansen, Packard)7 visualizava esses experimentos em termos da magnetizaçao macroscópica dos momentos magnéticos nucleares na presença de um campo magnético externo. Posteriormente, ficou evidente que ambas as explicaçoes eram complementares e por essa descoberta Bloch e Purcell receberam o Prêmio Nobel de Física em 1952. Os artigos iniciais da RMN foram publicados no mesmo fascículo da revista Physical Review em 1946. O trabalho de Purcell e colaboradores teve o título "Resonance Absorption by Nuclear Magnetic Moments in a Solid".6 O artigo de Bloch e colaboradores que relatou o experimento de RMN teve o título "The Nuclear Induction Experiment".7 Bloch também publicou outro artigo em que apresenta as equaçoes fenomenológicas para descrever o comportamento da magnetizaçao denominado de "Nuclear Induction".8 Desde entao as equaçoes de Bloch formam as bases para uma compreensao fenomenológica da ressonância magnética nuclear. A RMN é observada quando uma amostra que possui núcleos com spin nuclear I, sendo o momento angular (

onde, γ é a razao entre o momento magnético Uma vez que γ é uma constante, cada isótopo tem uma frequência de precessao única, conhecida também como frequência de Larmor (ϖ0). Para a grande maioria das aplicaçoes da RMN a frequência de ressonância em Hz (ϖ0/2π) situa-se na faixa das frequências de rádio (MHz). Apesar de o spin ser um fenômeno quântico, a RMN pode ser tratada classicamente como descrita por Bloch. Como há um pequeno excesso de núcleos com

No sistema de coordenadas de laboratório (x, y, z), a descriçao da RMN envolve movimentos tridimensionais complexos.1,2 Para simplificar a descriçao da RMN normalmente usa-se um sistema de coordenadas girantes. Neste sistema o plano xy, gira em torno do eixo Descriçao vetorial Para descrevermos matematicamente o comportamento da magnetizaçao macroscópica

Na presença do campo externo B0 ao longo do eixo

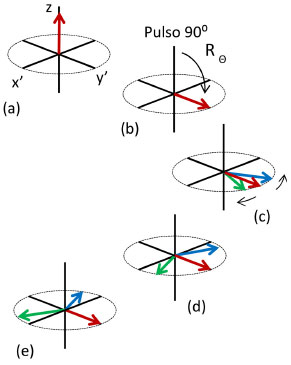 Figura 1. Diagrama vetorial da magnetizaçao macroscópica ao longo do eixo  (a), a rotaçao da magnetizaçao para o eixo y' devido à aplicaçao do pulso de r.f. (b) e a dispersao de três componentes da magnetizaçao (isocromatas) em funçao do tempo (c, d e e) em um sistema de coordenadas girantes com frequência ϖref . Para ϖ0 = ϖref, o vetor fica estacionário, ϖ0 < ϖref, o vetor sofre um atraso (gira no sentido anti-horário) e ϖ0 > ϖref, o vetor adianta (gira no sentido horário) (a), a rotaçao da magnetizaçao para o eixo y' devido à aplicaçao do pulso de r.f. (b) e a dispersao de três componentes da magnetizaçao (isocromatas) em funçao do tempo (c, d e e) em um sistema de coordenadas girantes com frequência ϖref . Para ϖ0 = ϖref, o vetor fica estacionário, ϖ0 < ϖref, o vetor sofre um atraso (gira no sentido anti-horário) e ϖ0 > ϖref, o vetor adianta (gira no sentido horário)
A RMN pulsada consiste da aplicaçao de pulsos de r.f., que rotaciona a magnetizaçao A matriz de rotaçao a ser utilizada depende da fase do pulso, por exemplo, para um pulso aplicado no eixo x' (um pulso de 90º com fase x', rotaciona a magnetizaçao para o eixo y') usa-se a matriz Rθx, equaçao 5.
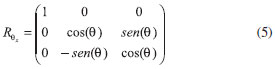
Para um pulso com fase y' usa-se a matriz Rθy.
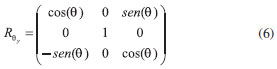
Assim, para aplicar um pulso de 90º com fase x' (Figura 1b), basta substituir os valor de θ na matriz (eq. 5) e multiplicar Rθ por
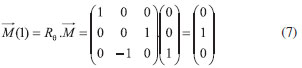
Após a aplicaçao do pulso, cada momento magnético individual ( As Figuras 1c a 1e ilustram o comportamento de três isocromatas, após o pulso, no sistema de coordenadas girante. A isocromata que está precessionando com frequência igual à frequência de referência (ϖ0 =ϖref) fica estacionada no eixo y'. As isocromatas com frequência ϖ0 >ϖref giram no sentido horário, enquanto que as isocromatas com frequência ϖ0 <ϖref giram no sentido anti-horário. Matematicamente o efeito da dispersao das isocromatas pode ser representado por outra matriz de rotaçao (RФ), equaçao 8, que descreve a defasagem de cada isocromata no plano x'y'.
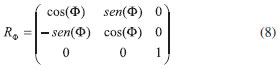
Por exemplo, para uma defasagem de 90º (Figura 2a a 2b) multiplica-se a matriz RФ pelo resultado da eq. 7,

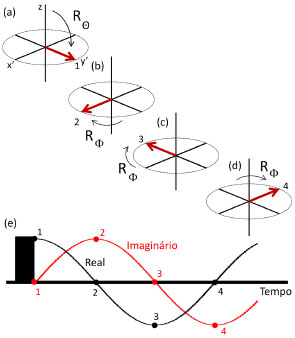 Figura 2. Diagrama vetorial de uma isocromata sob efeito de um pulso de 90º (a), seguido de três rotaçoes de 90º, RФ, no sentido horário (b) a (d). A Figura 2e representa a componente real (em y') e imaginária (em x') de um sinal fictício de RMN, com tempo de relaxaçao infinito. Os pontos 1 a 4 na Figura 2e representam os sinais dos vetores das Figuras 2a a d
Se aplicamos mais uma rotaçao de 90º, equaçao 10, a magnetizaçao chega à Figura 2c, apresentando componente no eixo -y'.

Com mais uma rotaçao calculamos
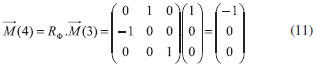
Nos experimentos de RMN podemos escolher a "posiçao" (fase) do detector no eixo de coordenadas girantes, definindo-o na sequência de pulsos. Vamos assumir que a componente Real do FID está posicionada no eixo y' e a componente Imaginária do FID no eixo x'. A Figura 2e representa a componente real e imaginária de um sinal fictício de RMN, com tempo de relaxaçao infinito. Os pontos 1 a 4 na Figura 2e representam os sinais dos vetores das Figuras 2a a d e consequentemente os resultados das equaçoes 7, 9, 10 e 11. Nas simulaçoes vamos calcular a rotaçao em pequenos incrementos de tempo, acompanhando o comportamento da magnetizaçao. A defasagem Ф utilizada na matriz de rotaçao é dada pela equaçao 12, que depende do offset de frequência da isocromata e do tempo.
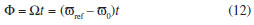
Como cada isocromata apresenta uma frequência Ω única, elas rotacionam no plano x'y' com velocidade diferente, causando o efeito da defasagem. Bloch também propôs que quando se desloca a magnetizaçao de sua posiçao de equilíbrio, ela tende a voltar a sua posiçao original, devido aos processos de relaxaçao, de modo que ocorrem dois efeitos distintos, a relaxaçao longitudinal (spin-rede), responsável pelo reaparecimento da relaxaçao no eixo longitudinal z (associada ao tempo T1) e a relaxaçao transversal (spin-spin), responsável pelo desaparecimento da magnetizaçao no plano transversal, x'y' (associada ao tempo T2). De forma fenomenológica, Bloch assumiu que esse desaparecimento e reaparecimento da magnetizaçao ocorrem de forma exponencial, ou seja, obedecem as seguintes equaçoes:1-2,9
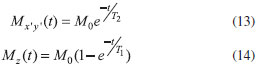
sendo T1 e T2 os tempos característico das exponenciais. Podemos reescrevê-las na forma matricial:
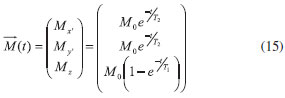
Para facilitar a escrita do código computacional usado na simulaçao, define-se a matriz E(t), que compoe os termos de relaxaçao
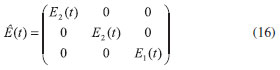
sendo E1 (t) = exp (-t/T1) e E2(t) = exp (-t/T2). Assim, após um pulso de rotaçao RФ, equaçao 7, cada isocromata começa a precessionar e relaxar de acordo com a matriz RФ e E(t), de modo que descreve-se a evoluçao temporal de cada isocromata, envolvendo a rotaçao do pulso, rotaçao de precessao e fenômenos de relaxaçao com a equaçao 17.
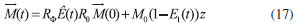
onde Ф = Ωt e M0 = 1. Reescrevendo a equaçao 17 na sua forma matricial temos a equaçao 18.
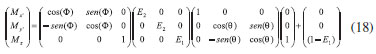
Lembrando que as matrizes R foram apresentadas na seçao anterior e sao compostas pelos termos de offset e r.f. onde, fisicamente, RФ é o operador que causa a rotaçao da magnetizaçao no plano Assim, após o pulso, a magnetizaçao resultante (
SIMULAÇAO COMPUTACIONAL DAS EQUAÇOES DE BLOCH Existem na literatura inúmeros métodos e software com o propósito de simular sinais no domínio do tempo e espectros de RMN.10-13 O objetivo deste artigo é apresentar uma descriçao simples do fenômeno utilizando as equaçoes de Bloch. Os códigos desenvolvidos foram criados de maneira semelhante a diversos outros trabalhos que utilizam soma de isocromatas pelas equaçoes de Bloch.13-15 Essa descriçao clássica1-4,9 nao permite explorar a total diversidade de fenômenos quânticos, entretanto, constitui um esquema simplificado e eficaz para a compreensao de diversos fenômenos da RMN. Além dos fenômenos físicos descritos acima, para a simulaçao real de um sinal de RMN tem-se que se levar em conta limitaçoes experimentais, como a nao-homogeneidade do campo magnético B0. Nao-homogeneidade do campo magnético B0 O campo magnético B0 de um espectrômetro de RMN nao é uniforme, possuindo uma variaçao espacial ∆B0 que depende das características do magneto e outras distorçoes experimentais. Dependendo da posiçao espacial, cada parte da amostra estará percebendo um campo magnético diferente. Assim, cada grupo de spins que está sob açao de um mesmo valor de campo magnético tem uma mesma frequência de precessao (isocromata). Desse modo, a nao-homogeneidade causa uma dispersao de frequências em torno da frequência central e consequentemente causa um alargamento da linha acima do previsto pela relaxaçao T2. Esse alargamento é denominado de T2* e depende tanto de T2 quanto ∆B0, de acordo com a equaçao 19.

sendo T2inom = 1/γ∆B0. O termo 1/T2* é representado por uma distribuiçao de isocromatas ao redor da frequência de Larmor ϖ0, e pode ser descrita por uma lorentziana (Figura 3), gaussiana ou outra distribuiçao. Assim, um sinal de RMN real nao corresponde a uma frequência de ressonância única, mas uma distribuiçao de frequências em torno da frequência central. Na Figura 3 também se vê que cada isocromata tem uma contribuiçao (intensidade) diferente na composiçao do sinal de RMN, que tem que ser levada em conta na simulaçao.
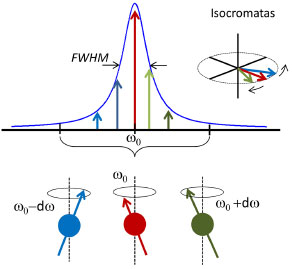 Figura 3. Distribuiçao Lorentziana de Isocromatas, conjunto de spins que sentem campo magnético diferente do central (B0) e precessionam com frequência ϖ0 ± dϖ
A distribuiçao lorentziana de frequências é dada por:2
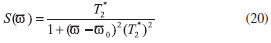
A largura da linha a meia altura (FWHM - Full width at half maximum) de uma linha lorentziana em Hertz é dada pela equaçao 21.

De modo a ter uma regiao razoável da distribuiçao das frequências de uma lorentziana, a regiao de isocromatas utilizadas na simulaçao deve ser um múltiplo da FWHM. O comportamento da magnetizaçao resultante será dado entao pela soma da contribuiçao de todas as isocromatas dentro desse intervalo de frequência. Assim, calcula-se primeiramente a evoluçao de cada isocromata no tempo, através das equaçoes 22-24 e posteriormente somamos todas essas contribuiçoes moduladas pela amplitude da lorentziana. ALGORITMO Devido ao caráter matricial das equaçoes de Bloch, uma maneira rápida e simples de realizar as simulaçoes é utilizando o software Matlab (MATrix LABoratory).16 A discretizaçao das equaçoes de Bloch (eq. 13 a 18) consiste em calcular o vetor magnetizaçao Para os pulsos instantâneos aplica-se a relaçao:
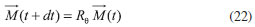
E após isso, calculamos a relaxaçao das isocromatas com:
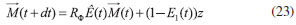
onde cada isocromata rotaciona no plano x'y' com velocidades diferente Ω. Para simplificar o programa podemos definir a relaxaçao que a magnetizaçao sofre num intervalo de tempo dt, definindo:
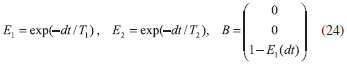
Na seçao Pulso Simples, temos o código desenvolvido para simular a aplicaçao de um pulso de ângulo θx na magnetizaçao. Nas linhas de 1 a 13, definem-se os parâmetros de entrada.
Os pulsos aplicados sao instantâneos causando rotaçao da magnetizaçao de acordo com a fase e ângulo do pulso aplicado θx. Para isso, nas linhas 14-17 escrevemos as matrizes de rotaçao Rθ (Rtheta), E e B, equaçoes 5 e 16. O próximo passo é criar o vetor Magnetizaçao onde armazenaremos a evoluçao das isocromatas no tempo, linhas 18-22, Figura 4.
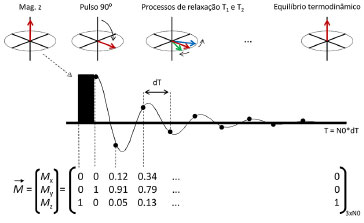 Figura 4. Esquema Simulaçao
Na linha 23 inicia-se o loop para simulaçao de cada uma das isocromatas, sendo o número total de isocromatas igual a 'length(df)'. Assim, para calcular a evoluçao de cada isocromata, primeiro calcula-se a matriz Rphi (RФ), equaçao 8. Em seguida, aplicamos o pulso de ângulo θ, através da equaçao 22 (linha 26), gerando a segunda coluna do vetor M(:,2), apresentado na Figura 4b. Após o pulso, inicia-se um novo loop onde a isocromata evolui sofrendo os processos de relaxaçao (equaçao 23), linhas 27-28, calculando os valores de M(:,3) até M(:,N0 -1). Para cada cálculo se utiliza o valor da magnetizaçao imediatamente anterior, equaçao 23. Após calculada toda a matriz M, nas linhas 29-33 efetuamos a soma das isocromatas com suas respectivas intensidades de acordo com a distribuiçao lorentziana assumida para a inomogeneidade de B0 (equaçao 20). Por fim, nas linhas 37-42 fornecemos os comandos para gerar a visualizaçao da simulaçao. Detalhes computacionais Alguns cuidados e "insights" sao necessários durante a escolha dos parâmetros da simulaçao. Caso defina um número insuficiente de isocromatas ("length(df)"), uma regiao errada ou pequena de frequências, artefatos disfarçados de 'ecos' podem surgir no sinal. É sempre necessário certificar-se que está simulando uma regiao efetiva da distribuiçao de inomogeneidade e que um número razoável de isocromatas está sendo utilizado. Por exemplo, se mudarmos o valor da inomogeneidade de campo (T2*), a largura de linha FWHM muda, e possivelmente o incremento e a regiao das isocromatas devem mudar, dentre outros parâmetros. Claramente, os códigos apresentados podem ser otimizados utilizando funçoes, dentre outras possibilidades do Matlab, no entanto, para facilitar ao leitor mais inexperiente escrevemos o código numa única folha de maneira direta e simples. Códigos para as sequências Spin-Eco e Inversao Recuperaçao estao disponíveis no material suplementar (Apêndices) com acesso livre no site da revista. Uma boa introduçao à programaçao em Matlab é a referência,17 entretanto, nossos códigos podem ser facilmente adaptados para outros softwares que trabalham diretamente com matrizes, como os softwares de distribuiçao livre Octave18 e Scilab.19
SEQUENCIAS DE PULSOS Podemos agora visualizar o comportamento da magnetizaçao para diversas sequências de pulsos. Nas Figuras 5 e 6 colocamos uma linha tracejada representando o decaimento exponencial, T2. Para todos os sinais utilizamos T1 = 600 ms, T2 = 400 ms e os demais parâmetros especificados no texto.
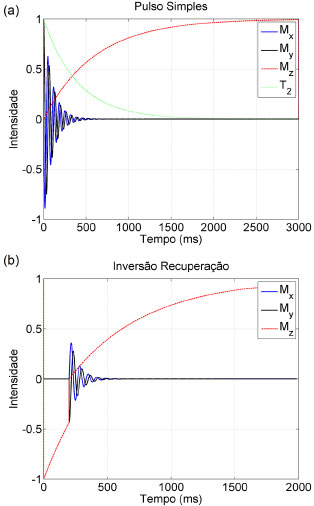 Figura 5. (a) Sinal FID simulado da aplicaçao de um pulso simples de ângulo θx 90°. Em (b) temos a simulaçao da sequência de Inversao Recuperaçao. Com T1 = 600 ms, T2 = 400 ms e T2inom = 200 ms
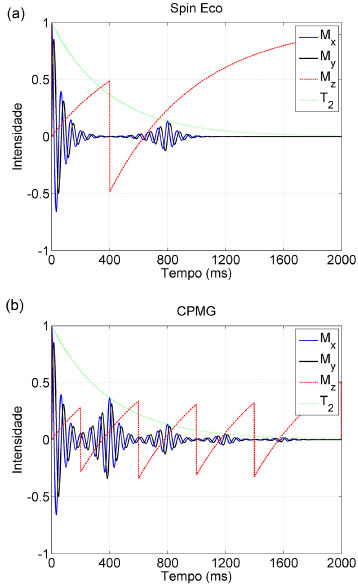 Figura 6. (a) Simulaçao para a sequência Spin-Eco, com τ =400 ms, resultando num eco em t = 800 ms. Em (b) temos a simulaçao da sequência CPMG, que consiste de um pulso de 90° y seguido após um tempo τ = 200 ms por um trem de pulsos de 180°x espaçados por τ = 400 ms, assim observamos ecos nos tempos t = 400 ms, 800 ms, 1200 ms e 1600 ms. Com T1=600 ms, T2=400ms e T2inom= 100 ms
Pulso Simples A Figura 5a apresenta a simulaçao da aplicaçao de um pulso simples θx = 90º. O decaimento da magnetizaçao evidencia o efeito dos tempos de relaxaçao T1, T2 e T2* até atingir o equilíbrio termodinâmico em aproximadamente 5T1. Nesta Figura nota-se que o decaimento do FID (T2*) ocorre mais rapidamente que o T2 intrínseco da amostra, devido à inomogeneidade de campo magnético. Sequência Inversao Recuperaçao A sequência de pulsos Inversao Recuperaçao consiste da aplicaçao inicial de um pulso de 180ºx seguido, após um tempo τ, por um pulso de 90ºx. Na Figura 5b, logo após o pulso de 180ºx a magnetizaçao é invertida na direçao - Sequência Spin-Eco A sequência de pulso Spin-Eco consiste da aplicaçao inicial de um pulso de 90ºy seguido após um tempo τ por um pulso de 180ºx. Na Figura 6a, logo após o pulso de 90ºy a magnetizaçao inicia os processos de relaxaçao. Após um tempo τ aplica-se o pulso de 180ºx que inverte as isocromatas do plano x'y' e, assim, surge um eco em t = 2τ. Como esperado, a sequência Spin-Eco produz um eco com amplitude máxima coincidente com a curva do decaimento T2. Essa mesma sequência pode ser utilizada para simular o Eco de Hahn. Para tal, devemos utilizar dois pulsos de 90ºy espaçados por t, assim, um eco de amplitude diferente surge no tempo t = 2τ. Sequência CPMG Na Figura 6b tem-se a simulaçao da sequência de Carr-Purcell-Meiboom-Gill (CPMG), que é o método padrao para medida de T2. A sequência consiste de um pulso de 90ºy seguido, após um tempo τ = 200 ms, por um trem de pulsos de 180ºx espaçados por τ = 400 ms. Assim, observamos ecos nos tempos t = 400 ms, 800 ms, 1200 ms e 1600 ms. As amplitudes dos ecos reproduzem o decaimento exponencial T2, possibilitando assim a medida experimental desse tempo de relaxaçao. Demais experimentos Diversos experimentos de RMN podem ser facilmente simulados utilizando a metodologia apresentada neste artigo. Algumas sugestoes a serem exploradas sao:
Dentre outros mais trabalhosos para implementar:
Além de diversas outras sequências de pulsos (Eco Estimulado, Eco de Hahn, CWFP, CP-CWFP, etc..), com obtençao de perfis de excitaçao ou experimentos em duas dimensoes.
CONCLUSAO A simulaçao através da descriçao semi-clássica da RMN nao reproduz todas as interaçoes e efeitos observados na prática experimental, no entanto, é fácil de implementar e fornece bons resultados quando queremos compreender o comportamento dos fenômenos spin-eco ou possibilitar uma melhor compreensao da influência dos diversos parâmetros experimentais. Através de códigos simples, desenvolvidos no Matlab, apresentamos simulaçoes das sequências Pulso Simples, Inversao Recuperaçao, Spin-Eco e CPMG.
MATERIAL SUPLEMENTAR Códigos para as sequências de pulso Spin-Eco, Inversao Recuperaçao e CPMG estao disponíveis no material suplementar com acesso livre no site da revista (http://quimicanova.sbq.org.br/). Caso o leitor queira obter códigos de outras sequências de pulso ou a versao com pacote de funçoes, podem entrar em contato com os autores pelo e-mail: tiagobuemoraes@gmail.com.
PULSO SIMPLES - MATLAB 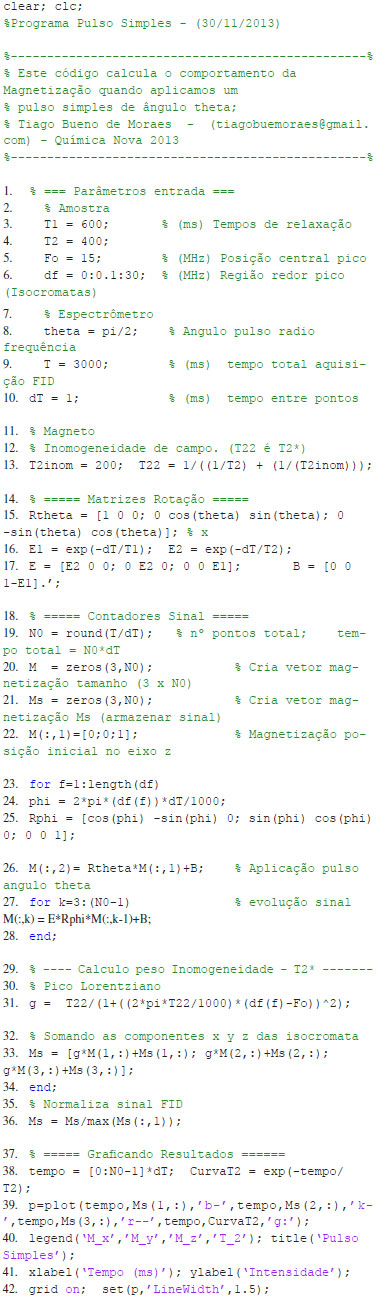
AGRADECIMENTOS A Embrapa Instrumentaçao pela infraestrutura cedida. A FAPESP pelo auxílio concedido Processo 2011/11160-3 e CNPq processo 301087/2009-1.
REFERENCIAS 1. Gil, V. M. S.; Geraldes, C. F. G. C.; Ressonância magnética nuclear: fundamentos, métodos e aplicaçoes, Fundaçao Calouste Gulbekian: Lisboa, 1987. 2. Levitt. M. H.; Spin Dynamics: Basics of Nuclear Magnetic Resonance, 2nd Edition, John Wiley & Sons, Ltd: Chichester, 2008. 3. Hoult, D. I., Bhakar, B.; Concepts Magn. Reson. 1997, 9, 277. 4. Hoult, D. I., Ginsberg. N. S.; J. Magn. Reson. 2001, 148, 182. 5. Ridgen, J. S.; Rev. Mod. Phys. 1986, 58, 433. 6. Purcell, E. M.; Torrey, H. C.; Pound, R. V.; Phys. Rev. 1946, 69, 37. 7. Bloch, F.; Hansen, W. W.; Packard, M.; Phys. Rev. 1946, 70, 474. 8. Bloch, F.; Phys. Rev. 1946, 70, 460. 9. Abragram, A.; The principles of nuclear magnetism, Oxford University Press: Londres, 1961. 10. Roberts, J. D.; Concepts Magn. Reson. 1991, 3, 27. 11. Bain, A. D.; Anand, C. K.; Nie, Z; J. Magn. Reson. 2010, 206, 227. 12. Madhu, P. K.; Kumar, A.; Concepts Magn. Reson. 1997, 9, 1. 13. Lars G. Hanson; Concepts Magn. Reson. 2008, 32A, 329. 14. Shkarin, P., Spencer, R. G. S.; Concepts Magn. Reson. 1996, 8, 253. 15. http://mrsrl.stanford.edu/~brian/bloch/, acessada em Agosto 2013. 16. MATLAB; version 7.10.0 (R2010a), MathWorks Inc., Natick, Massachusetts, EUA, 2010. 17. Palm III, W. J.; Introduçao ao MATLAB para Engenheiros, 3 ed., editora McGraw-Hill, 2013. 18. http://www.gnu.org/software/octave/, acessada em Novembro 2013. 19. http://www.scilab.org/, acessada em Novembro 2013. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






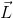 =
= 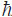
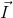 ) e momento magnético (
) e momento magnético (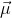 = γ
= γ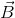 0) e um campo oscilante (
0) e um campo oscilante (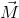 , sob a influência de
, sob a influência de