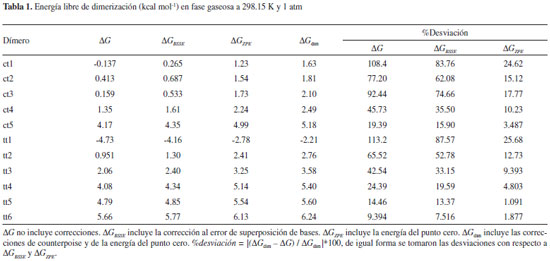
Artigo
|
|
| Exploración estocástica de las superficies de energía potencial de dímeros cis-trans y trans-trans del ácido fórmico Stochastic search on potential energy surface of cis-trans and trans-trans formic acid dimers |
|
Said F. Figueredo*; Adolfo E. Ensuncho; Jesús M. López
Universidad de Córdoba, Departamento de Química, Cra 6 Nº 76-103, Montería, Córdoba-Colombia Recebido em 27/03/2014 *e-mail: saifer87@gmail.com Potential energy surface (PES) of cis-trans and trans-trans formic acid dimers were sampled using a stochastic method, and the geometries, energies, and vibrational frequencies were computed at B3LYP/6-311++G(3df,2p) level of theory. The results show that molar free energy of dimerization deviated up to 108.4% when basis set superposition error (BSSE) and zero-point energy (ZPE) were not considered. For cis-trans dimers, C=O and O-H bond weakened, whereas C-O bonds strengthened due to dimerization. Also, trans-trans FA dimers did not show a trend regarding strengthening or weakening of the C=O, O-H and C-O bonds. INTRODUCCION La búsqueda computacional de geometrías de equilibrio se realiza típicamente construyendo las respectivas superficies de energía potencial (PES, por sus siglas en inglés) mediante métodos analíticos ó estocásticos.1 Aunque los métodos analíticos conllevan a puntos estacionarios de alta calidad, no son viables para una exploración exhaustiva del espacio conformacional por su imposibilidad de saltar sobre barreras de energía; además, las estructuras correspondientes a mínimos de energía dependen de una predicción inicial de la geometría molecular.2 Por otro lado, los métodos estocásticos realizan una búsqueda aleatoria del espacio conformacional3 generando estructuras candidatas para subsecuente refinamiento a partir de cálculos mecano-cuánticos. Estos métodos tienen la ventaja de no depender de una predicción inicial de la geometría, además de la habilidad de saltar sobre barreas de energía potencial.2,3 En el presente trabajo, se ha aprovechado la capacidad del programa ASCEC (annealing simulado con energía cuántica)4 de simular clusteres atómicos y moleculares1 para construir las PES de dímeros de ácido fórmico (FAD, por sus siglas en inglés) y obtener estructuras candidatas para subsecuente optimización por métodos analíticos. Los dímeros de ácido fórmico se han estudiado, tanto a nivel teórico5-8 como experimental,9-13 debido a que se consideran un prototipo para complejos moleculares con enlaces de hidrógeno,7 y a que son sistemas que exhiben una acentuada direccionalidad y cierto grado de cooperatividad en tales interacciones.12 Diversas investigaciones sobre los FAD también se han enfocado en los procesos de transferencia protónica que resultan similares a los que ocurren en sistemas químicos más complejos y en sistemas biológicos tales como el DNA.14,15 La forma cíclica de FAD11 ha sido estudiada por resonancia magnética nuclear,16,17 espectroscopia IR y Raman,18 difracción de electrones,19 entre otras técnicas experimentales;11,12,20 y por simulaciones de dinámica molecular21-23 y química cuántica.11,24 Esta estructura también ha sido de gran interés debido al doble enlace de hidrógeno simétrico que ocurre.18 Asimismo, formas no cíclicas de FAD11 también se han considerado importantes, ya que a bajas temperaturas, cristales de ácido fórmico (FA, por sus siglas en inglés) contienen pares FAD acíclicos como se ha demostrado a través de análisis de rayos-X y difracción de neutrones.25 Recientemente, Balabin11 encontró un FAD acíclico (polar) en fase gaseosa utilizando espectroscopia Raman para la extracción de datos vibracionales y de parámetros termodinámicos (entalpías de dimerización). También, Marushkevich y colaboradores10 encontraron cinco nuevas estructuras de FAD en una matriz de argón empleando métodos fotoquímicos. Atendiendo a que aún se siguen buscando nuevos dímeros de ácido fórmico,10 en el presente trabajo se empleó una metodología desarrollada recientemente en la exploración de las superficies de energía potencial de clústeres1,26-31 con el fin de generar estocásticamente las PES de los FAD cis-trans y trans-trans para determinar la estabilidad relativa de los diversos arreglos moleculares que ocurren en los dímeros de ácido fórmico, y a partir de estos, contribuir al entendimiento del efecto de la dimerización sobre la estructura electrónica de las sub-unidades monoméricas cis-FA y trans-FA.
METODOLOGIA COMPUTACIONAL Exploración de las superficies de energía potencial de los FAD con ASCEC El programa ASCEC dispone de una versión adaptada del algoritmo de optimización annealing simulado (AS),3,32 en la cual, la energía de cada configuración nuclear es calculada por métodos cuánticos llamando a un programa externo, en nuestro caso, Gaussian03 (rev. E.01.).33 Los movimientos atómicos que generan las diferentes configuraciones son aceptados de acuerdo a una versión modificada de la prueba de aceptación de Metropolis (consultar referencia 1 para más detalles). Una ejecución del programa ASCEC requiere los siguientes datos:1,27 (i) la longitud del cubo en el que el sistema estará envuelto (Å). (ii) Una ruta de enfriamiento: temperatura inicial, temperatura final, y una ruta de conexión entre estas. ASCEC permite elegir entre dos rutas de enfriamiento, una lineal (disminución de T por una cantidad constante) y una geométrica (disminución de T por un porcentaje constante). (iii) Número máximo de estructuras a evaluar a cada temperatura (MaxCyc). (iv) El número de elementos presentes en el clúster. (v) Una combinación Hamiltoniano/base para los cálculos de energía. (vi) La carga y la multiplicidad de espín del sistema. (vii) Número de moléculas que conforman el clúster. (viii) La geometría inicial de cada molécula en coordenadas cartesianas. (ix) Máximo desplazamiento permitido (Å) y el máximo ángulo de rotación (radianes) para las moléculas individuales dentro de la estructura del clúster. Se realizaron los corridos de ASCEC para los dímeros cis-trans (ct) y trans-trans (tt) del ácido fórmico, envolviendo estos sistemas bajo las condiciones del annealing dentro de un cubo de 8 Å de longitud; la ruta de enfriamiento fue geométrica con una temperatura inicial de 500 K, porcentaje de disminución del 5% y un total de 300 temperaturas. El máximo desplazamiento permitido y el máximo ángulo de rotación fueron respectivamente 1 Å y 1 rad. Se eligió el modelo semiempírico PM3 como Hamiltoniano cuántico para las evaluaciones de energía, ya que se ha reportado como una aproximación razonable en el tratamiento de sistemas con enlaces de hidrógeno.34,35 Con el propósito de encontrar nuevos mínimos locales sobre las PES de los FAD, se recurrió a los modelos AM1 y HF/3-21G como metodología mecano-cuántica para subsecuentes ejecuciones del programa ASCEC, lo que permitió encontrar estructuras candidatas adicionales para los cálculos de optimización analítica. Tratamiento de los puntos estacionarios El programa ASCEC genera una serie de estructuras candidatas, las cuales se optimizan posteriormente a través de métodos analíticos.30 Para llevar a cabo los cálculos de optimización y de frecuencias vibracionales, se utilizó el funcional híbrido B3LYP en conexión con la base 6-311++G(3df,2p), ya que este nivel de teoría ha proporcionado resultados consistentes con las medidas experimentales de las geometrías de equilibrio, energías y frecuencias vibracionales de monómeros y dímeros de ácido fórmico.11 Además, se tuvieron en cuenta las siguientes correcciones a la energía: (i) corrección de la energía del punto cero (ZPE, por sus siglas en inglés) debido a que la ZPE es significativa en sistemas con enlaces de hidrógeno;36,37 (ii) corrección del error por superposición de bases (BSSE, por sus siglas en inglés)38 ya que este conduce a una sobre-estimación de las energías de interacción.36,39 BSSE fue tomado en cuenta durante los cálculos de optimización utilizando el esquema propuesto por Boys y Bernardi40 (método counterpoise). La estabilidad termodinámica de los dímeros se analizó a partir de la energía libre molar (potencial químico termodinámico) de dimerización a 298 K y 1 atm, que en cada caso se calculó como ΔGdim = Gdímero - ΣGmonómeros. Todos los cálculos de optimización, frecuencias vibracionales y de energía, fueron realizados con el paquete computacional Gaussian03 (rev. E.01.).33 Adicionalmente, se analizaron las fortalezas relativas de las interacciones HO---H, C-O, y C=O a partir de los índices de enlace de Wiberg,41,42 calculados mediante el programa NBO43 (implementado en Gaussian03). Este parámetro, considerado como una medida de la multiplicidad del enlace entre dos átomos, se calculó como:44 WAB = Σµ∈AΣv∈B|Dµv|2, donde Dµv son los elementos de la matriz densidad. Las fortalezas de los enlaces C-O, C=O y O-H de los dímeros fueron comparadas con las de los respectivos monómeros para estudiar los efectos de la dimerización sobre la estructura electrónica y estabilidad de los dímeros.
RESULTADOS Y DISCUSION De las PES generadas por ASCEC, se seleccionaron varias estructuras candidatas (mínimos de energía) para los cálculos subsecuentes, sin embargo, durante los cálculos de optimización varias estructuras de partida convergieron a una misma geometría de equilibrio. La optimización geométrica con B3LYP/6-311++G(3df,2p) generó cuatro diferentes geometrías de equilibrio para los dímeros tt (tt1, tt2, tt3, tt4); y tres para los dímeros ct (ct1, ct2, ct3) optimizados con el mismo modelo. Con el objetivo de realizar una búsqueda exhaustiva del espacio conformacional de los FAD, también se construyeron las PES en AM1 de los sistemas ct y tt, en las que fue necesario descartar muchos mínimos de energía que tuvieran configuraciones atómicas similares debido a que podían converger a geometrías ya conocidas durante los cálculos de optimización. De hecho, solo se encontraron dos estructuras candidatas adicionales para ct y una para tt. Luego de optimizar estas estructuras con el modelo de trabajo B3LYP/6-311++G(3df,2p), se obtuvieron los dímeros ct4, ct5 y tt5. Además, se realizaron dos corridos adicionales de annealing simulado con el modelo HF/3-21G, de los cuales, se obtuvo una nueva estructura candidata tt para optimización y ninguna estructura nueva ct. La posterior optimización con B3LYP/6-311++G(3df,2p) generó el dímero tt6. En las Figuras 1 y 2 se muestran las estructuras de los dímeros tt y ct respectivamente en orden decreciente de estabilidad. En estas figuras, los enlaces de hidrógeno más importantes se representan mediante líneas punteadas, mostrando la longitud de enlace y el respectivo índice de enlace de Wiberg (orden de enlace) entre paréntesis.
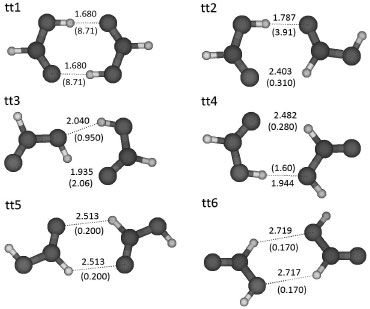 Figura 1. Geometrías optimizadas de los dímeros tt organizados en orden decreciente de estabilidad. Se muestran las longitudes de los enlaces de hidrógeno (Å) con sus respectivos órdenes de enlace (x10-2) entre paréntesis. Código de colores/átomo: blanco=hidrógeno, gris oscuro=carbono, gris=oxígeno
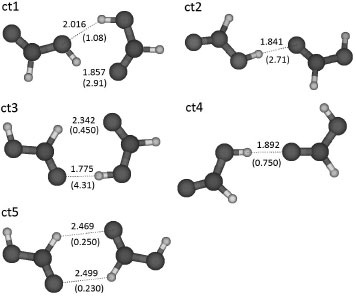 Figura 2. Geometrías optimizadas de los dímeros tt organizados en orden decreciente de estabilidad. Se muestran las longitudes de los enlaces de hidrógeno (Å) con sus respectivos órdenes de enlace (×10-2) entre paréntesis. Código de colores/átomo: blanco=hidrógeno, gris oscuro=carbono, gris=oxígeno
En total se encontraron seis dímeros trans-trans y cinco dímeros cis-trans sobre la superficie de energía potencial intermolecular. Todas las estructuras tt contienen dos enlaces de hidrógeno, y solo en tt1 y tt3 no hay ocurrencia de enlaces de hidrógeno secundarios (C-H---O). Tres de los cinco dímeros ct contienen dos enlaces de hidrógeno, pero solamente en ct1 ambas interacciones son del tipo primario. De las once estructuras calculadas para los dímeros del ácido fórmico, ocho están en buen acuerdo con las reportadas por Marushkevich y colaboradores.45 En su trabajo, el dímero trans-trans más estable (tt1), tiene estructura cíclica simétrica y una energía de interacción de -57.5 kJ mol-1 correspondiendo al dímero tt1 reportado aquí. Otras siete estructuras discutidas en su trabajo tienen patrones geométricos similares a nuestros dímeros tt2 (tt3), tt3 (tt4), tt4 (tt5), tt5 (tt6), ct1 (tc2), ct2 (tc3) y ct3 (tc1); por otro lado, sus estructuras tt3, tc4 y tc5 no fueron encontradas en el presente estudio. Las otras estructuras discutidas aquí (tt6, ct4 y ct5) no fueron consideradas en el artículo de Marushkevich y colaboradores.45 Adicionalmente, las estructuras tt1, tt3, tt4, y ct3 coinciden respectivamente con los dímeros FAD1, FAD7, FAD3 y FAD6 reportados por Roszak y colaboradores.46 En el presente trabajo se ha determinado la estabilidad relativa de los dímeros de ácido fórmico a partir de la variación en la energía libre de Gibbs.47,48 A pesar de que este término incluye parte de la energía de interacción, no es utilizado como una medida directa de las energías de interacción de los enlaces de hidrógeno, sino como una medida de la estabilidad relativa de los diferentes dímeros encontrados sobre las PES. En la Tabla 1 se muestran los resultados obtenidos para la energía Gibbs de dimerización (ΔGdim) con y sin las correcciones de la energía del punto cero (ZPE) y de counterpoise. Las correcciones anteriormente mencionadas fueron realizadas inicialmente sobre la energía electrónica total que resulta de los cálculos SCF (Self Consistent Field), y luego aplicadas a la energía de Gibbs, que se relaciona con la energía electrónica mediante la expresión G = Gterm + E0,47 donde la suma del lado derecho de la igualdad es obtenida a partir de los cálculos de frecuencias armónicas realizados por Gaussian03.33,49 También se dan las desviaciones porcentuales de la energía libre de dimerización con respecto a la energía libre no corregida (ΔG), la energía libre más la corrección del BSSE (ΔGBSSE), y la energía libre más la corrección de la ZPE (ΔGZPE). Se observa que el orden en la estabilidad de los dímeros no cambia al considerar correcciones sobre la energía libre de dimerización, excepto para las estructuras ct2 y ct3, que sin correcciones tienen energías libre de 0.413 y 0.159 kcal mol-1 respectivamente, y con la corrección del BSSE tienen energías libre de 0.687 y 0.533 kcal mol-1 respectivamente. Sin embargo, al tomar en cuenta la corrección de la ZPE, las energías libre de dimerización para ct2 y ct3 son 1.54 y 1.73 kcal mol-1, por lo tanto, se demuestra que al no considerar la corrección de la energía del punto cero puede ocurrir una inversión en la estabilidad de pares como ct2 y ct3 con respecto al orden de estabilidad esperado al tomar las correcciones sobre la energía.
Los porcentajes de desviación de la energía libre de dimerización con respecto a la energía libre no corregida, a la energía corregida por BSSE, y a la energía corregida por ZPE, disminuyen al disminuir la estabilidad de los dímeros, excepto para la secuencia ct2-ct3, ya que ct3 presenta mayor desviación en la energía libre que ct2 en los tres casos. Para los dímeros tt también se presenta esta tendencia, a mayor estabilidad, mayor porcentaje de desviación en la energía libre, sin embargo, ocurre una excepción para la estructura tt6, que siendo menos estable que tt5 tiene un mayor porcentaje de desviación de ΔGdim con respecto a la energía corregida por ZPE (ΔGZPE) (1.877 kcal mol-1 para tt6 y 1.091 kcal mol-1 para tt5). De los datos reportados en la Tabla 1, se observa que la energía libre de dimerización se desvía más al no tener en cuenta la ZPE que al no considerar el BSSE, por ejemplo, para tt1 la energía libre presenta un error del 25.68% al corregir la energía por inclusión de la ZPE y omisión del BSSE, un valor considerablemente menor que el error obtenido (87.57%) al tomar la corrección del BSSE y omitir la ZPE. De lo anterior, se infiere que la energía de vibración del punto cero (ZPE) contribuye mucho más a la energía libre que la energía debida al error de superposición de bases (BSSE). La mayor desviación ocurrida al no corregir la energía libre es del 113.2% para el dímero tt1, y la menor desviación es del 9.394% para la energía libre de tt6. Estos resultados ratifican la necesidad de considerar las correcciones de la ZPE y del BSSE para no sobre-estimar la estabilidad de las estructuras. Los enlaces de hidrógeno más fuertes tienen órdenes de enlace relativamente grandes, y por lo tanto, longitudes de interacción cortas, entre 1.680 y 1.841 Å. En la Figura 3 se muestra una gráfica que representa las longitudes de enlace frente a los órdenes de enlace respectivos para enlaces de hidrógeno entre 1.680 y 1.944 Å. Los datos de distancia de enlace (χ) como función de los órdenes de enlace (Φ) se ajustan bien a una regresión cúbica, sin embargo, una mejor correlación se obtuvo graficando e1/χ vs ø1/4, y luego aplicando la regresión cúbica.
 Figura 3. Longitud de los enlaces de hidrógeno (Å) en función de los órdenes de enlace (×10-2)
Para la gráfica dada en la Figura 4, se tiene una correlación cúbica con R2=1, de aquí que las distancias de interacción de los enlaces de hidrógeno primarios se pueden expresar en función de los órdenes de enlace a través de la ecuación:

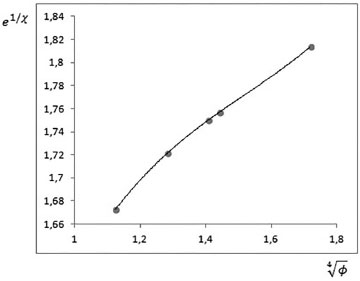 Figura 4. Los puntos en la gráfica corresponden a los datos de e1/χ y ø1/4, la línea continua es la línea de tendencia hallada por regresión cúbica (R2 = 1)
donde χ es la longitud del enlace de hidrógeno y ø es el correspondiente orden de enlace. Los parámetros de la regresión son: a =0.3835; b =-1.7465; c = 2.8441; d =0.1374. En la Tabla 2 se comparan los valores de las longitudes de algunos enlaces de hidrógeno primario con los valores calculados mediante la ec. 1.
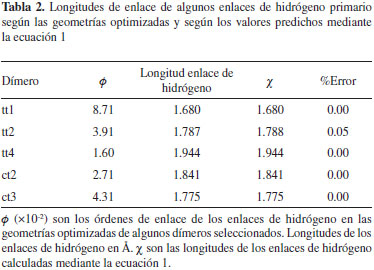
Con el propósito de comparar las fortalezas relativas de los enlaces C-O, C=O, O-H y C-H presentes en los mómeros cis y trans aislados, se calcularon los órdenes y longitudes de enlace de estas interacciones con el mismo nivel de teoría empleado para los dímeros. Los resultados se resumen en la Tabla 3. El enlace C-O en el monómero trans es más corto y tiene un mayor orden de enlace con respecto al monómero cis; asimismo, el enlace C-H en el monómero trans es más corto que en el cis, a pesar de que en este último el orden de enlace para la interacción C-H es mayor. Para la interacción C=O se observa una menor distancia de enlace (y un orden de enlace mayor) en el confórmero cis; y por último, el átomo de hidrógeno hidroxílico se encuentra más fuertemente unido al átomo de oxígeno en el confórmero cis-FA. De lo anterior, se infiere que la interacción C-O es más fuerte en el monómero trans, y que el doble enlace C=O en el confórmero cis es más fuerte. Estos resultados demuestran que la orientación espacial del grupo hidroxilo induce a cambios en la estructura electrónica global de las moléculas, donde el fortalecimiento o debilitamiento de cierto tipo de enlace promueve que las fortalezas de otros enlaces se vean modificadas considerablemente.
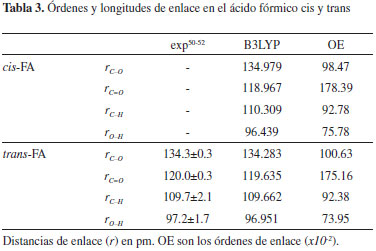
El efecto de la dimerización sobre la fortaleza de las interacciones C-O, C=O y O-H, se discute a partir de las desviaciones porcentuales de los órdenes de enlace en los dímeros con respecto a las interacciones en los monómeros aislados. Los resultados se muestran en la Tabla 4. El signo negativo indica una disminución en el orden de enlace (debilitamiento de la interacción) como consecuencia del proceso de dimerización. En los dímeros ct se observa que independientemente de la conformación de las sub-unidades (cis o trans), ocurre un debilitamiento de las interacciones C=O, que es más notable en los casos en los que el átomo de oxígeno participa en interacciones C=O--H, tal como ocurre en el residuo trans de todas las estructuras ct y en el residuo cis de ct3 y ct5. En las sub-unidades cis y trans de los dímeros ct, los enlaces O-H también se encuentran desfavorecidos en todos los casos (excepto para el enlace O-H del residuo cis del dímero ct5), siendo mayor este efecto cuando el grupo hidroxilo participa en enlaces de hidrógeno (sub-unidades cis y trans de ct1, sub-unidades cis de ct2 y ct4, sub-unidad trans de ct3). En la estructura ct1, el enlace O-H del residuo cis es aproximadamente 12% más débil con respecto al conformero cis aislado, lo que puede atribuirse al hecho de que el hidroxilo participa simultáneamente en dos enlaces de hidrógeno, a través del átomo de oxígeno y del hidrógeno respectivamente (ver Figura 2). La interacción C=O en la sub-unidad cis del dímero ct3 presenta la mayor desviación para este tipo de enlace: es aproximadamente 5.65% más débil con respecto al enlace C=O del monómero cis aislado; asimismo, la mayor desviación del enlace O-H ocurre en el residuo trans del dímero ct3, en el cual, el enlace O-H es aproximadamente un 13.4% más débil que en el residuo trans aislado. Para los dímeros ct, a excepción de ct1, se observa que los enlaces C-O están fortalecidos con respecto al enlace C-O de las sub-unidades cis y trans, siendo mayor en el residuo trans del dímero ct3, donde el enlace C-O es aproximadamente 5.96% más fuerte que en el monómero trans aislado.
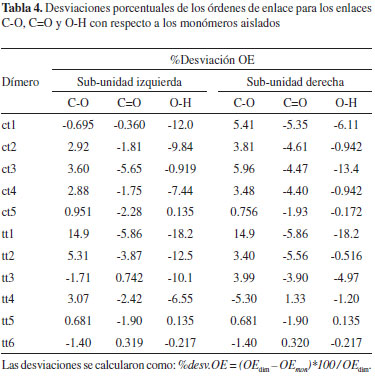
En el caso de las estructuras tt, no se observa una tendencia uniforme en cuanto al efecto de la dimerización sobre los enlaces C-O: en la sub-unidad izquierda de los dímeros tt1, tt2, tt4 y tt5, y en la sub-unidad derecha de los dímeros tt1, tt2, tt3 y tt5, se observó un fortalecimiento de las interacciones C-O. Los enlaces C=O están ligeramente debilitados en el residuo izquierdo de tt1, tt2, tt4 y tt5; así como en el residuo derecho de tt1, tt2, tt3 y tt5. Todos los enlaces O-H en las estructuras tt son menos fuertes que en los conformeros trans aislados, excepto en los dos residuos trans de la estructura simétrica tt5. Las sub-unidades trans en tt1 (el dímero más estable) presentan la mayor desviación sobre la fortaleza de los enlaces O-H, ya que los cálculos B3LYP/6-311++G(3df,2p) predicen que la fuerza de estas interacciones disminuyen en un 18.2% respectivamente con respecto al enlace O-H del conformero trans aislado. Los cálculos realizados predicen que el dímero más estable a 298.15 K es tt1 (figura 1) con una energía libre de dimerización de -2.21 kcal mol-1. Esta estructura ha sido estudiada extensivamente y se le atribuyen propiedades como apolaridad,9 direccionalidad y cooperatividad en los enlaces de hidrógeno, planaridad12 y ocurrencia de dos enlaces de hidrógeno simétricos. En la Tabla 5 se reportan las longitudes de enlace experimentales y calculadas para el dímero tt1. Al comparar los valores experimentales de las longitudes de enlace con los valores calculados, se observa que la menor desviación se presenta para la longitud de enlace C=O (aproximadamente 0.08%), seguida por la del enlace C-O. La mayor desviación de nuestros cálculos con respecto a los datos experimentales para tt1, se observa en la longitud de enlace C-H, donde la desviación es aproximadamente de 1.49%.
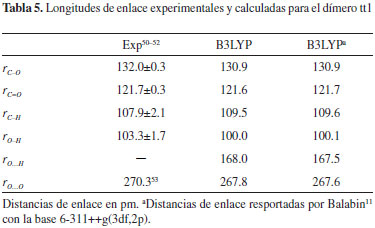
CONCLUSIONES Se encontraron seis dímeros trans-trans y cinco dímeros cis-trans estables sobre la superficie de energía potencial. De nuestro conocimiento, los dímeros tt6, ct4 y ct5 son reportados por primera vez. El algoritmo estocástico implementado en el programa ASCEC ha confirmado ser una herramienta razonable para la exploración de las superficies de energía potencial de agregados moleculares como los estudiados en el presente trabajo. Las energías libre de dimerización, órdenes de enlace y geometrías de equilibro de todos los dímeros, fueron computacionalmente evaluadas mediante el modelo B3LYP/6-311++G(3df,2p). La estabilidad termodinámica de los FAD fue determinada mediante la energía libre de dimerización, y los cambios en la estructura electrónica fueron discutidos a partir del índice de enlace de Wiberg. Se reportan desviaciones en la energía libre de dimerización entre aproximadamente un 9 y 100% al no considerar las correcciones de la ZPE y del BSSE, sin embargo, de acuerdo a nuestros cálculos, la energía de vibración del punto cero contribuye mucho más a la energía de dimerización que el error por superposición de bases. De lo anterior, se ratifica la pertinencia de tomar las correcciones de la ZPE y del BSSE en esta línea de trabajo. El dímero trans-trans más estable fue la estructura simétrica tt1 con una energía Gibbs de dimerización de -2.21 kcal mol-1, mientras que el dímero cis-trans termodinámicamente más favorable fue ct1 (ΔGdim = 1.63 kcal mol-1). La diferencia de energía entre el FAD más estable (tt1) y el menos estable (tt6) resultó ser de 8.45 kcal mol-1. Los enlaces de hidrógeno fuertes mostraron órdenes de enlace relativamente altos y longitudes de interacción cortas. Para enlaces de hidrógeno con distancias de interacción menores a 2 Å, se encontró una relación matemática cúbica para e1/χ como función de ø1/4 con un coeficiente de determinación de R2 =1. De los cálculos realizados sobre los monómeros aislados, se observó un debilitamiento de los enlaces C=O y O-H al pasar del confórmero cis al trans, dando lugar al fortalecimiento ocurrido en el enlace C-O del confórmero trans con respecto al cis. En el caso de los dímeros cis-trans, ocurre un fortalecimiento del enlace C-O en la mayoría de los casos, mientras que las fortalezas de los enlaces C=O y O-H se vieron disminuidas como consecuencia de la formación de los dímeros. En contraste, las estructuras trans-trans no mostraron tendencias uniformes en cuanto al fortalecimiento y/o debilitamiento de los diferentes enlaces. Estos resultados, en conexión con los reportados en otras investigaciones enfocadas en los cambios espectroscópicos ocurridos por la dimerización,45 demuestran los diversos cambios que ocurren en la densidad electrónica molecular de acuerdo a las distintas formas en que interactúan las unidades cis y trans del ácido fórmico.
AGRADECIMIENTOS Al Centro de Investigación Universidad de Córdoba (CIUC) por la financiación. Al Ph.D A. Restrepo por el soporte del programa ASCEC.
REFERENCIAS 1. Pérez, J. F.; Florez, E.; Hadad, C. Z.; Fuentealba, P.; Restrepo, A.; J. Phys. Chem. A 2008, 112, 5749. 2. Restrepo, A.; Marí, F.; González, C.; Química: Actualidad Futuro 1995, 5, 101. 3. Jensen, F.; Introduction to Computational Chemistry, 2th ed., John Wiley & Sons Ltd. : Chichester, 2006. 4. Pérez, J. F.; Restrepo, A.; ASCEC V-01: Annealing Simulado Con Energía Cuántica, Universidad de Antioquia, Colombia, 2008. 5. Yang, D.; Yang, Y.; Liu, Y.; Cent. Eur. J. Chem. 2013, 11, 171. 6. Okuyama, M.; Takatsuka, K.; Bull. Chem. Soc. Jpn. 2012, 85, 217. 7. Ito, F.; J. Chem. Phys. 2010, 133, 214502. 8. Zhou, P. P.; Qiu, W. Y.; Liu, S.; Jin, N. Z.; Phys. Chem. Chem. Phys. 2011, 13, 7408. 9. Birer, Ö.; Havenith, M.; Annu. Rev. Phys. Chem. 2009, 60, 263. 10. Marushkevich, K.; Siltanen, M.; Räsänen, M.; Halonen, L.; Khriachtchev, L.; J. Phys. Chem. Lett. 2011, 2, 695. 11. Balabin, R. M.; J. Phys. Chem. A 2009, 113, 4910. 12. Xue, Z.; Suhm, M.A.; J. Chem. Phys. 2009, 131, 054301. 13. Olbert-Majkut, A.; Ahokas, J.; Lundell, J.; Pettersson, M.; Chem. Phys. Lett. 2009, 468, 176. 14. Barnes, G. L.; Squires, S. M.; Sibert, E. L.; J. Phys. Chem. B 2008, 112, 595. 15. Bertran, J.; Oliva, A.; Rodríguez-Santiago, L.; Sodupe, M.; J. Am. Chem. Soc. 1998, 120, 8159. 16. Lazaar, K. I.; Bauer, S. H.; J. Am. Chem. Soc. 1985, 107, 3769. 17. Hippler, M.; Phys. Chem. Chem. Phys. 2002, 4, 1457. 18. Zielke, P.; Suhm, M. A.; Phys. Chem. Chem. Phys. 2007, 9, 4528. 19. Almenningen, A.; Bastiansen, O.; Motzfeldt, T.; Acta Chem. Scand. 1969, 23, 2848. 20. Zaleski, D. P.; Neill, J. L.; Muckle, M. T.; Steber, A. L.; Pate, B. H.; Douglass, K. O.; 66th International Symposium On Molecular Spectroscopy, Columbus, USA, 2011. 21. Miura, S.; Tuckerman, M. E.; Klein, M. L.; J. Chem. Phys 1998, 109, 5290. 22. Chocholoušová, J.; Vacek, J.; Hobza, P.; Phys. Chem. Chem. Phys. 2002, 4, 2119. 23. Markwick, P. R. L.; Doltsinis, N. L.; Marx, D.; J. Chem. Phys. 2005, 122, 054112. 24. Mališ, M.; Matanović, I.; Došlić, N.; J. Phys. Chem. A 2009, 113, 6034. 25. Madeja, F.; Havenith, M.; Nauta, K.; Miller, R. E.; Chocholoušová, J.; Hobza, P.; J. Chem. Phys. 2004, 120, 10554. 26. Mejía, S. M.; Orrego, J. F.; Espinal, J. F.; Mondragón, F.; Quim. Nova 2010, 33, 860. 27. Ensuncho, A. E.; López, J. M.; Carriazo, J. G.; Inf. Tecnol. 2011, 22, 95. 28. Mejía, S. M.; Espinal, J. F.; Restrepo, A.; Mondragón, F.; J. Phys. Chem. A 2007, 111, 8250. 29. David, J.; Guerra, D.; Restrepo, A.; J. Phys. Chem. A 2009,113, 10167. 30. Pérez, J. F.; Hadad, C. Z.; Restrepo, A.; Int. J. Quantum Chem. 2008, 108, 1653. 31. Yepes, D.; Kirk, S. R.; Jenkins, S.; Restrepo, A.; J. Mol. Model. 2012, 18, 4171. 32. Laarhoven, P. J. van; Aarts, E. H. In Simulated Annealing: Theory and Applications; Springer: Netherlands, 1987. 33. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, Jr., J. A.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; Pople, J. A.; Gaussian, Inc. (Rev. E.01) Wallingford CT, 2004. 34. Steward, J. J.; J. Comput. Chem. 1989, 10, 209. 35. James, J. P. S.; Stewart, J.; J. Comput. Chem. 1989, 10, 221. 36. Mejía, S. M.; Orrego, J. F.; Espinal, J. F.; Mondragón, F.; Quim. Nova 2010, 33, 860. 37. Mó, O.; Yáñez, M.; Elguero, J.; J. Chem. Phys. 1992, 97, 6628. 38. Liu, B.; McLean, A. D.; J. Chem. Phys. 1973, 59, 4557. 39. Van Duijneveldt, F. B.; van Duijneveldt-van de Rijdt, J. G. C. M.; van Lenthe, J. H.; Chem. Rev. 1994, 94, 1873. 40. Boys, S. F.; Bernardi, F.; Mol. Phys. 1970, 19, 553. 41. Mejía, S. M.; Espinal, J. F.; Mondragón, F.; Rev. Colomb. Quim. 2009, 38, 151. 42. Murillo, J.; David, J.; Restrepo, A.; Phys. Chem. Chem. Phys. 2010, 12, 10963. 43. Glendening, E. D.; Reed, A. E.; Carpenter, J .E.; Weinhold, F.; NBO Version 3.1, University of Wisconsin, USA, 2003. 44. Mayer, I.; J. Comput. Chem. 2007, 28, 204. 45. Marushkevich, K.; Khriachtchev, L.; Lundell, J.; Domanskaya, A.; Räsänen, M.; J. Phys. Chem. A 2010, 114, 3495. 46. Roszak, S.; Gee, R. H.; Balasubramanian, K.; Fried, L. E.; J. Chem. Phys. 2005, 123, 144702. 47. Kurtén, T.; Torpo, L.; Ding, C. G.; Vehkamäki, H.; Sundberg, M. R.; Laasonen, K.; Kulmala, M.; J. Geophys. Res.: Atmos. 2007, 112, D04210. 48. Nadykto, A. B., Yu, F., Jakovleva, M. V., Herb, J.; Xu, Y.; Entropy 2011, 13, 554. 49. Ochterski, J. W.; Thermochemistry in Gaussian; Gaussian, Inc., 2000. 50. Bertie, J. E.; Michaelian, K. H.; J. Chem. Phys. 1982, 76, 886. 51. Bertie, J. E.; Michaelian, K. H.; Eysel, H. H.; Hager, D.; J. Chem. Phys. 1986, 85, 4779. 52. Florio, G. M.; Zwier, T. S.; Myshakin, E. M.; Jordan, K. D.; Iii, E. L. S.; J. Chem. Phys. 2003, 118, 1735. 53. Lide, D. R.; CRC Handbook of Chemistry and Physics, 84th ed., CRC Press, 2003. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access