Educação
|
|
| Software para simulação de mecanismo de supressão da luminescência: modelo cinético de Stern-Volmer Software for simulation of luminescence quenching mechanism: the stern-volmer kinetic model |
|
Lauro Camargo Dias Júnior; Joao Batista Marques Novo*
Departamento de Química, Universidade Federal do Paraná, CP 19081, 81531-990 Curitiba - PR, Brasil Recebido em 25/04/2013 *e-mail: jbmnovo@ufpr.br A software that includes both Stochastic and Molecular Dynamics procedures has been developed with the aim of visualizing the Stern-Volmer kinetic mechanism of dynamic luminescence quenching. The software allows the student to easily simulate and graphically visualize the molecular collisions, the molecular speed distributions, the luminescence decay curves, and the Stern-Volmer graphs. The software named "SternVolmer" is written for the FreeBASIC compiler and can be applied to dynamic systems where luminescent molecules, during their excited state lifetimes, are able to collide with quenching molecules (collisional quenching). The good agreement found between the simulations and the expected results shows that this software can be used as an effective teaching aid for the study of luminescence and kinetic decay of excited states. INTRODUÇÃO O fenômeno de luminescência se refere à emissão de luz pelas substâncias em temperaturas relativamente baixas, sem a necessidade de aquecimento. Essa luz emitida é característica da amostra, pois é dependente da existência de estados eletrônicos característicos das moléculas que a compõem. Os fenômenos que ocorrem na luminescência podem ser resumidos pelas seguintes etapas cinéticas:1,2


onde o produto kqτ0 é conhecido como constante de Stern-Volmer, KSV.1,2 A Equação 1 se aplica a condições foto-estacionárias (medidas de intensidades, obtidas de espectros de emissão de luminescência convencionais), enquanto que a Equação 2 requer resolução temporal (medidas de tempos de vida de estados excitados, obtidas de curvas de decaimento de luminescência). Ambas, porém, evidenciam uma relação linear entre (I0/I) ou (τ0/τ) com a concentração de supressor, [Q]. O coeficiente angular fornece KSV e, a partir desse parâmetro, pode-se determinar kq (pois τ0 é conhecido). O mecanismo de supressão de luminescência de Stern-Volmer tem destacada importância em fotofísica e fotoquímica, na elucidação de mecanismos de luminescência, e também em química analítica, na determinação quantitativa de substâncias.3,4 Sendo assim, é um mecanismo importante a ser abordado no ensino de espectroscopia de luminescência e de cinética de estados excitados, conteúdos de disciplinas que fazem parte da grade curricular de cursos de Química. Para fins didáticos, recentemente utilizamos procedimentos Estocásticos (EST) no desenvolvimento de dois softwares: (1) "CinEstEx",5 para simular mecanismos de emissão de luminescência e de cinética de estados excitados; mas que também pode ser utilizado para a simulação de mecanismos complexos envolvendo cinética de primeira ordem de reações químicas; (2) "Perrin",6 para simulação da supressão estática da luminescência (modelo de Perrin). Nesse modelo, moléculas M* são suprimidas sempre que houver uma molécula Q dentro de uma esfera de volume Vq centrada em M*. Outros trabalhos com fins didáticos utilizando-se o Método Monte Carlo (que envolve o uso de números aleatórios e de estatística de probabilidade no tratamento do sistema de interesse7) também podem ser encontrados na literatura recente, para a simulação de equilíbrio químico com o emprego da urna de Ehrenfast8 e na resolução de equação de Schrödinger.9 Neste trabalho, apresentamos o software "SternVolmer" para demonstrar processos de supressão dinâmica da luminescência (supressão colisional). Para a simulação deste mecanismo, foi necessária a utilização de procedimentos (rotinas) de Dinâmica Molecular (DM) e, também, procedimentos Estocásticos (EST). Os procedimentos DM foram utilizados para a simulação dos movimentos de moléculas gasosas ou líquidas, governadas pelas leis de Newton. Os procedimentos EST foram utilizados na implementação do mecanismo cinético de Stern-Volmer propriamente dito: a etapa cinética seguida por cada molécula luminescente (ou seja, se ela tem ou não sua luminescência suprimida) é escolhida por meio de sorteios. Para a simulação DM, foi desenvolvido o programa denominado "DinMol", que inclui uma rotina de domínio público,10 para realizar os cálculos de dinâmica molecular com esferas rígidas. Foram adicionados a "DinMol" procedimentos para animação gráfica das movimentações moleculares e de gráfico da distribuição de velocidades das moléculas, não existentes no programa de domínio público. À exceção dessa rotina de domínio público inserida em "DinMol", todos os outros procedimentos (a saber: de apresentações gráficas das colisões moleculares, da distribuição de velocidades moleculares, das curvas de decaimento de luminescência, dos gráficos Stern-Volmer e incluindo também a simulação EST da cinética Stern-Volmer) foram originalmente desenvolvidos pelos autores do presente artigo. Os dois softwares, "SternVolmer" e "DinMol", estão disponíveis para uso e "download" da internet.11 O fato de se ter um código fonte aberto, permite que o professor possa utilizar a programação de computadores como incentivo à compreensão de fenômenos físicos e químicos, como é objetivo da disciplina de Tópicos Especiais "Desenvolvimento de Softwares em Química", ministrada no Departamento de Química da UFPR. Finalmente, utilizou-se o compilador gratuito "open-source" FreeBASIC.12
MÉTODOS O software "SternVolmer" O objetivo principal deste software é realizar simulações moleculares para se comprovar que, moléculas móveis, regidas pelas leis de movimento de Newton e por etapas cinéticas de desexcitação (com probabilidade kr+knr) e de supressão de luminescência (kq), se comportam conforme predito pela equação de Stern-Volmer, ou seja, apresentam tempos de vida de estado excitado que diminuem com o aumento da concentração de moléculas supressoras. Na simulação, as moléculas são representadas por circunferências de diferentes cores: as luminescentes excitadas são de cor verde, as luminescentes no estado fundamental são de cor cinza e as supressoras são azuis. Os fenômenos de desexcitação e de supressão também podem ser visualizados: Na desexcitação, um círculo verde aparece na posição da molécula luminescente; já na supressão, um círculo cinza aparece na posição da molécula luminescente que tem sua emissão suprimida, e um círculo azul na posição de sua parceira de colisão (molécula supressora). No início da simulação, todas as moléculas estão ordenadas: isto é necessário para que não ocorra sobreposição de moléculas. As velocidades iniciais de todas as moléculas são escolhidas pelo usuário e são iguais em módulo, mas com direções aleatórias, para fazer com que as moléculas se dispersem por todo sistema (cela cúbica na simulação 3D, ou cela quadrada na simulação 2D). Para se obter uma curva de decaimento válida, deve-se esperar primeiramente que todas as moléculas se distribuam homogeneamente no sistema, e isto é efetuado mais rapidamente por meio da tela de texto (tecla "t"). Somente após esta homogenização, o modo "randomizador" pode ser desligado (tecla "r") para se terminar a obtenção da curva de decaimento. Um ponto é então gerado e mostrado no gráfico Stern-Volmer. A simulação (experimento) é repetida, com uma concentração maior de moléculas supressoras, para obtenção de uma nova curva de decaimento e de mais um ponto no gráfico Stern-Volmer. Ao final do número de experimentos escolhido pelo usuário, o gráfico Stern-Volmer e os resultados quantitativos finais são mostrados. No início do experimento não existem moléculas no estado fundamental porque a existência destas moléculas somente acarretaria num maior consumo de memória e de processamento do computador, pois a colisão de moléculas excitadas com moléculas no estado fundamental não acarreta mudanças na concentração de moléculas excitadas. As curvas de decaimento continuariam a ser exponenciais, como se pode visualizar nos gráficos obtidos. Para fins didáticos, apresentamos a seguir algumas características do software, para permitir que os leitores interessados possam adaptar o programa às suas necessidades. O programa principal "SternVolmer.bas" contém a chamada ao procedimento "simulacaoControle", que é responsável pelas chamadas aos procedimentos DM e também de desexcitação e de supressão de luminescência. Estes dois últimos processos EST (desexcitação e supressão) são definidos por meio de sorteios. Resumidamente, o que ocorre neste procedimento é descrito a seguir: Inicialmente, o procedimento "simulacaoControle" atribui as configurações iniciais (posições e velocidades) para um conjunto de moléculas luminescentes M e supressoras Q e, em seguida, o procedimento "calculaUmaColisao" da DM é chamado para simular as movimentações moleculares e determinar quais moléculas estão colidindo e o respectivo tempo dessas colisões. Após isso, o procedimento EST "cineticaSternVolmer" é chamado para definir, por meio de sorteio, o que ocorre com o par de moléculas excitada e supressora que colide: se haverá supressão ou não da luminescência, de acordo com o mecanismo cinético de Stern-Volmer (M* + Q → M + Q). Após isso, outro procedimento EST denominado "desexcitacaoSorteio" também é chamado para verificar se haverá desexcitação de alguma molécula luminescente excitada, com probabilidade proporcional a kr+knr. É evidente, portanto, que a concentração de moléculas luminescentes no estado excitado, [M*], depende dessas simulações EST. O fluxograma do procedimento "simulacaoControle", pode ser descrito pela execução seqüencial das seguintes ações, na ordem: 1. Procedimento "entradaDados": responsável pela entrada de dados para as simulações. Detalhes dos parâmetros de entrada deste procedimento serão explicados mais adiante;Outros procedimentos e bibliotecas importantes no software são: Procedimento "visualizarDados": permite recuperar dados anteriormente gravados, visualizar o gráfico contendo todas as curvas de decaimento geradas na simulação e também o gráfico final Stern-Volmer, mostrando ainda os dados finais da regressão e da cinética. Isto é muito útil, pois permite a revisão e discussão dos resultados durante a aula. Biblioteca "lib-dinmol.bas": tratamento da DM segundo as leis da mecânica de Newton, contendo o procedimento calculaUmaColisao mencionado anteriormente. Biblioteca "lib-dinmol-graficos.bas": inclui os gráficos das movimentações moleculares e da distribuição de velocidades moleculares. Biblioteca "lib-sternvolmer-graficos.bas": apresenta a biblioteca gráfica correspondente para gráficos Stern-Volmer.
PARTE EXPERIMENTAL As simulações de mecanismo Stern-Volmer podem ser conduzidas tanto em uma configuração bidimensional (2D) como tridimensional (3D), para a caixa contendo as moléculas. São apresentadas, a seguir, três simulações tridimensionais: Simulação 1) Gráfico Stern-Volmer sob "condições padrão" Nesta simulação 3D, o procedimento "inicializaMoleculas" atribui valores não-nulos às componentes dos vetores posição e velocidade nos eixos x, y (na tela) e z (perpendicular à tela). Os demais parâmetros de entrada da simulação (procedimento "entradaDados") foram:
- Número de pontos no gráfico Stern-Volmer (número de experimentos, expSVmax)= 5Nesta simulação, foram gerados 5 pontos no gráfico Stern-Volmer (5 experimentos, com aquisição de um total de 5 curvas de decaimento). Estes experimentos correspondem às concentrações de moléculas supressoras [Q] = Nq/V = Nq/1 = Nq = 0, 18, 36, 54 e 72, para os pontos 1 a 5 respectivamente, do gráfico Stern-Volmer. Simulação 2) Efeito da velocidade das moléculas Esta simulação 3D foi realizada sob as mesmas "condições padrão" anteriores, obtendo-se um gráfico Stern-Volmer para cada uma das 5 diferentes velocidades iniciais das moléculas, Vp: 0,01; 0,02; 0,03; 0,04 e 0,05 (correspondentes a múltiplos Vp, 2Vp, 3Vp, 4Vp e 5Vp das velocidades sob condição "padrão", simulação 1). Portanto, nesta simulação foram obtidas 25 curvas de decaimento, ou seja, 5 curvas para cada velocidade molecular ou gráfico Stern-Volmer. Simulação 3) Efeito da densidade reduzida do sistema (caixa com moléculas) A densidade reduzida D pode ser calculada pela fórmula D = NL.σ3/V, onde V é o volume (unitário) da caixa e σ ("sigma") é o diâmetro molecular, que corresponde às distâncias entre os centros de duas moléculas (esferas) que estão colidindo.10,13 Esta simulação tridimensional foi realizada sob as mesmas "condições padrão" da simulação 1, obtendo-se um gráfico Stern-Volmer para cada uma das 5 diferentes densidades reduzidas do sistema, D: 0,017; 0,034; 0,051; 0,068 e 0,085 (correspondentes a múltiplos D; 2D; 3D; 4D e 5D das densidades sob "condição padrão", simulação 1). Portanto, nesta simulação foram obtidas 25 curvas de decaimento, ou seja, 5 curvas para cada densidade reduzida ou gráfico Stern-Volmer.
RESULTADOS E DISCUSSÃO A Equação de Stern-Volmer Para fins didáticos, a Equação 2 pode ser deduzida2,14 a partir das etapas cinéticas citadas anteriormente. Na ausência de moléculas supressoras Q, apenas os processos de emissão radiativa e não radiativa estão presentes (o processo de absorção é admitido como sendo realizado por fonte de excitação laser pulsado, muito rápido) e, assim, a lei de velocidade diferencial é descrita por:
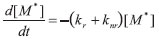
cuja integração resulta em:
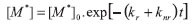
onde o tempo de vida de estado excitado τ0, na ausência de supressor, é dado por:
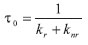
Na presença de moléculas supressoras Q, a lei de velocidade diferencial é descrita por:
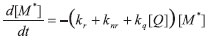
cuja integração ([Q] é constante durante a obtenção da curva de decaimento de estado excitado) resulta em:
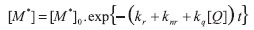
onde o tempo de vida de estado excitado τ, na presença de supressor, é dado por:
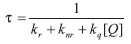
Pode-se então calcular a razão τ0 /τ:
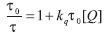
que é a equação de Stern-Volmer (Equação 2). De acordo com esta equação, o gráfico τ0 /τ vs.[Q] é linear, com coeficiente linear igual a 1 e, por meio da análise do coeficiente angular, o valor de kq pode ser obtido. Este é conhecido como gráfico de Stern-Volmer. O cálculo diferencial é muitas vezes inacessível principalmente para alunos dos primeiros períodos letivos, o que dificulta um pouco o entendimento das equações cinéticas acima. Entretanto, deve-se deixar claro que a simulação EST não necessita de conhecimento prévio e /ou resolução destas equações. Seus procedimentos estão baseados em sorteios e, sendo assim, é um método extremamente simples e útil para a simulação de sistemas de grande complexidade. Os leitores podem comprovar isto pelo programa fonte disponibilizado.11 Simulação 1) Gráfico Stern-Volmer sob "condições padrão" Na Figura 1 está o gráfico das curvas de decaimento obtidas nesta simulação. Observa-se a diminuição do tempo de decaimento das curvas (ou tempo de vida de estado excitado, τ) com o aumento da concentração do supressor, [Q]. Este comportamento é esperado para este mecanismo Stern-Volmer, e contrasta com o modelo de Perrin1,6 (supressão estática da luminescência), onde o tempo de decaimento das curvas permanece inalterado.
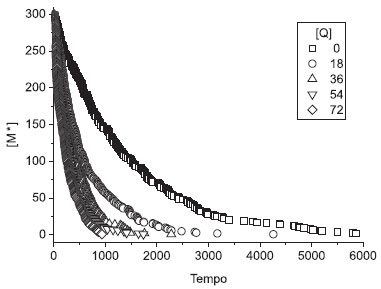 Figura 1. Gráficos das curvas de decaimento de estado excitado M* das moléculas luminescentes em função do tempo, em diferentes concentrações de moléculas supressoras, [Q], para a simulação tridimensional "padrão" (simulação 1). O volume do sistema é unitário e, portanto, a concentração de M* é igual ao número de moléculas luminescentes no estado excitado e a concentração de Q é o número de moléculas supressoras. A escala de tempo (u.a.) se refere aos tempos de colisões moleculares
Na Figura 2 está o gráfico Stern-Volmer para esta simulação "padrão". O resultado da regressão linear neste gráfico forneceu coeficiente angular Ksv = kqτ0 = 0,06591 e coeficiente linear igual a 1,079. Estas simulações forneceram τ0=1332 e kq=4,948 × 10-5. Pode-se notar a boa linearidade do gráfico, pelo valor do coeficiente de correlação igual a 0,9976.
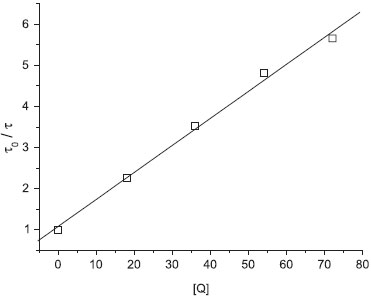 Figura 2. Gráfico Stern-Volmer para a simulação tridimensional "padrão" (simulação 1). τ0 é o tempo de vida de estado eletrônico excitado das moléculas luminescentes, na ausência de moléculas supressoras Q. A reta foi traçada pela regressão linear considerando todos os 5 pontos. Maiores detalhes no texto
Simulação 2) Efeito da velocidade inicial das moléculas, Vp Na Figura 3 está o gráfico construído para esta simulação. Este gráfico não faz parte do software original, podendo ser solicitado como atividade complementar aos alunos. Sua construção pode ser efetuada a partir dos tempos de vida de estado excitado contidos nos arquivos "SV". Neste gráfico estão presentes os tempos de vida de estado excitado τ, obtidos das curvas de decaimento, em função da velocidade das moléculas no início da simulação, Vp, e da concentração de moléculas supressoras, [Q]. Duas informações importantes estão contidas neste gráfico:
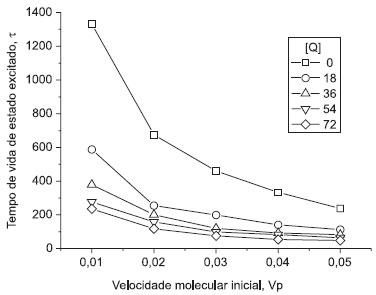 Figura 3. Efeito da velocidade molecular inicial Vp e da concentração de moléculas supressoras, [Q], sobre os tempos de vida de estado excitado τ das moléculas luminescentes (simulação 2). O volume do sistema é unitário e, portanto, a concentração de Q é o número de moléculas supressoras
Simulação 3) Efeito da densidade reduzida, D Na Figura 4 está o gráfico construído para esta simulação. Este gráfico também não faz parte do software original, podendo ser solicitado como atividade complementar aos alunos. Neste gráfico estão presentes os tempos de vida de estado excitado τ, obtidos das curvas de decaimento, em função da densidade reduzida, D, e da concentração de moléculas supressoras, [Q]. Pode-se notar a semelhança com o gráfico da Figura 3:
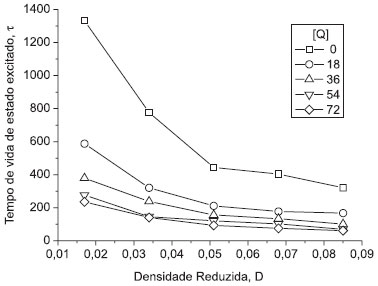 Figura 4. Efeito da densidade reduzida, D, e da concentração de moléculas supressoras, [Q], sobre os tempos de vida de estado excitado τ das moléculas luminescentes (simulação 3). O volume do sistema é unitário e, portanto, a concentração de Q é o número de moléculas supressoras
CONSIDERAÇÕES FINAIS As unidades utilizadas em todas as simulações são arbitrárias: as distâncias correspondem a frações do tamanho da cela, que tem lados unitários (u.a.), enquanto que os tempos correspondem a tempos de colisões moleculares (maiores detalhes na Referência10). Deste modo, τ0 e [Q] podem ser escalonadas para se adequarem aos valores empíricos de sistemas reais. A cinética de Stern-Volmer apresentada neste artigo trata da supressão por meio de colisões e, portanto, não se aplica a processos de transferência de energia de longo alcance. Neste caso, as desativações dos estados excitados M* poderiam ocorrer também nos intervalos entre as colisões. Existe uma limitação nas simulações feitas com este software: o menor intervalo de tempo que o procedimento DM consegue calcular é aquele intervalo entre duas colisões consecutivas. Portanto, eventos rápidos, da ordem de grandeza do tempo médio de colisões moleculares, não podem ser simulados, com precisão, com este software. Assim, consegue-se simular o comportamento cinético Stern-Volmer de moléculas de possuem τ0 >> tempo médio de colisões moleculares, ou seja, probabilidades de desexcitação DEXC (que é proporcional a k= 1/τ0 = kr + knr) relativamente baixas. Uma solução para esse problema seria a modificação dos procedimentos internos da biblioteca DM, de forma a introduzir tempos intermediários à das colisões moleculares. Entretanto, isto não foi efetuado no presente artigo, para não descaracterizar a biblioteca DM da literatura. Além disso, deve-se enfatizar que, mesmo no caso de se alterar esta biblioteca DM, ainda existiria um incremento de tempo limite a ser considerado no cálculo, ou seja, esta limitação sempre estaria presente. Como conseqüência da existência de processos extremamente rápidos, pode-se prever que, após uma excitação molecular por laser pulsado de curta duração, a emissão luminescente ocorreria com todas as moléculas praticamente imóveis (pois o tempo de vida do estado excitado destas moléculas seria extremamente curto). Neste caso, os modelos de supressão estática de Perrin1,6 ou de transferência de energia a longa distância poderiam ser válidos. Um esclarecimento sobre os procedimentos DM e EST utilizados neste software: a simulação dos movimentos e colisões moleculares é realizada exclusivamente por meio de procedimentos DM. A construção dos gráficos Stern-Volmer (Figura 2) depende da obtenção do tempo de vida de estado excitado (τ) das curvas de decaimento da luminescência (ou curvas de decaimento de estados excitados, Figura 1). O eixo x, nestas curvas, é o tempo de colisão molecular, que é calculado por meio dos procedimentos DM. Já o eixo y, é a concentração de moléculas luminescentes no estado excitado, [M*], que depende tanto da freqüência de colisões entre moléculas (depende da simulação DM), quanto dos sorteios relativos às etapas cinéticas do mecanismo Stern-Volmer (depende da simulação EST). Portanto, neste software, os dois procedimentos, DM e EST, agem em conjunto para a simulação do mecanismo de Stern-Volmer, ou seja, a união das duas simulações permite que se obtenham os dados cinéticos Stern-Volmer. As simulações efetuadas neste artigo demonstram que o software desenvolvido está funcionando adequadamente e que pode ser utilizado como recurso didático em aulas de ensino de luminescência e de cinética de estados eletrônicos excitados. Além disso, a simulação para a visualização do gráfico Stern-Volmer é rápida (15 minutos de duração aproximadamente) e pode ser perfeitamente aplicada durante o período de uma aula. O software traz muitos gráficos, que permitem que o professor discuta detalhes com os alunos: No gráfico de distribuição de velocidades moleculares, deve-se observar que, no início da simulação, as velocidades são todas iguais em módulo, mas, após um certo número de colisões, as moléculas têm suas velocidades aumentadas ou diminuídas, dependendo de como ocorre a colisão entre elas (princípio da conservação do momento linear), acarretando na bem conhecida distribuição de Maxwell. Nos gráficos das curvas de decaimento de estado excitado, deve-se atentar para os formatos exponenciais das curvas (cinética de 1ª ordem) e também aos seus diferentes comportamentos nos mecanismos de supressão estático (de Perrin)1,6 e o dinâmico, de Stern-Volmer: no primeiro, as curvas de decaimento de estado eletrônico excitado exibem o mesmo tempo de vida (τ), enquanto que no de Stern-Volmer ocorre uma diminuição em τ à medida que [Q] aumenta.
REFERÊNCIAS 1. Valeur, B.; Molecular Fluorescence, Principles and Applications, 1ª ed., Wiley-VCH: Weinheim, 2001; Turro, N. J.; Modern Molecular Photochemistry, 1ª ed., University Science Books: Sausalito, 1991. 2. Demas, J. N.; Excited State Lifetime Measurements, Academic Press: New York, 1983. 3. Sotomayor, M. D. P. T.; Dias, I. L. T.; Lanza, M. R. V.; Moreira, A. B.; Kubota, L. T.; Quim. Nova 2008, 31, 1755. 4. http://www.oceanoptics.com/Products/sensortheory.asp, acessada em Agosto 2013. 5. Winnischofer, H.; Araújo, M. P. de; Dias Jr, L. C.; Novo, J. B. M.; Quim. Nova 2010, 33, 225. 6. Novo, J. B. M.; Dias Jr, L. C.; Quim. Nova 2011, 34, 707. 7. Angelotti, W. F. D.; Fonseca, A. L.; Torres, G. B.; Custodio, R; Quim. Nova 2008, 31, 433. 8. López-Castillo, A.; Souza Filho, J. C.; Quim. Nova 2007, 30, 1759. 9. Custodio, R.; Custodio, M. R.; Creatto, E. J.; Quim. Nova 2012, 35, 2076. 10. Allen, M. P.; Tildesley, D. J.; Molecular Dynamics Of Hard Systems, 1ª ed., Oxford University Press: Oxford, 1987; http://www.ccp5.ac.uk/software/allen_tildersley.shtml acessada em Agosto 2013. 11. Novo, J. B. M.; Dias Jr., L. C.; Softwares Livres e Gratuitos; http://quimica.ufpr.br/jbmnovo, acessada em Agosto 2013. 12. Victor, A.; FreeBASIC Compiler; Free, open source BASIC Compiler; http://www.freebasic.net/, http://sourceforge.net/projects/fbc/. Debord, J.; FBMath; FreeBASIC Math library; http://sourceforge.net/projects/fbmath/, acessadas em Agosto 2013. 13. Metropolis, N.; Rosenbluth, A. W.; Rosenbluth, M. N.; Teller, A. H.; J. Chem. Phys. 1953, 21, 1087. 14. Grubbs, T. http://www2.stetson.edu/~wgrubbs/datadriven/quenching/quenchingwtg.html, acessada em Agosto 2013. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access





