JBCS

INTRODUÇÃO

Há muitos anos que a disciplina de química orgânica avançada vem sendo abordada pela apresentação e discussão de livros textos avançados tradicionais.^1,2 Entretanto, em um olhar atento ao capítulo 1 da versão mais atual do livro Advanced Organic Chemistry part A: structure and mechanisms² percebemos que a química computacional começa a ser amplamente debatida e apresentada aos estudantes que iniciam seus estudos no mestrado em química orgânica, sendo esta uma ferramenta imprescindível para que os estudantes obtenham sozinhos avanços na compreensão da estrutura molecular e suas reatividades.

Em conexão ao nosso interesse nos aspectos didáticos ao tema de ácidos e bases para química orgânica,³ introduzimos com amplo sucesso, nos dois últimos semestres em que ministramos a disciplina Química Orgânica Avançada, aspectos práticos para que os estudantes aprendessem a calcular computacionalmente, usando a teoria dos orbitais moleculares de fronteira,⁴ os valores de dureza (η) e moleza (σ) no estudo da teoria de Pearson (HSAB", acrônimo do inglês hard and soft acid and bases).⁵ Após os cálculos efetuados solicitamos que os alunos correlacionassem estes valores numéricos com aspectos estruturais intrínsecos de eletronegatividades, polarizabilidades, efeitos polares e de ressonância, que fazem parte da teoria da ligação de valência.⁶

A seguir abordaremos um resumo da teoria que vem sendo discutida, durante a nossa disciplina, sobre o tema. Em sequência apresentaremos um exercício proposto para ser individualmente resolvido.

Fundamentação teórica

Quando uma molécula ou íon é colocado entre cargas opostas, como um capacitor, a nuvem eletrônica desta espécie pode se polarizar (Figura 1), de acordo com a sua maior ou menor facilidade para isto (maior ou menor polarizabilidade).

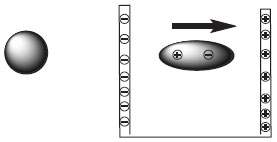Figura 1. Molécula ou íon sem açao do campo elétrico (a esquerda) e polarizada pelo campo elétrico (a direita)

Ralph Person⁵ definiu uma espécie mais polarizável como mole (ácido ou base) e menos polarizável como dura (ácido ou base). O valor de dureza (η) ou moleza (σ) é determinado usando-se os valores do potencial de ionização (PI) e da afinidade eletrônica (AE) destas espécies, mediante as equações 1 e 2.⁷

Entretanto, de acordo com a teoria dos orbitais moleculares de fronteira, definimos espécies com uma alta variação da energia entre o orbital ocupado de mais alta energia (HOMO, do inglês highest occupied molecular orbital) e do orbital desocupado de mais baixa energia (LUMO, do inglês lowest unoccupied molecular orbital) de espécies duras. Quanto menores forem as diferenças de energia entre os orbitais HOMO-LUMO desta espécie, mais mole ela será (Figura 2).

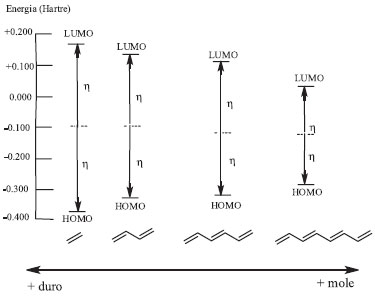Figura 2. Ordem de dureza (η) de sistemas conjugados, calculados pelo método ab-initio, no nível de calculo HF/6-31G^*

Podemos facilmente calcular a ordem de dureza e moleza das moléculas ou íons, usando programas como o ChemDraw3D^®,⁸ o Gaussian03W^®,⁹ o MOPAC (versões disponíveis para uso acadêmico são gratuitas em ambiente Windows ou Linux)¹⁰ entre outros, para calcular os valores de HOMO e LUMO das espécies em questão. Com os valores obtidos utilizamos as equações 3 e 4 para o cálculo de η e σ.

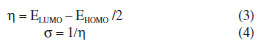
Cabe destacar que, dependendo do programa e do nível de cálculo utilizado, os valores numéricos podem alterar. Entretanto, a tendência da ordem de η e σ, que é o ponto mais importante nas suas interpretações qualitativas usando a teoria de valência, se mantém a mesma. No exercício teórico-prático proposto em sala de aula solicitamos que os alunos utilizem seus laptops implementados com programas de uso livre (para avaliação) como o ChemDraw3D^®, mas sugerimos aos programas de pós-graduação para que adquiram as devidas licenças destes programas. Como nível de cálculo, sugerimos os métodos semi-empiricos AM1¹¹ ou PM3,¹² devido à rapidez na obtenção dos dados, pois podem ser rapidamente obtidos em sala em qualquer laptop. Cabe enfatizar aqui que, neste exemplo didático, o uso de métodos simples e rápidos como os semi-empíricos AM1 ou PM3 são o diferencial na sala de aula durante os exercícios.

Mostramos na Figura 3 um breve resumo de como calcular os valores dos orbitais de fronteira com o programa ChemDraw3D^®. A manipulação do programa Gaussian03W^® via o visualizador GaussView não é complicada, mas de longa explicação neste breve relato. Entretanto, hoje em dia, percebemos que em aula há sempre um ou dois alunos mais habilidosos que sabem manipular bem estes programas e que ensinam facilmente aos seus colegas de sala, com apoio do professor.

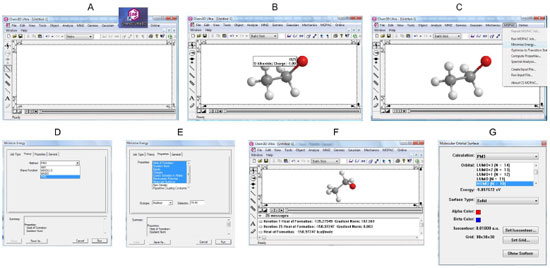Figura 3. Resumo das operaçoes (3A-3G) no ChemDraw3D^® para obtençao do valor dos orbitais HOMO e LUMO

Na Figura 3 sugerimos que após a instalação do programa no computador seja colocado um ícone na área de trabalho, para maior comodidade de uso. Para abrir o programa basta dar dois cliques no ícone e a tela 3A aparece. Desenha-se facilmente o composto usando os comandos do lado esquerdo da tela 3B, que neste caso foi o etanoato (ânion). Note na pose 3B que ao encostarmos o cursor em um átomo (no caso o oxiânion), o programa indica de que tipo é o átomo e a sua carga. Clicando no comando MOPAC (Pacote de Orbitais Moleculares, do inglês, molecular orbital package) nos comandos superiores, selecionamos minimize energy (3C) e depois escolhemos a teoria PM3 (3D). Se não selecionarmos nada o default (nível de cálculo padrão do programa) é o AM1. Selecionamos o comando properties e selecionamos de heat of formation até molecular surfaces (3E) e submetemos o cálculo, clicando em Run (3E). Após o cálculo terminado, devemos verificar se o Gradient Norm (abaixo da tela 3F, destacado em vermelho) está próximo de zero com uma casa decimal no mínimo (0.0...) para garantirmos que a molécula está com a geometria minimizada (geometria mais estável). Após isto visualizamos a energia de HOMO e LUMO facilmente (ou de qualquer outro orbital molecular) clicando em View, Molecular orbitals (comandos superiores). Por exemplo, selecionando HOMO encontramos a energia de -9,897672 eV (3G).

RESULTADOS

Exercício Proposto em aula. Calcule pela teoria dos orbitais moleculares (M.O., nível de cálculo PM3 do ChemDraw3D^®) a dureza (η) e moleza (σ) das 24 estruturas mostradas na figura abaixo (Figura 4) e faça análises relacionadas qualitativas, usando a teoria da ligação de valência (V.B.), como, por exemplo, os efeitos intrínsecos de eletronegatividades, polarizabilidade, ressonância e efeito polar.

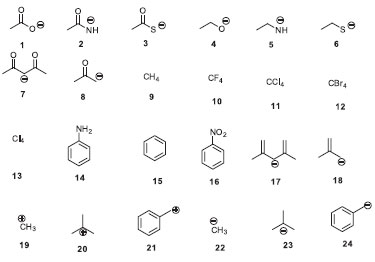Figura 4. Estruturas calculadas pelos métodos PM3 e que foram qualitativamente relacionadas pela teoria das ligaçoes de valência

Resolução: de acordo com a teoria de Pearson a dureza e moleza são determinadas pelas fórmulas mostradas a seguir.

onde PI = potencial de ionização e AE = afinidade eletrônica.

Entretanto, baseando-se na teoria dos orbitais de fronteira (HOMO-LUMO) podemos estimar a dureza e moleza usando a fórmulas mostradas abaixo.

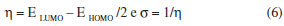
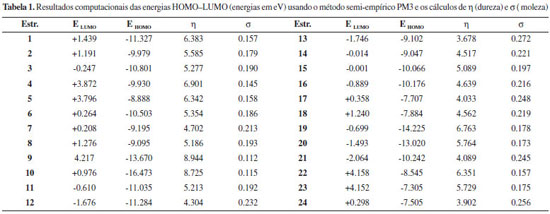
Os valores relativos à equação 6 foram calculados usando o método semi-empírico PM3, que está fundamentado na teoria dos orbitais moleculares e estes valores estão mostrados na Tabela 1.

DISCUSSÃO

Iniciamos nossa discussão pela série de moléculas aniônicas 1-6 (Figura 4 e Tabela 1). A ordem de moleza aumenta em 1-2-3 devido ao aumento da polarizabilidade dos átomos de O, N e S, ocasionado pelo maior volume atômico do átomo de S. A mesma tendência ocorre nas moléculas 4-5-6 devido rigorosamente ao mesmo motivo. Se compararmos as moléculas 1-4, 2-5, 3-6 notamos que os efeitos da ressonância que ocorrem em 1, 2 e 3 e que não ocorrem em 4, 5 e 6 (Figura 5a) são responsáveis pela maior dispersão da carga negativa, aumento da moleza destas espécies, que são corroboradas nos valores numéricos calculados. Em sequência, notamos que os valores numéricos de dureza aumentam na ordem para 7-8. A ressonância que ocorre com a carga negativa entre duas carbonilas em 7 faz que este íon seja mais disperso (mole) que 8, no qual somente uma carbonila é responsável pela ressonância (Figura 5b). Continuando as análises, a ordem numérica de moleza é crescente (Tabela 1) para a série de compostos 9-10-11-12-13. Neste caso, a polarizabilidade é ocasionada pelo alto volume molecular do tetraiodeto de carbono (13) quando comparada ao menos polarizável metano (9), como mostrado na Figura 5c.

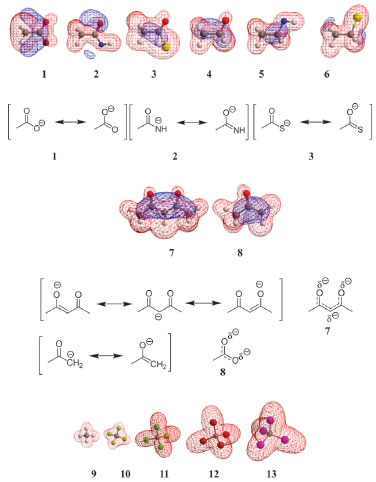Figura 5. (5a) Superfícies eletrostáticas potenciais calculadas para 1-6 e estruturas canônicas de 1-3. (5b) Superfícies eletrostáticas potenciais calculadas para 7-8 e estruturas canônicas de 7-8. (5c) Superfícies eletrostáticas potenciais relacionadas ao volume molecular, dispersao molecular e moleza de 9-13

Os dados numéricos calculados indicam que o benzeno (15) é mais duro que a anilina (14) e o nitrobenzeno (16). Neste caso, podemos aventar que tanto um grupo elétron-doador (NH₂) como um elétron-aceptor (NO₂) aumentam o volume molecular, aumentando a dispersão da nuvem eletrônica, aumentando a moleza de 14 e 16 em relação a 15 (Figura 6a). Uma comparação pertinente se dá entre os anions carbonilados 7 e 8 com os correspondentes hidrocarbonetos 17-18. A ressonância nos dois sistemas insaturados do ânion bis-alílico 17 em relação ao anion alílico 18 é o fator qualitativo responsável pela maior dispersão molecular de 17, corroborado pelos dados computacionais. Cabe destacar que 17 é mais mole que o análogo carbonilado 7 e o ânion 18 é mais mole que o 8. Isto é razoável, considerando a maior eletronegatividade do O em 7-8 em relação ao CH₂ em 17-18. Assim, os átomos de oxigênio tornam mais duros os seus correspondentes compostos (Figura 6b).

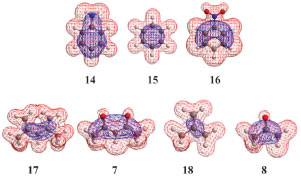Figura 6. (6a) Superfícies eletrostáticas potenciais calculadas para 14-16. (6b) Superfícies eletrostáticas potenciais comparadas para 17, 7, 18 e 8

Na série dos carbocátions, notamos um aumento da moleza na ordem 19-20-21. O efeito de hiperconjugação das três metilas em 20 aumenta consideravelmente a dispersão molecular do carbocátion terc-butila em relação ao cátion metila (Figura 7). Cabe destacar que o valor numérico de moleza do cátion benzílico é bem maior que o do cátion terc-butila. Considerando-se que o efeito de ressonância em 21 é mais efetivo na dispersão molecular que o efeito de hiperconjugação este fato torna-se compreensível. Finalmente, notamos que numericamente esta mesma tendência continua a ocorrer nos análogos aniônicos 22-23-24, sendo as explicações análogas às discutidas anteriormente para os cátions.

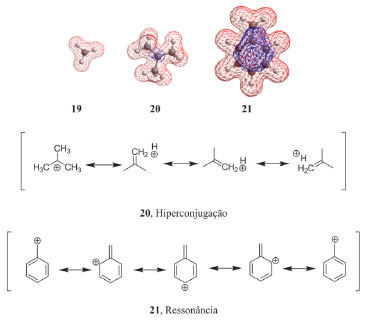Figura 7. Superfícies eletrostáticas potenciais calculadas para 19-20-21

CONCLUSÃO

Neste breve relato, concluímos que o ensino sobre a teoria de Pearson nas disciplinas avançadas de química orgânica pode ser feito estimulando os alunos ao cálculo computacional dos orbitais de fronteira HOMO e LUMO e, consequentemente, dos valores de dureza (η) e moleza (σ). O método semi-empírico PM3 mostrou ser totalmente adequado, rápido e acessível para fornecer dados numéricos confiáveis. Estes aspectos foram aplicados em sala mediante a aplicação de exercício, durante os últimos dois períodos letivos, em turma de 8-10 alunos. Percebemos a fascinação destes estudantes por conseguirem se inserir ativamente na construção do conhecimento sobre o tema, concluindo lentamente aspectos do assunto em pauta e fortalecendo seus conceitos, bem diferente da abordagem clássica atual, que é somente expositiva.

Neste artigo nós focamos somente os aspectos da maior ou menor dispersão de carga nos compostos moles e duros, relacionando-os com teorias mais convencionais como, por exemplo, a de ressonância. Uma continuação deste artigo será focada nas consequências destes aspectos nas reatividades do tipo duro-duro e mole-mole e também apresentaremos novas teorias complementares, como a teoria de Marcus,¹³ destacando casos onde a teoria HSAB apresenta limitações na compreensão das regiosseletividades, como ocorrem nos nucleófilos ambidentes.¹⁴

AGRADECIMENTOS

Aos estudantes que me estimularam a escrever esta experiência de aula. Ao CNPq e à CAPES pelo apoio financeiro e pela bolsa de produtividades.

REFERÊNCIAS

1. Smith, M. B.; March, J.; March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, 7^th ed., John Wiley & Sons: New Jersey, 2013.

2. Carey, F.A.; Sundberg, R. J.; Advanced Organic Chemistry, Part A: Structure and Mechanisms, 5^th ed., Springer: New York, 2007.

3. Costa, P.; Ferreira, V.; Esteves, P.; Vasconcellos, M.L.A.A.; Ácidos e Bases em Química Orgânica, Bookman: Porto Alegre, 2005.

4. Fukui, K.; Acc. Chem. Res. 1971, 4, 57; Fleming, I.; Frontier Orbitals and Organic Chemical Reactions, Wiley: New York, 1976.

5. Pearson, R. G.; J. Chem. Educ. 1968, 45, 581; Parr, R. G.; Tse-Lok, H; Chem. Rev. 1975, 75, 1; Pearson, R.G.; J. Am. Chem. Soc. 1983, 105, 7512.

6. Heitler, W.; London, F.; Z. Phys. 1927, 44, 455; Pauling, L.; J. Am. Chem. Soc. 1931, 53, 1367; Cooper, D. L.; Valence Bond Theory, Elsevier: Amsterdam, 2002; Gallup, G. A.; Valence Bond Methods: Theory and Applications, Cambridge University Press: Cambridge 2002.

7. Pearson, R. G.; J. Am. Chem. Soc. 1963, 85, 3533.

8. Consulte: http://www.cambridgesoft.com/; para acessar um tutorial, consulte http://www.camsoft.co.kr/services/documentation/chemdraw_8_english.pdf (acessados em Abril 2013).

9. Gaussian 03, Revision C.02, Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, Jr., J. A.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; and Pople, J. A.; Gaussian, Inc., Wallingford CT, 2004.

10. Downloads das versões do MOPAC 3 até MOPAC 7 podem ser efetuadas sem custo em http://openmopac.net/Downloads/Downloads.html (acessado em Julho 2013).

11. Dewar, M. J. S.; Zoebisch, E. G.; Healy, E. F.; Stewart, J. J. P.; J. Am. Chem. Soc. 1985, 107, 3902.

12. Stewart, J. J. P.; J. Comput. Chem. 1989, 10, 209.

13. Marcus, R. A.; Angew. Chem. Int. Ed. 1993, 32, 1111.

14. Mayr, H.; Breugst, M.; Ofial, A.R.; Angew. Chem. Int. Ed. 2011, 50, 6470.