Artigo
|
|
| Interacciones de la glicina en soluciones acuosas de tetrafluoroborato de 1-butil, 3-metilimidazolio a diferentes temperaturas Interactions of glycine in aqueous solutions of 1-butyl-3-methylimidazolium tetrafluoroborate at different temperatures |
|
Francisco Páez AriasI,*; Manuel Páez MezaI; Alfonso Portacio LamadridII
IDepartamento de Química, Facultad de Ciencias Básicas, Universidad de Córdoba, (Carrera 6 No. 76-103), Montería, Colombia Recebido em 11/06/2013 *e-mail: franpa2828@gmail.com Densities of glycine in aqueous solutions of ionic liquid 1-butyl-3-methylimidazolium tetrafluoroborate were determined at temperatures ranging from 283.15 to 313.15 K. The apparent molar volume, infinite dilution apparent molar volume, second derivative of the infinite dilution partial molar volume with respect to temperature, partial molar volume of transfer at infinite dilution, and the number of hydration were determined. It was found that the apparent molar volume at infinite dilution was positive, but decreased with increasing ionic liquid concentration and increased with increasing temperature. On the other hand, the partial molar volume of transfer at infinite dilution behaved in a similar manner, but was negative. INTRODUCCIÓN En los últimos años, se ha incrementado considerablemente el estudio del efecto que tienen los co-solutos como las sales y las sustancias iónicas en general, sobre el predominio de las interacciones moleculares que pueden estar presentes en las soluciones acuosas de aminoácidos.1-3 Los electrolitos orgánicos, incluyendo a los líquidos iónicos, pueden ayudar en el entendimiento acerca del efecto que tienen las interacciones electrostáticas e hidrofóbicas sobre la estabilidad de los aminoácidos. Así mismo, es de esperar, que estos compuestos tengan influencia sobre la conformación macromolecular de las biomoléculas, mediante el debilitamiento de las interacciones repulsivas o atractivas inter o intra cadena y carga-carga y afectando las interacciones hidrofóbicas de sus cadenas laterales con los grupos alquílicos.4 Pese a los grandes esfuerzos para comprender esta temática de estudio, el comportamiento de este tipo particular de sistemas aun no ha sido del todo bien entendido. El tetrafluroborato de 1-butil, 3-metilimidazolio es históricamente uno de los líquidos iónicos más importantes y comúnmente mas estudiado,5 desde el punto de vista estructural es considerado como una sustancia anfifílica debido a la presencia de cadenas alquílicas en su catión.6 Esta característica hace de el [BMIm][BF4] un candidato muy interesante para estudiar el efecto que este tipo de sustancias pueden tener sobre las interacciones predominantes en las soluciones de biomoléculas. Unas de las herramientas más utilizadas a través de los años para el estudio de las interacciones moleculares se he enfocado en el análisis de las propiedades termofísicas de las soluciones, dentro de las cuales, se han destacado de manera muy significativa las propiedades volumétricas de las mezclas,7,8 como los volúmenes molares aparentes y volúmenes molares de transferencia a dilución infinita.9-12 Estos estudios, han demostrado ser muy útiles en el entendimiento de la naturaleza de acción de aminoácidos, péptidos y proteínas en los sistemas vivos. La opinión predominante es que la estabilidad de la estructura nativa de las proteínas y el reconocimiento molecular es dominado por las fuerzas hidrofóbicas, sin embargo, en recientes años, se ha demostrado que las interacciones hidrofílicas pueden ser tan importantes como las hidrofóbicas.13 De acuerdo con esto, en este articulo, reportamos algunas propiedades volumétricas de las soluciones de glicina en mezclas acuosas de tetrafluoroborato de 1-butil, 3-metilimidazolio ([BMIm][BF4]) a las temperaturas de (283.15, 288.5, 293,15, 298.15, 303.15, 308.15 and 313.15) K. Dichas propiedades, fueron utilizadas para analizar el comportamiento de las interacciones soluto- soluto y soluto-solvente en estas mezclas.
MATERIALES Y MÉTODOS Glicina grado analítico (99%) adquirida de la casa comercial Alfa Aesar. [BMIn][BF4] (98%) obtenido de Aldrich. Antes de su uso la glicina fue recristalizada en soluciones acuosas de etanol y secada al vacio sobre P2O5.14 El agua utilizada fue doblemente destilada obteniéndose una conductividad menor a 2 mS cm-1. Las soluciones fueron preparadas en la escala de molalidad utilizando el método gravimétrico, en recipientes de vidrio con tapa, tomando todas las precauciones necesarias para evitar la contaminación de las muestras y la pérdida de masa por evaporación de los líquidos utilizados. Todas las medidas de masa fueron realizadas en una balanza analítica Ohaus con una sensibilidad de ± 0.1 mg. Las densidades de los componentes puros y sus mezclas fueron determinadas en un densímetro de tubo vibratorio Anton Para DMA 5000, que tiene una reproducibilidad de 110-5 g cm-3 y una exactitud en la determinación de la temperatura de (± 0.001 ºC).
RESULTADOS Y DISCUSIÓN Los valores de los volúmenes molares aparentes fueron calculados a partir de las medidas de densidad utilizando la ecuación (1):15
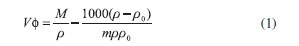
donde M es la masa molar del aminoácido, m es la molalidad de la glicina, que es definida como las moles de glicina por kilogramo de solvente (solución acuosa de [BMIm] [BF4] ), ρ y ρ0 son respectivamente la densidad de la solución (glicina + solución acuosa de [BMIm][BF4]) y la densidad del solvente (solución acuosa de [BMIm][BF4] a la molalidad deseada). La incertidumbre para los valores de VΦ fue menor que 0.06 cm3 mol-1. Los resultados para las densidades y los volúmenes molares aparentes son reportados en la Tabla 1 y en las Figuras desde la 1 hasta la 5. Se encontró una buena correlación lineal entre los valores de VΦ y la molalidad de la glicina en las soluciones a todas las concentraciones de [BMIm][BF4] a las temperaturas de trabajo. Para todos los casos, los volúmenes molares aparentes a dilución infinita VΦο fueron obtenidos mediante regresión lineal de la ecuación (2):

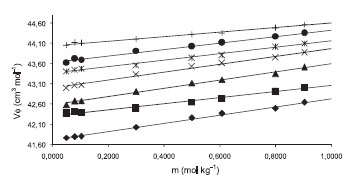 Figura 1. Volúmenes molares aparentes VΦ para la glicina en soluciones acuosas de [BMIm][BF4] 0.1000 mol kg-1 a las temperaturas de ♦ 283.15 K, ■ 288.15 K, ▲ 293.15 K, × 298.15 K, * 303.15 K, ● 308.15 K, + 313.15 K
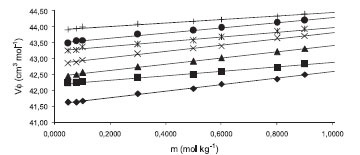 Figura 2. Volúmenes molares aparentes VΦ para la glicina en soluciones acuosas de [BMIm][BF4] 0.2000 mol kg-1 a las temperaturas de ♦ 283.15 K, ■ 288.15 K, ▲ 293.15 K, × 298.15 K, * 303.15 K, ● 308.15 K, + 313.15 K
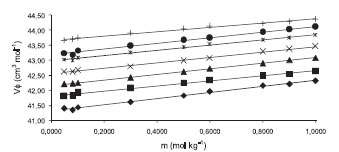 Figura 3. Volúmenes molares aparentes VΦ para la glicina en soluciones acuosas de [BMIm][BF4] 0.3000 mol kg-1 a las temperaturas de ♦ 283.15 K, ■ 288.15 K, ▲ 293.15 K, × 298.15 K, * 303.15 K, ● 308.15 K, + 313.15 K
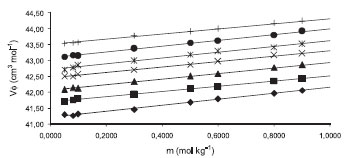 Figura. 4. Volúmenes molares aparentes VΦ para la glicina en soluciones acuosas de [BMIm][BF4] 0.4000 mol kg-1 a las temperaturas de ♦ 283.15 K, ■ 288.15 K, ▲ 293.15 K, × 298.15 K, * 303.15 K, ● 308.15 K, + 313.15 K
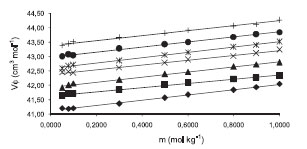 Figura. 5. Volúmenes molares aparentes VΦ para la glicina en soluciones acuosas de [BMIm][BF4] 0.5000 mol kg-1 a las temperaturas de ♦ 283.15 K, ■ 288.15 K, ▲ 293.15 K, × 298.15 K, * 303.15 K, ● 308.15 K, + 313.15 K
donde Sv es la pendiente experimental, tambien considerada como el coeficiente volumetrico virial, el cual caracteriza las interacciones par de las especies de soluto solvatados en la solución, mientras que VΦο refleja la presencia de interacciones soluto-solvente.16-18 Los valores de VΦο y Sv son mostrados en la Tabla 2. Los valores positivos de Sv para las mezclas de glicina sugieren que el coeficiente volumétrico virial par es dominado por las interacciones de los grupos funcionales cargados con los iones de los líquidos iónicos. Los valores de VΦο son positivos para todas las temperaturas y concentraciones del solvente mixto, y a la vez, disminuyen con el incremento de la concentración del [BMIm][BF4] para todas las temperaturas, lo cual podría ser interpretado como una contracción del volumen a dilución infinita debido al incremento de las interacciones soluto-solvente. Así mismo, los valores de VΦο incrementan sistemáticamente con los incrementos de temperatura, este comportamiento es mostrado en la Figura 6.
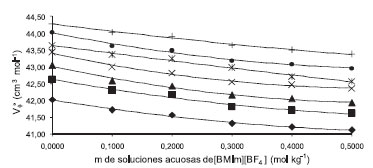 Figura 6. Volumen molar aparente VΦο dilución infinita para la glicinaen soluciones acuosas de [BMIm][BF4] a las temperaturas de ♦ 283.15 K, ■ 288.15 K, ▲ 293.15 K, × 298.15 K, * 303.15 K, ● 308.15 K, + 313.15 K
Los valores experimentales de Vf0 fueron correlacionados con temperatura usando la ecuación (3):

donde A, B y C son constantes y T es la temperatura. Los valores de (
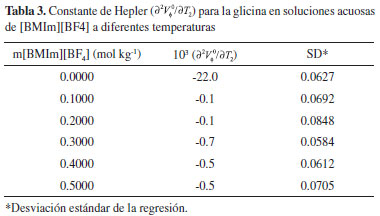
Los volúmenes molares de transferencia a dilución infinita ΔVΦο de la glicina desde el agua pura hasta las soluciones de [BMIm][BF4] fueron obtenidos utilizando la ecuación (4):

Estos valores son representados en la Tabla 4. Se observaron valores negativos para los ΔVΦο de la glicina a todas las temperaturas. De igual manera, los valores de ΔVΦο disminuyen con el incremento de la concentración de [BMIm][BF4] en las mezclas. A dilución infinita, las interacciones soluto-soluto son ausentes, por consiguiente, los volúmenes de transferencia proporcionan información acerca de la interacción de un co-solvente y un soluto.12,22
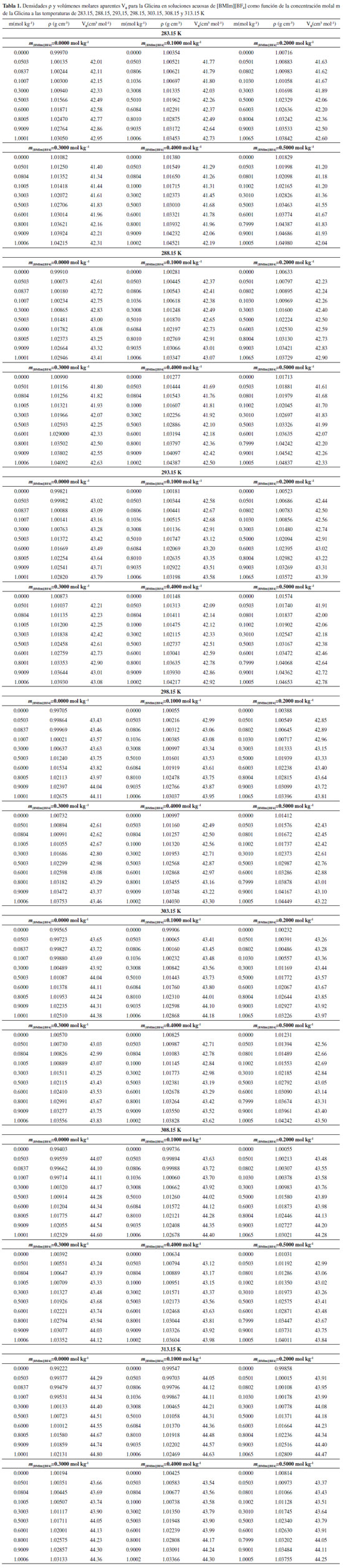
Por otra parte, siguiendo el modelo de las coesferas solapadas de Frank y Evans,8,18,23 y en virtud, a que en una solución de un aminoácido en mezclas acuosas de un líquido iónico se pueden presentar las siguientes interacciones:24 I. Interacciones ion-ion entre el anión del liquido iónico (en nuestro caso el grupo BF4-) y el catión del aminoácido (el grupo NH3+) y entre el catión del liquido iónico (en nuestro caso el grupo BMIm+) y el anión del aminoácido (el grupo COO-). II. Interacciones ion-hidrofóbica entre los grupos BMIm+/BF4- del líquido iónico y los grupos apolares presentes en los aminoácidos y entre los grupos NH3+/ COO- del aminoácido y los grupos alquílicos presentes en el liquido iónico. III. Interacciones hidrofóbica-hidrofóbica entre los grupos alquílicos presentes en el liquido iónico y los grupos apolares del aminoácido; los valores de DVf0 pueden ser analizados en términos de interacciones soluto co-soluto: El predominio de las interacciones tipo I produce valores positivos de ΔVΦο, mientras que el predominio de las interacciones tipo II y III da lugar a valores negativos ΔVΦο; en nuestro caso los valores negativos de ΔVΦο pueden ser interpretados como un predominio de las interacciones entre el grupo metilo de la glicina con los grupos metil, butil, y los centros cargados del [BMIm][BF4], así como de los centros cargados de la glicina con los grupos metil y butil del [BMIm][BF4]; este predomino de estas interacciones ocasiona un aumento de las moléculas de agua liberadas desde la esfera de hidratación hasta la fase voluminosa produciéndose una disminución en la estructura global del agua, producto del solapamiento de las coesferas.24 Así mismo, los valores de ΔVΦο disminuyen con el incremento de la concentración de [BMIm][BF4] lo cual indica que aumenta el, predominio de las interacciones tipo II. Estos resultados nos llevan a pensar que la glicina se comporta como un soluto disruptor de la estructura tridimensional del agua en soluciones de [BMIm][BF4], lo cual es consistente con los resultados encontrados de acuerdo al criterio de Hepler. Por otro lado, los VΦο para los aminoácidos pueden ser considerados como el resultado de la suma del volumen de Vander Waals Vvw, el volumen asociado con los huecos o espacios vacios VV y el volumen de contracción debido a la electrostricción VS.3,25 Asumiendo que VVW y VV tienen la misma magnitud en agua que en soluciones acuosas para la misma clase de solutos,26 los valores de ΔVΦ0 se pueden explicar de acuerdo al cambio en el volumen de contracción debido al efecto de electrostricción, según esto, en nuestro caso, la presencia [BMIm][BF4] aumenta el efecto de electrostricción causada por el aminoácido, a causa de los grupos metil y butil del [BMIm][BF4], lo cual resulta en un incremento de la contracción. Este efecto se debe reflejar en los valores de número de hidratación calculados utilizando el tratamiento de Millero.18,27,28 Según este modelo, el volumen molar aparente a dilución infinita se puede representar mediante la ecuación (5):

donde

donde
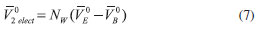
donde
CONCLUSIONES En este estudio, se obtuvieron datos volumétricos para la glicina en soluciones acuosas de [BMIm][BF4] a diferentes concentraciones. Los volúmenes molares aparentes limites Vf0 fueron positivos, disminuyen con el aumento de la concentración del [BMIm][BF4] e incrementan con el aumento de la temperatura. La segunda derivada de Vfο con respecto a la temperatura muestra que la glicina se comporta como un soluto disruptor de la estructura del solvente en soluciones acuosas de [BMIm][BF4]. Los volúmenes molares aparentes de transferencia a dilución infinita sugieren una disminución de la estructura del agua alrededor de los grupos hidrofóbicos e hidrofílicos. Finalmente, los resultados de los números de hidratación Nw muestran un efecto de deshidratación a medida que se incrementan los valores de temperatura; sin embargo, este procedimiento, no mostró sensibilidad respecto a los cambios en los valores de la concentración del [BMIm][BF4] en el solvente mixto.
AGRADECIMIENTOS Los autores agradecen a la Universidad de Córdoba por el apoyo financiero para la realización de este trabajo.
REFERENCIAS 1. Sinha, B.; Dakua, V. K.; Roy, M. N.; J. Chem. Eng. Data 2007, 52, 1768. 2. Rajagopal, K.; Jayabalakrishnan, S.; Chin. J. Chem. Eng. 2009, 17, 796. 3. Tome, L. I. N.; Domínguez-Pérez, M.; Cláudio, A. F. M.; Freire, M. G.; Marrucho, I. M.; Cabeza, O.; Coutinho, J. A. P.; J. Phys. Chem. B 2009, 113, 13971. 4. Shekaari, H.; Jebali, F.; J. Chem. Eng. Data 2010, 55, 2517. 5. Gao, H.; Qi, F.; Wang, H.; J. Chem. Thermodynamics 2009, 41, 888. 6. Malham, I. B.; Letellier, P.; Turmine, M.; J. Phys. Chem. B. 2006, 110, 14212. 7. Pal, A.; Kumar, S.; J. Mol. Liq. 2005, 121, 148. 8. Siddique, J.; Naqvi, S.; J. Chem. Eng. Data 2010, 55, 2930. 9. Lin, G.; Lin, R.; Ma, L.; Thermochim. Acta 2005, 430, 31. 10. Yuan, Q.; Li, Z. F.; Wang, B. H.; J. Chem. Thermodynamics 2006, 38, 20 11. Xu, L.; Ding, C.; Lin, R.; J. Solution Chem. 2006, 35, 191. 12. Pal, A.; Chauhan, N.; J. Chem. Thermodyn. 2011, 43, 140. " 13. Banipal, T. S.; Singh, K.; Banipal, P. K.; Kaur, J.; J. Chem. Thermodyn. 2010, 40, 1166. 14. Armarego, W. C.; Purification of laboratory chemicals, 3th ed., Heinemann, B: United States of America, 2009. 15. Wang, J.; Yan, Z.; Lu, J.; J. Chem. Thermodyn. 2004, 36, 281. 16. Mokhtarani, B.; Sharifi, A.; Mortaheb, H. R.; Mirzaei, M.; Mafi, M.; Sadeghian, F.; J. Chem. Thermodyn. 2009, 41, 323. 17. Shekaari, H.; Jebali, F.; Fluid Phase Equilib. 2010, 295, 68. 18. Banerjee, T.; Kishore, N.; J. Solution Chem. 2005, 34, 137. 19. Hepler, L.; Can. J. Chem. 1969, 47, 4613. 20. Zhenning, Q. Z.; WeiWei, L.; Jianji, W.; J. Chem. Eng. Data 2010, 55, 3560. 21. Banipal, T. S.; Kaur, J.; Banipal, P. K.; Singh, K.; J. Chem. Eng. Data 2008, 53, 1803. 22. Yan, Z.; Wang, J.; Kong, W.; Lu, J.; Fluid Phase Equilib. 2004, 215, 143. 23. Liu, C; J. Solution Chem. 2010, 39, 1253. 24. Singh, M.; Pandey, M.; Yadav, R. K.; Verma, H.; J. Mol. Liq. 2007, 135, 188. 25. Natarajan, M.; Wadi, R. K.; Gaur, H. C.; J. Chem. Eng. Data 1990, 35, 87. 26. Palani, R.; Balakrishnan, S.; Arumugam, G.; J. Phys. Sci. 2011, 22, 131. 27. Millero, F. J.; Surdo, L, A.; Shin, C.; J. Phys. Chem. 1978, 82, 784. 28. Choudhary, S.; Kishore, N.; J. Chem. Thermodyn. 2011, 43.1541. 29. Singh, S. K.; Kundu, A.; Kishore, N.; J. Chem. Thermodyn. 2004, 36, 7. 30. Wang, J.; Yan, Z.; Zhuo, K.; Lu, J.; Biophys. Chem. 1999, 80, 179. 31. Tyrrell, H. J. V.; Kennerley, M.; J. Chem. Soc., A: Inorg. Phys. Theor. 1968, 2724. 32. Yan, Z.; Wang, J.; Liu, W.; Lu, J.; Thermochim. Acta 1999, 334, 17. 33. Lark, B. S.; Bala, K.; Indian J. Chem. A., 1983, 22, 192. 34. Islam, M. N.;Wadi, R. K.; Phys. Chem. Liq. 2003, 41, 533. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






 2VΦο/
2VΦο/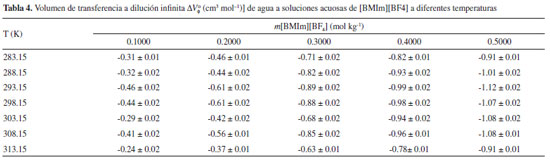
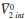 es el volumen molar parcial intrinseco del aminoácido, el cual se puede expresar como la adición del volumen de Van der Walls y el volumen debido al efecto de empaquetamiento y
es el volumen molar parcial intrinseco del aminoácido, el cual se puede expresar como la adición del volumen de Van der Walls y el volumen debido al efecto de empaquetamiento y 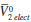 es el volumen de electrostricción. Los valores de
es el volumen de electrostricción. Los valores de 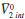 para los aminoácidos pueden ser obtenidos del volumen molar del cristal utilizando la ecuación (6):29
para los aminoácidos pueden ser obtenidos del volumen molar del cristal utilizando la ecuación (6):29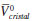 es el volumen del cristal y se obtiene dividiendo el peso molecular del cristal por su densidad. Tanto la densidad del sólido y el volumen del cristal se asumen constantes en todo el rango de temperatura de trabajo. Pese a que Millero utilizó esta ecuación para aminoácidos en agua, esta ha sido utilizada también en solventes acuosos mixtos.3,18,22,23,25,29,30 Conociendo el volumen de electrostricción es posible determinar el número de moléculas hidratadas alrededor del aminoácido o número de hidratación utilizando la siguiente ecuación:
es el volumen del cristal y se obtiene dividiendo el peso molecular del cristal por su densidad. Tanto la densidad del sólido y el volumen del cristal se asumen constantes en todo el rango de temperatura de trabajo. Pese a que Millero utilizó esta ecuación para aminoácidos en agua, esta ha sido utilizada también en solventes acuosos mixtos.3,18,22,23,25,29,30 Conociendo el volumen de electrostricción es posible determinar el número de moléculas hidratadas alrededor del aminoácido o número de hidratación utilizando la siguiente ecuación: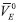 es el volumen molar del agua en la esfera de hidratación y
es el volumen molar del agua en la esfera de hidratación y 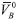 es el volumen molar del agua natural. Este modelo asume que por cada molécula de agua que pase desde la fase voluminosa hasta la región cercana al aminoácido el volumen decrece en
es el volumen molar del agua natural. Este modelo asume que por cada molécula de agua que pase desde la fase voluminosa hasta la región cercana al aminoácido el volumen decrece en 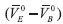 Usando los valores de -2.9, -3.3, -4.0 cm3 mol-1 a 288.15, 298.15 y 308.15 K respectivamente reportados por Yan et al,22 para la relación
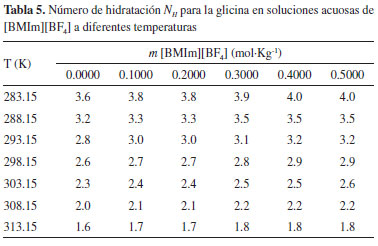
Usando los valores de -2.9, -3.3, -4.0 cm3 mol-1 a 288.15, 298.15 y 308.15 K respectivamente reportados por Yan et al,22 para la relación 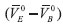 y obteniendo los valores a 283.15, 293.15, 303.15 y 313.15 K mediante la correlación de los datos obtenidos por Yan et al,22 se obtienen los valores de -2.7, -3.1, -3.6 y -4.6 cm3 mol-1 a las temperaturas de 288.15, 298.15 y 308.15 K respectivamente. Así, los números de hidratación pueden ser obtenidos como una aproximación utilizando la ecuación (7) y sus valores son mostrados en la Tabla 5. Los valores de Nw encontrados para la glicina en soluciones acuosas de [BMIm][BF4] son positivos, disminuyen conforme aumenta la temperatura y aumentan ligeramente con el incremento en la concentracion del [BMIm][BF4] en el solvente. Sin embargo, hay que anotar, que los valores en los números de hidratación no reflejan de manera marcada el aumento en la electrostricción obtenida previamente en el análisis de los volúmenes molares aparentes de trasferencia a dilución infinita, por tal motivo, pensamos que este procedimiento no es el más apropiado para la determinación de los números de hidratación, en este tipo de sistemas complejos.
y obteniendo los valores a 283.15, 293.15, 303.15 y 313.15 K mediante la correlación de los datos obtenidos por Yan et al,22 se obtienen los valores de -2.7, -3.1, -3.6 y -4.6 cm3 mol-1 a las temperaturas de 288.15, 298.15 y 308.15 K respectivamente. Así, los números de hidratación pueden ser obtenidos como una aproximación utilizando la ecuación (7) y sus valores son mostrados en la Tabla 5. Los valores de Nw encontrados para la glicina en soluciones acuosas de [BMIm][BF4] son positivos, disminuyen conforme aumenta la temperatura y aumentan ligeramente con el incremento en la concentracion del [BMIm][BF4] en el solvente. Sin embargo, hay que anotar, que los valores en los números de hidratación no reflejan de manera marcada el aumento en la electrostricción obtenida previamente en el análisis de los volúmenes molares aparentes de trasferencia a dilución infinita, por tal motivo, pensamos que este procedimiento no es el más apropiado para la determinación de los números de hidratación, en este tipo de sistemas complejos.