Artigo
|
|
| Estudo do efeito de matriz na determinação de metais em óleos básicos rerrefinados por fluorescência de raios X por energia dispersiva Study of matrix effect in determination of metals in re-refined basic oils by energy dispersive X-ray fluorescence - EDX |
|
Maristela L. S. MeloI,*; Jurandir R. de SouzaII
IAgência Nacional do Petróleo, Gás Natural e Biocombustíveis, SGAN 603, Módulo H, Asa Norte, Brasília - DF, Brasil Recebido em 19/08/2014 *e-mail: mlsilva@anp.gov.br In this article, the results of the study of the matrix effect in the determination of metals calcium, chromium, iron, nickel, copper, zinc, molybdenum, cadmium, barium and lead in base oil using Energy Dispersive X-Ray Fluorescence (EDX) are presented. Sensitivities obtained for each calibration curve were evaluated where calcium, chromium, copper, cadmium, barium and lead had the lowest sensitivities. In the case of cadmium, this parameter was lagging and the studies were not carried forward. The curves of the other metals in different base oils were evaluated for linearity. The elements chromium, copper, molybdenum and lead showed linearity problems in some cases. Therefore, curves in different base oils showed distinct mathematical behavior where the matrix effect was confirmed. The other curves were evaluated and existence of the matrix effect attributed to interference of C / H ratio was confirmed in the quantification of all elements. Metals iron, nickel and zinc exhibited the highest sensitivity and determination coefficients, showing that the method has application potential. INTRODUÇÃO O mundo contemporâneo está consumindo cada vez mais derivados de petróleo e existe uma tendência em se buscar fontes de energia renováveis que venham a substituir os combustíveis fósseis. Assim, os biocombustíveis estão sendo estudados exaustivamente, mas, além de combustíveis, o petróleo também é uma das fontes dos óleos básicos utilizados na fabricação de óleos e graxas lubrificantes. Esses materiais são usados entre duas superfícies em movimento para diminuir o atrito entre elas e são fundamentais na lubrificação de, dentre outros, motores de automóveis e máquinas industriais. Os óleos lubrificantes são compostos por uma mistura de um tipo ou mais de óleo básico e aditivos. O óleo básico pode ser um óleo mineral derivado de petróleo, constituído principalmente por hidrocarbonetos, ou ainda um óleo sintético produzido a partir de reações de síntese orgânica, os principais exemplos são as polialfaolefinas e os ésteres complexos. Os aditivos são substâncias utilizadas para melhorar algumas características desses básicos, tais como: dispersão e detergência (organometálicos de cálcio e magnésio); propriedades antioxidantes (ditiofosfato de zinco); índice de viscosidade (polialquilmetacrilatos) e produção e estabilização de espuma (silicone). Em seu uso ordinário, os óleos lubrificantes não são queimados, não sendo totalmente consumidos, por isso, podem ser reciclados, produzindo óleos básicos que retornam à cadeia de produção. Essa reciclagem é denominada rerrefino, o qual é definido como o tratamento do óleo lubrificante usado em uma sequência de processos que remove todos os contaminantes, incluindo água, partículas sólidas, produtos de diluição, produtos de oxidação e os aditivos previamente incorporados ao óleo básico.1 Existem inúmeros processos de rerrefino consolidados e alguns estudos que visam o seu aprimoramento.2-7 O óleo usado e contaminado é considerado um resíduo perigoso, por isso o seu rerrefino exige um controle de qualidade severo no que se refere à eliminação dos contaminantes, principalmente metais tóxicos como chumbo e cádmio e metais de aditivação como cálcio e zinco. O método de análise mais comumente utilizado para este controle é o ASTM D51858, cujo escopo contempla a análise de 22 elementos em óleos básicos e em óleos usados por espectrometria de emissão atômica de plasma indutivamente acoplado, ICP. Esse método, apesar de eficiente, exige a diluição da amostra em querosene ou xileno, além do alto consumo de gás argônio, o que motivou a busca por um método alternativo de fácil utilização e com menor quantidade de insumos. Existem diversos métodos consolidados para análise de óleos lubrificantes novos, como o método ASTM D49519, que também utiliza ICP, e o ASTM D 4628,10 que utiliza espectrometria de absorção atômica. Siveira et al.11 pesquisou a utilização da espectrometria de absorção atômica na análise de óleos lubrificantes usados provenientes de motores de ônibus da cidade de Teresina no Piauí. Devido à presença de material particulado e metais provenientes do desgaste físico das peças dos motores, foi necessário a mineralização das amostras por meio de reação com ácido sulfanílico e nitrato de lantânio. Apesar de se mostrar eficiente, o método empregado é bastante trabalhoso. Não foram encontradas pesquisas semelhantes sobre a determinação de metais em óleos básicos utilizando espectrometria de absorção atômica. A fluorescência de raios X por energia dispersiva é amplamente usada em análises qualitativas e quantitativas de metais em tipos diferentes de materiais.12-16 Na indústria do petróleo, esta técnica é utilizada na análise de enxofre em combustíveis e na determinação de fósforo, enxofre, cálcio e zinco em óleos lubrificantes acabados.17-20 A principal vantagem dessa técnica em relação às demais é não necessitar de preparo prévio das amostras, dispensando diluições ou mineralização. No entanto, essa técnica é mais suscetível a interferências por efeito de matriz, que afetam à seletividade dos métodos de análise. O método ASTM D6481,17 o qual se aplica à determinação de cálcio, zinco, enxofre e fósforo em óleos lubrificantes acabados novos, utiliza uma correção matemática para minimizar a absorção dos raios X dos elementos de interesse por outros elementos presentes, devido à aditivação do óleo básico. As concentrações mínimas das faixas de análise desse método, para cada elemento, varia entre 100 a 500 mg/kg e ele não se aplica a óleos usados, cuja matriz é complexa, nem a óleos básicos, cujos teores esperados são inferiores a 100 mg/kg. O método ASTM D429418 se aplica à determinação de enxofre total em petróleo e derivados de petróleo que sejam líquidos a temperatura ambiente. Nesse caso, o efeito de matriz pode ser causado pela diferença entre as razões carbono/hidrogênio (C/H) dos padrões e das amostras ou pela presença de outro heteroátomo.21 Simbolon22 estudou a utilização do EDX para determinar cromo, ferro e chumbo em óleos usados, verificando a ocorrência de efeito matriz devido a esses óleos serem formados por uma mistura de óleos básicos, aditivos (compostos organometálicos e polímeros), produtos de degradação e contaminantes típicos do uso do lubrificante. Para conseguir quantificar esses elementos, ele usou curva de adição de padrão, metodologia trabalhosa e demorada, uma vez que é feita uma curva analítica para cada amostra. Quando comparados aos demais materiais citados (óleo lubrificante usado e óleo lubrificante acabado novo), os óleos básicos rerrefinados apresentam uma matriz muito mais simples, pois não devem possuir aditivos ou produtos de degradação, sendo a determinação de metais necessária apenas para controle de descontaminação. No Brasil, esses básicos são classificados pela Portaria ANP nº130/99, de acordo com a sua viscosidade cinemática, em um dos seguintes tipos: parafínico spindle (PSP), parafínico neutro leve (PNL), parafínico neutro médio (PNM) e parafínico neutro pesado (PNP).23 A viscosidade cinemática está relacionada, entre outros fatores, à densidade e tamanho da cadeia carbônica do óleo básico. Portanto, as razões C/H observadas para estes básicos são distintas entre si, o que pode causar efeito de matriz na determinação de metais por EDX, afetando a sensibilidade do método caso se queira utilizar um método único para todos os tipos de básicos rerrefinados. Na busca bibliográfica realizada não foram encontrados estudos sobre a sensibilidade e a seletividade de métodos de análise dos elementos cálcio, cromo, ferro, níquel, cobre, zinco, molibdênio, cádmio, bário e chumbo em óleos básicos de primeiro refino ou rerrefinados utilizando fluorescência de raios X por energia dispersiva. A sensibilidade de um método é o gradiente da curva resposta, ou seja, a alteração na resposta do instrumento que corresponde a uma mudança na concentração do analito.24 Esse gradiente é dado pela inclinação da curva analítica. Dessa forma, a avaliação da sensibilidade do método está relacionada aos testes de verificação de linearidade e regressão linear. A seletividade depende de quanto ele é indiferente à presença de interferentes da matriz na determinação do analito.25 Assim, para que se possa propor e validar método de análise de metais em óleo básico rerrefinado utilizando EDX, é necessário estudar o efeito da matriz para comprovar que o método em questão é seletivo e que não existem diferenças significativas entre as matrizes dos padrões da curva analítica e das amostras. Neste trabalho, foi estudado o efeito de matriz na determinação de cálcio, cromo, ferro, níquel, cobre, zinco, molibdênio, cádmio, bário e chumbo em óleos básicos rerrefinados causado pelas diferentes viscosidades desses óleos. Para isso, curvas analíticas semelhantes, ou seja, com as mesmas conentrações dos elementos em questão, mas formuladas com os diferentes tipos de básicos foram comparadas entre si.
PARTE EXPERIMENTAL Experimento Foi utilizado o espectrômetro de fluorescência de raios X por energia dispersiva modelo 720 da Shimadzu, com tubo de Ródio e ambiente em ar atmosférico. A faixa de trabalho escolhida foi de 5 a 105 mg/kg, pois não é esperado que, em óleos rerrefinados, sejam encontrados os elementos aqui estudados em teores superiores a 100 mg/kg, pois teores a partir deste valor já são típicos de alguns óleos lubrificantes acabados, ou seja, próprios para o uso, como aqueles para motores 2 tempos. Foram preparadas quatro curvas analíticas, uma para cada básico, em cinco níveis na faixa de trabalho escolhida (5, 25, 45, 65, 85 e 105 mg/kg), com três padrões em cada nível. Todos os padrões foram preparados por diluição em massa, sendo utilizado básico de primeiro refino e material de referência certificado, MRC, multielementar, marca Conostan, contendo 900 mg/kg dos metais cálcio, cromo, ferro, níquel, cobre, zinco, molibdênio, cádmio, bário e chumbo e outros 11 elementos tipicamente encontrados em óleo usado. Após pesagem do MRC e do básico, a mistura foi aquecida em estufa a 45 ºC por 15 min e, depois, agitada em agitador magnético, também a 45 ºC, por 5 min. Um método inicial, denominado PNM1 (Parafínico Neutro Médio 1), foi elaborado de acordo com as sugestões tidas como padrão pelo equipamento (escolha da linha e dos filtros, voltagem de 50 kV e corrente de 100 µA), com algumas alterações nas voltagens e intensidade de corrente do tubo e sem utilização de filtros, conforme consta na Tabela 1. As curvas em PNM foram analisadas, sendo medidas aleatoriamente as intensidades de cada padrão. Em seguida, foram testadas quanto ao atendimento às premissas de linearidade, de acordo com o descrito na próxima seção. Para os casos nos quais a linearidade não foi comprovada, um novo método foi testado, sendo nomeado PNM3 (Parafínico Neutro Médio 3). As condições desse método também consta na Tabela 1. As demais curvas foram analisadas e testadas quanto às premissas da linearidade, novamente, nos casos em que elas não foram comprovadas, um novo método foi testado.
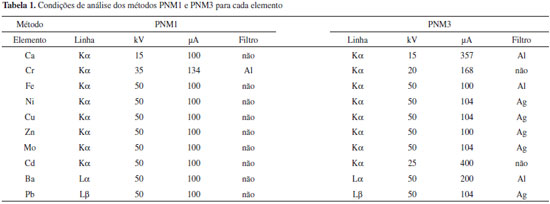
Análise estatística As curvas obtidas com o método PNM1 foram avaliadas quanto às premissas da linearidade: normalidade, homoscedasticidade, independência dos resíduos e inexistência de desvio da linearidade. Para isso, os resultados foram submetidos a tratamento de outliers utilizando o teste de resíduos Jacknife, o qual emprega uma estimativa da variância dos resíduos da regressão independente do ponto suspeito.26 À medida que um outilier é retirado, os cálculos são refeitos, até que não restem mais resultados deste tipo ou até alcançar a 22% dos dados avaliados. A normalidade foi testada pelo método Ryan-Joiner, a homoscedasticidade pelo método de Brown & Forsythe, a independência dos resíduos pelo método de Durbin-Watson e o desvio de linearidade pelo ANOVA. No teste de Ryan-Joiner, a hipótese nula de que os resíduos seguem a normal é confrontada com a alternativa de que eles seguem outra distribuição. A estatística adotada é o coeficiente de correlação do gráfico de probabilidade normal ou coeficiente de correlação de Ryan-Joiner, Req. Neste teste, é construído o gráfico dos resíduos, ei, calculado de acordo com a equação 1, em ordem crescente versus os pontos percentis de uma distribuição normal reduzida, qi, calculada conforme a equação 2. O coeficiente de correlação entre ei e qi é calculado conforme a equação 3. O coeficiente de correlação crítico, Rcrítico, com nível de significância α igual a 0,10, é calculado por interpolação polinomial pela equação 4.   Nas quais: ei o resíduo da regressão, yi a resposta obtida em análise e ŷi a resposta estimada; qi é a distribuição normal reduzida 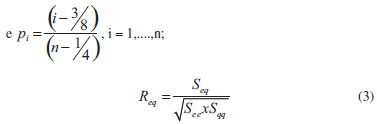 sendo: Req o coeficiente de correlação de Ryan-Joiner; 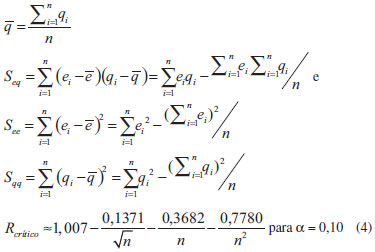 No método de Durbin-Watson, a hipótese nula afirma que não há autocorrelação dos resíduos e, a alternativa, que os resíduos são autocorrelacionáveis. A estatística deste teste é d, definido pela equação 5. Há dois limites críticos dL, limite inferior, e dU, limite superior, calculados de acordo com as equações 6 e 7, para um nível de significância α = 0,05. A independência dos resíduos é comprovada quando dU < d < 4 - dU. Se 4 - dU < d < 4 - dL, o teste é inconclusivo. Valores de d < dL e de d > 4 - dL indicam, respectivamente, autocorrelação positiva e negativa e rejeição da hipótese nula a um nível de significância de 2α. 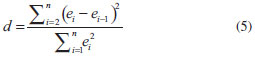 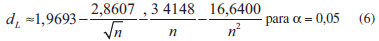 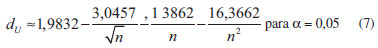 Os dados obtidos foram testados quanto à homocedasticidade utilizando o teste de Brown & Forsythe ou Levene modificado. Nesse teste, a hipótese nula de que as variâncias dos resíduos não diferem entre si é confrontada com a hipótese que elas são diferentes. A estatística do teste é o tL e a hipótese nula é rejeitada, com nível de confiança de 95%, quando a distribuição t de student de tL, p, for menor que 0,05. Os resíduos são divididos em dois grupos n1 e n2, sem separar as replicatas de um mesmo nível. Para cada grupo, é calculada a mediana e as diferenças, em módulo, entre ela e os resíduos. O tL é dado pela equação 8. 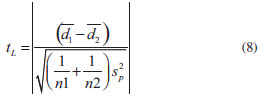 sendo:
nk, número de observações em cada grupo;
A análise de variância é o método mais usado para se avaliar numericamente a qualidade do ajuste de um modelo.27 Neste trabalho, a significância da regressão e o desvio da linearidade foram testados utilizando a tabela de Análise da Variância, ANOVA. Os testes de efeito de matriz foram realizados tomando a curva em PNM como padrão, pois esse óleo básico possui faixa de viscosidade intermediária entre os óleos mais leves (PSP e PNL) e o mais pesado (PNP), logo as demais curvas foram comparadas a ela. Antes da avaliação do efeito de matriz, a homogeneidade das variâncias dos resíduos de cada curva foi testada utilizando o teste F bilateral, cuja hipótese nula é de que há homocedasticidade e a alternativa é de que há heterodasticidade. A estatística do teste é a razão entre as variâncias F, sendo a maior variância o numerador e a menor o denominador, conforme equação 9. A hipótese nula é rejeitada quando o F calculado for maior que o F crítico, F(1-α/2;n1-2;n2-2), dado pela distribuição F.  na qual: F é a razão entre as variâncias, S2res1 é a maior variância e S2res2 é a menor variância. Em caso de homocedasticidade, as inclinações e interseções das curvas foram comparadas pelo teste t com variâncias combinadas. Neste teste, a hipótese nula é de que as inclinações e interseções não diferem entre si e, a alternativa é de que diferem. As estatísticas do teste, tb e ta, são calculadas de acordo com as equações 10 e 11 e a hipótese nula é rejeitada quando elas forem maiores que o valor crítico t(1-α/2;n1+n2-4), o qual é dado pela distribuição t de student. 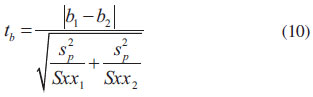 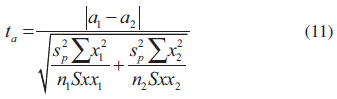
nas quais: b1 e b2 são as inclinações das curvas 1 e 2 respectivamente; a1 e a2 são as interseções das curvas 1 e 2 respectivamente;
Sxx1 e Sxx2 são calculados pela equação Em caso de heterodasticidade, o teste t é empregado utilizando as variâncias amostrais de cada curva. As estatísticas do teste são tb', contraste entre inclinações, e ta', contraste entre interseções, calculadas pelas equações 12 e 13, respectivamente. A hipótese nula, de que as inclinações e interseções não diferem entre si, é rejeitada quando tb' e ta' são maiores que o valor crítico t(1-α/2; ν), sendo ν definido pela equação 14. 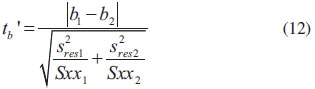 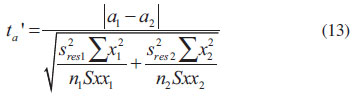 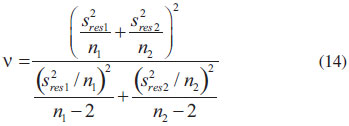
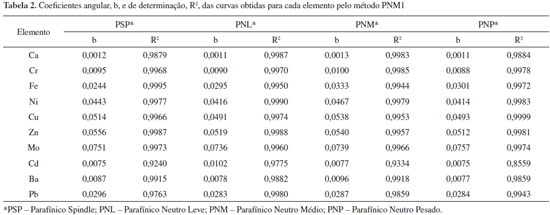
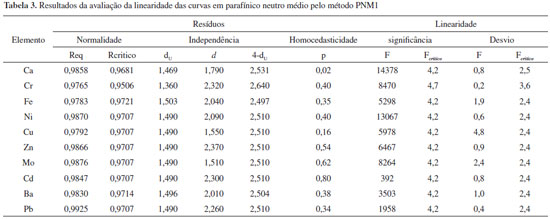
RESULTADOS E DISCUSSÃO A Tabela 2 apresenta os valores dos coeficientes angular, b, e de determinação, R2, obtidos para cada curva pelo método PNM1. De uma forma geral, os coeficientes angulares observados são baixos, indicando baixa sensibilidade do método. Cálcio, cromo, cádmio e bário demonstraram as menores sensibilidades. Os metais cádmio, bário e chumbo apresentaram os menores coeficientes de determinação, sendo todos inferiores ao desejado (0,99). Os resultados dos testes das premissas da linearidade para as curvas em PNM são apresentados na Tabela 3. A curva do cálcio apresentou heterocedasticidade dos resíduos e a do cobre, desvio da linearidade.
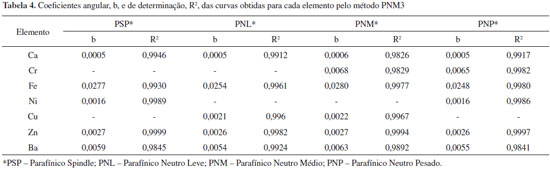
Com relação às curvas obtidas com os básicos PSP, PNL e PNP, a premissa de que os resíduos seguem a distribuição normal foi confirmada para todos os elementos pelo teste de Ryan-Joiner. Os resultados dos testes de Durbin-Watson confirmaram que os resíduos das curvas de todos os elementos, com exceção de níquel e bário, são independentes a um nível de significância α = 0,05. O teste foi não conclusivo para a curva de níquel em PNP e confirmou autocorrelação negativa no caso da curva de bário em PNP. A homocedasticidade dos resíduos foi confirmada para todos os elementos, exceto para chumbo em PNL, cujos testes acusaram a hetorodasticidade. Utilizando ANOVA, foi confirmado que a regressão de todas as curvas é significativa, mas ocorre desvio da linearidade nos seguintes casos: cromo, ferro, cobre, zinco e molibdênio em PNP e cobre e molibdênio em PNL. Nos casos em que as premissas da linearidade não foram confirmadas ou que a sensibilidade do método era muito baixa, duas possibilidades foram avaliadas: transformar os dados e refazer os testes ou modificar o método e reavaliar. A segunda opção foi escolhida, pois os modelos lineares são mais simples e fáceis de serem adotados cotidianamente. Assim, foi criado o método PNM3, cujas condições constam na Tabela 1. A Tabela 4 apresenta os valores dos coeficientes angular, b, e de determinação, R2, obtidos para cada curva pelo método PNM3, cuja linearidade foi confirmada. As premissas da linearidade não foram confirmadas para nenhuma das curvas dos metais molibdênio, cádmio e chumbo, para as curvas de cromo em PSP e PNL, de níquel em PNL e PNM e de cobre em PSP e PNP.
Os estudos com o cádmio não prosseguiram devido à baixa sensibilidade combinada a um coeficiente de determinação muito inferior ao desejado (0,99). A Figura 1 mostra as curvas obtidas para o cádmio pelos métodos PNM1 e PNM3. Observa-se, além da baixa sensibilidade, uma elevada dispersão dos dados, principalmente no caso do método PNM3.
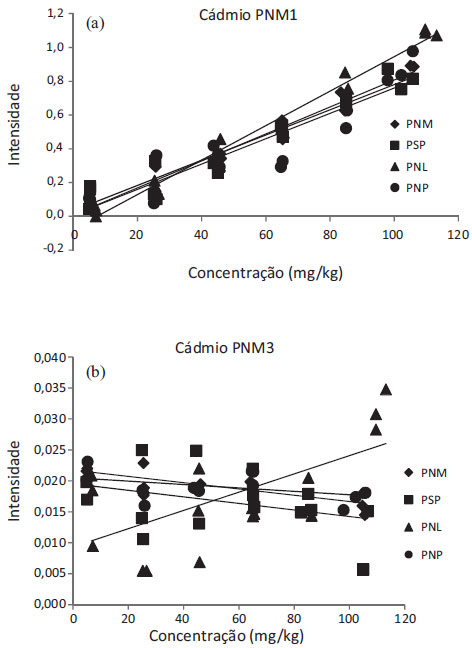 Figura 1. Gráfico de regressão linear das curvas de cádmio com os quatro tipos de básicos - (a) método PNM1 (b) método PNM3
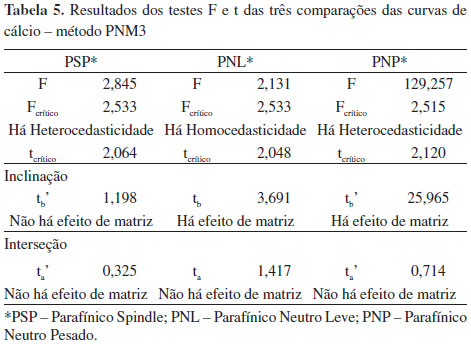
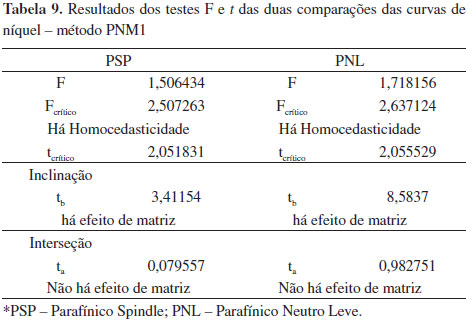
As avaliações de efeito de matriz das curvas dos metais molibdênio, chumbo, cobre e cromo não foram levadas adiante pelo fato de não se conseguir comprovar a linearidade das curvas em todos os básicos, o que de certa forma implica na existência deste efeito, visto que os comportamentos matemáticos das curvas obtidas são muito distintos. Cálcio e bário continuaram a apresentar baixa sensibilidade, além de coeficientes de determinação inferior a 0,99, para a curva de cálcio em PNM e para as curvas de bário em PSP, PNM e PNP. No entanto, todas as premissas de linearidade foram confirmadas para estes elementos e também para o ferro, por isso os testes de efeito de matriz foram realizados para as curvas desses três elementos obtidas com o método PNM3. A Figura 2 apresenta o gráfico da regressão obtido para as quatro curvas de cálcio pelo método PNM3. Observa-se que para os pontos de menor concentração, as curvas estão muito próximas, mas à medida que a concentração aumenta, elas se distanciam um pouco. A análise visual não é suficiente para que possa concluir sobre o real efeito da matriz, pois não é possível saber se as diferenças observadas entre as curvas se devem unicamente a uma flutuação aleatória. A Tabela 5 apresenta os resultados dos testes F e t realizados para cada tipo de básico. Foi comprovado o efeito matriz quando se compara as inclinações das curvas em PNM com as curvas em PNL e PNP.
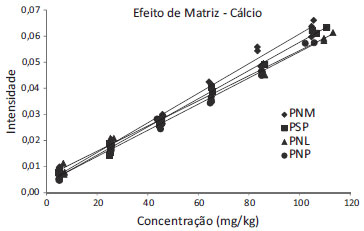 Figura 2. Gráfico de regressão linear das curvas de cálcio com os quatro tipos de básicos - método PNM3
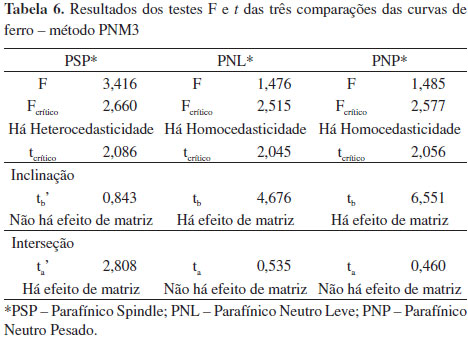
A Figura 3 apresenta o gráfico da regressão obtido para as quatro curvas de ferro pelo método PNM3. Assim como ocorreu com o cálcio, as curvas parecem convergir nas menores concentrações e se distanciam nas maiores. As curvas PNL e PNP quase se sobrepõem e parecem distintas das outras duas, que por sua vez aparentam ser paralelas nas maiores concentações. A análise visual indica a existência de efeito da matriz nos três casos. O teste t de variância combinada realizado para as curvas mostrou que há efeito de matriz na inclinação nos casos de PNL e PNP e efeito na interseção, no caso de PSP, confirmando a observação visual das curvas. Os resultados dos testes estatísticos são mostrados na Tabela 6.
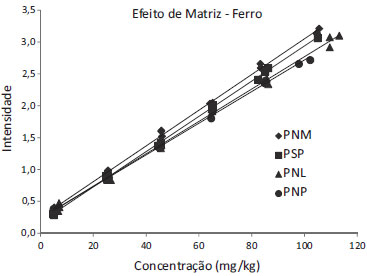 Figura 3. Gráfico de regressão linear das curvas de ferro com os quatro tipos de básicos - método PNM3
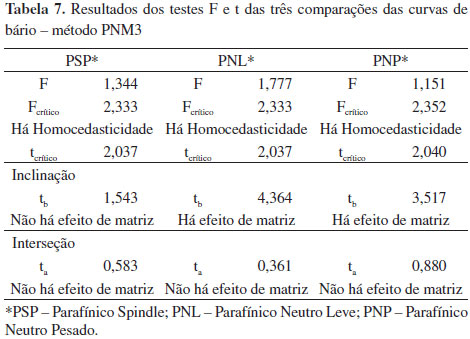
No caso do bário, as curvas em PNL e PNP se misturam, sendo visualmente diferentes da curva em PNM, como pode ser visto na Figura 4, o que sugere haver efeito de matriz nesses dois casos. A curva em PSP converge com PNM nas menores concentrações. O teste t de variância combinada realizado para as curvas, Tabela 7, mostrou que há efeito de matriz na inclinação nos casos de PNL e PNP, PSP não apresentou efeito de matriz de nenhum tipo.
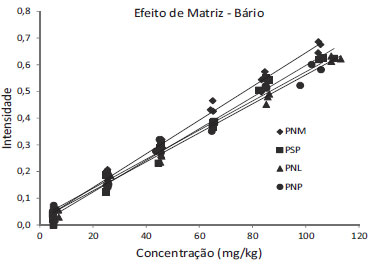 Figura 4. Gráfico de regressão linear das curvas de bário com os quatro tipos de básicos - método PNM3
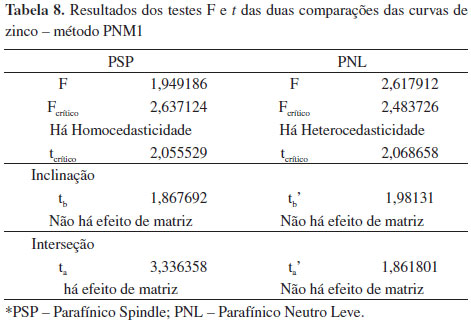
As curvas analíticas de zinco e níquel em PNP usando o método PNM1 não atenderam às premissas da linearidade e as curvas desses metais analisadas pelo método PNM3 apresentaram sensibilidade 10 vezes menor que as do primeiro método. Esse fato já é suficiente para que se conclua que existe efeito de matriz na análise desses metais por EDX. Ainda assim, as outras curvas foram testadas. A Figura 5 mostra o gráfico da regressão obtido para as curvas de zinco em PSP, PNL e PNP pelo método PNM1. É possível notar que a curva em PSP se distingue da curva em PNM nas menores concentrações, mas se sobrepõe a ela nas maiores. A curva em PNL é distinta da curva de PNM, sendo quase paralela a ela. A análise visual indica a existência de efeito da matriz nos dois casos. O teste t de variância combinada realizado para a curva em PSP mostrou que há efeito de matriz na interseção, confirmando a observação visual das curvas. O teste t de variância distinta realizado para a curva em PNL demonstrou não haver efeito matriz neste caso, ou seja, a diferença observada se deve a uma flutuação das medidas. Os resultados do teste são resumidos na Tabela 8.
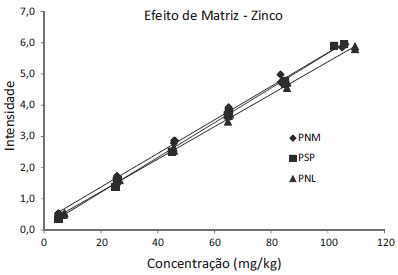 Figura 5. Gráfico de regressão linear das curvas de zinco com os básicos PSP, PNL e PNM - método PNM1
A Figura 6 apresenta o gráfico da regressão obtido para o níquel pelo método PNM1. As três curvas convergem nas menores concentrações. A análise visual indica a existência de efeito da matriz nos dois casos, o que foi confirmado pelo teste t de variância combinada o qual mostrou que o efeito ocorre na inclinação, conforme mostrado na Tabela 9.
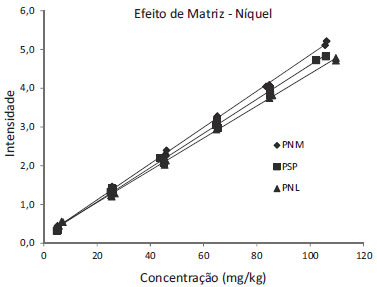 Figura 6. Gráfico de regressão linear das curvas de níquel com os básicos PSP, PNL e PNM - método PNM1
O fato dos padrões das curvas serem formulados com o mesmo material de referência certificado, MRC, e nas mesmas concentrações, implica que os efeitos de matriz observados neste estudo se devem exclusivamente às diferenças na composição dos básicos, ou seja, às distintas razões C/H. No entanto, o uso de MRC multielementar provavelmente é o responsável pela baixa sensibilidade em alguns casos. Deve ser estudada ainda a utilização de equipamentos com tubo de raios X distinto, como aqueles com tubos de prata, e atmosfera de hélio, a fim de averiguar se a mudança desses parâmetros poderia aumentar a sensibilidade do método de análise dos metais aqui estudados por EDX.
CONCLUSÃO O método de análise normalizado e amplamente utilizado para determinação de metais em óleo básico é o ASTM D5185, cuja técnica analítica adotada é o ICP. Neste método, as amostras precisam ser diluídas em querosene ou xileno e o consumo de gás argônio é alto. Os métodos de análise de lubrificantes por espectrometria de fluorescência de raios X não são adequados para análise de metais em óleos básicos rerrefinados, pois os teores esperados são mais baixos e a matriz é mais simples que a dos óleos lubrificantes acabados novos e usados. Na pesquisa apresentada, foram desenvolvidos métodos de análise dos metais cálcio, cromo, ferro, níquel, cobre, zinco, molibdênio, cádmio, bário e chumbo em óleos básicos minerais por EDX, sendo que, no caso dos elementos cálcio, cromo, cobre, cádmio, bário e chumbo, as sensibilidades obtidas foram baixas em relação aos demais. Além disso, os coeficientes de determinação obtidos foram inferiores a 0,99 em alguns casos. Neste aspecto, destaca-se o cádmio, cujo estudo do efeito de matriz não foi levado adiante, pois o R2 de todas as curvas foi inferior a 0,98. Os fatores que podem justificar a baixa sensibilidade e coeficiente de determinação envolvem o uso de material de referência certificado multielementar e atmosfera a ar, o que justifica novos estudos. Alguns metais não tiveram a linearidade de todas as curvas nos diferentes óleos básicos comprovadas, motivo pelo qual não foram testadas quanto ao efeito de matriz. Esse foi o caso do cromo, cobre, molibdênio e chumbo. No entanto, pode se concluir que o fato de serem obtidos resultados com comportamentos matemáticos distintos para cada óleo básico utilizado confirma a existência do efeito de matriz. Os metais ferro, níquel e zinco apresentaram coeficientes de determinação satisfatórios e sensibilidade maior em relação aos demais. As curvas de zinco e níquel em PNP apresentaram desvio da linearidade, mas as demais curvas desses elementos e as de ferro, cálcio e bário foram avaliadas quanto ao efeito de matriz, apresentando esse efeito na inclinação e/ou interseção. Conclui-se que houve a confirmação da interferência da razão C/H na quantificação de cromo, cobre, molibdênio, chumbo, zinco, níquel, ferro, cálcio e bário, sendo esse um importante passo para estudos futuros, os quais terão como desafio superá-la. A alternativa mais simples para tanto seria o uso de curvas analíticas individuais para cada tipo de básico, o que torna o método menos prático, mas não é um impeditivo para o seu uso. Os coeficientes de determinação e a sensibilidade obtida para as curvas dos metais ferro, níquel e zinco mostram que o método possui um potencial maior em ser aplicado na quantificação desses elementos. Os métodos avaliados não se mostraram promissores quanto à determinação de cádmio.
REFERÊNCIAS 1. Raldenes, E.; Assis, V. P.; Ornelas, R. B.; Atualidades do Conselho Nacional do Petróleo 1981, 78, 16. 2. Carreteiro, R. P.; Belmiro, P. N. A.; Lubrificantes e Lubrificaçao Industrial, 1 ed., Editora Interciência Ltda. e Instituto Brasileiro de Petróleo: Rio de Janeiro, 2006. 3. Mang, T.; Dresel, W.; Lubrication and Lubricants, 2nd ed., Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, 2007. 4. Rincón, J.; Cañizares, P.; Garcías, M. T.; Ind. Eng. Chem. Res. 2003, 42, 4867. DOI: http://dx.doi.org/10.1021/ie030013w 5. Rincón, J.; Cañizares, P.; Garcías, M. T.; Ind. Eng. Chem. Res. 2005, 44, 4373. DOI: http://dx.doi.org/10.1021/ie040254j 6. Rincón, J.; Cañizares, P.; Garcías, M. T.; Ind. Eng. Chem. Res. 2005, 44, 7854. DOI: http://dx.doi.org/10.1021/ie0580452 7. Hamawand, I.; Yusaf, T.; Rafat, S.; Energies 2013, 6, 1023. DOI: http://dx.doi.org/10.3390/en6021023 8. American Society for Testing and Materials, D5185, 2009. 9. American Society for Testing and Materials, D4951, 2009. 10. American Society for Testing and Materials, D4628, 2009. 11. Silveira, E. L. C.; Coelho, R. C.; Neto, J. M. M.; Moura, C. V. R.; Moura, E. M. M; Quim. Nova 2010, 33, 1863. DOI: http://dx.doi.org/10.1590/S0100-40422010000900008 12. Odumo, O. B.; Mustapha, A. O.; Patel, J. P.; Angeyo, H. K.; Bull. Environ. Contam. Toxicol. 2011, 87, 260. DOI: http://dx.doi.org/10.1007/s00128-011-0332-x PMID: 21681402 13. Natarajan, V.; Rajeswari, B.; Dhawale, B. A.; Hon, N. S.; Godbole, S. V.; Manchanda, V. K.; J. Radioanal. Nucl. Chem. 2009, 280, 27. DOI: http://dx.doi.org/10.1007/s10967-008-7384-3 14. Moraes, M. P. G.; Dissertaçao de Mestrado, Universidade Estadual de Campinas, Brasil, 2003. 15. Schidmidt, F.; Bueno, M. I. M. S.; Einzweiler, J.; Resumos do IV Congresso Brasileiro de Redes Neurais. ITA: Sao José dos Campos, 1999. 16. Ponce, L. C.; Zamora, P. P.; Bueno, M. I. M. S. Quim. Nova 1996, 19, 30. 17. American Society for Testing and Materials, D6481, 2010. 18. American Society for Testing and Materials, D4294, 2010. 19. American Society for Testing and Materials, D6445, 2004. 20. American Society for Testing and Materials, D7212, 2013. 21. Nadkarni, R. A. K.; Spectroscopy Analysis of Petroleum Products and Lubricants, Editora ASTM: Bridgeport, 2011. 22. Simbolon, S.; Atom Indonesia 1996, 22, 55. 23. BRASIL; Ministério de Minas e Energia. Agência Nacional do Petróleo, Gás Natural e Biocombustível. Portaria N130 de julho de 1999. Disponível em: http://www.anp.gov.br/?id=478 acessado em 2 de dezembro de 2013. 24. EURACHEM; The Fitness for Purpose of Analytical Methods - A Laboratory Guide to Method Validation and Related Topics, 1998. 25. Albano, F. M.; Raya-Rodrigues, M. T. Em Validaçao e Garantia da Qualidade de Ensaios Laboratoriais, 1 ed., Editora Rede Metrológica: Porto Alegre, 2009. 26. Souza, S. V. C.; Tese de Doutorado, Universidade Federal de Minas Gerais, 2007. 27. de Barros Neto, B.; Scarminio, I. S.; Bruns, R. E.; Como fazer Experimentos, 4 ed., Bookman: Porto Alegre, 2010. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






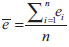 ;
;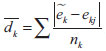 , média dos módulos das diferenças entre o j-ésimo resíduo e a mediana de cada grupo k = 1 e k=2;
, média dos módulos das diferenças entre o j-ésimo resíduo e a mediana de cada grupo k = 1 e k=2;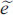 k, mediana de cada grupo;
k, mediana de cada grupo;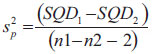 , variância combinada;
, variância combinada;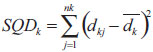 , soma dos quadrados dos desvios entre cada j-ésima diferença e a média de seu k-ésimo grupo para cada grupo.
, soma dos quadrados dos desvios entre cada j-ésima diferença e a média de seu k-ésimo grupo para cada grupo.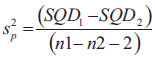 é a variância combinada;
é a variância combinada;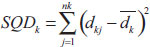 , soma dos quadrados dos desvios entre cada j-ésima diferença e a média de seu k-ésimo grupo para cada grupo.
, soma dos quadrados dos desvios entre cada j-ésima diferença e a média de seu k-ésimo grupo para cada grupo.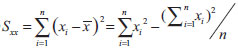 para cada curva. Sendo: xi a concentração conhecida do analito; yi resposta medida e ŷi a resposta estimada pela equação da regressão; n o número de pontos da curva analítica.
para cada curva. Sendo: xi a concentração conhecida do analito; yi resposta medida e ŷi a resposta estimada pela equação da regressão; n o número de pontos da curva analítica.