JBCS

INTRODUÇÃO

Vários métodos químico-quânticos amplamente utilizados atualmente^1-5 como o HF (Hartree-Fock), MP (teoria de perturbação de Møller-Plesset), DFT (teoria do funcional densidade) e Coupled-Cluster (coupled-cluster theory), por exemplo, são baseados numa função de onda descrita por um único determinante de Slater. Porém, se desejarmos estudar fotoquímica e fotofísica (quando é necessário descrever simultaneamente, e com a mesma precisão, diversos estados eletrônicos excitados), mecanismos de reação (quebra e formação de ligações químicas), compostos que não são representados por uma única configuração (como os representados por estruturas de ressonância), sistemas radicalares, estados de transição, dentre outros, é necessário utilizar métodos ab initio capazes de recuperar os efeitos de correlação eletrônica que, de acordo com Löwdin,⁶ representa a diferença entre a energia não relativística exata de um sistema e a energia Hartree-Fock. Dentre os métodos correlacionados estão os multiconfiguracionais,^1-5 que descrevem a função de onda empregando vários determinantes de Slater, introduzindo os efeitos de correlação eletrônica não dinâmica ou estática, proveniente da presença de configurações degeneradas (ou próximas à degenerescência, near-degeneracies). A outra parte da energia de correlação eletrônica, chamada de dinâmica, tem origem na posição relativa simultânea de dois elétrons, principalmente em regiões nas quais a distância entre eles é muito pequena (r_ij → 0), conhecida como cusp condition. Vale destacar que essa divisão da energia de correlação em duas partes deve-se, apenas, a uma questão de conveniência prática.

Em cálculos empregando métodos multiconfiguracionais a etapa mais importante é a construção do espaço ativo. Se o espaço ativo não estiver correto, os resultados não serão representativos. Nas próximas seções apresentaremos uma série de procedimentos que podem auxiliar os usuários na construção de espaços ativos. Os exemplos, envolvendo situações reais, poderão ser reproduzidos com o auxílio dos arquivos disponíveis no Material Suplementar, empregando softwares distribuídos gratuitamente pela internet. Para que o conteúdo seja melhor aproveitado, seria interessante o leitor ter algum conhecimento prévio sobre questões formais de química quântica computacional e teoria de grupo. Contudo, para aqueles ainda sem muita familiaridade com esses assuntos, esperamos que este trabalho seja uma fonte de inspiração para que eles aprimorem seus conhecimentos.

O método MCSCF: campo autoconsistente multiconfiguracional

Com o método MCSCF pretende-se recuperar a maior parte da energia de correlação estática. Para tratar os efeitos de correlação dinâmica é preciso combinar o método MCSCF com outros, como por exemplo interação de configurações,⁷ teoria de perturbação de muitos corpos (na sua forma mais usual, CASPT2), coupled-cluster⁸ e, inclusive, DFT^9,10 (embora ambos ainda em fase de desenvolvimento e testes).

Em um método multiconfiguracional, o espaço de orbitais moleculares é dividido, basicamente, em três subespaços: (i) inativo, (ii) ativo e (iii) virtual. Os orbitais pertencentes ao espaço ativo (ou orbitais ativos) são os que têm ocupação maior que zero e menor que dois. Orbitais com ocupação muito próxima a zero deverão ser incluídos no espaço virtual e os com ocupação próximas a dois, no espaço inativo. Em seguida, devemos escolher quais configurações utilizar e construir a função de onda como uma combinação linear (Equação 1), em que |I > (espaço de configurações) são determinantes de Slater ou funções adaptadas às simetrias espacial e de spin (CSF, configuration state function). Finalmente, os orbitais moleculares e os coeficientes (C_I) serão otimizados.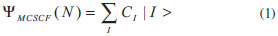

Analisando as etapas descritas anteriormente, identificamos algumas dificuldades práticas. Por exemplo, se o composto que está sendo investigado for conhecido, talvez não seja um grande problema identificar quais configurações serão incluídas na Equação 1. E se ele não for bem conhecido? No caso de uma molécula diatômica, por exemplo, é muito fácil identificar os produtos de dissociação; mas como seria no caso de uma molécula poliatômica? Em espectroscopia, poderíamos utilizar os orbitais moleculares HOMO e LUMO, inclusive alguns do tipo n (pares isolados), para gerar as configurações que irão compor a Equação 1; mas será que outras configurações importantes não seriam deixadas de lado? Portanto, uma maneira mais sistemática de se obter as configurações que serão utilizadas na Equação 1 é muito bem-vinda.

O método CASSCF

A construção do espaço de configurações e, principalmente, a solução das equações, eram um grande problema até a década de 1980, quando Roos e colaboradores^11-13 propuseram uma nova abordagem, denominada método CASSCF (complete active space self-consistent-field). Embora esse tipo de função de onda tivesse sido apresentada anteriormente por Ruedenberg e Sundberg,¹⁴ foi somente após a implementação proposta por Roos e colaboradores que o método CASSCF tornou-se uma ferramenta muito utilizada pelos pesquisadores. Revisões mais atuais sobre o método CASSCF, inclusive com a discussão de alguns casos, podem ser encontradas nas referências.^15-17

A diferença em relação ao método MCSCF é que no método CASSCF escolhemos um conjunto de orbitais moleculares com o qual construiremos todas as configurações a serem incluídas no espaço de configurações, ao invés de escolhermos um conjunto de configurações como no método MCSCF. O problema prático, agora, passa a ser a escolha dos orbitais moleculares; no entanto, uma vez definido o conjunto de orbitais moleculares, todas as configurações possíveis serão geradas automaticamente. Esse procedimento equivale a um full ci no espaço ativo; ou seja, gerar todos os determinantes de Slater (ou CSFs) fazendo todas as excitações possíveis, compatíveis com a simetria do sistema, dentro do espaço ativo.

Para realizar um cálculo CASSCF, é necessário ter um conjunto inicial de orbitais moleculares satisfazendo determinadas condições, como veremos a seguir.

O método CASSCF divide o conjunto total de orbitais moleculares em três subespaços (Figura 1), a saber:

Figura 1. Ilustraçao dos espaços de orbitais moleculares empregados no método CASSCF

- Espaço inativo: permanecerão duplamente ocupados, mas serão otimizados. Em alguns casos, os orbitais moleculares mais internos (caroço) poderão ser incluídos num subespaço no qual eles não serão otimizados, permanecendo como definidos originalmente (congelados, na maioria dos casos, como definidos pelo método RHF).

- Espaço ativo: a ocupação destes orbitais é variável; nele será feito um full ci, gerando todos os determinantes possíveis, ou todas as configurações adaptadas à simetria espacial e de spin (CSFs). Todos os orbitais moleculares ativos são otimizados.

- Espaço virtual: os orbitais moleculares pertencentes a este espaço permanecerão vazios; ou seja, nenhum elétron é permitido neste espaço.

É importantíssimo ressaltar que os orbitais moleculares devem ser, obrigatoriamente, colocados na sequência apresentada acima (inativo, ativo e virtual) antes do cálculo CASSCF ser realizado. Portanto, o conjunto inicial de orbitais moleculares deve ser construído após uma análise criteriosa dos orbitais disponíveis, para que eles possam ser ordenados corretamente antes de executar o cálculo CASSCF. Para facilitar a análise dos orbitais moleculares pode-se recorrer a programas de visualização como, por exemplo, o MOLDEN,¹⁸ GABEDIT¹⁹ e Jmol.²⁰

Supondo que os orbitais iniciais estejam na ordem correta, o espaço de configurações que será usado para formar a função de onda multiconfiguracional (Equação 1) é construído. Em seguida, aplicando o método variacional, os coeficientes CI e os orbitais moleculares (inativos e ativos) serão otimizados.

SUGESTÕES SOBRE COMO ESCOLHER O ESPAÇO ATIVO

Acabamos de descrever como ordenar corretamente os orbitais moleculares para que os espaços inativo, ativo e virtual estejam corretos. Precisamos, agora, saber escolher quais (e quantos) orbitais serão incluídos no espaço ativo e de um processo eficiente para obtê-los. Iniciaremos com algumas sugestões sobre quais orbitais incluir no espaço ativo e, a seguir, faremos uma coletânea de regras gerais obtidas a partir de sugestões feitas por Roos e colaboradores nos trabalhos mencionados anteriormente, incluindo algumas obtidas a partir da nossa própria experiência.^21-27

De uma forma geral, o espaço ativo deve conter todos os orbitais relevantes para descrever o problema em estudo. Por exemplo, se estivermos interessados em estudar a dissociação de um determinado grupo numa molécula é necessário incluir no espaço ativo o orbital molecular ligante (que faz a ligação química entre esse grupo e o restante da molécula) e o orbital molecular antiligante correspondente. Isso só pode ser feito com uma análise cuidadosa do processo que se pretende descrever. Em outros casos, por exemplo no estudo de estados excitados, deve-se incluir no espaço ativo todos os orbitais moleculares necessários para formar os estados excitados de interesse, ou seja, a escolha dos orbitais que farão parte do espaço ativo está muito longe de ser um procedimento automático; é necessária uma análise criteriosa do problema, aliada à intuição química.

No entanto, no caso de átomos, algumas regras simples são bastante úteis:

Elementos do 2º período: incluir os orbitais 2s e 2p.

Elementos do 3º período: incluir os orbitais 3s e 3p; em casos com mais do que 3 elétrons de valência, o orbital 3s poderá ser excluído.

Geralmente, conforme o grau de hibridização spⁿ diminui ao longo do período da tabela periódica, a inclusão do orbital s não é necessária.

Metais de transição do 1º período: incluir os orbitais 4s, 3d e 4p; havendo mais do que 5 elétrons d, considerar a necessidade de incluir uma camada d (4d) extra no espaço ativo (efeito da dupla camada d). Nos outros períodos de metais de transição, o efeito da dupla camada d é reduzido.

No caso dos lantanídeos, incluir os orbitais 4f, 6s, 6p e 5d. Para os actinídeos, incluir os orbitais 5f, 7s, 7p e 6d. É importante, também, investigar a necessidade de se utilizar uma dupla camada f.

Em moléculas, considere sempre a possibilidade de incluir no espaço ativo pares de orbitais correspondentes: π - π^*, σ - σ^*.

Sempre que possível, não separar conjuntos de orbitais que podem estar correlacionados por simetria. Por exemplo, incluir dois orbitais δ e não apenas um deles.

Em moléculas, verificar a necessidade de incluir orbitais moleculares do tipo n, para descrever excitações n → π^*, por exemplo.

Ligações CH podem ser incluídas no espaço inativo, a menos que estejam envolvidas em processos envolvendo a quebra da ligação CH.

Para compostos com elementos contendo número de oxidação alto, talvez seja necessário utilizar um número maior de orbitais ativos, porque as ligações se tornam muito covalentes.

Como veremos nas próximas seções, nem sempre será possível incluir todos os orbitais (elétrons), como sugerido acima, no espaço ativo. Portanto, mais uma vez, ressaltamos a necessidade de se examinar cuidadosamente o problema, antes de iniciar o cálculo.

Construindo o espaço ativo: alguns exemplos

Os resultados apresentados nas próximas seções foram obtidos com os programas FIREFLY²⁸ ou MOLCAS.²⁹ Para visualização dos orbitais, empregamos o GABEDIT.¹⁹

Na Figura 2, apresentamos os 10 primeiros orbitais moleculares para a molécula de etileno obtidos com o método RHF e bases atômicas 6-31G,³⁰ na geometria de equilíbrio calculada no mesmo nível, ordenados na sequência energética resultante do cálculo. Note que, com a base atômica 6-31G, temos 26 orbitais moleculares na molécula de etileno. Como o etileno tem 16 elétrons, temos 8 orbitais moleculares duplamente ocupados: OM1, OM2, ..., OM8. Os orbitais moleculares OM1 e OM2 representam os orbitais σ obtidos combinando-se linearmente os orbitais atômicos 1s dos átomos de carbono. Os orbitais moleculares OM3 ao OM7 são obtidos a partir das combinações lineares dos orbitais atômicos 2s e 2p dos átomos de carbono e os orbitais 1s dos átomos de hidrogênio. Os orbitais moleculares OM10, OM11, até o OM26 são os orbitais RHF não ocupados. Atenção especial deve ser dada aos orbitais moleculares OM8 e OM9, que representam os orbitais π e π^* obtidos combinando-se linearmente os orbitais atômicos 2p do carbono.

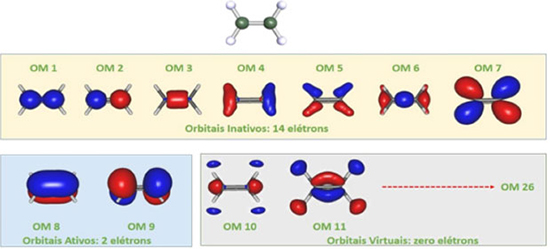Figura 2. Orbitais moleculares inativos, ativos e virtuais para o etileno. Estao representados os 11 primeiros orbitais moleculares canônicos obtidos com o método RHF e bases atômicas 6-31G, na geometria otimizada no mesmo nível de cálculo. Os orbitais estao ordenados na sequência energética obtida pelo cálculo

Se o objetivo for investigar o espectro de absorção na região do UV-VIS, as excitações eletrônicas relevantes envolvem transferência de elétrons dos orbitais moleculares π para os π^* (π → π^*); no caso do etileno, transições n → π^* não são relevantes espectroscopicamente. Portanto, os orbitais moleculares mais relevantes de simetria π e π^* deverão ser incluídos no espaço ativo. Teremos, portanto, 2 orbitais moleculares no espaço ativo (OM8 (π) e OM9 (π^*)) e 2 elétrons (do OM8), resultando na notação comumente empregada: CAS(2,2), na qual o primeiro dígito indica o número de elétrons no espaço ativo e o segundo o número de orbitais no espaço ativo (CAS(n,m): n elétrons em m orbitais). Os orbitais OM1, OM2, ..., OM7 serão mantidos no espaço inativo; ou seja, estarão sempre duplamente ocupados, mas serão otimizados variacionalmente. Os outros orbitais moleculares (OM10, OM11, ..., OM26) serão mantidos no espaço de orbitais virtuais e não serão ocupados.

Como podemos verificar na Figura 2, os orbitais moleculares gerados no cálculo RHF estão ordenados corretamente. Logo, podem ser empregados diretamente como o conjunto inicial de orbitais para o cálculo CASSCF.

Vamos considerar, agora, as transições eletrônicas π → π^* e n → π^* do tiofeno. O tiofeno (Figura 3) é um composto heterocíclico planar e aromático, composto por quatro átomos de carbono, um átomo de enxofre e quatro de hidrogênio. Devido às suas características estruturais e eletrônicas ele será utilizado para ilustrar vários aspectos mencionados anteriormente, além de um novo tópico importante envolvendo a exploração da simetria molecular.

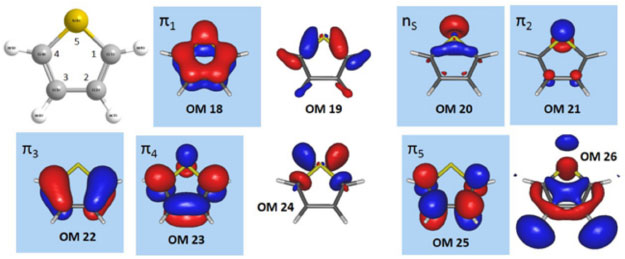Figura 3. Sequência de orbitais moleculares canônicos do tiofeno calculados no nível RHF/6-31G, na geometria de equilíbrio do estado fundamental obtida no mesmo nível de cálculo. Os orbitais moleculares canônicos assinalados deveriam estar no espaço ativo

Após otimizar a geometria (RHF/6-31G), a próxima etapa é determinar quais orbitais serão incluídos no espaço ativo. Neste caso, como o objetivo é investigar transições eletrônicas π → π^* e n → π^*, o espaço ativo deve conter os orbitais n, π e π^*. No caso do etileno não era difícil concluir que temos apenas 2 orbitais no espaço ativo, um π e o outro π^*. Porém, isso não é tão intuitivo para o tiofeno.

A próxima etapa do planejamento é, portanto, identificar quais orbitais deverão ser incluídos em cada um dos subespaços (inativo, ativo e virtual). Analisando a estrutura química do tiofeno, notamos que o conjunto de orbitais π de valência é composto por 2 orbitais π ligantes (4 elétrons) e 2 antiligantes (em torno dos átomos de carbono), um orbital π não ligante (isolado) (2 elétrons) sobre o átomo de enxofre e um par isolado do tipo σ (2 elétrons) também localizado no átomo de enxofre. Portanto, para descrever as transições eletrônicas π→π^* e n→π^* é necessário incluir no espaço ativo, pelo menos, 6 orbitais (2 π, 2 π^*, 1 π isolado e 1 σ), dentre os quais serão distribuídos 8 elétrons (CAS(8,6)).

Com o conjunto de bases atômicas 6-31G temos 76 orbitais moleculares, sendo alguns representados na Figura 3, dos quais 22 estão ocupados (tiofeno contém 44 elétrons e é uma molécula de camada fechada, i.e., todos os elétrons estão emparelhados). Portanto, se apenas 8 elétrons serão incluídos no espaço ativo, a sequência de orbitais deve ser (inativo, ativo, virtual):

Orbitais inativos: 1, 2, 3, ...,18;

Orbitais ativos: 19, 20, 21, 22, 23, e 24 (seis orbitais);

Orbitais virtuais: 25, 26, 27, ..., 76.

Na Figura 3, os orbitais moleculares 18, 19, 20, 21, 22, 23, 24, e 25, são apresentados na sequência gerada pelo cálculo RHF. Antes de prosseguir, devemos mencionar que os orbitais gerados pelo método RHF são ordenados seguindo critérios energéticos (maior energia, mais interno, para menor energia, mais externo). Como orbitais do mesmo tipo podem ter energias distintas, diferentes tipos de orbitais estarão dispostos sequencialmente seguindo a ordem energética, como acontece neste exemplo (Figura 3) no qual temos um do tipo σ (envolvendo ligações carbono-carbono e carbono-hidrogênio, OM19) na sequência de orbitais que estaria no espaço ativo; certamente ele não é relevante para descrever as transições eletrônicas π → π^* e n → π^* do tiofeno.

Observando a sequência de orbitais apresentada na Figura 3, notamos alguns problemas:

O orbital molecular 18 (OM18) é um orbital do tipo π, por isso ele deveria estar no espaço ativo (em uma das posições 19, 20, 21, 22, 23, ou 24), mas está na sequência de orbitais que compõem o espaço inativo (OM1 ao OM18).

O OM24 não é π, nem n localizado no átomo de enxofre; portanto, ele deveria estar no espaço virtual (numa das posições 25, 26, 27, ..., 76), mas está na sequência de orbitais ativos (OM19 até OM24).

O OM25 é um orbital π^* e, portanto, deveria estar no espaço ativo (posição 19, 20, 21, 22, 23, ou 24). No entanto, ele faz parte do espaço virtual (entre 25, 26, 27, ..., 76).

Portanto, a sequência de orbitais fornecidas pelo cálculo RHF não está correta. No entanto, a solução para este problema é simples: basta editar o conjunto de orbitais gerados no cálculo RHF, colocando o OM18 na posição 19, o OM19 na posição 18, o OM24 na posição 25 e o OM25 na posição 24. Com essas alterações, obtemos o conjunto de orbitais na sequência correta (Figura 4), que deverá ser utilizado como conjunto inicial de um cálculo CASSCF.

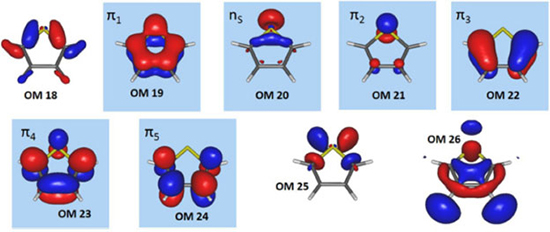Figura 4. Sequência correta de orbitais moleculares canônicos do tiofeno, calculados no nível RHF/6-31G e na geometria de equilíbrio do estado fundamental obtida no mesmo nível de cálculo. Os orbitais moleculares canônicos assinalados compoem o espaço ativo

QUANTOS TERMOS SERÃO INCLUÍDOS?

A função de onda CASSCF é determinada pelo número de orbitais inativos e ativos definidos pelo usuário. Como os orbitais virtuais permanecerão vazios (não serão ocupados), eles não participam da função de onda.

O número de termos gerados em um cálculo CASSCF equivale ao número de determinantes de Slater em um cálculo full ci no espaço ativo, dado pelo produto de coeficientes binomiais (Equação 2):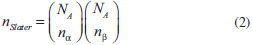

na qual N_A é o número de orbitais ativos, n_α e n_β representam o número de elétrons ativos (distribuídos entre os N_A orbitais ativos) com spin-α e spin-β, respectivamente. Uma forma alternativa de se obter uma função de onda multiconfiguracional a partir de full ci no espaço ativo é pelo método FORS (full optimized reaction space), desenvolvido por Ruedenberg e colaboradores.¹⁴ Apesar das semelhanças, o método CASSCF é mais vantajoso computacionalmente.^11-13

Se utilizarmos configurações adaptadas à simetria de spin (CSFs), normalmente uma combinação linear de determinantes de Slater, o número de configurações (N_CSF) (Equação 3) que serão incluídas na função de onda será menor, conforme dado pela expressão de Weyl-Robinson:³¹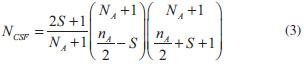

sendo S a multiplicidade de spin (singleto, tripleto, etc.) e N_A o número de elétrons ativos; está implícito que o espaço inativo contem N_I orbitais duplamente ocupados (2N_I elétrons). Como podemos notar, o número de determinantes de Slater e de CSFs cresce muito rapidamente em função da quantidade de orbitais no espaço ativo. Embora o uso de simetria espacial, através de teoria de grupo pontual, possa reduzir o número de determinantes de Slater e de CSFs, restrições computacionais (hardware) limitam o número máximo de orbitais ativos em cálculos rotineiros a, aproximadamente, 10 - 14 orbitais. Como exemplo do número de termos envolvidos, numa função de onda CAS(12,12) singleto teremos 853.776 determinantes de Slater e 226.512 CSFs; numa função de onda singleto CAS(14,14) teremos 11.778.624 determinantes de Slater e 2.760.615 CSFs.

Infelizmente, em algumas situações, o espaço ativo ideal pode ser muito grande e reduzi-lo a um tamanho computacionalmente viável não é uma tarefa fácil. Nestes casos, o método RASSCF^2-5 (Restricted Active Space SCF) pode ser de grande ajuda. No RASSCF também dividimos o conjunto de orbitais moleculares em inativos, ativos e virtuais. Os conjuntos de orbitais inativos e virtuais são definidos da mesma forma que no CASSCF; a diferença está na definição do espaço ativo.

No método RASSCF, o espaço ativo é divido em três subconjuntos, definidos da seguinte maneira:

- RAS1: número de elétrons excitados é limitado. Por exemplo, podemos impor somente excitações simples e duplas.

- RAS2: este subconjunto, tem a mesma propriedade do espaço ativo definido no método CASSCF, porém com um número menor de orbitais.

- RAS3: número máximo de elétrons é estipulado. Por exemplo, se permitimos apenas excitações simples e duplas a partir do RAS1, o número máximo de elétrons no RAS3 deve ser igual a dois. Em outras palavras, os elétrons do RAS1 serão excitados para o RAS3; portanto, o número máximo de elétrons permitido no RAS3 deve ser igual ao número máximo de elétrons excitados a partir do RAS1.

Se estivéssemos trabalhando com o método CASSCF, todos os orbitais pertencentes ao RAS1, RAS2 e RAS3 comporiam o espaço ativo, no qual é realizado um full ci gerando um número muito grande de configurações.

Com o método RASSCF podemos utilizar um número muito maior de orbitais, distribuídos nos espaços RAS1, RAS2 e RAS3, e analisar quais os orbitais são, realmente, mais relevantes para descrever o problema. Numa etapa seguinte, os orbitais escolhidos a partir dos cálculos RASSCF podem ser empregados na construção do espaço ativo num cálculo CASSCF.

ORBITAIS INICIAIS

Feita a escolha do espaço ativo (orbitais e elétrons), o passo seguinte é obter um conjunto de orbitais moleculares para iniciar o cálculo. Ou seja, a pergunta que devemos responder agora é: qual tipo de orbitais moleculares empregar como conjunto inicial para o cálculo CASSCF (ou MCSCF)?

A resposta poderia ser: orbitais RHF (provenientes do cálculo Hartree-Fock). No entanto, essa nem sempre será a melhor escolha. Os orbitais RHF, por definição, são delocalizados (pertencem à molécula como um todo), além dos orbitais virtuais desse tipo não serem bem definidos, pois não passam pelo processo de autoconsistência. Vamos analisar um caso concreto.

Na Figura 5, representamos os três últimos orbitais moleculares ocupados RHF para a molécula de benzeno, juntamente com os três primeiros orbitais virtuais, obtidos com um conjunto mínimo de bases atômicas (C : 2s1p/H : 1s) do tipo ANO (atomic natural orbitals).^32-36 Como pode-se observar na parte superior da Figura 5, os orbitais SCF estão delocalizados por toda a molécula. Ao contrário, os orbitais localizados, representados na parte inferior da Figura 5, estão restritos às regiões específicas, tornando-os mais apropriados para a descrição de fenômenos mais localizados. Neste caso, os orbitais foram localizados conforme proposto por Pipek e Mezey.³⁷ Porém, outro tipo de localização seria igualmente útil.^38,39

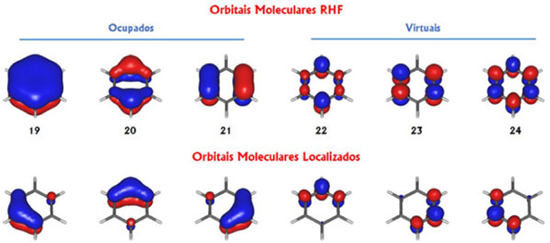Figura 5. Três últimos orbitais moleculares canônicos ocupados e os três primeiros orbitais canônicos virtuais para a molécula de benzeno, obtidos com o método RHF e conjuntos mínimos (C : 2s1p/H : 1s) de bases atômicas do tipo ANO (atomic natural orbitals), na geometria de equilíbrio obtida no mesmo nível de cálculo. Parte superior: orbitais canônicos; parte inferior: orbitais localizados de acordo com procedimento proposto por Pipek e Mezey

Outro caso pode ser empregado para ilustrar a vantagem de orbitais localizados sobre os SCF. Suponha que desejamos estudar a reação de decomposição do butadieno,

em que a ligação química entre os átomos centrais de carbono é quebrada. Neste caso, o espaço ativo deverá conter os orbitais π, π^*, o orbital σ entre os átomos centrais de carbono e o correspondente σ^*; ou seja, CAS(6,6) (seis elétrons em seis orbitais). Na Figura 6, ilustramos alguns orbitais RHF para o butadieno, obtidos com a mesma base mínima descrita anteriormente para o benzeno, em conjunto com os orbitais localizados conforme proposto por Pipek-Mezey. Qual conjunto de orbitais é mais apropriado para descrever essa quebra de ligação química? Como podemos observar na Figura 6, é mais prático empregar o conjunto de orbitais localizados.

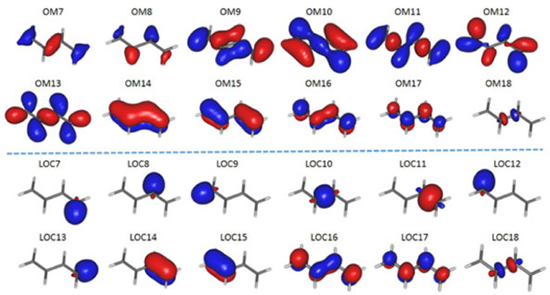Figura 6. Alguns orbitais moleculares canônicos (ocupados e virtuais) para a molécula de butadieno, obtidos com o método RHF e conjuntos mínimos de bases atômicas do tipo ANO (atomic natural orbitals), na geometria de equilíbrio obtida no mesmo nível de cálculo. Parte superior: orbitais canônicos; parte inferior: orbitais localizados de acordo com procedimento proposto por Pipek e Mezey

Em ambos casos anteriores, utilizamos um conjunto mínimo de bases atômicas para gerar os orbitais moleculares, porque essa é outra sugestão importante. Orbitais moleculares gerados a partir de conjuntos mínimos são mais fáceis de serem analisados, pois os orbitais moleculares serão descritos unicamente em função dos orbitais atômicos de valência (portanto, mais compactos), além dos cálculos serem mais rápidos. Alguns programas permitem o uso de uma estratégia muito útil: inicie o cálculo com um conjunto mínimo de bases atômicas, analise cuidadosamente os orbitais e defina o espaço ativo apropriado para descrever o problema. Em seguida, na fase final do trabalho, utilize um método que permita expandir o conjunto de orbitais moleculares obtidos com o conjunto mínimo de bases atômicas para uma base atômica maior.

Estabilidade do espaço ativo

Tendo definido o espaço ativo e o conjunto de orbitais iniciais, o cálculo CASSCF pode ser realizado.

Assim que o cálculo estiver concluído, é necessário analisar cuidadosamente os orbitais moleculares resultantes, para termos certeza de que todos os escolhidos para fazer parte do espaço ativo permaneceram nele. Porém, não surpreenda-se se os orbitais selecionados não estiverem mais no espaço ativo.

Antes de prosseguir com a análise dos orbitais, é preciso ressaltar que os orbitais moleculares relevantes para a análise das funções de onda CASSCF não são os orbitais canônicos obtidos com o método RHF mas os orbitais naturais,⁴⁰ que dentre suas características destacamos a ocupação fracionária, ao invés de 0, 1 ou 2 como os orbitais canônicos RHF. Portanto, além da natureza (π, σ, etc.) do orbital molecular devemos, agora, analisar o número de ocupação dos orbitais naturais correspondente.

Como vimos no início, a função de onda CASSCF é definida em função de três conjuntos de orbitais: (i) inativos: sempre duplamente ocupados (ocupação igual a dois); (ii) ativo: ocupação variável, fracionária; (iii) virtuais: sempre vazios (ocupação nula). O que acontecerá se tivermos no espaço ativo um orbital cuja ocupação é muito próxima de dois (duplamente ocupado) ou muito próxima de zero (vazio)? Haverá problemas durante o processo de otimização dos orbitais e eles poderão ser transferidos para o espaço inativo ou virtual, respectivamente, e outros incorporados ao espaço ativo.

Para manter os orbitais relevantes no espaço ativo é preciso ter, além dos pares correlacionados apropriados, orbitais cujo número de ocupação seja diferente de zero ou dois. Idealmente, orbitais com número de ocupação maiores que 1,999 ou menores do que 0,001 podem ser incluídos nos espaços inativo e virtual, respectivamente. Devemos, portanto, incluir no espaço ativo somente os orbitais cuja ocupação varie efetivamente durante o processo químico (excitação para um estado diferente, relaxamento para uma região específica da superfície de energia potencial com diferente natureza eletrônica, por exemplo).

Como obter números de ocupação diferentes de zero e dois? É necessário incluir simultaneamente no cálculo todos os estados eletrônicos relevantes, permitindo excitações eletrônicas a partir de orbitais específicos. Por exemplo, se estivermos interessados em estudar estados eletrônicos π, π^* e n, π^*, ao realizarmos um cálculo para os estados π, π^*, os orbitais moleculares do tipo n permanecerão duplamente ocupados (inativos); quando realizarmos o cálculo para os estados n, π^*, alguns orbitais do tipo π permanecerão duplamente ocupados (inativos). Logo, os resultados não são comparáveis, porque os espaços ativos são diferentes!

A solução é incluir num único cálculo todos os estados π, π^* e n, π^*, permitindo excitações simultâneas de todos os orbitais relevantes, fazendo com que eles tenham ocupação muito diferente de zero ou dois e, assim, sejam mantidos no espaço ativo. Isso é feito por meio do método SA-CASSCF (state averaged CASSCF),¹⁶ com o qual podemos gerar, simultaneamente, o número necessário de estados eletrônicos para estabilizar o espaço ativo (mantendo no espaço ativo sempre o mesmo número e tipo de orbitais). Dessa forma, ao invés de termos um conjunto de orbitais naturais para cada estado eletrônico, poderemos tratar todos os estados eletrônicos com um único conjunto de orbitais naturais (orbitais naturais médios), o que é bastante vantajoso para o cálculo de propriedades de transição eletrônicas como, por exemplo, força de osciladores. Note, no entanto, que isso só será possível se todos os orbitais relevantes estiverem no espaço ativo.

Em suma, antes de iniciar a fase de produção de resultados, é necessário verificar a estabilidade do espaço ativo, realizando cálculos SA-CASSCF variando o número de estados (raízes) calculados. A cada passo, analise cuidadosamente a natureza dos orbitais naturais obtidos, bem como os respectivos números de ocupação. A partir destas análises será possível concluir quais orbitais são realmente relevantes e quantos estados eletrônicos devem ser incluídos no cálculo.

Resumimos, então, algumas sugestões práticas sobre a escolha dos orbitais moleculares iniciais:

• Inicie o cálculo com um conjunto mínimo de bases atômicas.

• Utilize um programa para visualizar os orbitais moleculares.^18-20 É mais fácil analisá-los desta forma do que conferindo os coeficientes dos orbitais atômicos que compõem os orbitais moleculares.

• O conjunto de orbitais moleculares RHF pode ser um bom conjunto inicial em alguns casos. No entanto, sempre considere a possibilidade de empregar orbitais localizados, principalmente em se tratando dos orbitais virtuais.

• A energia dos orbitais RHF pode ser um critério para a escolha do espaço ativo; por exemplo, você poderia escolher os energeticamente mais próximos do HOMO e do LUMO. No entanto, é preciso muito cuidado: pares de elétrons isolados normalmente têm energia muito baixa e, portanto, não estarão energeticamente próximos ao HOMO.

• Existem algumas outras alternativas para se obter o conjunto inicial de orbitais moleculares. Em algumas situações pode ser interessante utilizar os orbitais moleculares do cátion, ao invés dos obtidos para a molécula neutra. Considere, também, a possibilidade de empregar os orbitais naturais, por exemplo os gerados pelo método MP2, como conjunto inicial. Isso não exclui a possibilidade de usar os orbitais naturais obtidos com o próprio método CASSCF, mesmo que empregando um conjunto menor de orbitais ativos.

• Examine cuidadosamente a natureza dos orbitais moleculares e escolha o conjunto mais apropriado para compor o espaço ativo.

• Faça vários testes para decidir sobre quais orbitais serão incluídos no espaço ativo. Lembre-se, sempre, do tamanho da função de onda (número de determinantes de Slater (Equação 2) ou de CSFs (Equação 3)) que será gerada.

• Realize alguns cálculos SA-CASSCF variando o número de estados (raízes) eletrônicos calculados. Após cada um dos cálculos, analise a natureza e o número de ocupação dos orbitais naturais que compõem espaço ativo, para verificar se os orbitais necessários estão presentes e se todos os estados eletrônicos desejados estão sendo descritos. Em alguns casos, essa etapa pode ser feita com um conjunto mínimo de bases atômicas; a projeção para um conjunto de bases atômicas maior poderá ser realizada após a definição da natureza e quantidade de orbitais no espaço ativo e quantos estados eletrônicos são necessários para a correta descrição do problema.

• Guarde o arquivo contendo o conjunto final de orbitais moleculares em um local seguro (faça backup), pois eles poderão ser necessários em outras etapas do trabalho.

Estudo de casos

Tendo exposto algumas sugestões práticas sobre como construir o espaço ativo para cálculos multiconfiguracionais, vamos ilustrá-las examinando alguns casos específicos.

O tiofeno: sem simetria espacial

Como vimos anteriormente, para descrever as transições eletrônicas π → π^* e n → π^* do tiofeno, o espaço ativo deve conter 2 orbitais π ligantes (4 elétrons), 2 orbitais π antiligantes (π^*), um orbital π não ligante (par isolado, 2 elétrons) sobre o átomo de enxofre e um par isolado do tipo σ (n, 2 elétrons) também localizado no átomo de enxofre; ou seja, uma função de onda singleto CAS(8,6). Neste item, todos os cálculos serão realizados sem nenhuma restrição à simetria espacial (isto é, serão realizados empregando o grupo pontual C₁), impondo apenas restrições à simetria de spin, restringindo os cálculos aos estados singletos. Além disso, os cálculos serão realizados empregando CSFs, reduzindo o número de termos incluídos na função de onda CASSCF.

Para facilitar a interação com os itens anteriores, cada etapa do cálculo será apresentada separadamente, acompanhando a sequência apresentada previamente. Os conjuntos de bases atômicas que serão empregados não são recomendados para cálculos quantitativos, servindo apenas para ilustrar aspectos qualitativos relacionados às etapas envolvidas em um cálculo CASSCF.

1. Otimização de geometria. A geometria do tiofeno é obtida com o método RHF e bases atômicas 6-31G (RHF/6-31G), conforme descrito anteriormente.

2. Construção do espaço ativo. O objetivo é descrever os estados eletrônicos ¹(nπ) e ¹(ππ^*). Portanto, o espaço ativo deve conter os 2 orbitais π ligantes (4 elétrons) e os 2 antiligantes (em torno dos átomos de carbono), um orbital π não ligante 2 elétrons) sobre o átomo de enxofre e um par isolado do tipo σ (2 elétrons) também localizado no átomo de enxofre, perfazendo um total de 8 elétrons distribuídos em 6 orbitais (2 π, 2 π^*, 1 π isolado e 1 σ), CAS(8,6). Como o tiofeno tem 44 elétrons, os primeiros 18 orbitais moleculares (36 elétrons) serão incluídos no espaço inativo, e os 6 seguintes (3 orbitais π, 2 π^* e 1 n) formarão o espaço ativo, dentre os quais serão distribuídos os 6 elétrons ativos.

3. Orbitais iniciais. O conjunto de orbitais canônicos (RHF) obtidos com a base atômica 6-31G será empregado como conjunto inicial de orbitais moleculares. Vale ressaltar que, em moléculas cuja estrutura eletrônica é mais complexa, pode-se empregar um conjunto mínimo de bases atômicas e orbitais localizados, para facilitar a classificação dos orbitais moleculares. Uma vez definido o conjunto de orbitais moleculares inicial, a próxima etapa é analisar cuidadosamente o conjunto de orbitais gerados, identificando o tipo de cada um. A sequência dos orbitais canônicos está representada na Figura 3. A sequência correta (orbitais inativos, ativos e virtuais) está representada na Figura 4.

4. Cálculo CASSCF inicial. Após colocar os orbitais moleculares iniciais na sequência correta, foi realizado o cálculo CAS(8,6) exclusivamente para o estado fundamental e os orbitais naturais relevantes estão apresentados na Figura 7, que serão analisados com base em dois critérios:

 

Figura 7. Espaço ativo para o tiofeno em termos dos orbitais naturais (e respectivos números de ocupaçao) obtidos com o método CASSCF (CAS(8,6)) e bases atômicas 6-31G, na geometria de equilíbrio otimizada no mesmo nível de cálculo. (a) Cálculo realizado para o estado fundamental; (b) Cálculo incluindo três estados eletrônicos; (c) Cálculo realizado incluindo cinco estados eletrônicos

 

1. Natureza dos orbitais: como pode ser observado na Figura 7, o conjunto de orbitais naturais resultante do cálculo para o estado fundamental, exclusivamente, não está correto. O orbital molecular OM18, que representa o orbital n_S localizado no átomo de enxofre, não está no espaço ativo; além disso, o OM20 não deveria estar no espaço ativo. Esse exemplo reforça a necessidade de se analisar a composição do espaço ativo em todos as etapas do cálculo, pois nada garante que a sequência inicialmente escolhida será mantida ao longo do processo de otimização dos orbitais moleculares e da função de onda CASSCF.

2. Número de ocupação dos orbitais ativos: Na Figura 7a, também incluímos o número de ocupação de cada um dos orbitais naturais representados. O que chama a atenção é a ocupação do OM20, muito próxima de 2. Como mencionado anteriormente, isso indica que esse orbital molecular deveria estar no espaço inativo, pois o espaço ativo deve conter, apenas, os orbitais moleculares com número de ocupação diferente de 2 ou zero.

5. Estabilidade do espaço ativo: com o cálculo CAS(8,6) para o estado fundamental, não foi possível obter o espaço ativo correto. Por outro lado, como estamos interessados em descrever estados eletrônicos excitados (¹(nπ^*) e ¹(ππ^*)) é necessário incluir no cálculo todos os estados de interesse. Para isso, vamos usar o método SA-CASSCF e testar diferentes quantidades de estados eletrônicos, lembrando sempre de iniciar todos os testes com os orbitais iniciais ordenados corretamente.

1. Três estados eletrônicos (estados fundamental e dois excitados): Iniciando com três estados eletrônicos, obtemos os orbitais naturais médios apresentados na Figura 7b). Como podemos observar, o espaço ativo resultante não está correto. Mesmo incluindo três estados eletrônicos no cálculo, ainda não conseguimos manter o orbital n_S (representado por OM18) no espaço ativo. Além disso, notamos claramente que o número de ocupação do OM20 indica que ele deveria estar no espaço inativo. Não há mais nada a fazer com esses resultados. É preciso fazer outro teste.

2. Cinco estados eletrônicos (estados fundamental e quatro excitados): Partimos, agora, para um novo teste com cinco estados eletrônicos, o fundamental e quatro estados excitados, representando os orbitais moleculares naturais médios na Figura 7c).

Vamos, então, partir para a análise, onde os seguintes pontos se destacam e devem chamar nossa atenção:

Finalmente, os orbitais moleculares que compõem o espaço ativo (OM19, OM20, ..., OM24) estão corretos. Temos o orbital n_S (OM20) e os orbitais moleculares π (OM19, OM22), π_S isolado no átomo de enxofre (OM21) e os π^* (OM23, OM24).

Os números de ocupação são bem diferentes de zero e dois. Esses fatos indicam que estamos no caminho certo. No entanto, é necessário satisfazer mais um critério: o estado excitado ¹(n π^*) deve ser um dos estados calculados.

Verificando a presença do estado eletrônico ¹(nπ^*) (Ou, analisando as funções de onda):

A função de onda ¹A (grupo pontual C₁, ou seja, sem simetria espacial) CAS(8,6), gera um total de 120 determinantes de Slater, que corresponde a 105 CSFs; como vimos anteriormente, o número de termos que serão incluídos na expansão full ci (Equação 1) no espaço ativo é muito menor quando trabalhamos com CSFs.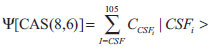

Neste exemplo, teremos cinco funções de onda CAS(8,6), cada uma delas caracterizadas por um conjunto de coeficientes CSF_i associados a cada uma das 105 CSFs (|CSF_i >); por sua vez, as CSFs são construídas a partir de um único conjunto de orbitais moleculares, que é composto pelos orbitais naturais médios.

A seguir, faremos as análises empregando os resultados obtidos com o programa MOLCAS (Figura 8); no entanto, o mesmo raciocínio pode ser feito para qualquer outro programa. A lista completa pode ser encontrada nos anexos (Material Suplementar).

Figura 8. Parte do arquivo de resultados gerados pelo MOLCAS para o cálculo CAS(8,6)/6-31G sem uso de simetria espacial. O arquivo completo pode ser encontrado no Material Suplementar

Na saída gerada pelo programa, encontramos o índice da configuração eletrônica e a respectiva ocupação dos orbitais ativos (sequência de 6 números, um para cada orbital do espaço ativo), na segunda coluna. Note que os orbitais ativos estão ordenados conforme sequência analisada no item anterior e ilustrada na Figura 7c. Normalmente, os orbitais ativos ocupados recebem o número 2 ou 1, indicando que ele está ocupado por 2 ou 1 elétron, respectivamente; o orbital ativo vazio é indicado pelo número zero. Na saída do MOLCAS, os orbitais unicamente ocupados são identificados pelas letras u e d, que representa elétrons com spin up ou spin down, respectivamente. Note que, neste caso, não se trata de ocupação de orbitais naturais, mas sim de uma representação de configurações eletrônicas. Acima das configurações eletrônicas (topo da 2a. coluna, 111111), encontramos o índice que indica a simetria espacial de cada um dos orbitais moleculares que compõem o espaço ativo; como anteriormente, temos 6 números representando a simetria espacial dos 6 orbitais moleculares do espaço ativo. Neste caso, estamos trabalhando com o grupo pontual C₁ e, portanto, todos os orbitais moleculares pertencem à representação irredutível A, a única presente no grupo pontual C₁. Na terceira coluna, temos o coeficiente CI da configuração eletrônica (cujo módulo quadrado é seu peso na expansão CASSCF, indicado na quarta coluna); quanto maior for o coeficiente (peso) de uma configuração, maior será sua participação na função de onda CASSCF.

Primeiro estado eletrônico: raiz 1. O primeiro estado eletrônico corresponde ao estado fundamental, dominado por uma única configuração (coeficiente = 0,95 e peso de 0,91, ou 91%) eletrônica com os orbitais moleculares OM19, OM20, OM21, e OM22 duplamente ocupados (222200).

Segundo estado eletrônico: raiz 2. No segundo estado eletrônico encontramos uma configuração (número 7) com coeficiente 0,79 (peso 62%), com participação bem superior à das outras configurações; portanto, consideramos que este estado também é bem descrito por uma única configuração eletrônica. A partir da ocupação dos orbitais ativos 22u2d0, observe que em relação ao estado fundamental 222200 a configuração dominante do segundo estado eletrônico é obtida excitando um único elétron do OM21 para o OM23, com natureza π e π^*, respectivamente (Figura 7c). Portanto, o segundo estado eletrônico é um estado ¹(ππ^*).

Terceiro estado eletrônico: raiz 3. Para o terceiro estado eletrônico, a maior contribuição para a função de onda CASSCF provém de uma única configuração eletrônica (coeficiente = 0,87, peso = 0,75), obtida a partir do estado fundamental a partir de uma excitação simples do orbital molecular OM22 (Figura 7c) (orbital molecular π ligante, localizado entre os carbonos C1C2 e C3C4) para o OM23 (orbital π^* antiligante, delocalizado entre os átomos pesados), resultando em outro estado ¹(ππ^*).

Quarto estado eletrônico: raiz 4. O quarto estado eletrônico apresenta um forte caráter multiconfiguracional, evidenciado pela participação de diversas configurações eletrônicas contribuindo significativamente para a função de onda CASSCF. A análise dos orbitais moleculares (Figura 7c) unicamente ocupados nas configurações eletrônicas mais relevantes revela que todos são de natureza π e π^*, indicando tratar-se de um outro estado eletrônico excitado ¹(ππ^*).

Quinto estado eletrônico: raiz 5. A função de onda CASSCF do quinto estado tem a participação predominante de uma única configuração eletrônica (coeficiente = 0,97 e peso = 0,94), derivada do estado fundamental por uma excitação eletrônica simples do OM20 para o OM23. Conforme podemos observar na Figura 7c, esses orbitais correspondem, respectivamente, ao orbital molecular n_S e ao orbital molecular π^* delocalizado no anel de cinco membros. Ou seja, o quinto estado eletrônico é obtido a partir da excitação n_S → π^*, resultando em um estado eletrônico ¹(n_Sπ^*). Portanto, o estado eletrônico obtido como a quinta raiz do cálculo CASSCF corresponde ao estado excitado ¹(n_Sπ^*) que desejamos estudar.

Finalizando os testes. Temos todos os estados eletrônicos que desejamos estudar (¹(ππ^*) e ¹(n_Sπ^*)). No entanto, antes de iniciar a fase de produção dos resultados, seria interessante certificar-se, mais uma vez, sobre a estabilidade do espaço ativo. Recomendamos, portanto, realizar mais um ou dois testes, aumentando o número de estados eletrônicos calculados (raízes). Comparando esses resultados com os anteriores, podemos decidir sobre o número de estados excitados que precisam ser calculados para garantir que todos aqueles relevantes para a descrição do problema estão sendo tratados.

Estabilizado o espaço ativo e obtido todos os estados eletrônicos desejados, pode-se partir para a etapa de produção de resultados. Não esqueça, no entanto, que o método CASSCF trata apenas de uma parte da correlação eletrônica, chamada não-dinâmica. Na maioria dos casos, será necessário empregar as funções de onda CASSCF como ponto de partida para cálculos visando a recuperação da energia de correlação dinâmica, por meio de métodos como MRCI ou CASPT2, por exemplo, para se obter resultados quantitativos.

O Tiofeno: explorando simetria espacial

No item anterior, comparamos o tamanho da expansão CASSCF, empregando determinantes de Slater e CSFs, e concluímos que o uso das CSFs é bastante vantajoso pois o número de termos na expansão é muito menor do que aquele que seria obtido se utilizássemos determinantes de Slater. No entanto, uma redução adicional pode ser obtida impondo uma restrição adicional à função de onda espacial, por meio da teoria de grupos pontuais. Infelizmente, nem todos os códigos computacionais exploram essa facilidade, mas isso é possível com alguns softwares como o MOLCAS²⁹ e o MOLPRO.⁴¹

Embora o tiofeno tenha simetria espacial C_2v (Figura 9), em todos os cálculos realizados anteriormente empregou-se o grupo pontual C₁, ou seja, sem nenhuma restrição à simetria espacial da função de onda. Quando se utiliza simetria espacial, os estados eletrônicos podem ser classificados de acordo com a representação irredutível à qual pertencem. Com isso, cálculos distintos podem ser realizados para cada conjunto de estados eletrônicos pertencentes à mesma simetria espacial. A seguir, serão descritas algumas etapas envolvidas no planejamento de cálculos empregando simetria espacial.

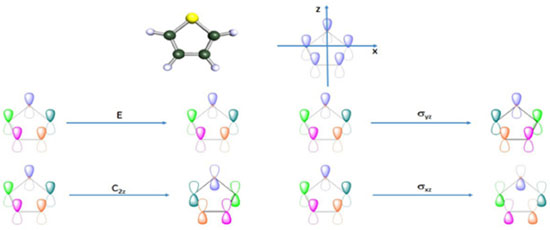Figura 9. Representaçao esquemática, com numeraçao, da molécula de tiofeno

A determinação do espaço ativo segue sendo uma parte de suma importância no cálculo, mas com pequenas diferenças em sua construção. A primeira etapa envolve a determinação do número de orbitais ativos pertencentes a cada uma das representações irredutíveis. No caso do tiofeno, pertencente ao grupo pontual C_2v (cuja tabela de caracteres está representada na Tabela 1), temos quatro representações irredutíveis: A₁, A₂, B₁ e B₂. Os orbitais moleculares serão classificados conforme a representação irredutível a qual eles pertencem e deverão ser ordenados, dentro de cada representação irredutível, como inativos, ativos e virtuais. Portanto, é preciso determinar quantos orbitais moleculares pertencem a cada uma das representações irredutíveis. A sequência de representações irredutíveis depende da orientação espacial da molécula, sendo apresentada na sessão referente ao cálculo das integrais moleculares. Portanto, recomenda-se analisar cuidadosamente essa parte do arquivo gerado pelo programa, para que a convenção adotada pelo programa seja utilizada corretamente.

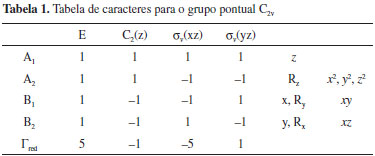
O processo para obter o número de orbitais moleculares pertencentes a cada uma das representações irredutíveis envolve dois passos: (i) obtenção da representação redutível, empregando como funções base os orbitais atômicos que irão formar os orbitais moleculares e (ii) decomposição da representação redutível em termos das representações irredutíveis do grupo pontual da molécula em estudo.

Como conjunto base para as operações de simetria, podemos empregar os orbitais atômicos utilizados para construir os orbitais moleculares do espaço ati, , vo. Neste caso, estamos interessados nos orbitais moleculares π, π^* e n_S. Supondo que a molécula esteja no plano molecular xz (Figura 9), empregaremos os orbitais atômicos p_y (perpendiculares ao plano xz), para construir os orbitais moleculares π e π^*, e o orbital atômico s do enxofre como orbital n_S. Orbitais do tipo n são totalmente simétricos e, portanto, pertencem à representação irredutível A₁.

Uma maneira prática de se obter uma representação redutível é contar o número de funções base, neste caso os orbitais atômicos que irão compor os orbitais moleculares π, que permanecem fixos no mesmo átomo em relação a cada uma das operações do grupo pontual ao qual a molécula pertence. Cada função base que permanecer com o mesmo sinal contribuirá com 1 para o caracter da operação correspondente na representação redutível; cada função que permanecer no mesmo átomo, porém com sinal contrário, contribuirá com -1 para o caracter da operação na representação redutível. Se a função não permanecer no mesmo átomo, ela não contribuirá para o caracter da operação na representação redutível.

Na Figura 9 representamos os cinco orbitais p_y nos átomos de carbono e enxofre da molécula de tiofeno. Na mesma figura, representamos o resultado de cada uma das operações de simetria do grupo pontual C_2v. A representação redutível (Γ_red) obtida como descrito na sequência do texto também pode ser vista na Tabela 1.

Após a realização da operação identidade (E), todos (5 funções) os orbitais permanecem na mesma posição; logo, o caracter da operação identidade na representação redutível é 5. Em relação à operação C₂(z), todos os orbitais atômicos mudam de posição, exceção ao orbital centrado no átomo de enxofre, que permanece nele com sinal trocado; logo, o caracter da operação C₂(z) na representação redutível é -1. Em relação à operação σ_xz, todas as funções permanecem em seus átomos de origem, porém com sinal trocado; portanto, seu caracter na representação redutível será -5. Finalmente, para a operação de simetria σ_yz, todas as funções mudam de posição, exceto a localizada no átomo de carbono que permanece nele com o mesmo sinal; assim, o caracter da operação σ_xz na representação redutível é 1.

Para grupos de ordem finita,^42,43 a redução de uma representação redutível pode ser feita pela seguinte equação: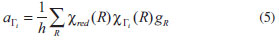

na qual, a_Γi corresponde ao número de vezes que a representação irredutível Γ_i aparece na representação redutível; h é a ordem do grupo pontual; R é a operação de simetria; χ_red(R) é o caracter da operação R na representação redutível Γ_red; χ_i(R) é o caracter da operação R na representação irredutível Γ_i; g_R é o número de membros da classe à qual a operação R pertence.

Na Tabela 2, ilustramos o uso da Equação 5 no nosso caso; lembre-se que a ordem do grupo pontual C_2v é igual a 4.

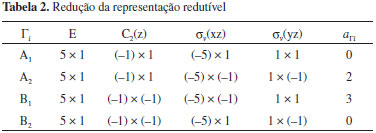
Portanto, a representação irredutível obtida empregando os orbitais atômicos py dos átomos localizados no anel do tiofeno se reduz a 2A₂ e 3B₁ (Γ_red = 2A₂ + 3B₁). Em outras palavras, os orbitais π e π^* do tiofeno pertencem às representações irredutíveis A₂ e B₁, sendo 3 com simetria A₂ e 2 com simetria B₁. Como o orbital n_S localizado no átomo de enxofre pertence à representação irredutível A₁, o espaço ativo de valência pode ser representado por (1230), lembrando que a sequência de representações irredutíveis é (A₁A₂B₁B₂). Tendo definido o espaço ativo, podemos planejar os cálculos dos estados excitados de valência. Os orbitais de valência π e π^* pertencem às representações irredutíveis A₂ e B₁ e o n_S, à A₁. Transições de valência π → π^* geram estados com simetria A₁ e B₂, obtidos a partir do produto direto das representações irredutíveis dos orbitais envolvidos. Por outro lado, transições n_S → π^* geram estados excitados com simetria A₂ e B₁.

Vamos comparar com os cálculos efetuados anteriormente, sem utilização de simetria. Empregando simetria C_2v podemos fazer uma partição do espaço ativo para calcular os diferentes estados excitados. Por exemplo, estados excitados ¹(ππ^*), que têm simetria A₁ e B₂, podem ser calculados empregando o espaço ativo (0230) e calculando estados excitados com simetria A₂, o que gera 28 CSFs (51 determinantes) e B₁, com 22 CSFs (24 determinantes); neste caso, temos uma função CAS(6,5), seis elétrons ativos (os dois elétrons do orbital n_S e ele próprio passam para o espaço inativo) distribuídos em cinco orbitais ativos. Anteriormente, no caso sem simetria, a função de onda era CAS(8,6), gerando 105 CSFs (120 determinantes). Portanto, o uso de simetria reduz o tamanho da expansão CASSCF e, sempre que possível, poderá ser utilizado.

CONCLUSÕES

Nesta contribuição, diversos aspectos envolvidos na construção do espaço ativo para cálculos quânticos multiconfiguracionais foram discutidos, dentre eles destacamos a relevância de uma análise criteriosa do problema, a escolha dos orbitais necessários para descrever os efeitos relevantes, algumas sugestões sobre a escolha do tipo de orbitais que serão empregados como ponto de partida para o cálculo multiconfiguracional, a análise das funções de onda e o emprego de teoria de grupo. Com o auxílio dos arquivos disponíveis no Material Suplementar, e de softwares disponíveis gratuitamente pela internet, os exemplos apresentados poderão ser utilizados como material de estudo. Com isso, pretendemos incentivar os leitores a utilizarem esses métodos quânticos em seus trabalhos de pesquisa.

MATERIAL SUPLEMENTAR

Os resultados apresentados podem ser reproduzidos empregando o material disponível na internet (http://quimicanova.sbq.org.br/).

AGRADECIMENTOS

Os autores agradecem o suporte acadêmico do CNPq (Conselho Nacional de Desenvolvimento Cientifíco e Tecnológico) e da FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo). Agradecem, também, os serviços oferecidos pelo LCCA (Laboratório de Computação Científica Avançada) da Universidade de São Paulo. Por fim, os autores agradecem ao NAP-PhotoTech, The USP Consortium for Photochemical Technology, por todo o suporte oferecido.

REFERÊNCIAS

1. Szabo, A.; Ostlund, N. S.; Modern Quantum Chemistry. Introduction to Advanced Electronic Structure Theory, 1 ed. rev., McGraw-Hill: New York, 1989.

2. Jensen, F.; Introduction to Computational Chemistry, John Wiley & Sons: Oxford, 1999.

3. Escola Brasileira de Estrutura Eletrônica; Santos, H. F.; Coura, P. Z.; Dantas, S. O.; Barone, P. M. V. B., eds.; Editora Livraria da Física: Sao Paulo, 2003.

4. Cramer, C.; Essentials of Computational Chemistry: Theories and Models, John Wiley & Sons: Oxford, 2005.

5. Métodos de Química Teórica E Modelagem Molecular, Morgon, N. H.; Coutinho, K. eds.; Editora Livraria da Física: Sao Paulo, 2007.

6. Löwdin, P. O. Em Advances in Chemical Physics; Prigogine, I., ed.; Interscience Publishers: New York, 1959, vol. 2.

7. Szalay, P. G.; Mueller, T.; Gidofalvi, G.; Lischka, H.; Shepard, R.; Chem. Rev. 2012, 112, 108. DOI: http://dx.doi.org/10.1021/cr200137a PMID: 22204633

8. Lyakh, D. I.; Musial, M.; Lotrich, V. F.; Bartlett, R. J.; Chem. Rev. 2012, 112, 182. DOI: http://dx.doi.org/10.1021/cr2001417 PMID: 22220988

9. Gusarov, S.; Malmqvist, P.-Å.; Lindh, R.; Roos, B. O.; Theor. Chem. Acc. 2004, 112, 84. DOI: http://dx.doi.org/10.1007/s00214-004-0568-1

10. Yamanaka, S.; Nakata, K.; Ukai, T.; Takada, T.; Yamaguchi, K.; Int. J. Quantum Chem. 2006, 106, 3312. DOI: http://dx.doi.org/10.1002/qua.21164

11. Roos, B. O.; Taylor, P. R.; Siegbahn, P. E. M.; Chem. Phys. 1980, 48, 157. DOI: http://dx.doi.org/10.1016/0301-0104(80)80045-0

12. Siegbahn, P.; Heiberg, A.; Roos, B. O.; Levy, B.; Phys. Scr. 1908, 21, 323. DOI: http://dx.doi.org/10.1088/0031-8949/21/3-4/014

13. Siegbahn, P. E. M.; Almlöf, J.; Heiberg, A.; Roos, B. O.; J. Chem. Phys. 1981, 74, 2384. DOI: http://dx.doi.org/10.1063/1.441359

14. Ruendenberg, K.; Sundeberg, K. R. Em Quantum Science: Methods and Structure - A Tribute to Per-Olov Lowdin; Calais, J.-L.; Goscinski, O.; Linderberg, J.; Ohrn, Y., eds.; Plenum Press: New York, 1976, pg. 515.

15. Roos, B. O. Em Advances in Chemical Physics; Ab Initio Methods in Quantum Chemistry - II; Lawley, K. P., ed.; John Wiley & Sons Ltd.: Oxford, 1987, pg. 399.

16. Roos, B. O., Em European Summerschool in Quantum Chemistry 2003, Book II ; Roos, B. O.; Widmark, P.-O., eds.; Lund University: Lund, 2003.

17. Roos, B. O., Em Theory and Applications of Computational Chemistry: The First 40 Years. A Volume of Technical and Historical Perspectives; Dykstra, C. E.; Frenking, G.; Kim, K. S.; Scuseria, G. E., eds.; Elsevier: Amsterdam, 2005, pg. 725.

18. Schaftenaar, G.; Noordik, J.; J. Comput. Aided Mol. Des. 2000, 14, 123. DOI: http://dx.doi.org/10.1023/A:1008193805436 PMID: 10721501

19. Allouche, A.-R.; J. Comput. Chem. 2011, 32, 174. DOI: http://dx.doi.org/10.1002/jcc.21600 PMID: 20607691

20. 20. Jmol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org/.

21. Borin, A. C.; Chem. Phys. 2001, 274, 99. DOI: http://dx.doi.org/10.1016/S0301-0104(01)00543-2

22. Borin, A. C.; Serrano-Andrés, L.; Ludwig, V.; Coutinho, K.; Canuto, S.; Int. J. Quantum Chem. 2006, 106, 2564. DOI: http://dx.doi.org/10.1002/qua.20967

23. Ando, R. A.; Borin, A. C.; Santos, P. S.; J. Phys. Chem. A 2007, 111, 7194. DOI: http://dx.doi.org/10.1021/jp071954f PMID: 17628052

24. Roos, B. O; Borin, A. C.; Gagliardi, L.; Ang. Chem. Int. Ed. 2007, 46, 1469. DOI: http://dx.doi.org/10.1002/anie.200603600

25. Serrano-Andrés, Merchán, M.; Borin, A. C.; Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 8691. DOI: http://dx.doi.org/10.1073/pnas.0602991103 PMID: 16731617

26. Giussani, A.; Merchán, M.; Gobbo, J. P.; Borin, A. C.; J. Chem. Theory Comput. 2014, 10, 3915. DOI: http://dx.doi.org/10.1021/ct5003175

27. Barbatti, M.; Borin, A. C.; Ullrich, S.; Em, Photoinduced Phenomena in Nucleic Acids I; Topics in Current Chemistry, Vol. 355; Barbatti, M.; Borin, A. C.; Ullrich, S., eds.; Springer: Berlim, 2015, pg. 1.

28. Granovsky, A. A.; Firefly version 8.0., http://classic.chem.msu.su/gran/firefly/index.html/

29. Aquilante, F.; Pedersen, T. B.; Veryazov, V.; Lindh, R.; WIREs Comput. Mol. Sci. 2013, 3, 143. http://molcas.org/ DOI: http://dx.doi.org/10.1002/wcms.1117

30. Hehre, W. J.; Ditchfield, R.; Pople, J. A.; J. Chem. Phys. 1972, 56, 2257. DOI: http://dx.doi.org/10.1063/1.1677527

31. Pauncz, R.; The Symmetric Group in Quantum Chemistry, CRC: Flórida, 1995.

32. Almlöf, J.; Taylor, P. R.; J. Chem. Phys. 1990, 92, 551. DOI: http://dx.doi.org/10.1063/1.458458

33. Almlöf, J.; Taylor, P. R. Em Advances in Quantum Chemistry, Vol. 22; Löwdin, P., ed., Academic Press: California, 1991, pg. 301.

34. Widmark, P.-O.; Malmqvist, P.-Å.; Roos, B. O.; Theor. Chem. Acc. 1990, 77, 291. DOI: http://dx.doi.org/10.1007/BF01120130

35. Widmark, P.-O.; Persson, B. J.; Roos, B. O.; Theor. Chim. Acta 1991, 79, 419. DOI: http://dx.doi.org/10.1007/BF01112569

36. Pou-Amérigo, R.; Merchán, M.; Nebot-Gil, I.; Widmark, P.-O.; Roos, B. O.; Theor. Chim. Acta 1995, 92, 149. DOI: http://dx.doi.org/10.1007/BF01114922

37. Pipek, J.; Mezey, P. G.; J. Chem. Phys. 1989, 90, 4916. DOI: http://dx.doi.org/10.1063/1.456588

38. Foster, J. M.; Boys, S. F.; Rev. Mod. Phys. 1960, 32, 300. DOI: http://dx.doi.org/10.1103/RevModPhys.32.300

39. Edmiston, C.; Ruedenberg, K.; Rev. Mod. Phys. 1963, 35, 457. DOI: http://dx.doi.org/10.1103/RevModPhys.35.457

40. Löwdin, P.-O.; Phys. Rev. 1955, 97, 1474. DOI: http://dx.doi.org/10.1103/PhysRev.97.1474

41. Werner, H.-J.; Knowles, P. J.; Knizia, G.; Manby, F. R.; Schütz, M.; WIREs Comput. Mol. Sci. 2012, 2, 242. http://www.molpro.net/ DOI: http://dx.doi.org/10.1002/wcms.82

42. Cotton, F. A.; Chemical Applications of Group Theory, 3rd edition, John Wiley & Sons; New York, 1990.

43. Harris, D. C.; Bertolucci, M. D.; Symmetry and Spectroscopy: An Introduction to Vibrational and Electronic Spectroscopy, Dover; New York, 1989.