Educação
|
|
| Compreensão matemática da difusão no contexto eletroquímico Mathematical approach of diffusion in the electrochemical context |
|
Sidineia Barrozo; Assis Vicente Benedetti*
Departamento de Físico-Química, Instituto de Química, Universidade Estadual Paulista, 14800-060 Araraquara - SP, Brasil Recebido em 27/05/2015 *e-mail: benedeti@iq.unesp.br The aim of this study was to explain in detail the mathematical methods used to deal with diffusion equations, mainly for students and researchers interested in electrochemistry and related areas. Emphasis was placed on the deduction and resolution of diffusion equations, as well as addressing cartesian, spherical and cylindrical coordinates. Different aspects of mass transfer processes were discussed including the importance of the resolution of Fick's laws equations to understand and derive parameters of the electroactive species (e.g., diffusion coefficients, formal electrode potentials) from the electrochemical techniques. As an example, the resolution of diffusion equations for a reversible reduction process of soluble oxidized species was presented for the chronopotentiometry technique. This study is envisaged to broaden the understanding of these frequently used methods, in which mathematical deductions are not always completely understood. INTRODUÇÃO O fenômeno da difusão está presente em nosso dia-a-dia em muitas situações como, por exemplo, no cheiro de um perfume que é percebido pela difusão de suas moléculas; ou ao deixar cair uma gota de tinta colorida e solúvel em água num recipiente com este solvente, em que facilmente se verifica o avanço da cor na solução, resultado da difusão de moléculas responsáveis pela cor da tinta. Neste caso, salienta-se que a queda da gota também produz convecção, o que facilita o transporte da tinta na solução. Outra situação em que o fenômeno da difusão é facilmente detectado é numa eletrólise, pois ao se formar íons hidroxila na superfície do cátodo imerso em solução contendo fenolftaleína (indicador ácido-base) verifica-se o aparecimento da cor rósea nas adjacências do eletrodo, e a intensidade de cor diminui à medida que aumenta a distância do cátodo devido à difusão do íon hidroxila a partir da superfície do eletrodo para o interior da solução. Em todos os casos tem-se um fluxo de massa a partir da fonte. Da simples observação macroscópica intui-se ser esse fluxo dependente da variação de concentração da espécie que se difunde entre dois pontos do sistema, por exemplo, num regime estacionário, e da variação da concentração entre dois pontos do sistema e do tempo num regime não estacionário. Em ambos os casos a constante de proporcionalidade, denominada coeficiente de difusão, é um parâmetro importante na descrição do sistema. Como será visto adiante e em trabalhos futuros, o valor do coeficiente de difusão pode ser obtido, por exemplo, empregando uma técnica eletroquímica, uma vez que se tenham as equações que expressam a relação das variáveis elétricas (corrente, potencial ou carga) entre si ou dessas com o tempo. Essas equações podem ser obtidas de forma simples quando é possível assumir que a difusão é praticamente a única forma de transporte de massa da espécie eletroativa no meio em estudo. Para tanto, um passo importante é resolver as equações de difusão assumindo determinadas condições iniciais e de contorno, objeto desse trabalho. Ou seja, não é possível interpretar, de forma quantitativa, grande parte dos processos de eletrodo sem resolver as equações de difusão. Isso se tornará claro ao final deste item. É de conhecimento geral que um eletrodo é constituído por um condutor eletrônico e um condutor iônico e, de forma simples, uma célula eletroquímica é formada por pelo menos dois eletrodos. No contato condutor eletrônico/iônico (solução iônica, sal fundido, eletrólito sólido, líquido iônico etc.) se estabelece uma interface que apresenta maior ou menor resistência à passagem de um fluxo de cargas, ou seja, corrente elétrica. O contato entre as fases representadas aqui pelos condutores eletrônico e iônico estabelece uma região tridimensional denominada interfase, que, muitas vezes para simplificar o sistema, é reduzida a uma superfície denominada interface. Na maioria das interfases há acúmulo de cargas de um mesmo sinal de um lado e de cargas de sinal oposto do outro lado da interface, o que resulta na presença de um campo elétrico. Este campo elétrico pode ser variado pela imposição, por exemplo, de um potencial elétrico externo, que modifica a cinética do processo de eletrodo. Não é recente a preocupação dos eletroquímicos e de profissionais de outras áreas que utilizam a eletroquímica com os processos que ocorrem na interfase eletrodo/solução. A parte da eletroquímica denominada iônica deixou de ser o objeto principal de estudo dos eletroquímicos. Por exemplo, um objeto de estudo da eletroquímica é medir a velocidade dos processos que ocorrem nessas interfases, então, é imprescindível estudar como se deslocam os reagentes até a superfície do eletrodo e como os produtos se afastam dessa superfície. Há três formas dos reagentes se deslocarem em direção à superfície do eletrodo: (a) em função das diferenças de potencial químico (diferença de atividade ou de concentração) em diferentes pontos do eletrólito, ou seja, gradiente de atividade ou, na maioria das técnicas eletroquímicas é suficiente considerar o gradiente de concentração, dC/dx. O movimento dessas espécies sempre ocorre do ponto ou região de maior concentração para um ponto ou região de menor concentração. Esta forma de transporte de massa é denominada difusão. A difusão é um exemplo de processo irreversível em que a diferença de concentração é diminuída por um processo espontâneo de transporte de massa; (b) devido à presença de um campo elétrico, ou seja, um gradiente de potencial elétrico (dE/dx), desde que as espécies reagentes sejam carregadas. Esta forma de transporte de massa é denominada migração; (c) as espécies reagentes e produtos podem também ser transportados pelo movimento da solução. Neste caso, o transporte de massa é denominado convecção. Para mais detalhes, conceitos, propriedades, parâmetros dos condutores iônicos, os leitores são aconselhados a consultar livros textos clássicos.1-5 Em condutores eletrônicos apenas elétrons e buracos são transportadores de carga, enquanto que em condutores iônicos há um grande número de espécies com diferentes tamanhos, cargas e estruturas que são transportadores de carga, e há também os condutores mistos.6,7 A condutividade de uma solução está intimamente relacionada com o fenômeno de migração de íons em solução iônica aquosa ou solução iônica de solventes orgânicos próticos e apróticos. A migração ocorre também em sais e óxidos fundidos, em eletrólitos sólidos e em líquidos iônicos. Em soluções iônicas muito diluídas a solvatação dos íons é praticamente o principal aspecto a ser considerado no estudo físico-químico do condutor iônico, enquanto que em soluções menos diluídas e concentradas devem ser levadas em consideração também as interações íon-íon. Essas interações íon-íon se estendem desde interações eletrostáticas de longo alcance até a formação de pares iônicos ou conjuntos de três ou mais íons. Nos eletrólitos fundidos e eletrólitos sólidos, os efeitos relacionados à associação de íons assumem ainda maior importância.2,3,8 Para os eletrólitos sólidos, a migração de íons pode ser um processo muito lento, cuja cinética é similar ao mecanismo de crescimento de fase sólida em campos elétricos elevados.9 A fração de carga qi transportada por uma espécie de íons i em um condutor iônico se denomina número de transporte ou número de transferência, ti.6,7 Em muitas técnicas eletroquímicas é conveniente fazer com que o número de transporte das espécies eletroativas se aproxime do valor nulo (ti esp. eletroativa → 0), ou seja, a contribuição da espécie eletroativa para o transporte de cargas no condutor iônico é considerada negligenciável. Isso é desejável porque evita que a espécie eletroativa seja transportada por difusão e migração, o que dificulta, por exemplo, a aplicação das equações de corrente - potencial para o processo de eletrodo, uma vez que não há como separar a corrente de difusão daquela devida à migração dessa espécie. Para tanto, espécies iônicas não eletroativas (eletrólito de suporte) no intervalo (de potencial ou corrente) de estudo do reagente devem ser adicionadas em concentração tal que o somatório dos valores de seus ti se aproxime de 1. Isto significa que a concentração do eletrólito de suporte deve ser da ordem de 102 a 103 vezes maior do que a concentração da espécie eletroativa.10 Em solução aquosa, por exemplo, essa concentração deve ser maior ou igual a 0,1 mol L-1. O eletrólito de suporte tem muitas outras funções, por exemplo, evitar a necessidade da correção de Frumkin na obtenção de parâmetros cinéticos, manter praticamente constante os coeficientes de atividade das espécies eletroativas etc. Sugere-se aos leitores consultarem a literatura.11,12 A convecção pode ocorrer pelo movimento do eletrodo, da solução ou de ambos e pode ser natural ou forçada. A convecção natural pode ser causada, por exemplo, por um gradiente de densidade, diferença de temperatura entre dois pontos na solução, ou por diferença de concentração entre a superfície do eletrodo e a solução adjacente ao eletrodo. A convecção forçada, como o próprio nome indica, é quando uma força externa é aplicada e movimenta o eletrodo, a solução, ou ambos. Nos processos interfaciais, o processo de difusão-convecção é o de maior interesse, por exemplo, difusão-convecção do eletrólito empregando um eletrodo de disco ou disco-anel rotatório.13 Se ambos, eletrodo e solução, forem estacionários e não houver gradientes de temperatura, o transporte de massa por convecção pode ser considerado negligenciável. Se ainda houver um excesso de eletrólito de suporte, é possível presumir que o transporte de massa relativo à espécie eletroativa ocorre fundamentalmente por difusão, e é este o caso que será abordado neste trabalho. Conhecidas as três formas de transporte de massa, para a eletroquímica deve se fazer a conexão entre o fluxo de massa no meio e o fluxo de cargas através da interface eletrodo/solução. Supondo que os leitores estejam familiarizados com o conceito de estado estacionário, basta lembrar que num processo de etapas sucessivas, todas as etapas ocorrem à mesma velocidade. Por exemplo, se as etapas são transferência de carga na interface, cuja densidade de corrente é jTC, e transporte de cargas na solução, cuja densidade de corrente é jTM, as densidades de corrente correspondentes a todas as etapas são iguais. Portanto,  Na interface, essa igualdade ocorre quando x = 0, ou no plano externo de Helmholts.14 Mas nesta situação tem-se  em que nF é a carga transportada por mol de íons e JTM é o fluxo, ou seja, número de moles de íons transportados por cm2 por segundo (mol cm-2 s-1). Se a espécie não for carregada (molécula) pode-se expressar o JTM como o número de moles que chega até a superfície do eletrodo (para se reduzir ou oxidar) por cm2 por segundo, ou seja,  Se a difusão for considerada a única forma de transporte de massa, tem-se  em que JD é o fluxo de difusão. A condição de igualdade de fluxos pode ser aplicada mesmo quando j e JTM variam com o tempo, bastando dividir o tempo em pequenos intervalos dt e considerar essa condição válida dentro desse tempo infinitesimal. Agora, se JTM = JD, então JD = j/nF com JD dado pela 1ª lei de Fick. Se a difusão está sujeita a um estímulo constante aplicado em t = 0, ou variável com o tempo, é preciso conhecer a variação da concentração com o tempo a uma distância particular da interface, para o quê é necessário resolver a 2ª lei de Fick. Ambas as situações serão abordadas no decorrer deste texto. Se a migração e a convecção forem negligenciáveis, ao se aplicar um potencial num eletrodo capaz de oxidar uma espécie em solução, haverá diminuição da concentração dessa espécie eletroativa na superfície do eletrodo. Isso gera um gradiente de concentração e, consequentemente, ocorrerá o transporte de espécies eletroativas a partir da solução em direção à superfície do eletrodo. A formação de espécies oxidadas na superfície do eletrodo cria um gradiente de concentração no sentido oposto que transporta tais espécies para longe da superfície do eletrodo, ou seja, em direção ao interior da solução. Como outros exemplos de difusão citam-se: o transporte de adátomos na superfície do eletrodo que pode controlar o processo de deposição; a difusão da espécie em fase volume do material no crescimento de camadas finas de fases sólidas; transporte de elétrons e buracos dentro de um semicondutor; o transporte de átomos de hidrogênio através de membranas delgadas de metal etc. O mais surpreendente é que equações relativamente simples das leis de difusão possam unificar tantos processos em um único parâmetro, D, o coeficiente de difusão, que, obviamente, assume valores diferentes para cada sistema. O coeficiente de difusão à temperatura ambiente assume valores que vão desde ~10-3 cm2 s-1 em fase gasosa, 10-5 a 10-7 cm2 s-1 em fase líquida (água e solventes orgânicos, exceto alguns líquidos iônicos, onde pode ser menor), e até ~10-18 cm2 s-1 em fase sólida, por exemplo, filmes de óxidos de metais.
DIFUSÃO Difusão é o movimento térmico de qualquer partícula de um líquido, gás e alguns sólidos a temperaturas acima do zero absoluto. A difusão pode ser discutida do ponto de vista das leis de Fick, na presença de um gradiente de concentração, ou do ponto de vista físico e atomístico considerando o movimento aleatório das partículas, por exemplo, das moléculas de água em água pura. A difusão causada pelo movimento aleatório de partículas (moléculas, íons, átomos) na ausência de um gradiente de concentração é denominada autodifusão (self-diffusion ou tracer diffusion) e corresponde à difusão de uma espécie individualmente. Isso pressupõe que numa mistura as espécies se difundem sem interação significativa entre elas, o que equivale à situação ideal, ou seja, por exemplo, uma solução muito diluída. O coeficiente de difusão é denominado coeficiente de autodifusão. A velocidade do movimento depende da temperatura, viscosidade do meio e da massa/tamanho da partícula. A difusão explica o fluxo líquido de matéria de uma região de maior concentração para uma de menor concentração. Ao se igualar as concentrações (atividades), esse fluxo líquido de massa cessa, porém, as partículas continuam em movimento, autodifusão. Tem-se, então, uma mistura gradual de materiais até chegar a uma distribuição uniforme, estabelecendo-se um equilíbrio com partículas em movimento, denominado equilíbrio dinâmico. A difusão continua, mas sem um fluxo líquido de matéria. Para maiores detalhes sobre autodifusão sugere-se consultar a literatura.3,4,5,15,16 Em particular, neste trabalho, tem grande interesse a análise da situação em que há fluxo líquido de matéria porque está diretamente relacionado com a maioria das técnicas eletroquímicas. A difusão é um fenômeno físico irreversível em que ocorre o transporte de massa pelo movimento de íons ou moléculas, na presença de um gradiente de potencial químico. O gradiente de potencial químico pode ser substituído por gradiente de concentração no uso de técnicas eletroquímicas. O movimento causado pelo gradiente se dá na direção de maior para menor concentração, procurando encontrar um equilíbrio. A difusão pode ocorrer em uma única direção (unidimensional), como no caso do fluxo sanguíneo por uma artéria, ou ser bidimensional, como no caso de uma gota de tinta se espalhando sobre uma superfície plana, ou tridimensional, como no caso de um gás se difundindo no espaço ou de espécies químicas se difundindo em solução ou num sólido. Matematicamente é descrita por uma equação diferencial parcial, envolvendo espaço e tempo, sendo que em coordenadas cartesianas sua forma geral é: 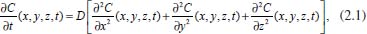 em que C representa a concentração da espécie que se difunde na posição (x,y,z) no instante de tempo t e D é chamado coeficiente de difusão. Dependendo da espécie, este coeficiente pode variar com a concentração, porém esta variação normalmente é muito pequena e, por isso, D é considerado constante na maioria dos casos, desde que não varie a temperatura. Esta equação pode também ser escrita em coordenadas esféricas ou cilíndricas, de acordo com o fenômeno que está sendo estudado, o que pode facilitar muito os cálculos. Nos processos eletroquímicos são utilizados eletrodos de diferentes geometrias como planar, cilíndrica, esférica etc. A difusão linear semi-infinita, ou seja, na direção perpendicular à superfície do eletrodo ocorre em eletrodos planos com raio maior que a espessura da camada de difusão. Nos outros casos há influência da difusão não linear: esférica (eletrodo de gota estática de mercúrio), eletrodo gotejador de mercúrio, microeletrodos, eletrodos micro heterogêneos como mini redes de metal onde a espessura do fio da rede é menor do que a espessura da camada de difusão, dentre outros.11 Assim, o objetivo deste trabalho é apresentar os métodos matemáticos presentes na equação de difusão aplicada à eletroquímica, em todos os seus detalhes, desde a dedução das equações até suas resoluções, abordando coordenadas cartesianas, esféricas e cilíndricas. Difusão planar Denomina-se difusão planar aquela que ocorre através de uma região plana, de área A, na direção (unidimensional) perpendicular ao plano. Considerando esta direção coincidente com o eixo-x no sistema cartesiano, isso significa que a concentração da espécie varia apenas na direção x, sendo constante nas direções y e z. Neste caso, o fluxo da espécie num ponto x e num instante t, J(x, t), é definido como sendo a quantidade de matéria m transferida por unidade de tempo, através da área A, ou seja, 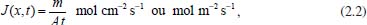 conforme ilustrado na Figura 1.
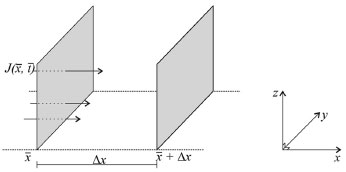 Figura 1. Representação geométrica de fluxo planar, na direção x
A 1ª lei de Fick estabelece que o fluxo de uma espécie, ou a quantidade de matéria que se difunde, por unidade de tempo, na direção perpendicular a uma região planar de área A, é proporcional ao gradiente de concentração da espécie. Matematicamente isso é descrito por  em que C(x,t) representa a concentração da espécie no ponto x e no instante t, D é o coeficiente de difusão ou difusividade e o sinal negativo indica que o fluxo ocorre sempre na direção de maior para menor concentração. É importante observar que a 1ª lei de Fick é aplicada a sistemas: estacionários,4 ou seja, quando não ocorre variação da concentração com o tempo; em estados transientes para descrever o fluxo em um instante de tempo em uma determinada posição; como uma condição de contorno na resolução da 2ª lei de Fick ou mesmo na explicação para se obter a 2ª lei. Assim, será utilizado o símbolo Como a maioria das leis físicas, esta também foi proposta a partir de observações empíricas, e para compreender sua dedução teórica apresentaremos aqui uma formulação sucinta, de forma mais intuitiva e sem grande rigor matemático e físico, porém para os leitores que desejarem compreendê-la mais detalhadamente, sugerimos os livros de A. J. Bard e L. R. Faulker10 ou de J. O'M. Bockris e A. K. N. Reddy.3,4 Suponha, sem perda de generalidade, que o fluxo de uma espécie esteja ocorrendo da esquerda para a direita na Figura 1, passando pelo plano em um ponto arbitrário  Portanto, considerando Δx ≈ 0, o fluxo no instante 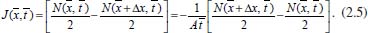 Em termos de concentração, em que o volume da região considerada é dado por V = AΔx, o fluxo é dado por 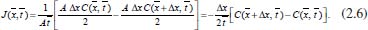 Se a variação Δx for muito pequena (Δx → 0)10 tem-se a forma contínua da equação (2.6) e, para a análise matemática. é interessante que se tenha a quantidade Δx no denominador, pois isso levará a uma derivada, facilitando o tratamento matemático. Assim, multiplicando e dividindo o lado direito da expressão (2.6) por Δx e rearranjando os termos adequadamente, obtém-se 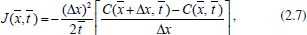 em que a concentração é dada em mol cm-3 ou mol m-3. O termo (Δx)2 pode ser interpretado como a média dos quadrados das distâncias percorridas por todas as moléculas presentes neste movimento,4,10 possuindo, portanto, dimensão cm2. Assim, considerando a equação de Einstein-Smoluchowski,3,4 (Δx)2 = 2D 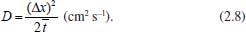 Considerando ainda que as espécies químicas estejam desacopladas (as partículas se movem sem interação significativa entre elas), o coeficiente de autodifusão (parâmetro microscópico) corresponde ao de difusão (parâmetro macroscópico) e, por isso, a equação (2.8) pode ser substituída em (2.7), tendo-se 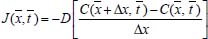 e, quando Δx → 0, obtém-se 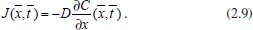 Como 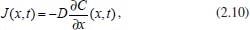 conforme anunciado na 1ª lei de Fick. O coeficiente de difusão D é bastante sensível à variação de temperatura e frequentemente segue uma equação do tipo Arrhenius:  em que Ea kJ mol-1 é a energia de ativação para difusão e D∞ é um valor hipotético de D a uma temperatura infinita T. Uma ilustração prática dessa lei de Fick é seu uso para caracterizar a difusão através de membrana biológica e outras membranas. Para aplicá-la a uma membrana celular de espessura ℓ há que se supor que ℓ seja tão pequeno que predomine a difusão de estado estacionário e que as fases solução em ambos os lados da membrana sejam bem misturadas. Neste caso, ∂C/∂x ~ (Cfora - Cdentro)/ℓ , em que Cfora e Cdentro representam as concentrações fora e dentro da membrana, respectivamente. O fluxo de difusão J é dado por D(Cfora - Cdentro)/ℓ, e D/ℓ é a permeabilidade.11 Como já observado, o desenvolvimento acima é válido apenas para difusão em estado estacionário, porém, a maioria das situações práticas envolvendo difusão ocorre em estado não estacionário, no qual a concentração da espécie varia tanto com a posição em que se encontra, quanto com o tempo. Se for considerada apenas a direção x, estas situações são usualmente representadas pela 2ª lei de Fick que, em coordenadas cartesianas (ou retangulares), é dada pela equação diferencial parcial  A dedução desta equação será feita inicialmente para o caso mais geral, ou seja, a difusão espacial, que ocorre no espaço tridimensional. Como caso particular tem-se a equação (2.12). Considere, portanto, um paralelepípedo como o mostrado na Figura 2 e suponha que a difusão esteja ocorrendo através dele, cujos fluxos ocorram nos sentidos de x para x + dx, de y para y + dy e de z para z + dz, através dos planos yz, xz e xy, respectivamente.
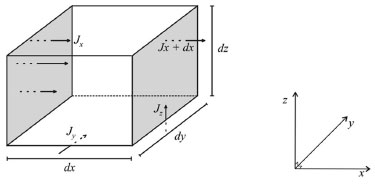 Figura 2. Representação geométrica de fluxo tridimensional
Se não existe produção de matéria no interior do paralelepípedo, então a taxa de variação da matéria neste paralelepípedo, em relação ao tempo, é dada pela diferença entre a matéria que entra e a matéria que sai, por unidade de tempo, ou seja, em termos de concentração tem-se 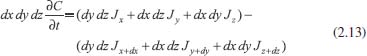 em que Jx representa o fluxo passando pelo plano em x, perpendicular à direção x; Jx+dx representa o fluxo passando pelo plano em x + dx, também perpendicular à direção x, e assim por diante; dx dy dz representa o volume do paralelepípedo; dy dz representa a área dos planos perpendiculares à direção x; dx dz representa a área dos planos perpendiculares à direção y e dx dy representa a área dos planos perpendiculares à direção z. Para simplificar a notação foi omitido o ponto (x, y, z, t). Observe que a unidade da equação é mol s-1 (matéria por unidade de tempo), pois do lado esquerdo tem-se cm3 mol cm-3 s-1 = mol s-1 e do lado direito cm2 mol cm-2 s-1 = mol s-1. Considerando dx, dy e dz suficientemente pequenos pode-se tomar a expansão de Taylor17 até primeira ordem nas expressões de fluxo de saída e, com isso obter 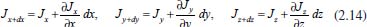 Substituindo na equação obtém-se 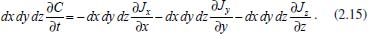 Dividindo pelo volume dx dy dz tem-se 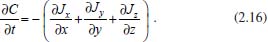 Utilizando agora a 1ª lei de Fick (2.10) para o fluxo em cada plano, a equação acima torna-se 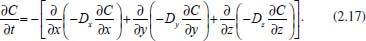 O coeficiente de difusão é função da concentração e, portanto, função de (x,y,z). Porém, num processo eletrolítico na presença de grande excesso de eletrólito de suporte a força iônica é virtualmente independente da concentração da espécie eletroativa e pode-se presumir que o coeficiente de difusão é independente de (x,y,z). Assim, considera-se, Dx = Dy = Dz = D constante e tem-se 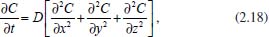 que é conhecida como equação de difusão tridimensional em coordenadas cartesianas. A difusão planar é, portanto, um caso particular da difusão tridimensional, onde se considera o fluxo ocorrendo apenas em uma direção, digamos x. Neste caso, a concentração não varia com y e z e, assim,  conforme afirmado na equação (2.12). Difusão esférica simétrica Por uma análise semelhante à que foi feita com coordenadas retangulares pode-se escrever a equação de difusão em coordenadas esféricas e cilíndricas, o que facilita a resolução de problemas que envolvem, por exemplo, eletrodos com estas geometrias. Neste caso será considerado o problema de difusão esférica simétrica, em que se supõe uma esfera de raio r, cuja difusão de espécies solúveis ocorre na direção de r a partir da superfície ou para a superfície dessa esfera (eletrodo). Esta difusão é também conhecida como difusão radial e o problema é, então, discutido apenas em termos de duas coordenadas: r que representa a distância a partir do centro do eletrodo, e t que representa o tempo decorrido a partir do início da eletrólise; não se leva em consideração as coordenadas angulares, usualmente presentes quando são utilizadas coordenadas esféricas. As relações entre as coordenadas retangulares e esféricas são dadas pelas equações: 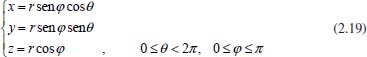 cuja interpretação geométrica é dada na Figura 3:
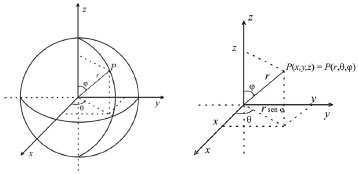 Figura 3. Visualização geométrica das coordenadas esféricas e sua relação com as coordenadas retangulares
Neste caso, o gradiente de concentração da espécie que está se difundindo é dado pelas derivadas parciais de C em relação às variáveis r, θ e φ. Utilizando a Regra da Cadeia17 para derivadas de funções de várias variáveis, tem-se:  No caso da difusão ser simétrica na direção do raio r pode-se tomar, sem perda de generalidade, o raio coincidindo com a direção x, ou seja, θ=0 e φ = 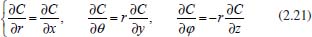 e o gradiente de concentração, em termos de coordenadas esféricas, dado por 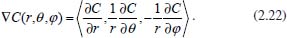 Considerando agora um fluxo de espécies em estado estacionário, do centro para a superfície de uma esfera de raio r, pode-se assumir que ao redor de um ponto ao longo do raio, ou seja, quando Δr → 0, Δθ → 0 e Δφ → 0, o fluxo se comporta segundo a 1ª lei de Fick, ou seja, é proporcional ao gradiente de concentração da espécie que se difunde. Isso é possível pelo fato da direção radial ser perpendicular ao plano tangente à esfera em cada ponto de interseção do raio com a superfície da esfera. Assim, em uma vizinhança suficientemente pequena deste ponto pode-se considerar o fluxo através do plano tangente à esfera (aproximação linear). Portanto, a ideia utilizada para a formulação teórica deste problema é análoga à utilizada no caso da difusão planar. Sejam dr, dθ e dφ variações infinitesimais no raio r e nos ângulos θ e φ, respectivamente. Com isso tem-se uma região de camada esférica tridimensional de espessura dr, formada entre a esfera de raio r e a esfera de raio r + dr, conforme mostra a Figura 4:
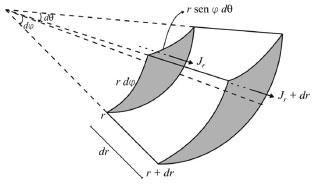 Figura 4. Representação geométrica da difusão esférica simétrica
Análogo ao que foi feito na equação (2.13), pode-se escrever 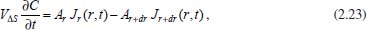 em que VΔS é o volume do pedaço da camada esférica, Ar é a área da parte da esfera de raio r, Ar+dr é a área da parte da esfera de raio r + dr, Jr é o fluxo passando por Ar e Jr+dr é o fluxo passando por Ar+dr. Como as dimensões dr, dθ e dφ são infinitesimais, pode-se tomar valores aproximados para o volume VΔS e para as áreas Ar e Ar+dr. Assim pode-se considerar: 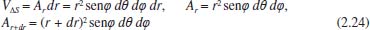 Logo, da equação tem-se 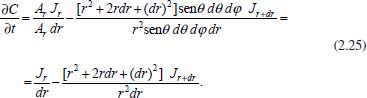 Utilizando a expansão de Taylor17 até primeira ordem para Jr+dr tem-se  Cancelando os termos semelhantes com sinais opostos e fazendo dr → 0 obtém-se: 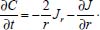 Utilizando a 1ª lei de Fick para o fluxo (lembrando que o gradiente é dado em termos de coordenadas esféricas) e considerando o coeficiente de difusão D constante, tem-se: 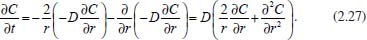 Portanto, em termos de coordenadas esféricas, a equação de difusão radial é dada por 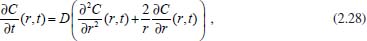 conforme pretendia-se mostrar. Difusão cilíndrica Considerando hipoteticamente que a difusão ocorra através de um cilindro circular reto, de raio r, na direção radial, ou seja, do eixo central do cilindro para a sua superfície ou da superfície para o eixo central. Neste caso é conveniente utilizar coordenadas cilíndricas, cujas relações com as coordenadas cartesianas são dadas pelas equações: 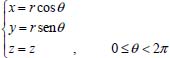 sendo sua interpretação geométrica mostrada na Figura 5:
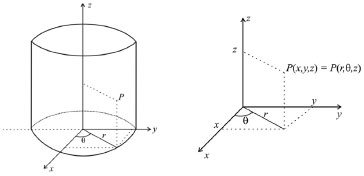 Figura 5. Visualização geométrica das coordenadas cilíndricas
O gradiente de concentração da espécie que está se difundindo, dado pelas derivadas parciais de C em relação às variáveis r, θ e z, é, então, dado por: 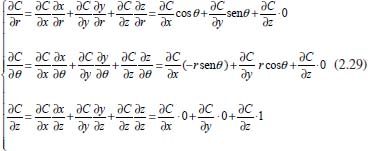 Análogo ao caso esférico, por existir simetria, pode-se considerar a difusão apenas na direção do raio r e, portanto, pode-se novamente tomar o raio coincidindo com a direção x, ou seja, θ = 0. Neste caso as derivadas parciais acima se tornam:  e o gradiente de concentração, em termos de coordenadas cilíndricas, é dado por 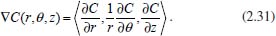 Tomando uma variação infinitesimal de tamanho dr no raio do cilindro, de dθ no ângulo e de dz na altura, tem-se uma região de camada cilíndrica tridimensional por onde o fluxo se difunde, conforme ilustrado na Figura 6:
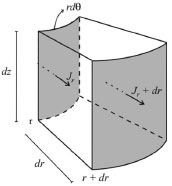 Figura 6. Representação geométrica da difusão cilíndrica simétrica
Como a ideia é exatamente a mesma dos casos anteriores, tem-se 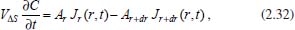 em que VΔS é o volume da região da camada cilíndrica, Ar é a área da parte do cilindro de raio r, Ar + dr é a área da parte do cilindro de raio r + dr, Jr é o fluxo passando por Ar e Jr + dr é o fluxo passando por Ar + dr. Como as dimensões dr, dθ e dz são infinitesimais, pode-se tomar valores aproximados para o volume VΔS e para as áreas Ar e Ar + dr, considerando  Logo, da equação (2.32) segue que 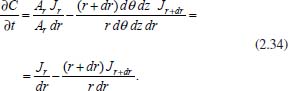 Utilizando a expansão de Taylor de primeira ordem para Jr + dr tem-se 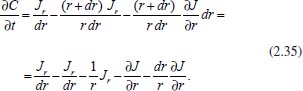 Novamente, cancelando os termos semelhantes com sinais opostos, fazendo dr tender a zero (dr → 0), utilizando a 1ª lei de Fick para o fluxo (lembrando que o gradiente agora é dado em termos de coordenadas cilíndricas) e considerando o coeficiente de difusão constante, obtém-se 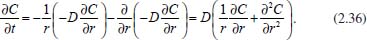 Portanto, em termos de coordenadas cilíndricas, a equação de difusão radial é dada por 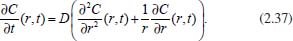
RESOLUÇÃO DA EQUAÇÃO DE DIFUSÃO Nesta seção serão apresentados alguns métodos matemáticos para a resolução da equação de difusão em coordenadas retangulares (difusão linear), esféricas e cilíndricas (difusão radial). Como visto na seção anterior, independentemente da geometria, a equação de difusão é sempre dada por uma equação diferencial parcial, envolvendo variáveis relacionadas ao tempo (t) e à posição da partícula em relação à superfície do eletrodo (x ou r). A sua resolução depende de pelo menos uma condição inicial relacionada à variável t, e pelo menos duas condições de contorno relacionadas à variável x ou à variável r. Estas condições dependem do fenômeno em estudo, da geometria do eletrodo e da técnica utilizada e, portanto, variam caso a caso. Leva-se em consideração, neste estudo, que não há reações químicas acopladas ao processo de transferência de carga e que as espécies O e R são solúveis e estáveis na solução. Coordenadas retangulares Considere um eletrodo plano de área A e um processo eletroquímico de oxidação ou redução, por exemplo, cujo fluxo das espécies se dá linearmente na direção perpendicular ao plano. De modo geral, a densidade de corrente j dada por I/A, sendo I a intensidade de corrente, relaciona-se com o fluxo da espécie oxidada O na superfície do eletrodo, JO (0,t), pela equação abaixo:10 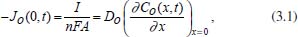 sendo que  e CO(x,t) e CR(x,t) representam, respectivamente, as concentrações das espécies O (oxidada) e R (reduzida) na posição x e no instante t, assim como JO e JR representam os fluxos destas espécies, DO e DR representam seus coeficientes de difusão, F é a constante de Faraday e q é o número de espécies que podem se reduzir. Em todos esses casos está sendo considerado que as espécies O e R não se solubilizam no eletrodo. As condições iniciais normalmente são determinadas pelo estado do sistema no início do processo, ou seja, em t = 0, enquanto que as de contorno levam em conta o que ocorre muito próximo da superfície do eletrodo (x → 0) ou distante dela, além da camada de difusão (x → ∞). Assim, em geral, tem-se:

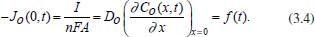 Pode-se utilizar também a conservação de massa na superfície do eletrodo. Assim, se O e R são solúveis na fase volume ou solução, para cada O que se reduz resulta um R e, consequentemente, 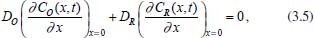 visto que JO(0,t) = -JR(0,t). A outra condição de contorno que possibilita a solução da equação de difusão depende da definição da técnica que será utilizada. Apresenta-se a seguir a resolução do caso geral da equação de difusão (2.12) considerando uma espécie com concentração C, que satisfaz a condição inicial e de contorno semi-infinita, conforme apresentado acima. Portanto, o objetivo é resolver a equação 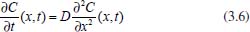 sujeita às condições inicial CO(x,0) = C0 e de contorno Este problema será resolvido de duas maneiras: inicialmente trabalhando com a equação original e, em seguida, utilizando uma mudança de variável que reduz o problema a uma equação diferencial ordinária de segunda ordem. Em ambos os casos, o método matemático principal utilizado para solucionar as equações é a transformada de Laplace,18,19 por ser um método que possibilita simplificar as equações, seja transformando uma equação diferencial parcial em uma equação diferencial ordinária, ou reduzindo uma equação diferencial ordinária em uma equação algébrica, simplificando, em ambos os casos, o tratamento matemático e, consequentemente, a resolução. Como não se trata de um assunto estudado em profundidade nos cursos de graduação optou-se por apresentar aqui a definição e as propriedades principais da transformada de Laplace, a fim de facilitar o entendimento das soluções que virão a seguir. A Transformada de Laplace Dada uma função f (t), definida e contínua para t > 0, a sua transformada de Laplace é uma função F(s), definida por  desde que a integral imprópria seja convergente, isto é, tenha um valor finito. A expressão e-st que aparece na transformada é denominada núcleo da transformação, sendo que a variável s pode ser real ou complexa, e seu significado normalmente está relacionado ao problema que está sendo estudado. Por exemplo, na Impedância Eletroquímica, representa a frequência e, com isso, a transformada de Laplace transforma um problema no domínio do tempo em outro no domínio da frequência, normalmente mais fácil de ser resolvido. De modo geral, em problemas que envolvem equações diferenciais lineares com coeficientes constantes, cujas soluções estão baseadas em funções exponenciais, a transformada de Laplace, por ter este núcleo, é particularmente útil. Se L[f(t)] existe, então existe também a transformada inversa, que é uma função que recupera a função original f(t), ou seja, existe L-1 tal que L-1[F(s)] = f(t). Observa-se que quanto mais complexa a função f(t), mais trabalhoso se torna o cálculo de sua transformada de Laplace, quando existir. Porém, a grande maioria das funções utilizadas nas áreas de Física, Química ou Engenharias possui sua transformada já calculada e apresentada em Tabelas. Hoje, com os recursos computacionais disponíveis, é possível calcular a transformada de Laplace (ou a transformada inversa) com muita facilidade. Um bom programa para fazer isso é o software Mathematica®,20 disponível para uso de docentes, alunos e pesquisadores na maioria das Universidades. Apresenta-se a seguir como calcular a transformada de Laplace de duas funções simples utilizando a definição e o software Mathematica®. Exemplo 1: Se f(t) = k, sendo k ≠ 0 é uma constante, então, sua transformada de Laplace é dada por Demonstração: Por outro lado, se Para calcular esta transformada utilizando o software Mathematica® basta executar o seguinte comando: LaplaceTransform[k, t, s], cujo retorno será Exemplo 2: Se f(t) = ekt, onde k ≠ 0 é uma constante, então, Demonstração: 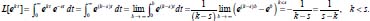 Note que se k > s a integral diverge e, portanto, não existe a transformada de Laplace. Por outro lado, se k < s, tem-se Analogamente mostra-se que se f(t) = e-kt, então, Utilizando o software Mathematica®, o comando para calcular a transformada é: LaplaceTransform[Exp[k*t], t, s], cujo retorno será Propriedades da transformada de Laplace Por ser definida por uma integral, esta transformada apresenta várias propriedades que a tornam muito útil na resolução de vários problemas matemáticos, em especial na resolução de equações diferenciais lineares com coeficientes constantes, uma vez que a transformada da derivada está relacionada de maneira simples com a transformada da função. Assim, uma equação diferencial em t é transformada em uma equação algébrica em s, cuja solução normalmente é simples, e o retorno para t é garantido pela transformada inversa. As propriedades principais são apresentadas a seguir: P1 (Linearidade): Se f e g são funções contínuas em [0, ∞) tais que suas transformadas de Laplace, L[f(t)] e L[g(t)], existam para todo t neste intervalo, então para quaisquer constantes a e b tem-se  Demonstração: Consequência imediata da linearidade do processo de integração.13 P2 (Transformada da derivada primeira): Se f é uma função contínua e diferenciável em [0, ∞) tal que sua transformada de Laplace L[f(t)] exista para todo t neste intervalo, então, a transformada da derivada de f, L[f'(t)], existe e satisfaz  Demonstração: Por definição, L[f'(t)] é dada por 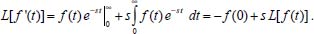
Portanto, se L[f (t)] é a transformada de Laplace de f (t), então, L[f'(t)] = s L[f (t)] - f (0)]. P3 (Transformada da derivada segunda): Se f é uma função contínua e diferenciável até segunda ordem em [0, ∞) tal que a transformada de Laplace de f e de sua derivada existam para todo t neste intervalo, então, a transformada da segunda derivada de f, L[f"(t)], existe e satisfaz 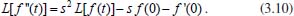 Demonstração: Por definição, L[f"(t)] é dada por 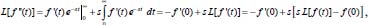 concluindo-se que 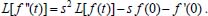 P4 (Transformada envolvendo funções de duas variáveis): Se f é uma função contínua nas variáveis x e t, então, a transformada de Laplace de f deve ser calculada parcialmente em relação a cada variável. E as transformadas sucessivas também podem ser calculadas conforme segue: 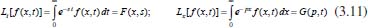 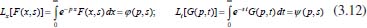 Demonstração: Consequência imediata da definição da transformada de Laplace e da integração de funções de várias variáveis.13 P5 (Transformada envolvendo derivadas de funções de duas variáveis): Se f (x, t) é uma função contínua com derivadas parciais contínuas até segunda ordem nas variáveis x e t, e se Lt[f(x,t)] = F(x, s), então 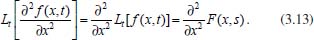 Demonstração: Isso é consequência imediata do fato de que, se f é contínua e possui derivadas parciais contínuas até segunda ordem, então a ordem de integração e de diferenciação de f em relação às variáveis x e t não importa. Assim, pela definição de Lt tem-se  Resolução 1 Retomando o problema de resolver a equação (3.6), dada por 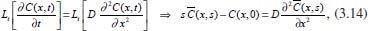 em que 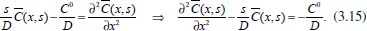 Aplicando a transformada de Laplace em relação à variável x tem-se:  Utilizando as propriedades P3 e P5 e o Exemplo 1 tem-se 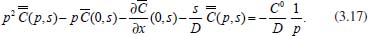 Os valores de 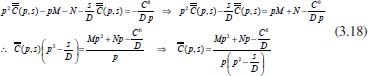 Tomando 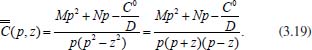 Separando o último termo em frações parciais2 tem-se: 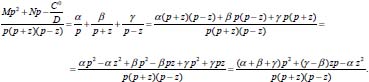 Logo, 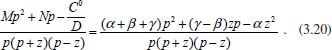 Portanto, considerando iguais os denominadores das frações em (3.20), a igualdade será verdadeira somente se os coeficientes dos termos semelhantes dos polinômios dos numeradores forem iguais, ou seja, se  Da terceira equação obtém-se 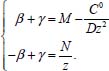 É um sistema linear de duas equações e duas incógnitas, cuja solução é facilmente calculada e dada por 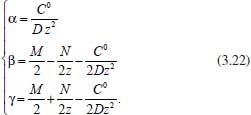 Como os valores de M e N não são conhecidos, pois dependem da técnica eletroquímica, os cálculos continuarão sendo feitos com β e γ para fins de simplificação da notação. Assim, 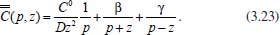 Aplicando a transformada inversa de Laplace para p, que está relacionado com a variável x: 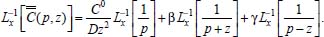 Utilizando uma Tabela ou um software para encontrar as transformadas inversas tem-se:  Observa-se que no caso do software Mathematica®, os comandos para calcular estas transformadas inversas são: InverseLaplaceTransform[1/p, p, x], com retorno: 1 InverseLaplaceTransform[1/(p+z), p, x], com retorno: e-xz InverseLaplaceTransform[1/(p-z), p, x], com retorno: exz Substituindo o valor de 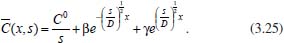 Utilizando a condição de contorno (3.6) pode-se calcular γ, pois 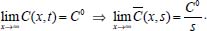 Portanto, calculando o limite da expressão (3.25), quando x → ∞, tem-se 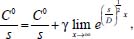 o que ocorre somente quando γ = 0. Logo, 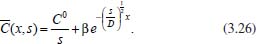 Aplicando a transformada inversa de Laplace para s, que está relacionado com a variável t, tem-se 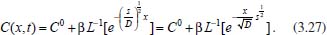 Esta transformada inversa não aparece com muita frequência nas Tabelas, porém, quando encontrada é usualmente apresentada na forma 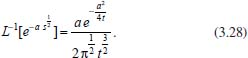 Considerando 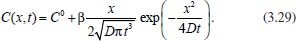 Utilizando-se o software Mathematica® para calcular esta transformada inversa, o resultado é obtido diretamente fazendo: InverseLaplaceTransform[Exp[-x*Sqrt[s/D]], s, t], cujo retorno é Observa-se que valor de β depende de outra condição de contorno definida pela técnica eletroquímica utilizada. Resolução 2 Outra maneira de resolver o problema apresentado em (3.6) é por meio de uma mudança de variável que possibilita trabalhar com a equação diferencial parcial na forma de uma equação diferencial ordinária linear homogênea de fácil solução. Seja, então,  a mudança que representa uma perturbação produzida na concentração inicial do sistema. Assim, C(x,t) = C0 -C1(x,t) e, derivando ambos os lados em relação à t obtém-se: 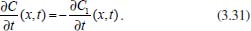 Por outro lado tomando a segunda derivada em relação à x tem-se: 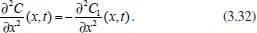 Substituindo (3.31) e (3.32) na equação (3.6), a mesma torna-se: 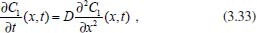 que é a equação de difusão conhecida, porém, as condições inicial e de contorno para C1 tornam-se, respectivamente, C1(x,0) e Aplicando a transformada de Laplace na equação (3.33) em relação à variável t e utilizando suas propriedades de derivadas obtém-se 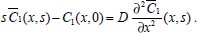 Como C1(x,0) = 0 segue que 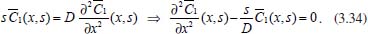 Fixando momentaneamente a variável s pode-se considerar a equação (3.34) como dependente apenas da variável x e, assim, obter uma equação diferencial ordinária de segunda ordem linear homogênea dada por  Para resolver tal equação deve-se supor que suas soluções sejam do tipo  Logo, a solução geral da equação (3.35) é dada por 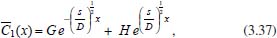 em que as constantes G e H devem ser obtidas a partir das condições de contorno. Como está sendo considerada apenas a condição semi-infinita 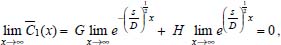 o que ocorre somente quando H = 0. Consequentemente, a solução é dada por 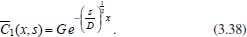 Como C(x,t)=C0 - C1(x,t), segue que 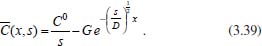 Aplicando a transformada inversa em relação à s obtém-se a expressão da concentração, ou seja, 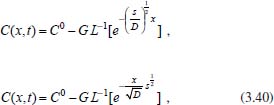 que é igual à solução encontrada em (3.27), onde G = -β, cuja determinação depende de uma segunda condição de contorno, dada pela técnica eletroquímica. Observa-se que a técnica define a forma de perturbação de potencial, corrente ou carga, o que determina, por exemplo, qual dos casos especiais da equação de Butler-Volmer será utilizado e isso possibilita encontrar os valores de β ou G. Aqui somente se fará referência a processos de eletrodo com transferência de carga reversível em solução e sem qualquer complicação causada por adsorção, reação química acoplada, formação de nova fase etc. Isso significa que a relação potencial - concentração será dada pela equação de Nernst. Por exemplo, no caso da cronoamperometria aplica-se uma perturbação de potencial deslocando-o instantaneamente de um valor onde não haja corrente faradáica (reação de oxidação ou redução) para valores em que ocorre a reação de interesse. Neste caso é possível obter uma expressão para a corrente em função do tempo e uma equação para o perfil de concentração da espécie reagente ou produto, em função do tempo e da distância da superfície do eletrodo. Ainda, se fixarmos o potencial numa condição em que a concentração da espécie eletroativa na superfície do eletrodo é nula, resulta na equação de Cottrell, com a qual é possível determinar, por exemplo, o coeficiente de difusão da espécie eletroativa. Se a técnica for a cronopotenciometria, aplica-se uma corrente constante e mede-se a variação do potencial em função tempo. Esta corrente constante determina um tempo para que a concentração na superfície do eletrodo seja nula, o que permite calcular o tempo de transição. Com a curva potencial-tempo e com o tempo de transição é possível também obter o potencial formal e o coeficiente de difusão do sistema em estudo. Para as técnicas potenciodinâmicas, a forma de variação do potencial com o tempo deverá ser considerada na resolução da equação, como será visto em detalhes num artigo em preparação. Para dar um exemplo simples da resolução das equações de difusão incluindo a técnica, será considerada a cronopotenciometria para um processo reversível de transferência de carga em solução, sem qualquer complicação cinética. Exemplo: cronopotenciometria Nesta técnica a corrente é a quantidade controlada e, portanto, o fluxo é dado pela equação 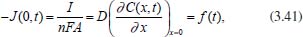 ou seja, a condição de contorno na superfície do eletrodo é dada por 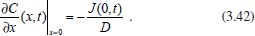 Admitindo-se que o fluxo na superfície do eletrodo seja dado por J(0,t) = 1 mol cm-2 s-1, que corresponde a uma densidade de corrente constante de 1 A cm-2, tem-se 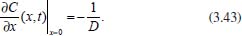 Neste caso, é mais fácil utilizar esta condição de contorno na equação (3.26) ou, de modo equivalente, na equação (3.39), pois derivando, por exemplo, a equação (3.26) em relação à x tem-se 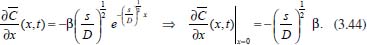 Por outro lado, aplicando a transformada de Laplace em relação a t na equação (3.43), tem-se 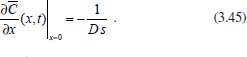 Logo, de (3.44) e (3.45) segue que 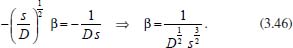 Substituindo em (3.26) tem-se 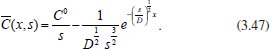 Utilizando uma tabela ou um software para encontrar as transformadas inversas do lado direito da expressão acima obtém-se 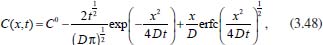 em que erfc é a função erro complementar, dada por erfc(x) = 1 - erf(x), onde erf é chamada função erro. Coordenadas esféricas A equação de difusão em coordenadas esféricas é dada por 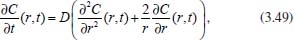 em que C é a concentração da espécie que se movimenta na direção radial, no sentido de se aproximar da superfície do eletrodo esférico de raio r. Considerando que na equação acima r representa a distância radial das moléculas ou íons até a origem da esfera, quando se considera um eletrodo de raio r0, a distância destas moléculas até a superfície do eletrodo é dada por r - r0, ou seja, na superfície do eletrodo tem-se r = r0. O método utilizado na Resolução 1 da seção anterior não é viável neste caso, pois o produto presente no lado direito da equação torna o cálculo da transformada de Laplace muito complexo. Assim, a resolução da equação será feita seguindo o método utilizado na Resolução 2 da seção anterior, ou seja, a partir da introdução de uma nova variável, que representa uma perturbação na concentração inicial da espécie, neste caso, definida adequadamente por 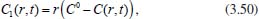 cuja derivada em relação à variável t é dada por: 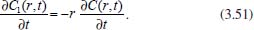 Por outro lado, as derivadas de primeira e segunda ordem em relação à r são dadas por  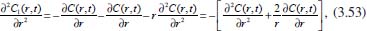 e da equação (3.50) tem-se 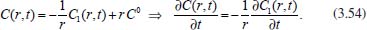 Assim, substituindo (3.53) e (3.54) na equação (3.49) tem-se  Portanto, a mudança de variável proposta em (3.50) transformou a equação diferencial (3.49) na equação de difusão resolvida no caso de coordenadas retangulares. Assim, utilizando o mesmo procedimento de resolução chega-se a  em que, neste caso, r = 0 indica a condição de contorno na superfície do eletrodo. Porém, como no caso de eletrodos esféricos a condição de contorno na superfície do eletrodo é dada quando r = r0, para que esta condição seja considerada, a solução da equação diferencial (3.55) deve, então, ser dada por 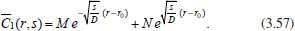 Como  Por outro lado, aplicando a transformada de Laplace em relação à variável t na expressão de C1 dada por (3.50) tem-se 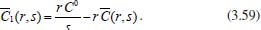 Assim, das equações (3.58) e (3.59) obtém-se 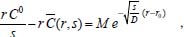 ou seja, 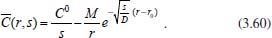 Análogo ao caso anterior, a constante M depende da técnica eletroquímica e aplicando a transformada inversa de Laplace em relação à s obtém-se a expressão da concentração da espécie em um tempo t qualquer e a uma distância r da superfície do eletrodo, que será dada por  ou 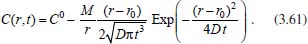 Coordenadas cilíndricas A equação de difusão em coordenadas cilíndricas é dada por 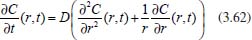 em que, análogo ao caso esférico, C é a concentração da espécie que se movimenta na direção radial, no sentido de se aproximar da superfície do eletrodo cilíndrico de raio r0. Assim, r - r0 é a distância do íon ou da molécula à superfície do eletrodo. Também análogo ao caso esférico, a equação será resolvida utilizando a variável r, já que uma mudança de variável do tipo z = r - r0 leva à mesma solução. Os métodos matemáticos empregados na resolução da equação de difusão com coordenadas retangulares ou esféricas não solucionam a equação (3.62), que será então resolvida pelo método de separação de variáveis.14,15 Tal método supõe que a função C(r,t) possa ser escrita como o produto de duas funções, sendo que uma depende apenas de r e a outra apenas de t, da seguinte forma: 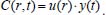 Derivando parcialmente C em relação à t e à r tem-se 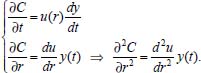 Substituindo na equação (3.62) tem-se 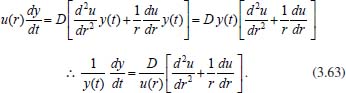 Como o lado esquerdo da equação acima só depende de t e o lado direito só depende de r, a igualdade só será satisfeita para todo t e todo r se os dois lados da equação forem iguais a uma constante k. Assim têm-se duas equações diferenciais ordinárias: 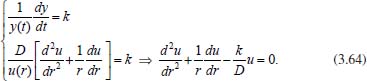 A primeira equação de (3.64) é simples e de fácil resolução e a segunda é uma equação de Bessel de ordem zero.18,19 Por conveniência toma-se  Para resolver a primeira equação basta integrar os dois lados em relação à variável t e a solução será dada por  em que M é a constante de integração. O método utilizado para resolver a equação de Bessel foi proposto por Frobenius e consiste em supor que a solução seja dada por uma série de potências do tipo 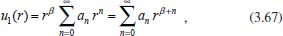 em que a0 ≠ 0, β e an são constantes que devem ser determinadas e r é não negativo (r > 0). Como se supõe que u1 seja uma solução da segunda equação em (3.65), deve satisfazê-la e, para isso, suas derivadas devem ser calculadas. Assim tem-se 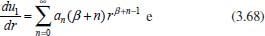  Substituindo na segunda equação de (3.65) tem-se 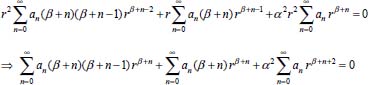 A expressão acima pode ser escrita como 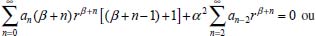 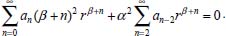 Expandindo o primeiro termo do somatório e rearranjando os termos a fim de utilizar um único somatório tem-se a equação 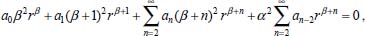 que pode ser escrita como 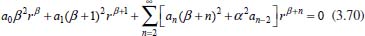 Como esta equação deve ser satisfeita para todo r > 0, o coeficiente de cada potência de r deve ser zero, ou seja: 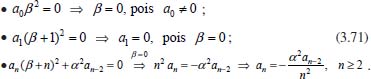 Uma simulação com vários valores de n na última expressão de (3.71) possibilita obter os coeficientes an em termos de a0, como se pode ver abaixo 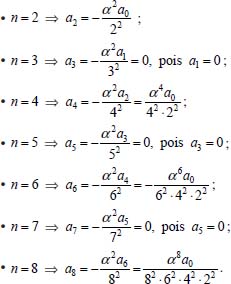 Observa-se que, como a1 = 0, tem-se an = 0 para todo n ímpar, enquanto que os denominadores dos termos com n par podem ser rearranjados da seguinte forma: 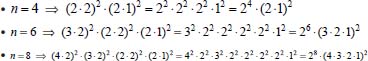 Portanto, o termo geral da série, an, pode ser escrito como 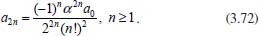 Assim, substituindo os valores obtidos para β e an na expressão de u1(r), dada por (3.67), obtém-se 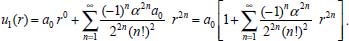 Como a expressão acima é uma solução para a equação em (3.65) independente do valor de a0, pode-se tomar a0 = 1 e, portanto, a solução procurada é usualmente dada por 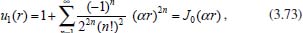 em que 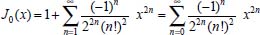 é conhecida como função de Bessel de primeira espécie de ordem zero. Segundo o método de Frobenius, quando β = 0 é possível encontrar uma segunda solução para a equação de Bessel dada por 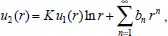 em que K é uma constante, u1(r) é a solução encontrada anteriormente e bn são coeficientes que devem ser determinados. Assim, a solução geral seria dada por 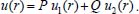 Porém, para o estudo em questão, esta segunda solução não é de interesse, pois quando r → 0, tem-se ln r → -∞ e, consequentemente, u2(r) → -∞. Como C(r,t) deve ser finita para todo r, Q deve ser zero e, portanto, a solução u2 não precisa ser determinada. Assim, retornando à equação (3.62), concluímos que sua solução é dada por 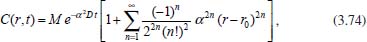 em que
CONCLUSÕES Neste trabalho foi detalhado o tratamento matemático dos processos de difusão linear semi-infinita para eletrodos planos, cilíndricos e esféricos. Estabeleceu-se um roteiro para a solução geral da equação de difusão, podendo-se chegar à solução final, uma vez estabelecidas as condições de contorno que são dependentes da técnica eletroquímica. Isso porque a técnica define a forma de perturbação de potencial, corrente ou carga, o que determina, por exemplo, qual dos casos especiais da equação de Butler-Volmer será utilizado. A forma especial da equação de Butler-Volmer para processos reversíveis é a equação de Nernst, enquanto que para processos irreversíveis assume a forma da equação de Tafel. Outra condição importante dependente da técnica é a magnitude da perturbação que leva a uma concentração nula da espécie eletroativa na superfície do eletrodo, o que permite obter equações mais simples, facilitando a determinação de parâmetros como o coeficiente de difusão e o potencial formal de eletrodo. A metodologia empregada na dedução e solução das equações de difusão permite o entendimento dos processos simples e oferece ferramentas matemáticas para desenvolver sistemas de maior complexidade.
AGRADECIMENTOS Os autores agradecem ao estudante Diego Batista Felix, do Curso de Licenciatura em Química, e ao Dr. Adriano Heleno Akita pela colaboração na confecção das figuras presentes no trabalho. O autor Assis Vicente Benedetti agradece ao CNPq (proc. 305890/2010-7).
REFERÊNCIAS 1. Wright, M. R.; An Introduction to Aqueous Electrolyte Solutions, John Wiley & Sons, Ltd.: England, 2007. 2. Fawcett, W. R.; Liquids, Solutions, and Interfaces - From Classical Macroscopic Descriptions to Modern Microscopic Details, Oxford University Press, Inc.: England, 2004. 3. Bockris, J. O'M.; Reddy, A. K. N.; Modern Electrochemistry volume 1. Ionics, 2nd ed., Plenum Press: New York, 1998. 4. Bockris, J. O'M.; Reddy, A. K. N.; Modern Electrochemistry, volume 1, 1st ed., Plenum Press: New York , 1970. 5. Robinson, R. A.; Stokes, R. H.; Electrolyte Solutions, 2nd ed., Dover Publications, Inc.: New York, 2002. 6. Oldham, K. B.; Myland, J. C.; Fundamentals of Electrochemical Science, Academic Press, Inc.: New York, 1994. 7. Hamann, C. H.; Hamnett, A.; Vielstich, W.; Electrochemistry, Wiley-VCH: New York, 1998. 8. Wright, M. R.; An Introduction to Aqueous Electrolyte Solutions, John Wiley & Sons, Ltd.: England , 2007. 9. Young, L.; Anodic Oxide Films, Academic Press: New York, 1961. 10. Bard, A. J.; Faulkner, L. R.; Electrochemical Methods - Fundamentals and Applications, John Wiley & Sons: New York, 1980. 11. Compton, R. G.; Banks, C. E.; Understanding Voltammetry, World Scientific Publishing Co. Pte. Ltd.: London, 2009 (reprinted). 12. Agostinho, S. M. L.; Villamil, R. F. V.; Agostinho Neto, A.; Aranha, H.; Quim. Nova, 2004, 27, 813. DOI: http://dx.doi.org/10.1590/S0100-40422004000500022 13. Levich, V. G.; Physicochemical Hydrodynamics, Prentice-Hall, Englewood Cliffs, N.J., 1962. 14. Bockris, J. O'M.; Reddy, A. K. N.; Modern Electrochemistry, volume 2, 1st ed., Plenum Press: New York , 1970. 15. Trinh, T. T.; Vlugt, T. J. H.; May-Britt Hägg, M-B.; Bedeaux, D.; Kjelstrup, S.; Front. Chem. 2013, 1 (dec), a38. 16. Lee, S. H.; Bull. Korean Chem. Soc. 2013, 34, 3800. DOI: http://dx.doi.org/10.5012/bkcs.2013.34.1.133 17. Stewart, J.; Cálculo - Volumes 1 e 2, 7th ed., Cengage Learning: São Paulo, 2013. 18. Boyce, W. E.; DiPrima, R. C.; Equações Diferenciais Elementares e Problemas de Valores de Contorno, 9th ed., LTC: Rio de Janeiro, 2010. 19. Oliveira, E. C.; Tygel, M.; Métodos Matemáticos para Engenharia, 2nd ed., SBM - Textos Universitários: Rio de Janeiro, 2010. 20. http://www.wolfram.com/mathematica, acessado em Outubro de 2015. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






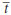 para representar esta situação, indicando que a concentração varia apenas com a posição em que a espécie se encontra em cada momento, não com o tempo.
para representar esta situação, indicando que a concentração varia apenas com a posição em que a espécie se encontra em cada momento, não com o tempo.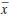 , que será aqui chamado de plano de transição em
, que será aqui chamado de plano de transição em  . Consequentemente, a equação de difusão planar, cujo fluxo ocorre na direção perpendicular ao plano, ou seja, perpendicular à superfície de um eletrodo do tipo disco plano, é dada por
. Consequentemente, a equação de difusão planar, cujo fluxo ocorre na direção perpendicular ao plano, ou seja, perpendicular à superfície de um eletrodo do tipo disco plano, é dada por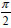 . Neste caso as derivadas parciais acima se tornam:
. Neste caso as derivadas parciais acima se tornam: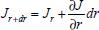 e, portanto,
e, portanto,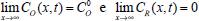 para qualquer t. No caso de células cujas paredes estão mais próximas da superfície do eletrodo do que o tamanho da espessura da camada de difusão (por exemplo, células de camada delgada), a perturbação na concentração alcança todo o volume da solução. Nestes casos, se a parede da célula está a uma distância ℓ do eletrodo, tem-se x → ℓ e não x → ∞.
para qualquer t. No caso de células cujas paredes estão mais próximas da superfície do eletrodo do que o tamanho da espessura da camada de difusão (por exemplo, células de camada delgada), a perturbação na concentração alcança todo o volume da solução. Nestes casos, se a parede da célula está a uma distância ℓ do eletrodo, tem-se x → ℓ e não x → ∞.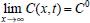 .
.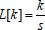 .
.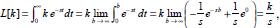 , uma vez que
, uma vez que 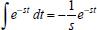 e o Teorema Fundamental do Cálculo afirma que se f é uma função contínua em um intervalo [a, b] e se
e o Teorema Fundamental do Cálculo afirma que se f é uma função contínua em um intervalo [a, b] e se 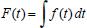 , então
, então 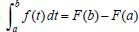 .
.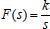 , então
, então 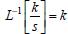 .
.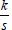 . Para calcular a transformada inversa, utiliza-se: InverseLaplaceTransform[k/s, s, t], cujo retorno será k.
. Para calcular a transformada inversa, utiliza-se: InverseLaplaceTransform[k/s, s, t], cujo retorno será k.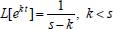 .
.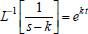 .
.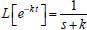 e, portanto,
e, portanto, 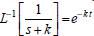 .
.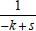 . Por outro lado, para calcular a transformada inversa faz-se: InverseLaplaceTransform[1/(s - k), s, t] e o retorno será: ekt.
. Por outro lado, para calcular a transformada inversa faz-se: InverseLaplaceTransform[1/(s - k), s, t] e o retorno será: ekt.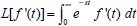 . O cálculo desta integral pode ser feito pelo método de integração por partes, que consiste na aplicação da seguinte fórmula:
. O cálculo desta integral pode ser feito pelo método de integração por partes, que consiste na aplicação da seguinte fórmula:  , em que, neste caso, considera-se u = e-st e dv = f'(t)dt. Calculando a diferencial de u e integrando dv obtém-se du = -se-stdt e v = f(t). Logo,
, em que, neste caso, considera-se u = e-st e dv = f'(t)dt. Calculando a diferencial de u e integrando dv obtém-se du = -se-stdt e v = f(t). Logo,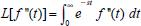 . Pelo método de integração por partes, considerando-se u = e-st e dv = f "(t)dt e, consequentemente, du = -se-stdt e v = f '(t), tem-se
. Pelo método de integração por partes, considerando-se u = e-st e dv = f "(t)dt e, consequentemente, du = -se-stdt e v = f '(t), tem-se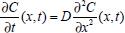 , aplica-se a transformada de Laplace em relação à variável t na equação e, considerando as propriedades P2 e P5 acima, tem-se:
, aplica-se a transformada de Laplace em relação à variável t na equação e, considerando as propriedades P2 e P5 acima, tem-se: (x,s) representa a transformada de Laplace de C em relação à variável t, s é a variável relacionada a t pela transformada e o coeficiente de difusão D é considerado constante. Utilizando a condição inicial C(x,0) = C0, a equação (3.14) torna-se
(x,s) representa a transformada de Laplace de C em relação à variável t, s é a variável relacionada a t pela transformada e o coeficiente de difusão D é considerado constante. Utilizando a condição inicial C(x,0) = C0, a equação (3.14) torna-se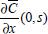 dependem de outras condições de contorno, referindo-se à transformada da concentração e à transformada da derivada da concentração, respectivamente, ambas na superfície do eletrodo. Portanto, essas condições de contorno serão definidas pela técnica eletroquímica. Por isso pode-se, neste instante, chamá-las de M e N, respectivamente, fazendo com que a equação (3.17) se torne:
dependem de outras condições de contorno, referindo-se à transformada da concentração e à transformada da derivada da concentração, respectivamente, ambas na superfície do eletrodo. Portanto, essas condições de contorno serão definidas pela técnica eletroquímica. Por isso pode-se, neste instante, chamá-las de M e N, respectivamente, fazendo com que a equação (3.17) se torne: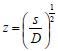 tem-se:
tem-se: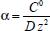 e substituindo este valor na primeira equação tem-se o seguinte sistema para ser resolvido, nas incógnitas β e γ:
e substituindo este valor na primeira equação tem-se o seguinte sistema para ser resolvido, nas incógnitas β e γ: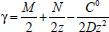 e
e 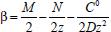 Portanto tem-se:
Portanto tem-se: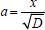 tem-se
tem-se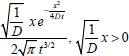 , que após uma pequena manipulação algébrica torna-se igual à expressão de (3.29).
, que após uma pequena manipulação algébrica torna-se igual à expressão de (3.29).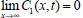 .
.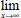 C(x,t)=0,
C(x,t)=0,  t, segue que
t, segue que 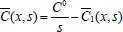 , ou seja,
, ou seja,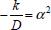 e multiplica-se a segunda equação por r2 a fim de que adquira o aspecto clássico da equação de Bessel. Com isso as equações a serem resolvidas são:
e multiplica-se a segunda equação por r2 a fim de que adquira o aspecto clássico da equação de Bessel. Com isso as equações a serem resolvidas são: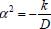 e as constantes k e M serão determinadas de acordo com as condições iniciais e de contorno.
e as constantes k e M serão determinadas de acordo com as condições iniciais e de contorno.