Educação
|
|
| Construção da curva de equilíbrio líquido-vapor usando uma equação de estado cúbica: uso do excel no ensino de físico-química Building the liquid-vapour equilibrium curve through a cubic equation of state: use of excel for teaching physical-chemistry |
|
Josefredo R. Pliego Jr.*
Departamento de Ciências Naturais, Universidade Federal de São João del Rei, 36301-160 São João del-Rei-MG, Brasil Recebido em 01/09/2015 *e-mail: pliego@ufsj.edu.br Cubic equations of state are able to predict the liquid-vapour coexistence curve of volatile substances. However, this property is rarely used to teach Physical Chemistry because solving the resulting equations require numerical technics and many mathematical operations. In this report was shown how the interactive method for finding the root of an equation can be applied with the Excel to determine the vapour pressure of the liquid, as well as the molar volumes of the gas and liquid phases. The generated points was used to build the curves of phase transition in the P × V and P × T graphics. INTRODUÇÃO Um dos primeiros tópicos de estudo de físico-química na graduação em química é sobre gases ideais e desvios da idealidade.1-3 A análise do comportamento de gases reais permite a discussão do diagrama de equilíbrio líquido-vapor e do ponto crítico, bem como leva a percepção do efeito das forças intermoleculares nas propriedades dos materiais.4,5 A famosa equação de van der Waals (1) introduz o efeito destas forças, uma vez que o parâmetro b está associado ao volume molecular (forças repulsivas) e a está associado a forças atrativas. A variável é o volume molar.  Como é bem conhecido, os parâmetros a e b estão relacionados à temperatura e pressão críticas dos gases, sendo possível a construção da curva de equilíbrio líquido-vapor com equações cúbicas de estado tais como a equação de van der Waals (VDW). De fato, sabe-se que abaixo da temperatura crítica, estas equações oscilam na região de condensação, como mostrado na Figura 1. Para determinar qual o volume molar do líquido e do vapor em equilíbrio a uma temperatura fixa, bem como qual a pressão correspondente (que também é a pressão de vapor do líquido), é necessário utilizar a regra das áreas de Maxwell.4 Em termos geométricos, esta regra diz que a curva de condensação é obtida traçando uma reta que tornam as áreas I e II equivalentes (Figura 1). A pressão correspondente é a pressão de vapor, e os volumes determinados pelo cruzamento da reta com a curva do gás correspondem aos volumes das fases líquida e gás. Os pontos correspondentes a estes volumes para cada temperatura geram a curva de equilíbrio líquido-vapor (Figura 1).
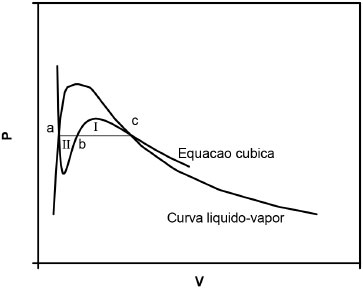 Figura 1. Comportamento de uma equação cúbica de estado, mostrando oscilação da função P( 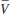 ) na região de condensação, sendo que a igualdade das áreas I e II determina os pontos que geram a curva de equilíbrio líquido-vapor ) na região de condensação, sendo que a igualdade das áreas I e II determina os pontos que geram a curva de equilíbrio líquido-vapor
Apesar da possibilidade de utilizar-se as equações de estado cúbicas para obter a curva de equilíbrio líquido-vapor, o que seria de grande valor no ensino deste tópico de Físico-Química, isso geralmente não é feito nos cursos de Físico-Química. O desafio reside na dificuldade do problema matemático envolvido, que seria extremamente trabalhoso, além da grande chance de erro devido à realização de várias operações matemáticas. Entretanto, nos dias atuais a maioria dos estudantes têm acesso a computadores (desktop ou notebooks). Com o uso de planilhas, é possível resolver uma série de problemas matemáticos que aparecem em Físico-Química com relativa facilidade. Tais problemas de maior complexidade poderiam inclusive fazer parte da avaliação de estudantes através de trabalhos em grupo. O objetivo deste artigo é mostrar como uma planilha como o Excel pode ser utilizada para obter a curva de equilíbrio líquido-vapor aplicando equações de estado cúbicas. A abordagem será discutida passo-a-passo, mostrando o resultado final e uma comparação com dados experimentais. Um arquivo xlsx é disponibilizado como material suplementar, o qual pode ser utilizado para executar os cálculos, acompanhando a exposição da solução do problema.
A REGRA DAS ÁREAS DE MAXWELL Será discutida aqui a derivação da regra das áreas, de forma a ficar claro seu embasamento na termodinâmica. O ponto de partida é considerar que na Figura 1, o ponto a é o líquido e c o gás. Na transição líquido-gás, as duas fases estão em equilíbrio, de forma que os potenciais químicos são iguais:  Como o sistema é de um componente apenas, podemos escrever a igualdade acima em termos de energia livre de Gibbs, ou ainda, energia de Helmholtz mais o termo PV:  o qual rearranjando, fica:  Uma vez que a temperatura é a mesma (isoterma), podemos usar a relação termodinâmica da variação de A com V e escrever A do gás em termos do A do líquido: 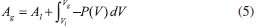 Substituindo (6) em (5), obtemos: 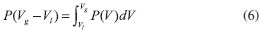 Na equação (6), a integral é feita ao longo da isoterma, sendo P(V) a equação de estado do gás. À esquerda temos P, a pressão sobre as duas fases em equilíbrio. Observando a Figura 1, vemos que a área sob a curva real de transição de fase (a reta ligando a e c) está à esquerda da equação (6), enquanto a área sub a curva da equação de estado é a integral do lado direito da equação (6). Como a reta corta a curva e as áreas sob a reta e sob a curva são iguais, fica claro que a área da região I deve ser igual a área da região II. Ao aplicar a regra das áreas para o gás de van der Waals, obtemos: 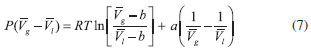 sendo que a equação já foi escrita com o uso de volume molar.
EQUAÇÃO DE ESTADO DE REDLICH-KWONG A equação (6) pode ser utilizada para qualquer equação de estado cúbica. Embora a equação de van der Waals é histórica e amplamente discutida em livros de Físico-Química, não é muito acurada. É interessante utilizar uma equação de estado que reproduza bem os dados experimentais, pois isso leva a uma melhor apreciação da mesma. Por este motivo, escolheu-se utilizar a equação de Redlich-Kwong (8) para ilustrar a metodologia, por ser mais a acurada do que a equação de van der Waals, mas ainda ser uma equação cúbica relativamente simples.6-8 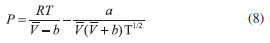 Os parâmetros a e b desta equação estão relacionados a temperatura e pressão crítica pelas equações (9) e (10): 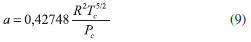  Utilizou-se o CO2 como exemplo, o qual tem os seguintes valores dos parâmetros da equação: a = 63,752 atm L2 mol-2 K1/2 e b = 0,029677 L/mol (valores da referência 5)
DETERMINAÇÃO DOS VOLUMES DAS FASES GASOSA E LÍQUIDA O leitor deve notar que não tem como sabermos a priori qual é a pressão correspondente ao equilíbrio líquido-vapor em uma isoterma, ou seja, a reta da Figura 1. Isso será feito em etapas, aplicando a regra das áreas de Maxwell. Mas o primeiro passo é determinar qual o volume das fases líquido e gás em uma isoterma, quando fixamos a pressão. Para este fim, utilizaremos o método iterativo. A abordagem consiste de reescrever a equação (8) na seguinte forma: 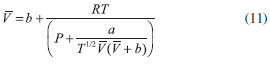 No procedimento, introduzimos um valor inicial para o volume molar na equação (11), e obtemos o volume molar da primeira iteração, mais próximo da solução. Com este novo volume, repetimos novamente o procedimento e fazemos assim de forma sucessiva até o valor do volume convergir. Para ficar mais claro, podemos colocar a equação (11) na forma: 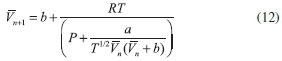 ou seja, usamos um valor de
Na planilha fornecida neste trabalho, o leitor pode verificar estes cálculos e testar novos valores de T e P.
DETERMINAÇÃO DA PRESSÃO DE CONDENSAÇÃO NA ISOTERMA Uma vez definida a temperatura (isoterma), temos que determinar em qual pressão o gás começa a se condensar. Pela regra das áreas de Maxwell (equação 6) aplicada a equação de Redlich-Kwong, temos: 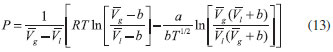 O problema matemático torna-se o seguinte: a pressão que leva aos valores de A Figura 2 mostra a operação na planilha. É necessário alterar somente a primeira linha de a, b, T, P,
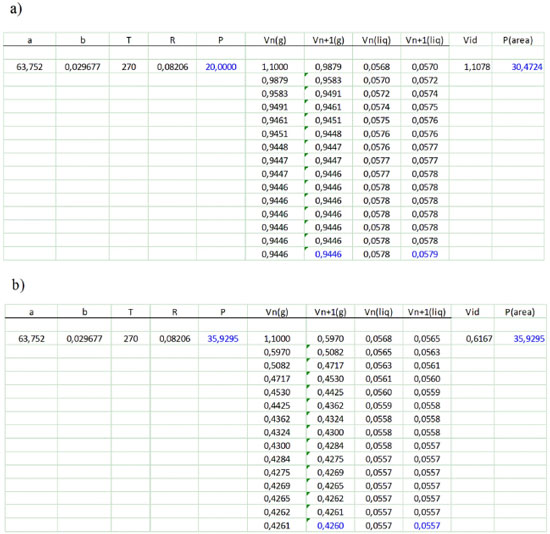 Figura 2. Operações na planilha: a) Valor inicial da pressão (P) e pressão obtida (P(área)). b) Convergência do processo iterativo. A temperatura de 270 K, a pressão de condensação é 35,9295 atm e os volumes molares obtidos são: fase gás a 0,4260 L e fase líquida 0,0557 L
Com base na discussão acima, podemos gerar os pontos da curva de equilíbrio líquido-vapor para cada temperatura diferente. Estes pontos podem ser agrupados para gerar o gráfico de ×
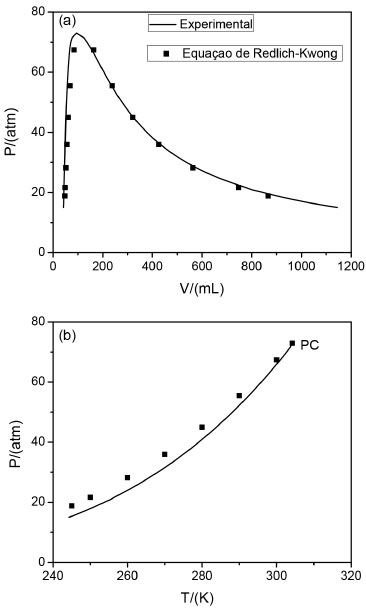 Figura 3. Curva de equilíbrio líquido-vapor para o CO2 no gráfico P × 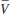 e curva da transição de fase líquido-vapor no gráfico P × T. Dados experimentais retirados da ref. 9 e curva da transição de fase líquido-vapor no gráfico P × T. Dados experimentais retirados da ref. 9
EXPERIÊNCIA EM SALA DE AULA Uma parte do problema aqui apresentado foi proposto como trabalho em grupo, a ser feito e casa, para alunos da disciplina de Físico-Química I na Universidade Federal de São João del-Rei. Foram utilizados os gases dióxido de carbono, etano, propano e butano como sistemas de estudo para diferentes grupos. Embora o trabalho tenha sido executado fora da sala de aula, houve constante interação com o professor conforme as dúvidas e resultados surgiam. As questões apresentadas foram as seguintes (todas usando a equação de Redlich-Kwong):
Os alunos tiveram várias dificuldades para resolver as questões propostas, algumas delas bem básicas. Um grupo traçou o gráfico de P versus De um modo geral, minha percepção foi que houve um importante aumento da compreensão do tópico pelos estudantes. A elaboração dos gráficos no Excel, a resolução da equação cúbica pelo método iterativo e a estimativa da região de transição (mesmo que aproximada) permitiu aos estudantes uma visão bem mais clara da equação de estado cúbica e da região de transição. Tal aprofundamento não me parece ocorrer para a maioria dos estudantes com o conteúdo padrão discutido em livros-texto de Físico-Química.
CONCLUSÃO Foi mostrado como o Excel pode ser utilizado com uma equação de estado Cúbica (Redlich-Kwong) na obtenção da curva de equilíbrio líquido-vapor para o CO2. O procedimento pode ser aplicado para outras equações cúbicas, bem como demais sistemas. Devo destacar 3 aspectos importantes desta abordagem no ensino de Físico-Química:
O problema discutido neste artigo é adequado para execução como trabalhos em grupo e uma parte da metodologia apresentada já foi testada em sala de aula.
MATERIAL SUPLEMENTAR O arquivo Excel usado para realizar os cálculos neste trabalho está disponível em http://quimicanova.sbq.org.br, na forma de arquivo xlsx, com acesso livre.
AGRADECIMENTOS O autor agradece o suporte das agências CNPq, FAPEMIG e CAPES.
REFERÊNCIAS 1. Castellan, G. W.; Physical Chemistry, 3ª ed., Addison Wesley, 1983. 2. Atkins, P.; de Paula, J.; Fisico-Quimica, 8ª ed., Livros Tecnicos e Cientificos: Rio de Janeiro, 2008. 3. Ball, D. W.; Físico-Química; Pioneira Thomson Learning: São Paulo, 2005. 4. Levine, I. N.; Physical Chemistry, 6ª ed., McGraw Hill: Singapore, 2009. 5. McQuarrie, D. A.; Simon, J. D.; Physical Chemistry: A Molecular Approach, University Science Books: Sausalito, 1997. 6. Valderrama, J. O.; Ind. Eng. Chem. Res. 2003, 42, 1603. DOI: http://dx.doi.org/10.1021/ie020447b 7. Tsonopoulos, C.; Heidman, J. L.; Fluid Phase Equilibr. 1985, 24, 1. DOI: http://dx.doi.org/10.1016/0378-3812(85)87034-5 8. Redlich, O.; Kwong, J. N. S.; Chem. Rev. 1949, 44, 233. DOI: http://dx.doi.org/10.1021/cr60137a013 PMID: 18125401 9. CRC Handbook of Chemistry and Physics; Hodgman, C. D., ed.; 44ª ed., CRC Press: Boca Raton, 1962. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






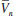 para gerar
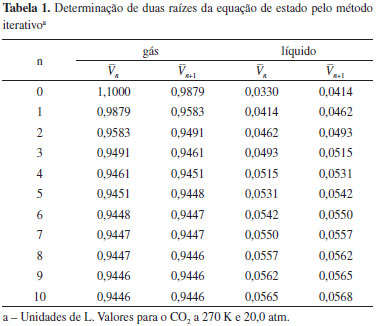
para gerar 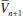 . No caso do volume da fase gás, uma boa estimativa inicial seria o volume do gás ideal. Já para obter o volume da fase líquida, uma possibilidade é utilizar um volume 10% maior do que b. Como exemplo, a Tabela 1 abaixo mostra a determinação dos volumes (molares) das duas fases a 270 K e 20 atm usando a planilha. Observe que o volume do gás já convergiu, enquanto que o líquido ainda precisa de mais iterações. Para isso, pode-se pegar o último valor do volume do líquido (0,0568 L) e utilizar como input novamente. Ao fazer isso, o volume depois de 10 iterações é 0,0578 L, estando praticamente convergido. É muito importante observar claramente a convergência. Em alguns casos ela é bem lenta, e ainda ambos podem convergir para um mesmo valor de volume, indicando neste caso que está em uma região de uma raiz apenas.
. No caso do volume da fase gás, uma boa estimativa inicial seria o volume do gás ideal. Já para obter o volume da fase líquida, uma possibilidade é utilizar um volume 10% maior do que b. Como exemplo, a Tabela 1 abaixo mostra a determinação dos volumes (molares) das duas fases a 270 K e 20 atm usando a planilha. Observe que o volume do gás já convergiu, enquanto que o líquido ainda precisa de mais iterações. Para isso, pode-se pegar o último valor do volume do líquido (0,0568 L) e utilizar como input novamente. Ao fazer isso, o volume depois de 10 iterações é 0,0578 L, estando praticamente convergido. É muito importante observar claramente a convergência. Em alguns casos ela é bem lenta, e ainda ambos podem convergir para um mesmo valor de volume, indicando neste caso que está em uma região de uma raiz apenas.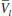 e
e 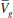 , as quais satisfazem a equação de estado (8), deve ser a mesma que se obtém na expressão (13). Portanto, são 3 equações com 3 incógnitas (na verdade, duas raízes da mesma equação), sendo que não é possível resolvê-las analiticamente. Novamente, usaremos o método iterativo, agora resolvendo 3 equações simultaneamente. O procedimento é o seguinte: Estima-se um valor inicial da pressão, que pode ser feito via análise do gráfico P ×
, as quais satisfazem a equação de estado (8), deve ser a mesma que se obtém na expressão (13). Portanto, são 3 equações com 3 incógnitas (na verdade, duas raízes da mesma equação), sendo que não é possível resolvê-las analiticamente. Novamente, usaremos o método iterativo, agora resolvendo 3 equações simultaneamente. O procedimento é o seguinte: Estima-se um valor inicial da pressão, que pode ser feito via análise do gráfico P ×