Artigo
|
|
| Comparação entre funcionais de densidade no estudo de propriedades eletrônicas de derivados da artemisinina Comparison of density functional in the study of electronic properties of artemisinin derivatives |
|
Victor H. S. C. BatistaI; Ana C. GranatoII; Wagner F. D. AngelottiI,*
IDepartamento de Matemática Aplicada, Instituto de Ciências Tecnológicas e Exatas, Universidade Federal do Triângulo Mineiro, 38064-200 Uberaba - MG, Brasil Recebido em 02/09/2015 *e-mail: angelotti@icte.uftm.edu.br The present paper demonstrates the application of functional GGA hybrids, with long-range corrections, for the calculation of the electronic properties of artemisinin and two of its derivatives - artemether e artesunate. Due to the relatively large amount of data obtained, the statistical method of Principal Component Analysis was employed. The functionals of the WB97 family are observed to be the most appropriate for the determining of reactivity indexes, which are the principal descriptors that, probably, are associated with the antimalarial and anticancer properties of this group of molecules. In addition, it was also observed that all the functionals obtained satisfactorily describe the geometric properties of the studied. INTRODUÇÃO Discorrer sobre os aspectos da Mecânica Quântica e não conseguir aplicá-los a sistemas de interesse tecnológico/biológico, por exemplo, pode torná-la uma teoria exótica e, inicialmente, sem utilidade. A principal barreira é que a equação de Schrödinger1 que descreve tais sistemas não possui, a não ser para sistemas simples e bem específicos, solução analítica, sendo necessário recorrer a métodos aproximados de solução. Para o caso eletrônico da equação, o método de Hartree-Fock (HF)2,3 é um dos mais conhecidos. Inicialmente, o método HF resolvia numericamente sistemas atômicos ou moleculares com poucos elétrons, não sendo viável para sistemas maiores. Uma alternativa inicialmente proposta por Slater, e depois formalizada por Roothaan,4 foi expandir a parte espacial dos spin-orbitais moleculares em termos de um número finito de funções conhecidas, chamadas de funções de base,5 o que reduziu a solução das equações íntegro-diferenciais acopladas de HF a um problema de álgebra matricial conhecido como método HF-Roothan (HFR - Hartree-Fock-Roothaan).6,7 Várias funções de base podem ser usadas no método HFR para cálculos atômicos e moleculares. As funções tipo Slater (STFs - Slater Type Functions) foram utilizadas com sucesso em cálculos atômicos.8,9 Boys, em 1950, propôs o uso de funções tipo Gaussianas (GTFs - Gaussian Type Functions) em cálculos moleculares que possuem mais de um núcleo, facilitando a solução das integrais.10 Por não levar em conta a correlação eletrônica, os métodos HF são utilizados como ponto de partida em relação aos demais métodos ab initio como, por exemplo, os métodos de Interação de Configuração (CI - Configuration Interaction)11 e a Teoria de Perturbação de Muitos Corpos (MBPT - Many Body Perturbation Theory).12 Uma classe alternativa a estes métodos, baseada na densidade eletrônica e originada na década de 60, é a Teoria do Funcional de Densidade (DFT - Density Functional Theory).13-15 De forma geral, o tempo computacional para cálculos DFT é da mesma ordem de cálculos HF, permitindo, assim, que sistemas de porte médio a grande possam ser estudados e, além disso, incluem efeitos de correlação eletrônica, tornando-o um interessante e importante aliado na obtenção de propriedades eletrônicas de átomos, moléculas e sólidos em seu estado fundamental.4,13 No método DFT, a energia de um sistema eletrônico pode ser descrita em termos da densidade de probabilidade eletrônica total, ρ.16,17 Para um sistema de N elétrons, ρ De posse de métodos teóricos e computacionais capazes de descrever sistemas cada vez maiores, uma importante aplicação em que a Mecânica Quântica pode ser uma grande aliada é a descoberta de novos fármacos. Antes de serem colocados no mercado, novos medicamentos são exaustivamente testados, demandando bastante tempo para tal, pois é preciso considerar desde o trabalho "bruto" com estudos de plantas, por exemplo, no laboratório, separação do composto, até os testes clínicos. Tais estudos são caros e, muitas vezes, estes compostos são descartados, pois não possuem o efeito desejado ou possuem diversos efeitos colaterais. Uma possibilidade de diminuir o tempo e barateá-lo é fazer uso de estudos computacionais na tentativa de predizer diversas propriedades que desvendem os caminhos de reação, a ação biológica, dentre outras interações moleculares. Neste cenário, é um fato a dificuldade em predizer tratamentos para novas doenças ou, simplesmente, tratar de forma mais eficiente doenças bem conhecidas, e muitas vezes negligenciadas, tais como a malária. O problema mais crítico para o tratamento da malária é o desenvolvimento de resistência a compostos antimaláricos quinolínicos clássicos, tais como a cloroquina. A partir de um programa de descoberta de novos fármacos realizado por químicos chineses na década de 1970 (Projeto 523), forneceu-se um dos antimaláricos mais potentes e eficazes até hoje, a artemisinina. A artemisinina e seus derivados são eficazes não só contra linhagens multi-resistentes de P. falciparum, mas tem ampla especificidade contra o ciclo de vida do Plasmodium.22 Representando uma nova classe de agentes antimaláricos, a artemisinina (Figura 1) é uma lactona sesquiterpeno trioxano cuja ponte endoperóxido é essencial para a atividade antimalárica.
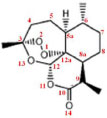 Figura 1. Estrutura química da artemisinina
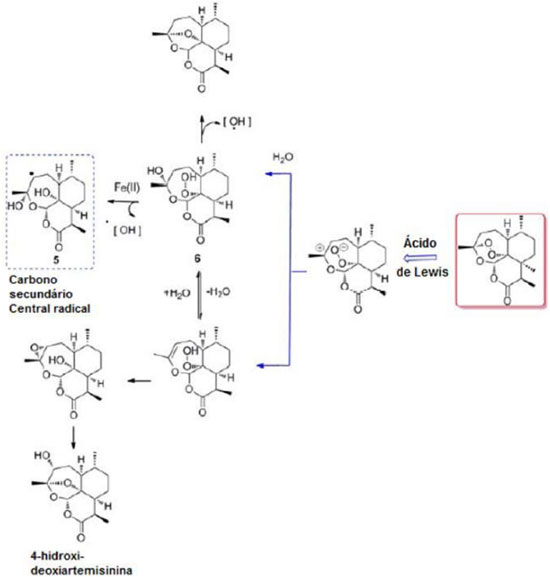
Um dos mecanismos de ação (Modelo Peróxido Aberto) sugere que a abertura do anel é impulsionada pela protonação do peróxido ou pela complexação do Fe2+ (Figura 2). Supõe-se que o ferro atue como ácido de Lewis para facilitar a forma iônica, ao invés de bioativação radicalar das artemisininas. Além disso, também se sugere que o oxigênio não peroxídico desempenha o papel de facilitar a abertura do anel peróxido para gerar o hidroperóxido aberto. O átomo de oxigênio fornece a estabilização da carga positiva e, de acordo com a Teoria do Estado de Transição, reduz a energia necessária para abertura do anel. A clivagem heterolítica da ponte endoperóxido e a subsequente captura de água conduzem à formação de um hidroperóxido insaturado 6, capaz de alterar irreversivelmente resíduos de proteínas por oxidação direta. A degradação do hidroperóxido 6 produz um radical hidroxila, uma espécie que pode subsequentemente oxidar os resíduos de aminoácidos-alvo. Para apoiar esta teoria, a artemisinina demonstrou mediar a N-oxidação de derivados de alquilaminas terciárias por meio da intermediação da forma aberta do anel peróxido da artemisinina. Este mecanismo alternativo pode ter o potencial para produzir uma série de espécies reativas de oxigênio que podem ter implicações para a atividade antimalárica desses compostos.22
Os derivados da artemisininas também foram investigados quanto aos seus efeitos anti-proliferativos contra uma vasta gama de linhagens de câncer. O promissor perfil in vitro de vários análogos semi-sintéticos levou os compostos à estudos clínicos mais adequados.22 Outros aspectos sobre estudos experimentais e teóricos, além de discussões levando-se em consideração os dois estudos, sobre a artemisinina e alguns de seus derivados (Figura 3) podem ser encontrados em outros importantes artigos científicos.23-28
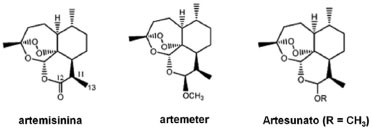 Figura 3. Estrutura da artemisinina e de alguns de seus derivados utilizados neste estudo
Desta forma, este trabalho teve como objetivo principal comparar o desempenho dos diversos funcionais de densidade do formalismo DFT, disponíveis no software The General Atomic and Molecular Electronic Structure System (GAMESS),29 que faz uso de código aberto (software livre), utilizando a artemisinina e alguns de seus derivados (Figura 3) como estudo de caso, na obtenção de propriedades eletrônicas destes compostos. De forma geral, a estrutura dos compostos abordados nesse estudo é de porte médio, sendo, assim, o DFT uma boa escolha para a solução aproximada da equação eletrônica de Schrödinger, já que computacionalmente é menos dispendioso quando comparado a outros como Coupled Cluster30 e Interação de Configurações e, também, mais eficiente quando comparado ao HF, já que leva em consideração a correlação eletrônica. Especificamente, tem-se o interesse em calcular as propriedades eletrônicas e, consequentemente, os índices de reatividade, da artemisinina e alguns de seus derivados, realizar um estudo estatístico via o método multivariado Análise de Componentes Principais31-34 para a interpretação conjunta dos vários dados obtidos e verificar o funcional, ou grupo de funcionais, mais indicado para o cálculo destas propriedades para os mesmos.
METODOLOGIA O estudo foi baseado em:
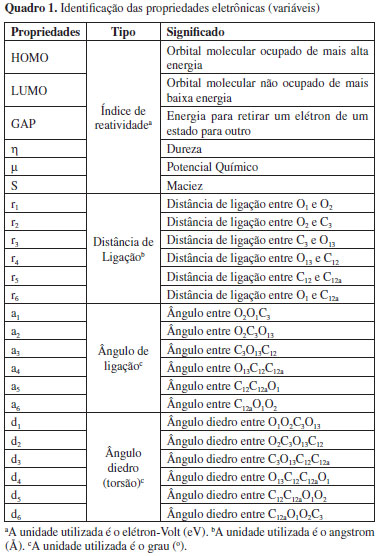
RESULTADOS E DISCUSSÃO No cálculo das propriedades foram testados todos os funcionais de troca e correlação disponíveis no programa GAMESS, porém apenas 17 funcionais convergiram para a estrutura de menor energia. Os valores calculados para as propriedades de índices de reatividade e geométricas da artemisinina, do artemeter e do artesunato se encontram, respectivamente, nas Tabelas 1S, 2S e 3S (vide Material Suplementar). Segundo o Teorema de Koopmans, a Energia de Ionização, ou Potencial de Ionização, de uma molécula, dentro da aproximação de orbital molecular congelado, é dada simplesmente como a energia do HOMO. Similarmente, a Afinidade Eletrônica de uma molécula neutra é dada pela energia do LUMO,5 ou seja, εHOMO = HOMO = Energia de Ionização ou Potencial de Ionização e εLUMO = LUMO = Afinidade Eletrônica. Entretanto, sabe-se que apenas dentro do formalismo Hartree-Fock é possível estimar-se a Energia de Ionização dentro do Teorema de Koopmans.4 Assim sendo, para sistemas com número não inteiro de elétrons, isto é, número fracionário, formalmente o Potencial de Ionização e a Afinidade Eletrônica são obtidos a partir das energias dos orbitais moleculares de Kohn-Sham. Na prática trata-se de uma aproximação, tendo em vista que não é conhecido o funcional de troca-correlação exato. Baseando-se na Teoria do Funcional da Densidade (DFT), várias propriedades importantes, tais como o índice de dureza (η), o potencial químico (µ), o índice de maciez (S), o índice de eletronegatividade (χ) e o índice de eletrofilicidade (ω) são definidos, respectivamente, pelas expressões abaixo41 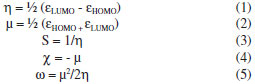 Levando-se em consideração o mecanismo de ação, o Ferro atua como um ácido de Lewis, isto é, recebendo um par de elétrons.22 Assim sendo, os funcionais de densidades foram analisados pelas propriedades LUMO e ω, que são descritores quânticos que mostram o poder em receber pares de elétrons por uma molécula (Tabela 1S, Material Suplementar). Dessa forma, para a artemisinina, levando-se em conta a energia do LUMO e a ω, apenas os funcionais B3LYP, B3P86, B3PW91, B97, B97-1, B98 e X3LYP descreveram satisfatoriamete essas propriedades, pois a partir desses cálculos é que foram obtidos os maiores valores de afinidade eletrônica (AE = - εLUMO) e de eletrofilicidade ω. Para o artemeter, somente os funcionais B3LYP, B3P86, B3PW91, B97 e X3LYP forneceram uma descrição apropriada para essas propriedades. Já para o artesunato, os funcionais B3LYP, B3P86, B3PW91, B97, B97-1, B97-2, B97-3, B98, PBE0 e X3LYP descreveram satisfatoriamente tais propriedades. Com relação às propriedades geométricas, todos os funcionais descrevem apropriadamente essas propriedades para o caso das três moléculas. Um fator impeditivo de uma comparação mais aprofundada está na dificuldade de encontrar dados experimentais para estas e também outras moléculas derivadas da artemisinina. Mesmo assim, parte da informação experimental/teórica para parâmetros geométricos pode ser encontrada nos trabalhos de Santos et al.37,38 para a artemisinina, que estão alocadas na última linha da Tabela 1S (vide Material Suplementar). Deste modo, faz-se necessária uma forma mais adequada para lidar com um volume relativamente grande de informações (neste caso, são os valores calculados) desta natureza. A técnica empregada com tal propósito foi a Análise de Componentes Principais. Os resultados obtidos a partir desta análise estão contidos nas Tabelas de 4S a 8S para a artemisinina, de 9S a 13S para o artemeter e de 14S a 18S para o artesunato (vide Material Suplementar). Como os dados possuem unidades de medida diferentes, estes foram autoescalados via matriz de correlação.31 As Tabelas 4S, 9S e 14S (vide Material Suplementar) apresentam a estatística descritiva para a artemisinina, artemeter e artesunato, respectivamente. O coeficiente de variação dos dados em questão, dado pela razão entre o desvio padrão e a média, indicou variabilidade alta para os parâmetros de reatividade e baixo para os geométricos, significando, especificamente, que os dados são não homogêneos para o caso reativo. A observação das Tabelas 5S, 10S e 15S (vide Material Suplementar) mostram a correlação entre as propriedades eletrônicas. É possível encontrar diversas amostras correlacionadas, como, por exemplo, na Tabela 5S, considerando (valor absoluto) os valores acima de 0,75 como referenciais, o orbital HOMO está correlacionado com as propriedades LUMO, GAP, η, S, r1, r3, a2, d3 e d4, isto é, o HOMO está relacionado a todos os parâmetros reativos, exceto o potencial químico, e apenas a cinco geométricos, sendo que os átomos de oxigênio têm um papel fundamental nesta última relação. O mesmo aspecto é verificado para o orbital LUMO e as demais variáveis de reatividade em relação às geométricas citadas e vice-versa. A mesma discussão orientada às Tabelas 10S e 15S (vide Material Suplementar) identifica um padrão para as correlações entre as variáveis, exceto pela substituição do HOMO pelo potencial químico, a inclusão de a4 e d2, no lugar de d3 e d4, respectivamente, para a molécula artemeter; para o artesunato são os mesmos parâmetros de reatividade da artemisinina, além de r1, r3, a2, a4, d1, d5 e d6. Em outras palavras, as propriedades de reatividade LUMO, GAP, dureza e maciez, somadas às propriedades geométricas r1, r3 e a2, formam o grupo de variáveis comuns entre tais moléculas. Um resultado importante da análise de Componentes Principais está no fato de que as três primeiras componentes explicam quase 90% da variabilidade dos dados para os três casos, conforme as Tabelas 6S, 11S e 16S (vide Material Suplementar). Especificamente, a componente 1 (CPrin1) explica mais da metade desta variabilidade, que somada à componente 2 (CPrin2) fica em torno de 80%. Neste ponto, como grande parte das informações é explicada por estas duas componentes, as Figuras de 6 a 9 ajudam a explicitar as Tabelas 7S, 12S e 17S (vide Material Suplementar) sobre os autovetores correspondentes aos autovalores das respectivas moléculas artemisinina, artemeter e artesunato, e a entender melhor o significado deste fato.
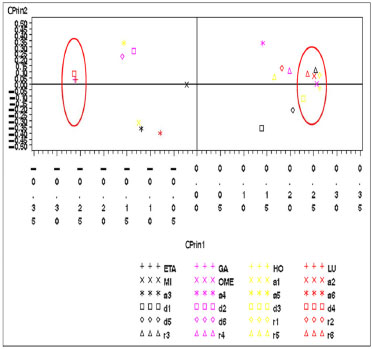 Figura 4. Gráfico das variáveis eletrônicas da artemisinina no primeiro plano fatorial (CPrin2 x CPrin1)
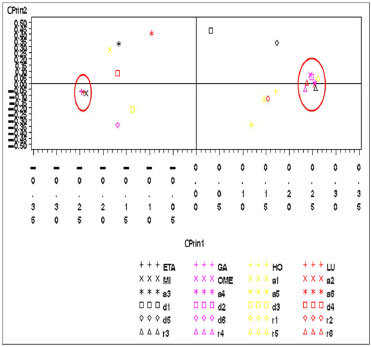 Figura 5. Gráfico das variáveis eletrônicas do artemeter no primeiro plano fatorial (CPrin2 x CPrin1)
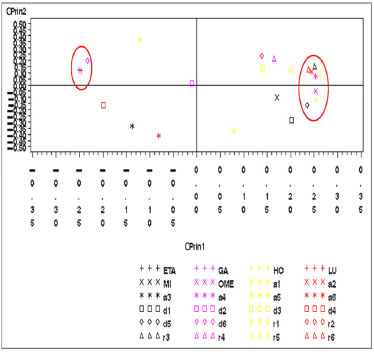 Figura 6. Gráfico das variáveis eletrônicas do artesunato no primeiro plano fatorial (CPrin2 x CPrin1)
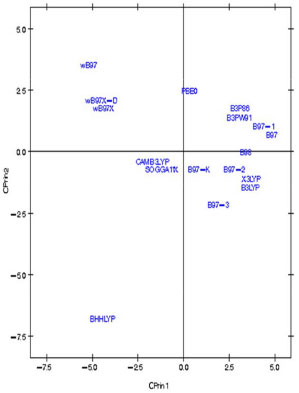 Figura 7. Gráfico dos dezessete funcionais de densidade relativos à artemisinina no primeiro plano fatorial (CPrin2 x CPrin1)
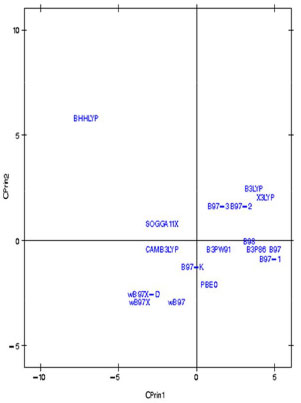 Figura 8. Gráfico dos dezessete funcionais de densidade relativos ao artemeter no primeiro plano fatorial (CPrin2 x CPrin1)
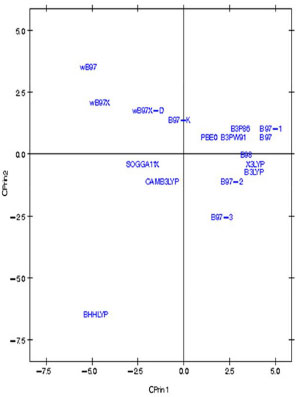 Figura 9. Gráfico dos dezessete funcionais de densidade relativos ao artesunato no primeiro plano fatorial (CPrin2 x CPrin1)
Os autovalores obtidos para CPrin1 e CPrin2 em relação aos funcionais de densidade e propriedades eletrônicas da artemisinina, artemeter e artesunato são, respectivamente, (13,18; 5,49), (13,78; 5,03) e (13,29; 4,73). Como a ideia central de Componentes Principais é reduzir a dimensionalidade das variáveis do estudo, eliminar sobreposições destas variáveis e escolher a forma mais representativa dos dados a partir de combinações lineares das variáveis originais, além de considerar que somente algumas variáveis são importantes à representatividade dos dados, foram utilizados os valores obtidos para o coeficiente de Pearson, que mede a "força" da correlação das variáveis, como critério de seleção das mesmas, sendo os valores próximos (e acima) de 0,8, dados nas Tabelas 8S, 13S e 18S (vide Material Suplementar), respectivamente, os mais significativos. Logo, as componentes são dadas pelas seguintes combinações lineares:  A representação destas equações, de forma completa, pode ser visualizada via gráfico das variáveis (propriedades eletrônicas) no plano fatorial formado por CPrin2 versus CPrin1, identificadas pelas Figuras 4, 5 e 6 da artemisinina, artemeter e artesunato, exatamente nesta ordem. Parte das coordenadas foi deixada de lado, ou seja, apenas a coordenada do HOMO referente a componente um está descrita, pois não acrescenta muita informação para a segunda componente, e assim, sucessivamente, para as demais propriedades. Por fim, as Figuras 7, 8 e 9 mostram o comportamento (scores) de todos os funcionais em relação às duas componentes principais (CPrin2 x CPrin1) para a artemisinina, artemeter e artesunato, respectivamente, levando-se em consideração as propriedades eletrônicas. Foi possível verificar nestas três (3) últimas figuras que, de forma geral, a componente principal CPrin1 opõe o grupo de funcionais WB97, WB97X e WB97X-D (que possuem scores moderados a altos e negativos, relacionando este fato às variáveis LUMO, GAP e η mostradas nas equações 6, 7 e 8, ou ainda nas Figuras 4, 5 e 6) aos demais funcionais, como, por exemplo, B3LYP, X3LYP, a família de funcionais B97, destacando, assim, as variáveis HOMO, S, r1, r3 e a2 para este grupo. Tal oposição evidencia o fato de que, enquanto os funcionais WB97, WB97X e WB97X-D descrevem de maneira satisfatória propriedades de índices de reatividade (LUMO, GAP e η), os funcionais B3LYP, X3LYP e a família de funcionais B97 descrevem melhor propriedades, em sua maioria geométricas, embora descreva também o orbital HOMO e S, que são parâmetros reativos. O fato dos funcionais CAMB3LYP, SOGGA11X e B97-K estarem localizados próximos à origem do plano fatorial indica que apresentam valores médios para todas as propriedades, não descrevendo de maneira destacada nenhuma delas. A variabilidade dos dados para estes funcionais talvez seja explicada pelo acréscimo de uma terceira ou mais componentes, porém, optou-se trabalhar somente com duas componentes a bem da redução da dimensionalidade do estudo. Já o funcional BHHLYP, diferentemente do exposto no início da discussão, está basicamente correlacionado com as propriedades a3 e a6 que descrevem os ângulos de ligação entre C3O13C12 e C12aO1O2, não tendo, a princípio, nenhuma participação efetiva no mecanismo de reação antimalárica e, provavelmente, anticâncer.
CONCLUSÃO Segundo os cálculos realizados, vários funcionais descreveram satisfatoriamente as propriedades de índices de reatividade e todos descreveram satisfatoriamente as propriedades geométricas das moléculas estudadas. Além disso, a Análise de Componentes Principais teve sucesso em discriminar os grupos de funcionais segundo as propriedades que descrevem os índices de reatividade e os parâmetros geométricos. Os funcionais WB97, WB97X e WB97X-D forneceram uma descrição satisfatoria à maioria dos índices de reatividade, principais descritores que, provavelmente, estão associados ao mecanismo de ação antimalária e anticâncer, além das outras propriedades eletrônicas, sendo, portanto, um bom indicativo de método para descrever tais propriedades para este grupo de moléculas. Como sugestão para trabalhos futuros indica-se a Análise de Cluster para estender a visualização dos resultados por meio de dendrogramas e a utilização de bases polarizadas para os cálculos das propriedades eletrônicas, desde que a base tenha um tamanho compatível com um custo computacional não muito dispendioso. Além disso, diferentes propriedades eletrônicas poderiam ser usadas como parâmetros (variáveis), das quais citamos modos vibracionais, momentos de dipolo, etc. Por fim, o estudo da artemisinina e alguns de seus derivados não expõe, provavelmente, o gigantesco leque de moléculas que também podem ou possuem atividade anticancerígina, porém, este protocolo pode ser de enorme valia, já que poucos estudos mostram este tipo de apontamento.
REFERÊNCIAS 1. Schrödinger, E.; Phys. Rev. 1926, 28, 1049. DOI: http://dx.doi.org/10.1103/PhysRev.28.1049 2. Hartree, D.; Proc. Cambridge Philos. Soc. 1928, 24, 89. DOI: http://dx.doi.org/10.1017/S0305004100011920 3. Fock, V. A.; Z. Physik 1930, 61, 126. DOI: http://dx.doi.org/10.1007/BF01340294 4. Morgon, N. H.; Coutinho, K.; Métodos de Química Teórica e Modelagem Molecular, Editora Livraria da Física: São Paulo, 2007. 5. Jensen, F.; Introduction to Computational Chemistry, 2th ed., John Wiley & Sons: West Sussex, 2007. 6. Roothaan, C. C. J.; Rev. Mod. Phys. 1951, 23, 69. DOI: http://dx.doi.org/10.1103/RevModPhys.23.69 7. Roothaan, C. C. J.; Rev. Mod. Phys. 1960, 32, 179. DOI: http://dx.doi.org/10.1103/RevModPhys.32.178 8. Arruda, P. M.; Dissertação de Mestrado, Universidade Federal do Espírito Santo, Brasil, 2009. 9. Clementi, E.; Roetti, C.; At. Data Nucl. Data Tables 1974, 14, 177. DOI: http://dx.doi.org/10.1016/S0092-640X(74)80016-1 10. Boys, S. F.; Proc. R. Soc. London Ser. A 1950, 200, 542. DOI: http://dx.doi.org/10.1098/rspa.1950.0036 11. Shavitt, I.; Mod. Theor. Chem. 1977, 3, 189. 12. Krishnan, R.; Frisch, M. J.; Pople, J. A.; J. Chem. Phys. 1980, 72, 4244. DOI: http://dx.doi.org/10.1063/1.439657 13. Parr, R. G.; Yang, W.; Density-functional Theory of Atoms and Molecules, Oxford University Press: New York, 1989. 14. Hohenberg, P.; Kohn, W.; Phys. Rev. 1964, 136, B864. DOI: http://dx.doi.org/10.1103/PhysRev.136.B864 15. Kohn, W.; Sham, L. J.; Phys. Rev. 1965, 140, A1133. DOI: http://dx.doi.org/10.1103/PhysRev.140.A1133 16. Vianna, J. D. M.; Canuto, S.; Fazzio, A.; Teoria Quântica de Moléculas e Sólidos, Livraria da Física: São Paulo, 2004. 17. Ziegler, T.; Chem. Rev. 1991, 91, 651. DOI: http://dx.doi.org/10.1021/cr00005a001 18. Narendrapurapu, B. S.; Richardson, N. A.; Copan, A. V.; Estep, M. L.; Yang, Z.; Schaefer, H. F.; J. Chem. Theory Comput. 2013, 9, 2930. DOI: http://dx.doi.org/10.1021/ct4002398 PMID: 26583976 19. Kozuch, S.; Martin, J. M. L.; J. Chem. Theory Comput. 2013, 9, 1918. DOI: http://dx.doi.org/10.1021/ct301064t PMID: 26583543 20. Li, W.; Walther, C. F. J.; Kuc, A.; Heine, T.; J. Chem. Theory Comput. 2013, 9, 2950. DOI: http://dx.doi.org/10.1021/ct400235w PMID: 26583978 21. Krykunov, M.; Ziegler, T.; J. Chem. Theory Comput. 2013, 9, 2761. DOI: http://dx.doi.org/10.1021/ct300891k PMID: 26583867 22. O'Neill, P. M.; Barton, V. E.; Bard, S. A.; Molecules 2010, 15, 1705. DOI: http://dx.doi.org/10.3390/molecules15031705 PMID: 20336009 23. Chaturvedi, D.; Goswami, A.; Saikia, P. P.; Barua, N. C.; Rao, P. G.; Chem. Soc. Rev. 2010, 39, 435. DOI: http://dx.doi.org/10.1039/B816679J PMID: 20111769 24. Lai, H. C.; Singh, N. P.; Sasaki, T.; Invest. New Drugs 2013, 31, 230. DOI: http://dx.doi.org/10.1007/s10637-012-9873-z PMID: 22935909 25. Vieira J. B.; Braga, F. S.; Lobato, C. C.; Santos, C. F.; Costa, J. S.; Bittencourt, J. A. H. M.; Brasil, D. S. B.; Silva, J. O.; Hage-Melim, L. I. S.; Macêdo, W. J. C.; Carvalho, J. C. T.; Santos, C. B. R.; Molecules 2014, 19, 10670. DOI: http://dx.doi.org/10.3390/molecules190810670 PMID: 25061720 26. Ferreira J. E. V.; Figueiredo, A. F.; Barbosa, J. P.; Pinheiro, J. C.; Em Chemometrics in Practical Applications; Varmuza K., ed.; In Tech, 2012, cap. 8. 27. Barbosa, J. P.; Ferreira, J. E. V.; Figueiredo, A. F.; Almeida, R. C. O.; Silva, O. P. P.; Carvalho, J. R. C.; da Cristino, M. G. G.; Pinheiro, J. C.; Vieira, J. L. F.; Serra, R. T. A.; J. Serb. Chem. Soc. 2011, 76, 1263. DOI: http://dx.doi.org/10.2298/JSC111227111B 28. Aghaei, M.; Ashtiani, H. A.; J. Pharm. 2012, 2, 49. 29. Schmidt, M. W.; Baldridge, K. K.; Boatz, J. A.; Elbert, S. T.; Gordon, M. S.; Jensen, J. J.; Koseki, S.; Matsunaga, N.; Nguyen, K. A.; Su, S.; Windus, T. L.; Dupuis, M.; Montgomery, J. A.; J. Comp. Chem. 1993, 14, 1347. DOI: http://dx.doi.org/10.1002/jcc.540141112 30. Bartlett, R. J.; Ann. Rev. Phys. Chem. 1981, 32, 359. DOI: http://dx.doi.org/10.1146/annurev.pc.32.100181.002043 31. Mingoti, S. A.; Análise de Dados através de Métodos de Estatística Multivariada: uma Abordagem Aplicada, Editora UFMG: Belo Horizonte, 2007. 32. Ferreira, M. M. C.; Antunes, A. M.; Melgo, M. S.; Volpe, P. L. O.; Quim. Nova 1999, 22, 724. DOI: http://dx.doi.org/10.1590/S0100-40421999000100003 33. Bruns, R. E.; Faigle, J. F. G.; Quim. Nova 1985, 8, 84. 34. Neto, B. B.; Scarmínio, I. S.; Bruns, R. E.; Quim. Nova 2006, 29, 1401. DOI: http://dx.doi.org/10.1590/S0100-40422006000600042 35. Hanwell, M. D.; Curtis, D. E.; Lonie, D. C.; Vandermeersch, T.; Zurek, E.; Hutchison, G. R.; J. Cheminf. 2012, 4, 1. DOI: http://dx.doi.org/10.1186/1758-2946-4-S1-P1 36. Lisgarten, J. N.; Potter, B. S.; Bantuzeko, C.; Palmer, R. A.; J. Chem. Crystallogr. 1998, 28, 539. DOI: http://dx.doi.org/10.1023/A:1023244122450 37. Santos, C. B. R.; Vieira, J. B.; Lobato, C. C.; Hage-Melim, L. I. S.; Souto, R. N. P.; Lima, C. S.; Costa, E. V. M.; Brasil, D. S. B.; Macêdo, W. J. C.; Carvalho, J. C. T.; Comput. Mol. Biosci. 2013, 3, 66. DOI: http://dx.doi.org/10.4236/cmb.2013.33009 38. Santos, C. B. R.; Vieira, J. B.; Lobato, C. C.; Hage-Melim, L. I. S.; Souto, R. N. P.; Lima, C. S.; Costa, E. V. M.; Brasil, D. S. B.; Macêdo, W. J. C.; Carvalho, J. C. T.; Molecules 2014, 19, 367. DOI: http://dx.doi.org/10.3390/molecules19010367 39. Woerdenbag, H. J.; Moskal, T. A.; Pras, N.; Malingré, T. M.; El-Feraly, F. S.; Kampinga, H. H.; Konings, A. W. T.; J. Nat. Prod. 1993, 56, 849. DOI: http://dx.doi.org/10.1021/np50096a007 PMID: 8350087 40. R CORE TEAM.; R: a Language and Environment for Statistical Computing; R Foundation for Statistical Computing, Austria, 2013. 41. Thanikaivelan, P.; Subramanian, V.; Rao, J. R.; Nair, B. U.; Chem. Phys. Lett. 2000, 323, 59. DOI: http://dx.doi.org/10.1016/S0009-2614(00)00488-7 |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






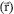 representa a densidade eletrônica total em um ponto
representa a densidade eletrônica total em um ponto  do espaço. A energia eletrônica, E, é um funcional desta densidade, representada como E[ρ], no sentido de que para uma dada função ρ
do espaço. A energia eletrônica, E, é um funcional desta densidade, representada como E[ρ], no sentido de que para uma dada função ρ