Educação
|
|
| Coeficientes de transmissão e reflexão pelo método da amplitude variável Transmission and reflection coefficients by the variable amplitude method |
|
Éderson D'M. CostaI; Luciano CordeiroII; Nelson H. T. LemesI,*; Joao P. BragaIII
IInstituto de Química, Universidade Federal de Alfenas, 37130-000 Alfenas - MG, Brasil Recebido em 22/10/2015 *e-mail: nelson.lemes@unifal-mg.edu.br In this work, a simple derivation of the variable amplitude method using the variation of parameters to solve a differential equation is presented. The variable amplitude method was originally devised by Tikochinsky in 1977, using the quantum theory of scattering. The method is applied to two model potentials, the rectangular potential barrier and the Eckart potential, both with analytical solutions for the reflection coefficient. Numerical results will be compared with the exact values for several energies. The problem of calculating the reflection coefficient, usually involving extensive algebra as described in several textbooks, is reduced to solving a first order differential equation with initial condition. The method is very simple to apply, representing an attractive tool for teaching introductory quantum mechanics. A simple computer code is available from which reflection coefficients for the Eckart potential can be calculated. INTRODUÇAO No estudo do movimento unidimensional de uma partícula de massa m e energia E, existem duas perspectivas: tratar o problema do ponto de vista da mecânica clássica ou de acordo com a mecânica quântica. No tratamento clássico, quando nao ocorre perdas de energia de qualquer forma, a partícula fica presa a uma regiao do espaço x, tal que sua energia potencial V(x) é sempre menor ou igual a E. Em outras palavras, a energia total é conservada, V(x)+mv2/2=E. Este é um dos aspectos mais fascinantes que distingue a mecânica quântica da mecânica clássica. Na teoria quântica o estado da partícula é representado por uma funçao ψ(x) obtida pela soluçao da equaçao de Schrödinger, cujo módulo ao quadrado |ψ(x)|2dx é interpretado como a probabilidade de encontrar a partícula na regiao x+dx. Neste caso, como a funçao é espalhada além do limite x0, em que x0 satisfaz a relaçao V(x0)=E, existe uma probabilidade finita de que uma partícula com energia total E penetre em uma regiao do espaço onde a energia total é menor que a energia potencial V(x). O processo, conhecido como tunelamento quântico, é de extrema relevância para explicaçao de várias fenômenos físicos e químicos, como o decaimento alfa,1,2 a emissao de elétrons por metais frios sob a influência de um campo forte,3 reaçoes de transferência de hidrogênio, fundamentais para a compreensao do efeito isotópico cinético H/D,4,5 mecanismos de transferência de elétrons6,7 e inversao espectral.8,9 Além disso, o tunelamento quântico é de importância para a fabricaçao de novos semicondutores e dispositivos eletrônicos.10 A compreensao das propriedades físicas dos sistemas requer em muitos casos a avaliaçao da equaçao unidimensional de Schrödinger para um potencial específico. No entanto, soluçoes analíticas sao limitadas a potenciais modelos, que embora sejam úteis para a análise da situaçao física em questao, nem sempre representam sistemas reais. Podemos destacar o potencial degrau e o potencial barreira retangular apresentado em diversos livros-textos para introduçao do assunto.11,12 Exemplos de potenciais para os quais se tem soluçoes analíticas podem ser encontrados na referência Razavy.13 Dentre os métodos numéricos destaca-se o método da matriz de transferência que é amplamente utilizado para cálculos de coeficientes de transmissao/reflexao.14-17 O trabalho de Rozman et al.18 destaca algumas deficiências do método, como o aumento do esforço computacional decorrente do aumento de segmentos em que o potencial é dividido e erros numéricos de arredondamento ao lidar com barreiras opacas. Outro método, originalmente apresentado por Tikochinsky em 1977,19 consiste em estabelecer uma equaçao diferencial de primeira ordem para a amplitude de reflexao similar a equaçao de Calogero.20,21 A equaçao de Calogero relaciona o deslocamento de fase ao potencial intermolecular e tem sido utilizada na identificaçao de estados ligados22 e no estudo do problema inverso da obtençao do potencial intermolecular a partir de dados de deslocamento de fase.23 O método de Tikochinsky, método da amplitude variável, se aplica de forma geral a potenciais localizados e consiste de uma ferramenta simples e de fácil implementaçao computacional. Nesse trabalho busca-se enfatizar a simplicidade do método proposto por Tikochinsky para cálculos de coeficientes de transmissao/reflexao. Embora, na literatura, tenha sido aplicado na maioria dos casos para potenciais com limites assintóticos V(x →±∞) = 0,24 o método também é aplicável a potenciais com condiçoes de contorno diferentes, como será discutido. Uma derivaçao da equaçao diferencial será feita por um novo caminho utilizando o método da variaçao dos parâmetros, uma poderosa ferramenta matemática para resolver equaçoes diferenciais lineares nao homogêneas de ordem superior. Soluçoes numéricas serao obtidas para coeficientes de transmissao/reflexao e comparadas com resultados analíticos para potenciais modelos.
EQUAÇAO DIFERENCIAL PARA A AMPLITUDE DE REFLEXAO Uma derivaçao da equaçao diferencial para a amplitude de reflexao, com o enfoque principalmente voltado para a física de espalhamento,25 pode ser encontrada no livro de Calogero e Degasperis.26 Nesta seçao, diferentemente da abordagem adotada no livro citado, a equaçao diferencial é obtida utilizando o método da variaçao dos parâmetros conforme método geral apresentado no trabalho de Ronveaux.27 Considerando a equaçao unidimensional de Schrodinger 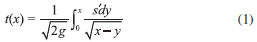 busca-se a soluçao em termos das soluçoes particulares para o problema homogêneo associado, isto é, ψ1 = eikx e ψ2 = e-ikx. A quantidade U(x) se relaciona com o potencial V(x) por U(x) = 2mV(x)/ħ2 e o número de onda k se relaciona com a energia E por A soluçao para o problema original, Equaçao 1, é colocada na forma 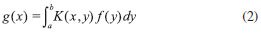 com a suposiçao de que 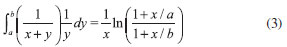 que é a idéia básica do método da variaçao dos parâmetros.28 A substituiçao de ψ e sua segunda derivada na Equaçao 1 fornece 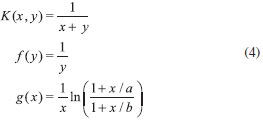 As Equaçoes 3 e 4 compoe o sistema de equaçoes  ou na forma matricial WX' = UWX, na qual 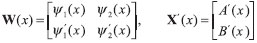 e  O vetor X' é encontrado por X' = MX com M = W-1UW, isto é, 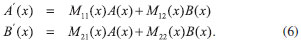 As funçoes A(x) e B(x) modulam as amplitudes das funçoes de onda incidente e refletida, portanto, segundo a interpretaçao de Born, o quadrado da razao destas amplitudes, em x → -∞, definem a probabilidade de reflexao ou coeficiente de reflexao desejado. Assim, assumindo r(x) como r(x) = B(x) / A(x), obtém-se a equaçao diferencial 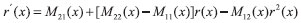 ou 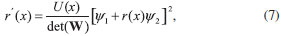 que é uma equaçao de Riccati,27 cuja soluçao em x → -∞ fornece o coefiente de reflexao R = |r(x → -∞)|2. A probabilidade de transmissao ou coeficiente de transmissao pode ser facilmente obtida da relaçao R+T = 1, que reflete a conservaçao de partículas no processo. Neste último caso, para avaliar os elementos da matriz M, calcula-se a inversa de W analiticamente. A Equaçao 7 aplica-se na condiçao em que o potencial para x → -∞ tem o valor zero. Essa condiçao pode ser sempre alcançada somando-se uma constante à energia e ao potencial. A condiçao inicial para resoluçao numérica do problema, desde que as partículas incidam sobre a barreira da esquerda para a direita, é dada por 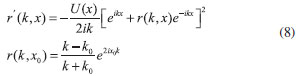 A quantidade r0 é a amplitude de reflexao para o potencial degrau V(x0)H(x - x0) com H sendo a funçao de Heaviside. O termo é de importância para potenciais com limites assintóticos VD = V(x → +∞) ≠ 0 para levar em conta a contribuiçao do potencial a direita de x0 ao se iniciar a integraçao nesse ponto. Para o caso em que V(x → +∞) = 0, nao existem partículas que se deslocam para a esquerda à direita da barreira, consequentemente, a condiçao inicial r(x → ∞) deve ser nula, portanto, r0 se reduz a zero para valores grandes de x.
RESULTADOS E DISCUSSAO Devido à importância pedagógica do potencial barreira retangular, esse potencial será considerado como um primeiro exemplo. O segundo potencial abordado será o potencial de Eckart.29 O potencial apresenta o limite assintótico, VD ≠ 0, o que possibilita mostrar a eficiência do método para uma condiçao de contorno diferente. Para os dois casos, considerou-se que a partícula incide da esquerda para a direita. A integraçao numérica foi realizada para valores de coordenada de 20 a -20 utilizando o método de Runge-Kutta quarta e quinta ordem com passo adaptativo.30 Os cálculos foram feitos em unidades atômicas. Potencial barreira retangular Um potencial contínuo que representa uma barreira pode ser estabelecido com a funçao, 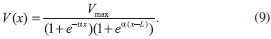 No limite de α grande, o potencial tende ao potencial barreira retangular (Figura 1), em que Vmax é o máximo do potencial e L a largura da barreira.
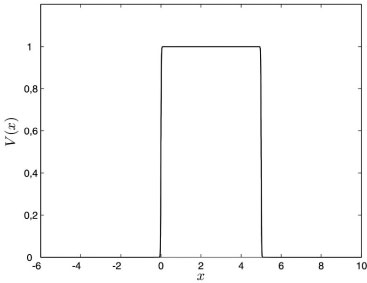 Figura 1. Aproximaçao para o potencial barreira retangular, α = 100, Vmax = 1 e L = 5
As soluçoes exatas do caso limite para E > Vmax e E < Vmax, sao dadas, respectivamente, por 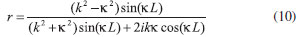 e 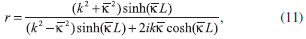 com A soluçao numérica para o coeficiente de transmissao, T = 1 - R, em que R = |r|2, com parâmetros a = 100, Vmax = 1 e L = 5, é apresentada na Figura 2 em comparaçao com as soluçoes exatas.
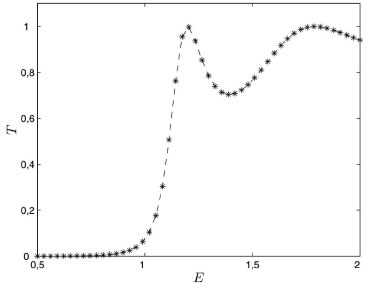 Figura 2. Coeficiente de transmissao para o potencial barreira retangular, (asteriscos) soluçao numérica da Eq. (8), (linha tracejada) soluçao analítica
O erro médio cometido é menor que 0,05%, neste caso, o erro além de ser funçao dos parâmetros ajustáveis do método de resoluçao da equaçao diferencial que controla a precisao, é também funçao do valor α considerado para a aproximaçao. A soluçao correta é obtida tanto para E > Vmax, quanto para E < Vmax. Os valores de T > 0 para E < Vmax indicam o tunelamento das partículas, isto é, mesmo que as partículas tenham energia menor que a da barreira, ainda há uma probabilidade finita de essas a atravessarem, o que classicamente nao seria permitido. Também, mesmo que as partículas possuam energia maior que a da barreira, E > Vmax, ainda se observa T < 1, quando classicamente se esperaria T = 1. O potencial considerado se anula assintoticamente, tanto para valores negativos, quanto para valores positivos de x, um caso com condiçoes de contorno diferentes pode ser ilustrado com o potencial de Eckart.29 Potencial de Eckart O potencial de Eckart é dado pela funçao,13,29 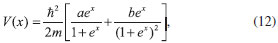 em que a e b sao parâmetros arbitrários. O potencial possui limites diferentes como funçao dos parâmetros e possui soluçao analítica para o tunelamento o que permite a comparaçao com os resultados numéricos. Na Figura 3 é apresentado o potencial de Eckart onde se verifica a modificaçao no limite VD em funçao da modificaçao dos parâmetros.
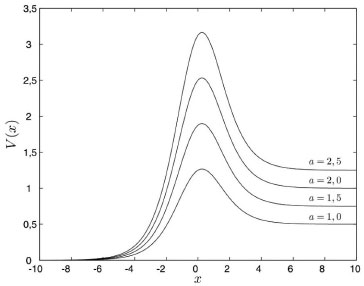 Figura 3. Potencial de Eckart para diferentes valores do parâmetro a com b = 8a
A Figura 4 apresenta os coeficientes de reflexao, R, para valores de energia tomados no intervalo, 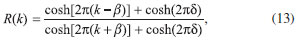 em que β =
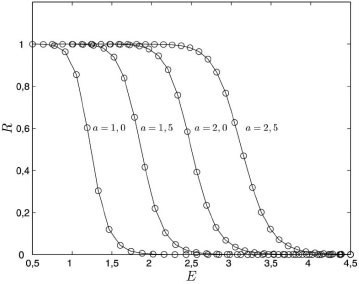 Figura 4. Coeficiente de reflexao R para o potencial de Eckart para diferentes valores de a com b = 8a, (linha contínua) exato, (círculos) soluçao numérica
reflexao para b > 1/4. Como se verifica, a resoluçao da Equaçao 8 leva a valores de coeficientes de reflexao corretos. O erro médio em relaçao à soluçao analítica foi de 1,54 × 10-6%. Uma das vantagens de se utilizar o método da amplitude variável é a possibilidade de utilizar técnicas de integraçao com passo adaptativo, o que contorna os problemas citados por Rozman et al.18 no método da matriz de transferência.
CONCLUSAO A abordagem pelo método da amplitude variável consiste em um caminho elementar para reduzir os cálculos dos coeficientes de transmissao ou reflexao a um problema de valor inicial, utilizando uma equaçao diferencial de primeira ordem. A equaçao diferencial pode ser resolvida pelas técnicas com passo adaptativo, o que leva a uma soluçao precisa com um mínimo esforço computacional. Utilizando uma condiçao inicial adequada o método torna-se aplicável de maneira geral a potenciais localizados com diferentes condiçoes de contorno. O método aqui apresentado pode ser adaptado para o cálculo da matriz de espalhamento e versoes em mais de uma dimensao devem ser investigadas. De simples implementaçao computacional, o método representa uma ferramenta atrativa para compreender os processos de tunelamento para os mais diversos potenciais. A exemplo da equaçao de Calogero, a equaçao diferencial para a amplitude de reflexao pode ser utilizada para estudar o problema inverso de recuperaçao do potencial a partir de dados de coeficiente de transmissao ou reflexao.
MATERIAL SUPLEMENTAR Um exemplo de código para cálculos de coeficiente de reflexao desenvolvido em MATLAB está disponível como material suplementar em http://quimicanova.sbq.org.br, com acesso livre.
AGRADECIMENTOS Gostaríamos de agradecer à CAPES, ao CNPq e à Fapemig pelo suporte financeiro.
REFERENCIAS 1. Gamow, G.; Z. Phys. 1928, 51, 204. DOI: http://dx.doi.org/10.1007/BF01343196 2. Gurney, R. W.; Condon, E. U.; Phys. Rev. 1929, 33, 127. DOI: http://dx.doi.org/10.1103/PhysRev.33.127 3. Fowler, R. W.; Nordheim, L.; Proc. R. Soc. London, Ser. A 1928, 119, 173. DOI: http://dx.doi.org/10.1098/rspa.1928.0091 4. Bell, R. P.; The Tunnel Effect in Chemistry, Chapman and Hall: London, 1980. 5. Johnston, H. S.; Rapp, D.; J. Am. Chem. Soc. 1961, 83, 1. DOI: http://dx.doi.org/10.1021/ja01462a001 6. Levich, V. G.; Dogonadze, R. R.; Dokl. Akad. Nauk SSSR 1960, 133, 158. 7. Marcus, R. A.; J. Chem. Phys. 1966, 45, 4493. DOI: http://dx.doi.org/10.1063/1.1727528 8. Khairutdinov, R. F.; Zamaraev, K. I.; Zhdanov, V. P. Em Comprehensive Chemical Kinetics; Compton, R. G., eds.; Elsevier: Amsterdam, 1989, vol. 30. 9. Tserkis, S. T.; Moustakidis, Ch. C.; Massen, S. E.; Panos, C. P.; Phys. Lett. A 2014, 378, 497. DOI: http://dx.doi.org/10.1016/j.physleta.2013.12.004 10. Johnson, E. A. Em Low-Dimensional semiconductor structures; Barnham, K., Vvedensky, D., eds.; Cambridge Univ. Press: Cambridge, 2001, cap. 2. 11. Powell, J. L.; Crasemann, B.; Quantum Mechanics, Addison-Wesley: Massachusetts, 1961. 12. Cohen-Tannoudji, C.; Diu, B.; Laloë, F.; Quantum Mechanics, Wiley: New York, 1977, vol. 1. 13. Razavy, M.; Quantum Theory of Tunneling, World Scientific: New Jersey, 2003. 14. Vatannia S.; Gildenblat, G.; IEEE J. Quantum Electron. 1996, 32, 1093. DOI: http://dx.doi.org/10.1109/3.502388 15. Sanchez-Soto, L. L.; Monzona, J. J.; Barriuso, A. G.; Carinena, J. F.; Phys. Rep. 2012, 513, 191. DOI: http://dx.doi.org/10.1016/j.physrep.2011.10.002 16. Mukherjee, S.; Karmakar, R.; Deyasi, A.; International Journal of Soft Computing and Engineering 2011, 1, 41. 17. Das, S.; Am. J. Phys. 2015, 83, 590. DOI: http://dx.doi.org/10.1119/1.4916834 18. Rozman, M. G.; Reineker, P.; Tehver, R.; Phys. Rev. A: At., Mol., Opt. Phys. 1994, 49, 3310. DOI: http://dx.doi.org/10.1103/PhysRevA.49.3310 19. Tikochinsky, Y.; Ann. Phys. 1977, 103, 185. DOI: http://dx.doi.org/10.1016/0003-4916(77)90268-8 20. Viterbo, V. D.; Lemes, N. H. T.; Braga, J. P.; Rev. Bras. Ensino Fis. 2014, 36, 1310. 21. Calogero, F.; Variable phase approach to potential scattering, Academic Press: New York, 1967. 22. Braga, J. P.; Murrell, J. N.; Mol. Phys. 1984, 53, 295. DOI: http://dx.doi.org/10.1080/00268978400102311 23. Lemes, N. H. T.; Braga, J. P.; Alves, M. O.; Costa, É. D'M.; J. Mol. Model. 2014, 20, 2317. DOI: http://dx.doi.org/10.1007/s00894-014-2317-2 PMID: 24935112 24. Kidun, O.; Fominykh, N.; Berakdar, J.; Phys. Rev. A: At., Mol., Opt. Phys. 2005, 71, 022703. DOI: http://dx.doi.org/10.1103/PhysRevA.71.022703 25. Pliego Jr., J. R.; Braga, J. P.; Bosanac, S. D.; Phys. Rev. A: At., Mol., Opt. Phys. 1995, 53, 342. DOI: http://dx.doi.org/10.1103/PhysRevA.52.342 26. Calogero, F.; Degasperis, A. Em Studies in Mathematics and its Applications; Lions, J. L., Papanicolaou, G., Rockafeliar, R. T., Fujita, H., eds.; North-Holland: Amsterdam, 1982, vol. 13. 27. Ronveaux, A.; Am. J. Phys. 1969, 37, 135. DOI: http://dx.doi.org/10.1119/1.1975426 28. Zill, D. G.; Cullen, M. S.; Equaçoes Diferenciais, Makron Books: Sao Paulo, 2007. 29. Eckart, C.; Phys. Rev. 1930, 35, 1303. DOI: http://dx.doi.org/10.1103/PhysRev.35.1303 30. Forsythe, G. E.; Malcolm, M. A.; Moler, C. B.; Computer Methods for Mathematical Computations, Prentice Hall: New Jersey, 1977. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






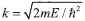 , em que m é a massa da partícula e ħ a constante reduzida de Planck.
, em que m é a massa da partícula e ħ a constante reduzida de Planck.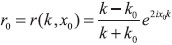 , em que
, em que 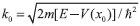 e x0 é um valor grande da coordenada. Com a substituiçao de ψ1, ψ2 e do determinante det(W) = -2ik na Equaçao 7, tem-se o problema de valor inicial a ser resolvido,
e x0 é um valor grande da coordenada. Com a substituiçao de ψ1, ψ2 e do determinante det(W) = -2ik na Equaçao 7, tem-se o problema de valor inicial a ser resolvido,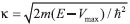 e
e 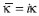 .15
.15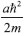 < E < 4,5. Os resultados estao em comparaçao com a soluçao analítica,
< E < 4,5. Os resultados estao em comparaçao com a soluçao analítica,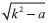 e δ =
e δ = 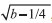 , apropriada para descrever o coeficiente de reflexao para b > 1/4.
, apropriada para descrever o coeficiente de reflexao para b > 1/4.