JBCS

INTRODUCCIÓN

Los carbonilos metálicos son una de las familias de compuestos organometálicos más importante de la química inorgánica. Son de gran interés tanto desde el punto de vista teórico como experimental. En el pasado, la mayoría de los estudios teóricos sobre estos complejos se han centrado en la interpretación de la función de onda a través del análisis de los orbitales moleculares.^1-6

Recientemente, se han sintetizado una variedad de carbonilos metálicos. En este sentido, Geier y col.⁷ han desarrollado un método para sintetizar sales del complejo [Mn(CO)₆]⁺, y determinaron sus estructuras moleculares por difracción de rayos X. De acuerdo a estos autores, las propiedades espectroscópicas y estructurales del [Mn(CO)₆]⁺ encajan perfectamente con los de las especies isoelectrónicas [V(CO)₆]^-, Cr(CO)₆, y [Fe(CO)₆]²⁺. Brathwaite y col.⁸ han sintetizado y caracterizado los iones [Cu(CO)_n]⁺ (n = 1-8). El catión [Cu(CO)₄]⁺ es el más estable de la serie y tiene una estructura tetraédrica. También han estudiado los cationes [M(CO)_n]⁺ (M = Ti, Zr, Hf; n = 6-8)⁹ donde las especies con n=6 resultaron los complejos totalmente coordinados. Cui y col.^10,11 han caracterizado cationes dinucleares [Cu₂(CO)₆]⁺, [Cu₂(CO)₇]⁺, [Co₂(CO)₈]⁺, [Co₂(CO)₉]⁺, trinucleares [Cu₃(CO)₇]⁺, [Cu₃(CO)₈]+, [Cu₃(CO)₉]⁺, [Co₃(CO)₁₀]⁺, [Co₃(CO)₁₁]⁺, y tetranucleares [Cu₄(CO)₈]⁺, [Co₄(CO)₁₂]⁺. En la mayoría de estos trabajos las geometrías y estados electrónicos de estos complejos son determinados por el número de bandas activas en el espectro infra rojo, sus frecuencias vibracionales y las intensidades relativas comparadas con predicciones teóricas calculadas con métodos de la teoría del funcional de la densidad.

Por otra parte, Reed y col.¹² han estudiado los cationes Mn(CO)_n⁺ (n=1-9). Estos autores han encontrado que la multiplicidad de espín decrece con el agregado sucesivo de ligandos. Al catión [MnCO]⁺ se lo ha detectado en los estados quintete y sextete, el catión [Mn(CO)₂]⁺ se ha detectado solo como quintete, mientras que los cationes [Mn(CO)₃]⁺ y [Mn(CO)₄]⁺ ambos son tripletes y [Mn(CO)₅]⁺ y [Mn(CO)₆]⁺ son singuletes, al igual que los complejos más grandes. Además han determinado que el complejo [Mn(CO)₆]⁺ es un singulete en su estado fundamental al igual que su análogo isoelectrónico [V(CO)₆]. De manera similar Xie y col.¹³ han sintetizado y estudiado las geometrías y estados electrónicos de los complejos [La(CO)₈]⁺, [Ce(CO)₈]⁺, [U(CO)₈]⁺ y [Y(CO)₈]⁺. Los estudios teóricos de estas especies han mostrado que tienen una geometría con simetría O_h en el estado triplete y ligeramente distorsionada en el estado cuartete.

La unión M-C en los carbonilos metálicos es usualmente interpretada en términos del mecanismo de Dewar-Chatt-Duncanson que involucra la transferencia electrónica desde el par libre del C carbonílico hacia los orbitales d vacantes del metal (donación-σ) y la transferencia de carga electrónica reciproca desde los orbitales atómicos d ocupados del catión metálico hacia los orbitales moleculares antienlazantes π* del CO (retrodonación-π).

La estabilidad de estos complejos, donde el metal tiene estado de oxidación nulo (carbonilos metálicos neutros) o negativo (carbonilos metálicos aniónicos), se le atribuye a la gran capacidad que tiene el ligando CO para aceptar densidad electrónica del metal por retrodonación-π. Mientras que, la estabilidad de los carbonilos metálicos catiónicos se le atribuye a la donación-σ desde el par libre del átomo de C del CO hacia los orbitales vacantes d del catión metálico. Ehlers y col.¹⁴ en su estudio teórico de carbonilos metálicos determinaron que la donación-σ aumenta con el incremento del estado de oxidación del metal, mientras que la retrodonación-π decrece con el aumento de la carga positiva de la especie metálica. En otras palabras, para las especies neutras y negativas es más importante la retrodonación-π, mientras que para las especies con carga positiva es más importante la donación-σ.

La Teoría Cuántica de Átomos en Moléculas (QTAIM),^15-17 a través del análisis topológico de la densidad electrónica y de su función Laplaciana, ofrece otro punto de vista, y se la puede utilizar para caracterizar los enlaces químicos. Uno de los atractivos de la QTAIM es que puede ser aplicada a densidades electrónicas determinadas tanto experimentalmente como en forma teórica, y actualmente se la utiliza de forma rutinaria para los estudios de densidad de carga electrónica experimental. Esta metodología ya fue aplicada al estudio de carbonilos metálicos en donde el metal actúa con bajo estado de oxidación. MacDougall y Hall,¹⁸ Macchi y Sironi¹⁹ y Cortés-Guzmán y Bader²⁰ han analizado, las interacciones M∙∙∙C por medio de la topología del Laplaciano de la densidad electrónica. En estos trabajos se mostró la forma cúbica que presenta la distribución electrónica de la especie metálica en los complejos de coordinación octaédrico. Recientemente, esta teoría también ha sido utilizada para caracterizar interacciones metal-metal y metal-ligando con densidades electrónicas obtenidas experimentalmente y por métodos de la teoría del funcional de la densidad.^21,22

Por otra parte, recientemente hemos mostrado por medio de la QTAIM que muchas interacciones como los enlace de hidrógeno,^23,24 enlaces de litio,²⁵ enlaces de berilio,²⁵ enlaces de boro²⁵ y enlaces de halógeno,^26-29 débiles y no tan débiles, pueden ser caracterizadas en base a la topología de la densidad electrónica y su función derivada el Laplaciano de la densidad electrónica. En estos trabajos hemos discutido acerca de la covalencia de las interacciones y en varios sistemas hemos observado que la transferencia de carga y la interacción electrostática entre el núcleo del ácido de Lewis y el par electrónico de la base juegan un rol importante no solo en la estabilización del complejo sino también en la determinación de la geometría molecular de los mismos. Es nuestro interés indagar si estos hallazgos se presentan también en los complejos metálicos aquí estudiados.

En los clásicos carbonilos metálicos, la frecuencia de estiramiento del CO se reduce en comparación con su valor en la molécula libre. Probablemente debido a una disminución neta de densidad electrónica enlazante del orbital σ_C≡O y un incremento en la densidad electrónica antienlazante de los orbitales π*_C≡O. La interacción entre estos orbitales (σ_C≡O y π*_C≡O) ha sido reconocido durante muchos años. Sin embargo, algunos trabajos sugieren que las interacciones electrostáticas entre la especie metálica y la molécula de CO pueden proporcionar efectos adicionales interesantes en estos sistemas. Los cálculos sugieren que la carga de metal puede desempeñar un papel importante en la polarización de la densidad electrónica del CO.^30-32 Desafortunadamente, hay pocos estudios de carbonilos metálicos aislados en fase gaseosa en donde investigar estas predicciones. En este trabajo se estudia, entre otras cosas, como varia la polarizabilidad del para electrónico del C del CO y su influencia en la estabilidad de la especie metálica.

Se conocen una gran variedad de complejos que forma el CO con cationes metálicos y se siguen sintetizando y estudiando nuevos carbonilos metálicos.^{8-13,21,22,33} Por otra parte, es conocido el hecho que en la molécula de CO el átomo de carbono tiene carga positiva (+1,17) y el átomo de oxígeno tiene carga negativa (-1,17).³⁴ Esto nos lleva a preguntarnos ¿Cómo es posible que cationes metálicos interactúen atractivamente con átomos de C en los carbonilos metálicos? ¿Cuánto influye la donación-σ y la retrodonación-π en la estabilización de estos complejos? ¿Cuál es la magnitud física, en el contexto QTAIM, que determina la extensión de la donación-σ y la retrodonación-π? ¿Cuál es el fundamento físico que explica la estabilidad de las interacciones estabilizantes M^δ+∙∙∙^δ+C? Con el objeto de dar respuesta a estos interrogantes, en el presente trabajo se realizó un estudio teórico profundo de la distribución electrónica que presentan los complejos isoelectrónicos [Ti(CO)₆]^2-, [V(CO)₆]^-, [Cr(CO)₆], [Mn(CO)₆]⁺, [Fe(CO)₆]²⁺ y [Co(CO)₆]³⁺ mediante el análisis topológico de la densidad de carga electrónica y de su función Laplaciana en el marco de la QTAIM.

MÉTODO DE CÁLCULO

Las geometrías de todos los monómeros y complejos fueron optimizados sin ninguna restricción con el paquete de programas Gaussian 03,³⁵ utilizando el funcional híbrido B3LYP,³⁶ el cual ha demostrado ser adecuado para el tratamiento teórico de sistemas similares,^7,12,37 con el conjunto de funciones bases 6-311++G(2d,2p). De acuerdo a la teoría del campo del ligando,³⁸ la molécula de CO es un ligando de campo alto, en consecuencia se espera que cuando la coordinación es completa el estado fundamental sea un singulete de capa cerrada. Todos los cálculos han sido realizado en el estado singulete.

Los puntos estacionarios sobre la superficie de energía potencial fueron confirmados como mínimos verdaderos por la ausencia de frecuencias vibracionales imaginarias. Las energías de interacción (ΔE) de los complejos fueron calculadas como la diferencia entre la energía total del complejo y la suma de la energía de los monómeros aislados. El análisis topológico de la distribución de la densidad de carga electrónica y de su función Laplaciana fueron realizados con el programa AIMAll³⁹ y AIM2000.⁴⁰ El análisis topológico de la función de localización electrónica (ELF) fue realizado con el programa Multiwfn.⁴¹ Ambos análisis (AIM y ELF) se realizaron sobre las funciones de onda obtenidas al nivel B3LYP/6-311++G(2d,2p).

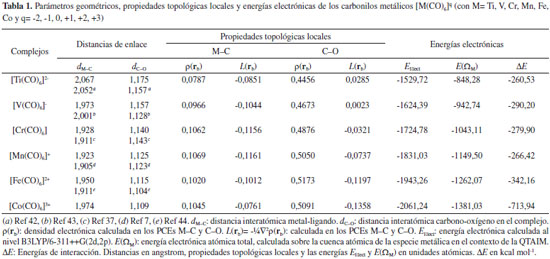
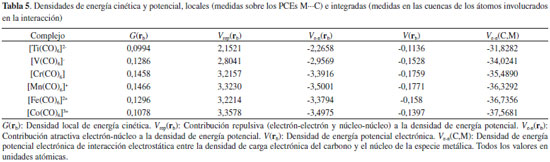
RESULTADOS Y DISCUSIÓN

En este trabajo se estudiaron los complejos de coordinación octaédricos [M(CO)6]^q (con M= Ti, V, Cr, Mn, Fe, Co y q= -2, -1, 0, +1, +2, +3 respectivamente). Los metales y sus correspondientes estados de oxidación fueron seleccionados de forma tal que, todos los complejos sean isoelectrónicos.

Parámetros geométricos y energéticos

En la Tabla 1 se informan las distancias de enlace M-C y C-O, parámetros topológicos locales seleccionados, las energías electrónicas de los complejos y las energías atómicas QTAIM de la especie metálica. Las distancias de enlace M-C y C-O calculadas están en buen acuerdo con las distancias experimentales y teóricas informadas por otros autores.^7,37,42-44 De acuerdo a Orpen y col.⁴⁵ la longitud promedio de los enlaces V-C, Cr-C, Mn-C y Fe-C en carbonilos metálicos son 1,946, 1,866, 1,808, y 1,782 Å, respectivamente. Como era de esperar, estas longitudes disminuyen al aumentar el número atómico del metal, debido a que en este sentido disminuye el radio iónico de los metales de transición. Las longitudes de enlace M-C de los carbonilos isoelectrónicos estudiados aquí no siguen la misma tendencia, sin embargo están en el mismo orden que los parámetros geométricos hallados por Geier y col.⁷ Estas longitudes de enlace están comprendidas en un intervalo bastante estrecho [1,923-2,067] Å.

En la Tabla 1 se observa un decrecimiento de las longitudes de enlace C-O en el miso sentido en que aumenta el estado de oxidación de la especie metálica. Un decrecimiento en la longitud de enlace es muy probable que conduzca a un incremento en la fortaleza del mismo con el correspondiente incremento en su frecuencia de absorción en el espectro infrarrojo, IR. Esta disminución en la longitud de enlace C-O está de acuerdo con las frecuencias de absorción IR del enlace C-O en las especies [V(CO)₆]^-, [Cr(CO)₆], [Mn(CO)₆]⁺ y [Fe(CO)₆]²⁺, informadas en el trabajo de Geier y col.,⁷ siendo estas de 1897, 2029, 2125 y 2209 cm^-1 respectivamente.

Energía electrónica

La energía electrónica de átomos isoelectrónicos es una medida de la estabilidad electrónica de los mismos y puede considerarse como una medida de lo ligado que están los electrones del sistema al núcleo atómico. En los complejos estudiados aquí, la única diferencia entre ellos es la carga nuclear del metal. Por lo tanto, puede considerarse que la estabilidad electrónica de estos complejos viene dada por la energía electrónica, E_Elect, del sistema. En la Tabla 1 se informan los valores de E_Elect calculados a nivel B3LYP/6-311++G(2d,2p), en ella se observa que la E_Elect se incrementa en magnitud en el sentido [Ti(CO)₆]^2- < [V(CO)₆]^- < [Cr(CO)₆] < [Mn(CO)₆]⁺ < [Fe(CO)₆]²⁺ < [Co(CO)₆]³⁺.

Por otra parte, en la Figura 1 se observa una muy buena correlación lineal entre la E_Elect y la carga nuclear Z de la especie metálica. Podemos establecer entonces que la estabilidad electrónica de estos complejos es directamente proporcional a la carga nuclear de la especie metálica.

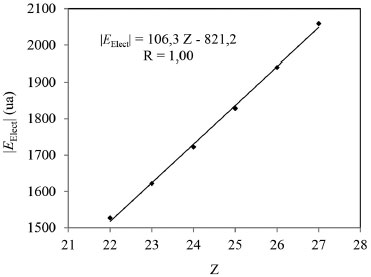Figura 1. Variación de la energía electrónica con la carga nuclear de la especie metálica

En el contexto de la QTAIM, la energía electrónica atómica total, E(Ω), puede considerarse como una medida de la estabilidad electrónica del átomo en la molécula.^15,16 Los valores de esta energía para la especie metálica, E(Ω_M), se incrementan en magnitud en el mismo sentido en que lo hace la E_Elect del sistema. Más aún, entre ambas magnitudes existe una muy buena correlación lineal, como se observa en la Figura 2. Esto demuestra que la estabilización electrónica de los complejos estudiados aquí se debe principalmente a la estabilización electrónica de la especie metálica.

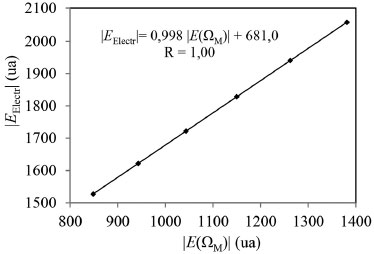Figura 2. Variación de la energía electrónica con la energía electrónica atómica total de la especie metálica

En la última columna de la Tabla 1 se informan las energías de interacción (ΔE). En ella se observa que para todos los complejos ΔE < 0, lo cual indica que los complejos son estables y las interacciones M^δ+∙∙∙^δ+C son estabilizantes, aún cuando estas se establecen entre átomos cargados positivamente.

Por otra parte, en el contexto de los enlaces de hidrógeno (EH), Grabowski⁴⁶ propuso considerar que aquellos EH cuyas energías de interacción sean inferiores a las -50 kcal mol^-1 sean consideradas como covalentes. Por la simetría que presentan estos carbonilos metálicos podríamos considerar la energía de interacción de cada enlace M-C como la energía de interacción de la supermulécula dividido seis (ΔE_M-C = ΔE/6), y realizar un análisis similar al efectuado por Grabowski para los EHs. En este sentido, se observa que ΔE_M-C toma valores inferiores a -50 kcal mol^-1 solo para los complejos [Fe(CO)₆]²⁺ y [Co(CO)₆]³⁺, en el resto los valores de ΔE_M-C son ligeramente superiores a -50 kcal mol^-1. En base a este análisis, podríamos considerar que las interacciones M^δ+∙∙∙^δ+C son covalentes o al menos tienen cierto grado de covalencia.

Topología de la densidad electrónica

La densidad electrónica, ρ(r), es una magnitud física real que tiene asociado un valor en cada punto del espacio. Se define como el número de electrones por unidad de volumen.^15,16 Se trata, por lo tanto, de un campo escalar definido sobre el espacio tridimensional. La forma de la distribución de carga electrónica en un sistema molecular es la manifestación física de las fuerzas que actúan en el sistema.^15,16 Entre esas fuerzas domina la fuerza atractiva ejercida por los núcleos sobre los electrones que rodean a los átomos, la cual es una consecuencia de la naturaleza localizada de la carga nuclear. Esta interacción es la principal responsable de la topología de la densidad electrónica en una molécula o cristal. El mapa de densidad electrónica de una molécula presenta una serie de peculiaridades topológicas muy interesantes, que nos proporcionan información muy valiosa sobre la estructura electrónica molecular. La formación del enlace químico genera una línea de máxima densidad electrónica que une a ambos núcleos interactuantes llamada camino de enlace, CE. Cualquier desplazamiento lateral de este camino nos lleva a una región con valores menores de la densidad electrónica. A lo largo del CE, los valores de la densidad electrónica es menor que en los núcleos, debido a la capacidad atractora de los mismos. Además, a lo largo del CE existe un punto en el cual la densidad electrónica presenta su valor más bajo. Se trata, de un punto de silla de segundo orden (mínimo respecto a la línea de enlace y máximo respecto al plano perpendicular al eje internuclear). Ese punto se denomina punto crítico de enlace, PCE^15-17 y se encuentra presente entre cada par de átomos que están enlazados químicamente.

Para el estudio de interacciones atómicas es importante destacar que un CE es un indicador universal de la existencia de una interacción enlazante.^15,16 La presencia física de un CE entre dos átomos implica una estabilización energética, ya que cada CE se manifiesta también en un camino de densidad de energía potencial que une los mismos núcleos, a lo largo del cual la densidad de energía potencial electrónica está máximamente estabilizada. En todos los complejos estudiados se observa (ver Figuras 3c y 3d) que existe un CE entre la especie metálica y el átomo de C del CO, esto confirma que estos átomos están unidos químicamente.

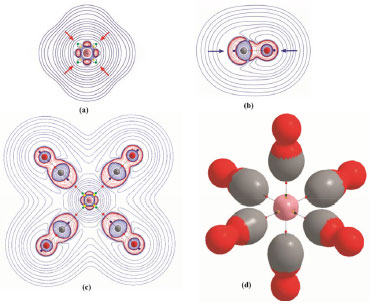Figura 3. Mapas de contorno de la función L(r) y superficies envolventes "envelops" [L(r)=0 ua] del complejo [Co(CO)₆]³⁺. Los mapas de contorno están dibujados en un plano que contiene: a) el núcleo del catión Co³⁺ aislado en su configuración electrónica más estable. Se indican los PCs (3,+1) y (3,+3) de la topología de L(r) en amarillo y verde respectivamente. Con flechas rojas se indican las regiones ácidas; b) los núcleos de la molécula de CO aislada. Se indican los PCs (3,-3) de la topología de L(r) en azul. Con flechas azules se indican las regiones básicas; y c) el núcleo del catión Co³⁺ y los núcleos de 4 moléculas de CO del complejo [Co(CO)₆]³⁺. Se indican los PCs (3,+1), (3,+3) (3,-3) de la topología de L(r) en amarillo, verde y azul respectivamente. En todos los casos se indican con líneas azules las regiones de depresión de carga electrónica y con líneas rojas las regiones de acumulación de carga electrónica. d) Superficie envolvente "envelop" L(r)=0 ua del complejo [Co(CO)₆]³⁺. Se indican además los caminos de enlace con sus respectivos PCs (3,-1) de ρ(r) en rojo y los PCs (3,+1) y (3,+3) de la topología de L(r) en amarillo y verde respectivamente

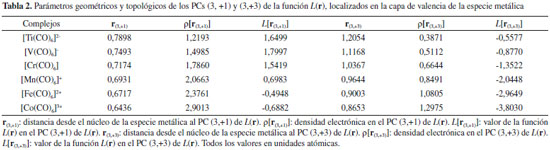
El valor de la densidad de carga electrónica en la región internuclear, en particular en el PCE, ρ(r_b), es una medida de la fortaleza de la interacción (especialmente cuando comparamos interacciones atómicas entre el mismo par de átomos), cuanto mayor es el valor de ρ(r_b) más fuerte es la interacción. Sin embargo, en la Tabla 1 se observa que estos valores no se incrementan en el mismo sentido en que lo hacen las E_Elect, por lo que ρ(r_b), para estos complejos, parece no ser un buen indicador de la estabilidad electrónica de los mismos.

Los valores de ρ(r_b) varían entre 0,0787 y 0,1069 ua, estos están en el mismo orden de magnitud que los valores informados por otros autores para interacciones similares.³⁰ Estos valores son relativamente altos comparados con los valores de ρ(r_b) en interacciones débiles como enlaces de hidrógeno y enlaces de halógeno [ρ(r_b) ≈ 0,03 ua], y relativamente bajos comprado con enlace covalentes convencionales [ρ(r_b) (C-H) ≈ 0,30 ua]. Los valores de la función L(r_b) = ‑¼∇²ρ(r_b) < 0, lo cual es indicativo de interacciones de capa cerrada, mientras que H(r_b) < 0 en todos los casos. Una situación similar se observa en el clásico aducto de Lewis H₃N-BH₃ [ρ(r_b) = 0.1006 ua, L(r_b) = ‑0.1197 ua y L(r_b)=-0.0612 ua]. Por lo tanto, las interacciones M∙∙∙C podrían considerarse como enlaces covalentes dativos.

De acuerdo al teorema del virial local, las densidades de energía cinética, G(r_b), y potencial, V(r_b), están relacionadas por la expresión: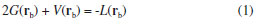

La ecuación anterior establece un balance entre la densidad de energía cinética, G(r_b), y la densidad de energía potencial, V(r_b), corregido por el valor de L(r_b) en el PCE. Puesto que G(r_b) es una magnitud positiva y V(r_b) es siempre negativa, L(r_b) será negativo cuando |V(r_b)| < 2G(r_b) y positivo en el caso contrario. Por otra parte, la densidad de energía electrónica total, H(r_b), está relacionada con G(r_b) y V(r_b) por la expresión: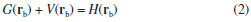

El análisis conjunto de las propiedades topológicas locales ρ(r_b), L(r_b) y H(r_b) permite investigar sobre la naturaleza de las interacciones interatómicas. Un valor negativo de H(r_b) indica que la energía potencial predomina sobre la cinética, y de acuerdo al teorema del virial, puede interpretarse como una consecuencia de la acumulación de carga electrónica en el PCE. Así, interacciones donde |V(r_b)| > 2G(r_b) y H(r_b) < 0, son interacciones de capa compartida. Mientras que cuando |V(r_b)| < 2G(r_b) y H(r_b) > 0 la interacción es de capa cerrada. Una situación interesante se presenta cuando H(r_b) < 0 pero |V(r_b)| < 2G(r_b), [L(r_b) < 0]. En este sentido, recientemente hemos mostrado^23,24 que en situaciones como esta, el decrecimiento de H(r_b) junto con el incremento de la densidad electrónica en el PCE es un indicador de la estabilización del complejo debido al incremento de la componente electrostática de la interacción. En la Tabla 1 se observa que los valores de H(r_b) siguen la misma tendencia que ρ(r_b). Más aún, existe una buena correlación lineal entre estas dos magnitudes (R=0,99 figura no mostrada). Por lo tanto, queda claro que el decrecimiento de H(r_b) junto con el incremento de ρ(r_b) en el PCE es un indicador de la estabilización de las interacciones M∙∙∙C.

Por otra parte, el análisis de las propiedades topológicas locales en el PC (3,-1) del enlace C-O, revela que la fortaleza de este enlace se incrementa en el mismo sentido en que lo hace la E_Elect. En otras palabras, a medida que se estabiliza el complejo el enlace C-O se hace más fuerte. No se observan cambios de elipticidad para este enlace, esta es nula en todos los complejos, lo cual implica que no hay cambio en el orden del enlace de la molécula CO.

Topología del Laplaciano de la densidad electrónica

El análisis topológico de la densidad electrónica constituye una excelente herramienta para abordar una investigación profunda de las propiedades electrónicas de un sistema molecular, permitiendo la exploración de interacciones interatómicas. Por otra parte su función derivada, el Laplaciano de la densidad electrónica, ∇²ρ(r), es más sensible y brinda información complementaria del sistema electrónico molecular en observación. Para el análisis topológico de este campo escalar es más útil analizar la función L(r) = -¼∇²ρ(r). La topología de esta función permite identificar regiones de concentración [L(r) > 0] y de depresión [L(r) < 0] de carga electrónica.

Una propiedad importante que presenta la topología de L(r) es que muestra la estructura de capas cuánticas de los átomos a partir de una función derivada de una propiedad física real. Para cada capa cuántica principal, la función L(r) muestra pares de regiones, una negativa y otra positiva, siendo las regiones internas, zonas de concentración de carga electrónica y las zonas externas de depresión de carga electrónica. El número de capas definidas en términos de la función L(r) puede ser menor que el número cuántico principal para elementos situados en el sistema periódico después del Calcio. La distribución de esta función si bien exhibe el número requerido de máximos y mínimos exteriores para elementos con Z > 40, no presenta los correspondientes cambios de signo.^47,48 A la concentración de carga de la capa más externa de un átomo se la llama concentración de carga de la capa de valencia, CCCV, y a la depresión de carga más externa se la llama depresión de carga de la capa de valencia, DCCV.

Basados en esta topología, Bader y col.^15,16 enunciaron el Principio de Complementariedad, el cual establece que: "Un máximo de concentración de carga electrónica, de un átomo en una molécula se combina con un mínimo de concentración de carga de otro átomo". Por lo tanto, la función L(r) constituye una excelente herramienta para explorar las regiones que rodean a la especie metálica M que serán susceptibles para el ataque nucleofílico, y los cambios electrónicos que se producen cuando M interacciona con los ligandos para formar los complejos de coordinación.

De acuerdo a Bader y col. la topología de la función L(r) en el espacio real es una consecuencia del apareamiento de los electrones determinada por la densidad condicional de pares en seis dimensiones espaciales.⁴⁹ Además, la topología de L(r) provee la base física para la localización de los pares electrónicos de la teoría de Lewis.

En la Figura 3 se muestran los PCs (3,-3) de L(r) de los átomos de carbono y oxígeno y los PCs (3,+1) y (3,+3) de la función L(r) de la especie metálica. En ella se observa que la molécula de CO tiene dos máximos no enlazantes [PCs (3,-3) de L(r)] y por lo tanto dos pares libres, uno sobre el átomo de C y otro sobre el átomo de O. El máximo de CCCV del C está más alejado del núcleo del C (≈ 0,9 Å), que el máximo de CCCV del O del núcleo del O (≈ 0,6 Å). Este hecho hace que el par libre del C sea más polarizable que el par libre del O, razón por la cual el CO produce su ataque nuclefílico por el lado del C, a pesar que este átomo esté cargado positivamente. Luego de la complejación, el par libre del átomo de C experimenta cambios significativos, observándose una importante polarización de su CCCV en la dirección de la interacción Co³⁺∙∙∙C (ver Figuras 3b y 3c), producto de la interacción electrostática entre el par libre del átomo de C y la carga nuclear del catión Co³⁺. Una situación similar se ha observado en las interacciones enlazadas por halógeno.^27-29

Además, en las Figuras 3c y 3d también se observa que las moléculas se orientan de modo que las regiones de CCCV de los átomos de carbono [PCs (3,-3) de L(r)], se alinean con las regiones de máxima depresión de carga de la capa de valencia [PCs (3,+1) y (3,+3) de L(r)] de la especie metálica. En otras palabras, en todos los complejos se observa (ver Figura S1 de la información soporte) que las regiones de acumulación de carga electrónica ("lump" - región básica) de la base de Lewis se complementan con las regiones de depresión de carga electrónica ("hole" - región ácida) de la especie metálica. Este "hole" en M alrededor de los PCs (3,+1) y (3,+3) de L(r) permite la interacción electrostática entre el núcleo desprotegido de M y el "lump" (par libre) de la base de Lewis CO.

En un trabajo previo sobre interacciones moleculares enlazadas por halógenos, hemos determinado que la fortaleza de las interacciones Cl∙∙∙N en los sistemas FCl∙∙∙NX₃ (con X= -H, -F, -CH₃) correlaciona muy bien con propiedades topológicas locales medidas en el PC (3,+1) de L(r) del átomo de cloro, localizado en la dirección axial opuesta al enlace σ_F-Cl.²⁷ En el presente trabajo hemos explorado cómo se comportan las propiedades topológicas locales medidas sobre los PCs (3,+1) y (3,+3) de L(r) perteneciente a la especie metálica. En la Tabla 2 se informan estos valores.

En todos los complejos estudiados se observa que r_(3,+1) < r_(3,+3). Además, ambas distancias disminuyen en el sentido [Ti(CO)₆]^2- < [V(CO)₆]^- < [Cr(CO)₆] < [Mn(CO)₆]⁺ < [Fe(CO)₆]²⁺ < [Co(CO)₆]³⁺. Es decir, las distancias r_(3,+1) y r_(3,+3) siguen la misma tendencia que el radio atómico, que disminuye de izquierda a derecha en un período de la tabla periódica. La densidad electrónica medida en los PCs (3,+1) y (3,+3) de L(r), ρ[r_(3,+1)] y ρ[r_(3,+3)] respectivamente, se incrementa en el mismo sentido que la magnitud E_Elect. Más aún, la Figura 4 muestra una buena correlación lineal entre ρ[r_(3,+1)] y ρ[r_(3,+3)] y la E_Elect, lo cual pone de manifiesto que el aumento de la estabilidad electrónica del sistema guarda relación directa con el aumento de la densidad electrónica en las regiones acidas de la especie metálica. En otras palabras, a medida que se incrementa la estabilidad electrónica del sistema aumenta la donación-σ.

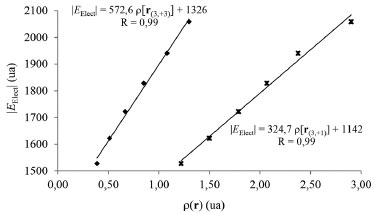Figura 4. Variación de la energía electrónica con la densidad electrónica calculada en los PCs (3,+1) y (3,+3) de la función L(r)

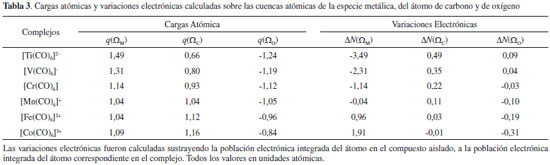
De acuerdo a la IUPAC, un enlace covalente coordinado resulta de la interacción entre dos especies moleculares, una de las cuales actúa como donante y otra como aceptor de un par electrónico que se comparte en el complejo formado, por ejemplo, el enlace N→B en el aducto de Lewis H₃N→BH₃.⁵⁰ De acuerdo a la información brindada por el análisis topológico de L(r), resulta evidente que el aumento de la densidad electrónica en las regiones acidas de la especie metálica se debe al aporte electrónico que realiza el par libre de la base de Lewis. En otras palabras, la transferencia electrónica desde la base de Lewis a la especie metálica (donación-σ) puede considerarse la evidencia física de la formación de un enlace covalente coordinado entre la especie metálica y el átomo de carbono, C→M. Además, de acuerdo a la tendencia observada en el incremento de ρ[r_(3,+1)] y ρ[r_(3,+3)] conforme aumenta la estabilidad del complejo, podemos decir que el carácter de enlace covalente dativo C→M se incrementa en el sentido C→Ti < C→V < C→Cr < C→Mn < C→Fe < C→Co.

De acuerdo con la discusión precedente, se puede establecer que la topología del Laplaciano de la densidad electrónica muestra claramente que parte de la estabilidad de las interacciones M^δ+∙∙∙^δ+C se debe a la donación-σ y a la fuerza electrostática que el núcleo metálico ejerce sobre cada par libre del C carbonílico debido a la depresión de carga electrónica que la especie metálica posee en las direcciones de los vértices de un octaedro regular. Además, el incremento de la carga electrónica en las regiones ácidas de la especie metálica [PCs (3,+1) y (3,+3) de L(r)] puede considerarse la evidencia física de la formación de un enlace covalente coordinado entre la especie metálica y el átomo de carbono, C→M.

Cargas atómicas

La idea cualitativa de que los átomos en las moléculas son más negativos o más positivos que otros ha sido muy útil en la racionalización y la predicción del comportamiento químico. Sin embargo, los intentos por cuantificar esta idea no han sido del todo satisfactorios. Ni la electronegatividad ni la carga atómica son observables físicos, y por lo tanto no tienen una fórmula matemática única. A pesar de esto son numerosos los procedimientos que han sido, y siguen siendo, propuestos para la asignación de valores numéricos a electronegatividades y cargas atómicas. En este apartado queremos llamar la atención sobre las predicciones erróneas en las que podemos incurrir si solo consideramos las cargas atómicas para predecir el comportamiento de los átomos presentes en una molécula. Cuando se asigna una carga a un átomo, estamos dando un valor numérico a todo el átomo y pasamos a considerarlo una partícula. En la Tabla 3 se informan las cargas atómicas de la especie metálica y de los átomos de C y O. En ella se observa que en todos los casos la especie metálica central tiene carga positiva, y esta disminuye en el sentido [Ti(CO)₆]^2- < [V(CO)₆]^- < [Cr(CO)₆] < [Mn(CO)₆]⁺ < [Fe(CO)₆]²⁺ < [Co(CO)₆]³⁺, mientras que en este mismo sentido se incrementa la carga positiva sobre el átomo de carbono y disminuye en magnitud la carga negativa sobre el átomo de oxígeno.

Es importante notar aquí que esta situación es un tanto inusual, la carga atómica del átomo de carbono es siempre positiva y la carga atómica de la especie metálica también, sin embargo entre ellos se produce una interacción estabilizante. En este punto es conveniente recordar que los átomos cuando se combinan para formar moléculas deforman su densidad electrónica esférica, acumulando carga electrónica en algunas regiones. En este sentido, recientemente Clark⁵¹ ha señalado que muchos átomos unidos covalentemente no pueden ser representados adecuadamente por una carga atómica neta, porque los átomos en una molécula se ven negativos en algunas direcciones y positivos en otras. En el caso particular de la molécula de CO, es lógico suponer que sobre el átomo de carbono, en la región axial opuesta al enlace C-O, se verá una carga parcial negativa que interacciona con la carga positiva de la especie metálica, a pesar de que la carga total del átomo de carbono es positiva.

Análisis de la transferencia de carga electrónica por QTAIM

El análisis de la cantidad de electrones presentes en cada una de las cuencas atómicas es una herramienta muy útil que ofrece la QTAIM para hacer un análisis directo de como se altera la población electrónica en las cuencas atómicas de los átomos interactuantes. En la Tabla 3, se informan estos valores para la especie metálica y para los átomos de C y de O. En ella se observa que el metal cede carga electrónica [ΔN(Ω_M) < 0] al CO en los complejos [Ti(CO)₆]^2-, [V(CO)₆]^-, [Cr(CO)₆] y [Mn(CO)₆]⁺ mientras que en los complejos [Fe(CO)₆]²⁺ y [Co(CO)₆]³⁺ el metal acepta carga electrónica [ΔN(Ω_M) > 0] de la base de Lewis. En consecuencia, pareciera ser que la retrodonación-π se incrementa en mismo sentido en que lo hace la carga positiva (QTAIM) de la especie metálica y la donación-σ se incrementa en sentido opuesto al incremento de la carga positiva (QTAIM) del metal. En el complejo [Mn(CO)₆]⁺ prácticamente no se observa transferencia de carga electrónica en ningún sentido, probablemente en este complejo la donación-σ este compensada por la retrodonación-π. Por otra parte, una buena correlación lineal se ha encontrado entre la carga transferida [ΔN(Ω_M)] y la |E_Elect| (ver Figura 5). Por lo tanto, la transferencia de carga electrónica juega un papel muy importante en la estabilidad electrónica de estos complejos.

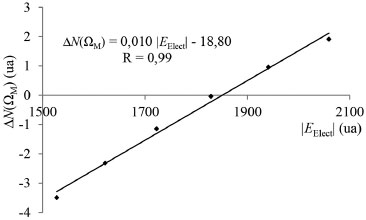Figura 5. Variación de la carga electrónica transferida entre el metal y la base de Lewis, medida sobre la cuenca electrónica del metal, y la energía electrónica del sistema

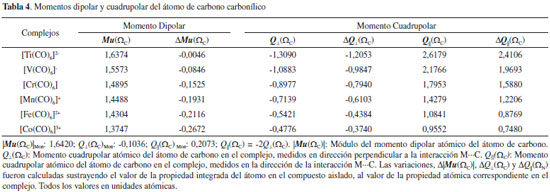
Momento dipolar y cuadrupolar

Los momentos dipolares y cuadrupolares atómicos son magnitudes muy útiles para analizar las variaciones electrónicas que experimentan los átomos cuando estos forman parte de un enlace químico. En la Tabla 4 se informan están magnitudes y sus correspondientes variaciones medidas sobre la cuenca atómica del átomo de C de la molécula de CO. En todos los carbonilos metálicos estudiados aquí, se observa que el módulo del momento dipolar del átomo de carbono es menor en el complejo [ΔMu(Ω_C) < 0]. Este decrecimiento se puede interpretar como un reordenamiento de la nube electrónica del carbono, producto de la interacción con la especie metálica. Este reordenamiento electrónico es directamente proporcional a la estabilidad electrónica de los complejos estudiados. La Figura 6, muestra La correlación lineal encontrada entre |E_Elect| y Mu(Ω_C).

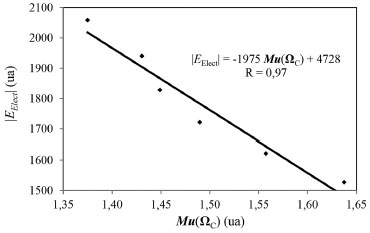Figura 6. Variación de la energía electrónica del sistema con el momento dipolar atómico del átomo de C

El momento cuadrupolar de una molécula lineal proporciona una medida de la acumulación o depresión de carga electrónica a lo largo del eje molecular y en la dirección perpendicular al mismo. El momento cuadrupolar atómico, Q(Ω), se define como la traza del tensor momento cuadrupolar atómico.^15,16 Sobre el átomo de C en la molécula de CO solo hay dos componentes independientes, la componente paralela, Q_||(Ω_C), medida sobre el eje de simetría de la molécula y dos componentes perpendiculares, Q_⊥(Ω_C), equivalentes por simetría, medidas en direcciones perpendiculares al eje molecular.

Los cambios en Q_||(Ω_C) y Q_⊥(Ω_C) proporcionan una determinación directa de la extensión de transferencia de densidad electrónica entre el metal y el ligando. De acuerdo a Bader y col.⁵² las magnitudes Q_||(Ω_C) y Q_⊥(Ω_C) proporcionan una medida directa de la donación-σ desde el CO al metal y de la retrodonación-π desde el metal al CO respectivamente. La disminución de Q_||(Ω_C) indica un aumento de la donación-σ y el incremento en magnitud de Q_⊥(Ω_C) indica un aumento de la retrodonación-π. En otras palabras, las magnitudes Q_||(Ω_C) y Q_⊥(Ω_C) proporcionan una evidencia directa del mecanismo de Dewar-Chatt-Duncanson que explica la estabilidad de los carbonilos metálicos. Estas magnitudes se informan en la Tabla 4.

En la Tabla 4 se observa un incremento dramático de estas magnitudes cuando la molécula de CO se acompleja. Así Q_⊥(Ω_C)_Mon= -0,1036 ua, mientras que en los complejos esta magnitud varía entre -1,3090 y -0,4776 ua. De manera análoga Q_||(Ω_C)_Mon=0,2073 ua, mientras que en los complejos varía entre 2,6179 y 0,9552 ua.

Los valores de Q_⊥(Ω_C) se incrementan en magnitud en el sentido [Co(CO)₆]³⁺ < [Fe(CO)₆]²⁺ < [Mn(CO)₆]⁺ < [Cr(CO)₆] < [V(CO)₆]^- < [Ti(CO)₆]^2-, lo cual pone en evidencia que la retrodonación-π se incrementa en este orden. Por otra parte, los valores de Q_||(Ω_C), medidos en la dirección de la interacción M∙∙∙C disminuyen en el sentido [Ti(CO)₆]^2- > [V(CO)₆]^- > [Cr(CO)₆] > [Mn(CO)₆]⁺ > [Fe(CO)₆]²⁺ > [Co(CO)₆]³⁺, lo cual indica que en este sentido se incrementa la donación-σ.

Por otra parte, la energía electrónica de las especies metálicas isoelectrónicas puede considerarse como una medida de lo ligado que están los electrones del sistema al núcleo atómico. El incremento en magnitud de la energía electrónica hace que los electrones de valencia del átomo central estén más ligados a su núcleo atómico y en consecuencia estén menos disponibles para la transferencia electrónica π desde el metal hacia el CO. En la Tabla 4 se observa que |E_Elect| se incrementa en el mismo sentido en que Q_⊥(Ω_C) y Q_||(Ω_C) disminuyen en magnitud. Es decir, el aumento de la carga nuclear de la especie metálica provoca que los electrones que rodean al átomo central se sientan fuertemente atraídos por su núcleo disminuyendo la capacidad de transferirse por retrodonación-π e incrementando la transferencia de carga electrónica desde la base de Lewis por donación-σ. En otras palabras, la retrodonación-π disminuye y la donación-σ se incrementa con el aumento de la carga nuclear de la especie metálica.

Comportamiento de V(r) y G(r)

Las densidades de energía potencial y cinética son magnitudes muy importante para la comprensión del enlace químico, por lo que, un análisis exhaustivo de estas magnitudes en los PCE M∙∙∙C y sobre las cuencas de los átomos interactuantes debe dar información crucial para la comprensión sobre la naturaleza de las interacciones atómicas. La densidad local de energía potencial en el PCE, V(r_b), puede dividirse en dos contribuciones; V_e-n(r_b): contribución atractiva (atracción electrón-núcleo) y V_rep(r_b): contribución repulsiva (repulsión electrón-electrón y repulsión núcleo-núcleo). Por otra parte, la integración de la densidad electrónica sobre la cuenca atómica de un átomo permite determinar la energía de interacción electrostática entre la distribución de carga electrónica de un átomo A y el núcleo de un átomo B, V_e-n(A,B). En la Tabla 5, se informan las densidades locales de energía cinética, G(r_b), y potencial, V_rep(r_b), V_e-n(r_b) y V(r_b) medidos sobre los PCE M∙∙∙C, y las densidades de energía potencial de interacción electrostática electrón-núcleo V_e-n(C,M).

La contribución atractiva V_e-n(r_b), es una medida de la fuerza con que los núcleos de los átomos interactuantes atraen la densidad electrónica localizada en la región internuclear cercanas al PCE. Mientras que la contribución repulsiva V_rep(r_b), es una medida de las fuerzas repulsivas que experimenta el sistema en la región internuclear. En todos los dímeros estudiados, se observa que |V_e-n(r_b)| > V_rep(r_b) (ver Tabla 5), lo cual indica que la atracción electrostática electrón-núcleo es superior a las fuerzas electrostáticas repulsivas presentes en la región internuclear de los átomos interactuantes. Además, la magnitud V_e-n(r_b) siguen la misma tendencia que las E_Elect, lo cual sugiere que la interacción electrostática entre la densidad electrónica localizada entre los átomos interactuantes y sus núcleos juega un papel importante en la estabilización de estos complejos.

La densidad de energía potencial en el PCE, V(r_b), es una medida de la capacidad que tiene el sistema para concentrar electrones en este punto, mientras que el valor de la densidad de energía cinética en el PCE, G(r_b), brinda información acerca de la tendencia que tienen los electrones a diluirse del mismo.⁵³ En la Tabla 5 se observa que |V(r_b)| > G(r_b) lo cual pone de manifiesto que la capacidad que tiene el sistema para concentrar electrones en la región internuclear de los átomos interactuantes M y C es mayor que la capacidad para difuminarlos. Esta acumulación de carga electrónica en la región interatómica de la interacción M∙∙∙C permite a los electrones sentir la atracción de ambos núcleos, lo que incrementa en magnitud su energía potencial.

Un análisis similar sobre el PC (3,+1) de L(r) perteneciente a la especie metálica se llevo a cabo. En la Figura 7 se muestra la relación existente entre la densidad de carga electrónica en el PC (3,+1) de L(r) y las densidades locales de energía potencial y cinética en el mismo punto. La correlación lineal pone de manifiesto que V[r_(3,+1)] es un buen indicador de la capacidad que tiene el sistema para concentrar electrones en las regiones ácidas de la especie metálica. Además, en la Figura 7 se observa, una relación lineal entre G[r_(3,+1)] y la densidad electrónica en el PC (3,+1) de L(r), esto indica, que a medida que el sistema aumenta la capacidad para concentrar electrones en el PC (3,+1) de L(r), también incrementa la capacidad para difuminarlos. Sin embargo, la pendiente de la recta - V[r_(3,+1)] Vs. ρ[r_(3,+1)] es de 19,27, mientras que la recta G[r_(3,+1)] Vs. ρ[r₍₃₊₁₎] tiene una pendiente de 10,48. Es decir, a medida que aumenta la fortaleza de las interacciones M∙∙∙C, el sistema incrementa la capacidad de acumular densidad electrónica en el PC (3,+1) más rápidamente que la capacidad para difuminarlos. El incremento de densidad electrónica en el PC (3,+1) de L(r) se debe a la transferencia de carga electrónica desde el par libre de la base de Lewis hacia la especie metálica. Por lo tanto, pareciera que la magnitud V[r_(3,+1)] es un buen indicador del carácter de enlace covalente dativo que presentan estos complejos.

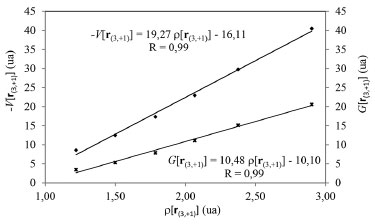Figura 7. Correlación entre las densidades locales de energía potencial y cinética y la densidad electrónica en el PC (3,+1) de L(r)

La energía de interacción electrostática entre la distribución de carga electrónica del átomo de carbono y el núcleo del metal es medida por V_e-n(C,M). En la Tabla 5 se observa que esta magnitud crece con el incremento de la carga nuclear del metal, siguiendo el mismo orden que las E_Elect. Más aun, la Figura 8 muestra una buena correlación cuadrática entre ambas magnitudes. Esto nos permite establecer que cuanto mayor es la carga nuclear del metal, más ligados están los electrones de la base de Lewis al núcleo del metal.

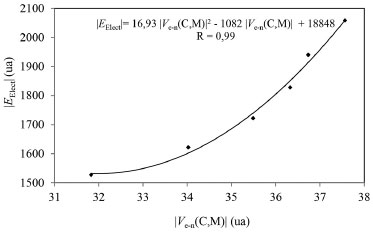Figura 8. Variación de la energía electrónica con la energía de interacción electrostática entre la distribución de carga electrónica del átomo de carbono y el núcleo del metal

Análisis de la función de localización electrónica

La función de localización electrónica (ELF) al igual que la densidad electrónica es una función escalar susceptible de análisis topológico. La función ELF, propuesta por Becke y Edgecombe,⁵⁴ puede ser entendida como una medida de la localización de los electrones en los sistemas atómicos y moleculares. En otras palabras, es la probabilidad promediada esféricamente de encontrar en los alrededores de un electrón que se toma como referencia otro del mismo espín. Desde un punto de vista físico, esta función permite determinar las regiones de un sistema polielectrónico que están dominadas por la probabilidad de encontrar pares de electrones apareados. El análisis topológico de la función ELF revela la existencia de máximos locales, llamados atractores, y las regiones del espacio asociados a las mismas denominadas cuencas. Estas cuencas, pueden clasificarse en cuencas nucleares (C) que contienen electrones de las capas internas de los átomos, o de valencia (V) asociada con los electrones externos, esta última vinculada a los pares electrónicos enlazados y los pares electrónicos no compartidos.

En la Figura 9 se muestran las isosuperficies de la función ELF para la molécula aislada de CO, el catión Co³⁺ y el complejo [Co(CO)₆]³⁺ y se informan las poblaciones electrónicas de la cuenca de valencia correspondiente al par libre del átomo de carbono en el monómero y complejo. El análisis de estas poblaciones electrónicas pone de manifiesto la redistribución electrónica que se produce en el par libre del átomo de carbono como resultado de la interacción con la especie metálica. Se observa una disminución de la población electrónica en el complejo respecto del monómero aislado de 0,22e. Esta variación revela la transferencia de carga electrónica que se produce desde el par libre del átomo de carbono hacia la especie metálica, como resultado de la formación del complejo.

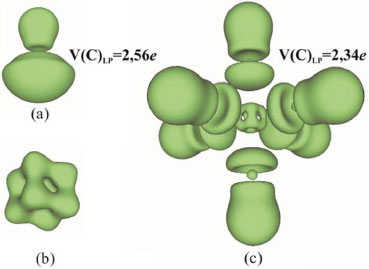Figura 9. Isosuperficie de la función ELF para a) CO b) Co³⁺ c) Complejo [Co(CO)₆]³⁺ a un isocontorno de η=0,70

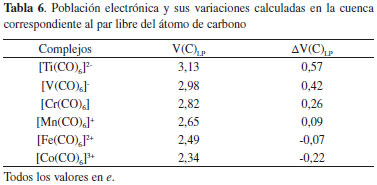
En la Tabla 6 se informan las poblaciones de la cuenca de valencia correspondiente al par libre del átomo de carbono en el complejo [V(C)_LP] y las variaciones respecto del monómero aislado [ΔV(C)_LP]. En ella se observa que V(C)_LP disminuye en el mismo sentido en que la E_Elect se incrementa en magnitud. El análisis de ∆V(C)_LP muestra que, está magnitud es directamente proporcional a E_Elect (R=1,00; figura no mostrada). Además, ∆V(C)_LP revela que en los complejos [Ti(CO)₆]^2-, [V(CO)₆]^-, [Cr(CO)₆] y [Mn(CO)₆]⁺ la población electrónica del par libre del carbono se incrementa, probablemente debido a que en estos predomina la retrodonación-π, mientras que en los complejos [Fe(CO)₆]²⁺ y [Co(CO)₆]³⁺ ocurre lo contrario, debido al predominio de la donación-σ. En otras palabras la retrodonación-π se incrementa en el sentido [Co(CO)₆]³⁺ < [Fe(CO)₆]²⁺ < [Mn(CO)₆]⁺ < [Cr(CO)₆] < [V(CO)₆]^- < [Ti(CO)₆]^2- y la donación-σ en sentido inverso. Estos resultados están de acuerdo con los resultados QTAIM discutidos anteriormente.

CONCLUSIONES

En este trabajo se realizó un análisis de la distribución de la densidad de carga electrónica y su función Laplaciana en el marco de la QTAIM en los complejos de coordinación isoelectrónicos [Ti(CO)₆]^2-, [V(CO)₆]^-, [Cr(CO)₆], [Mn(CO)₆]⁺, [Fe(CO)₆]²⁺ y [Co(CO)₆]³⁺.

El análisis de las energías electrónicas de los complejos y de la especie metálica revela que la estabilidad de los carbonilos metálicos estudiados aquí se debe principalmente a la estabilización electrónica de la especie metálica.

De acuerdo con la topología del Laplaciano de la densidad electrónica, la formación de los complejos resulta de la interacción electrostática entre la densidad de carga electrónica provista por el par libre del C carbonílico y el núcleo atómico de la especie metálica.

El análisis de la densidad de energía potencial y cinética muestra que a medida que aumenta la estabilidad de los complejos, , , , , el sistema incrementa la capacidad de acumular densidad electrónica en las regiones internucleares M∙∙∙C y en la regiones ácidas de la especie metálica. Los resultados sugieren que la densidad de energía potencial medida en las regiones ácidas de la especie metálica, V[r_(3,+1)], es un buen indicador del carácter de enlace covalente dativo que presentan los complejos aquí estudiados. Finalmente, la magnitud V_e-n(C,M) muestra que cuanto mayor es la carga nuclear del metal, más ligados están los electrones de la base de Lewis al núcleo del metal.

Este estudio demuestra que el análisis QTAIM es una herramienta muy confiable para el estudio de los complejos de coordinación, explica la geometría que presentan los mismos y permite dilucidar la naturaleza electrónica de las interacciones Metal-Ligando. Finalmente, las conclusiones de este trabajo están basadas en un observable físico real, la distribución de la densidad de carga electrónica, la cual puede ser obtenida experimentalmente o por métodos computacionales.

AGRADECIMIENTOS

Los autores agradecen a la Secretaría General de Ciencia y Técnica de la Universidad Nacional del Nordeste, (SEGCYT-UNNE) por el aporte financiero.

REFERENCIAS

1. Frenking, G.; Frölich, N.; Chem. Rev. 2000, 100, 717. DOI: http://dx.doi.org/10.1021/cr980401l PMID: 11749249

2. Frenking, G.; Wichmann, K.; Frölich, N.; Loschen, C.; Lein, M.; Frunzke, J.; Rayon, V. M.; Coord. Chem. Rev. 2003, 238, 55. DOI: http://dx.doi.org/10.1016/S0010-8545(02)00285-0

3. Davidson, E. R.; Machado, F. B. C.; J. Phys. Chem. 1993, 97, 4397. DOI: http://dx.doi.org/10.1021/j100119a024

4. Barnes, L. A.; Liu, B.; Lindh, R.; J. Chem. Phys 1993, 98, 3978. DOI: http://dx.doi.org/10.1063/1.464026

5. Ehlers, A. W.; Frenking, G.; J. Am. Chem. Soc. 1994, 116, 1514. DOI: http://dx.doi.org/10.1021/ja00083a040

6. Fonseca Guerra, C.; Handgraaf, J.-W.; Baerends, E. J.; Bickelhaupt, F. M.; J. Comput. Chem. 2004, 25, 189. DOI: http://dx.doi.org/10.1002/jcc.10351 PMID: 14648618

7. Geier, J.; Willner, H.; Lehmann, C. W.; Aubke, F.; Inorg. Chem. 2007, 46, 7210. DOI: http://dx.doi.org/10.1021/ic700798z PMID: 17616186

8. Brathwaite, A. D.; Reed, Z. D.; Duncan, M. A.; J. Phys. Chem. A 2011, 115, 10461. DOI: http://dx.doi.org/10.1021/jp206102z PMID: 21861528

9. Brathwaite, A. D.; Duncan, M. A.; J. Phys. Chem. A 2013, 117, 11695. DOI: http://dx.doi.org/10.1021/jp400793h PMID: 23485174

10. Cui, J.; Zhou, X.; Wang, G.; Chi, C.; Liu, Z.; Zhou, M.; J. Phys. Chem. A 2013, 117, 7810. DOI: http://dx.doi.org/10.1021/jp405250y PMID: 23895186

11. Cui, J.; Zhou, X.; Wang, G.; Chi, C.; Li, Z. H.; Zhou, M.; J. Phys. Chem. A 2014, 118, 2719. DOI: http://dx.doi.org/10.1021/jp411237p PMID: 24673590

12. Reed, Z. D.; Duncan, M. A.; J. Am. Soc. Mass. Spectrom. 2010, 21, 739. DOI: http://dx.doi.org/10.1016/j.jasms.2010.01.022 PMID: 20188586

13. Xie, H.; Wang, J.; Qin, Z.; Shi, L.; Tang, Z.; Xing, X.; J. Phys. Chem. A 2014, 118, 9380. DOI: http://dx.doi.org/10.1021/jp504079k PMID: 25203282

14. Ehlers, A. W.; Ruiz-Morales, Y.; Baerends, E. J.; Ziegler, T.; Inorg. Chem. 1997, 36, 5031. DOI: http://dx.doi.org/10.1021/ic970223z

15. Bader, R. F. W.; Atoms in Molecules. A Quantum Theory, Clarendon: Oxford, 1990.

16. Popelier, P.; Atoms in Molecules: An Introduction, Prentice Hall: Harlow, 2000.

17. Gillespie, R. J.; Popelier, P. L. A.; Chemical Bonding and Molecular Geometry, Oxford University Press: Oxford, 2001.

18. MacDougall, P. J.; Hall, M. B.; Trans. Am. Cryst. Assoc. 1990, 26, 105.

19. Macchi, P.; Sironi, A.; Coord. Chem. Rev. 2003, 238, 383. DOI: http://dx.doi.org/10.1016/S0010-8545(02)00252-7

20. Cortés-Guzmán, F.; Bader, R. F. W.; Coord. Chem. Rev. 2005. 249, 633. DOI: http://dx.doi.org/10.1016/j.ccr.2004.08.022

21. Farrugia, L. J.; Senn, H. M.; J. Phys. Chem. A 2010, 114, 13418. DOI: http://dx.doi.org/10.1021/jp1098624 PMID: 21182291

22. Farrugia, L. J.; Evans, C.; Senn, H. M.; Hänninen, M. M.; Sillanpää, R.; Organometallics 2012, 31, 2559. DOI: http://dx.doi.org/10.1021/om2011744

23. Angelina, E. L.; Duarte, D. J. R.; Peruchena, N. M.; J. Mol. Model. 2013, 19, 2097. DOI: http://dx.doi.org/10.1007/s00894-012-1674-y PMID: 23187685

24. Duarte, D. J. R.; Angelina, E. L.; Peruchena, N. M.; J. Mol. Model. 2014, 20, 2510. DOI: http://dx.doi.org/10.1007/s00894-014-2510-3 PMID: 25367044

25. Duarte, D. J. R.; Silva Miranda, M.; Esteves da Silva, J. C. G.; Struct. Chem. 2015, 26, 565. DOI: http://dx.doi.org/10.1007/s11224-014-0519-y

26. Duarte, D. J. R.; Vallejos, M. M.; Peruchena, N. M.; J. Mol. Model. 2010, 16, 737. DOI: http://dx.doi.org/10.1007/s00894-009-0558-2 PMID: 19820973

27. Duarte, D. J. R.; Sosa, G. L.; Peruchena, N. M.; J. Mol. Model. 2013, 19, 2035. DOI: http://dx.doi.org/10.1007/s00894-012-1624-8 PMID: 23076553

28. Duarte, D. J. R.; Angelina, E. L.; Peruchena, N. M.; Comput. Theor. Chem. 2012, 998, 164. DOI: http://dx.doi.org/10.1016/j.comptc.2012.07.019

29. Duarte, D. J. R.; Peruchena, N. M.; Alkorta, I.; J. Phys. Chem. A 2015, 119, 3746. DOI: http://dx.doi.org/10.1021/jp511118s PMID: 25826009

30. Goldman, A. S.; Krogh-Jespersen, K.; J. Am. Chem. Soc. 1996, 118, 12159. DOI: http://dx.doi.org/10.1021/ja960876z

31. Lupinetti, A. J.; Jonas, V.; Thiel, W.; Strauss, S. H.; Frenking, G.; Chem. Eur. J. 1999, 5, 2573. DOI: http://dx.doi.org/10.1002/(SICI)1521-3765(19990903)5:9<2573::AID-CHEM2573>3.0.CO;2-J

32. Lupinetti, A. J.; Fau, S.; Frenking, G.; Strauss, S. H.; J. Phys. Chem. A 1997, 101, 9551. DOI: http://dx.doi.org/10.1021/jp972657l

33. Li, H.; Sun, F. W.; King, R. B.; Schaefer, H. F.; Inorg. Chem. 2013, 52, 6893. DOI: http://dx.doi.org/10.1021/ic400797b PMID: 23721544

34. Matta, C. F.; Gillespie, R. J.; J. Chem. Educ. 2002, 79, 1141. DOI: http://dx.doi.org/10.1021/ed079p1141

35. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Zakrzewski, V. G.; Montgomery Jr., J. A.; Stratmann, R. E.; Burant, J. C.; Dapprich, S.; Millam, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G. A.; Ayala, P. Y.; Cui, Q.; Morokuma, K.; Rega, N.; Salvador, P.; Dannenberg, J. J.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Cioslowski, J.; Ortiz, J. V.; Baboul, A. G.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Andres, J. L.; Gonzalez, C.; Head-Gordon, M.; Replogle, E. S.; Pople, J. A.; Gaussian 03, Revision D.01, Gaussian Inc., Wallingford, CT, 2004.

36. Becke, A. D.; J. Chem. Phys. 1993, 98, 5648; Lee, C.; Yang, W.; Parr, R. G.; Phys. Rev. B 1988, 37, 785. DOI: http://dx.doi.org/10.1063/1.464913

37. Farrugia, L. J.; Evans, C.; J. Phys. Chem. A 2005, 109, 8834. DOI: http://dx.doi.org/10.1021/jp053107n PMID: 16834287

38. Schläfer, H. L.; Gliemann, G.; Basic Principles of Ligand Field Theory, Wiley Interscience: New York; 1969.

39. Keith, Todd A. AIMAll (Version 11.12.19); TK Gristmill Software, Overland Park KS, 2011

40. Blieger-König S. F.; Schönbohn J., AIM2000 Program Package, Version. 2.0 Copyright 2002, Chemical adviser by Bader, R.F.W., Büro fur Innovative Software Strieibel Blieger-König, Germany, 2000.

41. Lu, T.; Chen, F.; J. Comp. Chem. 2012, 33, 580. DOI: http://dx.doi.org/10.1002/jcc.22885

42. Fischer, P. J.; Young, V. G. Jr.; Ellis, J. E.; Chem. Commun. 1997, 1249. DOI: http://dx.doi.org/10.1039/a701143a

43. Bellard, S.; Rubinson, K. A.; Sheldrick, G. M.; Acta Cristallogr. 1979, B35, 271. DOI: http://dx.doi.org/10.1107/S0567740879003332

44. Bernhardt, E.; Bley, B.; Wartchow, R.; Willner, H.; Bill, E.; Kuhn, P.; Sham, I. H. T.; Bodenbinder, M.; Bro1chler, R.; Aubke, F.; J. Am. Chem. Soc. 1999, 121, 7188. DOI: http://dx.doi.org/10.1021/ja990958y

45. Orpen, A. G.; Brammer, L.; Allen, F. H.; Kennard, O.; Watson, D. G.; J. Chem. Soc., Dalton Trans. 1989, S1. DOI: http://dx.doi.org/10.1039/dt98900000s1

46. Grabowski, S. J.; Chem. Rev. 2011, 111, 2597. DOI: http://dx.doi.org/10.1021/cr800346f PMID: 21322583

47. Sagar, R. P.; Simas, A. M.; Smith, V. H.; Ku, A. C. T.; J. Chem. Phys. 1988, 88, 4367. DOI: http://dx.doi.org/10.1063/1.453796

48. Shi, Z.; Boyd, R. J.; J. Chem. Phys. 1988, 88, 4375. DOI: http://dx.doi.org/10.1063/1.454711

49. Bader, R. F. W.; Heard, G. L.; J. Chem. Phys. 1999, 111, 8789. DOI: http://dx.doi.org/10.1063/1.480226

50. IUPAC; Compendium of Chemical Terminology, 2^nd ed. (the "Gold Book"), Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). XML on-line corrected version: http://goldbook.iupac.org (2006) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN 0-9678550-9-8. doi:10.1351/goldbook. DOI: http://dx.doi.org/10.1351/goldbook

51. Clark, T.; WIREs Comput. Mol. Sci. 2013, 3, 13. DOI: http://dx.doi.org/10.1002/wcms.1113

52. Cortés-Guzmán, F.; Bader, R. F. W.; Coord. Chem. Rev. 2005. 249, 633. DOI: http://dx.doi.org/10.1016/j.ccr.2004.08.022

53. Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E.; Chem. Phys. Lett. 1998, 285, 170. DOI: http://dx.doi.org/10.1016/S0009-2614(98)00036-0

54. Becke, A. D.; Edgecombe, K. E.; J. Chem. Phys. 1990, 92, 5397. DOI: http://dx.doi.org/10.1063/1.458517