Artigo
|
|
| Propriedades ópticas não lineares de clusters do BC5 Nonlinear optical properties of BC5 clusters |
|
Marconi B. S. Costa*; Ana E. de A. Machado
Departamento de Química Fundamental, Universidade Federal de Pernambuco, 50670-901 Recife - PE, Brasil Recebido em 12/12/2015 *e-mail: marconi.costa@ufpe.br The first (β) and second (γ) hyperpolarizabilities of BC5 clusters were investigated through the PM6, PM3, and MNDO-d semiempirical Hamiltonians. The I INTRODUÇAO O BC5 é um material caracterizado experimentalmente na literatura que possui excepcionais propriedades térmicas e mecânicas. Em adiçao, estudos teóricos indicam um caráter metálico e supercondutor.1-5 Por ser superabrasivo e apresentar elevada dureza, existe a possibilidade deste material substituir o diamante em aplicaçoes tecnológicas.6,7 Várias propriedades do BC5 têm sido exploradas em investigaçoes teóricas e experimentais, todavia, as propriedades ópticas nao lineares (ONL) ainda nao foram contempladas. A maioria dos estudos sobre esse material abordam a sua real estrutura cristalina, uma vez que o padrao de difraçao de raios-X do BC5 nao permite determiná-la devido aos valores similares dos números atômicos dos átomos de B e C. Alguns grupos teóricos sugerem que mais de uma fase reproduz satisfatoriamente o padrao de difraçao de raios-X e indicam quais as fases que sao termodinamicamente mais estáveis.7 Até o presente momento nao há unanimidade em relaçao à real estrutura do BC5 (bulk). Esse sistema é descrito através de ligaçoes multicentros visto que o B e o C formam ligaçoes sp3 hibridizadas, porém o B possui deficiência de elétrons de valência e nao forma quatro ligaçoes. Assim, os elétrons sao compartilhados entre unidades de B-C-B formando duas ligaçoes de dois elétrons e três centros. Também, a deslocalizaçao de elétrons nas ligaçoes (planos) do B-C-B foi demonstrada através de cálculos de estrutura de banda.7 Em nossa investigaçao, consideramos modelos de clusters para quatro fases do BC5, que sao I Diversos fatores influenciam a magnitude das hiperpolarizabilidades β e γ, dos quais podemos destacar a dimensionalidade, a simetria e a ressonância.13 Assim, consideramos nesse estudo as fases do BC5 que satisfatoriamente reproduzem o padrao de difraçao de raios-X e que sao termodinamicamente estáveis, permitindo a indicaçao de quais clusters exibem os valores mais significativos de β e/ou γ. Através dos valores dos coeficientes β e γ é possível estimar o potencial uso de um material como meio óptico nao linear. Novas classes de materiais que apresentam propriedades ONL sao requeridas para o desenvolvimento de dispositivos mais eficientes bem como para a implementaçao de tecnologias avançadas.14-16 O BC5 abre uma nova perspectiva de aplicaçoes em razao dos relevantes valores dos coeficientes β e γ obtidos nesta investigaçao.
PROCEDIMENTO COMPUTACIONAL A otimizaçao de geometrias dos clusters do BC5 e o cálculo de magnitudes das hiperpolarizabilidades β e γ foram realizados usando os Hamiltonianos semiempíricos: PM6 (Parametric Method Number 6),10 PM3 (Parametric Method Number 3)11 e MNDO-d (Modified Neglect of Diatomic Overlap com orbitais d)12 implementados no MOPAC2012.9 A característica central dos métodos semiempíricos é que eles sao parametrizados para a reproduçao de dados experimentais ou de resultados ab initio.9 Uma de suas principais vantagens é a possibilidade de investigar sistemas com um número elevado de átomos sem exigir uma infraestrutura computacional robusta associada a obtençao de resultados satisfatórios.9,17 Isso é particularmente útil em nosso trabalho, uma vez que os modelos de cluster que usamos para representar o BC5 possuem mais de 200 átomos. Para sistemas contendo os átomos de C, B e H, é demonstrado que o Hamiltoniano PM6 produz resultados mais realísticos.9,10 Para esses átomos, o erro médio do calor de formaçao, do comprimento de ligaçao, do momento de dipolo e do potencial de ionizaçao para o PM6 é menor em comparaçao com os outros Hamiltonianos selecionados.9,10 Além das vantagens mencionadas acima, os métodos semiempíricos têm alcançado sucesso através de uma concordância satisfatória entre os valores teóricos e experimentais das hiperpolarizabilidades β e γ para várias classes de moléculas que apresentam propriedades ONL.17 A magnitude das hiperpolarizabilidades β e γ para os processos de geraçao de segundo (SHG) e terceiro (THG) harmônicos é obtida através das seguintes equaçoes, 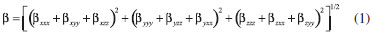 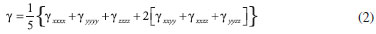 Os valores estáticos de β e γ sao calculados via método Coupled Perturbed Hartree-Fock (CPHF),18 enquanto que as magnitudes dependentes da frequência sao obtidas através da técnica Time-Dependent Hartree-Fock (TDHF).19 A interaçao com o campo elétrico externo em um sistema de camada fechada é calculada pelo método TDHF através da introduçao de uma perturbaçao na parte eletrônica da equaçao de Schrödinger. Para investigar o efeito de dispersao, foram selecionados os comprimentos de onda de 2479 nm (0,5 eV) e 1060 nm (1,17 eV). O comprimento de onda de 1060 nm é comumente usado na caracterizaçao experimental de β em estudos que utilizam o laser de Nd3+:YAG.13 Tendo em vista a inviabilidade computacional de modelar um cristal inteiro em cálculos de orbitais moleculares, o uso de modelos de cluster para representar um sistema cristalino é uma estratégia utilizada na literatura.21 As propriedades eletrônicas e estruturais de clusters permanecem um dos problemas relevantes em ciência de materiais.22 Os clusters podem exibir propriedades que nao sao características dos átomos ou do estado sólido. Por exemplo, os níveis de energia nos átomos sao discretos e bem separados, em contraste os sólidos têm estados contínuos (bandas de energia). Os clusters podem residir entre estes limites.22 Uma correlaçao entre as propriedades do cluster e a do cristal correspondente pode ser estabelecida usando modelos que contenham no mínimo a célula unitária do cristal envolta em seu ambiente químico original. A determinaçao das dimensoes de um cluster que reproduza as propriedades de um sólido cristalino nao é trivial. Modelos de clusters também podem ser úteis quando se trata de nanopartículas e filmes finos em razao de suas dimensoes.23 Em nosso estudo, selecionamos modelos de clusters que reproduzem as condiçoes periódicas de contorno da célula unitária até um limite computacionalmente viável. A Figura 1 apresenta os modelos de clusters das fases do BC5 utilizados em nossos cálculos. De modo a completar as valências livres dos átomos na fronteira dos clusters, os mesmos foram saturados com átomos de hidrogênio (nao exibidos na Figura 1). As fórmulas resultantes sao C132B24H96 (I
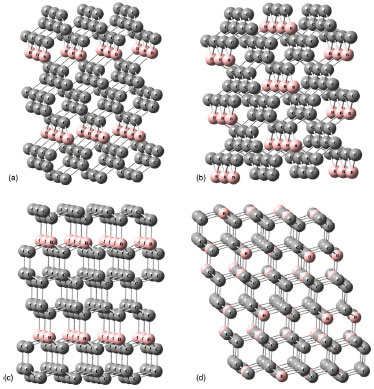 Figura 1. Modelos de clusters para as fases investigadas do BC5: (a) I 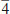 m2, (b) Imm2, (c) P3m1, (d) P m2, (b) Imm2, (c) P3m1, (d) P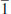 . Carbono ( . Carbono ( ); Boro ( ); Boro ( ) )
A escolha adequada dos ligantes para a saturaçao dos átomos de fronteira do cluster é crucial para obtençao de resultados satisfatórios. O uso do átomo de hidrogênio apresenta vantagens, pois torna a computaçao significativamente mais simples em comparaçao quando se usa ligantes maiores. Nesse último caso, podem causar efeitos estéricos e reduzir o número de ligantes a serem adicionados a um dado cluster. Também, os átomos de hidrogênio nao promovem efeitos adicionais devido à transferência de carga que ocorreria pelo uso de ligantes mais eletronegativos ou eletropositivos.24 A estratégia de saturaçao com átomos de hidrogênio tem sido empregada na literatura pois minimiza os efeitos de borda indesejáveis que ocorrem em modelos de clusters e evita a formaçao de ligaçoes flutuantes. Este procedimento impede que os elétrons das ligaçoes flutuantes (dangling bonds) sejam injetados no cluster, otimizando o tempo computacional ao evitar o excesso de carga negativa. Na ausência deste artifício, os elétrons ocuparao níveis de energia que originalmente nao estao presentes no sistema. Cálculos de estrutura eletrônica e densidade de estados das fases do BC5, realizados através dos métodos Projector-Augmented Wave (PAW) e Generalized Gradient Approximation Perdew-Burke-Ernzerhof (GGA-PBE) relatados na literatura,7 indicam uma deslocalizaçao de elétrons de valência nas ligaçoes B-C-B. Ademais, esses estudos demonstram que os estados eletrônicos próximos do nível de Fermi consistem predominantemente destas ligaçoes, resultando em fraco caráter metálico. Este efeito é relevante nas fases I
AVALIAÇAO DA METODOLOGIA PARA O CALCULO DAS PROPRIEDADES OPTICAS NAO LINEARES Para uma avaliaçao dos métodos semiempíricos no estudo de propriedades ONL, selecionamos um grupo de moléculas promissoras caracterizadas na literatura.25 As moléculas investigadas em relaçao à hiperpolarizabilidade β sao apresentadas na Figura 2. Os valores teóricos (PM6, PM3 e MNDO-d) da primeira hiperpolarizabilidade estática (β0) e dinâmica (β1060) sao mostrados na Tabela 1. Os valores experimentais de β0 das moléculas investigadas se encontram disponíveis na literatura, como também as magnitudes de β1060 para os sistemas 1 e 4 (Tabela 1).
Para a frequência da radiaçao incidente nula (β0), os valores teóricos sao inferiores aos experimentais, a única exceçao observada é para o sistema 2 utilizando o Hamiltoniano PM6. Em relaçao aos valores dependentes da frequência (1060 nm), o resultado obtido para o sistema 1 reproduz satisfatoriamente o valor experimental, enquanto que um comportamento oposto é observado para a molécula 4. Para a frequência da radiaçao incidente nula, a metodologia também nao reproduz a magnitude experimental para esse composto. A estrutura otimizada obtida através dos métodos semiempíricos para a molécula 4, que é octopolar, deve contribuir para os resultados obtidos, visto que o valor de β é influenciado pela geometria molecular de acordo com estudos multidisciplinares.13,17 Deve ser destacado que a metodologia semiempírica nao aborda o efeito de solvente,26 a formaçao de pontes de hidrogênio,27 a transferência de carga intramolecular e intermolecular,28 os defeitos na cadeia,29 a correlaçao eletrônica e efeitos vibracionais30 que influenciam a magnitude das hiperpolarizabilidades β e γ. Portanto, os resultados obtidos com as técnicas semiempíricas sao geralmente inferiores aos experimentais, como observado nas prediçoes dos valores da β0 (Figura 3) para as moléculas orgânicas investigadas.
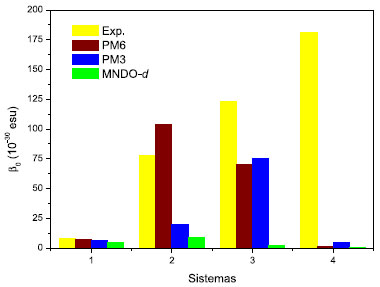 Figura 3. Valores experimentais (Exp.) e teóricos da hiperpolarizabilidade β0 para as moléculas orgânicas
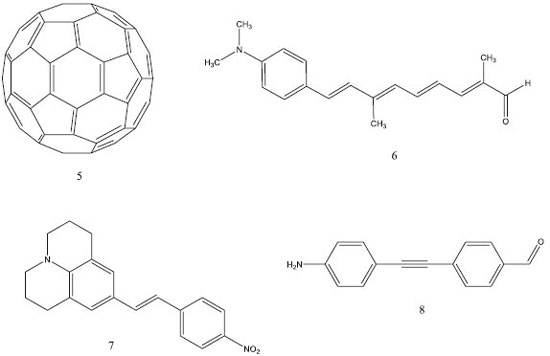
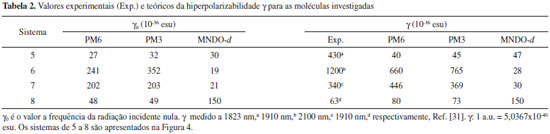
Recentemente, o cálculo da hiperpolarizabilidade β0 para a p-nitroanilina (molécula 1), entre outras moléculas ONL, foi realizado através da teoria da perturbaçao de Møller-Plesset de segunda ordem (MP2) e da teoria do funcional de densidade (DFT) utilizando 31 diferentes funcionais e considerando 71 conjuntos de base distintos.17 Santos e Paschoal verificaram que o uso de funçoes difusas e de polarizaçao (d e f) contribuem para os resultados de β0 mais próximos dos valores experimentais.17 Observaram que o erro associado é o menor para a p-nitroanilina, que é o sistema que contém uma quantidade de átomos inferior aos outros investigados. Os resultados obtidos para a β0 da p-nitroanilina através dos Hamiltonianos PM6 e PM3 mostram um comportamento similar (Tabela 1) e demonstram a vantagem da eficiência computacional da metodologia semiempírica13 em comparaçao com os métodos mais rigorosos que demandam um maior suporte computacional. Contudo, a dependência da hiperpolarizabilidade com o comprimento da cadeia entre grupos doador e receptor de elétron nao é adequadamente estimada para moléculas orgânicas push-pull através da técnica semiempírica.13 Selecionamos outro grupo de moléculas (Figura 4) para as quais as magnitudes experimentais de γ dependentes da frequência sao relatadas na literatura,31 uma vez que nao é disponibilizada as medidas desse coeficiente para os sistemas usados na avaliaçao de β. Desta forma, a prediçao dos valores de γ para cada molécula foi realizada para os comprimentos de onda das respectivas medidas experimentais (Tabela 2). Em adiçao, calculamos os valores da segunda hiperpolarizabilidade para a frequência da radiaçao incidente nula (γ0).
Para os sistemas 7 e 8, os valores de γ calculados através dos Hamiltonianos PM3 e PM6 reproduzem satisfatoriamente a tendência experimental, enquanto que para os sistemas 5 e 6 é observado um comportamento distinto, visto que os valores teóricos sao inferiores aos respectivos valores experimentais (Figura 5).
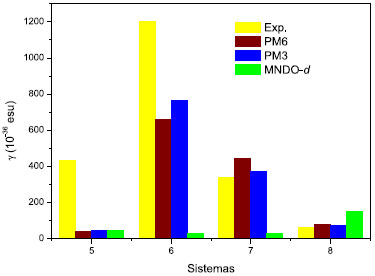 Figura 5. Valores experimentais (Exp.) e teóricos da hiperpolarizabilidade γ (dinâmica) para as moléculas orgânicas
Para a frequência da radiaçao incidente nula, os valores teóricos exibem a mesma tendência observada para os valores de γ dependentes da frequência, considerando cada método semiempírico. Os resultados indicam que o Hamiltoniano MNDO-d nao é adequado para o cálculo de propriedades ONL de moléculas orgânicas contendo um número elevado de átomos. As magnitudes de β e γ sao fortemente influenciadas pela geometria molecular de acordo com estudos experimentais e teóricos.13,17 Em geral, os sistemas planos exibem valores mais elevados das hiperpolarizabilidades. Assim, a diferença observada nas estruturas otimizadas para os compostos orgânicos é resultante do uso dos diferentes métodos selecionados neste trabalho. Por exemplo, o método MNDO-d produz torçoes na estrutura da molécula 6 em comparaçao com a estrutura obtida com o Hamiltoniano PM6 (Figura 6), o que resulta no valor inferior de γ . Em adiçao, a estrutura otimizada para essa molécula através do método PM3 é similar àquela obtida com o PM6. Esse efeito nao é relevante para o BC5, uma vez que os dados utilizados na construçao dos modelos de clusters sao referentes à estrutura cristalina, a qual se encontra no estado fundamental.7
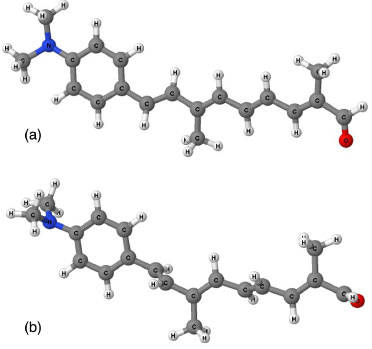 Figura 6. Estrutura da molécula 6 otimizada através dos métodos (a) PM6 e (b) MNDO-d
A análise da metodologia realizada demonstra que a técnica semiempírica pode ser utilizada para indicar moléculas orgânicas que apresentam propriedades ONL. Em adiçao, devemos destacar que para uma comparaçao entre os valores teóricos e experimentais da hiperpolarizabilidade se faz necessário o uso de um fator de correçao, já que os cálculos foram realizados na fase gás. A caracterizaçao experimental dos coeficientes nao lineares pode ser efetuada nas fases gás e condensada, e as técnicas utilizadas em geral fazem uso de solventes.13 Uma prescriçao de Willets e colaboradores39 tem sido usado como referência na literatura por grupos teóricos.17,40 Contudo, Reis41 introduziu outro protocolo devido à discrepância observada entre os valores experimentais e teóricos na literatura, como também devido à existência de diversas convençoes usadas pelos grupos experimentais que resulta em diferentes valores para as hiperpolarizabilidades.
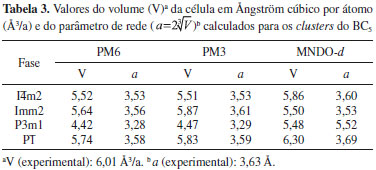
RESULTADOS E DISCUSSAO Calculamos o volume (V) e o parâmetro de rede (
Embora nao seja o objetivo deste trabalho determinar a fase real do BC5, realizamos uma análise da estabilidade dos clusters. Observamos a mesma sequência para os Hamiltonianos usados, i.e., P3m1 > I
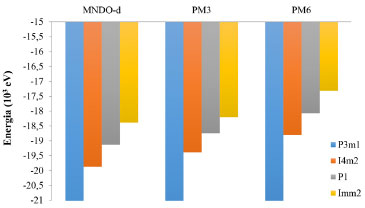 Figura 7. Energia total dos clusters do BC5
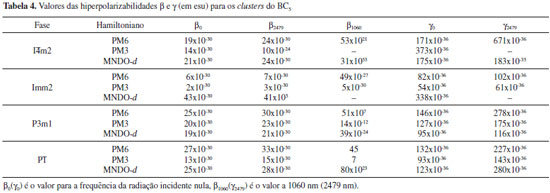
A satisfatória reproduçao de parâmetros experimentais do BC5 obtidos neste trabalho demonstra o potencial das técnicas semiempíricas para o estudo deste sistema. Os valores das hiperpolarizabilidades para os clusters do BC5, calculados utilizando os Hamiltonianos PM6, PM3 e MNDO-d sao apresentados na Tabela 4. Para β0, observamos que todas as fases apresentam magnitudes da ordem de 10-30 esu, enquanto para γ0 todos os valores sao da ordem de 10-36 esu. Também os valores de β a 2479 nm sao da mesma ordem de grandeza de β0, exceto para as fases I
Os resultados das magnitudes de β dependentes da frequência indicam a existência de propriedades ópticas nao lineares para os clusters do BC5. De acordo com a literatura,13 os valores de β sao considerados elevados quando se encontram no intervalo de 10 a 100x10-30 esu para moléculas orgânicas do tipo doador-receptor, medido a 1910 nm (0,65 eV). A maioria dos valores de β a 2479 nm, que corresponde a 0,50 eV, estao contidos nesse intervalo. Um comprimento de onda maior (menor energia) foi selecionado na investigaçao dos clusters do BC5, de modo que os valores teóricos obtidos para a hiperpolarizabilidade β sao relevantes. Os valores dinâmicos de γ2479 nao sao obtidos para as fases I Embora nao seja possível avaliar a performance do BC5 em relaçao aos materiais inorgânicos tradicionais como KDP (KD2PO4) e KTP (KTiOPO4), visto que as susceptibilidades de segunda χ(2) e terceira χ(3) ordem do BC5 ainda nao foram medidas, apresentamos na Tabela 5 os valores de χ(2) e χ(3) a 1064 nm para alguns materiais ONL tradicionais.20,32,33 Para as espécies microscópicas de um material, o coeficiente óptico nao linear γ (ou β) é associado ao tensor χ(3) (ou χ(2)), o qual é caracterizado experimentalmente.13 Valores da hiperpolarizabilidade γ da ordem de 10-30 esu correspondem a cerca de 10-8 esu para a susceptibilidade macroscópica χ(3).13 Em geral, um requerimento para os materiais candidatos de terceira ordem é que devem exibir um valor de χ(3) superior a 10-8 esu para uso em dispositivos que realizam o chaveamento de luz.13 Em relaçao aos materiais de segunda ordem, é necessária a otimizaçao da resposta nao linear em comparaçao aos valores da literatura atual, tendo em vista aplicaçoes em tecnologias avançadas.13
Os resultados indicam a ocorrência de flutuaçoes nos valores de β1060 (1,17 eV) para as fases do BC5 (Tabela 4), independente do método selecionado. O comportamento observado é decorrente das parametrizaçoes dos modelos de química quântica, como também devido às diferenças entre as fases (parâmetros de rede, coordenadas atômicas e grupo espacial). Para uma caracterizaçao teórica do comportamento de β, investigamos o efeito de dispersao no intervalo de energia de 0 a 1,3 eV (Tabela 6). Verificamos que na faixa de energia de 0 a 0,75 eV, a sequência observada para os valores de β obtidos através do Hamiltoniano PM6 é I
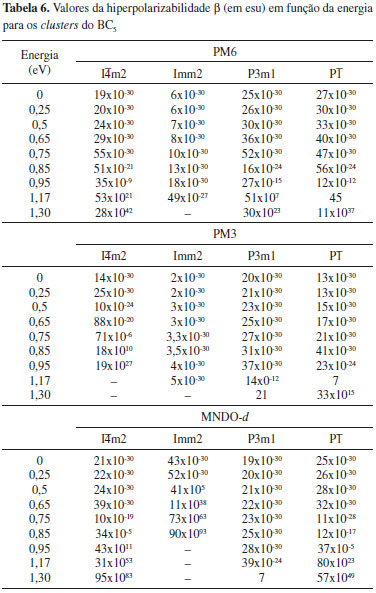
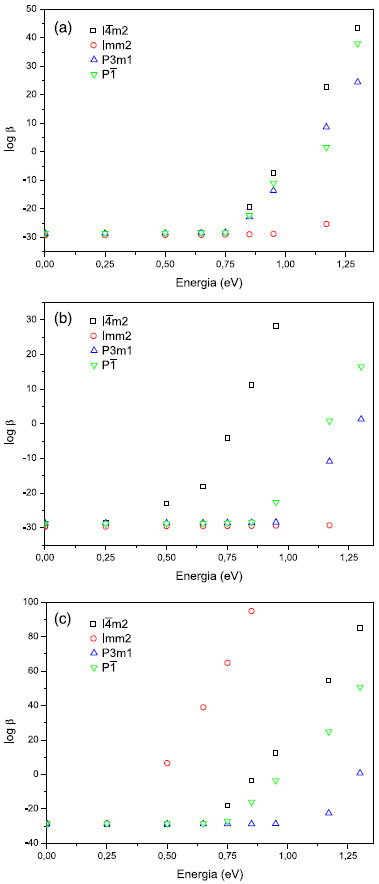 Figura 8. Variaçao da hiperpolarizabilidade β em funçao da energia: (a) PM6; (b) PM3; (c) MNDO-d
Os resultados de β obtidos via métodos PM3 e PM6, para as fases Imm2, P3m1 e P Existe a possibilidade da ocorrência de instabilidades numéricas no cálculo de β (TDHF) em razao da mudança observada por várias ordens de grandeza a valores mais altos de energia.35 É fundamental a síntese dos clusters investigados neste trabalho para a caracterizaçao experimental dos coeficientes ópticos nao lineares, o que permitirá ratificar ou nao os resultados obtidos de β. A separaçao de cargas, que ocorre em funçao da ressonância nao sincronizada de ligaçoes covalentes como previsto por Pauling,34 pode contribuir para as propriedades ONL do BC5. A ressonância sincronizada é mostrada na Figura 9(a), enquanto a nao sincronizada que resulta em separaçao de cargas é apresentada na Figura 9(b). Como destacado anteriormente, os átomos de B sao deficientes de elétrons, o que implica na presença de várias bandas vazias acima do nível de Fermi. Esta deficiência permite que os átomos de B recebam elétrons dos átomos de C resultando em separaçao de cargas conforme o esquema (Figura 9).
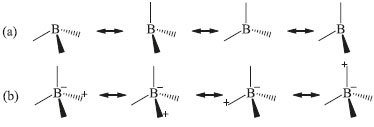 Figura 9. Ressonância (a) sincronizada e (b) nao sincronizada das ligaçoes covalentes para o Boro
A transferência de elétrons sugerida pelo mecanismo RVB (Resonating-Valence-Bond)34 foi analisada através da distribuiçao de cargas atômicas nos átomos de B em cada cluster. Apresentamos a quantidade de átomos de B que exibem carga negativa para as quatro fases do BC5 na Tabela 7.
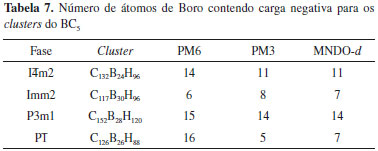
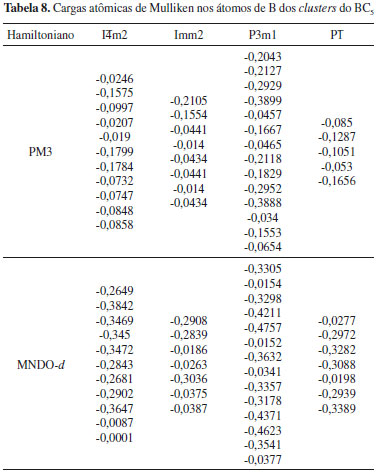
Como esperado, todos os átomos de B nao apresentam carga negativa, pois ambas as ressonâncias podem ocorrer no material. Deve ser destacado que a fase Imm2, que apresenta o menor valor de β1060, possui a menor quantidade de átomos de B com carga negativa, enquanto que as fases que apresentam as magnitudes mais elevadas de β1060 possuem uma quantidade maior de átomos de B negativamente carregado. A fase I A distribuiçao de cargas atômicas de Mulliken para os clusters do BC5 calculada através do método PM6 é apresentada na Figura 10. A escala de cor indica a variaçao de carga, sendo que o vermelho e o azul representam a carga positiva e negativa, respectivamente. A Tabela 8 exibe as cargas atômicas de Mulliken dos átomos de B nos clusters do BC5 obtidas com os métodos PM3 e MNDO-d, as quais nao sao apresentadas na Figura 10. De acordo com a teoria RVB, o boro é classificado como um elemento hipoeletrônico, i.e., possui uma quantidade maior de orbitais de ligaçao do que de elétrons de valência, o que permite incrementar a sua valência recebendo um elétron.34 Portanto, os átomos de B no interior dos clusters que se encontram ligados a quatro átomos de C apresentam carga negativa, enquanto aqueles posicionados nas bordas exibem carga positiva. Embora os modelos de cluster possuam limitaçoes, esse resultado reforça o mecanismo RVB da separaçao de cargas (Figura 9) e está em concordância com estudos teóricos da estrutura eletrônica do BC5.7
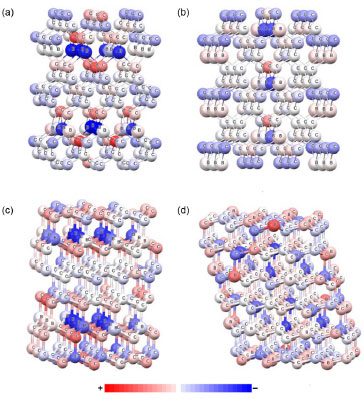 Figura 10. Distribuiçao de cargas atômicas de Mulliken nos clusters do BC5 calculada através do método PM6: (a) I  m2, (b) Imm2, (c) P3m1, (d) P m2, (b) Imm2, (c) P3m1, (d) P
Os elevados valores de β obtidos a 1060 nm devem ser considerados com cautela, visto que as instabilidades numéricas inerentes ao MOPAC2012 podem contribuir para esses resultados.35 Também deve ser destacado que os efeitos nao lineares exibem descontinuidades próximas de frequências de absorçao. Estas descontinuidades podem causar diferenças por várias ordens de grandeza nos resultados. Todavia, como o espectro de absorçao do BC5 nao está disponível na literatura, nao é possível ratificar ou nao esse efeito. Em adiçao ao estudo das propriedades ONL, apresentamos na Figura 11 o comportamento da polarizabilidade (α) em funçao da energia para todos os clusters do BC5. Os resultados obtidos com o método PM3 sao similares àqueles calculados com o PM6, por isso nao sao mostrados na Figura 11. A sequência em ordem decrescente para os valores obtidos de α é idêntica para todos os métodos selecionados (P3m1 > I
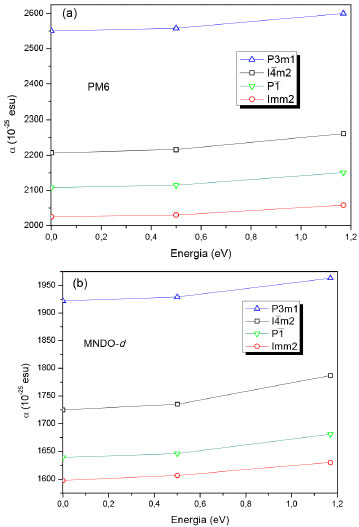 Figura 11. Polarizabilidade (α) em funçao da energia para os clusters do BC5 calculada através dos métodos PM6 (a) e MNDO-d (b) (α (unidade): 1 a.u. = 1.48184709x10-25 cm3)
Compostos apresentando elevados valores de α sao requeridos para aplicaçoes, por exemplo, em fibras ópticas.36 Nestas, o aumento da polarizabilidade da regiao interna da fibra é obtido pela adiçao de dopantes como o óxido de germânio (GeO2). Esta técnica resulta em um ganho relevante da reflexao interna total na interface núcleo-revestimento, restringindo as ondas de luz dentro da fibra óptica, que resulta na otimizaçao do seu desempenho.36 Em geral, estas fibras sao feitas de SiO2 de elevado grau de pureza. Os valores teóricos de α para os clusters do BC5 sao da mesma ordem de magnitude do observado para oligômeros do dietinilsilano, cujas magnitudes foram calculadas via DFT e MP2.37 O polidietinilsilano (PDES) é um material de terceira ordem que apresenta uma rápida resposta óptica na faixa de frequência de sub-terahertz.37 Os clusters de boro, como também de carbono, exibem valores da polarizabilidade estática que aumentam em funçao do tamanho do sistema de acordo com estudos ab initio.38 Em particular, o cluster contendo 14 átomos de B apresenta um valor para α de 444x10-25 cm3.
CONCLUSAO Os resultados obtidos demonstram que o sistema BC5 apresenta valores significativos das hiperpolarizabilidades β e γ, independente do Hamiltoniano semiempírico selecionado, indicando um potencial uso como meio óptico nao linear. A síntese dos clusters investigados e a caracterizaçao de suas propriedades ópticas nao lineares é um interessante tópico em ciência de materiais tendo em vista aplicaçoes tecnológicas. Pesquisas estao sendo realizadas em nosso grupo para a otimizaçao das magnitudes das hiperpolarizabilidades β e γ dos clusters do BC5, que pode ser obtida através de processos de dopagens, introduçao de defeitos e funcionalizaçao.
AGRADECIMENTOS Os autores agradecem às agências de fomento FACEPE e CAPES pelo suporte financeiro e ao CENAPAD - Sao Paulo.
REFERENCIAS 1. Solozhenko, V. L.; Kurakevych, O. O.; Andrault, D.; Godec, Y. L.; Mezouar, M.; Phys. Rev. Lett. 2009, 102, 015506. DOI: http://dx.doi.org/10.1103/PhysRevLett.102.015506 PMID: 19257210 2. Lazar, P.; Podloucky, R.; Appl. Phys. Lett. 2009, 94, 251904. DOI: http://dx.doi.org/10.1063/1.3159627 3. Zhao, W. J.; Wang, Y. X.; Solid State Commun. 2011, 151, 478. DOI: http://dx.doi.org/10.1016/j.ssc.2010.12.032 4. Zhang, J.; Cheng, X.; Comput. Mater. Sci. 2011, 50, 2249. DOI: http://dx.doi.org/10.1016/j.commatsci.2011.02.037 5. Jiang, C.; Lin, Z.; Zhao, Y.; Phys. Rev. B 2009, 80, 184101. DOI: http://dx.doi.org/10.1103/PhysRevB.80.184101 6. Liang, Y.; Zhang, W.; Zhao, J.; Chen, C.; Phys. Rev. B 2009, 80, 113401. DOI: http://dx.doi.org/10.1103/PhysRevB.80.113401 7. Yao, Y.; Tse, J. S.; Klug, D. D.; Phys. Rev. B 2009, 80, 094106. DOI: http://dx.doi.org/10.1103/PhysRevB.80.094106 8. Karamanis, P.; Pouchan, C.; Maroulis, G.; Phys. Rev. A 2008, 77, 013201; Maroulis, G.; Karamanis, P.; Pouchan, C.; J. Chem. Phys. 2007, 126, 154316. DOI: http://dx.doi.org/10.1103/PhysRevA.77.013201 9. Stewart, J. J. P.; MOPAC2012: Molecular Orbital PACkage; Stewart Computational Chemistry, Colorado Springs, CO, USA, 2012. 10. Stewart, J. J. P.; J. Mol. Model. 2007, 13, 1173. DOI: http://dx.doi.org/10.1007/s00894-007-0233-4 PMID: 17828561 11. Stewart, J. J. P.; J. Mol. Model. 2004, 10, 155; Stewart, J. J. P.; J. Comput. Chem. 1989, 10, 209. DOI: http://dx.doi.org/10.1007/s00894-004-0183-z PMID: 14997367 12. Thiel, W.; Voityuk, A.; J. Phys. Chem. 1996, 100, 616; Thiel, W.; Voityuk, A.; Theor. Chim. Acta 1992, 81, 391. DOI: http://dx.doi.org/10.1021/jp952148o 13. Champagne, B.; Kirtman, B. Em Nonlinear Optical Materials; Nalwa, H. S., ed.; Academic Press: San Diego, 2001, cap. 2; Kanis, D. R.; Ratner, M. A.; Marks, T. J.; Chem. Rev. 1994, 94, 195; Brédas, J. L.; Adant, C.; Tackx, P.; Persoonst, A.; Pierce, B. M.; Chem. Rev. 1994, 94, 243. 14. Song, W. N.; He, C. Y.; Zhang, W.; Gao, Y. C.; Yang, Y. X.; Wu, Y. Q.; Chen, Z. M.; Li, X. C.; Dong, Y. L.; Carbon 2014, 77, 1020. DOI: http://dx.doi.org/10.1016/j.carbon.2014.06.018 15. Seidler, T.; Stadnicka, K.; Champagne, B.; J. Chem. Phys. 2014, 141, 104109. DOI: http://dx.doi.org/10.1063/1.4894483 PMID: 25217906 16. Costa, M. B. S.; Machado, A. E. de A.; Pavao, A. C.; J. Mater. Sci. 2013, 48, 192; Costa, M. B. S.; Pavao, A. C.; Machado, A. E. de A.; J. Mater. Sci. Res. 2013, 2, 77. DOI: http://dx.doi.org/10.1007/s10853-012-6728-0 17. Paschoal, D.; dos Santos, H. F.; J. Mol. Model. 2013, 19, 2079; Machado, A. E. de A.; Gama, A. A. S.; Neto, B. B.; Chem. Phys. 2011, 388, 19; Cardoso, C.; Abreu, P. E.; Nogueira, F.; J. Chem. Theory Comput. 2009, 5, 850; Ibersiene, F.; Hammoutène, D.; Boucekkine, A.; Katan, C.; Blanchard-Desce, M.; J. Mol. Struct. (THEOCHEM) 2008, 866, 58; Machado, A. E. H.; Neto, N. M. B.; Ueno, L. T.; Paula, L. F. de; Araújo, D. M. S.; Oliveira, G. S.; Gomes, W. R.; Paula, R. De; Franzen, P. L.; Zilio, S. C.; Oliveira-Campos, A. M. F.; Fonseca, A. M.; Rodrigues, L. M.; Nkeonye, P. O.; Hrdina, R. J. Photochem. Photobiol. A 2008, 199, 2; Boeglin, A.; Barsella, A.; Fort, A.; Mançois, F.; Rodriguez, V.; Diemer, V.; Chaumeil, H.; Defoin, A.; Jacques, P.; Carré, C.; Chem. Phys. Lett. 2007, 442, 298; Machado, A. E. de A.; Gama, A. A. S.; J. Mol. Struct. (THEOCHEM) 2003, 620, 21; Machado, A. E. de A.; Petrov, D. V.; Falcao, E. H. L.; da Gama, A. A. S.; de Azevêdo, W. M.; Chem. Phys. Lett. 2002, 356, 451; Machado, A. E. de A.; Gama, A. A. S.; J. Braz. Chem. Soc. 2008, 19, 1381; Silva, A. M. Jr.; Junqueira, G. M. A.; Santos, H. F.; Carvalho, A. C. M.; Quim. Nova 2009, 32, 315. DOI: http://dx.doi.org/10.1007/s00894-012-1644-4 PMID: 23149760 18. Dykstra, C. E.; Jasien, P. G.; Chem. Phys. Lett. 1984, 109, 388. DOI: http://dx.doi.org/10.1016/0009-2614(84)85607-9 19. Dupuis, M.; Karna, S.; J. Comput. Chem. 1991, 12, 487; Kurtz, H. A.; Stewart, J. J. P.; Dieter, K. M.; J. Comput. Chem 1990, 11, 82. DOI: http://dx.doi.org/10.1002/jcc.540120409 20. Boyd, R. W.; Nonlinear Optics, 3th ed., Elsevier: New York, 2008. 21. Li, T.; Goldberger, J. E.; Chem. Mater. 2015, 27, 3549; Kuklja, M. M.; Zerilli, F. J.; Sushko, P.; MRS Online Proc. Libr. 2003, 800, AA6.2. DOI: http://dx.doi.org/10.1021/cm5022239 22. Fehlner, T.; Halet, J. F.; Saillard, J. Y.; Molecular Clusters - A Bridge to Solid-State Chemistry, Cambridge University Press, 2007; Causà, M.; Barone, V.; Stener, M.; Fronzoni, G.; J. Phys.: Conf. Ser. 2008, 117, 012009; Berrondo, M.; Rivas-Silva, J. F.; Int. J. Quantum Chem. 1996, 57, 1115; Nieuwpoort, W. C.; Broer, R.; Nato ASI Ser. 1992, 283, 505. 23. Dollinger, A.; Park, E. J.; Strobel, C. H.; Bleuel, H.; Marsteller, A.; Seo, H. O.; Kim, Y. D.; Gantefor, G.; Phys. Chem. Chem. Phys. 2015, 17, 20873; Grabow, M. H.; Gilmer, G. H.; Surf. Sci. 1988, 194, 333. DOI: http://dx.doi.org/10.1039/C5CP03147H PMID: 26214654 24. Xu, K.; Li, X.; Chen, P.; Zhou, D.; Wu, C.; Guo, Y.; Zhang, L.; Zhao, J.; Wu, X.; Xie, Y.; Chem. Sci. 2015, 6, 283; Villegas, C. E. P.; Mendonça, P. B.; Rocha, A. R.; Sci. Rep. 2014, 4, 6579; Costa, M. B. S.; Bastos, C. C.; Pavao, A. C.; J. Braz. Chem. Soc. 2012, 23, 1305; Machado, A. E. de A.; dos Santos, H. F.; Almeida, W. B.; Chem. Phys. Lett. 2011, 514, 134. DOI: http://dx.doi.org/10.1039/C4SC02576H 25. Kaatz, P.; Donley, E. A.; Shelton, D. P.; J. Chem. Phys. 1998, 108, 84; Molinos-Gómez, A.; Vidal, X.; Maymó, M.; Velasco, D.; Martorell, J.; López-Calahorra F.; Tetrahedron 2005, 61, 9075; Blanchard-Desce, M.; Wortmann, R.; Lebus, S.; Lehn, J.-M.; Krämer, P.; Chem. Phys. Lett. 1995, 243, 526. 26. Lu, S.; Chiu, C.; Wang, Y.; J. Chem. Phys. 2011, 135, 134104. DOI: http://dx.doi.org/10.1063/1.3644336 PMID: 21992279 27. Góra, R. W.; Zaleśny, R.; Zawada, A.; Bartkowiak, W.; Skwara, B.; Papadopoulos, M. G.; Silva, D. L.; J. Phys. Chem. A 2011, 115, 4691. DOI: http://dx.doi.org/10.1021/jp110226h PMID: 21491879 28. Fukuda, K.; Nakano, M.; J. Phys. Chem. A 2014, 118, 3463. DOI: http://dx.doi.org/10.1021/jp412634q PMID: 24761772 29. Nakano, M.; Shigemoto, I.; Yamada, S.; Yamaguchi, K.; J. Chem. Phys. 1995, 103, 4175. DOI: http://dx.doi.org/10.1063/1.470657 30. Yartsev, V. M.; Chem. Phys. Lett. 1999, 313, 241. DOI: http://dx.doi.org/10.1016/S0009-2614(99)01024-6 31. Gisbergen, S. J. A.; Snijders, J. G.; Baerends, E. J.; Phys. Rev. Lett. 1997, 78, 3097; Puccetti, G.; Blanchard-Desce, M.; Ledoux, I.; Lehn, J.M.; Zyss, J.; J. Phys. Chem. 1993, 97, 9385; Alain, V.; Thouin, L.; Blanchard-Desce, M.; Gubler, U.; Bosshard, C.; Günter, P.; Muller, J.; Fort, A.; Barzoukas, M.; Adv. Mater. 1999, 11, 1210; Bures, F.; RSC Adv. 2014, 4, 58826. DOI: http://dx.doi.org/10.1103/PhysRevLett.78.3097 32. Buschow, K. H. J.; Cahn, R. W.; Flemings, M. C.; Ilschner, B.; Kramer, E. J.; Mahajan, S.; Veyssière, P.; Encyclopedia of Materials: Science and Technology, Elsevier Science, 2001. 33. Andrews, D. L.; Demidov, A. A.; An Introduction to Laser Spectroscopy, 2ª ed., Springer U.S., 2002. 34. Costa, M. B. S.; Barros, K. A.; Revista Virtual de Química 2012, 4, 130; Herman, Z. S. Em Pauling's Legacy: Modern Modelling of the Chemical Bond; Maksić, Z. B., Orville Thomas, W. J., eds.; Elsevier Science B. V.: Amsterdam, 1999, cap. 28; Pauling, L.; Herman, Z. S.; Valence Bond Theory and Chemical Structure, Elsevier Science Publishers B. V.: Amsterdam, 1990; Pauling, L.; Herman, Z. S.; Advances in Boron and the Boranes, VCH Publishers: New York, 1988. DOI: http://dx.doi.org/10.5935/1984-6835.20120011 35. Comunicaçao recebida via e-mail (mrmopac@att.net) dos desenvolvedores do MOPAC em 27 de Julho de 2015. 36. Fulay, P.; Lee, J. K.; Electronic, Magnetic, and Optical Materials (Advanced Materials and Technologies), CRC Press, 2010. 37. Machado, A. E. de A.; de Souza, L. A.; dos Santos, H. F.; de Almeida, W. B.; J. Polym. Sci., Part B: Polym. Phys. 2011, 49, 1410; Wong, K. S.; Han, S. G.; Vardeny, Z. V.; Shinar, J.; Pang, Y.; Ijadi-Maghsoodi, S.; Barton, T. J.; Grigoras S.; Parbhoo, B.; Appl. Phys. Lett. 1991, 58, 1695. DOI: http://dx.doi.org/10.1002/polb.22324 38. Abdurahman, A.; Shukla, A.; Seifert, G.; Phys. Rev. B 2002, 66, 155423. DOI: http://dx.doi.org/10.1103/PhysRevB.66.155423 39. Willetts, A.; Rice, J. E.; Burland, D. M.; Shelton, D. P.; J. Chem. Phys. 1992, 97, 7590. DOI: http://dx.doi.org/10.1063/1.463479 40. Paschoal, D.; Dos Santos, H. F.; Org. Electron. 2016, 28, 111. DOI: http://dx.doi.org/10.1016/j.orgel.2015.10.019 41. Reis, H.; J. Chem. Phys. 2006, 125, 014506. DOI: http://dx.doi.org/10.1063/1.2211611 PMID: 16863315 |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






 m2, Imm2, P3m1, and P
m2, Imm2, P3m1, and P phases that are pointed out in literature as likely candidates of the BC5 superhard diamondlike real structure were investigated. In this way, the stability analysis of the BC5 clusters was performed. Moreover, insights into the nonlinear mechanisms were obtained via Resonating Valence Bond (RVB) theory. The semiempirical methodology was evaluated in relation to the β and γ hyperpolarizabilities by considering fully characterized nonlinear organic molecules reported in the literature. The high values of the dynamic β and γ hyperpolarizabilities exhibited by the BC5 phases demonstrate that these clusters present potential applications as nonlinear optical media.
phases that are pointed out in literature as likely candidates of the BC5 superhard diamondlike real structure were investigated. In this way, the stability analysis of the BC5 clusters was performed. Moreover, insights into the nonlinear mechanisms were obtained via Resonating Valence Bond (RVB) theory. The semiempirical methodology was evaluated in relation to the β and γ hyperpolarizabilities by considering fully characterized nonlinear organic molecules reported in the literature. The high values of the dynamic β and γ hyperpolarizabilities exhibited by the BC5 phases demonstrate that these clusters present potential applications as nonlinear optical media.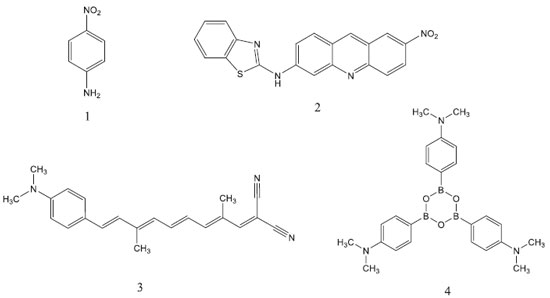

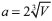 ) da célula para as fases do BC5 selecionadas (I
) da célula para as fases do BC5 selecionadas (I