Artigo
|
|
| Desarrollo de los índices de poder electrofílico y nucleofílico dentro del marco conceptual de la teoría del funcional de la densidad Development of electrophilic and nucleophilic power indices within the conceptual framework of density functional theory |
|
Said F. FigueredoI,*; Manuel S. PáezI; Jong-Won SongII
IDepartamento de Química, Universidad de Córdoba, Cra. 6 Nº 74-103, Montería, Córdoba, Colombia Recebido em 14/12/2015 *e-mail: saifer87@gmail.com In this work, the electrophilic and nucleophilic power indices were developed in the basis of canonical and grand canonical ensembles respectively, also local versions of these indices has been derived in analogy to philicity concept by Chattaraj. It can be observed that local electrophilic power and local nucleophilic power contain a third order response function, namely the hyperhardness, which recently has been considered for its chemical relevance. Also, the reactivity indices proposed here were tested by predicting the relative reactivity of molecules within three series of compounds (butyl-lithium isomers, carbonyl compounds, and aromatic motifs). In general, the global reactivity indices were in agreement with the experimental observations, while local versions shown a good representation of the site reactivity of the majority of studied system giving better results in some of cases if matched with both the Fukui functions and dual descriptor. INTRODUCCION Entre los primeros ejemplos exitosos de la teoría de funciones de onda aplicada al entendimiento de la reactividad molecular están la teoría de los orbitales moleculares frontera (FMO, por sus siglas en inglés) de Fukui,1 y las reglas de Woodward-Hoffman,2 siendo los orbitales moleculares más alto ocupado (HOMO, por sus siglas en inglés) y más bajo desocupado (LUMO, por sus siglas en inglés) las cantidades más importantes en ambas teorías. Una desventaja de estas representaciones orbitales es que utilizan una descripción orbital basada en partículas independientes donde la dinámica asociada a la correlación electrónica es totalmente omitida.3 Esta correlación a menudo juega un papel importante en el fenómeno de la reactividad química,4,5 no obstante, si la correlación electrónica es tomada en cuenta, el enfoque orbital desaparece y la FMO se vuelve irrelevante.3 Por otro lado, la inclusión de los efectos de correlación electrónica en la Teoría de Funcionales de la Densidad (DFT, por sus siglas en inglés)6,7 no afecta el poder interpretativo de los descriptores de reactividad basados en la densidad electrónica,3 lo que ha justificado el desarrollo del marco conceptual de la DFT hacia un esquema más comprensible de la reactividad química en comparación con el enfoque orbital.3 Concretamente, la DFT6,7 es un formalismo mecano-cuántico en el que la variable principal es la densidad de probabilidad electrónica, a partir de la cual, es posible en principio, determinar todas las propiedades de un sistema electrónico. No obstante, dentro del esquema conceptual de la DFT, es posible representar la energía y cualquier otra propiedad del sistema mediante el número de electrones y el potencial externo (ensamble canónico), esto es:3,6  En esta representación, si un agente externo interactúa con el sistema provocando una perturbación en este, el cambio en la energía correspondiente con las variaciones en N y ν(r) se puede escribir mediante la siguiente expansión de Taylor de segundo orden:3,8 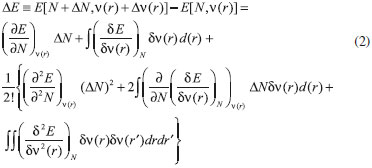 Una de las observaciones clave en la DFT conceptual ha sido que varias de las derivadas que aparecen en la ecuación 2 (funciones respuesta) pueden ser identificadas con propiedades químicas que solo habían sido tratadas de forma cualitativa.9 En particular:   donde µ, el multiplicador de Lagrange asociado con la minimización de la energía en DFT,9 es precisamente el potencial químico electrónico,10 una propiedad global que mide la tendencia de los electrones a escapar desde un sistema molecular en equilibrio; η es la dureza,11 un descriptor global que mide la resistencia que oponen los electrones a ser transferidos desde un sistema electrónico en equilibrio. Adicionalmente, la suavidad (S) ha sido identificada como el recíproco de la dureza:12  Esta propiedad es una medida de la reactividad molecular, y ha mostrado estar relacionada con la polarizabilidad.3 Además, la ecuación 2 contiene la derivada de la densidad electrónica con respecto al número de electrones, que es una propiedad local reconocida por Parr y Yang como la función de Fukui (FF, por sus siglas en inglés) f (r):13 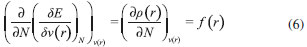 f (r) es un descriptor local de reactividad que ha sido útil para el estudio de la regioselectividad14-17 y la formación de enlaces covalentes.9,18 La derivada de la función de Fukui con respecto al número de electrones equivale a otro índice local de reactividad conocido como el descriptor dual f (2)(r):19 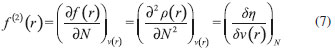 Los sitios moleculares donde f (2)(r) es positivo son regiones electrofílicas donde es probable que ocurra el ataque de un nucleófilo; mientras que valores negativos de f (2)(r) son característicos para las regiones nucleofílicas de una molécula. A partir de los conceptos de potencial químico y dureza, Parr y colaboradores20 propusieron una minimización de la energía de un sistema electrónico dentro del ensamble canónico para dar lugar al índice de electrofilicidad,20,21 definido como la energía de estabilización del sistema cuando es saturado con electrones. Aunque este concepto ha sido utilizado para el estudio de la reactividad de diversos sistemas moleculares,22-25 su descripción de la reactividad relativa ha resultado ser inconclusa en algunos casos.26 Similarmente, los índices de filicidad propuestos por Chattaraj,27 y que se derivan del concepto de electrofilicidad, no dan información adicional a la proporcionada por la suavidad local y las funciones de Fukui cuando se estudian aspectos relacionados con la reactividad intramolecular,28 además, para tendencias de reactividad intermolecular, los índices de filicidad pueden ser utilizados solo en limitados casos.29 Con la intención de obtener descriptores de reactividad más consistentes con las observaciones experimentales, numerosos trabajos han sido realizados en el ámbito de la DFT conceptual,30-33 incluyendo la publicación de Gázquez, Cedillo y Vela34 concerniente a los índices definidos como poder electroaceptador y poder electrodonador,35 además del trabajo recientemente publicado por Morell y colaboradores36 donde se introdujeron nuevos índices locales de electrofilicidad y nucleofilicidad. En este escenario, los índices de poder electrofílico y nucleofílico, así como sus versiones locales han sido desarrollados y son discutidos en el presente trabajo. Inicialmente, se realiza una breve presentación teórica de los índices de electrofilicidad, poder electroaceptador y poder electrodonador, para posteriormente presentar la elaboración de los dos índices globales definidos aquí como poder electrofílico y poder nucleofílico respectivamente. Interesantemente, las versiones locales de estos descriptores quedaron expresadas en términos del potencial químico, dureza, funciones de Fukui, descriptor dual y la hiperdureza, una función de respuesta de tercer orden cuya relevancia química ha sido recientemente discutida.37 Por último, los índices desarrollados fueron probados para predecir la reactividad relativa y de sitio de algunos sistemas moleculares cuyo comportamiento reactivo se encuentra bien definido.
DESCRIPTORES GLOBALES DE ELECTROFILICIDAD Y NUCLEOFILICIDAD Indice de electrofilicidad De acuerdo a las ecuaciones 2, 3 y 4, la variación en la energía cuando el potencial externo permanece constante está dada por (modelo mono-parabólico de Parr y Pearson):11 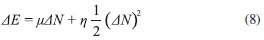 En la situación en la que una especie es saturada con electrones, el máximo número de electrones que son transferidos durante el proceso se obtiene por optimización del cambio en la energía del sistema, de modo que:36  Debido a que µ < 0, la ecuación 9 predice que ΔNmax debe ser positivo cuando el sistema adquiere electrones. La energía óptima asociada al proceso está dada entonces por: 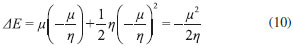 De acuerdo a la ecuación 10, la variación de la energía cuando un sistema molecular adquiere electrones es siempre negativa, por lo que equivale a una energía de estabilización. Atendiendo a este resultado, Parr y colaboradores20 expresaron el índice de electrofilicidad global (ω) como:  Poder electrodonador y electroaceptador Gázquez, Cedillo y Vela (GCV)34 introdujeron los conceptos de poder electrodonador (ω+) y poder electroaceptador (ω-) dentro de un ensamble gran canónico en el cual la molécula es un sistema cuántico abierto capaz de intercambiar electrones con en el entorno. En el esquema de interpolación bi-parabólico GCV, se asume que el sistema de referencia responde de manera distinta cuando acepta o dona electrones; de este modo, los cambios en la energía cuando el sistema dona y acepta electrones, se escriben respectivamente como: 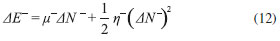 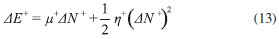 Cuando el sistema entra en contacto con un reservorio de electrones con potencial químico µbath, el sistema disminuye su potencial químico cediendo electrones al reservorio si µbath < µ-. Por otro lado, si µbath > µ+ el sistema incrementa su potencial químico aceptando electrones provenientes del reservorio. En la situación correspondiente a los pequeños cambios de la energía del sistema producidos por el entorno en el que este está inmerso, Gázquez y colaboradores34 asumieron que µbath = α-µ-, donde α- es una constante cuyo valor es ligeramente mayor que 1 para garantizar que µbath < µ- cuando el sistema dona electrones; y µbath = α+µ+ si el sistema acepta electrones, en cuyo caso α+ debe ser una constante ligeramente menor que 1, de modo que µbath > µ+. En este escenario, el poder electrodonador y poder electroaceptador fueron definidos respectivamente como:34,35   donde se ha considerado que η- = η+ = η.34 Las especies moleculares más electrofílicas exhibirán valores altos de ω+; mientras que valores pequeños de ω- serán característicos para sistemas que actúan mejor como nucleófilos.34,35,38 Para complementar la información proporcionada aquí, una revisión bibliográfica más profunda sobre el desarrollo teórico de la DFT conceptual, así como los descriptores que se derivan de ella, puede ser realizada en las publicaciones correspondientes a las referencias 3, 9, 39, 40, 41 y 42.
DESARROLLO DE LOS INDICES DE PODER ELECTROFILICO Y NUCLEOFILICO Poder electrofílico global y local Siguiendo los argumentos discutidos en otros trabajos,20,34,36 los índices de reactividad electrofílica fueron desarrollados en términos de los cambios ocurridos en la energía de un sistema electrónico cuando es saturado con electrones. No obstante, en el desarrollo presentado a continuación se consideró la evolución del potencial químico durante el proceso de aceptación de electrones, de este modo, manteniendo el potencial externo constante, el cambio instantáneo de la energía asociado a la respuesta del sistema a la aceptación de carga eléctrica se define por la siguiente expansión de Taylor de segundo orden: 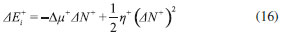 Donde µ+ es el potencial químico instantáneo, cuyo valor inicial es µ0+, aumentando su valor hasta cero cuando el sistema se satura con la máxima cantidad de electrones que puede adquirir. En esta representación canónica, cada vez que el sistema de referencia incrementa su número de electrones, debe ocurrir un cambio diferente en la energía del sistema. Expresando el potencial químico instantáneo mediante una expansión de Taylor alrededor del número de electrones del sistema de referencia se tiene:40 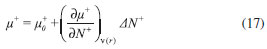  Por lo que el cambio instantáneo en el número de electrones se puede tomar como:  Introduciendo este resultado en la ecuación 16, se obtiene la siguiente expresión para el cambio instantáneo de la energía del sistema:  Ya que el primer valor del potencial químico es µ+ = µ0+, la ecuación 19 predice que al inicio del proceso el número de electrones adquiridos por el sistema es ΔN = 0, lo que es consistente con el hecho de que en este punto el sistema aún no ha adquirido la carga proveniente de los alrededores. Por otro lado, de acuerdo a la ecuación 20, la variación en la energía del sistema se puede aproximar a una función cuadrática del potencial químico instantáneo, que a su vez depende del número de electrones. Además, la máxima estabilización del sistema ocurre cuando µ+ = 0, en cuyo caso el cambio en la energía del sistema es: 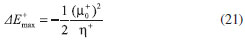 De aquí, se define el poder electrofílico como:  Ya que la energía de estabilización asociada al proceso de aceptación de carga es negativa, valores altos de ϕ+ serán característicos de especies altamente electrofílicas. No obstante, a diferencia de w, el poder electrofílico definido por la ecuación 22 es un concepto que parte del hecho de considerar las variaciones del potencial químico durante el proceso de transferencia electrónica, además de hacer énfasis en que el potencial químico inicial del sistema de referencia es diferente cuando el sistema acepta y recibe electrones. Considerando ahora que el potencial químico instantáneo puede escribirse en términos del potencial químico inicial, se tiene que:  Aquí, α+ es una función cuyo valor inicial es 0 tendiendo a 1 cuando el sistema es saturado con electrones, es decir, cuando µ+ se aproxima a 0. La derivada de α+ con respecto al número de electrones será de utilidad más adelante en la presente discusión, 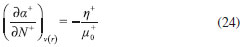 A partir de la ecuación 23, la ecuación 20 se re-escribe como: 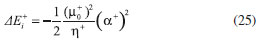 De esta manera, se define la función de respuesta electrofílica como:  Cuando el sistema es saturado con electrones, ϕi+ se convierte en: 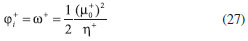 recuperándose así el concepto de poder electroaceptador.34 Como se mencionó antes, dentro del ensamble gran canónico Gázquez y colaboradores34 definieron una constante que multiplica el valor del potencial químico instantáneo del sistema para relacionarlo con el potencial químico de un baño de electrones en el que el sistema está inmerso. Por otra parte, en el presente desarrollo se optó por tomar el potencial químico inicial del sistema como parámetro fijo y definir una función α+ que da cuenta de la evolución del potencial químico durante el proceso en términos de su valor inicial. En analogía con el concepto de filicidad introducido por Chattaraj,27 el producto de ϕi+ por la función de Fukui se define como función de respuesta electrofílica local:  Asumiendo que ϕi+(r) es una función diferenciable, su derivada con respecto al número de electrones manteniendo el potencial externo constante es: 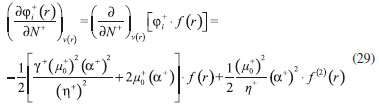 Aquí, se utilizaron las relaciones dadas por las ecuaciones 7 y 24, además γ es la hiperdureza, que ha sido definida como:43-46  En la situación límite en la que el sistema de referencia es saturado con la máxima cantidad de electrones, el potencial químico tiende a 0 debido a que el valor de α+ tiende a 1; en estas condiciones se define el poder electrofílico local como: 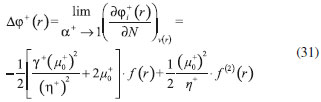 Debido a que el potencial químico es siempre negativo, Δϕ+(r) exhibirá valores positivos altos en las regiones del sistema donde existe un mayor poder electrofílico ya que en estas regiones el descriptor dual es positivo. Poder nucleofílico global y local En la representación gran canónica, un sistema electrónico es un sistema abierto capaz de intercambiar electrones, siendo el gran potencial la fuerza que conduce el proceso. Aplicando una transformación de Legendre47-49 para cambiar el número de electrones de la representación canónica por el potencial químico, se obtiene la siguiente expresión para el gran potencial (la función conjugada):36 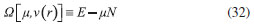 Dentro de esta representación, Morell y colaboradores36 demostraron que cuando el sistema de referencia cede electrones, la variación en el número de electrones debe ser negativa, de modo que:  mientras que la variación del gran potencial en términos de los cambios en el potencial químico y número de electrones es: 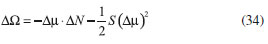 Las ecuaciones 33 y 34 fueron re-escritas aquí como:  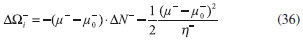 Introduciendo el valor de ΔN- de la ecuación 35 en la ecuación 36, la variación instantánea del gran potencial queda dada por: 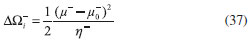 Para expresar el potencial químico instantáneo asociado al proceso de donación de electrones en términos del potencial químico inicial, µ- fue expresado como:  donde α- es una función que es igual a 0 al comienzo del proceso de transferencia electrónica (cuando se supone que µ- = µ0-), y tiende a 1 al final del proceso cuando µ- se aproxima a 0. La variación de α- con respecto al número de electrones es:  Combinando las ecuaciones 37 y 38, se tiene: 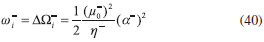 Donde el poder electro-donador instantáneo (ωi-) se define como el cambio instantáneo del gran potencial del sistema de referencia cuando este cede electrones. Como las variaciones en el gran potencial son siempre positivas, ωi- equivale a la energía instantánea de desestabilización del sistema mientras ocurre el proceso de transferencia electrónica, por ello, los sistemas electrónicos con mayor poder nucleofílico serán los que exhiban valores positivos pequeños de ωi-. Al final del proceso cuando α- se aproxima a 1, ωi- se convierte en 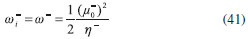 que equivale al concepto de poder electrodonador.34 La respuesta nucleofílica local sobre el sistema de referencia mientras dona electrones, se obtiene multiplicando el recíproco de ωi-(ϕi-) por la función de Fukui:  Donde ϕi- es la función de respuesta nucleofílica:  Tomando la derivada de ωi-(r) con respecto al número de electrones a potencial externo constante, se obtiene: 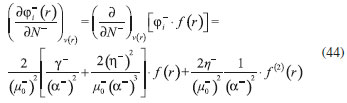 En la situación en la que el sistema de referencia dona la máxima cantidad de electrones, el potencial químico tiende a 0 debido a que el valor de α- tiende a 1; en estas condiciones se define el poder nucleofílico local como: 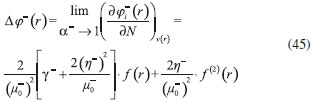 Ya que el potencial químico es negativo, Δϕ-(r) exhibirá valores negativos altos en las regiones del sistema donde existe un mayor poder nucleofílico debido a que en estas regiones el descriptor dual debe tomar valores negativos. Derivadas laterales Como las derivadas de la energía y la densidad electrónica con respecto al número de electrones son diferentes cuando se evalúan desde la izquierda y la derecha, tiene sentido considerar que la respuesta de un sistema molecular a la donación de carga es diferente al comportamiento del mismo cuando acepta electrones, lo que ha sido resaltado en el presente trabajo utilizando los super-índices - y + para indicar que el sistema dona o recibe electrones respectivamente. De este modo, el poder electrofílico local y el poder nucleofílico local de las ecuaciones 31 y 45 se convierten respectivamente en: 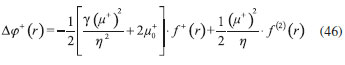 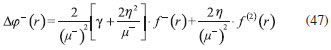 donde se ha removido el subíndice cero, η+ = η- = η, y 34,36  Además, f+(r) y f-(r) son las funciones de Fukui nucleofílica y electrofílica respectivamente.50,51 En particular, para sistemas moleculares, las regiones o sitios que muestren valores positivos altos de Δϕ+(r), tenderán a ser fuertemente electrofílicos; mientras que los sitios con los valores más negativos de Δϕ-(r) serán aquellos donde más probablemente ocurrirá el ataque de un electrófilo.
ESTUDIO DE LA REACTIVIDAD DE MOLÉCULAS ORGANICAS Los índices de reactividad desarrollados en el presente trabajo fueron utilizados caracterizar algunos sitios reactivos de moléculas orgánicas incluyendo derivados de órgano-litio (serie 1), compuestos carbonílicos (serie 2), y compuestos aromáticos (serie 3); que fueron seleccionados debido a su comportamiento reactivo bien establecido. Metodología Las moléculas estudiadas fueron construidas con el programa Avogadro52 y optimizadas por mecánica molecular con el campo de fuerzas UFF (Universal Force Fields).53 Posteriormente, las conformaciones moleculares de mínima energía fueron reoptimizadas utilizando el programa NWChem54 mediante el modelo químico PBE0/6-311+G(d,p)55 siguiendo así la metodología propuesta por Morell y colaboradores36 para el estudio computacional de estos mismos sistemas moleculares. Los potenciales químicos fueron calculados utilizando el esquema de interpolación de Gázquez, Cedillo y Vela:34   En este contexto, los valores de dureza se calcularon utilizando la ecuación 48. Las energías de ionización (I), y afinidades electrónicas (A) fueron aproximadas utilizando el teorema de Koopmans,56-58 donde I y A se toman como -εHOMO y -εLUMO. Asimismo, los valores de hiperdureza se aproximaron por:59 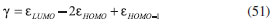 Las energías orbitales requeridas para la implementación de las ecuaciones 49, 50 y 51 se determinaron a partir del funcional B3LYP60,61 (como ha sido sugerido en numerosos trabajos teóricos de reactividad química)32,62-64 en conexión con las funciones de base 6-311++G(d,p) utilizando el programa Gaussian 0965 mediante cálculos de punto singular sobre las geometrías moleculares previamente optimizadas. Por otro lado, las funciones de Fukui fueron aproximadas mediante las expresiones:43,51,66,67   donde qkN-1, qkN y qkN+1 son las cargas atómicas del k-ésimo átomo de una molécula con N - 1, N y N + 1 electrones respectivamente. Las cargas atómicas fueron calculadas mediante el análisis de población de Mulliken (MPA, por sus siglas en inglés)68 al nivel de teoría B3LYP/6-311+G(d,p) utilizando el programa NWChem.54 Aunque ha habido durante muchos años un debate en la comunidad científica sobre la viabilidad de utilizar las cargas de Mulliken para condensar los valores de las funciones de Fukui, Roy e Hirao69 demostraron que no hay un problema totalmente definido en cuanto al signo negativo de las funciones de Fukui obtenidas en el esquema MPA; además aunque las cargas de Mulliken tienden a depender de las funciones de base,69 las ecuaciones de diferencias finitas 52 y 53 para condensar las funciones de Fukui fueron originalmente derivadas dentro del esquema de Mulliken,70-72 que sigue siendo utilizado aún en diversos trabajos teóricos de reactividad para el cálculo de las FF's.73-75 Por último, los valores del descriptor dual se aproximaron por:3,19,36 
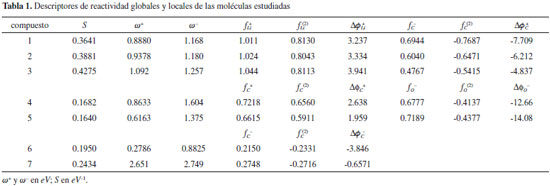
RESULTADOS Y DISCUSION La reactividad global relativa dentro de cada subgrupo de compuestos fue discutida mediante los índices S, ω+ y ω-, que fueron obtenidos mediante las ecuaciones 5, 27 y 41 respectivamente. Por otro lado, los valores condensados de Δϕk+ y Δϕk- fueron calculados respectivamente como: 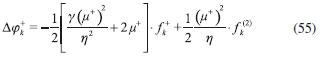 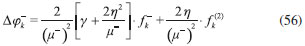 Estos nuevos índices locales, junto con las funciones de Fukui y el descriptor dual, se utilizaron para discutir los aspectos relacionados con la reactividad local de sitios moleculares pertinentes en cada caso. Todos los índices de reactividad obtenidos fueron recogidos en la Tabla 1, mientras que en la Figura 1 se muestran las estructuras de las moléculas estudiadas.
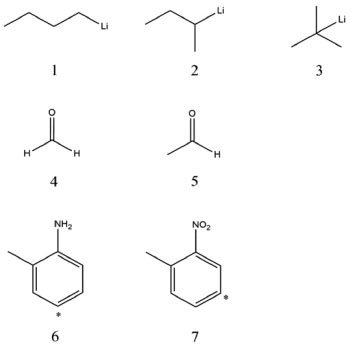 Figura 1. Estructuras de los derivados órgano-litio de la serie 1 (1, 2 y 3), derivados carbonilo de la serie 2 (4, y 5), y derivados aromáticos de la serie 3 (6 y 7). Con asterisco con los átomos de carbono más reactivos de los compuestos 6 y 7
Serie 1: n-butil-Li, sec-butil-Li, y terc-butil-Li Para esta serie de compuestos organo-litio (Figura 1), se sabe que la electrofilicidad molecular se encuentra concentrada sobre el átomo de Li, siendo el terc-butil-litio (3) el más electrofílico de los tres derivados, seguido por el sec-butil-litio (2) y n-butil-litio (1) respectivamente.36,76 Los valores de ω+ de la Tabla 1 reproducen de manera correcta esta observación. Asimismo, los valores de suavidad predicen un incremento de reactividad en el sentido 1 - 2 - 3. Desde el punto de vista local, los valores del descriptor dual no dieron una descripción correcta de la reactividad relativa del átomo de Li presente en los compuestos 1, 2 y 3, no obstante, los valores de fLi+ y de ΔϕLi+ aumentaron desde el n-butil-litio hasta el terc-butil-litio, mostrando así una buena representación de la reactividad electrofílica relativa del átomo de litio en estos derivados. Los valores de ω- de los organo-litios sugieren un incremento del carácter nucleofílico en el sentido 3 - 2 - 1, lo que va en desacuerdo con observaciones realizadas en otros trabajos.77 Los valores de ΔϕC- del carbono nucleofílico enlazado a Li tampoco dieron la predicción correcta del orden relativo de reactividad de este sitio molecular, que debe aumentar desde el n-butil-litio hasta el terc-butil-litio. Esta falla podría deberse a una descripción incorrecta de las cargas atómicas condesadas como consecuencia de la capacidad de la densidad electrónica de extenderse hacia los grupos alquilo enlazados al átomo de carbono terminal. Un inconveniente similar fue reportado por Morell y colaboradores36 al estudiar la misma serie de compuestos mediante los índices locales propuestos en su trabajo basados en el esquema de cargas atómicas de Hirshfeld. Serie 2: Compuestos carbonilo La serie de compuestos carbonilo está conformada por el formaldehído (4) y acetaldehído (5), (Figura 1) que son moléculas comúnmente conocidas por su carácter electrofílico concentrado sobre el átomo de carbono carbonilo. Experimentalmente, se ha observado una mayor reactividad electrofílica por parte del formaldehído en comparación con el acetaldehído.78 Los datos de S y ω+ reportados en la Tabla 1 corroboran el orden relativo de reactividad y electrofilicidad de los dos compuestos carbonilo estudiados; además, los valores de ΔϕC+ referidos al átomo de carbono carbonilo, mostraron el mismo orden relativo de reactividad dado por fC(2), lo que significa que tanto la selectividad hacia especies nucleofílicas como el poder electrofílico local del carbono carbonilo se incrementan en el sentido acetaldehído - formaldehído, lo que es de esperarse debido a que el grupo metilo del acetaldehído aporta electrones inductivamente al C carbonilo disminuyendo su potencial electrofílico.78 Por otro lado, el orden relativo de nucleofilicidad dado por los valores de ω- sugieren que, en fase gaseosa, el formaldehído es menos nucleofílico que el acetaldehído, por lo que este podría interactuar de manera más efectiva con un electrófilo adecuado. En concordancia con esta observación, los valores de ΔϕO- sugieren que el compuesto 5 tiene un mayor poder nucleofílico local sobre el átomo de O carbonilo, mostrando así el mismo orden de selectividad dado por los valores de fO- y fO(2). Serie 3: Compuestos aromáticos En la Tabla 1 se muestran los valores de S, ω+ y ω- de los compuestos 6 (o-toluidina) y 7 (o-nitro-tolueno). Estos derivados aromáticos (Figura 1) fueron seleccionados siguiendo los argumentos de Morell y colaboradores.36 Desde el punto de vista experimental, se ha observado que la o-toluidina y el o-nitro-tolueno solo dan lugar a productos sustituidos en posición para y meta con respecto a los grupos exocíclicos amino y nitro respectivamente,79,80 por lo que la reactividad local de estos carbonos fue racionalizada utilizando el índice de poder nucleofílico local, además de los valores de fC- y fC(2). De los dos compuestos aromáticos estudiados, el o-nitro-tolueno resultó ser el más reactivo en virtud de su alto potencial electrofílico alojado sobre el grupo nitro; mientras que la o-toluidina es un sistema más nucleofílico debido al grupo amino exocíclico, que además es un fuerte activador del anillo aromático favoreciendo el carácter nucleofílico de los carbonos en posición orto/para con respecto a este sustituyente.78 Por otro lado, el compuesto 7 contiene un sustituyente nitro que desactiva el anillo aromático orientando así la sustitución electrofílica hacia la posición meta.78 Aunque desde el punto de vista intramolecular las funciones de Fukui y el descriptor dual dan razón de estas observaciones, la selectividad de sitio dada por estos índices falla al comparar la reactividad de los carbonos más nucleofílicos de los compuestos 6 y 7. En este sentido, los valores de ΔϕC- demuestran que el carbono para de la o-toluidina es más reactivo que el carbono en posición meta del o-nitro-tolueno, lo que está en buen acuerdo con el hecho de que el primer derivado mencionado está fuertemente activado por el grupo amino que aporta electrones al anillo aromático mediante resonancia; mientras que el segundo debe ser menos reactivo hacia la sustitución electrofílica debido al grupo nitro que actúa como extractor de electrones.78
CONCLUSIONES Considerando la evolución del potencial químico, los ensambles canónico y gran canónico fueron utilizados para expresar las variaciones de la energía de un sistema electrónico en procesos en los que acepta y dona electrones respectivamente; de este modo, los conceptos de función de respuesta electrofílica y función de respuesta nucleofílica fueron introducidos (ecuaciones 26 y 43). En las situaciones límite en la que el sistema es saturado con electrones o cede la máxima cantidad de carga, los índices globales desarrollados aquí se convierten respectivamente en los conceptos de poder electroaceptador y poder electrodonador, propuestos originalmente por Gázquez, Cedillo y Vela,34 y re-definidos recientemente por Morell y colaboradores.36 Además, como ha sido propuesto en estos trabajos, no solo se consideraron las derivadas laterales de la función de Fukui, sino también del potencial químico, dando cuenta así de la diferencia en las respuestas del sistema a la aceptación y donación de carga. El poder electrofílico local (Δϕ+(r)) y poder nucleofílico local (Δϕ-(r)), fueron desarrollados como la razón de cambio de las funciones de respuesta electrofílica y nucelofílica respectivamente, quedando expresados en términos de los potenciales químicos, dureza, las funciones de Fukui, el descriptor dual, y la derivada de la dureza con respecto al número de electrones (hiperdureza) (ecuaciones 46 y 47, respectivamente) que apareció de forma natural durante el desarrollo de Δϕ+(r) y Δϕ-(r). Los índices de reactividad propuestos fueron probados para el estudio de la reactividad de tres series de sistemas moleculares con propiedades químicas bien establecidas. La estructura electrónica de las moléculas estudiadas fue modelada mediante el funcional de la densidad híbdrido B3LYP en conexión con las bases 6-311++G(d,p). En general, los índices w+ y w- mostraron buenos resultados en la predicción de la reactividad relativa dentro de cada serie de compuestos; mientras que los valores de Δϕk+ y Δϕk- dieron una descripción razonable de la reactividad local de la mayoría de los sistemas estudiados, dando resultados comparables a los de las funciones de Fukui y el descriptor dual. No obstante, para la serie de compuestos aromáticos Δϕk- dio mejores resultados que fk- y fk(2) en cuanto a la comparación de la reactividad intermolecular de los átomos de carbono nucleofílicos; por lo tanto, los índices de poder electrofílico local y poder nucleofílico local propuestos aquí podrían ser probados para predecir la reactividad de otras moléculas con reactividad conocida con el propósito de complementar la validación de estos nuevos índices para el estudio de la reactividad local de sistemas moleculares más complejos.
AGRADECIMIENTOS Los autores agradecen a la Universidad de Córdoba por el apoyo prestado para la realización de este trabajo. Los autores agradecen también el soporte proporcionado por la beca de investigación 20160316 de la Universidad Daegu.
REFERENCIAS 1. Fukui, K.; Angew. Chem., Int. Ed. Engl. 1982, 21, 801. DOI: http://dx.doi.org/10.1002/anie.198208013 2. Ponec, R. Overlap determinant method in the theory of pericyclic reactions, Springer Science & Business Media: Berlim, 2012, vol. 65. 3. Liu, S.-B.; Acta Phys.-Chim. Sin. 2009, 25, 590. 4. Ponec, R.; Strnad, M.; Int. J. Quantum Chem. 1992, 42, 501. DOI: http://dx.doi.org/10.1002/qua.560420311 5. Wilson, S. Electron correlation in molecules, 2nd ed., Dover Publications, Inc.: New York, 2014. 6. Parr, R. G.; Yang, W.; Density-functional theory of atoms and molecules; Oxford University Press, 1989; Vol. 16. 7. Dreizler, R. M.; Gross, E. K.; Density functional theory: an approach to the quantum many-body problem; Springer Science & Business Media: Berlim, 2012. 8. Liu, S.; Parr, R. G.; J. Chem. Phys. 1997, 106, 5578. DOI: http://dx.doi.org/10.1063/1.473580 9. Proft, F. D.; Ayers, P. W.; Geerlings, P. En The Chemical Bond: Fundamental aspects of chemical bonding; Frenking, G.; Shaik, S., eds.; Wiley-VCH Verlag GmbH & Co. KGaA: New Jersey, 2014, cap. 7. 10. Parr, R. G.; Donnelly, R. A.; Levy, M.; Palke, W. E.; J. Chem. Phys. 1978, 68, 3801. DOI: http://dx.doi.org/10.1063/1.436185 11. Parr, R. G.; Pearson, R. G.; J. Am. Chem. Soc. 1983, 105, 7512. DOI: http://dx.doi.org/10.1021/ja00364a005 12. Pearson, R. G.; J. Am. Chem. Soc. 1963, 85, 3533. DOI: http://dx.doi.org/10.1021/ja00905a001 13. Parr, R. G.; Yang, W.; J. Am. Chem. Soc. 1984, 106, 4049. DOI: http://dx.doi.org/10.1021/ja00326a036 14. Cerda-Monje, A.; Ormazábal-Toledo, R.; Cárdenas, C.; Fuentealba, P.; Contreras, R.; J. Phys. Chem. B 2014, 118, 3696. DOI: http://dx.doi.org/10.1021/jp5009994 PMID: 24617616 15. Berger, G.; Comput. Theor. Chem. 2013, 1010, 11. DOI: http://dx.doi.org/10.1016/j.comptc.2012.12.029 16. Scales, S.; Johnson, S.; Hu, Q.; Do, Q.-Q.; Richardson, P.; Wang, F.; Braganza, J.; Ren, S.; Wan, Y.; Zheng, B.; Faizi, D.; McAlpine, I.; Org. Lett. 2013, 15, 2156. DOI: http://dx.doi.org/10.1021/ol4006695 PMID: 23600718 17. Saha, S. K.; Banerjee, P.; RSC Adv. 2015, 5, 71120. DOI: http://dx.doi.org/10.1039/C5RA15173B 18. Zhou, P.; Ayers, P. W.; Liu, S.; Li, T.; Phys. Chem. Chem. Phys. 2012, 14, 9890. DOI: http://dx.doi.org/10.1039/c2cp40488e PMID: 22711288 19. Morell, C.; Grand, A.; Toro-Labbé, A.; J. Phys. Chem. A 2005, 109, 205. DOI: http://dx.doi.org/10.1021/jp046577a PMID: 16839107 20. Parr, R. G.; Szentpaly, L. v; Liu, S.; J. Am. Chem. Soc. 1999, 121, 1922. DOI: http://dx.doi.org/10.1021/ja983494x 21. Chattaraj, P. K.; Sarkar, U.; Roy, D. R.; Chem. Rev. 2006, 106, 2065. DOI: http://dx.doi.org/10.1021/cr040109f PMID: 16771443 22. Zhang, J.; Qiao, G.; Hu, S.; Yan, Y.; Ren, Z.; Yu, L.; Corros. Sci. 2011, 53, 147. DOI: http://dx.doi.org/10.1016/j.corsci.2010.09.007 23. Mebi, C. A.; J. Chem. Sci. 2011, 123, 727. DOI: http://dx.doi.org/10.1007/s12039-011-0131-2 24. Singh, O.; R Kakularam, K.; Reddanna, P.; Aparoy, P.; Protein Pept. Lett. 2015, 22, 903. DOI: http://dx.doi.org/10.2174/0929866522666150622102131 PMID: 26095375 25. Ghiasi, R.; Pasdar, H.; Russ. J. Phys. Chem. A 2013, 87, 973. DOI: http://dx.doi.org/10.1134/S0036024413060368 26. Mendoza Huizar, L. H.; Rios-Reyes, C. H.; Olvera-Maturano, N. J.; Robles, J.; Rodriguez, J. A.; Open Chem. 2015, 13, 52. DOI: http://dx.doi.org/10.1515/chem-2015-0008 27. Chattaraj, P. K.; Maiti, B.; Sarkar, U.; J. Phys. Chem. A 2003, 107, 4973. DOI: http://dx.doi.org/10.1021/jp034707u 28. Roy, R. K.; J. Phys. Chem. A 2004, 108, 4934. DOI: http://dx.doi.org/10.1021/jp038025i 29. Roy, R. K.; Usha, V.; Paulovič, J.; Hirao, K.; J. Phys. Chem. A 2005, 109, 4601. DOI: http://dx.doi.org/10.1021/jp046505j PMID: 16833797 30. Roy, R. K.; Krishnamurti, S.; Geerlings, P.; Pal, S.; J. Phys. Chem. A 1998, 102, 3746. DOI: http://dx.doi.org/10.1021/jp973450v 31. Padmanabhan, J.; Parthasarathi, R.; Elango, M.; Subramanian, V.; Krishnamoorthy, B. S.; Gutierrez-Oliva, S.; Toro-Labbé, A.; Roy, D. R.; Chattaraj, P. K.; J. Phys. Chem. A 2007, 111, 9130. DOI: http://dx.doi.org/10.1021/jp0718909 PMID: 17715901 32. Chamorro, E.; Duque-Noreña, M.; Notario, R.; Pérez, P.; J. Phys. Chem. A 2013, 117, 2636. DOI: http://dx.doi.org/10.1021/jp312143t PMID: 23350794 33. Sánchez-Márquez, J.; J. Mol. Model. 2015, 21, 1. DOI: http://dx.doi.org/10.1007/s00894-014-2561-5 34. Gazquez, J. L.; Cedillo, A.; Vela, A.; J. Phys. Chem. A 2007, 111, 1966. DOI: http://dx.doi.org/10.1021/jp065459f PMID: 17305319 35. Orozco-Valencia, A. U.; Vela, A.; J. Mex. Chem. Soc. 2012, 56, 294. 36. Morell, C.; Gázquez, J. L.; Vela, A.; Guégan, F.; Chermette, H.; Phys. Chem. Chem. Phys. 2014, 16, 26832. DOI: http://dx.doi.org/10.1039/C4CP03167A PMID: 25375814 37. Morell, C.; Grand, A.; Toro-Labbé, A.; Chermette, H.; J. Mol. Model. 2013, 19, 2893. DOI: http://dx.doi.org/10.1007/s00894-013-1778-z PMID: 23475291 38. Martínez-Araya, J. I.; Salgado-Morán, G.; Glossman-Mitnik, D.; J. Phys. Chem. B 2013, 117, 6339. DOI: http://dx.doi.org/10.1021/jp400241q PMID: 23656309 39. Geerlings, P.; De Proft, F.; Langenaeker, W.; Chem. Rev. 2003, 103, 1793. DOI: http://dx.doi.org/10.1021/cr990029p PMID: 12744694 40. Geerlings, P.; De Proft, F.; Phys. Chem. Chem. Phys. 2008, 10, 3028. DOI: http://dx.doi.org/10.1039/b717671f PMID: 18688366 41. Chattaraj, P. K. Chemical reactivity theory: a density functional view, CRC Press: New York, 2009. 42. Geerlings, P.; Fias, S.; Boisdenghien, Z.; De Proft, F.; Chem. Soc. Rev. 2014, 43, 4989. DOI: http://dx.doi.org/10.1039/c3cs60456j PMID: 24531142 43. Senet, P.; J. Chem. Phys. 1996, 105, 6471. DOI: http://dx.doi.org/10.1063/1.472498 44. Senet, P.; J. Chem. Phys. 1997, 107, 2516. DOI: http://dx.doi.org/10.1063/1.474591 45. Fuentealba, P.; Cedillo, A.; J. Chem. Phys. 1999, 110, 9807. DOI: http://dx.doi.org/10.1063/1.478033 46. Fuentealba, P.; Parr, R. G.; J. Chem. Phys. 1991, 94, 5559. DOI: http://dx.doi.org/10.1063/1.460491 47. De Proft, F.; Liu, S.; Parr, R. G.; J. Chem. Phys. 1997, 107, 3000. DOI: http://dx.doi.org/10.1063/1.474657 48. Ayers, P. W.; Fuentealba, P.; Phys. Rev. A 2009, 80, 032510. DOI: http://dx.doi.org/10.1103/PhysRevA.80.032510 49. Guégan, F.; Tognetti, V.; Joubert, L.; Chermette, H.; Luneau, D.; Morell, C.; Phys. Chem. Chem. Phys. 2015. PMID: 26662022 50. Ayers, P. W.; Levy, M.; Theor. Chem. Acc. 2000, 103, 353. DOI: http://dx.doi.org/10.1007/s002149900093 51. Ayers, P. W.; Yang, W.; Bartolotti, L. J. En Chemical reactivity theory: A density functional view; Chattaraj, P. K., Ed.; CRC Press: New York, 2009, cap. 18. 52. Hanwell, M. D.; Curtis, D. E.; Lonie, D. C.; Vandermeersch, T.; Zurek, E.; Hutchison, G. R.; J Cheminformatics 2012, 4, 17. DOI: http://dx.doi.org/10.1186/1758-2946-4-17 53. Rappé, A. K.; Casewit, C. J.; Colwell, K. S.; Goddard, W. A.; Skiff, W. M.; J. Am. Chem. Soc. 1992, 114, 10024. DOI: http://dx.doi.org/10.1021/ja00051a040 54. Valiev, M.; Bylaska, E. J.; Govind, N.; Kowalski, K.; Straatsma, T. P.; Van Dam, H. J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T. L.; Jong, W. A.; Comput. Phys. Commun. 2010, 181, 1477. DOI: http://dx.doi.org/10.1016/j.cpc.2010.04.018 55. Adamo, C.; Barone, V.; J. Chem. Phys. 1999, 110, 6158. DOI: http://dx.doi.org/10.1063/1.478522 56. Lewars, E. G. Computational chemistry: introduction to the theory and applications of molecular and quantum mechanics, 2nd ed., Springer Science & Business Media: New York, 2010. 57. Cramer, C. J. Essentials of computational chemistry: theories and models, 2nd ed., John Wiley & Sons: Chichester, 2013. 58. Helgaker, T.; Jorgensen, P.; Olsen, J.; Molecular electronic-structure theory, John Wiley & Sons: Chichester, 2014. 59. Cárdenas, C.; Rabi, N.; Ayers, P. W.; Morell, C.; Jaramillo, P.; Fuentealba, P.; J. Phys. Chem. A 2009, 113, 8660. DOI: http://dx.doi.org/10.1021/jp902792n PMID: 19580251 60. Becke, A. D.; Phys. Rev. A 1988, 38, 3098. DOI: http://dx.doi.org/10.1103/PhysRevA.38.3098 61. Lee, C.; Yang, W.; Parr, R. G.; Phys. Rev. B 1988, 37, 785. DOI: http://dx.doi.org/10.1103/PhysRevB.37.131 62. Cardona, W.; Guerra, D.; Restrepo, A.; Mol. Simul. 2014, 40, 477. DOI: http://dx.doi.org/10.1080/08927022.2013.822077 63. Domingo, L. R.; Pérez, P.; Org. Biomol. Chem. 2011, 9, 7168. DOI: http://dx.doi.org/10.1039/c1ob05856h PMID: 21842104 64. El Adnani, Z.; Mcharfi, M.; Sfaira, M.; Benzakour, M.; Benjelloun, A. T.; Touhami, M. E.; Corros. Sci. 2013, 68, 223. DOI: http://dx.doi.org/10.1016/j.corsci.2012.11.020 65. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, Jr., J. A.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; and Pople, J. A.; Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009. 66. Yang, W.; Parr, R. G.; Pucci, R.; J. Chem. Phys. 1984, 81, 2862. DOI: http://dx.doi.org/10.1063/1.447964 67. Ayers, P. W.; Theor. Chem. Acc. 2001, 106, 271. DOI: http://dx.doi.org/10.1007/PL00012385 68. Mulliken, R. S.; J. Chem. Phys. 1955, 23, 1833. DOI: http://dx.doi.org/10.1063/1.1740588 69. Roy, R. K.; Hirao, K.; Krishnamurty, S.; Pal, S.; J. Chem. Phys. 2001, 115, 2901. DOI: http://dx.doi.org/10.1063/1.1386699 70. Yang, W.; Mortier, W. J.; J. Am. Chem. Soc. 1986, 108, 5708. DOI: http://dx.doi.org/10.1021/ja00279a008 PMID: 22175316 71. Contreras, R. R.; Fuentealba, P.; Galván, M.; Pérez, P.; Chem. Phys. Lett. 1999, 304, 405. DOI: http://dx.doi.org/10.1016/S0009-2614(99)00325-5 72. Domingo, L. R.; Pérez, P.; Sáez, J. A.; RSC Adv. 2013, 3, 1486. DOI: http://dx.doi.org/10.1039/C2RA22886F 73. Oftadeh, M.; Mahani, N. M.; Hamadanian, M.; Res. Pharm. Sci. 2013, 8, 285. PMID: 24082898 74. Saravanan, S.; Balachandran, V.; Spectrochim. Acta, Part A 2014, 130, 604. DOI: http://dx.doi.org/10.1016/j.saa.2014.04.058 75. Gece, G.; Bilgiç, S.; Ind. Eng. Chem. Res. 2012, 51, 14115. DOI: http://dx.doi.org/10.1021/ie302324b 76. Setzer, W. N.; Schleyer, P. v R.; Adv Organomet Chem 1985, 24, 353. 77. Farah, D.; Karol, T. J.; Kuivila, H. G.; Organometallics 1985, 4, 662. DOI: http://dx.doi.org/10.1021/om00123a008 78. Bruice, P. Y.; Organic Chemistry, 4th ed., Pearson Prentice Hall, 2004. 79. Bigelow, L. A.; J. Am. Chem. Soc. 1919, 41, 1559. DOI: http://dx.doi.org/10.1021/ja02231a010 80. Fergwon, P. R.; J. Chem. Educ. 1971, 48, 405. DOI: http://dx.doi.org/10.1021/ed048p405 |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access