Educação
|
|
| Problemas inversos mal colocados em química Ill-posed inverse problems in chemistry |
|
Joao P. BragaI,*; Nelson H. T. LemesII; Emílio BorgesIII; Rita C. O. SebastiaoI
IDepartamento de Química, Universidade Federal de Minas Gerais, 31270-901 Belo Horizonte - MG, Brasi Recebido em 18/11/2015 *e-mail: jpbraga@ufmg.br What is an ill-posed inverse problem? The answer to this question is the main objective of the present paper and the pre-requisite to follow the material requires only elementary calculus. The first mathematical formulation of an inverse problem, due to N. H. Abel, together with the fundamental work by Jacques Hadamard, are explored at the beginning of the paper. A prototype system is used to consider the regularization concept. Three numerical methods, the Tikhonov regularization, the decomposition into singular values and the Hopfield neural networks, applied to remove the singularity are examined. General aspects of the ill-posed inverse problems in chemistry with emphasis in thermodynamics and a set of general rules for other areas of science are also analyzed. INTRODUÇAO O que sao problemas inversos mal colocados? Problemas inversos mal colocados sao importantes em química? O que faz um problema inverso ser mal colocado? Por que o estudante de graduaçao provavelmente nunca lidou com problemas inversos mal colocados? Uma apresentaçao didática dessas respostas, enfatizando a importância de problemas inversos mal colocados em química e em ciências de forma geral, será abordada. Retirar alguma informaçao de dados experimentais é um problema inverso. Por exemplo, obter uma seçao de choque de colisao de forma teórica ou experimental seria um processo direto, enquanto retirar a energia potencial da seçao de choque experimental seria um problema inverso. Fica evidente que ao lidar com problemas inversos o cientista tem de estar familiarizado com o problema teórico direto relacionado e com a natureza do experimento realizado. Mas é preciso reconhecer que ao tratar com dados experimentais tem-se que respeitar a existência do erro experimental, muitas vezes desprezado ou mesmo filtrado numa primeira análise. Problemas inversos na presença de erros experimentais sao denominados problemas inversos mal colocados.1 O primeiro problema inverso resolvido foi provavelmente elaborado por Eratóstenes entre 276-196 a.C, mas é preciso deixar claro que nao existe consenso sobre esse ponto histórico, e por vezes esse fato é atribuído também a Archimedes.2 Entretanto, a primeira formulaçao matemática e consciente de um problema inverso foi desenvolvida por N. H. Abel em 1826.3 O trabalho de Abel, apesar de nao considerar erros experimentais, foi essencial no desenvolvimento da teoria de problemas inversos, pois indicou um caminho matemático e rigoroso para se lidar com tais problemas. Em 1923, Jacques Hadamard formula as condiçoes para um problema inverso ser mal colocado,4 condiçoes essas que serao discutidas. Diretamente relacionado com essa definiçao de Hadamard observa-se que problemas inversos mal colocados envolvem também a remoçao de uma singularidade. Técnicas especiais que removem essa singularidade serao apresentadas, com maior ênfase no estudo de redes neurais recorrentes, devido a sua importância na aplicaçao em problemas inversos. Uma revisao de problemas inversos mal colocados em termodinâmica será discutida, evidenciando a importância do estudo de tais problemas em química.
NIELS HENRIK ABEL, 1826 Em um artigo publicado em 1826,3 Abel formula o problema da tautocrônica como se segue. Considere uma curva BDMA qualquer na qual observa-se um ponto (ou um anel) que cai livremente sob a açao da gravidade. O problema proposto por Abel consiste em: sendo dado o tempo de queda em várias alturas, pode-se determinar o formato da curva BDMA?
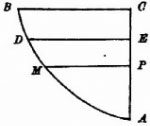 Figura 1. Figura original usada por N.H. Abel 3
Portanto, sendo medida a funçao t(h), t sendo o tempo de queda nas várias alturas h, pede-se o formato da curva. O problema direto é relativamente simples. A conservaçao da energia ao longo da curva s fornece 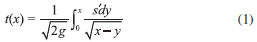 com
JACQUES HADAMARD, 1923 O passo decisivo para um entendimento mais geral de problemas inversos foi dado por Jacques Hadarmard em 1923,4 trabalho em que introduziu o conceito de problemas inversos mal colocados. Problemas inversos mal colocados em química, física, medicina, e em ciências de forma geral, sao problemas em que a soluçao pode nao existir, nao ser única ou nao ser contínua em relaçao à informaçao inicial. Se essas três condiçoes sao satisfeitas, o problema é denominado de bem-colocado. Nao é difícil perceber que essas três condiçoes estao associadas com a presença do erro experimental, o que será evidenciado por três exemplos simples. O fator de compressibilidade, O espalhamento de duas partículas num campo central ilustra a segunda condiçao de um problema ser mal colocado. O ângulo de espalhamento máximo nesse caso vale 1800, quando o choque for frontal, correspondendo ao parâmetro de impacto igual a zero. Se numa medida experimental obteve-se esse ângulo igual a 1850, pergunta-se: qual a energia potencial que forneceria 1850? O leitor um pouco familiarizado com a teoria de espalhamento responderia que tal potencial nao existe. A terceira condiçao de um problema ser mal colocado pode ser exemplificada considerando-se a integral, O entendimento de existência, unicidade e continuidade é um pré-requisito para o entendimento adequado de problemas inversos mal colocados. Estudar um problema em que a soluçao nao existe, nao é única ou nao é contínua certamente é um desafio em química e em ciências. Como o próprio Hadamard provocou em 1923,7 inexperienced people will not handle this kind of problem.
EQUAÇAO INTEGRAL DE FREDHOLM A equaçao (1) é um caso particular da integral de Fredholm de primeira ordem, 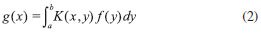 A interpretaçao dessa equaçao, para os propósitos do presente artigo, deve ser a seguinte:
Para entender os problemas que aparecem quando se tenta inverter uma equaçao integral de Fredholm de primeira ordem, protótipo de uma classe de problemas inversos lineares na forma integral, pode-se tomar uma equaçao desse tipo com soluçao conhecida. A equaçao integral de Fredholm,8, 9 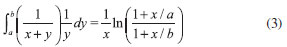 com a < y < b, foi escolhida como protótipo e servirá de base teórica e numérica para o entendimento de problemas reais. Nesse caso a entrada, a saída e a transformaçao sao conhecidas, 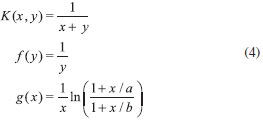 Sabendo-se a saída e o que causou essa saída, pergunta-se qual a entrada. O resultado esperado nesse problema inverso, a funçao f(y), é entao conhecida. A representaçao da equaçao integral numa forma algébrica é o próximo passo para resolver esse problema. Isso deve ser feito escolhendo-se uma base adequada, como por exemplo, uma base quadrada ou uma base de Legendre.10 A precisao da representaçao está relacionada com o tamanho dessa base, de dimensao n. Após transformaçoes algébricas adequadas,9 chega-se a uma expressao da forma,  com ƒ ∈ Rn, g ∈ Rm e K ∈ Rm×n, indicando as dimensoes dessas três quantidades. A equaçao algébrica terá duas dimensoes a serem consideradas, uma relacionada com essa representaçao e outra com o número de dados experimentais, m. Numa primeira discussao considera-se o caso hipotético em que o número de dados experimentais é igual à dimensao da base. Portanto, pode-se tentar a soluçao do problema inverso simplesmente fazendo-se ƒ = K-1 g. Assim procedendo, para m = n =32 numa base quadrada, encontra-se o resultado da funçao ƒ como na figura 2. A funçao 
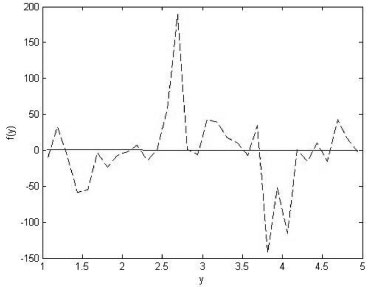 Figura 2. Resultado invertido usando o critério dos mínimos quadrados (linha pontilhada) juntamente com o resultado exato (linha contínua)
Entretanto o resultado obtido para ƒ é idêntico ao da Figura 2, pois nao se pode mudar o posto (rank) de uma matriz simplesmente somando as suas linhas, como em KTK. Qual a origem desses resultados tao discrepantes? Para o caso particular apresentado pode-se analisar, de forma bem mais restrita, o determinante da representaçao para KTK ou para K. Nesse caso tem-se, para m = n = 32, det(K) = 10-40, praticamente zero. Para n = m = 64 calcula-se det(K) = 0.0. Portanto existe uma singularidade no cálculo da matriz inversa que depende do inverso do valor do determinante. Obviamente que a soluçao desse problema existe, mas certamente terá de envolver conceitos adicionais de álgebra.
MÉTODOS NUMÉRICOS PARA REGULARIZAÇAO Técnicas numéricas especiais devem ser desenvolvidas para tratar de problemas inversos mal colocados. A transformada pode nao ter inversa, como ilustrado, e mesmo quando houver os possíveis erros em g, mesmo o da discretizaçao numérica, serao enormemente amplificados. Até aproximadamente 1996, dois eram basicamente os métodos usados para se resolver um problema inverso: a regularizaçao de Tikhonov1 e a decomposiçao em valores singulares.10 Na regularizaçao de Tikhonov remove-se a singularidade adicionando-se uma informaçao extra ao problema original, como por exemplo, a procura da soluçao de norma mínima. Na decomposiçao em valores singulares essa singularidade é removida usando-se os dois espaços vetoriais básicos da álgebra linear, um relativo aos dados de entrada e outro relativo aos dados de saída. De acordo com o teorema fundamental da álgebra11 esses espaços sao ortogonais e complementares. Trabalhando-se no sub-espaço adequado, encontra-se a soluçao desejada do problema inverso. Uma comparaçao detalhada desses dois métodos, usando a equaçao (3) como modelo, aparece na referência.9 Entretanto, tanto na regularizaçao de Tikhonov quanto na decomposiçao em valores singulares é necessário um passo empírico, no qual sao computados o peso da restriçao ou o tamanho do sub-espaço. Um outro método mais poderoso, usando redes neurais de Hopfield,12 será apresentado com mais detalhes no presente trabalho. Esse método foi estendido para problemas lineares e nao lineares13, sendo mais robusto do que a regularizaçao de Tikhonov ou a decomposiçao em valores singulares. Redes neurais artificais, no presente contexto, sao programas numéricos que simulam o funcionamento do cerébro. Por conseguinte, esses programas sao capazes de aprender, no sentido de otimizar, sobre um problema formulado. A rede neural de Hopfield12 mostrou-se a mais apropriada, pois pode-se tratar indistintamente problemas lineares e nao lineares. Como na regularizaçao de Tikhonov ou na decomposiçao em valores singulares procura-se também a soluçao que satisfaça o mínimo de E = Φ(ƒ) = || Kƒ - g ||2, com a condiçao de que 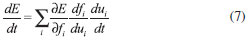 Um passo importante nas redes neurais é prosseguir com a analogia com a biologia, assumindo que a funçao ativaçao ƒ sempre aumenta com o estado do neurônio isto é,  em que i = 1, 2, ..., n, n é o número de neurônios no sistema e também o número de equaçoes de Hopfield. A resposta desejada é obtida pela soluçao desse sistema de equaçoes diferenciais acopladas, denominadas equaçoes de Hopfield. Observe que em nenhum momento a inversa do operador foi requerida. A medida que o tempo de aprendizado avança, os neurônios vao se adaptando para obter a soluçao desejada. O resultado invertido do problema apresentado na equaçao (3), usando-se as redes recorrentes com n=32 e uma condiçao inicial igual a ui = 0, ou seja, nenhuma informaçao, é apresentado na figura 3 para um tempo de aprendizado de t = 2 e na figura 4 para t = 16000. Observa-se que à medida que a rede aprende sobre o problema formulado, o resultado melhora. Essa garantia é única das redes neurais de Hopfield, pois as equaçoes (8) foram obtidas sujeitas a essa restriçao, isto é,
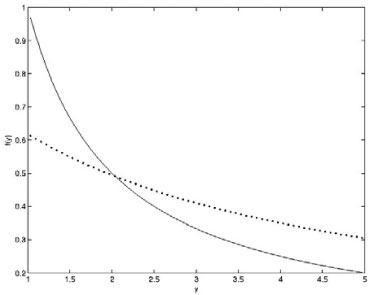 Figura 3. Resultado invertido com redes neurais para t = 2 (linha pontilhada) juntamente com o resultado exato (linha contínua)
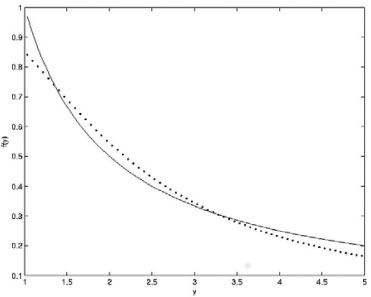 Figura 4. Resultado invertido com redes neurais para t = 16000 (linha pontilhada) juntamente com o resultado exato (linha contínua)
EXEMPLO NUMÉRICO Um protótipo interessante para ilustrar o uso da rede de Hopfield em problemas mal colocados constitui-se na análise da soluçao de um problema linear Ax=b, na forma 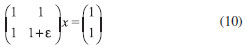 O posto da matriz A é completo e o determinante da matriz A é dado por ε. A soluçao obtida pelo cálculo da inversa, xcal = A-1berr, é expresso como 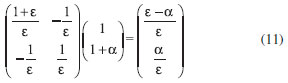 em que berr representa os dados de entrada com erros da ordem de |α|. Observe que existem dificuldades numéricas para o cálculo da inversa quando det(A)= ε é próximo de zero. A norma do resíduo, para a soluçao obtida a partir do cálculo da inversa, é dada por  e tem a mesma magnitude do erro em b. Por outro lado, a norma do erro, para esta soluçao, é dada por  Como pode-se observar a norma do erro na soluçao é maior que a norma do erro introduzido em b por um fator ε. Quando o sistema é aproximadamente linearmente dependente, isto é, |ε| ≅ 0, a norma do erro cometido em xcal diverge. O cálculo da inversa nao é apropriado para a soluçao do problema (10), quando erros sao introduzidos em b. Por exemplo, usando a equaçao (11), com ε=10-2 e α=10-1, obtém-se x=[-9,10], enquanto o valor esperado é x=[1,0]. Entretanto, pode-se encontrar uma soluçao adequada usando-se a rede de Hopfield, equaçao (8), que para um problema linear tem a forma 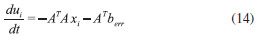 em que ui=tanh-1(xi). Essa equaçao pode ser resolvida usando-se as técnicas usuais para soluçao de sistema de equaçoes diferenciais ordinárias, tal como o método de Runge-Kutta. Com a equaçao (14), usando como valor inicial x=[0,0], obtém-se x=[0,9988, 0,0462], mostrando como a rede de Hopfield trata adequadamente o problema mal colocado.
PROBLEMAS INVERSOS EM TERMODINAMICA CLASSICA Os problemas inversos em termodinâmica clássica, para a equaçao de estado, envolvem a expansao virial,  com as variáveis tendo o seu significado usual. Para sistemas com simetria esférica e usando a termodinâmica estatística clássica, a relaçao entre a energia potencial Ep e o segundo coeficiente do virial é dada por,14 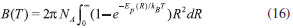 Portanto, este é um problema inverso nao linear. Por analogia com a equaçao (2) escreve-se, 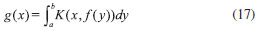 Esse é o tipo de problema a ser abordado na inversao de dados de fator de compressibilidade. Nesse caso a temperatura T e a coordenada R representam as duas variáveis independentes x e y, respectivamente. Nesse ponto fica mais clara a natureza das dimensoes m e n. O número de pontos, n, para representar a integral está relacionado com a coordenada R, enquanto o número de dados experimentais está relacionado com a variável m. Dificilmente ter-se-ía m = n, isto é, a precisao da representaçao igual ao número de dados experimentais, enfatizando a discussao já apresentada. O problema direto é relativamente simples, mesmo para o caso nao linear. Vários exemplos sao trabalhados na biografia.14 Por exemplo, se Ep(R) = 0 é substituído na equaçao (16), retira-se B(T) = 0 e pV = NkBT. Por outro lado o problema inverso, mesmo bem colocado, nao é trivial. A primeira tentativa de se retirar alguma informaçao microscópica do segundo coeficiente do virial foi feita por Lennard-Jones em 1924,15 usando um potencial da forma Ep(R) = λn / Rn -λm / Rm, conhecido hoje como o potencial de Lennard-Jones. Neste trabalho os parametros λn e λm foram determinados usando-se uma combinaçao gráfica com o uso de variáveis universais. Na verdade essa proposta consistia num ajuste gráfico, o que nao pode ser considerado como um problema inverso. Em 1959 Keller e Zumino,16 tratando a energia potencial como variável, reescreveram a equaçao (16) na forma,  com 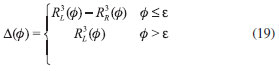 Para o caso do potencial puramente repulsivo, situaçao aproximadamente válida para altas temperaturas, obtém-se Δ(Φ) = RL3(Ep), permitindo que se determine de forma única a funçao Ep(R) de dados do coeficiente do virial. Propondo uma funçao analítica para B(T), Jonah and Rowlinson17, em 1960, foram capazes de determinar a energia potencial. Esse método, importante para a época, é certamente limitado, pois assume-se um ajuste para o segundo coeficiente, filtrando assim os erros experimentais. Maitland e Smith18 transformaram a equaçao de Keller e Zumino numa forma matricial, com posterior aplicaçao de um método proposto por Bellman e Kalaba.19 Apesar de o método ter sido aplicado somente a potenciais repulsivos o trabalho de Maitland e Smith representa uma primeira abordagem de um problema inverso mal colocado aplicada à equaçao de estado, já que dados experimentais foram tratados como um primeiro passo. Dados do segundo coeficiente do virial foram gerados, pela equaçao (16), utilizando-se um potencial repulsivo na forma, Ep(R) = Ae-aR, com A = 0,2 keV e a = 4,20 Å, aproximadamente adequado para o sistema He-He. Para temperaturas na faixa de 500K - 1500K e com erros em B(T) da ordem de 1% obteve-se o potencial desejado, usando-se a regularizaçao de Tikhonov e a decomposiçao em valores singulares.20 Em ambos os casos recupera-se o potencial, dentro do erro esperado. O critério de norma mínima e do tamanho do espaço foram utilizados nos métodos teóricos discutidos. O trabalho, apesar de usar dados simulados e um potencial aproximado, foi importante para futuros assuntos na mesma linha de pesquisa. As redes de Hopfield foram utilizadas pela primeira vez, em um problema inverso mal colocado em química, para o sistema HeNe.21 Ainda na mesma linha investigativa do primeiro trabalho,20 com dados simulados e potencial modelo, o uso das redes recorrentes mostrou-se um método mais estável e robusto em relaçao aos erros experimentais quando comparado com a regularizaçao de Tikhonov ou decomposiçao em valores singulares.20 A transformada de Keller e Zumino16 fornece uma estratégia para obtençao do potencial de curto alcance de forma única. Entretanto existe um ambiguidade para o potencial de longo alcance pois tem-se Δ(ƒ) = RL3(Φ) - RR3(Φ). Assumindo RL conhecido e usando a decomposiçao em valores singulares e dados experimentais, obteve-se 20, 21 o coeficiente de dispersao do sistema Ar-Ar. Essa primeira fase para tratar problemas inversos mal colocados relacionados com a equaçao de estado é caracterizada pelo uso da equaçao de Keller e Zumino, com dados simulados. O potencial foi sempre obtido em duas partes. Entretanto, o passo definitivo para uma análise global desse problema inverso foi dado em 2003. 22 Em 2003, foi dado o primeiro passo para um tratamento geral de redes neurais, aplicadas indistintamente a problemas lineares ou nao. Usando a equaçao (11), dados experimentais em conjunto com redes recorrentes, obteve-se o potencial global da interaçao Ar-Ar. O potencial obtido é o mais adequado na literatura para aquela propriedade, pois foi invertido de dados experimentais. Uma comparaçao foi feita com outros potenciais mostrando a qualidade do potencial invertido. O presente trabalho também originou a apresentaçao de um algoritmo global para qualquer problema inverso mal colocado desejado,22 que foi aplicado a diversos problemas inversos mal colocados em química, como em espectroscopia23, ressonância magnética nuclear24, aniquilaçao de pósitrons25 e cinética química.26,27
ASPECTOS GERAIS DE PROBLEMAS INVERSOS Nao existe uma limitaçao para a aplicabilidade de problemas inversos mal colocados em química. Vários exemplos foram fornecidos, mas o assunto encontra espaço também em outras áreas, como por exemplo em geofísica,28 astrofísica,29 teoria de controle,30,31 espalhamento quântico inverso,32,33 física médica34 e economia.35 Independente da área em que se estuda um problema inverso, tem de se estar atento para os seguintes pontos comuns:
Uma hierarquia entre os dados tratados é algo comum e deve ser respeitada. Por exemplo, nao se espera que um potencial obtido do coeficiente do virial seja adequado no cálculo da seçao de choque. Mas o oposto é certamente verdade. Médias sao feitas na termodinâmica, perdendo-se assim informaçao importante sobre o potencial. O dado mais refinado, apesar de nao ter uma medida experimental direta, é a fase de espalhamento, como abordado na bibliografia.33
CONCLUSOES Uma abordagem geral sobre problemas inversos mal colocados foi apresentada. O protótipo de um problema inverso linear foi discutido, após uma introduçao histórica sobre o assunto. Foi evidenciado que sao necessárias técnicas especiais, que removam uma singularidade, para tratar de problemas inversos mal colocados. Três dessas técnicas foram apresentadas de forma geral, com ênfase em redes neurais de Hopfield. Uma aplicaçao específica em termodinâmica foi apresentada, para exemplificar problemas em químicas, indicando, em termos gerais, como o problema deve ser abordado em outra área do conhecimento. A discussao apresentada evidenciou que os fundamentos de problemas inversos sao válidos em qualquer área das ciências e que o problema inverso tem de ser feito com dados experimentais. Além disso, uma falta de informaçao experimental nao pode ser substiuída por um artifício matemático e as decisoes importantes sao feitas com informaçoes insuficientes. Portanto, é sempre desejável a colaboraçao com o cientista experimental na área em que o problema inverso é tratado. É importante observar que, na verdade, todo cientista que trabalha em um problema direto terá um problema inverso associado, pronto para ser resolvido. Espera-se que o presente trabalho, apresentado de forma tao didática quanto possível, motive o leitor a explorar a área de problemas inversos mal colocados.
AGRADECIMENTOS Gostaríamos de agradecer ao CNPq, à CAPES e à FAPEMIG pela ajuda financeira.
REFERENCIAS 1. Tikhonov, A. N.; Goncharski, A. V.; Ill- Posed Problems in the Natural Sciences, Mir Publishers: Moscow, 1987. 2. Groetsch, C. W.; Inverse Problems: Activities for Undergraduates, Mathematical Association of America: Washington, 1999. 3. Abel, N. H. Em Oeuvres complètes de Niels Henrik Abel; Sylow, L.; Lie, S., eds.; Cambridge University Press: Cambridge, 2012, vol. 1. 4. Hadamard, J.; Lectures on Cauchy's Problem in Linear Partial Differential Equations, Yale University Press: New Haven, 1923. 5. Gorenflo, R.; Vessella, S.; Abel Integral Equations: Analysis and Applications, Springer-Verlag: Berlin-Heidelberg, 1991. 6. Alves, M. O.; Oliveira, J. M.; Lemes, N. H. T.; Braga, J. P.; Int. J. Quantum Chem. 2012, 112, 3141. DOI: http://dx.doi.org/10.1002/qua.24031 7. Wing, G. M.; Zahrt, J. D.; A Primer on Integral Equations of the First Kind: The Problem of Deconvolution and Unfolding, Society for Industrial and Applied Mathematics: Philadelphia, 1991. 8. Riele, H. J. J.; Comput. Phys. Commun. 1985, 36, 423. DOI: http://dx.doi.org/10.1016/0010-4655(85)90032-3 9. Braga, J. P.; J. Math. Chem. 2001, 29, 151. DOI: http://dx.doi.org/10.1023/A:1010983230567 10. Leon, S. J.; Linear Algebra With Applications, 8th ed., MacMillan: New York, 1990. 11. Strang, G.; Amer.Math.Monthly 1993, 100, 848. DOI: http://dx.doi.org/10.2307/2324660 12. Hopfield, J. J.; Tank, D. W.; Biol. Cybern. 1985, 52, 141. PMID: 4027280 13. Lemes, N. H. T.; Borges, E.; Braga, J. P.; J. Braz. Chem. Soc. 2007, 18, 1342. DOI: http://dx.doi.org/10.1590/S0103-50532007000700008 14. Braga, J. P.; Físico-Química - Aspectos Moleculares e Fenomenológicos, 3ª ed., UFV: Viçosa, 2013. 15. Jones, J. E.; Proc. R. Soc. Lond. A 1924, 106, 463. DOI: http://dx.doi.org/10.1098/rspa.1924.0082 16. Keller, J. B.; Zumino, B.; J. Chem. Phys. 1959, 30, 1351. DOI: http://dx.doi.org/10.1063/1.1730184 17. Jonah, D. A.; Rowlinson, J. S.; Trans. Faraday Soc. 1960, 62, 1067. DOI: http://dx.doi.org/10.1039/tf9666201067 18. Maitland, G. C.; Smith, E. B.; Mol. Phys. 1972, 24, 1185. DOI: http://dx.doi.org/10.1080/00268977200102281 19. Bellman, R.; Kalaba, R.; Dynamic Programming and Modern Control Theory, Academic Press: New York, 1966. 20. Lemes, N. H. T.; Braga, J. P.; Belchior, J. C.; Chem. Phys. Lett. 1998, 296, 233. DOI: http://dx.doi.org/10.1016/S0009-2614(98)01042-2 21. Braga, J. P.; de Almeida, M.; Braga, A. P.; Belchior, J. C.; Chem. Phys. 2000, 260, 347. DOI: http://dx.doi.org/10.1016/S0301-0104(00)00218-4 22. Sebastiao, R. C. O.; Lemes, N. H. T.; Virtuoso, L.; Braga, J. P.; Chem. Phys. Lett. 2003, 378, 406. DOI: http://dx.doi.org/10.1016/j.cplett.2003.07.006 23. Borges, E; Lemes, N. H. T.; Braga, J. P.; Chem. Phys. Lett. 2006, 423, 357. DOI: http://dx.doi.org/10.1016/j.cplett.2006.03.090 24. Sebastiao, R. C. O.; Braga, J. P.; J. Magn. Reson. 2005, 177, 146. DOI: http://dx.doi.org/10.1016/j.jmr.2005.07.017 PMID: 16125428 25. Viterbo V.; Braga J. P.; Braga A. P; Almeida M.; J. Chem. Inform. Comput. Sci. 2001, 41, 309. DOI: http://dx.doi.org/10.1021/ci0000833 26. Lemes, N. H. T.; Borges, E.; Braga, J. P.; Chemom. Intell. Lab. Syst. 2009, 96, 84. DOI: http://dx.doi.org/10.1016/j.chemolab.2009.01.006 27. Menezes, D. C.; Borges, E.; Torres, M. F.; Braga, J. P.; Chem. Phys. Lett. 2012, 548, 85. DOI: http://dx.doi.org/10.1016/j.cplett.2012.07.078 28. Parker, R.L., Geophysical Inverse Theory, Princeton University Press: New Jersey, 1994. 29. Hedmana, M. M.; Burnsa, J. A.; Hamilton, D. P.; Showalterd, M. R.; Icarus 2012, 217, 322. DOI: http://dx.doi.org/10.1016/j.icarus.2011.11.006 30. Warren, W. S.; Rabitz, H.; Dahleh, M.; Science 1993, 229, 1581. DOI: http://dx.doi.org/10.1126/science.259.5101.1581 31. Bryson, A; Ho, Y.; Applied Optimal Control: Optimization, Estimation and Control, CRC Press: Washington, DC, 1975. 32. Newton, R.G.; Inverse Schrödinger Scattering in Three Dimensions, Springer-Verlag: Berlin-Heidelberg, 2012. 33. Lemes N. H. T.; Braga J. P.; Alves M. O.; Costa E. M, J. Mol. Model. 2014, 20, 2317. DOI: http://dx.doi.org/10.1007/s00894-014-2317-2 PMID: 24935112 34. Börgers, C.; Natterer, F.; Computational Radiology and Imaging: Therapy and Diagnostics, Springer: New York, 2012. 35. Horowitz, J. L.; Annual Review of Economics: Ill-Posed Inverse Problems in Economics 2014, 6, 21. DOI: http://dx.doi.org/10.1146/annurev-economics-080213-041213 |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






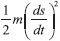 + mgy + mgx, com as quantidades tendo seu significado usual. Essa equaçao pode ser rearranjada na forma,
+ mgy + mgx, com as quantidades tendo seu significado usual. Essa equaçao pode ser rearranjada na forma,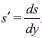 . A equaçao integral de Abel representa, de forma genérica, uma enorme variedade de problemas diretos e inversos em ciências,5 como por exemplo em espalhamento clássico inverso.6
. A equaçao integral de Abel representa, de forma genérica, uma enorme variedade de problemas diretos e inversos em ciências,5 como por exemplo em espalhamento clássico inverso.6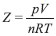 , expressa a relaçao entre pressao, volume e temperatura. Num primeiro curso de termodinâmica é difícil encontrar um estudante que nao responda corretamente à seguinte pergunta: se pV = nRT, qual seria a força entre as partículas? A nao existência de força, ou seja um gás ideal, é a resposta fornecida. De certa forma um estudante já sabe fazer um problema inverso, apesar de ser bem colocado. Se um pequeno erro experimental, for considerado, digamos Z = 1,1, e se a mesma pergunta for feita ninguém irá responder que se trata de um gás ideal. Mas, se esse erro estiver dentro do erro experimental pode-se ainda ter o gás ideal como resposta, apesar dela, em geral, nao ser fornecida pelo estudante. Esse exemplo simples evidencia que o erro experimental é sempre desprezado em consideraçôes teóricas. O problema proposto ainda encerra uma outra resposta, pois se a temperatura é a de Boyle pode-se ainda ter pV = nRT para um gás real. Tem-se aqui uma das condiçoes de um problema mal colocado. A resposta pode nao ser única.
, expressa a relaçao entre pressao, volume e temperatura. Num primeiro curso de termodinâmica é difícil encontrar um estudante que nao responda corretamente à seguinte pergunta: se pV = nRT, qual seria a força entre as partículas? A nao existência de força, ou seja um gás ideal, é a resposta fornecida. De certa forma um estudante já sabe fazer um problema inverso, apesar de ser bem colocado. Se um pequeno erro experimental, for considerado, digamos Z = 1,1, e se a mesma pergunta for feita ninguém irá responder que se trata de um gás ideal. Mas, se esse erro estiver dentro do erro experimental pode-se ainda ter o gás ideal como resposta, apesar dela, em geral, nao ser fornecida pelo estudante. Esse exemplo simples evidencia que o erro experimental é sempre desprezado em consideraçôes teóricas. O problema proposto ainda encerra uma outra resposta, pois se a temperatura é a de Boyle pode-se ainda ter pV = nRT para um gás real. Tem-se aqui uma das condiçoes de um problema mal colocado. A resposta pode nao ser única.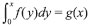 para o caso especial em que f(y) = 1 e, consequentemente, g(x) = x. Se a derivada de g(x) no ponto x = y é calculada, isto é,
para o caso especial em que f(y) = 1 e, consequentemente, g(x) = x. Se a derivada de g(x) no ponto x = y é calculada, isto é, 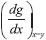 , recupera-se f(y) = 1. As consequências de um erro experimental podem ser analisadas nesse exemplo puramente matemático. Se, devido ao erro experimental, a quantidade a ser derivada fosse, por exemplo, gerro = g(x) + χ(x), em que χ(x) representa o erro experimental, é fácil observar que nao se obteria a derivada igual à unidade. Também é natural esperar que se χ(x) → 0 entao gerro → g(x), propriedade que chamamos de continuidade. No entanto, mesmo com esse erro pequeno as derivadas seriam funçoes oscilantes, com amplitudes que podem ser grandes dependendo da natureza mal-colocada do problema. Portanto, quando o erro na soluçao é maior que o erro no dado inicial, dizemos que a soluçao nao é contínua. Observe que tomar derivadas numéricas é um processo bastante comum em química, como por exemplo, em cinética química ou quando filtros sao usados para suavizar uma funçao.
, recupera-se f(y) = 1. As consequências de um erro experimental podem ser analisadas nesse exemplo puramente matemático. Se, devido ao erro experimental, a quantidade a ser derivada fosse, por exemplo, gerro = g(x) + χ(x), em que χ(x) representa o erro experimental, é fácil observar que nao se obteria a derivada igual à unidade. Também é natural esperar que se χ(x) → 0 entao gerro → g(x), propriedade que chamamos de continuidade. No entanto, mesmo com esse erro pequeno as derivadas seriam funçoes oscilantes, com amplitudes que podem ser grandes dependendo da natureza mal-colocada do problema. Portanto, quando o erro na soluçao é maior que o erro no dado inicial, dizemos que a soluçao nao é contínua. Observe que tomar derivadas numéricas é um processo bastante comum em química, como por exemplo, em cinética química ou quando filtros sao usados para suavizar uma funçao.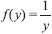 representada no gráfico aparece como se fosse um valor constante igual a zero, completamente mascarada pelo resultado obtido pelo operador inverso. Numa situaçao mais real, em que m nao será igual a n, deve-se procurar a soluçao que satisfaça o critério de mínimo quadrado, ou seja,
representada no gráfico aparece como se fosse um valor constante igual a zero, completamente mascarada pelo resultado obtido pelo operador inverso. Numa situaçao mais real, em que m nao será igual a n, deve-se procurar a soluçao que satisfaça o critério de mínimo quadrado, ou seja,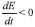 . Aqui fica evidente o conceito de aprendizado em redes neurais: o erro do objetivo do problema sempre irá decair. O tempo t deve ser associado com o conceito de tempo de aprendizado. A restriçao
. Aqui fica evidente o conceito de aprendizado em redes neurais: o erro do objetivo do problema sempre irá decair. O tempo t deve ser associado com o conceito de tempo de aprendizado. A restriçao 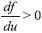 . Essas duas restriçoes, e
. Essas duas restriçoes, e 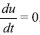 , refletindo que a rede neural nao tem mais nada a aprender sobre o problema. Uma característica muito importante de redes reside nesse fato. Se a condiçao inicial é a exata, entao nao há nada a aprender. Portanto, uma condiçao inicial adequada pode resolver o problema com um aprendizado mais rápido.
, refletindo que a rede neural nao tem mais nada a aprender sobre o problema. Uma característica muito importante de redes reside nesse fato. Se a condiçao inicial é a exata, entao nao há nada a aprender. Portanto, uma condiçao inicial adequada pode resolver o problema com um aprendizado mais rápido.