Artigo
| Enzyme kinetic modelling and analytical solution of nonlinear rate equation in the transformation of D-methionine into L-methionine in batch reactor using the new homotopy perturbation method |
|
Pavithra Sivasamy; Jansi Rani Palaniyandi Ganapathy; Iswarya Thinakaran; Rajendran Lakshmanan*
Department of Mathematics, Sethu Institute of Technology, Pulloor, Kariapatti - 626115, Virudunagar District - Tamilnadu, India Recebido em 18/04/2016 *e-mail: dr.rajendran.l@gmail.com A mathematical model of biotransformation of D-methionine into L-methionine in the cascade of the enzymes such as, D-amino acid oxidase (D-AAO), L-phenylalanine dehydrogenase (L-PheDH) and formate dehydrogenase (FDH) is discussed. The model is based on a system of coupled nonlinear reaction equations under non steady-state conditions for biochemical reactions occurring in the batch reactor that describes the substrate and product concentration within the catalyst. Simple analytical expressions for the concentration of substrate and product have been derived for all values of reaction parameters using the new homotopy perturbation method (NHPM). Enzyme reaction rate in terms of concentration and kinetic parameters are also reported. The analytical results are also compared with experimental and numerical ones and a good agreement is obtained. The graphical procedure for estimating the kinetic parameters is also reported. INTRODUCTION The development of cascade conversions (i.e. enzyme membrane catalytic reactions without intermediate recovery steps as taking place in living cells) is considered as one of the important future directions for carrying out sustainable organic syntheses with inherently safer designs.1,2 Hence, the enzyme is very important for the industrial application in the purification and determination of certain amino acids. Bae et al., developed a multi-enzyme system composed of glutamate race mase, thermo stable D-amino acid amino transferase, glutamate dehydrogenase and formate dehydrogenase for the production of aromatic D-amino acids, D-phenylalanine and D-tyrosine, from the corresponding α-keto acids, phenylpyruvate and hydroxyl phenylpyruvate, respectively.3 Hummel et al. discussed the biocatiytic membrane reactors using laboratory scale in enzyme systems. Mathematical models for separate reactions steps, as well as for the complete system are developed and validated in the batch reactor experiments.4 Enzymes are large complex protein molecules, which proceed as a catalyst to speed up chemical reactions in living organisms. In biochemistry, Michaelis-Menten kinetics is one of the simplest and important models to enzyme kinetics. In this model the rate of enzymatic reactions is a nonlinear function of concentration of a substrate. Also these reactions are essential in biochemistry because most of cell processes need enzymes to find a significant rate.5,6 The mathematical model of mono-enzymatic biosensor involving Michaelis-Menten kinetics is presented.7 The theoretical model for amperometric enzymes reactions for steady state condition is discussed and the various analytical methods for solving the non-linear reaction diffusion equation in enzyme biosensors has been reviewed recently.8 The approximate expression of steady state current for amperometric polymer molecular electrodes for the first-order and zero-order kinetics using Danckwert's expression is derived.9 The steady state concentration and current occurring at microdisk and the microcylinder enzyme electrodes for amperometric biosensor using homotopy perturbation method is obtained.10 All the above models have two enzyme systems. Mathematical modellings of two enzyme systems are quite common.11,12 But it is not easy in the case of three or more enzyme systems. Findrik et al. developed a kinetic model of amino acid oxidation catalyzed by a new D-amino acid oxidase from Arthrobacter protophormiae. In developing the enzyme-catalyzed reaction for large-scale production, mathematical modeling of the reaction of kinetics plays an important role. Therefore, the subject of this study is focused on the kinetics of the oxidative deamination, a very complex reaction system, which is catalyzed by D-AAO from Arthrobacter protophormiae using its natural substrate D-methionine and the aromatic amino acid 3,4-dihydroxyphenyl-D-alanine (D-DOPA).13-15 Findrik et. al. have developed a mathematical model for biotransformation of D-methionine into L-methionine in the cascade of four enzymes systems.1 This model is formulated as a set of non-linear differential equations describing the mass balance of the concentration of D-methionine, 2-oxo-4-methylthiobutyric acid, L-methionine, ammonium, nicotinamide adenine dinucleotide coenzyme and nicotinamide adenine dinucleotide hydrogen. It is observed that even though the results are compared with experimental results, they are only be obtained at discrete points depending on the step size provided. This creates a shortcoming since four cascade enzyme models are represented as a dynamical system using coupled PDE. However, to the best of our knowledge, till date there is no general analytical result corresponding to the non-steady state concentration for four enzyme system has been reported. The purpose of this communication is to derive the analytical expression of concentration of four enzyme systems based on new homotopy perturbation method. This is an effective tool for solve the nonlinear problems in chemical sciences.16 These analytical results are helpful to understand the mechanism and physical effects of parameters through the model problem. It is also useful to validate the numerical results and the experimental data.
NOMENCLATURE 
MATHEMATICAL FORMULATION OF THE PROBLEM The reaction scheme of four enzyme systems D-AAO, L-PheDH, FDH and coupled system of D-methionine into L-methionine are represented in Figure 1. The mass balance equations with corresponding boundary conditions and analytical expressions for the concentrations are shown in the following sections.
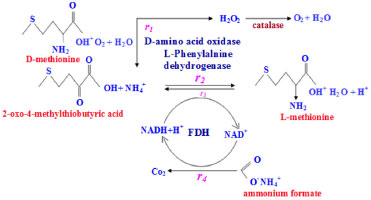 Figure 1. Kinetic scheme of D-AAO, L-PheDH, FDH and Coupled system of D-methionine bioconversion into L-methionine1
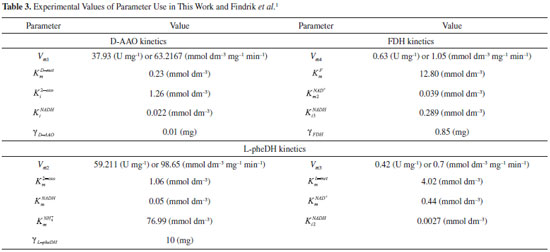
D-AAO Kinetics Mass balances equations for D-methionine and 2-oxo-4-methylthibutyric acid, in the batch reactor with the Michaelis-Menten kinetics are formulated as:1   The enzyme reaction rate of D-AAO catalyzed by D-methionine oxidation (r1) is  The initial conditions for above equations (1) and (2) are given below: 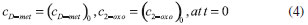 where cD-met, c2-oxo are the concentration of D-methionine and 2-oxo-4-methylthibutyric acid (competitive product). Vm1 is the maximal enzyme reaction rate, KmD-met is the Michaelis-Menten constant of D-methionine and Ki2-oxo is the product inhibition constant of 2-oxo-4-methylthiobutyric acid. Solving the above nonlinear equations (1)-(2) using new homotopy perturbation method (Appendix A), we can obtain the analytical expressions of concentration of D-methionine and 2-oxo- 4-methylthibutyric acid as follows: 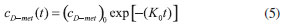 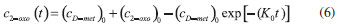 where, 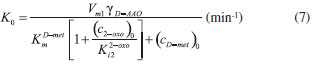 Substituting c2-oxo from the Equation 6 in the Equation 1, we can write the rate Equation 8a as 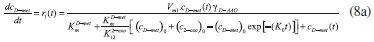 Similarly the rate equation r1 in terms of concentration c2-oxo can be obtained as follows: 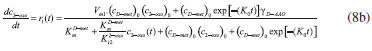 Equation 8a represents the new simple expression of the enzyme reaction rate of D-methionine in terms of cD-met, whereas the Equation 8b represents enzyme reaction rate of 2-oxo-4-methylthibutyric acid in terms of c2-oxo. L-PheDH Kinetics In this case, the rate equations of concentration of L-methionine, 2-oxo-4-methylthiobutyric acid, ammonium, nicotinamide adenine dinucleotide and nicotinamide adenine dinucleotide hydrogen are given as follows:1 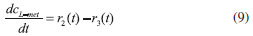 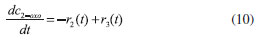 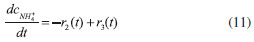 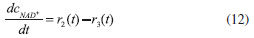 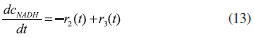 The enzyme reaction rate of reductive amination of 2-oxo-4-methylthiobutyric acid (r2 in Equation 14) is described by three substrate Michaelis-Menten kinetics. The enzyme reaction rate of the reverse reaction, L-methionine oxidation (r3 in Equation 15) is described by double-substrate Michaelis-Menten equation with the inclusion of the competitive NADH inhibition. 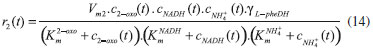 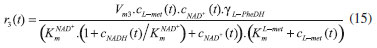 The initial conditions for above equations are given below: 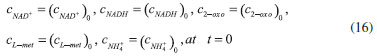 whereVm2 and Vm3 are maximum enzyme reaction rate, Km2-oxo, KmNADH, KmNH4+, KmNAD+, KmL-met are the Michaelis-Menten constant of 2-oxo-4-methylthiobutyric acid, Nicotinamide adenine dinucleotide hydrogen, Ammonium, Nicotinamide adenine dinucleotide respectively. Ki2NADH is the product inhibition constant of nicotinamide adenine dinucleotide hydrogen. Solving the above non-linear equations 9-13 using new HPM (Appendix A), the analytical expression of concentration of L-methionine, 2-oxo-4-methylthiobutyric acid, ammonium, nicotinamide adenine dinucleotide (NAD+) and nicotinamide adenine dinucleotide hydrogen (NADH) are obtained as follows: 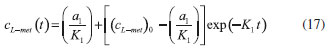 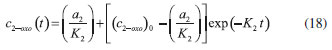 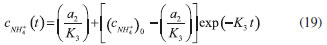 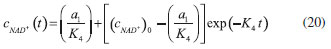  where the parameters a1, a2 and K1 to K5 are given in the Appendix B. FDH Kinetics In this case, the mass balance equation for formate, nicotinamide adenine dinucleotide coenzyme and nicotinamide adenine dinucleotide hydrogen oxidase enzyme membrane reactor are represented as follows: 1  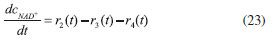 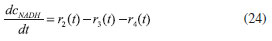 The enzyme reaction rate of NAD+ reduction by FDH kinetics (Eqn (25)) is 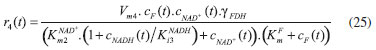 The Eqns (22-24) are solved for the following initial conditions: 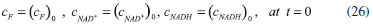 where Vm4 is a maximum enzyme reaction rate and Km2NAD+, KmF are the Michaelis-Menten constant of Nicotinamide adenine dinucleotide and Formate. Ki3NADH is the product inhibition constant of Nicotinamide adenine dinucleotide hydrogen. Solving the above mentioned non-linear equations (22) - (24) using new Homotopy perturbation method (Appendix A), we get the analytical expression of concentrations of formate, nicotinamide adenine dinucleotide (NAD+) and nicotinamide adenine dinucleotide hydrogen (NADH) oxidase in enzyme membrane reactor as follows: 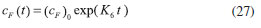 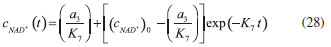 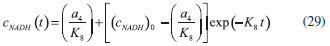 where the parameters a3, a4 and K6 to K8 are given in the Appendix B Coupled kinetics In this case, the rate equation of 2-oxo-4-methylthiobutyric acid and ammonium are given as follows:1 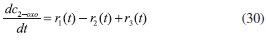 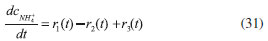 where the reaction rate is 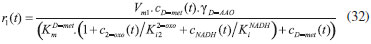 The reaction rate r2 and r3 are given in the Equations 14 and (15). The initial conditions for the above equations are given below: 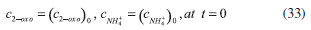 Solving the non-linear Equations 30 and (31) using new Homotopy perturbation method, we can obtain the approximate analytical expression for the concentration of 2-oxo-4-methylthiobutyric acid and ammonium as follows: 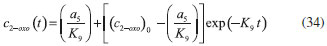 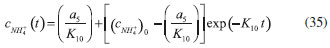 where the parameters a5 and K9 to K10 are given in the Appendix B.
NUMERICAL SIMULATION The non-linear differential equations 1, 2, 9-13, 22-24, 30 and 31 are also solved using numerical methods. The function pdex4 in Scilab software which is the function of solving the initial value problems for ordinary differential is used to solve this equation. Our theoretical results for the concentration of cD-met using Equation 5 and c2-oxo using Equation 6 for the D-AAO kinetics are compared with simulation results (Scilab program 4.1) in Tables 1-2. The Scilab program is also given in Appendix C. We run scilab 4.1 on apple imac core i5. The maximum error between our analytical results and simulation results 0.5%. Similarly our analytical results for the concentration of ammonium, nicotinamide adenine dinucleotide coenzyme and nicotinamide adenine dinucleotide hydrogen are compared with numerical results and available experimental results1 in Figures 2-7. Satisfactory agreement is found for all values of time t.
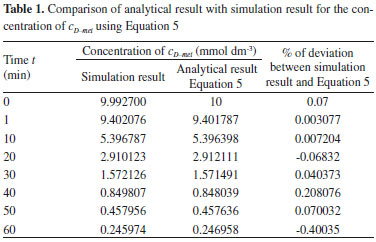
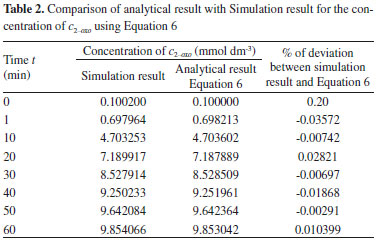
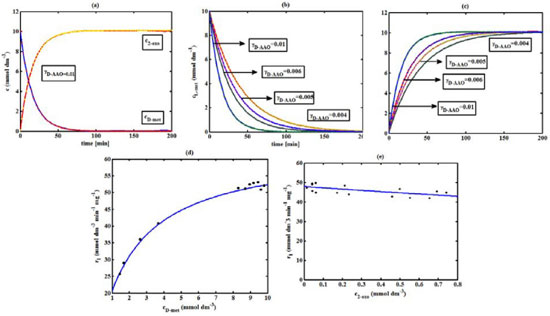 Figure 2. D-AAO kinetics (a) Comparison between the theoretical results (Equations 5 and (6)) and simulation results. (b) Comparison between theory (Equation 5) and simulations results. (c) Comparison between theory (Equation 6) and simulation results. (d)-(e) Comparison of theoretical results with experimental results1 for the reaction rate r1. The numerical value of the kinetic parameters used for the above figure is given in Table 1
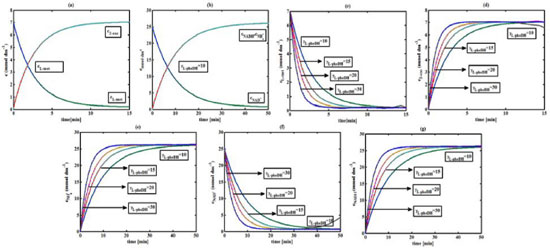 Figure 3. L-pHeDH kinetics (a) Comparison between the theoretical results (Equations 17 and (18)) and simulation results. (b) Comparison between the theoretical results (Equations 19, (20) and (21)) and simulation results. Concentration of (c) L-methionine (Equation 17), (d) 2-oxo-4-methylthiobutyric acid (Equation 18), (e)Ammonium (Equation 19), (f) Nicotinamide adenine dinucleotide (Equation 20), (g) Nicotinamide adenine dinucleotide hydrogen (Equation 21) versus time t. The numerical value of the kinetic parameters used for the above figure is given in Table 1. Key to the graph: (___) represents the (Equations 17-(21)) and (....) represents the numerical results
 Figure 4. Comparison of theoretical results with the experimental results1 for the reaction rate r2 and r3.The numerical value of the kinetic parameters used for the above figure is given in Table 1
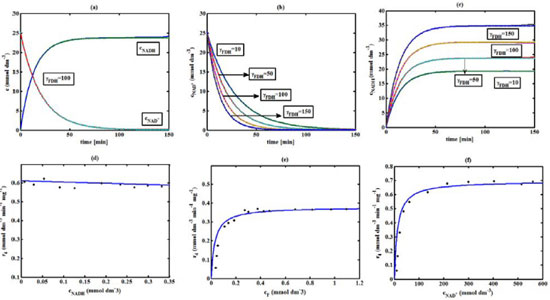 Figure 5. FDH kinetics (a) Comparison between the theoretical results (Equations(28) and (29)) and simulation results. (b) Concentration of Nicotinamide adenine dinucleotide (Equation 28), (c) Nicotinamide adenine dinucleotide hydrogen (Equation 29) versus time t. (d-f) Comparison of theoretical results with the experimental results 1 for the reaction rate r4.The numerical value of the kinetic parameters used for the above figure is given in Table 3
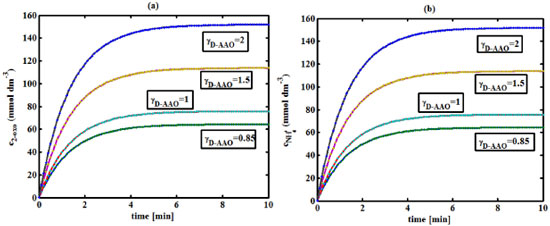 Figure 6. (a) Variation of the concentration of 2-oxo-4-methylthiobutyric acid (c2-oxo) with time t at different γD-AAO using Equation 34. (b) Variation of the concentration of ammonium (cNH4+) with time t at different γD-AAO using Equation 35
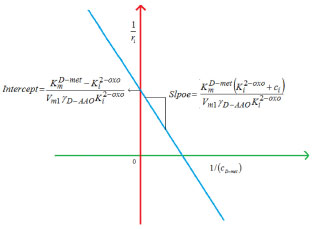 Figure 7. Estimation of kinetic parameters KmD-met and Ki2-oxo using Equation 36.The numerical value of the kinetic parameters used for the above figure is given in Table 3
RESULTS AND DISCUSSION D-AAO Kinetics Equations 5 and 6 are the new and simple approximate analytical expression of the concentrations of D-methionine and 2-oxo-4-methylthiobutyric acid. The rate of reaction can be determined from the graphs for a specified time, by measuring the gradient of the graphs using a tangent. Figure 2(a) signifies the comparison of the concentration of 2-oxo-4-methylthiobutyric acid and D-methionine versus time t. From Figure 2(b), it is observed that when concentration D-met increases when the parameter γD-AAO decreases. From Figure 2(c), it is inferred that when concentration 2-oxoincreases when the parameter γD-AAO increases. Our analytical results for the enzyme reaction rate (r1) versus concentration of D-methionine (Equation 8a) and concentration of 2-oxo-4-methylthiobutyric acid (Equation 8b) are compared with experimental results for some fixed values of parameters in Figure 2(d) and 2(e) and satisfactory agreement is noted. L-PheDH Kinetics Equations 17-21 represent the analytical expressions of the concentrations of L-methionine, 2-oxo-4-methylthiobutyric acid, Ammonium, Nicotinamide adenine dinucleotide and Nicotinamide adenine dinucleotide hydrogen. Figures 3(a)-3(g) signifies the concentrations of L-methionine, 2-oxo-4-methylthiobutyric acid, Ammonium, Nicotinamide adenine dinucleotide and Nicotinamide adenine dinucleotide hydrogen for various values of parameter γL-PheDH and for all time it remains domain. Figure 3(a), signifies that the comparison of L-methionine, 2-oxo-4-methylthiobutyric acid versus time t. Figure 3(b), represents the comparison of the concentration of ammonium, Nicotinamide adenine dinucleotide and Nicotinamide adenine dinucleotide hydrogen versus time t. From Figures 3(c) and 3(f), it is noted that the concentrations of L-methionine and Nicotinamide adenine dinucleotide decreases when the parameter γL-PheDH increases. From Figures 3 (d), (e) and 3(g), it is obvious that the concentration of 2-oxo-4-methylthiobutyric acid, Ammonium and Nicotinamide adenine dinucleotide hydrogen increases when the parameter γL-PheDH increases. Our analytical results for enzyme reaction rate (r2) versus the concentrations of 2-oxo-4-methylthiobutyric acid, Nicotinamide adenine dinucleotide hydrogen, Ammonium are compared with experimental results for some fixed values of parameters in Figures 4(a)-4(c). The enzyme reaction rate (r3) versus the concentrations of L-methionine, Nicotinamide adenine dinucleotide and Nicotinamide adenine dinucleotide are compared with the experimental results for some fixed values of other parameters in Figures 4(d)-4(f). FDH Kinetics Equations 27-29 identify the analytical expressions of the concentrations of formate, Nicotinamide adenine dinucleotide and Nicotinamide adenine dinucleotide hydrogen. Figure 5(a) represents the comparison of the concentration of Nicotinamide adenine dinucleotide and Nicotinamide adenine dinucleotide hydrogen versus time t. From Figure 5(b) it is clear that when the parameter γFDH increases the concentration of Nicotinamide adenine dinucleotide decreases. From Figure 5(c) it is evident that when the concentration γFDH increases the concentration of Nicotinamide adenine dinucleotide hydrogen also increases. In our analytical results, enzyme reaction rate (r4) versus the concentration of formate cF, Nicotinamide adenine dinucleotide and Nicotinamide adenine dinucleotide coenzyme are compared with the experimental results for some fixed values of other parameters in Figures 5(d)-5(f). Coupled kinetics Equations 34 and 35 characterizes the analytical expressions of the concentration of 2-oxo-4-methylthiobutyric acid and Ammonium. From Figure 6(a) and 6(b) show the concentration of 2-oxo-4-methylthiobutyric acid and Ammonium versus time t for some fixed values of other parameters. Concentrations of 2-oxo-4-methylthiobutyric acid and Ammonium decreases when the parameter γD-AAO increases. Influence of the parameter on the concentration is also reported. Estimation of Kinetic Parameters To check the validity of the model against the experimental data, the model equation, which contains three kinetic parameters, is transformed so that a linear plot of the data can be made. The plot has yielded reasonable linearity, and the parameter values can be estimated from the plot. The three parameters in Equation 1 can be evaluated by means of non-linear least-squares fit. Equation 3 can be rewritten as 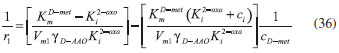 As shown in Figure 7, Plot of 1/r1 versus 1/(cD-met) gives the slope Also the rate equation (1) can be written as 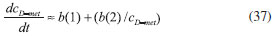 where the constant 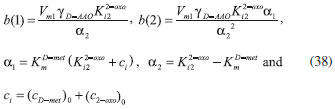 If we know the experimental data i.e (ti, cD-met), we can obtain the numerical values of the constant b(1) (=0.7721) and b(2) (=1.9645) using the Matlab program (Appendix D). From the numerical values, the kinetic constant KmD-met, Ki22-oxo, Vm1 and γD-AAO can be obtained. Estimation of parameter from our analytical result Eqn (5 ) The Equation 5 can be rewritten as, 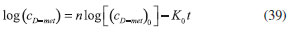 Using the method of Least chi-square we get, 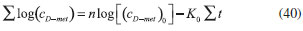 The parameter K0 can be obtained from the above Equation 40. From this parameter we can obtain the Vm1, γD-AAO, KmD-met, Ki2-oxo by changing the initial concentration of cD-met. Similarly the parameter for other kinetics scheme can be obtained. The numerical value of the parameter b(1) estimated from the Equation 39 is 0.773 where as the value of the parameter estimated from the Matlab/Scilab program is 0.07721. This validate our analytical model against the experimental data.
CONCLUSIONS A non-linear time dependent reaction equations in enzyme kinetics have been solved analytically using new Homotopy perturbation method. In this paper we have presented approximate analytical expression of the concentration of 2-oxo-4-methylthiobutyric acid, L-methionine, Ammonium, Nicotinamide adenine dinucleotide, Nicotinamide adenine dinucleotide hydrogen and Formate. The analytical expressions are compared to the numerical simulation using Scilab software. Good agreement is noted. Theoretical evaluation of the kinetic parameter is also reported.
SUPPLEMENTARY MATERIAL The supplementary data associated with this article can be found at http://qumicanova.sbq.org.br in pdf format with free access.
ACKNOWLEDGEMENTS The author very much grateful to the referees for the valuable suggestions. The authors are thankful to Mr. S. Mohamed Jaleel, The Chairman, Dr. A. Senthilkumar, The Principal, Sethu Institute of Technology, Kariapatti-626115, Tamilnadu, India for their encouragement.
REFERENCES 1. Findrik, Z.; Vasić-Rački, Ð.; Biotechnol. Bioeng. 2007, 98, 956. 2. Bruggink, A.; Schoevaart, R.; Kieboom, T.; Org. Process Res. Dev. 2003, 7, 622. 3. Bae, H. S.; Lee, S. G.; Hong, S. P.; Kwak, M. S.; Esaki. N., Soda, K.; J. Mol. Catal. B: Enzym. 1999, 6, 241. 4. Hummel, W.; Schmidt, E.; Wandrey, C.; Kula, M. R.; Appl Microbiol Biotechnol. 1986, 25, 175. 5. Michaelis, L.; Menten, M. L.; Biochem. Z. 1913, 49, 333. 6. Murray, J. D.; Mathematical Biology, Springer-Verlag: New York, 2002. 7. Kirthiga, O. M.; Rajendran, L.; J. Electroanal. Chem. 2015, 751, 119. 8. Rajendran, L.; Anitha, S.; Electrochim. Acta 2013, 102, 474. 9. Rajendran, L.; Rahamathunissa, G.; J. Math. Chem. 2008, 44, 849. 10. Eswari, A.; Rajendran, L.; J. Electroanal. Chem. 2010, 641, 35. 11. Cho, B. K.; Cho, H. J.; Park, S. H.; Yun, H.; Kim, B. G.; Biotechnol. Bioeng. 2003, 81, 783. 12. Cho, B. K.; Seo, J. H.; Kang, T. J.; Kim, J.; Park, H. Y.; Biotechnol. Bioeng. 2006, 94, 842. 13. Findrik, Z.; Vasić-Rački, Ð.; Lütz, S.; Daubmann, T.; Andrey, C.; Biotechnol. Lett. 2005, 27, 1087. 14. Findrik, Z.; Vasić-Rački, Ð.; Geueke, B.; Kuzu, M.; Hummel, W.; Eng. Life Sci. 2005, 5, 550. 15. Findrik, Z.; Geueke, B.; Hummel, W.; Vasić-Rački, Ð.; Biochem. Eng. J. 2006, 27, 275. 16. He, H. J.; Electrochim. Acta 2013, 109, 617. 17. Lineweaver, H.; Burk. D.; J. Am. Chem. Soc. 1934, 56, 658. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






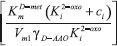 and y-intercept
and y-intercept 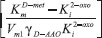 . If we know the maximum enzyme reaction rate Vm1, we can obtain the other parameter Michaelis-Menten constant of D-methionine KmD-met and product inhibition constant of 2-oxo-4-methylthiobutyric acid Ki2-oxo. As Ki tends to infinity the equation reduces to the form of Michaelis-Menten kinetics10 for which the Lineweaver-Burk plot17 is commonly used to determine the parameter values.
. If we know the maximum enzyme reaction rate Vm1, we can obtain the other parameter Michaelis-Menten constant of D-methionine KmD-met and product inhibition constant of 2-oxo-4-methylthiobutyric acid Ki2-oxo. As Ki tends to infinity the equation reduces to the form of Michaelis-Menten kinetics10 for which the Lineweaver-Burk plot17 is commonly used to determine the parameter values.