Artigo
|
|
| Índices de poder electrofílico global y local para el estudio teórico de la reactividad química: aplicación a derivados carbonilo α,β-insaturados Global and local electrophilic power indices for theoretical study of the chemical reactivity: application to α,β-unsaturated carbonyl derivatives |
|
Said F. Figueredo1,*; Manuel S. Páez1; Francisco Torres2,3
1. Departamento de Química, Universidad de Córdoba, Cra. 6 N° 74-103, Montería, Córdoba - Colombia Recebido em 15/09/2016 *e-mail: saifer87@gmail.com In this study two new global descriptors for chemical reactivity are proposed, namely the electrophilic power and nucleophilic power. These have been developed by performing the normalization of the local electrophilic power and local nucleophilic power respectively, which were recently proposed elsewhere. In particular, the usefulness of both global and local electrophilic power was evaluated by studying the chemical reactivity of six series of α,β-unsaturated carbonyl compounds whose experimental reactivity measures toward the nucleophile glutathione are available. It was observed in the majority of the cases the global and local electrophilic powers work as better than the popular global and local electrophilicity indices, respectively. INTRODUCCION Entre los primeros ejemplos exitosos de la teoría de funciones de onda aplicada al entendimiento de la reactividad molecular están la teoría de los orbitales moleculares frontera (FMO, por sus siglas en inglés) de Fukui,1 y las reglas de Woodward-Hoffman,2 siendo los orbitales moleculares más alto ocupado (HOMO, por sus siglas en inglés) y más bajo desocupado (LUMO, por sus siglas en inglés) las cantidades más importantes en ambas teorías. Una desventaja de estas representaciones orbitales es que utilizan una descripción orbital basada en partículas independientes donde la dinámica asociada a la correlación electrónica es totalmente omitida.3 Esta correlación a menudo juega un papel importante en el fenómeno de la reactividad química,4,5 no obstante, si la correlación electrónica es tomada en cuenta, el enfoque orbital desaparece y la FMO se vuelve irrelevante.3 Por otro lado, la inclusión de los efectos de correlación electrónica dentro de la Teoría del Funcional de la Densidad (DFT, por sus siglas en inglés)6,7 no afecta el poder interpretativo de los descriptores de reactividad basados en la densidad electrónica,3 lo que ha justificado el desarrollo del marco conceptual de la DFT como un esquema más comprensible de la reactividad química en comparación con el enfoque orbital.3 La teoría del funcional de la densidad (DFT)6,7 es una formulación mecánico-cuántica en la que la variable principal es la densidad de probabilidad electrónica ρ(  Aquí, N es una propiedad global y ν( 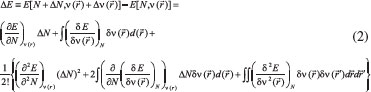 Una observación crucial en la DFT conceptual ha sido que varias de las derivadas que aparecen en la ecuación 2 (funciones respuesta) pueden ser identificadas con propiedades químicas de interés.9 Como se discutirá más adelante, Entre los logros notables de la DFT destacan el establecimiento de la conexión entre el potencial químico y la electronegatividad de Mulliken,9 así como el desarrollo de índices de reactividad que han ayudado a comprender conceptos químicos que solo habían sido tratados de forma intuitiva. En este contexto, la dureza química fue establecida como una medida de la estabilidad de cualquier sistema electrónico.16,17 No obstante, la reactividad de sistemas moleculares complejos no puede ser racionalizada solo mediante este parámetro, dando lugar a la necesidad de considerar otros descriptores de reactividad.18 Atendiendo a esto, han surgido conceptos derivados tales como el índice de electrofilicidad,19 poder electrodonador y poder electroaceptador,20,21 electrofugalidad y nucleofugalidad,22,23 índice de nucleofilicidad,24 entre otros. De los descriptores anteriormente mencionados, el índice de electrofilicidad ω ha sido el más ampliamente utilizado en la literatura para reproducir y ayudar a entender el comportamiento electrofílico de múltiples sistemas moleculares,3,25-27 sin embargo, su definición podría carecer de rigor considerando el hecho de que fue construido a partir de un modelo donde la energía del sistema es considerada como una función continua y diferenciable con respecto al número de electrones, lo que implica que las respuestas de una especie química a los procesos de donación o aceptación de carga deberían ser iguales.21 En efecto, desde una perspectiva química, tiene sentido diferenciar las respuestas de un sistema frente a la donación y aceptación de carga, situación que indica que las derivadas izquierda y derecha de la energía con respecto al número de electrones deberían ser distintas.20 Aunque esta diferenciación siempre ha sido reconocida para las funciones de Fukui,28 donde ƒ-(r) caracteriza los sitios moleculares susceptibles al ataque de un electrófilo, y ƒ+(r) caracteriza los sitios para un ataque nucleofílico, solo hasta hace pocos años se ha tenido en cuenta para el caso del potencial químico y la dureza.29 De hecho, en la mayoría de los estudios teóricos basados en estas cantidades, el análisis de tendencias de reactividad se lleva a cabo mediante un solo valor de µ y η para caracterizar tanto la donación como la aceptación de electrones. Con el propósito de resolver las limitaciones inherentes a la definición del índice de electrofilicidad, Gázquez, Cedillo y Vela20,21 modelaron los cambios en el potencial químico de un sistema que interactúa con un baño de electrones dando lugar a los índices poder electrodonador y poder electroaceptador,20,21 que miden respectivamente, la habilidad nucleofílica y electrofílica de sistemas moleculares a partir de los cambios que ocurren en la energía del sistema asociados a pequeñas fluctuaciones en la densidad electrónica. En analogía con el trabajo de Gázquez, Cedillo y Vela,20,21 recientemente, Figueredo y colaboradores30 propusieron describir la evolución del potencial químico durante los procesos de aceptación y donación de carga a través de una función ficticia del número de electrones, conduciendo al desarrollo de los conceptos locales denominados funciones de respuesta electrofílica y nucleofílica, asociados respectivamente a las definiciones de los índices de poder electrofílico local y poder nucleofílico local.30 Como una continuación del trabajo anteriormente mencionado, aquí se propone formalmente el desarrollo de las versiones globales de estos descriptores. En particular, el índice de poder electrofílico propuesto fue probado junto con otros descriptores electrofílicos globales para reproducir las tendencias de reactividad relativas dentro de una serie de derivados carbonilo α,β-insaturados, cuya reactividad química ha sido ya evaluada experimentalmente frente a glutatión (GSH).31 Desde el punto de vista químico, estos compuestos son especies conjugadas que tienen la habilidad de reaccionar vía adición nucleofílica de Michael con nucleófilos suaves como los grupos tiol.26,31 El mecanismo molecular para la reacción entre GSH y carbonilos α,β-insaturados es considerado como una adición nucleofílica por medio del grupo tiol en el átomo de carbono β del enlace múltiple carbono - carbono.31,32 Atendiendo a estas observaciones, la reactividad local del átomo de carbono β de los derivados α,β-insaturados fue objeto de estudio mediante el índice de poder electrofílico local. En general, el índice electrofílico desarrollado en el presente trabajo así como su versión local, resultaron ser de utilidad para describir las tendencias relativas de reactividad de los compuestos estudiados.
FUNDAMENTOS TEORICOS Dentro del marco conceptual de la DFT,3,6 el potencial químico µ, que mide la tendencia de escape de los electrones desde un sistema en equilibrio,14,33 está definido como:  donde χ es la electronegatividad de Mulliken definida por Iczcowski y Margrave.34 Sin embargo, debido al comportamiento de la energía como una función de N a temperatura cero,35 la derivada de E evaluada en algún valor integral de N tendrá, en general, dos valores diferentes al ser evaluadas desde la izquierda y la derecha respectivamente. Esto es,20 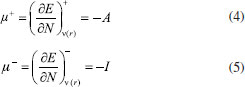 donde A e I son la afinidad electrónica y la energía de ionización respectivamente. Aunque tiene sentido diferenciar las respuestas del sistema frente a la donación y aceptación de carga, un solo valor de µ (el promedio entre µ+ y µ-) es utilizado en estudios de tendencias de reactividad para describir los procesos de donación y aceptación de carga.20,21 De esta manera, el potencial químico ha de ser aproximado como:36  Gázquez y colaboradores20,21 han propuesto un esquema alternativo de interpolación de la energía como función del número de electrones dando lugar a las siguientes expresiones para µ+ y µ-: 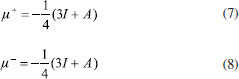 En esta perspectiva, µ+ y µ- son los potenciales químicos asociados a las respuestas del sistema frente a la aceptación y donación de carga, respectivamente. Por otro lado, la dureza16 e híperdureza37-40 han sido formalmente definidos como: 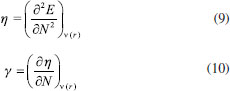 La dureza η es un índice global de reactividad que puede ser entendido como la resistencia de los electrones a ser transferidos desde un sistema en equilibrio.14,33 A partir de una aproximación de diferencias finitas, los valores de η pueden ser calculados como: 3,41  La híperdureza es una función de respuesta de tercer orden cuyo significado ha sido revisado recientemente.42 En particular, se considera que valores grandes positivos de híperdureza corresponden a sistemas moleculares que son altamente estables, mientras que los sistemas más reactivos tenderán a exhibir valores pequeños de γ.42,43 Uno de los predictores de reactividad más ampliamente utilizado13,14,26,33 ha sido el índice de electrofilicidad ω,19 que se define como la energía de estabilización de un sistema electrónico cuando es saturado con electrones provenientes de los alrededores:13  A nivel local, un descriptor de reactividad llamado función de Fukui (FF)28 es utilizado cuando las interacciones de tipo covalente son preponderantes entre las moléculas. Formalmente, la FF se define como:28 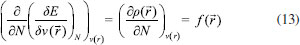 La función ƒ( 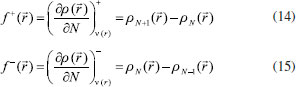 Una molécula es susceptible a un ataque nucleofílico en sitios en los que ƒ+( 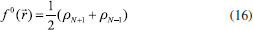 La derivada de FF con respecto al número de electrones conduce a otro índice local de reactividad que fue identificado por Morell y colaboradores45 como descriptor dual (DD) ƒ(2)( 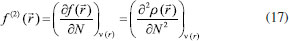 Los valores de ƒ(2)( 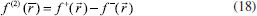 Se puede demostrar que las funciones de Fukui y el descriptor dual están normalizados como sigue:3,45  Recientemente, Figueredo, Páez and Song30 introdujeron los siguientes dos descriptores locales de reactividad: 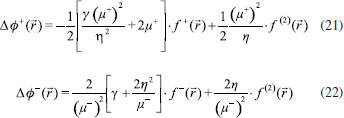 El primero de ellos es el poder electrofílico local Δφ+( 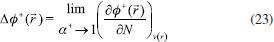 La función φ+(  donde  φ+ es la función de respuesta electrofílica,30 una función del número de electrones que fue formulada como la versión instantánea del índice de electrofilicidad. Mientras que φ+( El índice Δφ-( 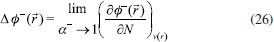 La función φ-(  donde  φ- es la función de respuesta nucleofílica,30 una función del número de electrones que equivale al valor instantáneo del recíproco del poder electrodonador. Nuevamente, mientras que φ-(
METODOLOGIA COMPUTACIONAL Desde el punto de vista computacional, las propiedades electrónicas y estructuras de los compuestos carbonilo α,β-insaturados considerados en el presente trabajo fueron tratados de acuerdo al siguiente procedimiento. Inicialmente, las geometrías moleculares de los 18 derivados fueron pre-optimizadas por mecánica molecular mediante el Campo de Fuerzas Universal (UFF)48 implementado en el programa Avogadro.49 Posteriormente, las conformaciones de mínima energía fueron re-optimizadas analíticamente utilizando el paquete de programas NWChem 6.3 a partir del modelo químico DFT B3LYP/6-31+G(d) 50,51 sin la observación de frecuencias imaginarias. Los valores del potencial químico y dureza fueron calculados luego aplicando el teorema de Koopmans52 sobre las aproximaciones de diferencias finitas dadas por las ecuaciones 6 y 11:13-15,33 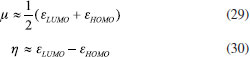 donde εLUMO y εHOMO son los valores propios de los orbitales moleculares desocupado de más baja energía y ocupado de mayor energía, respectivamente (LUMO y HOMO, por sus siglas en inglés). Asimismo, la ecuación de trabajo para el cálculo de hiperdureza queda expresada como:41,42 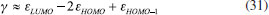 Los valores de µ+ también fueron obtenidos mediante el teorema de Koopmans: 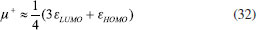 Las energías orbitales necesarias para el desarrollo de las ecuaciones 29 a 32 fueron obtenidas mediante cálculos de punto singular de energía sobre las geometrías previamente optimizadas, resolviendo iterativamente las ecuaciones de Kohn-Sham al nivel de teoría B3LYP/6-311++G(2d,2p)50,51,53 mediante el paquete de programas ab initio PSI4.54 Por otro lado, los valores condensados de las funciones de Fukui fueron aproximados como:37,55-57  donde  Con el propósito de comparar la habilidad descriptiva del índice de poder electrofílico con la del índice de electrofilicidad, ambos predictores fueron utilizados para racionalizar la reactividad electrofílica de los carbonilos α,β-insaturados. Los valores de Δφ+ y ω fueron calculados empleando las ecuaciones 40 y 12, respectivamente. Desde el punto de vista de la reactividad local, la electrofilicidad del átomo de carbono β fue discutida por medio de los valores condesados del índice de electrofilicidad local ωk+59 y el poder electrofílico local,30 dados respectivamente por: 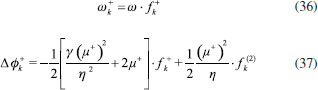 Adicionalmente, la reactividad de los átomos de carbono carbonilo (C) fue considerada por medio del poder electrofílico local calculado de acuerdo a la ecuación 37.
RESULTADOS Y DISCUSION Desarrollo de los índices de poder electrofílico y nucleofílico Figueredo, Páez y Song30 definieron la función de respuesta electrofílica tal como aparece en la ecuación 25. En esta expresión, α+ es una función del número de electrones que describe la evolución del potencial químico durante un proceso de aceptación de carga en un sistema cerrado. α+ fue formalmente definido como:30  Con la condición de potencial externo constante, la expansión de Taylor alrededor del número de electrones para α+ está dada por: 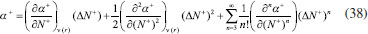 donde se ha utilizado el hecho de que α0+ es igual a cero al inicio del proceso. La ecuación 38 contiene las derivadas primera y segunda de α+ con respecto al número de electrones. Debido a que no existe una ecuación explícita para α+ en función de N, tales derivadas pueden ser obtenidas implícitamente a partir de la ecuación 37: 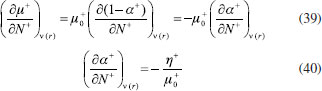 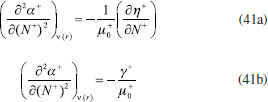 Ahora bien, derivando la ecuación 25 con respecto al número de electrones a potencial externo constante, se tiene: 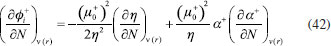 Tal como sugiere el esquema de interpolación de Gázquez, Cedillo y Vela, en este punto se ha considerado que η+ = η. La derivada de α+ que aparece en la ecuación 42 puede ser sustituida por la expresión de la ecuación 40 conduciendo a: 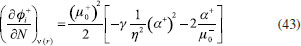 Como se mencionó antes, en la situación límite en la que el sistema de referencia es saturado con la máxima cantidad de electrones, la función α+ tiende a 1 haciendo que el potencial químico aumente hasta 0, de modo que 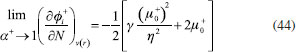 Ya que la función de respuesta electrofílica es una función global, su valor crítico correspondiente al límite de la ecuación 44 debe corresponder a una cantidad local. Por otro lado, integrando sobre todo el espacio la expresión que define al poder electrofílico local dado por la ecuación 21 se obtiene: 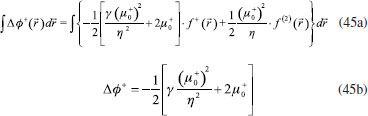 donde se han utilizado las condiciones de normalización de la función de Fukui y del descriptor dual, dadas por las ecuaciones 19 y 20 respectivamente. Ya que la integral del poder electrofílico local sobre todo el espacio es la sumatoria del poder electrofílico sobre cada punto La ecuación 44 puede ser re-escrita como: 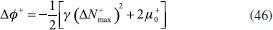 donde la máxima cantidad de electrones transferidos está dada mediante la expresión:  Debido a que ΔN+max es positivo y µ0+ es siempre negativo, los sistemas moleculares más electrofílicos serán aquellos con potenciales químicos altamente negativos y valores pequeños (o incluso negativos) de la híper-dureza indicando que el sistema en cuestión es bastante reactivo. Por lo tanto, se concluye que los sistemas moleculares más electrofílicos deberán exhibir valores altos positivos de Δφ+. De manera análoga al rol de α+, el término α- que aparece en la función de respuesta nucleofílica es una función del número de electrones que describe la evolución del potencial químico durante un proceso de donación de carga:  Así como α+, el valor inicial de α-debe ser 0 haciendo que µ- = µ0- al comienzo del proceso; y cuando el sistema cede la máxima cantidad de electrones, α- debe tender a 1 para garantizar que en este punto el potencial químico se hace cero (µ- = 0). Considerando que α- es infinitamente diferenciable, y con la condición de potencial externo constante, la expansión de Taylor alrededor del número de electrones para α- está dada por: 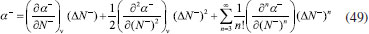 donde se ha considerado el hecho de que el valor inicial de α- es 0. La ecuación 49 contiene las derivadas de α- con respecto al número de electrones a ν(r) constante. Estas derivadas pueden obtenerse implícitamente a partir de la ecuación 48: 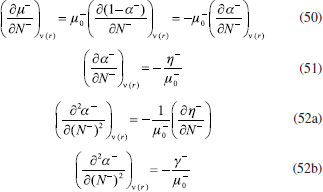 Aquí, se ha utilizado la definición de híper-dureza dada por la ecuación 10. Por otro lado, tomando la derivada de la función de respuesta nucleofílica con respecto al número de electrones a potencial externo constante, se obtiene: 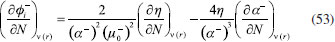 Nuevamente, siguiendo el esquema de Gázquez, Cedillo y Vela, se hizo la consideración de que η- = η. Utilizando las ecuaciones 10 y 51, la ecuación 53 se convierte en: 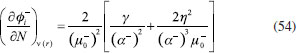 En la situación límite en la que el sistema dona la máxima cantidad de carga, se tiene: 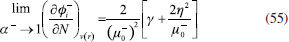 Para comparar este resultado con el concepto de poder nucleofílico local es necesario tomar la integral de esta función sobre todo el espacio de la misma forma en que se hizo para el poder electrofílico local, es decir: 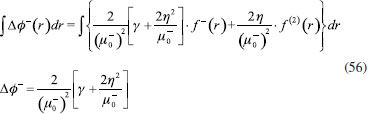 ahora, en virtud de que la integral del poder nucleofílico local dada por la ecuación 56 equivale a la sumatoria del poder nucleofílico sobre cada punto  es posible re-escribir la ecuación 55 como: 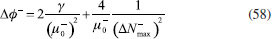 Debido a que la máxima cantidad de carga que el sistema dona en el proceso de transferencia electrónica es siempre positiva, los sistemas más nucleofílicos serán aquellos que exhiban valores bajos negativos del potencial químico y valores bajos positivos o incluso valores negativos de la híper-dureza indicando nuevamente que el sistema es bastante reactivo. Reactividad química de compuestos carbonilo α,β-insaturados Con el objetivo de evaluar la eficacia de los índices de poder electrofílico global y local, estos nuevos descriptores fueron utilizados para reproducir la reactividad relativa de una serie de 18 derivados carbonilo α,β-insaturados (ver Figura 1) incluyendo ésteres, cetonas y aldehídos.
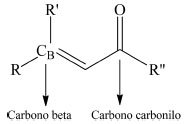 Figura 1. Estructura general de un compuesto carbonilo α,β-insaturado. El enlace múltiple carbono-carbono puede ser doble o triple
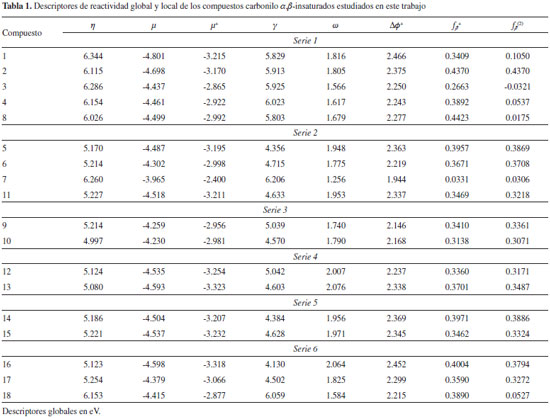
Para estos compuestos, las medidas experimentales de reactividad hacia GSH fueron reportadas por Schultz y colaboradores31 por medio de la concentración efectiva máxima media (EC50). Desde el punto de vista teórico, los valores de los descriptores de reactividad global junto con los valores de las funciones de Fukui y del descriptor dual, fueron recogidos en la Tabla 1; además, siguiendo el esquema comparativo de reactividad empleado por Schultz,31 los compuestos estudiados fueron separados en seis sub-grupos teniendo en cuenta sus características estructurales: (i) los compuestos de la serie 1 se utilizaron para analizar el efecto de la ocurrencia de dobles o triples enlaces sobre la reactividad del sistema carbonilo α,β-insaturado; (ii) los compuestos de la serie 2 fueron utilizados para estudiar el efecto de la posición del doble enlace olefina; (iii) los derivados de las series 3 y 4 se consideraron como modelo para verificar el efecto de la substitución con grupos metilo sobre la reactividad hacia GSH de los sistemas carbonilo-olefina conjugados; (iv) los compuestos de la serie 5 permitieron comparar la reactividad relativa de vinil cetonas con sus isómeros tipo aldehído; y (v) los análogos de la serie 6 se utilizaron para comparar la reactividad relativa de esteres carbonilo α,β-insaturados teniendo grupos vinileno o grupos etilo adicionales, respectivamente.31 En particular, la Tabla 1 muestra los valores de η, µ, µ+, γ, que fueron necesarios para el cálculo de los índices electrofílicos ω y Δφ+; asimismo, se reportan los valores de la función de Fukui y del descriptor dual condensados sobre el carbono β (ƒβ+ y ƒβ(2), respectivamente). Cabe resaltar que los valores del potencial químico electrofílico µ+ resultaron ser mayores que los del potencial químico µ, lo que es de esperarse debido a que este último representa un promedio del potencial químico asociado a las respuestas del sistema frente a la adición o sustracción de carga, una situación que implica que los valores de µ subestiman la habilidad de los sistemas estudiados para actuar como aceptadores de carga. Una segunda observación con respecto a los descriptores registrados en la Tabla 1, es que aunque la dureza e hiperdureza son conocidos por ser indicadores de la reactividad química de los sistemas electrónicos, sus valores por sí solos no describen de forma correcta las escalas experimentales de reactividad de los sistemas moleculares considerados.
Las Figuras 2, 3, 4, 5, 6 y 7 muestran las estructuras de los compuestos estudiados en cada serie junto con los valores condesados sobre el carbono β del índice de electrofilicidad ωβ+ y el poder electrofílico local Δφβ+. Además, la reactividad local del átomo de carbono carbonilo fue tratada mediante el poder electrofílico local (ΔφC+). De hecho, el átomo de carbono β (Cβ) de los compuestos estudiados mostró ser el sitio más probable de reacción para el ataque nucleofílico, excepto para los compuestos 1 y 3 de la serie 1, y el compuesto 7 de la serie 2, donde el carbono carbonilo resultó ser el sitio de reacción más prominente (ver Figuras 2 y 3).
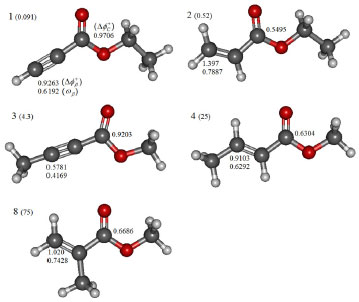 Figura 2. Estructuras moleculares de los compuestos 1 (etil propiolato), 2 (etil acrilato), 3 (metil but-2-inoato), 4 (metil but-2-enoato) and 8 (metil metacrilato). Δφβ+, ωβ y ΔφC+ en eV, valores de EC50 entre paréntesis
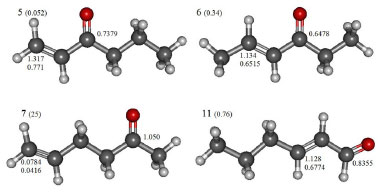 Figura 3. Estructuras moleculares de los compuestos 5 (hex-1-en-3-ona), 6 (hex-4-en-3-ona), 7 (hex-5-en-2-ona) and 11 (trans-hex-2-enal)
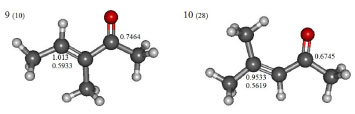 Figura 4. Estructuras moleculares de los compuestos 9 (3-metilpent-3-en-2-ona) and 10 (4-metilpent-3-en-2-ona
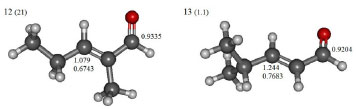 Figura 5. Estructuras moleculares de los compuestos 12 (2-metil-pent-2-enal) y 13 (4-metil-pent-2-enal)
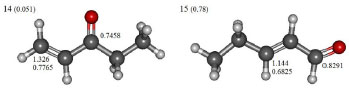 Figura 6. Estructuras moleculares de los compuestos 14 (pent-1-en-3-one) and 15 (trans-pent-2-en-al)
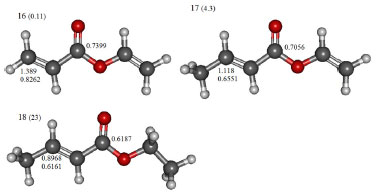 Figura 7. Estructuras moleculares de los compuestos 16 (vinil acrilato), 17 (vinil but-2-enoato) and 18 (etil but-2-enoate)
Serie 1 Las medidas experimentales de reactividad de los compuestos 1, 2, 3 y 4 hacia GSH revelan que el etil propiolato es el más reactivo, seguido por 2, 3 y 4 consecutivamente.31 Una segunda observación sugiere que los derivados con sustituyentes etinil o etinileno son más reactivos que sus análogos vinil o vinileno.31 Examinando los datos de la Tabla 1 se hace evidente que los valores del poder electrofílico Δφ+ perfectamente reproducen estas observaciones a diferencia de ω que resultó no ser una medida apropiada de la electrofilicidad relativa dentro de esta serie de análogos. Desde el punto de vista local, los valores de ωβ+ y Δφ+ fallaron al describir la reactividad relativa del carbono β de los derivados etinil y etinileno asi como sus los análogos sustituidos con grupos vinil y vinileno. En este sentido, la función de Fukui nucleofílica (ƒβ+) y el descriptor dual por sí solos no dieron mejores resultados. Dentro de los argumentos de Schultz y colaboradores,31 los derivados carbonilo α,β-insaturados sustituidos con grupos etinil o etinileno son más reactivos que sus análogos sustituidos con grupos vinil y vinileno debido a que el sistema π del enlace C≡C es intrínsecamente un arreglo más deficiente de electrones. La comparación de los valores de EC50 de los isómeros 2, 4 y 8 sugiere que la sustitución con metilo sobre un carbono vinileno reduce la reactividad del sistema conjugado, siendo mayor el efecto si la sustitución se realiza sobre el carbono β. En este sentido, solamente las escalas de reactividad relativa dadas por los valores del descriptor dual (ƒβ(2)) fueron consistentes con estas observaciones. Serie 2 En buen acuerdo con los datos experimentales de reactividad,31 los valores de Δφ+ muestran que hex-1-en-3-ona (Δφ+ = 2.363) es mucho más reactivo que hex-4-en-3-ona (Δφ+ = 2.219), que a su vez es más reactivo que el derivado no α,β-insaturado 5-hexen-3-ona (Δφ+ = 1.944). Esta misma observación fue reproducida por los valores de ω, así como por los índices locales Δφβ+, ωβ+, ƒβ+ y ƒβ(2) (ver Figura 3 y Tabla 1). Ya que hex-5-en-2-ona no es un sistema conjugado olefina-carbonilo, el carbono β de este compuesto no es el sitio más efectivo para la adición nucleofílica. En efecto, la comparación de los valores de Δφβ+ y ΔφC+ corrobora que el carbono carbonilo del compuesto 7 es el sitio más electrofílico de este sistema, sin embargo, experimentalmente se ha demostrado que no es selectivo hacia nucleófilos suaves como los grupos tiol,31 lo que explica el por qué el compuesto 7 es menos reactivo que sus isómeros 5 y 6. Siguiendo el procedimiento de Schultz y colaboradores,31 se compararon los efectos de ubicar en posición terminal a los enlaces C=C (vinil cetonas) y C=O (aldehídos). De este modo, se comparó la reactividad de la estructura trans-hex-2-enal con la de los compuestos 5 y 6. Experimentalmente,31 se sabe que el orden de reactividad de estos compuestos es el siguiente 5 > 6 > 11, pero desde el punto de vista teórico, los órdenes relativos de reactividad dados por los valores de Δφ+, ω, y ωβ+ no fueron consistentes con estas observaciones. No obstante, los valores condensados del poder electrofílico local Δφβ+ perfectamente reproducen la reactividad relativa de los compuestos 5, 6 y 11: hex-1-en-3-ona > hex-4-en-3-ona > trans-hex-2-enal, confirmando así que las vinil cetonas son más reactivas que sus isómeros aldehídos. Serie 3 Nuevamente, se evaluó la calidad de los índices de poder electrofílico global y local para predecir el efecto del grupo metilo sobre la reactividad de los compuestos 9 y 10, que son mostrados en la Figura 4. De acuerdo a lo reportado por Schultz,31 la reducción de la reactividad es mayor si el grupo metilo se encuentra enlazado al carbono β, de modo que el 3-metil-3-penten-2-ona es más electrofílico que 4-metil-3-penten-2-ona. Aunque los valores de Δφ+ y ω no reprodujeron estas observaciones, los valores condensados de Δφβ+ y ωβ+ lo hicieron satisfactoriamente. Además, las funciones de Fukui nucleofílicas y así como los valores del descriptor dual condensados sobre el carbono β (ver Tabla 1), también dieron el orden correcto de selectividad de los compuestos 9 y 10 hacia glutatión. Serie 4 Mientras que el 2-metil-2-pentenal tiene el sustituyente metilo en posición α, su isómero 4-metil-2-pentenal (ver Figura 5) presenta la sustitución con metilo en posición δ exhibiendo por lo tanto una mayor reactividad sobre el carbono β. Esto ocurre debido a que el carácter electrofílico del carbono β del 4-metil-2-pentenal es menos afectado por el sustituyente metilo que actúa como inductor electrónico. En este contexto, los valores de Δφβ+ y ω junto con los de Δφβ+ y ωβ+ mostraron ser descriptores de reactividad apropiados para racionalizar estas observaciones. Serie 5 Similar a lo discutido para los compuestos 5, 6 y 11 de la serie 2, el compuesto pent-1-en-3-ona (14) es más reactivo que su isómero aldehído (trans)-pent-2-enal (15). Las estructuras de estos dos compuestos son mostradas en la Figura 6. Nuevamente, mientras que la reactividad relativa dada por el índice de electrofilicidad ω no está en concordancia con los experimentos, los valores del poder electrofílico Δφ+ correctamente predicen la mayor reactividad del compuesto 14 con respecto al 15. A nivel local, los valores de Δφβ+ y ωβ+ también sugieren que el átomo de carbono β del compuesto 14 es más electrofílico, de lo cual se concluye que las vinil cetonas son más reactivas que sus análogos tipo aldehído. Serie 6 Las medidas de EC50 muestran que el vinil-acrilato (16) es el más reactivo de los compuestos de la serie 6 (Figura 7), seguido consecutivamente por el vinil-crotonato (17) y etil-crotonato (18). En este sentido, los valores de Δφ+ y ω están en buen acuerdo las observaciones descritas. Ya que los valores condensados de Δφβ+ y ωβ+ siguen esta misma tendencia, es posible considerar que la reactividad química de los compuestos 16, 17 y 18 está gobernada por las propiedades electrónicas del sistema olefina-carbonilo conjugado más que por otros factores tales como el efecto del solvente e impedimentos estéricos. Asimismo, tal como fue señalado por Schultz y colaboradores,31 la introducción de un grupo metilo sobre el carbono β disminuye su electrofilicidad local, lo que puede ser evidenciado comparando los valores de Δφβ+ del etil-crotonato (Δφβ+ = 0.8968), vinil-crotonato (Δφβ+ = 1.118), y vinil-acrilato (Δφβ+ = 1.389). Desde el punto de vista estructural, el remplazo del grupo etilo de los compuestos 2 y 18 por sustituyentes vinilo da lugar a los compuestos 16 y 17, respectivamente, lo que va acompañado por un decremento en la reactividad electrofílica relativa para cada par de análogos. En concordancia con estos resultados,31 los valores del poder electrofílico Δφ+ correctamente describen la reactividad relativa de los compuestos 2, 16 y 18, 17. No obstante, los valores condensados de Δφβ+ no racionalizaron estas observaciones. Cabe resaltar que para esta serie de análogos, el índice de electrofilicidad local ωβ+ describe correctamente el orden relativo de reactividad que sigue la secuencia 2 < 16 y 18 < 17.
CONCLUSIONES A partir de los índices locales de poder electrofílico y nucleofílico recientemente propuestos, las respectivas versiones globales de estos descriptores fueron desarrolladas dando lugar a las definiciones de las ecuaciones 40 y 45. Desde el punto de vista interpretativo, los sistemas que exhiban valores altos positivos del poder electrofílico (Δφ+) tenderán a ser más susceptibles a interactuar covalentemente con especies nucleofílicas; mientras que las moléculas con valores altos negativos del poder nucleofílico (Δφ-) podrían ser altamente susceptibles al ataque de ciertos sistemas electrofílicos. La utilidad de los índices electrofílicos local y global como conceptos razonables para la reactividad química fue demostrada estudiando la reactividad de una serie de dieciocho derivados carbonilo α,β-insaturados que reaccionan con sistemas nucleofílicos suaves actuando como aceptores de Michael. Con este propósito, los valores de Δφ+ y Δφk+ fueron utilizados para predecir la reactividad relativa dentro de seis subgrupos de análogos carbonilo α,β-insaturados reportados por Schultz y colaboradores31 por su reactividad hacia glutatión. Después del modelamiento de las geometrías moleculares de equilibrio, todos los descriptores de reactividad, incluyendo los índices de electrofilicidad global y local, poder electrofílico global y local, y funciones de Fukui, fueron calculados a partir de la información electrónica obtenida por el nivel de teoría B3LYP/6-311++G(2d,2p), el cual mostró ser una elección razonable para los propósitos del presente trabajo. En general, la comparación de tendencias de reactividad predichas por los valores de Δφ+ y ω con respecto a los datos experimentales, sugiere que Δφ+ fue más consistente con los experimentos; también, en la mayoría de los casos considerados, los valores condensados de Δφβ+ fueron mejores para reproducir la reactividad local intermolecular del carbono β de los derivados estudiados en comparación con el popular índice de electrofilicidad local (ωβ+). A pesar de que la calidad del poder electrofílico local obviamente depende de una buena condensación atómica de las funciones de Fukui, las tendencias de reactividad local intermoleculares dadas por los valores de Δφβ+ fueron mejores que al considerar solamente los valores de ƒβ+ para el tratamiento de la selectividad de sitio. Debido a que la utilidad de los índices de poder electrofílico global y local ha sido solo parcialmente demostrada, estos nuevos índices de reactividad podrían ser nuevamente evaluados para una validación más formal y general que permita definirlos como conceptos apropiados para el tratamiento teórico de las tendencias de reactividad de sistemas moleculares.
AGRADECIMIENTOS Los autores agradecen a la Universidad de Córdoba y a la Universidad Cooperativa de Colombia por el soporte del presente trabajo.
REFERENCIAS 1. Fukui, K.; Angew. Chem., Int. Ed. Engl. 1982, 21, 801. 2. Ponec, R. In Overlap Determinant Method in the Theory of Pericyclic Reactions; Springer, 1995; pp. 10-17. 3. Liu, S.-B.; Acta Phys.-Chim. Sin. 2009, 25, 590. 4. Ponec, R.; Strnad, M.; Int. J. Quantum Chem. 1992, 42, 501. 5. Wilson, S.; Electron Correlation in Molecules; Courier Corporation: North Chelmsford, 2014. 6. Parr, R. G.; Yang, W.; Density-functional theory of atoms and molecules; Oxford University Press: Oxford, 1989; Vol. 16. 7. Dreizler, R. M.; Gross, E. K. Density functional theory: an approach to the quantum many-body problem; Springer Science & Business Media: Berlin, 2012. 8. Liu, S.; Parr, R. G.; J. Chem. Phys. 1997, 106, 5578. 9. Proft, F. D.; Ayers, P. W.; Geerlings, P. In The Chemical Bond: Fundamental Aspects of Chemical Bonding; Frenking, G., Shaik, S., ed.; Wiley-VCH Verlag GmbH & Co. KGaA: New Jersey, 2014, cap. 7. 10. Labet, V.; Morell, C.; Tognetti, V.; Syzgantseva, O. A.; Joubert, L.; Jorge, N.; Grand, A.; Cadet, J. In Structure, Bonding and Reactivity of Heterocyclic Compounds; Springer: Berlin, 2014; pp. 35-70. 11. El Adnani, Z.; Mcharfi, M.; Sfaira, M.; Benzakour, M.; Benjelloun, A. T.; Touhami, M. E.; Corros. Sci. 2013, 68, 223. 12. Srivastava, A.; Rawat, P.; Tandon, P.; Singh, R. N.; Comput. Theor. Chem. 2012, 993, 80. 13. Glossman-Mitnik, D.; Procedia Comput. Sci. 2013, 18, 816. 14. Martínez-Araya, J. I.; Salgado-Morán, G.; Glossman-Mitnik, D.; J. Chem. 2013, 2013. 15. Mendoza-Huizar, L. H.; J. Chem. 2015, 2015, e751527. 16. Parr, R. G.; Pearson, R. G.; J. Am. Chem. Soc. 1983, 105, 7512. 17. Pearson, R. G.; Inorg. Chem. 1988, 27, 734. 18. Sánchez-Márquez, J.; Zorrilla, D.; Sánchez-Coronilla, A.; Desireé, M.; Navas, J.; Fernández-Lorenzo, C.; Alcántara, R.; Martín-Calleja, J.; J. Mol. Model. 2014, 20, 1. 19. Parr, R. G.; Szentpaly, L. v; Liu, S.; J. Am. Chem. Soc. 1999, 121, 1922. 20. Gazquez, J. L.; Cedillo, A.; Vela, A.; J. Phys. Chem. A 2007, 111, 1966. 21. Orozco-Valencia, A. U.; Vela, A.; J. Mex. Chem. Soc. 2012, 56, 294. 22. Bentley, T. W.; Chem. Eur. J. 2006, 12, 6514. 23. Campodónico, P. R.; Pérez, C.; Aliaga, M.; Gazitúa, M.; Contreras, R.; Chem. Phys. Lett. 2007, 447, 375. 24. Domingo, L. R.; Pérez, P.; Org. Biomol. Chem. 2011, 9, 7168. 25. Pinter, B.; Nagels, N.; Herrebout, W. A.; De Proft, F.; Chem. Eur. J. 2013, 19, 519. 26. Cardona, W.; Guerra, D.; Restrepo, A.; Mol. Simul. 2014, 40, 477. 27. Morales-Bayuelo, A.; Vivas-Reyes, R.; J. Math. Chem. 2013, 51, 125. 28. Parr, R. G.; Yang, W.; J. Am. Chem. Soc. 1984, 106, 4049. 29. Gomez, B.; Likhanova, N. V.; Dominguez-Aguilar, M. A.; Martinez-Palou, R.; Vela, A.; Gazquez, J. L.; J. Phys. Chem. B 2006, 110, 8928. 30. Figueredo, S. F.; Páez, M. S.; Song, J.-W.; Quim. Nova 2016, 39, 817. 31. Schultz, T. W.; Yarbrough, J. W.; Johnson, E. L.; SAR QSAR Environ. Res. 2005, 16, 313. 32. Freidig, A. P.; Verhaar, H. J.; Hermens, J. L.; Environ. Toxicol. Chem. 1999, 18, 1133. 33. Glossman-Mitnik, D.; Chem. Cent. J. 2013, 7, 1. 34. Mulliken, R. S.; J. Chem. Phys. 1934, 2, 782. 35. Perdew, J. P.; Parr, R. G.; Levy, M.; Balduz Jr, J. L.; Phys. Rev. Lett. 1982, 49, 1691. 36. Parr, R. G.; Donnelly, R. A.; Levy, M.; Palke, W. E.; J. Chem. Phys. 1978, 68, 3801. 37. Senet, P.; J. Chem. Phys. 1996, 105, 6471. 38. Senet, P.; J. Chem. Phys. 1997, 107, 2516. 39. Fuentealba, P.; Cedillo, A.; J. Chem. Phys. 1999, 110, 9807. 40. Fuentealba, P.; Parr, R. G.; J. Chem. Phys. 1991, 94, 5559. 41. Cárdenas, C.; Rabi, N.; Ayers, P. W.; Morell, C.; Jaramillo, P.; Fuentealba, P.; J. Phys. Chem. A 2009, 113, 8660. 42. Morell, C.; Grand, A.; Toro-Labbé, A.; Chermette, H.; J. Mol. Model. 2013, 19, 2893. 43. Mohajeri, A.; Omidvar, A.; Phys. Chem. Chem. Phys. 2015, 17, 22367. 44. Ayers, P. W.; J. Math. Chem. 2008, 43, 285. 45. Morell, C.; Grand, A.; Toro-Labbé, A.; J. Phys. Chem. A 2005, 109, 205. 46. Martínez-Araya, J. I.; J. Math. Chem. 2014, 53, 451. 47. Morell, C.; Hocquet, A.; Grand, A.; Jamart-Grégoire, B.; J. Mol. Struct. THEOCHEM 2008, 849, 46. 48. Rappé, A. K.; Casewit, C. J.; Colwell, K. S.; Goddard III, W. A.; Skiff, W. M.; J. Am. Chem. Soc. 1992, 114, 10024. 49. Hanwell, M. D.; Curtis, D. E.; Lonie, D. C.; Vandermeersch, T.; Zurek, E.; Hutchison, G. R.; J. Cheminformatics 2012, 4, 17. 50. Becke, A. D.; Phys. Rev. A 1988, 38, 3098. 51. Lee, C.; Yang, W.; Parr, R. G.; Phys. Rev. B 1988, 37, 785. 52. Jensen, F.; Introduction to computational chemistry; John Wiley & Sons, 2013. 53. Schuchardt, K. L.; Didier, B. T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T. L.; J. Chem. Inf. Model. 2007, 47, 1045. 54. Turney, J. M.; Simmonett, A. C.; Parrish, R. M.; Hohenstein, E. G.; Evangelista, F. A.; Fermann, J. T.; Mintz, B. J.; Burns, L. A.; Wilke, J. J.; Abrams, M. L.; Russ, N. J.; Leininger, M. L.; Janssen, C. L.; Seidl, E. T.; Allen, W. D.; Schaefer, H. F.; King, R. A.; Valeev, E. F.; Sherrill, C. D.; Crawford, T. D.; Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 556. 55. Yang, W.; Parr, R. G.; Pucci, R.; J. Chem. Phys. 1984, 81, 2862. 56. Ayers, P. W.; Theor. Chem. Acc. 2001, 106, 271. 57. Ayers, P. W.; Yang, W.; Bartolotti, L. J.; Chemical Reactivity Theory: A Density Functional View 2009, 18, 255. 58. Mulliken, R. S.; J. Chem. Phys. 1955, 23, 1833. 59. Chattaraj, P. K.; Maiti, B.; Sarkar, U.; J. Phys. Chem. A 2003, 107, 4973. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






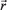 ), de la cual es posible, en principio, determinar todas las propiedades de un sistema electrónico. No obstante, otras representaciones han sido derivadas conduciendo a los bien definidos ensambles de la DFT.3,6 Por ejemplo, es posible representar la energía (y cualquier otra propiedad) del sistema a través del número de electrones y el potencial externo (ensamble canónico), es decir: 3,6
), de la cual es posible, en principio, determinar todas las propiedades de un sistema electrónico. No obstante, otras representaciones han sido derivadas conduciendo a los bien definidos ensambles de la DFT.3,6 Por ejemplo, es posible representar la energía (y cualquier otra propiedad) del sistema a través del número de electrones y el potencial externo (ensamble canónico), es decir: 3,6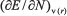 es precisamente la electronegatividad;
es precisamente la electronegatividad; 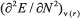 es la dureza química;
es la dureza química; 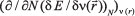 es la función de Fukui; y
es la función de Fukui; y 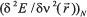 es la función respuesta.3 Estos conceptos han contribuido al entendimiento de la reactividad química y selectividad de sitio de diversos sistemas moleculares.10-15
es la función respuesta.3 Estos conceptos han contribuido al entendimiento de la reactividad química y selectividad de sitio de diversos sistemas moleculares.10-15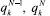 y
y 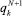 son las cargas atómicas del catión radical, molécula neutra y anión radical respectivamente. Las cargas atómicas47 fueron calculadas a punto simple mediante el nivel de teoría B3LYP/6-311++G(2d,2p) utilizando el esquema de partición de Mulliken58 implementado en el programa NWChem. Finalmente, los valores del descriptor dual atómico fueron calculados mediante la expresión:45
son las cargas atómicas del catión radical, molécula neutra y anión radical respectivamente. Las cargas atómicas47 fueron calculadas a punto simple mediante el nivel de teoría B3LYP/6-311++G(2d,2p) utilizando el esquema de partición de Mulliken58 implementado en el programa NWChem. Finalmente, los valores del descriptor dual atómico fueron calculados mediante la expresión:45