Educação
|
|
| Estruturas de fulerenos: estabelecendo interfaces no ensino de matemática e química em nível superior Structures fullerenes: establishing interface in mathematics education and chemistry in higher education |
|
Thiago H. B. Corrêa*; Joana D'arc da Silva Reis
Instituto de Ciências Exatas, Naturais e Educação, Universidade Federal do Triângulo Mineiro, 38064-200 Uberaba - MG, Brasil Recebido em 14/02/2017 *e-mail: correa.uftm@gmail.com The objective of this paper is to study fullerene geometry properties and attempt to stablish a dialogue between the teaching of mathematics and chemistry concepts using hands-on cardboard geometric models, in classroom, in order to facilitate the understanding of fullerene structures. This approach to the study of such molecules represents a unique opportunity to explore a complex and rich array of concepts that are essential to the teaching of chemistry at university level and have to be applied by the students along their course. At the same time the study of fullerenes can also profit from a mathematics approach to it, especially from a geometry perspective as argued here. In our research, the use of paper-made geometric models has proven to help the students to visualize and understand such molecular structures, their chemical bonds and their physical-chemical properties. These models have also contributed to overcome representational constraints of such tiny structures, which often come close to a "quasi-abstract' dimension, in a scale that can be manually handled by the students and at the same time played into multiple possible variations that allow them to test concepts and compare different molecular structures and arrangements. INTRODUÇAO Descoberto em 1985 pelo inglês Harold W. Kroto e os americanos Robert F. Curl e Richard E. Smalley, os fulerenos (chamados inicialmente de buckminsterfulereno, em homenagem ao arquiteto estadunidense Richar Buckminster Fuller (1895-1983), por seus trabalhos com cúpulas geodésicas) têm revelado ser um promissor campo de pesquisa e aplicaçao em diversas áreas da Química. Empregados no desenvolvimento de novos materiais, demonstrando, inclusive, atividade antioxidante, neuroprotetora, antimicrobiana e antirretroviral, o grupo de nanomoléculas esferoidais constituídas apenas por átomos de carbono (C), figurou o Prêmio Nobel de Química de 1996.1 Previstos desde 1966 por cálculos teóricos, a existência de "gaiolas" estáveis formadas exclusivamente por carbonos somente foi confirmada em 1990 pelo especialista em cromatografia Roger Taylor, o qual obteve amostras puras de C60 e C70. Foi também neste ano o desenvolvimento, por Krätschmer,2 de um método para a síntese de C60 em quantidades "macroscópicas", representando uma etapa decisiva para o campo que se tornou, nos últimos 25 anos, um dos maiores temas da química contemporânea com reflexos importantes nas áreas de supercondutividade, biologia e ciência dos materiais.1 Tema de nove entre dez artigos mais citados na área de Química, e de todos os dez em 1992, a terceira forma alotrópica do C - e a primeira molecular - vem despertando grande interesse de pesquisadores.3 Os trabalhos sobre fulerenos oportunizaram, também, o surgimento de novas técnicas de produçao de nanotubos de ponta aberta, o que tem se tornado um novo campo de investigaçao. Vale destacar que o estudo destes compostos exibe uma riqueza conceitual que pode ser explorada e utilizada no ensino de Química em nível superior. Além do mais, o presente trabalho vai ao encontro do exposto e evidencia a viabilidade de interlocuçao da Matemática e da Química na compreensao destas estruturas químicas regidas pela geometria (molecular). Diante do apresentado, este artigo visa explorar a relaçao das propriedades geométricas de fulerenos e apresentar um estudo introdutório sobre simetria molecular dos fulerenos a partir da manipulaçao de um material didático, assim como retratar uma experiência vivenciada na oficina Geometria de Fulerenos, ofertada aos estudantes do curso de Licenciatura em Química da Universidade Federal do Triângulo Mineiro (UFTM - Uberaba/MG).
DESENVOLVIMENTO A oficina supracitada foi idealizada no intuito de promover a introduçao ao estudo dos fulerenos, priorizando a relaçao matemática-química das estruturas e discutindo, subsequentemente, a interpretaçao de suas propriedades sob a ótica da Geometria/Topologia. A proposta inicia com a apresentaçao dos fulerenos, utilizando um material manipulável (modelo em anexo); os resultados do trabalho de Kroto4 em seu artigo 'The stability of the fullerenes Cn, with n=24, 28, 32, 36, 50, 60 and 70' publicado na revista científica Nature; e, como material de referência e consulta, o An Atlas of Fullerenes.5 Discutiremos a relaçao da estabilidade de fulerenos - C24 até C70 - a partir de um conjunto de regras químicas e sua estrutura geométrica. Seguimos com a proposta de estudo e investigaçao sobre grupo de simetria pontual das moléculas de fulerenos e algumas de suas aplicaçoes na química. A fim de representar as estruturas citadas, utilizaremos o mesmo material empregado na oficina, o qual foi confeccionado com papel cartao e elásticos. O material é de simples manuseio e barato, que permite investigar e representar as estruturas dos fulerenos.
EXPLORANDO AS ESTRUTURAS Atualmente é utilizado por consenso o termo fulereno para toda a família de "gaiolas" compostas inteiramente por átomos de carbono sp2 hibridizados, posicionados nos vértices de um poliedro formado por h hexágonos e 12 pentágonos, constituindo uma vasta família de nanomoléculas, formadas por número par de átomos de carbono C2n.6,7 Cinco argumentos empíricos para justificar a relativa estabilidade dos fulerenos foram apresentados no estudo de Kroto, os quais serviram de objeto de análise na oficina tendo como aporte o material utilizado.
Investigaçao I: a piramidalizaçao e o C60 Foi proposto aos estudantes que utilizassem somente as peças hexagonais do material para montar uma estrutura totalmente fechada, na forma de um poliedro. O mesmo foi proposto para o caso de usar somente as peças pentagonais. Posteriormente, foi sugerido que estes descrevessem suas observaçoes a respeito das experiências. Os pentágonos sao importantes na estrutura do fulereno, pois os grupos formados somente por hexágonos sao sempre planos - como um piso ladrilhado - inclusive na estrutura cilíndrica. Nota-se que a cada pentágono adicionado, a forma adquire curvatura, o que é possível ser visualizado manipulando o material. Ao incluir os 12 pentágonos, a "bola" se fecha completamente, uma vez que estes sao responsáveis pela mudança de ângulo das ligaçoes e, consequentemente, pela forma tridimensional da estrutura. A medida do ângulo interno (ai) de um polígono regular pode ser calculada do seguinte modo: ai = 180(n - 2)/n, sendo n o número de lados do polígono. Assim, a medida de um ângulo interno do pentágono regular é 1080 e do hexágono regular 1200, conforme observado no material da Figura 1.
 Figura 1. Representaçao dos ângulos internos dos polígonos (hexágonos e pentágonos) a partir do material da oficina
Como é possível perceber, a curvatura e as propriedades especiais dos fulerenos devem-se muito à presença dos pentágonos.7 A tensao associada à piramidalizaçao dos átomos é a razao da alta reatividade do C60 - o mais abundante e representativo dos fulerenos - quando comparado a outras formas de carbono, de modo que, ao reagirem, estes átomos passam a ser sp3 (Figura 2).
 Figura 2. Demonstraçao da piramidalizaçao
Investigaçao II: regra do pentágono isolado Nesta etapa da oficina, foi proposto que os estudantes usassem as peças pentagonais e hexagonais do material para montar uma estrutura totalmente fechada, na forma de um poliedro convexo, em que todas as faces pentagonais estao isoladas uma da outra, de modo que todo pentágono fique rodeado por um "anel" de faces hexagonais. A regra do pentágono isolado, conhecida por seu acrônimo em inglês IPR (Isolated Pentagon Rule), afirma que os fulerenos mais estáveis sao aqueles que nao apresentam pentágonos adjacentes, ou seja, cada um dos 12 pentágonos está rodeado de hexágonos. Usando os dois tipos de peças (pentagonais e hexagonais), na oficina apareceram duas estruturas C80 e C60. Ambas totalmente fechadas, nas quais todas as faces pentagonais estao isoladas uma da outra, de modo que todo pentágono fique rodeado por um "anel" de faces hexagonais. O C80 aparece como resultado devido à escolha das arestas que sao compostas por peças pentagonais e hexagonais. Entretanto, o C60, representado na Figura 3, é a menor estrutura que cumpre esta regra.
 Figura 3. Demonstraçao do C60
Foram necessárias exatamente 12 peças pentagonais e 20 peças hexagonais para fechar a estrutura, sendo descrito apenas um modo de montar o C60 com todos os pentágonos separados. O princípio é uma consequência da característica de Euler-Poincaré, que é um invariante topológico e pode ser calculado usando V-A+F=2, sendo V o número de vértices, A o número de arestas e F o número de faces do poliedro convexo. Com base nesta teoria, estabelecemos que para fechar qualquer rede esférica consistindo de h hexágonos, exceto para h = 1 sao necessários doze pentágonos. O menor fulereno observado foi o C20, composto apenas por doze pentágonos e zero hexágono. Como cada uma das arestas está ligada a dois vértices e em cada vértice do fulereno há um encontro de três arestas, temos que: V=2A/3. Substituindo em V+F-A=2, obtemos F=A/3+2. Sabemos que F=F5+F6, isto é, o total de faces (F) é soma do número de pentágonos (F5) e hexágonos (F6). Como cada aresta do poliedro é compartilhada por arestas de duas faces, A = (5F5 + 6F6)/2. Substituindo-se F = F5+F6 e A = (5F5 + 6F6)/2 em F = A/3+2, temos: F5 = 12 (exatamente 12 pentágonos). Portanto, F =12 + F6. Quanto aos vértices, como V = 2A/3, entao A=3V/2. Substituindo-se A= 3V/2 e F =12 + F6 em V+F-A=2, obtém-se V=20+2F6. Vale destacar que para fulerenos menores que o C60 nao podemos aplicar a regra do pentágono isolado, sendo a estabilidade dos diferentes isômeros dada pela regra da penalidade do pentágono adjacente, também conhecida como PAPR (Pentagon Adjacency Penalty Rule), que afirma que entre os possíveis isômeros na regra dos pentágonos isolados, o mais estável é o que minimiza o número de arestas comuns entre pentágonos, ou seja, aquele com o menor número de ligaçoes pentágono-pentágono.8 Podemos afirmar, entao, que fulerenos do tipo Cn, com n<60, com todos os pentágonos isolados nao existe. Nesse caso, Kroto argumenta que a estabilidade está relacionada com o isômero de menor número de fusoes de pentágonos e maior simetria para cada um desses fulerenos. Para discutir a afirmaçao, os estudantes foram incitados a utilizar o material para encontrar e representar a estrutura do menor fulereno Cn que possa existir sem a fusao de pentágono do tipo III ou fusao sequencial dos pentágonos, isto é, o tipo I e II sao suficientes. Outro resultado que nao é observado de imediato, mas depois de dicas e algumas tentativas podemos chegar, é que o menor fulereno sem a fusao de pentágono do tipo III, ou fusao sequencial dos pentágonos é o C50 - formado por 12 peças pentagonais e 15 peças hexagonais (Figura 4).
 Figura 4. Demonstraçao do C50
O C60 possui seis subunidades, denominadas piracelênicas, constituídas por dois pentágonos e dois hexágonos, sendo que é nesta parte da molécula que ocorrem as reaçoes, geralmente na posiçao 1, 22 (Figura 5).
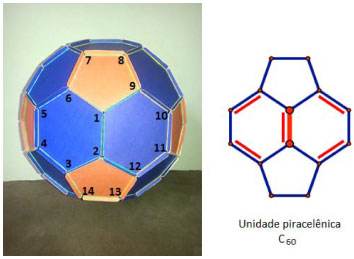 Figura 5. Demonstraçao da unidade piracelênica do C60
A maioria dos autores nao consideram o C60 uma molécula aromática, pois seus carbonos nao possuem um ângulo de 120º com carbonos usuais sp2 [C = C], porém, sao ligeiramente piramidalizados de forma que a molécula nao contém superfícies planares, o que, por sua vez, impede a existência de correntes anelares. Outro aspecto a ser considerado é que o fulereno nao apresenta reaçoes típicas de arenos, como adiçoes eletrofílicas. Estes reagem de forma análoga à olefinas deficientes de elétrons, sendo passível de ataques nucleofílicos, radicalares e até mesmo reaçoes de cicloadiçoes. Acredita-se que a força motriz para a alta reatividade resida na tensao resultante de seus carbonos piramidalizados, que passa a ser aliviado após as transformaçoes deles em carbono sp3 [C - C]3. Harold Kroto decidiu pôr a terminaçao eno no nome do C60 (Buckminsterfulereno), por analogia com benzeno (C6H6), dada a existência de ligaçoes ϖ alternadas, as quais poderiam conferir ao C60 algum carácter aromático. É evidente que, dada a esfericidade deste, os orbitais p - nao envolvidos na hibridaçao sp2 - nao serao exatamente paralelos (como acontece no benzeno), o que nao propicia uma boa junçao para garantir ligaçoes ϖ fortes e também nao propicia uma deslocalizaçao eficiente, o que deve se refletir no fato de, no C60, existir uma fraca aromaticidade. Isto pode ser confirmado pelas distâncias internucleares entre os átomos de carbono: enquanto numa camada de grafite, em que a deslocalizaçao é perfeita, todas as ligaçoes têm o mesmo comprimento (1,42 Å), no C60 existem dois valores para o comprimento da ligaçao carbono-carbono: 1,455 Å, para as ligaçoes C-C, e 1,391 Å para as ligaçoes C=C.9 Sabe-se que a molécula de C60, embora rica em elétrons, se comporta como uma espécie eletronegativa capaz de aceitar reversivelmente de um até seis elétrons, formando os ânions correspondentes. O caráter eletrônico deficitário deste fulereno foi comprovado por cálculos teóricos e atribuído aos orbitais moleculares LUMO nao-ligantes, que estao em um patamar de energia muito baixo.1 O excesso de densidade de carga negativa se acumula principalmente nos pentágonos, já que é a zona mais "piramidalizada" da estrutura esférica.6 Investigaçao III: a exceçao do C22 Com o material da oficina, foi requerido aos estudantes a construçao de uma estrutura fechada na forma de um poliedro convexo utilizando 12 peças pentagonais e uma hexagonal, em que se verificou a nao existência do fulereno C22. O emprego do material pode colaborar nesta investigaçao, pois permitiu aos estudantes demonstrar que o poliedro sugerido nao é possível, uma vez que a estrutura nao fecha (I). Pode-se constatar, ainda, que a partir do C24, este retoma o formato de "gaiolas" (II) - (Figura 6).
 Figura 6. Demonstraçao do C22
Com base nesta investigaçao, estabelecemos que podemos fechar qualquer rede esférica consistindo de 12 pentágonos e F6 hexágonos, exceto para F6= 1. V=20+2F6. Com F6=0, obtemos V=20, menor fulereno observado (C20), composto apenas por doze pentágonos e zero hexágono. Assim, com n vértices, um fulereno Cn existe para todo n ≥ 20 e n ≠22 e F6=n/2-10. Investigaçao IV: o C70 Nesta investigaçao foi pedido aos estudantes que usassem as peças pentagonais e hexagonais do material para representar a estrutura totalmente fechada do C70 de modo que todas as faces pentagonais ficassem isoladas. Conforme demonstrado matematicamente na investigaçao II, já era previsto que, para representar o C70, seriam necessárias 12 peças pentagonais e 25 peças hexagonais. Nao é óbvio de imediato, mas assim como no caso do C60, também existe apenas um isômero do C70 que mantém a regra de todos os pentágonos isolados (Figura 7). Para montar, basta acrescentar um "anel" com 5 peças hexagonais na parte que divide o C60 em dois hemisférios. Este argumento foi usado para explicar a predominância do C60 e C70, apresentado por Kroto.
 Figura 7. Demonstraçao do C70
Investigaçao V: C36, C32, C28, C26, C24 De acordo com o argumento 3 descrito na introduçao deste artigo, utilizamos o material para representar e comparar os fulerenos C24; C26; C28; C32; e, C36. Na oficina, os estudantes foram conduzidos a construir as estruturas, considerando os tipos de fusao de pentágonos4 (Figura 8), seguindo as seguintes orientaçoes:
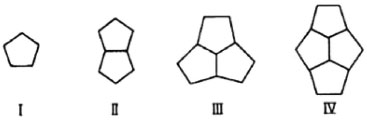 Figura 8. Tipos de fusao de pentágonos
Comparar os resultados obtidos com o recurso disponível na Web,10 fornecido e mantido por David Tomanek e Nick Frederick, do Michigan State University Computational Nanotechnology Lab. Segue uma tabela para apresentar os resultados desse trabalho investigativo. Usamos Cn para designar o fulerenos de n vértices (átomos de carbono) e F6 o número de hexágonos necessários para construçao dos casos de fulerenos investigados (Tabela 1).

FULERENOS E SEU GRUPO PONTUAL DE SIMETRIA A Matemática é uma ciência que fornece ferramentas para a construçao de muitos conceitos científicos. Além disso, é possível observar na natureza, um recorrente padrao geométrico que alicerça e influi em arranjos espaciais, desde o formato de um favo de mel até a disposiçao de um cristal de gelo, todos tendendo a variaçoes hexagonais. Para entender tais variaçoes, precisamos identificar a geometria das formas, que agem, desde seu nível mais básico, buscando a soluçao mais eficiente em termos de espaço e energia. No nível submicroscópico, o mundo também é estruturado em torno de leis geométricas, tendo a Química muitos exemplos: estruturas cristalinas, redes de Bravais, nanocompostos e clusters. Na Química, a simetria é deveras importante para determinar as propriedades físicas de compostos; orientar como as reaçoes podem ocorrer; justificar os orbitais híbridos que sao possíveis em determinadas moléculas; construir diagramas de energia de orbitais moleculares; discutir a estrutura eletrônica; discutir vibraçoes moleculares e atribuir transiçoes em espectroscopia eletrônica. O estudo da simetria nao deixa de ser relevante nos fulerenos, os quais têm a sua estabilidade, assim como muitas propriedades, associada à simetria das estruturas.1 Seguimos com a proposta de estudo e investigaçao sobre grupo de simetria das moléculas de fulerenos e algumas de suas aplicaçoes na Química. Para isso, introduzimos o assunto de forma oral e expositiva e utilizamos, como meio de referência e consultas, o recurso da Web fornecido por Nick Frederick no Michigan State University Computational Nanotechnology Lab.10 Para representar as estruturas, utilizou-se o mesmo material empregado nas atividades anteriores e um espelho plano. Elementos e operaçoes básicas de simetria O tipo de simetria para o qual uma molécula pertence é conhecida como seu grupo pontual. O grupo pontual de qualquer molécula é o conjunto das operaçoes de simetria que consiste em mover um corpo de tal maneira que sua posiçao final, após o movimento, seja equivalente à inicial. Um elemento de simetria é uma entidade geométrica (ponto, reta ou plano) com relaçao a qual se efetua uma ou mais operaçoes de simetria. As operaçoes de simetria estao baseadas em elementos de simetria, e ambos (operaçoes e elementos) sao condiçoes necessárias para definir simetria. No estudo de sistemas finitos, tais como moléculas, aglomerados moleculares, etc., existem somente quatro tipos de operaçoes (Tabela 2). Em um cristal, as operaçoes de translaçoes também dever ser incluídas.

Grupos pontuais de simetria Um grupo pontual é representado por um conjunto de operaçoes de simetria. Para esta atividade os estudantes utilizaram o material proposto na oficina e um espelho. Segue um esquema bastante difundido nos textos didáticos para classificar a molécula (Figura 9).
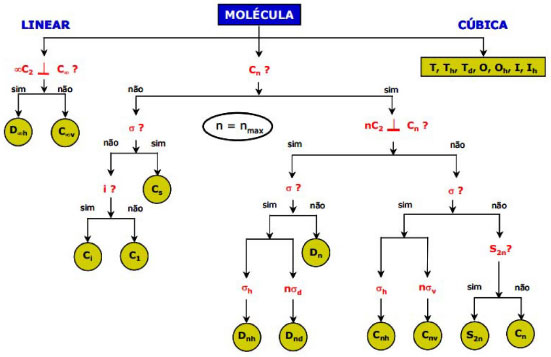 Figura 9. Fluxograma para classificaçao do grupo de simetria de moléculas11
Após a apresentaçao deste estudo introdutório de forma expositiva, continuamos com a investigaçao proposta a seguir. Investigaçao VI: A proposta foi explorar a página da Web10 construída e mantida por Frederick para auxiliar na visualizaçao e na escolha de isômeros do fulereno que representem exemplos dos grupos de simetria apresentados. O material manupulável foi utilizado para representá-los. Seguem as tabelas com os resultados deste trabalho investigativo. I) Grupos de baixa simetria (Tabela 3)
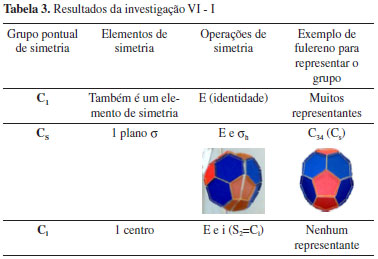
II) Grupos com um único eixo de simetria (Tabela 4)
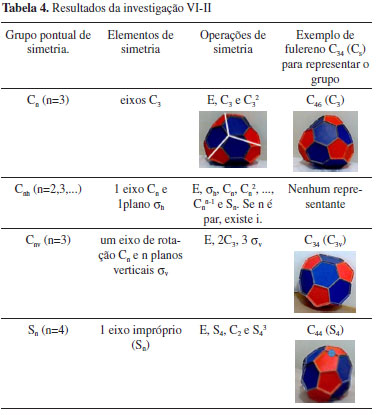
III) Grupos com um eixo Cn e n eixos C2 (Tabela 5)
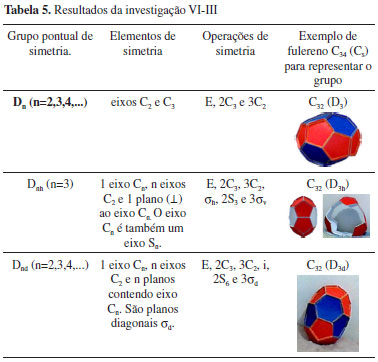
IV) Grupos de alta simetria (Tabela 6)
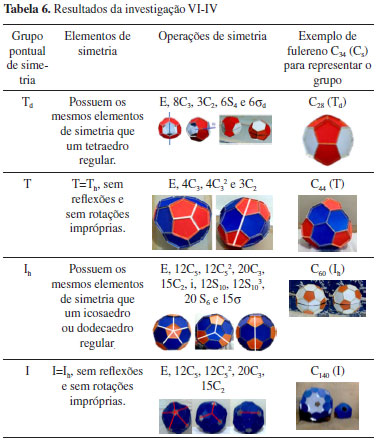
Estes grupos estao relacionados com as propriedades de simetria dos poliedros regulares (poliedros platônicos): tetraedro, cubo, octaedro, dodecaedro e icosaedro. Simetria, polaridade e moléculas quirais As aplicaçoes de simetria estao relacionadas à polaridade e à quiralidade das moléculas. Uma molécula com centro de inversao é apolar, sendo que a inversao implica na distribuiçao de carga igual em todos os pontos opostos diametralmente a um centro (i). Assim, moléculas polares nao apresentam centro de inversao. O momento dipolo nao pode estar perpendicular aos planos de reflexao e também nao pode estar perpendicular ao eixo de rotaçao, pois moléculas que possuem C2 perpendicular a um eixo Cn ou σh perpendicular a um eixo Cn tem a resultante do momento dipolo igual a zero, ou seja, sao apolares. Assim, uma molécula nao pode ser polar se ela pertencer a qualquer dos grupos D e seus derivados, os grupos cúbicos T e O, o grupo icosaédrico I e suas modificaçoes. Uma molécula quiral nao pode ser sobreposta na sua imagem de reflexao e é opticamente ativas quando observadas. Uma molécula quiral e sua imagem (reflexao) sao chamados enantiômeros. Os pares de enantiômeros giram o plano da luz polarizada na mesma magnitude, mas para lados opostos. Para ser quiral uma molécula nao pode ter Sn. Os grupos que apresentam Sn sao Dnh, Dnd e os grupos Td, Oh e Ih. Para os eixos Sn disfarçados (σ=S1; i=S2), moléculas com um plano de reflexao ou com um centro de inversao nao podem ser quirais.
POTENCIALIDADES DO MATERIAL E O APELO TEMATICO DOS FULERENOS Como se pode perceber, todos os conteúdos das atividades da oficina foram trabalhados a partir do material apresentado. Este foi empregado de modo a demonstrar elementos da estrutura de fulerenos que estao limitados à abstraçao do conteúdo químico. Em outras palavras, o material revelou um expressivo valor para o ensino de Química no que diz respeito a "materializaçao" de conceitos, ajudando o estudante a compreender estruturas químicas regidas pela geometria [molecular], e assumindo a Matemática como uma indispensável ferramenta no estudo de fulerenos,12 estudo este que demonstrou riqueza conceitual e apelo frente à atualidade do tema em importantes pesquisas de Química. Além do mais, o material auxiliou na compreensao dos artigos selecionados na oficina, o que aproximou os estudantes à esfera da pesquisa, e, consequentemente, da escrita científica. Pontuamos, ainda, que o desenvolvimento da habilidade de representar mentalmente um objeto que nao está ante os olhos, depende da exploraçao de modelos, programas computacionais ou materiais que possibilitem ao estudante a construçao de imagens mentais. Em consonância, o material utilizado contribuiu para a percepçao do arranjo espacial dos fulurenos, permitindo o desenvolvimento da noçao da tridimensionalidade, assim como o diálogo e a inter-relaçao de diferentes áreas do conhecimento, numa rede de comunicaçao, isto é, num saber unificado. Em suma, nao podemos descartar o fato de que transformar artigos científicos em recursos didáticos - em especial nos cursos de graduaçao - pode ser uma forma de socializar a produçao científica, favorecendo o processo de ensino e a proposiçao de metodologias. Embora algumas iniciativas sobre a utilizaçao dos artigos científicos no ensino superior de Química sejam relatadas na literatura internacional, o Brasil ainda carece de trabalhos pautados nesta prática.13
CONCLUSAO Ao contrário do que se pode imaginar, os fulerenos nao sao objetos de estudo exclusivos da Química ou da Física, mas dao lugar a problemas puramente matemáticos. Neste artigo buscamos explorar as propriedades básicas destas moléculas sob o ponto de vista matemático, demonstrando a riqueza conceitual deste tema, além da possibilidade de utilizaçao para o ensino superior, tecendo, em especial, um diálogo com a Química sob o enfoque geométrico. Ressaltamos, inclusive, as potencialidades de um material de fácil acesso que demonstrou contribuir para o estudo dos fulerenos e a superaçao das limitaçoes representacionais relacionadas à abstraçao exigida. Assim, o material apresentado foi uma valiosa ferramenta/estratégia que possibilitou a materializaçao de conceitos matemáticas e químicos. Como é possível notar, a visao geométrica das moléculas - garantida pelo material utilizado na oficina - é fundamental para a compreensao das estruturas, das ligaçoes químicas e das propriedades físico-químicas dos fulerenos.
REFERENCIAS 1. Santos, J.; Rocha, P.; Alves, B.; Freitas, P.; Quim. Nova 2010, 33, 680. 2. Krätschmer, W.; Lamb, D.; Fostiropoulos, K.; Huffman, R.; Nature 1990, 347, 354. 3. Rodrigues, V.; Dissertaçao de Mestrado, Universidade Federal de Minas Gerais, Brasil, 2011. 4. Kroto, W.; Nature 1987, 329, 529. 5. Fowler, W.; Manolopoulos, E.; An atlas of fullerenes, Dover Publications: New York, 2007. 6. Alegret, N.; Rodríguez-Fortea, A.; Poblet, M.; An. Quim. 2014, 110, 121. 7. Dias, M.; Quim. Nova 1995, 18, 592. 8. Gan, L.; Zhao, J.; Hui, Q.; J. Comput. Chem. 2010, 31, 1715. 9. http://www.spq.pt/magazines/BSPQ/631/article/30001382/pdfAcessada em dezembro de 2016. 10. http://www.nanotube.msu.edu/fullerene/fullerene-isomers.htmlAcessada em julho de 2016. 11. http://www.lqes.iqm.unicamp.br/images/vivencia_lqes_index_classificacao_moleculas.pdfAcessada em julho de 2016. 12. Reis, S.; Corrêa, B.; Resumos do XVIII Encontro Nacional de Ensino de Química, Florianópolis, Brasil, 2016. 13. Massi, L; Santos, R.; Ferreira, Q.; Queiroz, L.; Quim. Nova 2009, 32, 503. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access





