JBCS

INTRODUCTION

Electrocatalysis at modified electrodes has diverse applications, especially in sensors and biosensors and bio fuel cells. The model presented accounts for three processes, viz. (i) diffusion of reactant from solution into a layer of film, (ii) a chemical reaction between reactant and catalytically active centers of a film, and (iii) diffusion of charge carriers. Naujikas et al. and Puida et al. developed a mechanical of electrocatalytic processes taking place at conducting polymer modified electrodes.^1,2 This model takes into account the diffusion of solution specifies into polymer film, diffusion of charge carrier within the film and chemical redox reaction within the film. Theoretical modeling of biosensors implies the use of a nonlinear term related to Michaelis-Menten kinetic scheme for enzyme-catalyzed reactions.² Lyons et al. discussed the theoretical analysis of the steady-state amperometric response for a polymer modified electrode system which exhibits Michaelis-Menten kinetics.³ Lyons et al. also described a analytical model of the transient response of an amperometric chemical sensor in which the sensing elements bound in a surface deposited polymer film interact with the substrate via Michaelis-Menten reaction kinetics.⁴ Albery et al. recognized the most models for polymer modified electrodes. These models are rather complex and sophisticated, but are limited in their applicability, in that they concern the evaluation of the steady state response associated with mediated electrocatalysis at polymer film.⁵ Lyons et al. developed the mathematical analysis of the steady state amperometric response for a conducting polymer microelectrodes.⁶ Uma et al. reported the theoretical analysis corresponding to irreversible homogeneous reaction on finite-layer diffusion impedance. It is also relevant for solid electrolytes and membranes.⁷

Recently, Naujikas et al. and Puida et al. developed a mathematical model of electrocatalysis at conducting polymer modified electrodes.^1,2 However to the best of author knowledge, no general analytical results for the concentration of reactant, reaction product and charge carrier have been published. The purpose of this communication is to derive the analytical expression of the concentration of reactant, reaction product and charge carrier for all values of the parameter using the homotopy perturbation method.

MATHEMATICAL FORMULATION OF THE PROBLEM

The diffusion of reactant into a modified electrode is described by the Fick's law:

where R means the concentration of reactant, t is the time, x is a space coordinate, and D is the diffusion coefficient for reactant. We can assume that constant suitable electrode potential is applied for the electrochemical conversion of reactant into product. In this reaction, the reaction rate are expressed as the concentration of the reactant and of the charge carrier. The reaction rate is change in concentration of either product or reactant. The concentration of reactant decreases with time while concentration of charge carrier increases. So, the reaction rate is expressed as, where k is a second order rate constant. In this model the electrode surface is assumed to be covered with a uniform layer of a film. It is also supposed that there is no concentration gradient outside of the film which means that the process proceeds under ideal stirring condition. The diffusion coefficients of reactants and product are assumed to be equal. Also the diffusion coefficients of charge carrier is not equal to diffusion coefficients of reactants or product (D_n ≠ D). Hence the nonlinear reaction diffusion equations for reactant (R), reaction product (P) and charge carrier (n) can be expressed as follows¹: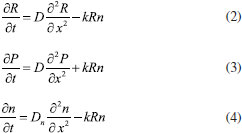

where x ∈ [0, d], and t>0. While formulating the above equation for the diffusion of the reactants pertaining to a modified electrode, its applicability is well known in other contexts. Among them, mention may be made of the following: (i) CE mechanisms at a microdisc electrodes⁸ (ii) reaction kinetics between oxirane and carbon dioxide.⁹

The schematic diagram of modified electrodes is given in Figure.1. Let x=0 represent the electrode/ film boundary while x = d is the thickness of a film. The electrocatalytic processes start when the reactant appears over the surface of a electrode. The electrode process starts when the reactant appears over the surface of the film. The initial conditions are: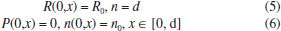

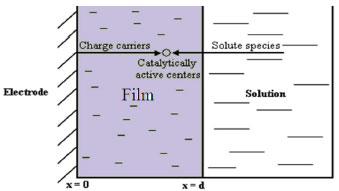Figure 1. Schematic diagram of modified electrodes. Theoretical model of catalytic processes at modified electrodes are discussed. Mathematical solu tion of nonlinear reaction diffusion equations were obtained

Consequently, the boundary conditions are (t>0)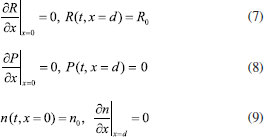

We introduce the following set of dimensionless parameters,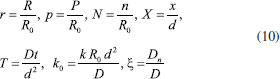

The governing nonlinear reaction/diffusion Eqns. (2-4) are expressed in the following non - dimensional form: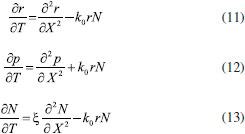

The dimensionless initial and boundary conditions becomes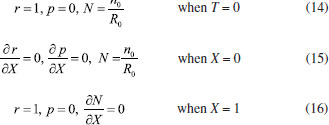

The dimensionless current density ψ(T) obtained explicitly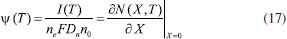

ANALYTICAL EXPRESSION OF NON-STEADY STATE CONCENTRATIONS USING HPM

Recently, many authors have applied the HPM to various problems and demonstrated the efficiency of the HPM for handling nonlinear structures and solving various physics and engineering problems.^10-14 This process is a combination of homotopy in topology and classic perturbation techniques. Ji-Huan He used the HPM to solve the Lighthill equation,¹¹ the Duffing equation ¹² and the Blasius equation.¹³ The idea has been used to solve nonlinear boundary value problems,¹⁴ integral equations,^15-17 Klein-Gordon and Sine-Gordon equations,¹⁸ Emden-Flower type equations¹⁹ and various other problems. This wide variety of applications shows the power of the HPM to solve functional equations. The HPM is unique in its applicability, accuracy and efficiency.

More recently, the system of coupled nonlinear reaction diffusionequations in an electroactive film deposited on aninlaid microdisc electrodes are solved using homotopy perturbation method.^23,24 The basic concept of homotopy perturbation method is given in Appendix A. By solving the Eqns. (12) - (14), using this method (see Appendix B), the concentration of reactant (R),reaction product (P) and charge carrier (n) can be obtained as follows:

The current becomes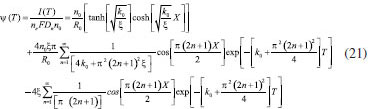

ANALYTICAL EXPRESSION OF STEADY STATE CONCENTRATIONS AND CURRENT USING HPM

When T = ∞ the above Eqn. (18) - (20) we get,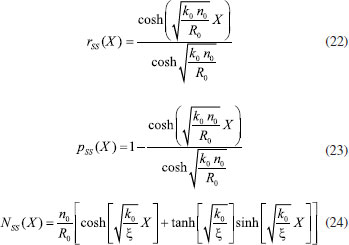

Eqn. (22) - (24) represents new simple analytical expressions of concentration of reactant (R), reaction product (P) and charge carrier (n) for steady state condition.

The steady state current becomes,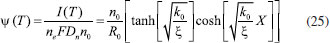

VALIDATION OF THE RESULT

The non-steady state nonlinear differential equations (11)-(13)are also solved using numerical methods. The function pdex4 in Scilab software which is the function of solving the initial value problems for ordinary differential is used to solve this equation. Our theoretical results for the concentration of reactant (Eqn. (18)), reaction product (Eqn. (19)) and charge carrier (Eqn. (20)) are compared with simulation results (Scilab program 4.1) in Figures 2-4. Satisfactory agreement is found for all values of time T. The Scilab program is also given in Appendix C. We run Scilab 4.1 on Apple iMac Core i5.

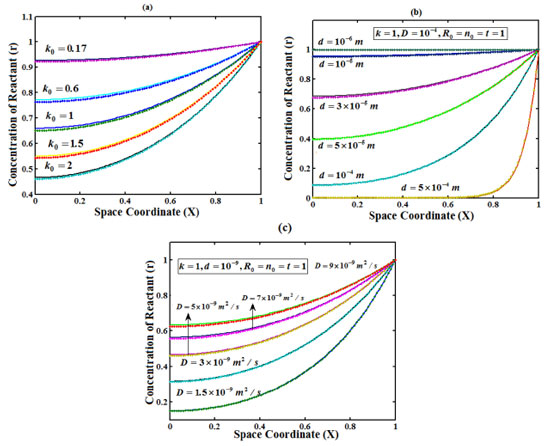Figure 2. Plot of concentration of reactant versus distance from the electrode surface for various values of k₀, d and D, when time T=1. (___) denotes Eqn. (18) and (...) denotes the numerical simulation for the experimental values of the parameters (Appendix C)

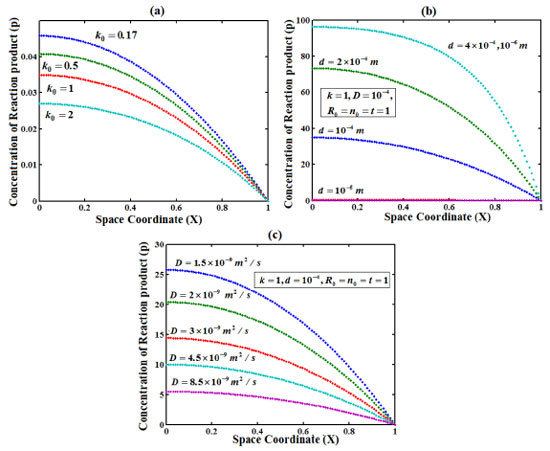Figure 3. Plot of concentration of reaction product versus distance from the electrode surface for various values of k₀, d and D, when time T=1. (... ) denotes Eqn. (19)

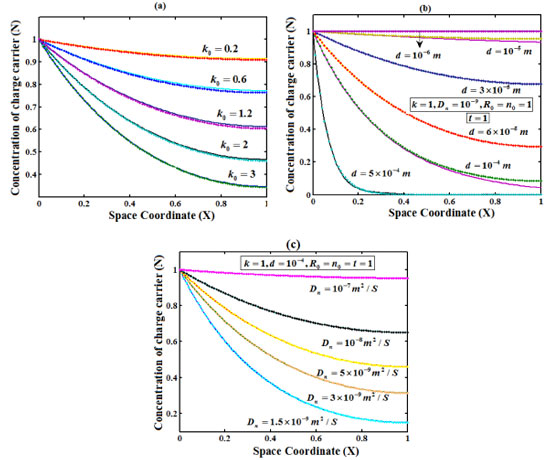Figure 4. Plot of concentration of charge carrier versus distance from the electrode surface for various values of k₀, d and D, when time T=1. (___) denote Eqn. (20) and (...) denotes the numerical simulation for the experimental values of the parameters (Appendix C)

RESULT AND DISCUSSIONS

Eqns. (18)-(20) represents the concentration of the reactant (R), reaction product (P) and charge carrier (n) for non-steady state condition. Eqn. (21) represents the dimensionless current density. Eqns. (22)-(25) represents the corresponding steady-state concentrations and current.

The concentration of the reactant, reaction product and charge carrier on depends upon the reaction rate, thickness of the film and diffusion coefficient.The reaction rate for a given chemical reaction is the measure of the change in concentration of the reactant or product per unit time. The thickness of the film and diffusion coefficient are always critical parameters.

Figures 2(a)-(c) represent the concentration of reactant versus distance from the electrode. Here the concentration is calculated for various values of the parameter k₀, d and D respectively. From Figure 2 (a), it is observed that concentration of reactant decreases when parameter k₀ increases. From Figure 2 (b)-(c), it is inferred that the concentration of reactant decreases when parameter d and D decreases.

Figure 3 (a)-(c) presents the dependence of the parameter k₀, d and D on the concentration of reaction product. From Figures 3 (a) - (c) it is inferred that the concentration of reaction product decreases at the electrode surface when all the parameters are increases.

Figure 4(a)-(c) represent the concentration of charge carrier versus the distance from the electrode for various values of parameters. In Figure 4 (a) and (c) the concentration decreases when the parameter k₀, k and ID increases. In Figure 4 (b), the concentration decreases when thickness of film d decreases.

Figure 5 represent the steady state concentration of reactant, reaction product and charge carrier respectively. From the Figure 5, it is observed that the concentration of reactant and reaction product are increasing function whereas charge carrier is a decreasing function from the film/solution interface.

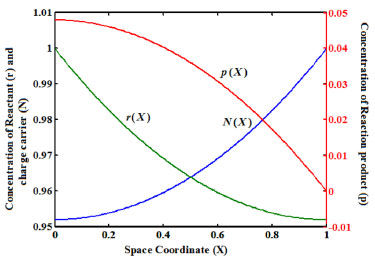Figure 5. Plot of steady state concentration of reactant, reaction product and charge carrier versus distance from the electrode surface

From Figure 6 (a), it is inferred that the current density increases when k₀ increases. Also the current density increases when R₀ (initial substrate concentration) and d (thickness of the film) decreases. Also from Figure 6(b), it is obversed that the current density increases when D_n decreases.

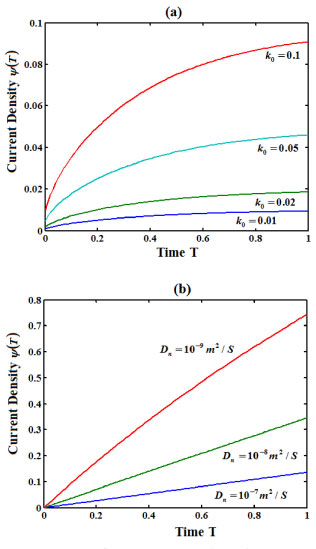Figure 6. Current versus the time for various values of k₀ and D_n

CONCLUSIONS

Electrocatalysis of solute species at modified electrodes is discussed. The concentration of reactant, reaction product and charge carrier are obtained by solving the nonlinear reaction diffusion equation using homotopy perturbation method. Analytical results are compared with simulation result. A satisfactory agreement with the numerical results is noted. Based on the proposed model, optimization of reaction system parameters could be made for any particular case to get an optimum efficiency or reactant to product conversion. These analytical results are useful to predict and optimize the kinetic parameters in modified electrodes.

SUPPLEMENTARY MATERIAL

Appendix A, Appendix B, Appendix C and Appendix D can be found at http://qumicanova.sbq.org.br in pdf format with free access.

ACKNOWLEDGEMENTS

The authors are very much grateful to the referees for the valuable suggestions. The authors are thankful to Mr. S. Mohamed Jaleel, The Chairman, Dr. A. Senthilkumar, The Principal, Dr. P. G. Jansi Rani, Head of the Department of Mathematics, Sethu Institute of Technology, Kariapatti-626115, Tamilnadu, India for their encouragement.

REFERENCES

1. Naujikas, R.; Malinauskas, A.; Ivanauskas, F.; J. Math. Chem. 2007, 42, 1069.

2. Puida, M.; Malinauskas, A.; Ivanauskas, F.; J. Math. Chem. 2011, 49, 1151.

3. Lyonsa, G.; Greera, C.; Fitzgerald, A.; Bannon, T.; Barlett, N.; Analyst 1996, 121, 715.

4. Lyons, G.; Bannon, T.; Hinds. G.; Rebouilat, S.; Analyst 1998, 123, 1947.

5. Albery, J.; Hilman, R.; J. Electroanal. Chem. 1984, 170, 27.

6. Lyons, G.; Bannon, G.; Rebouilat, S.; Analyst 1998, 123, 1961.

7. Maheswari, M.; Rajendran, L.; International Journal of Mathematical Archive 2012, 3, 1.

8. Streeter, I.; Compton, G.; J. Electroanal. Chem. 2008, 615, 154.

9. Park, W.; Park, W.; Kim, Y.; Park, Y.; Oh, J.; Catal. Today 2004, 98, 493.

10. He, H.; International Journal of Non-Linear Mechanics 2000, 35, 37.

11. He, H.; Computer Methods in Applied Mechanics and Engineering 1999, 178, 257.

12. He, H.; Applied Mathematics and Computation 2003, 135, 73.

13. He, H.; Applied Mathematics and Computation 2003, 140, 217.

14. He, H.; Phys. Lett. A 2006, 350, 87.

15. Golbabai, A.; Keramati, B.; Chaos, Soliton Fractals 2008, 37, 1528.

16. Ghasemi, M.; Kajani, M.; Babolian, E.; Applied Mathematics and Computation 2007, 188, 446.

17. Biazar, J.; Ghazvini, H.; Chaos, Soliton Fractals 2009, 39, 770.

18. Odibat, Z.; Momani, S.; Phys. Lett. A 2007, 365, 351.

19. Chowdhury, H.; Hashim, I.; Phys. Lett. A 2007, 368, 305.