JBCS

INTRODUÇAO

O tema fotocatálise já foi alvo de diversas revisoes na literatura, inclusive em alguns manuscritos de cunho exaustivo com centenas de referências. Nesse sentido, destacam-se entre os trabalhos clássicos o do professor Michael R. Hoffmann e col.¹ que acumula mais de 17 mil citaçoes desde 1995 e os do professor Akira Fujishima e col.^2,3 sobre o TiO₂, com cerca de 7 mil e 4 mil citaçoes desde os anos de 2000 e 2008, respectivamente. No Brasil, em língua portuguesa, sobressaem-se os trabalhos de revisao do professor Wilson Jardim e col.^4,5 visando a discussao da aplicaçao do TiO₂ para remediaçao ambiental e a discussao de mecanismos de fotodegradaçao de compostos orgânicos catalisados por ele. A fotoeletrocatálise, entretanto, nunca foi focalizada em trabalhos de revisao em vernáculo. Por algumas vezes, ela foi abordada em trabalhos de inovaçao técnica contemplando novas aplicaçoes,^6-9 mas nao uma visao fundamentada e sistematizada do tema balizada em literatura selecionada e acompanhada de discussao crítica do estado da arte e possíveis tendências. A fundamentaçao teórica da fotoeletrocatálise remonta ao final da Segunda Guerra Mundial, com os estudos da semiconduçao no silício e germânio orientados por Lark-Horovitz¹⁰ e que desencadearam o enorme avanço tecnológico representado por componentes eletrônicos como diodos e transistores, formados por junçoes entre semicondutores com dopagem diferente, presentes hoje em praticamente todos os dispositivos eletrônicos. Os componentes semicondutores também se impuseram na detecçao e emissao de radiaçao eletromagnética, servindo de exemplos os fotodiodos e os diodos emissores de luz (LEDs). Assim, segue a fundamentaçao teórica da matéria.

A TEORIA DE BANDA

Por definiçao simples, um semicondutor é um material com condutividade elétrica mensurável que, ao contrário dos condutores metálicos, aumenta com a temperatura. Para compreender melhor os seus mecanismos de conduçao, é importante conhecer um pouco de suas características físicas e, principalmente, alguns dos princípios da teoria do orbital molecular.

Os sólidos podem ser considerados a uniao de um número virtualmente infinito de átomos, de modo que o seu posicionamento sucessivo em linha leva à superposiçao dos orbitais adjacentes para a formaçao de ligaçoes. Através da combinaçao linear de dois orbitais atômicos é originado um orbital molecular ligante e um orbital molecular antiligante (dois orbitais moleculares). A medida que mais átomos sao enfileirados, mais orbitais moleculares sao formados pela interferência das funçoes de onda de seus orbitais atômicos, levando à formaçao de um conjunto de orbitais nao-degenerados com baixa diferença de energia entre níveis consecutivos. Sugere-se de modo aproximado a formaçao de um contínuo de níveis de energia entre o orbital ligante de menor energia e o orbital antiligante de maior energia, a chamada banda (Figura 1). Quanto maior a força de interaçao entre os átomos vizinhos, maior é a diferença de energia entre esses níveis e, portanto, mais larga é a banda. O aumento do número de átomos enfileirados e orbitais moleculares formados eleva o número de níveis internos da banda e a chamada densidade de estados (número de níveis contidos em uma fraçao de largura infinitesimal da banda), reduzindo a diferença de energia entre níveis consecutivos e tornando o modelo ainda mais próximo do real.¹¹

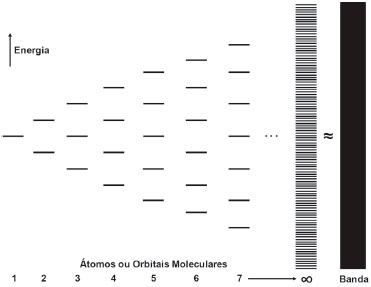Figura 1. Representaçao esquemática puramente pictorial do enfileiramento crescente de átomos com a combinaçao linear de seus orbitais atômicos do tipo s para a formaçao de orbitais moleculares σ_s e σ_s^*. Quando o número de átomos enfileirados tende ao infinito, observa-se a formaçao de um quasi-contínuo de níveis que é aproximado a um contínuo, constituindo-se o modelo de banda. Exemplo de banda s. Baseado em figura da obra de Shriver e Atkins¹¹

Cada banda pode ser classificada de acordo com o tipo de orbital atômico que a constitui. A Figura 1 representa a formaçao de uma "banda s", sendo possível a formaçao de "banda p" ou ainda "banda d" pela combinaçao dos respectivos orbitais atômicos quando disponíveis. Como os orbitais "d" sao mais energéticos do que os "p" que, por sua vez, sao mais altos que os "s" em uma mesma camada de valência, há frequentemente a formaçao de uma falha entre as bandas formadas, uma regiao vazia entre níveis ou orbitais moleculares, chamada de banda proibida. A diferença de energia delimitada pela sua largura é chamada de Band Gap (Eg). A existência da banda proibida (Band Gap) está condicionada à largura das bandas consecutivas e à separaçao energética dos tipos de orbitais envolvidos na formaçao de cada uma. Forças interatômicas elevadas e energias de orbitais atômicos similares geralmente induzem a sobreposiçao de bandas.

A ocupaçao dos orbitais em bandas é ditada pela distribuiçao de Fermi-Dirac, um algoritmo estatístico sigmoidal semelhante à distribuiçao de Boltzmann, mas com a restriçao de ocupaçao de apenas dois elétrons por nível.¹²

em que f(E) representa a probabilidade de um estado com energia "E" estar ocupado após o equilíbrio termodinâmico ser alcançado, T é a temperatura absoluta do sistema em Kelvin, k é a constante de Boltzmann e µ representa o potencial químico total dos elétrons. Em especial, a energia equivalente ao potencial químico do sistema (E = µ) merece atençao: neste valor, a probabilidade atinge 50 % (0,5/1,0) de chance de ocupaçao. Esse nível é chamado de nível de Fermi (E_f). O nível de Fermi nao corresponde necessariamente a um nível real, podendo se localizar no meio da banda proibida (falha) onde nao há orbitais. É um parâmetro de suma importância na caracterizaçao de materiais, pois, juntamente com a estrutura, possibilita prever seu comportamento elétrico. A banda localizada imediatamente acima do nível de Fermi é chamada de Banda de Conduçao (BC ou Banda Vazia), e por se constituir de orbitais de maior energia, apresenta níveis de baixa probabilidade de ocupaçao. A banda localizada imediatamente abaixo do nível de Fermi é chamada de Banda de Valência (BV ou Banda Cheia) e, por constituir-se de orbitais de menor energia, encontra maior probabilidade de ocupaçao. Em sólidos, os elétrons apenas podem atuar como transportadores de carga quando há estados eletrônicos vacantes na banda, uma circunstância plausível somente quando há promoçao de parte dos elétrons da banda de valência para a banda de conduçao.

Em metais, como as bandas sao largas e os níveis mais altos da BV sao energeticamente comparáveis aos mais baixos da BC, observa-se a sobreposiçao de bandas com o E_f localizado nessa regiao (Figura 2). Os elétrons da BV conseguem atingir a BC como estados termicamente acessíveis, de modo que à temperatura ambiente (298,15 K), a BC encontra-se parcialmente ocupada e a BV nao completamente preenchida. Assim, pela açao de um campo elétrico, é possível transportar carga. Em isolantes, E_f encontra-se dentro de um Band Gap largo (Figura 2), muito distante das bordas de qualquer uma das bandas e de qualquer estado com capacidade de transporte de carga. Os elétrons permanecem isolados na banda de valência cheia, nao apresentando estados que permitam mobilidade frente a um campo elétrico. Em semicondutores, a distância da BC para a BV é pequena (Figura 2 - Band Gap < 4 eV), sendo que o nível de Fermi se encontra aproximadamente no centro do Band Gap (E_f = ½ Eg). Desse modo, alguns níveis inferiores da Banda de Conduçao sao termicamente acessíveis para elétrons no topo da Banda de Valência à temperatura ambiente (≈ 298,15 K) que, após a excitaçao, transformam-se em transportadores de carga (e^-_BC), assim como os estados vacantes deixados na BV, chamados de lacunas (h⁺_BV), que conferem maior grau de liberdade ao restante de elétrons ali contidos. Esses níveis de transportadores de carga formados puramente por excitaçao térmica sao conhecidos como níveis intrínsecos.

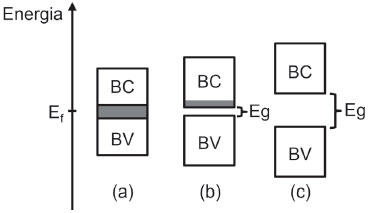Figura 2. Representaçao esquemática de diagramas de bandas típicos para (a) condutores eletrônicos (p. ex. metais), (b) semicondutores e (c) isolantes. E_g: Band Gap; BV: banda de valência; BC: banda de conduçao; E_f: nível de Fermi a 298,15 K; Sombreamento cinza aponta a presença de estados ocupados com capacidade de transporte de carga

A formaçao de transportadores de carga (e^-_BC/h⁺_BV) em semicondutores lhes confere condutividade superior a de um isolante nas mesmas condiçoes. Entretanto, a condutividade de ambos os materiais apresenta uma dependência com a temperatura do tipo de Arrhenius,¹³ à qual se aplica o valor de gap de energia entre o fundo da banda de conduçao (E_BC) e o nível de Fermi (E_f) em analogia à Energia de Ativaçao (E_a = E_BC - E_f ≈ Eg/2):

em que σ é a condutividade em S cm, σ₀ é um fator pré-exponencial, Eg é a energia de separaçao entre a borda das bandas (Band Gap), k é a constante de Boltzmann e T é a temperatura absoluta em Kelvin. Qualitativamente, é possível concluir que o gap de energia entre o fundo da BC e o nível de Fermi (E_BC - E_f) é um parâmetro determinante da condutividade de um semicondutor intrínseco ou isolante, qualquer que seja a temperatura de estudo. Inclusive, esse pode ser o principal parâmetro de diferenciaçao, uma vez que isolantes até podem ser considerados semicondutores em temperaturas elevadas e, em zero Kelvin, todo semicondutor será um isolante.

Um novo rearranjo da Eq. 2, apresentado abaixo na Eq. 3, explicita a relaçao de decaimento exponencial do produto das concentraçoes dos transportadores intrínsecos (lacunas e elétrons) com a energia de Band Gap (Eg), atenuado pela energia térmica do sistema (kT) e de acordo com um fator pré-exponencial correspondente à densidade efetiva de estados nas bordas das bandas de conduçao e valência, N_c e N_v respectivamente:¹⁴

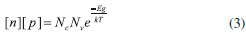
Os valores de densidade de estados N_c e N_v costumam ser da ordem de 10¹⁹ cm^-3, de modo que quando a excitaçao térmica é o único mecanismo de geraçao de transportadores de carga, [n] = [p] e a concentraçao total de transportadores decai fortemente com o aumento da energia de Band Gap para uma dada temperatura. A exemplo disso, em temperatura ambiente (298,15 K), o produto kT é de 0,0257 eV, o que para os valores propostos acima indica a classificaçao de isolante para materiais com Eg a partir de 0,5 eV.¹⁴ Sendo assim, nao é surpreendente que à temperatura ambiente semicondutores intrínsecos apresentem um número limitado de aplicaçoes por sua baixa condutividade. Ao determinar na prática¹⁵ a populaçao de elétrons excitados em semicondutores intrínsecos típicos, como o Si ou o GaAs, é possível encontrar valores no intervalo entre 10⁶ e 10¹⁰ cm^-3, o que se compara desfavoravelmente ao número de transportadores livres disponíveis em metais, que chega a ordem de 10²⁸ cm^-3. Portanto, o aumento de condutividade do material é essencial, havendo algumas estratégias para isso. A mais comum é a dopagem.

A dopagem consiste na adiçao (por difusao em fornos ou por implantaçao de íons) de uma concentraçao muito baixa de átomos com um elétron de valência a mais ou a menos do que o elemento do qual é constituído o semicondutor (p. ex., respectivamente, P ou B para o Si) em sua rede cristalina, havendo a substituiçao. Semicondutores dopados com elementos com elétrons a mais na camada de valência sao chamados de semicondutores extrínsecos do tipo n, enquanto que os dopados com elementos com um déficit de elétrons sao chamados semicondutores extrínsecos tipo p.¹⁵

Nos semicondutores do tipo n, como os elétrons excedentes encontram-se fracamente ligados aos seus átomos dopantes parentais (energia de ligaçao da ordem de décimos de eV), eles geralmente sao facilmente ionizados e promovidos para a Banda de Conduçao, sendo representados em um diagrama de bandas na forma de uma linha pontilhada ou uma sub-banda doadora localizada cerca de 0,1 eV abaixo da BC (Figura 3). Isso nao significa que estados eletrônicos acessíveis foram gerados no meio do Band Gap, mas sim aponta para a existência de elétrons que podem ser muito facilmente levados a estados que permitem transporte de carga. É importante ressaltar que os transportadores de carga majoritários aqui sao os elétrons (e^-). Nos semicondutores do tipo p, a inserçao de níveis aceptores de elétrons pela introduçao de átomos com um elétron de valência a menos induz ao transporte de carga majoritário por lacunas (h⁺), de modo que esses níveis sao representados por uma sub-banda receptora logo acima da banda de valência¹⁵ (Figura 3).

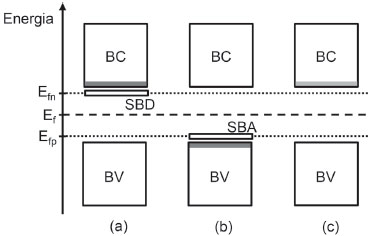Figura 3. Representaçao esquemática de um diagrama de bandas para semicondutores extrínsecos (a) do tipo n e (b) p em comparaçao a (c) um intrínseco. BC: banda de conduçao; BV: banda de valência; E_f: nível de Fermi do semicondutor intrínseco; E_fn: nível de Fermi do semicondutor n; E_fp: nível de Fermi do semicondutor p; SBD: sub-banda doadora; SBA: sub-banda aceptora. Diagrama esquemático representado à temperatura ambiente (≈ 298,15 K). Sombreamento cinza gradual apontando a presença de níveis acessíveis para transporte de carga

Como representado na Figura 3, a posiçao do nível de Fermi (E_f) observada no semicondutor intrínseco é deslocado de acordo com o tipo de dopagem. A temperatura ambiente, o nível de Fermi encontra-se aproximadamente na metade do Band Gap. Mantendo-se a temperatura constante, o nível de Fermi se desloca linearmente em funçao do logaritmo da densidade de dopagem seguindo no sentido de valores mais próximos da borda da banda de conduçao para o tipo n e da de valência para o tipo p.^14-16 A distância do E_f à borda da banda adjacente é um fator importante para determinar a concentraçao do transportador majoritário ([n] ou [p]), como mostrado a seguir nas Eqs. 4 e 5, deduzidas a partir da Eq. 3.

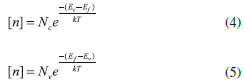
Do ponto de vista matemático, ao elevar a concentraçao de um dos transportadores de carga através da dopagem n ou p ([n] ou [p]), os termos que se alteram na igualdade para acompanhar esse aumento sao as diferenças (E_c - E_f) ou (E_f - E_v) e, quando essa diferença se aproxima de 0 (mais precisamente cerca de 0,1 eV referente à energia de ionizaçao/associaçao dos elétrons com os átomos/íons dopantes), a concentraçao de transportadores se iguala à densidade de estados nas bordas da banda mais próxima, chegando ao limite máximo de condutividade do material como um semicondutor. Por isso, raramente se excede o limite de concentraçao de dopantes da ordem de 10¹⁹ cm^-3. Como a energia de ativaçao dos elétrons aos níveis que permitem o transporte de carga é muito baixa, no estado de equilíbrio termodinâmico, a concentraçao do transportador majoritário é praticamente igual à concentraçao do dopante em temperatura ambiente. Assim, ao ultrapassar o limite de dopagem citado, o semicondutor inicia a chamada degeneraçao, em que o nível de Fermi adentra a banda adjacente e o material se torna um quase-condutor, perdendo suas características.¹⁴ Essa estratégia é especificamente utilizada em aplicaçoes em que se deseja estipular contato ôhmico (nao-retificado) entre um condutor e um semicondutor, como em contatos elétricos de dispositivos eletrônicos.

É importante ressaltar que, mesmo sob qualquer um dos tipos de dopagem, ainda há transportadores provindos da semiconduçao intrínseca, porém, com uma contribuiçao muito baixa frente aos transportadores introduzidos pela impureza dopante em temperatura ambiente, principalmente por parte dos transportadores de carga inversa à da dopagem (p. ex., h⁺_BV em dopagem n).

A contribuiçao dos transportadores intrínsecos para a condutividade do material dopado pode aumentar com a temperatura do sistema e até se tornar majoritária em casos extremos, deslocando o nível de Fermi das vizinhanças da banda novamente para o centro do Band Gap^15,16 (Figura 3). Isso ocorre pela transiçao do mecanismo gerador de transportadores majoritários, que passa de um controle pelo grau de ionizaçao dos dopantes a baixas temperaturas (ambiente) à transferência térmica dos transportadores da BV à BC em elevadas temperaturas.¹⁶

TRANSIÇOES ELETRONICAS ENTRE BANDAS

Como mencionado anteriormente, em um semicondutor a banda de conduçao (BC) encontra-se predominantemente vazia, enquanto a banda de valência (BV) encontra-se cheia. Além da estratégia apontada de dopagem, a condutividade deste tipo de material pode ser aumentada através de uma perturbaçao externa, como, por exemplo, a absorçao de fótons com energia igual ou superior ao Band Gap para a promoçao de elétrons à BC, deixando lacunas na BV.¹⁴

A lacuna é uma quasipartícula que pode, assim como o elétron, ser descrita em termos de carga (e⁺), spin (s = ½) e massa efetiva (m_ef). A massa efetiva é uma grandeza para contabilizaçao do efeito da interaçao da partícula com a rede cristalina na sua mobilidade. Valores superiores à massa do elétron livre no vácuo representam partículas com mobilidade retardada pela interaçao com a rede, enquanto valores inferiores representam um incremento de mobilidade. Paralelamente, a massa efetiva também pode ser um representativo da extensao espacial da funçao de onda da partícula no material, de modo que massas efetivas menores representam alta deslocalizaçao do transportador.¹⁷

O par elétron/lacuna (e^-_BC/h⁺_BV), formado por excitaçao eletrônica, interage por força de Coulomb devido às respectivas cargas opostas, podendo ser tratado unitariamente como uma quasipartícula: o éxciton.¹⁸ A formaçao do éxciton envolve uma quantidade mínima de energia (Eg), assim como também requer a conservaçao de momento (Figura 4).^18,19

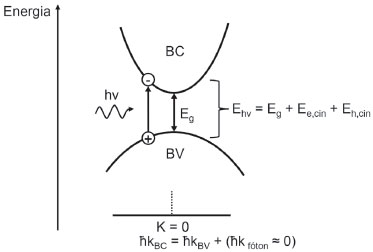Figura 4. Representaçao esquemática da transiçao eletrônica direta de um elétron da banda de valência (BV) à banda de conduçao (BC) em um semicondutor de Band Gap direto. E_hν = energia do fóton; E_g = Band Gap; E_e,cin = energia cinética do elétron na banda de conduçao; E_h,cin = energia cinética da lacuna na banda de valência; ћ constante reduzida de Planck (ћ = h/2π); k_BC, k_BV e k_fóton = vetor de onda do elétron na banda de conduçao, da lacuna na banda de valência e do fóton. Adaptado da tese de Groeneveld²⁰

A energia quantizada do fóton pode caracterizar o éxciton formado em "quente" ou "frio", sendo que fótons com energia superior ao Band Gap induzem a excitaçao do elétron a orbitais acima da borda de fundo da BC, como também geram lacunas mais profundas abaixo da borda de topo da BV, conferindo aos elétrons mobilidade interorbital nas bandas que se caracteriza como a energia cinética do transportador fotogerado (E_e,cin ou E_h,cin da Figura 4). A transiçao também deve ser acompanhada da manutençao do momento do sistema e, como o fóton apresenta momento p desprezível (≈ 10^-28), o vetor de onda k da BC deve coincidir com o da BV para que seja observada uma transiçao direta.^18,19 Daí deriva-se o conceito de Band Gap direto e indireto.^15,21

O Band Gap direto é aquele em que o vetor de onda do nível mais alto da BV coincide com o vetor de onda do nível mais baixo da BC, permitindo a transiçao direta apenas pela absorçao de fótons (quando satisfeitas as regras ópticas de permissao de transiçao). Quando os níveis mencionados das bandas nao coincidem no mesmo momento, o processo de fotoexcitaçao depende também da interaçao do elétron com um fônon (quantum de vibraçao da rede cristalina) para transferência de momento, reduzindo a probabilidade de ocorrência do fenômeno.^15,21 Em termos práticos, o coeficiente de absorçao de semicondutores com Band Gap indireto apresenta ganhos menos acentuados com o aumento da energia dos fótons para fotoexcitaçao e exigem, mesmo para comprimentos de onda consideravelmente menores do que o equivalente ao Band Gap, espessuras de filme maiores para um bom aproveitamento da radiaçao incidente.¹⁴

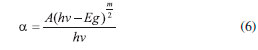
Na Eq. 6, α representa o coeficiente de absorçao, A uma constante, m = 1 para uma transiçao de Band Gap direta, m = 4 para transiçao de Band Gap indireta, h é a constante de Planck e ν é a frequência da radiaçao incidente.

Como anteriormente mencionado, o excesso de energia de um fóton em relaçao ao Band Gap do material pode caracterizar a formaçao de um éxciton quente, em que os elétrons e lacunas ocupam estados excitados da BC e BV, respectivamente. Neste caso, ambos tendem a relaxar para que o éxciton decaia para o seu estado fundamental através de etapas rápidas de relaxaçao intrabanda nao-radiativas, liberando o excesso de energia na forma de calor.^17,22 Como essas transiçoes nao sao restritas por regras de seleçao, elas ocorrem em intervalos muito curtos (< 1 ps), seja pelo acoplamento à um fônon de energia compatível ou pela transferência de energia entre transportadores de carga pelo espalhamento Auger.^22,23

Uma vez que o éxciton tenha atingido o estado fundamental, qualquer relaxaçao adicional deve ocorrer pela recombinaçao do par e^-_BC/h⁺_BV, havendo o retorno do elétron da BC para a BV. A energia relativa a essa transiçao (igualmente sujeita às regras de seleçao como a excitaçao) pode ser liberada radiativamente (com emissao de fóton) ou por processo nao-radiativo.¹⁹

A emissao radiativa pode ocorrer sob influência de gatilho de uma frequência ressonante à transiçao eletrônica de retorno, a chamada emissao estimulada, comum na emissao de radiaçao coerente em LASERs; ou ainda pode ocorrer de modo espontâneo, mediante combinaçao linear dos orbitais do estado fundamental e excitado por flutuaçoes de vácuo ou modos de vácuo, apresentando dependência com a amplitude de momento de dipolo da transiçao, com a frequência da radiaçao de excitaçao e, principalmente, com a densidade de modos ópticos acoplados à transiçao de retorno.¹⁷

A recombinaçao nao-radiativa geralmente está condicionada à presença de defeitos ou impurezas na composiçao do semicondutor, uma vez que requer o acoplamento com um número muito elevado de fônons. Por outro lado, defeitos na rede cristalina ou ainda alguns estados presentes na superfície do semicondutor sao capazes de gerar os chamados traps, os quais reduzem a sobreposiçao de fases das funçoes de onda dos transportadores entre si, induzindo ao quenching da emissao e viabilizando a relaxaçao nao-radiativa por acoplamento com vibraçoes locais (fônons). É importante ressaltar que a recombinaçao radiativa, mesmo com menor probabilidade, ainda pode ocorrer com o éxciton em trap, porém a energia do fóton emitido é mais baixa (λ maior) e o rendimento quântico do processo é bastante limitado.¹⁷ Um último caso de recombinaçao nao-radiativa própria de Quantum Dots (d < 6 nm) é a transferência da energia do éxciton entre diferentes partículas,²⁴ de modo que um QD doador sofre uma recombinaçao e através de uma interaçao dipolo-dipolo é capaz de induzir um éxciton em um QD aceptor. Abaixo seguem sumarizados os diferentes tipos de recombinaçao discutidos (Figura 5).

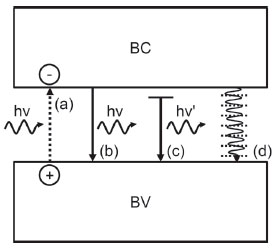Figura 5. Ilustraçao esquemática apresentando os diferentes tipos de recombinaçao de transportadores de cargas vista em semicondutores: (a) excitaçao; (b) recombinaçao radiativa (c) recombinaçao radiativa assistida por um defeito ou estado superficial (v>v'); (d) recombinaçao nao-radiativa. Adaptado da tese de Groeneveld²⁰

Um dos principais supressores da recombinaçao, mesmo na ausência de aceptores eletrônicos, é o fenômeno anteriormente mencionado de trapping. Um trap (armadilha) é uma regiao espacial do cristal em que o transportador de carga (e^-_BC ou h⁺_BV em semicondutores) se move para ganho de energia livre do sistema, atingindo um mínimo de potencial eletroquímico. Há uma boa relaçao de energia a um trap que, se muito profundo, pode comprometer o potencial de oxidaçao e/ou reduçao de lacunas e elétrons, respectivamente, podendo também inibir o transporte ou a transferência de carga. Se muito raso, os efeitos de supressao de recombinaçao sao bastante reduzidos, elevando a probabilidade de emissao de fótons (Figura 5c) ou calor e limitando a energia efetiva acumulada nos estados para os processos fotocatalíticos. O resultado disso é a inibiçao cinética das reaçoes químicas adjacentes.²⁵ O fenômeno de trapping costuma ser bastante benéfico quando localizado na superfície do material, regiao onde há interesse em suprimir a recombinaçao e elevar a localizaçao dos transportadores na interface para captura por espécies químicas (reaçoes interfaciais). Muitos sao os parâmetros que podem regular os estados de trap superficiais, dentre eles a estrutura local (defeitos), a presença de adsorbatos e a aplicaçao de potencial por sistemas eletroquímicos.^25,26

Igualmente aos traps, o fenômeno de space-charge layer ou, mais precisamente, a sua modulaçao pela aplicaçao de potencial por sistemas eletroquímicos, é capaz de suprimir eficientemente a recombinaçao e^-_BC/h⁺_BV pela separaçao espacial desses transportadores. Ao operar em células fotoeletroquímicas, há sempre a formaçao de uma interface semicondutor/eletrólito, regiao onde se faz mais relevante a supressao da recombinaçao para obtençao de maior número de transportadores e, consequentemente, maiores velocidades de transferência de carga com o eletrólito. Segue o tratamento desse modelo importante.

O MODELO DE SPACE-CHARGE LAYER

A space-charge layer (SCL) é um fenômeno essencial para a separaçao de cargas em interfaces de semicondutores, além de representar o principal modelo para caracterizaçao do comportamento de retificaçao em junçoes p-n e eletrólito/semicondutor. Essencialmente ela apresenta quatro modelos de conformaçao (Figura 6).

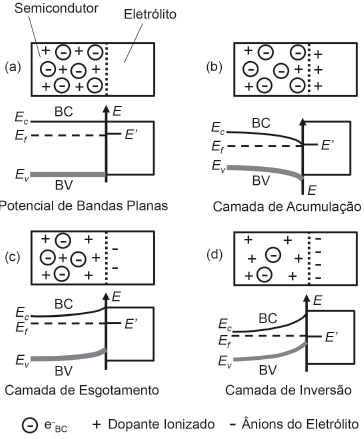Figura 6. Diagrama esquemático de visao pictorial do modelo de space-charge layer desenvolvido na interface de um semicondutor do tipo n com um eletrólito de suporte contendo espécies aceptoras dos elétrons proveniente da sua banda de conduçao (e^-_BC) e os respectivos diagramas de bandas à temperatura ambiente (298,15 K) de acordo com o caso: (a) potencial de bandas plano; (b) camada de acumulaçao; (c) camada de esgotamento; (d) camada de inversao. Todos os sistemas foram representados em equilíbrio (E_f = E'). BC: banda de conduçao; BV: banda de valência; E': potencial formal do par redox da espécie eletroativa no eletrólito; E_c: potencial da banda de conduçao; E_v: potencial da banda de valência. Adaptado do trabalho de insight de Grätzel²⁷

Na Figura 6, aplicou-se como exemplo a interface de um semicondutor do tipo n (dopado) com um suposto eletrólito de suporte contendo uma espécie aceptora (eletroativa) de potencial redox formal E'.²⁷ Quando ambos sao colocados em contato, uma corrente flui através da junçao até que o equilíbrio seja atingido no momento em que o nível de Fermi do semicondutor (E_f) e o potencial redox da espécie aceptora no eletrólito (E') se igualam. E' é simplesmente um potencial Nernstiano e representa "o nível de Fermi" do eletrólito em uma analogia em que o estado ocupado é representado pela espécie reduzida e o estado vacante pela espécie oxidada. A velocidade com que o equilíbrio é alcançado depende da velocidade de transferência de carga do material e costuma ser mais lenta para semicondutores do que para metais.¹⁴ Na interface do eletrólito, o carregamento interfacial se constitui na dupla camada elétrica, composta pela zona compacta (modelo de Helmholtz) e pela zona difusa (modelo de Gouy-Chapman). Do lado do semicondutor na junçao, o arqueamento de banda (Band Bending) depende da posiçao do nível de Fermi, de modo que se ele se igualar ao potencial de banda plana (E_f = E' = E_FB), nao se observa a formaçao de space-charge layer e, portanto, o potencial relativo às bandas permanece plano desde a regiao de bulk até a interface (Flat Band Potential - Figura 6a).²⁷

em que "E_B" é o potencial (ou energia) de arqueamento de banda (Band Bending), "E_f" é o potencial relativo ao nível de Fermi, E' é o potencial formal desenvolvido pela espécie eletroativa na interface. Caso haja acúmulo de elétrons pelo lado do semicondutor na interface e a induçao de carregamento positivo na dupla-camada elétrica, observa-se a formaçao da camada de acumulaçao (Figura 6b). Por outro lado, se os elétrons forem esgotados na interface do semicondutor, cargas positivas imóveis provindas dos estados doadores ionizados do dopante (semicondutor tipo n) sao deixadas para trás, havendo a formaçao da camada de esgotamento (Figura 6c) com carregamento negativo da dupla camada elétrica. Caso o esgotamento de elétrons prossiga a uma extensao com concentraçao inferior ao nível intrínseco, a superfície adquire caráter p (excesso de cátions imóveis do dopante) frente ao bulk do material, sendo possível a formaçao da camada de inversao (Figura 6d).²⁷

O potencial de banda plana (E_FB) é um parâmetro importante para ser determinado por auxiliar na determinaçao do nível de Fermi e, consequentemente, no potencial da banda de conduçao.²⁷ Sua determinaçao pode ser feita pela medida da capacitância da junçao semicondutor-eletrólito em potenciais crescentes para polarizaçao reversa da junçao, na qual o modelo de Mott-Schottky se aplica.²⁸

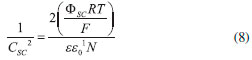
em que C_SC é a capacitância medida, Φ_SC é o decaimento de potencial observado na space-charge layer (Φ_SC = V - V_FB), R é a constante universal dos gases (8,314 J K^-1 mol^-1), T a temperatura absoluta em Kelvin, F a constante de Faraday (96485 C mol^-1), ε a constante dielétrica do semicondutor, ε₀ a permissividade no vácuo e ¹N é a concentraçao de dopante ionizado. Há tanto a capacitância da space-charge layer (C_SCL) como da camada de Helmholtz (C_H) a serem consideradas, sendo que ambas podem ser ponderadas como em série, em analogia a circuitos eletrônicos. No regime de esgotamento (Figura 6c) C_SCL < C_H e, portanto, a capacitância medida é predominantemente característica da space-charge layer. Ao plotar os valores do recíproco do quadrado da capacitância com o potencial de polarizaçao reversa aplicado, obtém-se uma relaçao linear, a qual, ao ser extrapolada ao ponto 1/C_SC² = 0, revela o valor de potencial de banda plana (E_FB).^27,29 Como nesse ponto nulo do recíproco do quadrado da capacitância em que o E_FB é atingido, também E_B = 0 (banda plana), o nível de Fermi se iguala ao potencial redox da espécie eletroativa em soluçao e corresponde, aproximadamente, ao potencial da banda de conduçao para semicondutores n suficientemente dopados a 298,15 K (Eq. 7). Por isso, o potencial de banda plana exprime, para semicondutores n, o poder redutor dos elétrons na banda de conduçao e permite avaliar termodinamicamente a viabilidade de reaçoes de reduçao no material de acordo com o potencial do par redox (E') em soluçao. Conhecendo-se a energia de Band Gap (Eg), é possível igualmente determinar o potencial das lacunas na banda de valência (E_BV = E_BC + Eg) e, através da comparaçao com o potencial redox formal de solutos intencionados, estimar seu poder oxidante.²⁸ A junçao dos dados de potencial das bandas de valência e conduçao juntamente ao Band Gap gera um diagrama de posiçao de bandas (Figura 7), extremamente útil para a seleçao do material mais adequado para as aplicaçoes químicas desejadas.²⁷

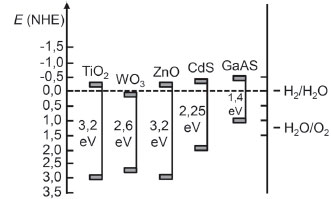Figura 7. Diagrama de posiçao de bandas para alguns exemplos de semicondutores apresentando as respectivas posiçoes em V frente ao eletrodo normal de hidrogênio (NHE) em pH = 1, o Band Gap de cada material (eV) e a posiçao do potencial padrao (vs. NHE) de um exemplo de reaçoes redox para a decomposiçao da água em hidrogênio e oxigênio. Adaptado do trabalho de insight de Grätzel²⁷

Semicondutores com potencial da banda de valência alto (p. ex. TiO₂, WO₃ e ZnO) apresentam lacunas com elevado poder oxidante, além de boa estabilidade à corrosao e fotocorrosao. Mas, geralmente, esses semicondutores apresentam Band Gap dentro da faixa UV (Eg = 3,2 eV ≈ 390 nm), o que reduz a eficiência de aplicaçoes com aproveitamento do espectro solar como fonte de radiaçao. Quanto maior for o poder redutor e oxidante simultaneamente de um semicondutor, mais distantes sao suas bandas, maior o seu caráter isolante e menores os comprimentos de onda requeridos para promover sua fotoexcitaçao.

Outro parâmetro importante é o potencial de arqueamento de bandas (E_B) que corresponde ao fotopotencial de circuito aberto.²⁷ Para a reaçao apontada na Figura 7 de decomposiçao da água, o par redox do eletrólito para um fotoanodo é o O₂/H₂O, com potencial de 1,23 V vs. NHE. Para que a eletrólise da água seja realizada puramente pela açao da luz incidente, E_B deve exceder 1,23 V, de modo que a banda de conduçao (E_BC ≈ E_f) se situe no mínimo 1,23 V abaixo do par O₂/H₂O e, portanto, abaixo do par H⁺/H₂.²⁸ Caso essa circunstância nao possa ser atingida apenas pela açao da luz, é possível ainda aplicar um potencial em um suposto substrato condutor utilizado como leito do filme semicondutor. Daí consolida-se um dos papeis do potencial de polarizaçao (E_bias) nesses eletrodos: caso E_B (fotopotencial) seja menor do que o potencial do par redox do eletrólito (mais a sobretensao), E_bias pode completar a demanda energética restante.²⁸ No exemplo da eletrólise da água sob irradiaçao em fotoânodos de TiO₂, a luz permite eletrolisar a água em aproximadamente +0,2 V vs. NHE,²⁸ mais de 1,0 V abaixo do potencial termodinâmico exigido, mas ainda com a necessidade do complemento elétrico para a efetivaçao da reaçao. Este é considerado, conceitualmente, o verdadeiro efeito fotoeletrocatalítico, em que a luz é capaz de reduzir (ou extinguir) a tensao termodinâmica e a sobretensao elétricas exigidas para a efetivaçao de uma reaçao, ainda com cinética mensurável.

Um segundo papel da aplicaçao de potencial de polarizaçao ao substrato condutor consiste em influenciar a cinética da reaçao interfacial através do aumento da disponibilidade de um dos transportadores na interface. Nessa funçao, a velocidade e até a natureza do processo Faradaico (anódico ou catódico) tornam-se dependentes do potencial aplicado (E_bias).¹⁴ Este efeito é totalmente explicado utilizando os modelos de space-charge layer apresentados na Figura 6. Por simplificaçao, inicialmente, o efeito do potencial será tratado na ausência de luz na forma de um processo eletroquímico no escuro. Em seguida, serao tratados os processos sob a incidência de luz.

MODULAÇAO DA SPACE-CHARGE LAYER

A aplicaçao de um potencial para polarizaçao do substrato afeta a posiçao das bordas das bandas de valência e conduçao e, de acordo com o seu arqueamento (band bending), observam-se as diferenças de natureza das reaçoes interfaciais. Primeiramente, ao aplicar um potencial constante pode-se observar a formaçao de três regioes com potencial elétrico variável: a space-chage layer na interface do semicondutor, a zona compacta e a difusa da dupla camada elétrica. Ao operar com concentraçoes suficientemente elevadas de eletrólito de suporte (> 0,1 mol L^-1), a espessura da zona difusa se torna muito baixa (≈ 10 Angstroms) e o potencial que decai através dela pode ser negligenciado, permitindo assumir que todo o potencial deve decair somente através da space-charge layer e da camada de Helmholtz. De acordo com o princípio da soma de capacitores em séries (1/C_T = 1/C_SCL + 1/C_H), o lado da interface que apresenta o menor número de transportadores de carga sofre as maiores mudanças com a modulaçao de potencial e, de acordo com os níveis típicos de dopagem (no intervalo entre 10¹⁵ e 10¹⁹ cm^-3), o semicondutor apresenta algumas ordens de grandeza a menos de transportadores do que eletrólitos fortes em meio aquoso (≈ 10²⁰ cm^-3 para concentraçao 0,1 mol L^-1 de um sal de estequiometria 1:1). Portanto, a modulaçao de potencial afeta predominantemente a distribuiçao de carga interfacial do semicondutor e, consequentemente, o arqueamento de bandas.¹⁴

A diferença de potencial observada na space-charge layer é produto da distribuiçao desigual dos transportadores majoritários (elétrons ou lacunas), como também dos sítios carregados provindos dos dopantes, observando-se uma variaçao suave do potencial através de sua extensao. O arqueamento se deve à diferença gradual de energia dos elétrons em regioes de potencial elétrico variável, o que confere um caráter positivo ou negativo de curvatura à borda das bandas. A magnitude do arqueamento é igual ao decaimento de potencial através da SCL e uma consequência importante disso é a perturbaçao das concentraçoes dos elétrons e lacunas na interface frente ao bulk. O nível de Fermi permanece constante sob essa circunstância e o arqueamento induz a uma mudança na distância relativa das bordas das bandas ao E_f, o que, de acordo com as Eqs. 4 e 5, leva ao acúmulo de um tipo de transportador e o esgotamento daquele de carga oposta. Para o caso de arqueamento positivo, elétrons tendem ao esgotamento na interface e lacunas ao acúmulo; para arqueamento negativo, elétrons tendem ao acúmulo na interface enquanto lacunas ao esgotamento.¹⁴

Para a determinaçao do arqueamento das bandas, um parâmetro novamente importante é o potencial de banda plana (E_FB), além do tipo de semicondutor utilizado. Em um semicondutor intrínseco (Figura 8), a aplicaçao de potencial acima dele (E_bias > E_FB) gera um arqueamento de bandas positivo, com afastamento da Banda de Conduçao e aproximaçao da Banda de Valência ao nível de Fermi, indício de leve acúmulo de lacunas (h⁺_BV) na interface. A aplicaçao de potencial abaixo dele (E_bias < E_FB) leva ao arqueamento negativo, aproximando a Banda de Conduçao e afastando a Banda de Valência do nível de Fermi, o que significa um leve acúmulo de elétrons na interface (Figura 8). Esse processo leva à separaçao espacial de cargas, acumulando um tipo de transportador na interface do eletrodo de trabalho.

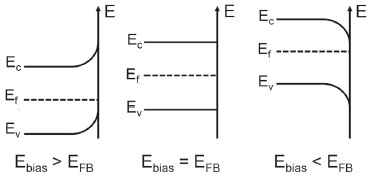Figura 8. Fenômeno de arqueamento de bandas (band bending) para um semicondutor intrínseco sob diferentes condiçoes de polarizaçao pela aplicaçao de um potencial externo no substrato condutor. E_bias: potencial de polarizaçao do substrato; E_FB: potencial de banda plana; E_f: nível de Fermi; E_V: potencial da borda da banda de valência; E_C: potencial da borda da banda de conduçao. Adaptado da obra FINKLEA¹⁴

De fato, como o nível de Fermi em um semicondutor intrínseco encontra-se no meio do Band Gap, a polarizaçao até pode induzir ao arqueamento e leve acúmulo de carga na interface, mas mesmo quando E_bias >> E_FB ou E_bias << E_FB, todos os efeitos práticos sao dependentes do Band Gap (Eg) e, portanto, dos níveis intrínsecos de transportadores que costumam ser baixos para Eg > 0,5 eV. Entretanto, caso o semicondutor intrínseco seja livre de estados superficiais, absolutamente todo o potencial aplicado diferente do E_FB é aproveitado no fenômeno de arqueamento de bandas e essa condiçao interessante pode ser extrapolada a semicondutores extrínsecos p e n.¹⁴

Em um semicondutor extrínseco, a magnitude do potencial aplicado é de suma importância para a caracterizaçao do modelo de SCL desenvolvido. Ao polarizar levemente o substrato com E_bias > E_FB em um semicondutor n, ambas as bandas sofrem um arqueamento positivo de modo que a BC se distancia do E_f e a BV se aproxima. Mas, como o nível de Fermi ainda se encontra bastante distante da BV mesmo após o arqueamento, o que realmente se observa é o esgotamento de transportadores na interface, formando a camada de esgotamento (Figura 6C). O mesmo pode-se dizer de um semicondutor p levemente polarizado negativamente (E_bias < E_FB), com a diferença de que se observa um arqueamento negativo com afastamento da BV do E_f e leve aproximaçao da BC.¹⁴ Sob esse modelo de esgotamento, além de ser possível a determinaçao do E_FB através do modelo de Mott-Schottky como anteriormente descrito (Eq. 8) é possível estimar a espessura (W) da SCL:

em que N_d é o nível de dopante, ε é a constante dielétrica na direçao normal à superfície, ε₀ é a permissividade do vácuo, E_bias é o potencial externo de polarizaçao, E_FB é o potencial de banda plana e q é o valor de carga elementar. Esse equacionamento assume que (i) todos os níveis aceptores ou doadores do dopante estao ionizados; (ii) uniformemente distribuídos e imóveis; (iii) o nível de Fermi (E_f) encontra-se a mais de 2 kT (0,05 eV) de distância da banda mais próxima (semicondutor nao-degenerado); e (iv) a intensidade de polarizaçao nao fez a SCL atingir o modelo de inversao. Essas consideraçoes mostram a importância do modelo de esgotamento (Figura 6C) para a determinaçao da espessura da SCL, bem como para a determinaçao do E_FB. Nele, a quantidade de transportadores na interface do semicondutor é muito menor do que na interface do eletrólito e até do que os níveis intrínsecos. Desse modo, o potencial aplicado nao afeta o decaimento de potencial na camada de Helmholtz.¹⁴ Para que isso aconteça, a concentraçao de transportadores de carga majoritários do semicondutor deve se equiparar à de íons do eletrólito, algo possível com a aplicaçao do potencial suficientemente abaixo do E_FB para semicondutores n ou suficientemente acima para semicondutores p, para além dos limites do modelo de camada de acumulaçao (Figura 6B).

Ao aplicar E_bias << E_FB ou E_bias >> E_FB para semicondutores tipo n e p, respectivamente, os transportadores majoritários do material inundam a interface, elevando a concentraçao de transportadores de carga a nível comparável ao de metais. O E_f adentra a banda adjacente e, portanto, a interface adota caráter de um semicondutor degenerado (quase-condutor). Nessa condiçao, o arqueamento de bandas costuma ser desconhecido e o potencial aplicado passa a controlar também o potencial interfacial das bandas (intersecçao com o eixo de energia e/ou potencial).¹⁴

A última consideraçao diz respeito à transiçao entre os modelos de esgotamento e inversao (Figura 6C e 6D). Como já explicado, ao se aplicar potencial acima do E_FB a qualquer semicondutor n, ou abaixo para semicondutores p, inicialmente, drena-se os transportadores majoritários da interface permanecendo apenas os estados ionizados e imóveis do dopante (átomos substituídos na rede cristalina do material) com carga oposta. Nessa circunstância diz-se que o eletrodo se encontra em estado de bloqueio, pois nao há concentraçao de transportadores suficiente para a conduçao de reaçoes faradáicas interfaciais. Contudo, ao se elevar a amplitude do potencial aplicado (ainda mais positivo para n e mais negativo para p), dois fenômenos diferentes podem ocorrer de acordo com a largura do Band Gap do material (Figura 9).

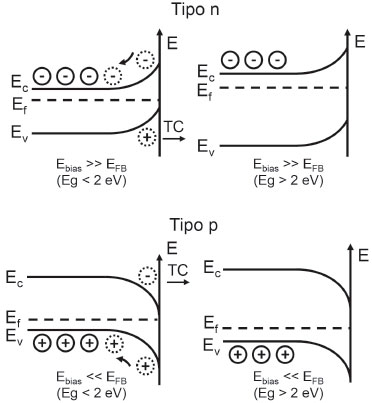Figura 9. Modulaçao da space-charge layer pela aplicaçao de potencial de polarizaçao reverso de amplitude além dos limites da camada de esgotamento, formando a camada de inversao para semicondutores com Band Gap abaixo de 2 eV e a camada de esgotamento profundo para semicondutores com Band Gap acima de 2 eV. E_bias: potencial de polarizaçao do substrato; E_FB: potencial de banda plana; E_f: nível de Fermi; E_C: potencial da borda da banda de conduçao; E_V: potencial da borda da banda de valência; E_g: Band Gap. TC: transferência de carga com o eletrólito interfacial. Adaptado da obra de FINKLEA¹⁴

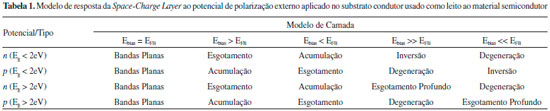
Caso Eg < 2 eV, além do estado de esgotamento, a elevaçao da amplitude faz o nível de Fermi se aproximar da banda inicialmente mais distante, que seria a banda de valência para um semicondutor n e a banda de conduçao para o tipo p, de modo a desenvolver o modelo de camada de inversao (Figura 6D). Para o tipo n a transferência de carga (TC) ocorre com a BV através dos níveis intrínsecos de lacunas (h⁺_BV), do mesmo modo que para o tipo p os processos faradáicos ocorrem pelos níveis intrínsecos de elétrons na BC (e^-_BC). Agora, se Eg > 2 eV, tanto para semicondutores n ou p, o aumento da amplitude do potencial aplicado frente a E_FB leva a space-charge layer a um estado de esgotamento profundo, já que o nível de transportadores intrínsecos é muito baixo e o eletrodo permanece no estado de bloqueio.¹⁴ As diferentes respostas de modulaçao da space-charge layer frente ao potencial de polarizaçao encontram-se sumarizadas na Tabela 1 a seguir.

Cabe analisar as circunstâncias também sob o prisma da irradiaçao da interface com fótons contendo energia igual ou superior ao Band Gap do semicondutor. O material dopado apresenta uma grande disparidade entre a concentraçao dos dois tipos de transportadores, sendo que ao ser irradiado para a geraçao de um éxciton (e^-_BC/h⁺_BV), pouca diferença se observa na concentraçao do transportador de carga majoritário, mas um grande aumento se observa para o transportador minoritário. Assim, para que o foto-efeito possa ser mais pronunciado, os transportadores fotogerados devem dominar a resposta do eletrodo, o que é possível através da polarizaçao do substrato para a geraçao de uma camada de esgotamento na interface irradiada (Figura 6C).¹⁴

Por exemplo, quando um semicondutor n é submetido (com o auxílio de um potenciostato) à polarizaçao positiva suficientemente acima do E_FB, a corrente no escuro é muito baixa devido ao efeito de bloqueio do eletrodo. Ao ser irradiado com comprimentos de onda abaixo do Band Gap, observa-se valores consideravelmente altos de fotocorrente devido á geraçao e disponibilizaçao de lacunas (h⁺_BV - transportador minoritário) na interface. Ao absorver luz e gerar o par e^-_BC/h⁺_BV na camada de esgotamento (Figura 6C), o campo elétrico da regiao separa os transportadores de modo que os elétrons migram ao bulk do cristal e as lacunas para a superfície. Mesmo quando o éxciton é formado fora da regiao da camada de esgotamento, considera-se que os transportadores difundem até a regiao do campo elétrico e, a partir daí, sao separados por migraçao. Esse é o principal mecanismo de separaçao espacial e supressao da recombinaçao em eletrodos de semicondutores extrínsecos. As lacunas na interface apresentam o poder oxidante relativo ao potencial da borda da banda de valência (E_BV) e sao capazes de oxidar quaisquer moléculas no estado reduzido com potencial formal inferior a ele no eletrólito, termodinamicamente falando. Para semicondutores com Band Gap largo, como é o caso do TiO₂, as lacunas sao capazes de oxidar a própria água, quando esse é o solvente do eletrólito. Os elétrons sao conduzidos até o substrato condutor e seguem por um circuito externo até o eletrodo auxiliar (intermediados, p.ex., pelo conversor corrente/tensao e amplificador do potenciostato), provendo a carga transferida em processos de reduçao.¹⁴

Agora focando nos processos anódicos, acometendo um eletrodo de trabalho constituído de semicondutor n sobre leito condutor, polarizado a um potencial acima do potencial de banda plana (E_bias > E_FB: Esgotamento - Figura 6C) e sob um fluxo de fótons (I₀), os efeitos da fotoexcitaçao e dos processos de injeçao de carga nas lacunas levam a um formato característico de voltamograma (Figura 10) que foi alvo de modelamento por um número elevado de autores.^30-36

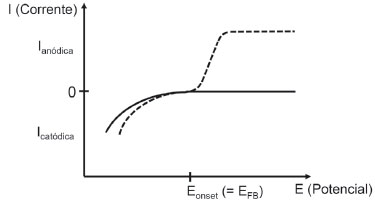Figura 10. Voltamogramas apresentando a dependência da corrente no escuro (--) e da fotocorrente (---) com a aplicaçao de potencial de polarizaçao crescente em eletrodo de semicondutor extrínseco n. E_onset: potencial no qual se inicia a medida de corrente anódica; E_FB: potencial de banda plana. Baseado em figura da obra de Finklea¹⁴

O formato do voltamograma depende dos seguintes fatores: a distribuiçao de energia dos fótons incidentes; o coeficiente de absorçao do semicondutor; a distância de difusao para as lacunas e elétrons fotogerados até atingir a SCL; e a taxa de recombinaçao e^-_BC/h⁺_BV. A condiçao de análise mais simples se dá quando os fótons sao absorvidos na própria camada de esgotamento, onde o campo elétrico permite condiçao de mínima recombinaçao entre os transportadores. Desconsiderando-se as limitaçoes de transporte de massa da espécie doadora de elétrons no eletrólito, a eficiência de fotoconversao de fótons em elétrons compondo a fotocorrente no filme se aproxima da unidade. A partir do momento em que a espessura da camada de esgotamento excede a penetrabilidade da radiaçao incidente no filme, a eficiência quântica da fotocorrente passa a nao mais depender do potencial, por isso nota-se o nivelamento da fotocorrente (Figura 10). Mas, à medida que o potencial se aproxima do E_FB, a espessura da camada de esgotamento diminui e limita a açao de supressao de recombinaçao do campo elétrico, levando ao encontro dos valores de fotocorrente e corrente no escuro. Em potenciais abaixo do E_FB, o eletrodo inicia o desenvolvimento de uma camada de acumulaçao e sai do estado de bloqueio, apresentando corrente pequena, pouco acima da corrente catódica no escuro. Geralmente sao valores baixos, uma vez que elétrons fotogerados pouco alteram a concentraçao de elétrons superficiais que sao fortemente controlados pelo nível de dopagem.¹⁴

Como anteriormente mencionado, muitos modelamentos foram criados para o transporte de carga sob o estímulo das condiçoes descritas. O modelo mais simples e útil (Eq. 12) foi derivado assumindo-se a inexistência de recombinaçao na space-charge layer, de tal modo que toda lacuna gerada dentro ou difundida para a camada de esgotamento gera fotocorrente e que a fotocorrente é somente governada pelo fluxo de lacunas para interface, desprezando-se limitaçoes cinéticas ou por transporte de solutos redutores.

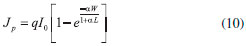
em que J_p é a densidade de fotocorrente; I₀ é fluxo de fótons incidente; W é a espessura da camada de esgotamento; L é o comprimento de difusao para os transportadores minoritários fotogerados; q é o valor de carga elementar; e α é o coeficiente de absorçao do material. O rearranjo da Eq. 10 com a Eq. 9 e a Eq. 6 leva a um modelo capaz de descrever completamente a camada de esgotamento em termos da resposta de fotocorrente-potencial e fotocorrente-comprimento de onda. Através da manipulaçao desenvolvida por Fornarini et al.,³⁷ é possível gerar relaçoes lineares simples que levam à determinaçao da energia do Band Gap e do tipo de transiçao (direto ou indireto) do semicondutor. Ao utilizar comprimentos de onda em que nao se observa uma forte absorçao por parte do semicondutor, p. ex. próximo à Eg, a luz é capaz de penetrar além da camada de esgotamento e, com αW e αL << 1 a Eq. 10 pode ser transformada na Eq. 11.

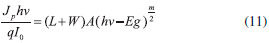
em que J_p é a densidade de fotocorrente; h é a constante de Planck; ν é a frequência da radiaçao incidente; q é o valor de carga fundamental; I₀ é o fluxo incidente de fótons, L é o comprimento de difusao para os transportadores minoritários fotogerados; W é a espessura da camada de esgotamento; A é uma constante; Eg é a energia de Band Gap; e m é o fator de transiçao do Band Gap (direto ou indireto). Ao plotar um gráfico de log [J_phν/qI₀] vs. Log (hν - Eg) sob potencial de polarizaçao constante, obtêm-se uma funçao de dependência linear com coeficiente angular igual a ½ (m = 1 para Band Gap direto) ou 2 (m = 4 para Band Gap indireto). Em outra abordagem, ao plotar [(J_phν/qI₀)]^2/m vs. hν obtêm-se o valor de Eg do semicondutor como intersecçao do eixo das ordenadas (coeficiente linear da funçao).

Na abordagem apresentada até aqui, pode-se perceber a importância dada aos modelos de space-charge layer para o desenvolvimento da ciência de semicondutores e, mais especificamente, a versatilidade dos ensaios fotoeletroquímicos na sua caracterizaçao a ponto de até propriedades fundamentais puramente ópticas poderem ser determinadas por eles. Com o desenvolvimento da ciência de nanomateriais, muitos desses conceitos fortemente sedimentados ao final da década de 1980 foram revistos vez que nao se aplicavam aos filmes compostos por nanopartículas. Dentre esses conceitos pode-se apontar a refutaçao inclusive do desenvolvimento de uma space-charge layer,³⁸ como será discutido no tópico a seguir.

FOTOEXCITAÇAO, SEPARAÇAO E TRANSPORTE DE CARGA EM FILMES NANOPARTICULADOS E SUA COMPARAÇAO COM ELETRODOS MONOCRISTALINOS DOPADOS

Nanopartículas muito pequenas podem ser vistas como moléculas gigantes ou clusters, contendo de algumas dezenas a milhares de átomos e orbitais atômicos (Build up Approach). Ou ainda, como pequenos cristais separados do bulk (Top-Down Approach).¹⁷ A classe de nanopartículas tendendo a diâmetros da ordem de algumas unidades de nanômetro (< 6 nm) é chamada de Quantum Dots.^17,39,40 Sua estrutura eletrônica pode ser caracterizada pela elevada densidade de estados no centro da banda, e pela formaçao de níveis discretos nas bordas (Figura 11).

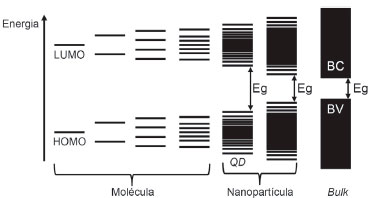Figura 11. Organizaçao dos níveis de energia ou orbitais moleculares partindo (da direita à esquerda) de uma molécula diatômica ao bulk. E_g: Band Gap; BC: banda de conduçao; BV: banda de valência; LUMO: lowest unoccupied molecular orbital; HOMO: highest occupied molecular orbital; QD: quantum dots. Adaptado da tese de Groeneveld²⁰

Essas evidências observadas na estruturaçao dos níveis ocorrem de acordo com o Efeito de Confinamento Quântico.^17,39,40 Além de representar a quebra de quasi-continuidade de níveis de energia da teoria de banda em bulks, demonstra o aumento da energia de Band Gap com a reduçao dos diâmetros de partícula através da diferença de energia entre os orbitais HOMO e LUMO (Figura 11). Os limites de dimensao para o regime de confinamento, classificado em forte ou fraco, sao ditados por um parâmetro criado em analogia ao raio atômico de Bohr do Hidrogênio: o raio de Bohr do éxciton (r_B).^17,38

em que r_B é o raio de Bohr do éxciton; h é a constante de Planck normalizada; ε₀ é a permissividade do vácuo; ε é a constante dielétrica da partícula; "e" é o valor de carga elementar; e m_ef é a massa efetiva. O r_B determina a distância mais provável entre o elétron e a lacuna em um éxciton, de modo que para raios de partículas inferiores ou iguais a r_B, observa-se o regime de confinamento forte, no qual a energia cinética de ambos os transportadores supera em muito a sua interaçao coulombiana, podendo, portanto, cada um ser tratado independentemente do ponto de vista energético. A soma de suas energias relativas leva à energia de confinamento que, somada à energia de Band Gap original do material, induz ao novo valor referente a comprimentos de onda de excitaçao mais baixos. Quando o raio da nanopartícula supera o r_B até o limite do seu dobro ou triplo, o regime de confinamento é classificado como fraco e, apesar de serem observadas mudanças nos níveis de energia, essas sao muito mais moderadas do que no regime de confinamento forte.¹⁷

Particularmente útil é a relaçao que r_B apresenta com o Band Gap dos materiais: quanto maiores os valores de Eg, menores os de r_B. Essa relaçao mostra que materiais diferentes experimentam o regime de confinamento em tamanhos distintos, como por exemplo: para o PbSe, Eg = 0,26 eV (4769 nm) e r_B = 46 nm; para o ZnS, Eg = 3,7 eV (335 nm) e r_B = 1,5 nm. Quanto mais isolante for o material (Eg elevado), maior a localizaçao do éxciton (m_ef maiores) e menores os tamanhos de partícula requeridos para que o material sofra os fatores de confinamento.¹⁷

Afora as diferenças nas propriedades ópticas causadas pelo confinamento quântico, a reduçao dos tamanhos de partícula, mesmo a diâmetros de dezenas de nm, ainda apresenta outras particularidades importantes. Ao dividir finamente um material semicondutor dopado, limita-se fortemente a quantidade de sítios de dopante ionizados presentes em cada nanopartícula formada, aproximando-as do estado de semiconduçao intrínseca.^38,41 Em alguns casos, quando aplicada concentraçao de dopante análoga ao estado monocristalino, a maioria das partículas encontra-se sem nenhum átomo dopante, enquanto a minoria restante tem de um a dois átomos.⁴¹ O esgotamento de transportadores acaba sendo ainda mais pronunciado pelo fato de que filmes nanoparticulados sao penetrados pelo eletrólito interfacial, de modo que para atingir o equilíbrio dos níveis de Fermi entre as fases (E_f = E') observa-se a transferência dos transportadores das partículas aos aceptores no eletrólito, aprofundando ainda mais a depleçao.^38,41

A distribuiçao de potencial em semicondutores esféricos foi derivada a partir de uma equaçao linearizada de Poisson-Boltzmann e, a partir dela, determinou-se o decaimento de potencial observado em nanopartículas de acordo com o seu raio (Eq. 13).³⁸

em que ΔΦ₀ é a diferença de potencial entre o centro e a borda da partícula; k é a constante de Boltzmann; T é a temperatura absoluta em Kelvin; r₀ é o raio da partícula; e L_D é o comprimento de Debye (L_D decai proporcionalmente com a raiz quadrada da concentraçao de dopante). Como o raio de nanopartículas é pequeno, a dopagem deve atingir valores altos para que o comprimento de Debye decaia suficientemente e aumente a diferença de potencial entre as bordas e o núcleo da partícula, havendo assim o desenvolvimento de um campo elétrico com efeito prático. Com o esgotamento de transportadores majoritários protagonizado principalmente pela percolaçao de eletrólito no filme nanoparticulado,⁴¹ conclui-se que a principal forma de transporte de carga através das partículas é a difusao. Uma regra prática mostra que a diferença, de potencial entre as bordas e o núcleo das partículas deve atingir o valor de 50 mV para que o transporte seja realizado predominantemente por migraçao elétrica ao invés de difusao.³⁸ Valores abaixo disso denotam um campo desprezível, podendo-se igualmente desprezar a formaçao de space-charge layer (Figura 12). Sugere-se, nessa circunstância, que o eletrodo permanece com bandas planas e que qualquer variaçao de potencial deve decair na camada de Helmholtz ([eletrólito] > 0,1 mol L^-1), representando uma mudança na posiçao da borda das bandas.

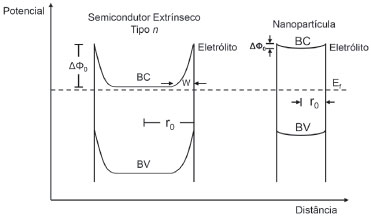Figura 12. Formaçao da space-charge layer em partículas grandes de semicondutores extrínsecos do tipo n e em nanopartículas de semicondutores em equilíbrio com uma espécie redox do eletrólito com potencial formal igual ao nível de Fermi (E_f). A nanopartícula encontra-se praticamente esgotada de transportadores, com o nível de Fermi localizado aproximadamente no centro do Band Gap e arqueamento de bandas negligenciável. BC: banda de conduçao; BV: banda de valência; r₀: raio da partícula; W: espessura da space-charge layer medida no modo de camada de esgotamento; ΔΦ₀: decaimento de potencial na space-charge layer relativo ao arqueamento de bandas. Adaptado do trabalho de revisao de Hagfeldt e Grätzel³⁸

Em filmes nanoparticulados, o esgotamento de transportadores causado tanto pelo efeito de reduçao de diâmetro como pela penetraçao de eletrólito faz com que os transportadores gerados por fotoexcitaçao possam se tornar majoritários e, assim, a condutividade do material passe a ser controlada pela etapa limitante do processo de injeçao de carga interfacial.^42,43 Ao irradiar um filme nanoparticulado com fótons com energia superior ao Band Gap, há igualmente a formaçao de elétrons excitados na banda de conduçao (e_BC^-) e lacunas na banda de valência (h⁺_BV). Tanto a acepçao do elétron como a captura da lacuna por espécies no eletrólito podem ser reaçoes plausíveis, de modo que o tipo de reaçao predominantemente mais rápida leva a um novo tipo de classificaçao do material.

Semicondutores nanoparticulados n sao aqueles em que a cinética de reaçao da lacuna (h⁺_BV) com o eletrólito é mais rápida e os elétrons provenientes tanto da excitaçao como da transferência de carga sao chamados de transportadores de vida longa.⁴² Eles levam a um carregamento negativo do filme e, ao se aplicar potenciais positivos frente ao potencial de corrente nula E_onset (≈ E_FB), sao os transportadores que apresentam mobilidade e podem ser medidos sob forma de uma corrente anódica durante registros voltamétricos. Semicondutores nanoparticulados p sao aqueles em que o elétron reage mais rápido com um componente do eletrólito, de modo que as lacunas passam a ser os transportadores de vida longa que conferem um carregamento positivo ao filme e sao transportados através dele pela aplicaçao de potenciais mais negativos frente ao E_onset, sendo medida uma corrente catódica durante registros voltamétricos.⁴²

No início dos estudos de fotoanodos com semicondutores nanoparticulados, o transporte de carga através desses filmes era visto como algo efetivamente pouco provável, uma vez que nao se observava o campo elétrico provindo do arqueamento de bandas da space-charge layer para a separaçao espacial dos transportadores de carga oposta, que inicialmente deveriam recombinar em massa. Além disso, o transporte de carga inter-partícula também parecia algo complicado, uma vez que o transportador deveria vencer uma barreira coulombiana de até 50 meV, dependendo do contato entre os cristalitos,⁴¹ com resistividades da ordem de 10⁹ Ω cm.⁴⁴ Afora isso, o efeito favorável de ganho de área pela penetraçao do eletrólito, que é estimado em 1000 vezes para um filme com algumas unidades de µm de espessura,⁴¹ parecia bastante promissor, principalmente para o desenvolvimento de células solares fotosensibilizadas por corante.

A resposta a esses problemas veio a partir da própria natureza dos processos, que mostraram certa capacidade de transporte de carga nos filmes nanoparticulados. Por exemplo, em semicondutores nanoparticulados n a lacuna (h⁺_BV) é um transportador que apresenta tempo de vida curto.³ Em outras palavras, ou ela é gerada e reage com um doador em soluçao ou ela recombina com um elétron fotoexcitado.⁴² O tempo de vida do éxciton é aumentado pelo processo de trapping, ampliando o período para a incidência de reaçoes interfaciais antes da recombinaçao.²⁵ Após a injeçao de um elétron na lacuna, o elétron na BC (ou no trap) é transportado para o eletrodo polarizado positivamente. Caso o filme seja composto por Quantum Dots, a funçao de onda dos transportadores é espalhada por toda a extensao espacial da partícula, de modo que os mesmos nao precisam se difundir do ponto de onde foram gerados para as bordas. Assim, os elétrons se deslocam ao condutor sem encontrar pela frente lacunas para se recombinar. Há chances de sequestro desse elétron por reaçoes com aceptores eletrônicos presentes no eletrólito durante a etapa de transferência inter-partícula, já que o eletrólito circunda a maior parte das partículas componentes do filme poroso. O potencial redox disponível para tanto será o da borda da banda de conduçao do material ou do potencial relativo do elétron no estado de relaxamento do trap, sendo que as perdas de fotocorrente dependem também da cinética de captura do elétron pelo suposto aceptor.

Quanto à improvável transferência de transportadores entre diferentes partículas, a presença do eletrólito entre elas facilita este processo. O desenvolvimento da carga negativa das partículas n pela presença de elétrons acumulados no filme leva ao pareamento de cátions e orientaçao do dipolo das moléculas do solvente (se polarizável, como H₂O), o que reduz a barreira coulombiana para valores termicamente acessíveis à temperatura ambiente, como reportado por Brus.⁴⁵ Todavia, a eficiência do transporte de carga em filmes nanoparticulados é bastante prejudicada frente aos eletrodos monocristalinos.

Mesmo em semicondutores intrínsecos, no estado monocristalino, a aplicaçao de potencial leva ao transporte vetorial dos transportadores, o que nao ocorre em filmes nanoparticulados devido ao seu caráter descontínuo. Considera-se que o transporte de carga se dá inteiramente pela difusao causada pelo gradiente de concentraçoes do transportador ao longo do filme nanoparticulado.³⁸ Essas características se refletem nos respectivos coeficientes de difusao do elétron (D₀) em cada tipo de estrutura.⁴⁶ Por exemplo, em monocristais D₀ está próximo a valores de 4,0 10^-1 cm² s^-1, enquanto que para filmes nanoparticulados é de cerca de 1,4 10^-3 cm² s^-1, ou seja, quase 300 vezes menor.

Em filmes nanoparticulados, durante o transporte de carga, o transportador pode ser eliminado principalmente pela recombinaçao (fator comum aos eletrodos monocristalinos) e pela sua captura por aceptores na etapa de transferência inter-partícula (fator próprio). Todavia, em monocristais dopados a existência da SCL permite o decaimento do potencial em sua extensao (no mínimo de 50 mV)³⁸ de modo a formar um campo elétrico que separa espacialmente lacunas de elétrons para evitar a recombinaçao na interface. Um dos transportadores é levado à interface para se transferir a uma espécie eletroativa, gerando o aumento da concentraçao do transportador oposto, o qual migra sob efeito do campo elétrico em direçao ao bulk do semicondutor. Nessa regiao há alta concentraçao de transportadores da sua própria espécie e ínfima concentraçao do transportador oposto, sendo, portanto, muito baixa a probabilidade de recombinaçao. A existência do campo elétrico na interface, nesse caso, suprime fortemente a recombinaçao na profundidade de penetraçao da radiaçao incidente, e é essa a principal funçao da dopagem de semicondutores nas células fotoeletroquímicas condutivas. Utiliza-se o transportador fotogerado de carga oposta à dopagem para a reaçao química com as espécies no eletrólito.

De outro lado existem os filmes nanoparticulados que nao suportam a formaçao de SCL e assim nao apresentam campo elétrico para separaçao de cargas. A melhor condiçao encontrada para supressao de recombinaçao é em Quantum Dots, em que o transportador reativo depende apenas da cinética da reaçao de transferência de carga para ser extinto e o transportador de vida longa deve percorrer um filme praticamente isento do transportador oposto, sendo realmente baixa a possibilidade de recombinaçao.⁴² Nesse caso a maior fonte de perdas de transportadores no percurso ao eletrodo polarizado é a captura por espécies durante a transferência inter-partícula.⁴² Já em nanopartículas maiores (r >> r_B), ambos os transportadores difundem dentro das partículas e a chance de recombinaçao é muito maior durante o transporte ao condutor. Assim, desponta a importância de utilizar filmes nanoparticulados finos, principalmente quando se trabalha acima do limite de tamanho dos Quantum Dots e enseja-se alta eficiência de coleta.⁴⁷ Apesar do menor coeficiente de absorçao (α) e consequentemente menor extensao de reaçao interfacial, ao reduzir o percurso do transportador diminui-se drasticamente a probabilidade de recombinaçoes, sequestro por espécies eletroativas na transferência inter-partícula e inclusive a resistência ôhmica do filme, diminuindo o potencial de polarizaçao mínimo para otimizaçao do fator de coleta.

E, por fim, cabe apreciar o papel da aplicaçao de potencial de polarizaçao em substratos condutores modificados com filmes de materiais nanoparticulados. Nao se observam muitos trabalhos dispostos a essa discussao e alguns autores⁴⁸ se limitam a dizer que a aplicaçao do potencial nao causa a supressao da recombinaçao e exaltam a necessidade da dopagem. Outros, como Jiang et al.,⁴⁹ mostram que a aplicaçao de potencial, dependendo do valor, possibilita coletar os elétrons de modo a evitar seu acúmulo na interface e, indiretamente, reduzir a taxa de recombinaçao. Esse último grupo de autores discute uma possível inconsistência no transporte puramente por difusao, defendendo a formaçao de um campo elétrico e o transporte de carga com pouca dependência, em termos de mobilidade eletrônica, dos efeitos de blindagem dos cátions (e solvente) interfaciais do eletrólito.

O que se confirma na prática é que o comportamento do nanomaterial na forma de um filme nanoporoso se aproxima de um isolante, com uma faixa linear em regioes logo após o potencial de corrente nula (acima ou abaixo de E_onset dependendo se semicondutor tipo n ou p) seguindo até o nivelamento da fotocorrente em um valor constante, ou seja, nao mais dependente do aumento do potencial aplicado: a corrente de saturaçao. De fato, a fotocorrente depende em larga faixa do potencial aplicado. Entretanto, ele nao regula a cinética de reaçoes interfaciais.⁴³ Os transportadores sao fotogerados pela luz e reagem com espécies na interface em decorrência do potencial conferido pela sua respectiva borda de banda,²⁷ sendo os transportadores de vida longa drenados ao substrato condutor. Caso um potencial abaixo do mínimo necessário para atingir a fotocorrente de saturaçao seja aplicado, isso nao significa que a reaçao interfacial possui velocidade mais lenta, mas sim que o potencial aplicado nao é suficiente para coletar todos os transportadores acumulados para um mesmo tempo de irradiaçao.

A reaçao de fotooxidaçao interfacial depende apenas do fluxo radiante da fonte de excitaçao e da concentraçao de doadores (para reagir com lacunas) ou aceptores (para reagir com elétrons) na interface.⁴³ Assim, o potencial de polarizaçao tem a funçao de drenar os transportadores acumulados, sem um compromisso com a cinética das fotorreaçoes ou mesmo com o complemento do potencial termodinâmico para a efetivaçao delas. Caso a banda do respectivo transportador nao tenha o potencial necessário para reagir com a espécie interfacial, o potencial aplicado nao complementa a demanda energética, nao sendo o processo viável.

Portanto, conclui-se a grande contribuiçao que eletrodos nanoparticulados podem trazer à eletroquímica de semicondutores: a possibilidade de construir dispositivos que visem o estudo cinético da etapa limitante das reaçoes dos transportadores fotogerados com as espécies eletroativas de interesse nos diferentes tipos de sítio de reaçao, já que o eletrodo polarizado funciona como uma sonda das reaçoes interfaciais.⁴⁹ Em alguns tipos de sítio a reaçao pode eventualmente ser controlada por transporte, de modo a poder-se estudar o decaimento da concentraçao do soluto de acordo com seu coeficiente de difusao em soluçao.^50,51 Em outros tipos, o decaimento da concentraçao do soluto pode ser dependente da cinética de formaçao dos complexos superficiais.^50,51 Isso é particularmente útil no estudo da degradaçao de poluentes orgânicos solubilizados visando, por exemplo, novos métodos de tratamento de águas baseado nesse processo oxidativo avançado.⁵²

APLICAÇOES DA FOTOELETROCATALISE

Na literatura internacional há uma vasta gama de artigos revendo aplicaçoes do processo fotoeletrocatalítico para as mais diversas áreas e finalidades, além de apresentar perspectivas e novos desafios. Bessegatto et al.⁵² revisaram as aplicaçoes das estruturas com diferentes morfologias nanométricas do TiO₂ para (i) a degradaçao de poluentes orgânicos através de reaçoes de transferência de carga de suas lacunas (h⁺) com elevado poder oxidante, diretamente com o soluto orgânico ou via reaçao indireta com a formaçao de radicais hidroxila (HO^•); (ii) reduçao de contaminantes inorgânicos via transferência de carga de seus elétrons com a espécie em soluçao; (iii) inativaçao de microorganismos patógenos pela reaçao de lacunas/radicais hidroxila com os compostos constituintes de sua membrana plasmática, organelas e até seu DNA; (iv) produçao de hidrogênio através da decomposiçao da água, pela simultânea reduçao de algumas moléculas com os elétrons fotoexcitados (H₂O/H₂) e oxidaçao de outras com as lacunas (H₂O/O₂) em fotopotencial de circuito aberto. Outro aspecto interessante revisado pelos autores é a reduçao do gás carbônico a espécies de forte valor comercial agregado, como hidrocarbonetos puros ou oxigenados (p. ex. CO₂/CH₃OH), com elevada eficiência de conversao. Utilizando um composto de sacrifício para reaçao com lacunas ou aplicando potencial de polarizaçao abaixo do potencial de bandas planas em semicondutores p, pode-se elevar a taxa de conversao da fotorreaçao, atingindo-se valores bastante interessantes em algumas horas (> 95 %) para eletrodos de materiais de baixo custo, como o CuO/Cu. Daghrir et al.⁵³ revisaram as aplicaçoes ambientais dos processos fotoeletrocatalíticos envolvendo eletrodos de TiO₂ de um ponto de vista pragmático, através do estudo dos reatores e os fatores que afetam sua eficiência para a degradaçao de diversos poluentes orgânicos e inativaçao de microorganismos (E. coli), como a fonte de radiaçao UV implementada, aplicaçao de potencial externo, intensidade de luz, temperatura, e os fatores atrelados à amostra em tratamento, como o pH, concentraçao de oxigênio dissolvido e concentraçao de eletrólitos. Zhang et al.⁵⁴ revisaram muitos dos mesmos parâmetros voltados para a degradaçao de poluentes orgânicos recalcitrantes (p. ex. Fenol) com eletrodos de filme de TiO₂, mas também a influência da estrutura cristalina do filme de semicondutor, da sua espessura, do material usado como substrato leito, da dopagem do TiO₂ com metais e nao-metais, além de propor uma revisao dos mecanismos e a cinética para a degradaçao fotoeletrocatalítica de poluentes orgânicos. Egerton,⁵⁵ comparando a eficiência do processo fotoeletrocatalítico frente ao fotocatalítico em suspensao para quatro reaçoes diferentes de oxidaçao do nitrofenol, oxalato, inativaçao da bactéria E. coli e degradaçao do corante reativo laranja, chegou a conclusao de que, ao aplicar um pequeno potencial acima do potencial de bandas planas, há um aumento da taxa de oxidaçao dos poluentes; todavia nao o suficiente para tornar o processo tecnologicamente viável. O autor desenvolveu sua discussao de acordo com as possíveis limitaçoes impostas pelo design do reator frente àquelas previstas pelo tipo de material semicondutor e, em última análise, creditou ao material o baixo desempenho. Ao revisar o uso de nanotubos de TiO₂, igualmente chegou à conclusao de que sua performance também nao atende à demanda tecnológica de custo. Certamente, o caráter ôhmico de filmes nanoparticulados e a inaplicabilidade da separaçao de cargas por desenvolvimento de camada de esgotamento da space-charge layer discutidos nesta revisao sao capazes de explicar parte dos resultados observados pelo autor. Zhang et al.⁵⁶ resumiram em seu artigo de revisao o desenvolvimento de materiais fotocatalisadores aplicáveis no tratamento de remediaçao ambiental e/ou em rotas de síntese. O trabalho foca nos diferentes materiais testados, como o TiO₂, ZnO, SnO₂, WO₃, Fe₂O₃ e CdS, e suas implicaçoes no uso prático em fotocatálise, como a estabilidade química e fotoquímica, a modificaçao físico-química dos materiais para o aumento das velocidades de reaçao e rendimento, a extensao da sensibilidade dos materiais para janela dentro do espectro visível e o desenvolvimento de semicondutores de óxidos mistos com valores de Band Gap deliberadamente moduláveis. Os autores mostram que tanto cálculos teóricos como os resultados experimentais obtidos sao convincentes em provar que os materiais desenvolvidos até entao sao fotocatalisadores altamente eficientes com significância para profundas mudanças no campo ambiental e econômico, prontos para servir de base, juntamente ao conhecimento gerado, para o desenvolvimento de fotocatalisadores de alta eficiência para fotoconversao solar. Karanasios et al.⁵⁷ revisou o uso da oxidaçao fotoeletrocatalítica como um método oxidativo avançado para a degradaçao de poluentes, dando ênfase na aplicabilidade sob iluminaçao na regiao do visível. Deste modo, os materiais utilizados como fotoanôdos na regiao do visível foram abordados, podendo ser classificados em semicondutores monocomponente, bi-componente ou materiais de TiO₂ modificados, incluindo a dopagem com ametais, como C-, N- e S-, e a nanodecoraçao com metais, como Pt, Au e Ag. Os autores concluem que o processo fotoeletrocatalítico é um método eficiente para aumentar o desempenho da fotocatálise convencional para o caso de semicondutores imobilizados em substratos, sendo viável para tratamentos de água em pequena escala com reatores modulares e a purificaçao de ar. Eles acreditam que o processo tem futuro promissor, principalmente por acoplar o tratamento de águas com a geraçao de hidrogênio ou energia elétrica em fotocélulas combustível. Dentre os materiais sensíveis a luz solar, os materiais de TiO₂ dopados com -N ou -C ou ainda nanodecorados com Ag ou Au sao apontados como os mais promissores. Lianos⁵⁸ recentemente revisou os aspectos fundamentais de células fotoeletrocatalíticas desenvolvidas para a produçao de eletricidade ou hidrogênio, a partir da oxidaçao de um agente de sacrifício orgânico ou inorgânico e a reduçao da água, de prótons ou mesmo de oxigênio. Os aspectos principais de células fotoeletrocatalíticas foram revisados, como fotoânodos, fotocátodos, contra-eletrodos, os eletrólitos e os designs incluindo células em tandem e combinaçao de eletrodos. Os materiais para a construçao de todos os componentes e as respectivas eficiências obtidas foram discutidos, chegando-se à conclusao de que poucos trabalhos efetivamente estudam materiais de considerável absorçao do espectro solar, como WO₃, BiVO₄ ou Fe₂O₃, em fotoânodos de fotocélulas combustível. Sua eficiência depende da capacidade dos fotoânodos em oxidar os combustíveis, bem como dos processos de reduçao no contra-eletrodo, como a reduçao do oxigênio. Parte deste conhecimento pode ser adquirido dos estudos de célula combustível, levando em conta o desenvolvimento de materiais eletrocatalisadores da reduçao de oxigênio sem Pt ou outros metais nobres, o que prejudica a relaçao de custos dos projetos de célula. Ou seja, pouca atençao é dada ao material constituindo o contra-eletrodo, já que elevada complexidade é encontrada nos processos envolvendo o fotoeletrodo de trabalho, e isso certamente prejudica o desenvolvimento dos protótipos de fotocélulas. Afora esses aspectos, o autor conclui que as células fotoeletrocatalíticas alcançaram maturidade tecnológica, sendo importante confrontar os tradicionais problemas de ampliaçao de escala (scale-up). As células em tandem ainda constituem uma curiosidade científica longe de viabilidade prática devido ao design e os custos dos materiais, sendo ainda preferível o acoplamento de células fotoeletrocatalíticas com células fotovoltaicas comerciais.

CONSIDERAÇOES FINAIS

No limitado número de páginas de um artigo de revisao, seria impossível tratar em profundidade de todo o corpo de conhecimento teórico e experimental em que se apoia a compreensao atual dos fenômenos envolvidos nos processos de fotoeletrocatálise em semicondutores e sua aplicaçao prática, tampouco de analisar criticamente a vasta e crescente literatura sobre o assunto. Acredita-se ter sido possível, no entanto, selecionar e introduzir em linguagem acessível aos químicos interessados a ingressar nesse ativíssimo campo de pesquisa os aspectos essenciais da ciência de semicondutores e do desenvolvimento dos modelos vigentes para explicaçao do papel da eletrocatálise aos fenômenos fotocatalíticos de semicondutores, inclusive nanoparticulados e imobilizados em substratos condutores. A compreensao dos diversos mecanismos envolvidos permite melhor controle dos processos fotocatalíticos, viabilizando o desenvolvimento - também no país - da inventividade nesse campo da ciência com geraçao de dispositivos mais avançados e competitivos frente a tecnologias existentes. Entre os exemplos dessas possibilidades estao as células solares,^52,58 novos processos oxidativos avançados para tratamento de águas,⁵² purificadores de ar⁵⁶ e também diversos dispositivos analíticos com viés ambiental, exemplificados pela digestao de compostos orgânicos para determinaçao da concentraçao total de metais em amostras de água^59-61 e a determinaçao da Demanda Química de Oxigênio.⁶²

AGRADECIMENTOS

Os autores agradecem ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) pela concessao de uma bolsa de doutorado (processo nº 141734-2012-4) e uma de produtividade (processo nº 311324/2014-2).

REFERENCIAS

1. Hoffmann, M. R.; Martin, S. T.; Choi, W.; Bahnemann, D. W.; Chem. Rev. 1995, 95, 69.

2. Fujishima, A.; Rao, T. N.; Tryk, D. A.; J. Photochem. Photobiol., C 2000, 1, 1.

3. Fujishima, A.; Zhang, X.; Tryk, D. A.; Surf. Sci. Rep. 2008, 63, 515.

4. Nogueira R. F. P.; Jardim, W. F.; Quim. Nova 1998, 21, 69.

5. Ziolli, R. L.; Jardim, W. F.; Quim. Nova 1998, 21, 319.

6. Catanho, M.; Malpass, G. R. P.; Motheo, A. J.; Quim. Nova 2006, 29, 983.

7. Cervantes, T. N. M.; Zaia, D. A. M.; Santana, H.; Quim. Nova 2009, 32, 2423.

8. Brunelli, T. F. T.; Guaraldo, T. T.; Paschoal, F. M. M.; Zanoni, M. V. B.; Quim. Nova 2009, 32, 67.

9. Frade, T.; Gomes, A.; Pereira, M. I. S.; Lopes, A.; Ciríaco, L.; Quim. Nova 2012, 35, 30.

10. Lark-Horovitz, K.; The present state of physics: The New Electronics; F. S. Brackett: Washington D. C., 1954, pp. 57-157.

11. Shriver, D. F.; Atkins, P.W.; Em Química Inorgânica; Porto Alegre: Bookman, 2003, pp. 128-136.

12. Reif, F.; Fundamentals of Statistical and Thermal Physics; McGraw-Hill: New York, 1965, p. 341.

13. Madhusudan Reddy, K.; Manorama, S. V.; Ramachandra Reddy, A.; Mater. Chem. Phys. 2002, 78, 239.

14. Finklea, H. O.; Semiconductor Electrodes; Elsevier: New York, 1988, pp. 1-18.

15. http://www.doitpoms.ac.uk/tlplib/semiconductors/direct.php, acessada em novembro de 2017.

16. Van Zeghbroech Em Principles of Semiconductor Devices; disponível em http://ecee.colorado.edu/~bart/book/, acessada em novembro de 2017.

17. Koole, R.; Groeneveld, E.; Vanmaekelbergh, D.; Meijerink, A.; Donegá, C. M. Em Nanoparticles; Donegá, C. M., ed.; Springer: Verlag-Berlin-Heidelberg, 2014; cap. 2.

18. Gaponenko, S. V.; Em Introduction to Nanophotonics, Cambridge University Press: Cambridge, 2010; cap. 4.

19. Henderson, B.; Imbusch, G. F.; Optical Spectroscopy of Inorganic Solids, Clarendon Press: Oxford, 1989; cap. 4 e 5.

20. Groeneveld, E.; Tese de Doutorado, Utrecht University, Holanda, 2012.

21. López, R.; Gómez, R.; J. Sol-Gel Sci. Technol. 2012, 61, 1.

22. Klimov, V. I.; Annu. Rev. Phys. Chem. 2007, 58, 635.

23. Kambhampati, P.; J. Phys. Chem. C 2011, 115, 22089.

24. Rogach, A. L.; Klar, T. A.; Lupton, J. M., Meijerink, A.; Feldmann, J.; J. Mater. Chem. 2009, 19, 1208.

25. Minero, C.; Bahnemann, D.; Robertson, P. Em Environmental Photochemistry Part III; Bahnemann, D., Robertson, P., eds.; Springer: Verlag-Berlin-Heidelberg, 2013, pp. 23-44.

26. Fu, Y.; Cao, W. H.; J. Appl. Phys. 2006, 100, 84324.

27. Grätzel, M.; Nature 2001, 414, 338.

28. Bolts, J. M.; Wrighton, M. S.; J. Phys. Chem. 1976, 80, 2641.

29. Gerischer, H.; Physical Chemistry, Academic Press: New York, 1970; Cap. 5.

30. Lewerenz, H. J.; Heller, A.; Di Salvo, F. J.; J. Am. Chem. Soc. 1980, 102, 1877.

31. Lewerenz, H. J.; Gerischer, H.; Lubke, M.; J. Electrochem. Soc. 1984, 131, 100.

32. Canfield, D.; Furtak, T.; Parkinson, B. A.; J. Appl. Phys. 1980, 51, 6018.

33. Shockley, W.; Queisser, H. J.; J. Appl. Phys. 1961, 32, 510.

34. Razzini, G.; Bicelli, L. P.; Pini, G.; Scrosati, B.; J. Electrochem. Soc. 1981, 128, 2134.

35. Bicelli, L. P.; Razzini, G., Surf. Technol. 1983, 20, 383.

36. White, H. S.; Abruna, H. D.; Bard, A. J.; J. Electrochem. Soc. 1982, 129, 265.

37. Fornarini, L.; Stirpe, F.; Scrosati, B.; J. Electrochem. Soc. 1983, 130, 2184.

38. Hagfeldt, A.; Grätzel, M.; Chem. Rev. 1995, 95, 49.

39. Alivisatos, P.; Pure Appl. Chem. 2000, 72, 3.

40. Rabouw, F. T.; Donega, C. M.; Top. Curr. Chem. 2016, 374, 58.

41. Cahen, D.; Grätzel, M.; Guillemoles, J. F.; Hodes, G. Em Electrochemistry of Nanomaterials; Hodes, G., ed.; Wiley: VCH Verlag, 2001, p. 201.

42. Hodes, G.; Howell, I. D. J.; Peter, L. M.; J. Electrochem. Soc. 1992, 139, 3136.

43. Jiang, D.; Zhao, H.; Zhang, S.; John, R.; J. Phys. Chem. B 2003, 107, 12774.

44. Hodes, G.; Albu-Yaron, A.; Decker, F.; Motisuke, P.; Phys. Rev. B 1987, 36, 4215.

45. Brus, L., Phys. Rev. B 1996, 53, 4649.

46. Villanueva-Cab, J.; Jang, S-R.; Halverson, A. F.; Zhu, K.; Frank, A. J.; Nano Lett. 2014, 14, 2305.

47. Baccaro, A. L. B.; Gutz, I. G. R.; Electrochim. Acta 2016, 214, 295.

48. Berger, T.; Lana-Villarreal, T.; Monllor-Satoca, D.; Gómez, R.; Electrochem. Commun. 2006, 8, 1713.

49. Jiang, D.; Zhao, H.; Zhang, S.; John, R.; J. Catal. 2004, 223, 212.

50. Regazzoni, A. E.; Mandelbaum, P.; Matsuyoshi, M.; Schiller, S.; Bilmes, S. A.; Blesa, M. A.; Langmuir 1998, 14, 868.

51. Jiang, D.; Zhao, H.; Zhang, S.; John, R.; J. Photochem. Photobiol. A 2006, 177, 253.

52. Bessegato, G. G.; Guaraldo, T. T.; Brito, J. F.; Brugnera, M.F.; Zanoni, M. V. B.; Electrocatalysis 2015, 6, 415.

53. Daghrir, R.; Drogui, P.; Robert, D.; J. Photochem. Photobiol. A 2012, 238, 41.

54. Zhang, Y.; Xiong, X.; Han, Y.; Zhang, X.; Shen, F.; Deng, S.; Xiao, H.; Yang, X.; Yang, G.; Peng, H.; Chemosphere 2012, 88, 145.

55. Egerton, T. A.; J. Chem. Technol. Biotechnol. 2011, 86, 1024.

56. Zhang, H; Chen, G.; Bahnemann, D. W.; J. Mater. Chem. 2009, 19, 5089.

57. Karanasios, N.; Georgieva, J.; Valova, E.; Armyanov, S.; Litsardakis, G.; Sotiropoulos, S.; Curr. Org. Chem. 2015, 19, 512.

58. Lianos, P.; Appl. Catal., B 2017, 210, 235.

59. Cavicchioli, A.; Gutz, I. G. R.; Anal. Chim. Acta 2001, 445, 127.

60. Daniel, D.; Gutz, I. G. R.; Electrochem. Commun. 2007, 9, 522.

61. Baccaro, A. L. B.; Gutz, I. G. R.; Electrochem. Commun. 2013, 31, 28.

62. Zhao, H.; Jiang, D.; Zhang, S.; Catterall, K.; John, R.; Anal Chem. 2004, 76, 155.