JBCS

INTRODUÇAO

Na prática docente vivenciamos situaçoes recorrentes ao longo da carreira onde estudantes, temporal e geograficamente distintos, apresentam as mesmas dificuldades de compreensao de conceitos e fenômenos relacionados à química orgânica.¹ Antes de ser uma limitaçao intrínseca dos estudantes, a origem destas dificuldades pode residir na forma como esses conceitos e fenômenos sao apresentados aos graduandos,² bem como da sofisticada representaçao pictórica da fenomenologia química.³

A aromaticidade e a degenerescência dos orbitais moleculares do benzeno e correlatos se enquadram neste cenário pois, nos textos didáticos, sao tao somente apresentados como fatos, e o fato passa a ser a explicaçao sem uma deduçao que possa levar à compreensao. Isto é particularmente deletério, pois a química dos compostos aromáticos e o fenômeno da aromaticidade sao temas balizares na formaçao dos profissionais da química,⁴ ensinados nos cursos teóricos de química orgânica, que deve resultar na compreensao da estabilidade e reatividade diferenciada do anel benzênico, quando comparado aos alcenos.⁵

Em continuaçao à nossa abordagem de ensino de orbitais moleculares nos cursos básicos de química orgânica na graduaçao,^6-8 apresentamos aqui um método operacional para avaliar as energias relativas dos orbitais moleculares de hidrocarbonetos aromáticas e antiaromáticas, e dos alcenos conjugados correspondentes, Figura 1.

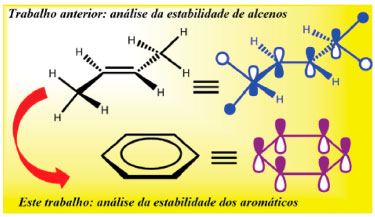Figura 1. Dos alcenos aos polienos e aromáticos: estabilidade e orbitais moleculares

A proposta se baseia na construçao da topologia dos orbitais moleculares⁹ que representa a combinaçao linear dos orbitais atômicos p do carbono, permitindo deduzir a natureza ligante e antiligante de cada orbital e avaliar qualitativamente suas energias relativas e, assim, comparar a energia total de estabilizaçao dos elétrons dos polienos cíclicos conjugados e íons orgânicos com a dos correspondes polienos acíclicos. Dessa forma, a degenerescência dos orbitais do benzeno e também a energia relativa dos orbitais dos polienos sao deduzidas pelo próprio estudante, suplantando a descriçao estática dos livros textos amplamente empregados na graduaçao.¹⁰

Critérios apresentados nos livros de graduaçao para avaliar aromaticidade e energias relativas dos orbitais moleculares

Para verificar o tipo de argumentaçao didática presente nos textos de graduaçao, uma amostra representativa de treze livros foi analisada, desde clássicos como o Morrison e Boyd até livros mais recentes, e assim avaliar a perenidade dos critérios empregados na explicaçao da aromaticidade tendo o benzeno como modelo.¹⁰ A maioria tem traduçao para a língua portuguesa, sendo dois de autores brasileiros, e na Figura 2 estao reunidos os recursos gráficos empregados nestes livros para ensinar os argumentos que conduzem o estudante a compreender a maior estabilidade do benzeno, em funçao da aromaticidade, quando comparada aos polienos de cadeia aberta. Nao foi incluída a comparaçao entre reaçao de adiçao a alcenos versos substituiçao eletrofílica aromática, que evidencia a diferença de reatividade, pois esta nao é a explicaçao da aromaticidade, é a sua consequência.

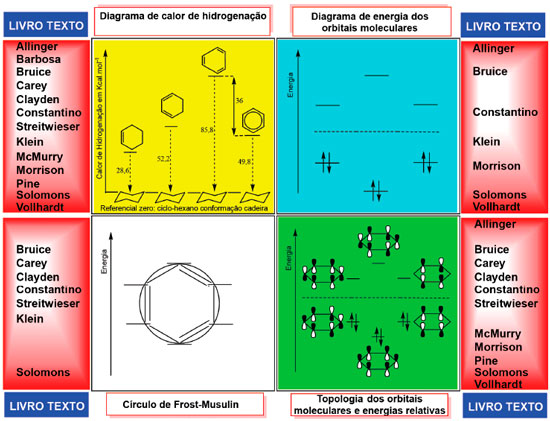Figura 2. Recursos gráficos empregados nos livros textos de Química Orgânica para explicar a aromaticidade e a degenerescência dos orbitais moleculares do benzeno

O critério da estabilidade termodinâmica introduzida por Pauling,¹¹ que faz a comparaçao do calor de hidrogenaçao, prevalece em todos os livros. Ao empregar este critério para demonstrar a maior estabilidade do sistema de elétrons π do anel aromático, comparam o calor de hidrogenaçao do ciclo-hexeno e do hipotético ciclo-hexatrieno com o do benzeno, e a diferença destas energias é denominada energia de estabilizaçao por ressonância, Figura 2. Em seguida, os textos apresentam o diagrama de energia indicando a existências de orbitais moleculares degenerados com a corresponde topologia (em alguns casos é reapresentado sem a topologia). Por fim, concluem que os elétrons π no sistema aromático sao mais estabilizados no seu conjunto, com menor energia eletrônica que os elétrons π dos alcenos conjugados de igual número de átomos de carbono.

O método mnemônico do círculo e polígono desenvolvido por Frost e Musilin¹² é apresentado na minoria dos textos de graduaçao, sendo este recurso o único empregado para julgar a degenerescência dos orbitais. Em nenhum deles há uma deduçao passo-a-passo para se chegar à conclusao da existência da degenerescência dos orbitais moleculares dos sistemas com elétrons π conjugados quando se passa de uma substância acíclica para uma cíclica, ou qualquer discussao sobre a topologia dos orbitais moleculares que conduza e este fim. Adicionalmente, a topologia dos orbitais π do benzeno é apresentada sem qualquer explicaçao de como é construída ou deduzida. Nem mesmo há indicaçao de que sao topologias calculados pelo método de Hückel^5,13 ou outro método químico-quântico e que representam a combinaçao linear dos orbitais atômicos p do carbono. A regra de Huckel¹⁴ é enunciada em todos os livros analisados, mas a consequência do "número mágico" de elétrons π do sistema conjugado monocíclico, que resulta no comportamento aromático, é representada graficamente de formas diversas nestes mesmos livros.

Ao aplicar todas estas consideraçoes os livros procuram contemplar os critérios energéticos e estruturais necessários à compreensao da aromaticidade. Apesar desta estratégia de apresentaçao e conceituaçao ser largamente empregada, os textos de graduaçao nao demonstram como avaliar a energia de estabilizaçao dos elétrons π nos polienos cíclicos que seguem a regra de Hückel, quando comparados aos respectivos alcenos acíclicos de igual número de átomos de carbono e de elétrons π conjugados. Por outro lado, nos cursos avançados de química orgânica na pós-graduaçao e mesmo na graduaçao, é possível lançar mao de expressoes matemáticos e/ou de pacotes computacionais baseados nos métodos químico-quânticos para calcular as energias dos orbitais moleculares.^15-17 Entretanto, esta abordagem nao é diretamente transponível aos cursos básicos de química orgânica, o que leva à apresentaçao dos níveis de energia do benzeno, por exemplo, sem qualquer deduçao, mesmo que qualitativa.

Do exposto, há, portanto, uma clara lacuna didática nos textos de química orgânica na graduaçao na explicaçao das energias dos polienos acíclicos e cíclicos, da degenerescência dos orbitais moleculares e da aromaticidade. Deduzir a topologia dos orbitais moleculares é necessário para, como consequência, deduzir as energias relativas do conjunto dos orbitais em análise. Um método que proporcione o aprendizado de um conjunto de passos que conduza a estas deduçoes pode ser útil ao estudante. Um procedimento que o dota desta capacidade de análise é a seguir descrito.

Estratégia alternativa para deduzir as energias relativas dos orbitais de polienos e íons cíclicos e acíclicos com elétrons π conjugados

A estratégia alternativa para deduzir as energias relativas dos orbitais de moléculas neutras ou espécies iônicas consiste na aplicaçao dos Passos 1-7 que proporciona deduzir as energias relativas dos orbitais moleculares da maioria dos exemplos tradicionalmente estudados nos textos didáticos da graduaçao. Para exemplificar, os Passos 1-7 foram aplicados na deduçao das energias relativas dos orbitais π de moléculas e íons acíclicos conjugados de dois a seis átomos, e em moléculas e íons cíclicos de três a sete membros.

Na execuçao dos Passos 1-7 as premissas detalhadas na explicaçao de cada um deles sao conhecidas pelos estudantes desde os cursos básicos de química geral onde tópicos de teoria atômica e de ligaçao química sao trabalhados, como a conservaçao do número total de orbitais atômicos que se combinam para formar os moleculares, a existência de planos nodais nos orbitais moleculares, o cancelamento de uma interaçao ligante por uma antiligante, e a noçao de que quanto maior o número de interaçoes ligantes mais estável deve ser o orbital.

O recomendável é que o estudante inicie a análise com os polienos acíclicos, se aproprie do procedimento descrito nos Passo 1-3 da Figura 3 e entao aplique-os ao polieno imediatamente superior em número de átomos, fazendo toda a análise até o sistema com seis átomos, um de cada vez. Para exemplificar a construçao do diagrama dos orbitais π e deduçao das energias relativas, fazemos o detalhamento para o 1,3-butadieno e o cátion ciclopropenila na Figura 3.

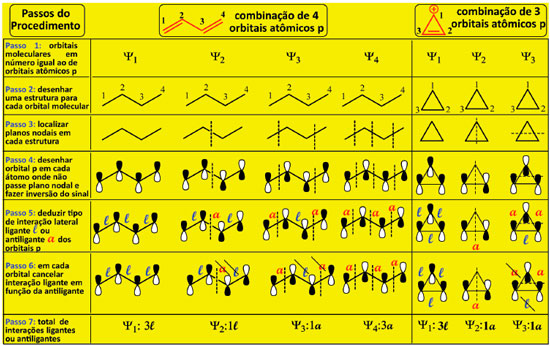Figura 3. Procedimento alternativo de deduçao da topologia dos orbitais π e das energias relativas para o 1,3-butadieno e cátion ciclopropenila

O Passo 1 é determinar o número de orbitais atômicos p paralelos e adjacentes da estrutura em análise que dao origem aos orbitais moleculares Ψ. Para os sistemas π conjugados aqui descritos, cada átomo contribui com um orbital atômico p para formar o circuito de elétrons π. Assim, a construçao da combinaçao linear dos orbitais atômicos de um dado sistema de n átomos na estrutura resulta em n orbitais moleculares, ou seja, Ψ₁, Ψ₂, até Ψ_n (ver Passo 1 da Figura 3 para o anel de três carbonos).

O Passo 2 é desenhar uma estrutura de linhas para cada Ψ_n.

O Passo 3 consiste em localizar o plano nodal em cada estrutura desenhada, com a máxima simetria possível e, para os polienos acíclicos, sao empregados planos verticais que sao distribuídos tendo como referencial o centro geométrico do sistema π conjugado. Havendo mais de um plano, estes sao localizados equidistantes a este centro guardando a máxima simetria possível, como se em cada orbital molecular Ψ_n o centro geométrico do sistema π conjugado fosse uma espécie de espelho interno, que reflete cada plano de uma metade do sistema π da molécula na outra metade, sendo indicado na Figura 3 para o butadieno. Os planos nodais verticais sao distribuídos em número crescente, iniciando em Ψ₂ pois todo Ψ₁ nao possui plano nodal.

Para os demais polienos acíclicos sao empregados planos verticais tantos quantos forem necessários, sempre distribuídos tendo como referencial o centro geométrico do sistema π conjugado, sempre localizados equidistantes a este centro, com a máxima simetria possível, como indicado no Passo 3, o que resulta na Figura 4. É por este critério que, quando o sistema π conjugado está contido em número ímpar de átomos, alguns planos ficam localizados diretamente no átomo central do sistema.

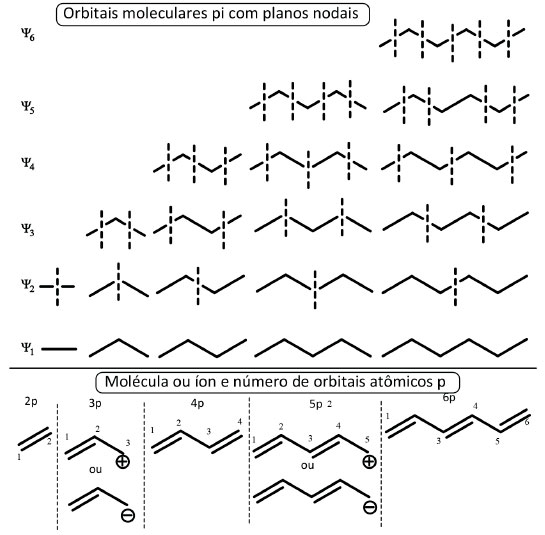Figura 4. Localizaçao dos planos nodais dos orbitais π para moléculas e íons acíclicos de 2 a 6 átomos empregando os Passos 1-3 do procedimento alternativo

Aplicando a estratégia descrita para os Passos 1-3 aos polienos conjugados acíclicos, cujo número de planos nodais de um dado orbital molecular Ψ_n é n-1, é possível localizar os planos nodais para os entes químicos de dois a seis átomos (o eteno foi incluído na análise como molécula de referência), Figura 4. O resultado final apresentado na Figura 4 deve ser reproduzido antes que o estudante avance na deduçao das energias de cada orbital, para que possa seguir com segurança na etapa da comparaçao das energias do sistema acíclico com o cíclico abaixo descrita.

No Passo 4 é inferida a topologia dos orbitais moleculares pois, uma vez distribuídos os planos nodais em cada orbital molecular Ψ_n, os orbitais atômicos p sao desenhados em cada átomo de todas as estruturas onde nao passe plano nodal, levando-se em conta a existência de inversao do sinal da fase determinada pela presença do plano nodal entre dois carbonos ou passando diretamente por um dos átomos da estrutura, como ilustrado na Figura 3.

No Passo 5, cada interaçao adjacente construtiva (em fase) dos orbitais atômicos p resulta em uma interaçao ligante energeticamente favorável à estabilizaçao do sistema, designada aqui pela letra l. No caso contrário, quando a interaçao adjacente ocorre com os orbitais atômicos p fora de fase, resulta em uma interaçao antiligante, energeticamente desfavorável à estabilizaçao do sistema, designada aqui pela letra a.

No Passo 6 sao avaliados os orbitais Ψ_n que possuem simultaneamente interaçoes ligantes e antiligantes, de forma que uma interaçao l é cancelada por uma a.

No Passo 7 é determinado o cômputo do número de interaçoes resultantes em cada orbital molecular Ψ_n totalizando as interaçoes ligantes e antiligantes de cada orbital, Figura 3. Quao maior o número de interaçoes ligantes resultante, mais estável é o orbital e menor a sua energia. Quao maior o número de interaçoes antiligantes resultante, maior a energia do orbital. A energia de cada orbital molecular é entao expressa em termos de energia ligante l e energia antiligante a.

Na Figura 5 encontra-se representado o resultado da aplicaçao dos Passos 1-7 para a série dos compostos acíclicos de dois a seis átomos de carbonos. Para a deduçao do valor da energia de um dado orbital é necessário que a designaçao da interaçao como ligantes l ou antiligantes a atenda rigorosamente o que preconiza o Passo 5. Por exemplo, nos orbital Ψ₂ do cátion alílico nao há interaçoes adjacentes, uma vez que o plano nodal secciona a cadeia no átomo central, o que resulta em densidade eletrônica nula neste carbono neste orbital. Assim, como nao existem interaçoes adjacentes entre dois orbitais atômicos, esta combinaçao gera um orbital molecular cuja energia é a mesma do orbital atômico p, Figura 5. Outra possibilidade de um orbital molecular ter este valor de energia é quando o número de interaçoes l é igual a de a.

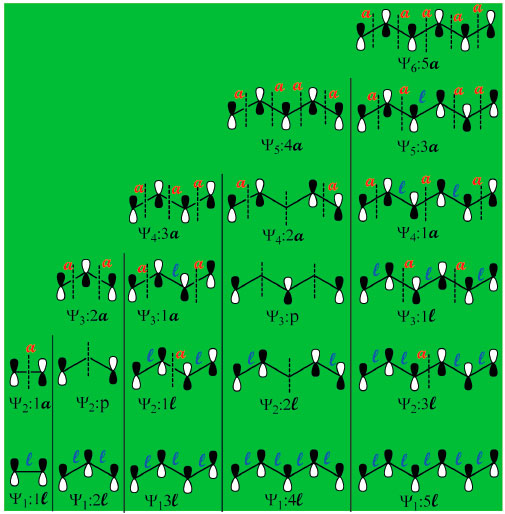Figura 5. Topologia e energias relativas dos orbitais π para moléculas e íons acíclicos conjugados de 2 a 6 átomos empregando o procedimento alternativo

Para fins de comparaçao, a estratégia alternativa foi estendida a moléculas e íons cíclicos, e assim poder comparar a energia total de estabilizaçao dos elétrons dos polienos cíclicos conjugados com os correspondes polienos acíclicos. A execuçao dos Passos 1 e 2 é idêntica para os sistemas acíclicos e cíclicos, mas para o Passo 3 é preciso uma pequena adaptaçao para os polienos cíclicos, pois sao empregados planos verticais e horizontais, distribuídos nesta ordem, de forma alternada e em número crescente, iniciando em Ψ₂. Assim, para a estrutura que corresponde a Ψ₂, localizar o plano vertical que divide a estrutura ao meio na vertical; em seguida, para Ψ₃ localizar o plano horizontal que divide a estrutura ao meio na horizontal. Ambos os planos passam pelo centro geométrico da estrutura, como ilustrado na Figura 3 (ver Passos 1 a 3 para o anel de três carbonos).

Caso a estrutura admita um maior número de orbitais moleculares Ψ_n, empregar dois planos nodais na vertical para Ψ₄ seguidos de dois na horizontal para Ψ₅, que sao localizados equidistantes do centro geométrico da estrutura e o mais afastado possível deste centro, tanto na vertical quanto na horizontal. Quando for necessário empregar três planos nodais, o processo passa a ser, para o novo orbital Ψ₆, uma combinaçao das localizaçoes dos planos verticais de Ψ₂ com Ψ₄ seguido dos planos horizontais de Ψ₃ com Ψ₅ para o novo Ψ₇. Na Figura 6 estao descritos os Passos 1-3 para os monociclos de três a sete átomos de carbonos.

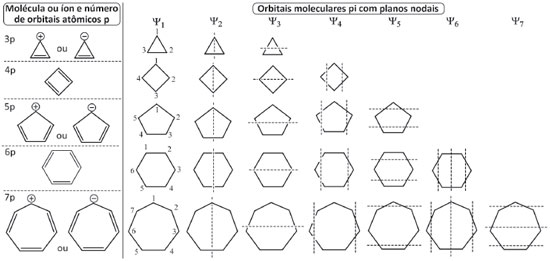Figura 6. Localizaçao dos planos nodais dos orbitais π para moléculas e íons cíclicos conjugados de 3 a 7 átomos empregando o procedimento alternativo dos Passos 1-3

É importante destacar que as estruturas devem ser escritas com um dos lados para baixo, exceto para o anel de quatro átomos, que é escrito com um vértice para baixo, Figura 4, e que a localizaçao dos planos sempre inicia em Ψ₂ pela vertical, mantendo-se daí em diante a alternância vertical/horizontal até preencher todos orbitais moleculares Ψ_n. Para cumprir o critério de máxima simetria na localizaçao de número ímpar de planos nodais, alguns planos podem ficar localizados diretamente sobre um ou dois átomos da estrutura em alguns Ψ_n ao passar por seu centro geométrico, dividindo-a ao meio.

O recomendável é que o estudante inicie a análise pelo anel de três átomos, aproprie-se do procedimento descrito nos Passo 1-3 da Figura 3 e entao aplique-os ao anel imediatamente superior em número de átomos, fazendo toda a análise até o anel de sete átomos, um de cada vez. O resultado apresentado na Figura 7 deve ser reproduzido antes que o estudante avance na deduçao das energias de cada orbital, para que possa seguir com segurança na etapa da comparaçao das energias do sistema cíclico com o acíclico abaixo descrita.

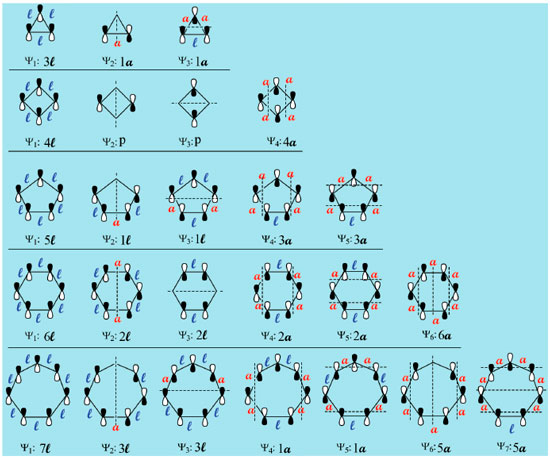Figura 7. Topologia dos orbitais π e deduçao das energias relativas para moléculas e íons cíclicos conjugados de 3 a 7 átomos empregando o procedimento alternativo

De posse das topologias e deduzidas as energias dos orbitais moleculares dos sistemas acíclicos e cíclicos, é possível proceder à comparaçao da estabilidade relativa destas duas classes de polienos conjugados.

Comparaçao das energias relativas dos orbitais de polienos e íons cíclicos e acíclicos empregando a estratégia alternativa e consequências químicas

Uma vez deduzida a topologia dos orbitais moleculares dos polienos, é possível avaliar a energia relativa dos orbitais moleculares dos orbitais moleculares π das substâncias e íons insaturados conjugados cíclicos e acíclicos, através da estratégia alternativa, e agora comparar a estabilidades das mesmas.

O método aqui proposto guarda analogia com os aspectos qualitativos do método de Hückel,¹⁶ no qual sao considerados apenas os elétrons π dos sistemas conjugados. Também a quantificaçao da energia dos orbitais moleculares é feita em unidades intrínsecas do método (unidades de α e β no método de Hückel, e unidades de interaçoes ligantes l e antiligantes a no método qualitativo alternativo aqui proposto).

Para um dado orbital, quanto maior o número de interaçoes ligantes l menor é a sua energia e, ao contrário, quanto maior o número das interaçoes antiligantes a maior é a energia do orbital Ψ_n, levando-se em conta que uma interaçao l é cancelada por uma a. Para uma espécie química específica, quanto maior o número de interaçoes ligantes l mais estável ela é.

Como cada elétron assume a energia do orbital que ocupa, na avaliaçao da energia de cada orbital é levado em consideraçao a quantidade dos elétrons e a correspondente energia de cada orbital para o somatório e a designaçao da energia eletrônica total (EET) dos elétrons π de cada molécula ou íon. Dessa forma, a EET é o somatório da energia de cada orbital molecular ocupado multiplicado pelo número de elétrons destes orbitais.

Na Figura 8 é apresentado o diagrama de energia dos orbitais dos alcenos conjugados de quatro a oito átomos de carbono, e do eteno para fins de comparaçao, cujos valores de energia de cada orbital molecular foram deduzidos de acordo com a Figura 5. Para um dado orbital ocupado Ψ_n de energia maior, há a repulsao com os elétrons do orbital molecular ligante imediatamente inferior Ψ_n-1. É por este motivo que o orbital Ψ₂ do butadieno, apesar de ter o valor algébrico 1l igual ao orbital Ψ₁ do eteno, encontra-se em patamar energético superior. É também por este motivo que os orbitais ocupados dos demais alcenos conjugados têm a posiçao relativa como indicado na Figura 8. Além disto, nos polienos acíclicos conjugados há a simetria na distribuiçao da energia dos orbitais ligantes e antiligantes em relaçao ao ponto central do diagrama de energia, que corresponde à energia do orbital atômico p do carbono. Dessa forma, quanto maior a energia de um dado orbital molecular ligante menor é a energia do seu correspondente antiligante, e fica fácil perceber que quanto maior for a energia do HOMO menor será a energia do LUMO de um dado polieno.

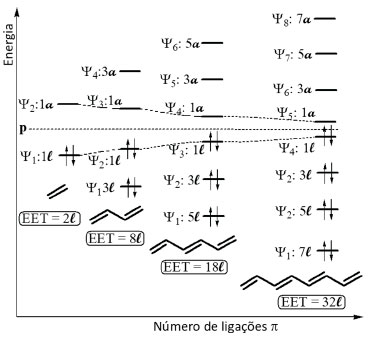Figura 8. Comparaçao da energia relativa dos orbitais π e da energia eletrônica total (EET) de alcenos empregando o procedimento alternativo

Uma consequência do arranjo energético deduzido para os polienos acíclicos conjugados é que o aumento do grau de conjugaçao faz diminuir a banda de energia HOMO-LUMO, o que justifica o fato de produtos naturais que apresentam esta unidade estrutural absorvam na regiao do visível, sendo corantes naturais, como o licopeno, o betacaroteno e a bixina, por exemplo. Outra consequência que emana da análise da Figura 8 é a deduçao da maior reatividade dos polienos de maior grau de conjugaçao nas reaçoes onde se comportam como nucleófilos, pois maior é a energia do HOMO em funçao do incremento do grau de instauraçao, sendo assim mais fácil doar os elétrons mais externos.

Um aspecto que é ensinado nos cursos de química orgânica é que o aumento da conjugaçao estabiliza melhor o conjunto dos elétrons π.¹⁰ Para explicar este fato, os textos de graduaçao lançam mao da teoria de ressonância, justificando que quanto maior o número de estruturas de ressonância para um polieno conjugado mais estável ele é, e assim discrimina-se a maior estabilidade do polieno conjugado em relaçao ao nao conjugado. Propomos aqui empregar o método alternativo para ampliar a explicaçao através dos orbitais moleculares. Para isto é necessário comparar as energias deduzidas na Figura 8. Entretanto, a comparaçao direta da EET entre os polienos acíclicos conjugados diferentes nao pode ser feita, pois tanto a quantidade de elétrons quanto de carbonos varia ao longo da série. É necessário normalizar o valor da EET por cada átomo de carbono do sistema conjugado. Empregando os dados da Figura 8 e exemplificando com o 1,3-butadieno e o 1,3,5-hexatrieno, a razao EET/n^o_Carbono para o 1,3-butadieno e o 1,3,5-hexatrieno é dada por 8l/4 e 18l/3, o que corresponde à razao de 2l/C e 3l/C, respectivamente. Assim, fica explicitado que o hexatrieno estabiliza mais o conjunto de elétrons π que o butadieno, por unidade de átomo de carbono do sistema conjugado. Aplicando esta linha de raciocínio para polienos acíclicos conjugados superiores, chega-se à conclusao de que o aumento da conjugaçao estabiliza melhor o conjunto dos elétrons π.

Uma vez compreendido o diagrama de energia para os polienos conjugados acíclicos da Figura 8, é possível empregar o mesmo método na construçao do diagrama dos polienos cíclicos, levando-se em consideraçao o valor da energia de cada orbital deduzido de acordo com a Figura 7. Para fins de exemplificaçao, na Figura 9 sao apresentados, num mesmo diagrama de energia, os orbitais moleculares do 1,3,5-hexatrieno e do benzeno, e também do par 1,3-butadieno/ciclobutadieno, para assim explicitar as consequências eletrônicas da aromaticidade e da anti-aromaticidade.

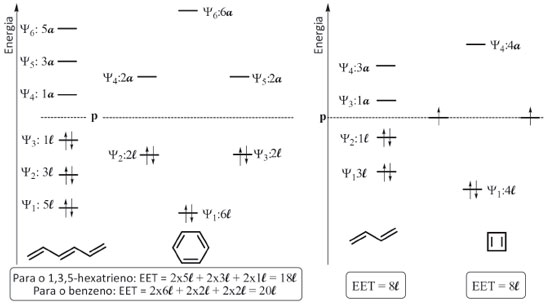Figura 9. Comparaçao das energias relativas dos orbitais π e da energia eletrônica total (EET) entre benzeno/1,3,5-hexatrieno e entre ciclobutadieno/1,3-butadieno empregando o procedimento alternativo

No cômputo da EET do benzeno, os seis de átomos de carbono sao capazes de estabilizar mais intensamente a mesma quantidade de elétrons π que o mesmo número de átomos no 1,3,5-hexatrieno, uma vez que a EET destas duas moléculas sao 20l e 18l, respectivamente, Figura 9. Como o número de carbonos é o mesmo, podemos aplicar diretamente estes valores como indicativos da maior estabilidade do benzeno em relaçao ao polieno acíclico; ao se aplicar a razao EET/n^o_Carbono, chega-se ao valor 3,3l, que é 10% superior ao do 1,3,5-hexatrieno. Por ambas as análises se conclui que essa melhor acomodaçao dos elétrons π no benzeno, consequência da existência de orbitais degenerados e da menor energia relativa destes elétrons, é funçao da sua aromaticidade.

Para ilustrar a aplicaçao do método alternativo na análise de antiaromaticidade, é feita a comparaçao do ciclobutadieno com o 1,3-butadieno na Figura 9. Pelo método alternativo chega-se ao mesmo valor de EET para as duas substâncias e nao num valor menor para o polieno cíclico, como evidenciado para o par benzeno/1,3,5-hexatrieno. O fato do ciclobutadieno nao estabilizar os elétrons π mais intensamente que o correspondente polieno acíclico é agravado pela verificaçao da existência de dois orbitais moleculares degenerados cujas energias sao de igual valor ao do orbital atômico p do carbono, e que dois elétrons desemparelhados ocupam estes dois orbitais moleculares, o que confere um caráter de biradical à substância. Todos estes aspectos explicam o comportamento antiaromático do ciclobutadieno e, portanto, sua maior instabilidade em comparaçao ao 1,3-butadieno, que possui todos os elétrons π emparelhados e num patamar energético inferior ao do orbital atômico p do carbono.

CONCLUSAO

A abordagem didática desenvolvida conduz o estudante à autonomia na análise da aromaticidade e suas consequências, pois permite que deduza a topologia dos orbitais π de moléculas, cátions e ânions de polienos acíclicos e cíclicos e, em seguida, deduza as energias relativas dos orbitais π destes sistemas conjugados, conclua por ocorrência de degenerescência como no benzeno e análogos, e assim possa comparar a estabilidade relativa de espécies químicas e julgar aromaticidade e antiaromaticidade. O estudante pode aplicá-la e nao ser refém das apresentaçoes estáticas dos textos de graduaçao (e muitos de pós-graduaçao) que apresentam estes fatos como coisa pronta.

AGRADECIMENTOS

O autor agradece o suporte financeiro do Conselho Nacional de Desenvolvimento Científico e Tecnológico – CNPq, da Coordenaçao de Aperfeiçoamento de Pessoal de Nível Superior – CAPES, e da Fundaçao de Amparo à Pesquisa do Estado da Bahia – FAPESB. Também agradecemos ao CNPq a bolsa de produtividade em pesquisa e ao Instituto Nacional de Ciência e Tecnologia-INCT em Energia e Ambiente.

REFERENCIAS

1. Halford, B.; Chem. Eng. News 2016, March 28, 24. Para um editorial interessante sobre dificuldade de aprendizado relacionado à existência de conflito de informaçao química entre livros-texto, e-book e informaçoes da Internet ver: Pienta, N. J.; J. Chem. Educ. 2018, 95, 187.

2. Sendur, G.; Toprak, M.; Chem. Educ. Res. Pract. 2013, 14, 431; Grove, N. P., Bretz. S. L.; Chem. Educ. Res. Pract. 2012, 13, 201.

3. Araujo Neto, W. N.; Quim. Nova Esc. 2007, 13; Pessoa Jr, O.; Quim. Nova Esc. 2007, 25; Gois, J.; Giordan, M.; Quim. Nova Esc. 2007, 34.

4. Mullins, J. J.; J. Chem. Educ. 2008, 85, 83.

5. Caramori, G. F.; Oliveira, K. T.; Quim. Nova 2009, 32, 1871; Glukhovtset, M.; J. Chem. Educ. 1997, 74, 132; Stanger, A.; Chem. Commun. 2009, 1939.

6. Cunha, S.; Quim. Nova 2003, 26, 948.

7. Cunha, S.; Quim. Nova, no prelo, doi: 10.21577/0100-4042.20170197.

8. Para contribuiçao recente de outros autores ver: Martins, B. S.; Lüdtke, D. S.; Moro, A. V.; Quim. Nova 2017, 40, 342; de Freitas, J. J. R.; Avelino, R. A.; Mata, M. M. S.; Santos, C. S.; Almeida, C. L. A.; Freitas, J. C. R.; Freitas Filho, J. R.; Rev. Virtual Quim. 2017, 9, 1597.

9. Pearson, R. G.; J. Chem. Educ. 1981, 58, 753.

10. Allinger, N. L.; Cava, M. P.; de Jongh, D. C.; Johnson, C. R.; Lebel, N. A.; Stevens, C. L.; Química Orgânica, Guanabara Dois: Rio de Janeiro, 1978; Barbosa, L. C. A.; Introduçao à Química Orgânica; Pearson: Sao Paulo, 2011; Bruice, P. Y.; Química Orgânica, 4^a ed., Prentice Hall: Sao Paulo, 2006, vols. 1 e 2; Carey, F. A.; Química Orgânica, 7^a ed., McGraw-Hill-Bookmann: Sao Paulo, 2011, vols. 1 e 2; Streitwieser, A.; Heathcock, C. H.; Kosover, E. M.; Introduction to Organic Chemistry, 4^th ed., Macmillan Publishing Company: New York, 1992; Clayden, J., Greeves, N., Warren, S.; Organic Chemistry, 2^nd ed., Oxford University Press: Oxford, 2012; Constantino, M. G.; Química Orgânica Curso Básico Universitário, LTC: Rio de Janeiro, 2008, vols. 1 e 2; Klein, D.; Química Orgânica, 2^a ed., LTC: Rio de Janeiro, 2016, vols. 1 e 2; McMurry, J.; Química Orgânica, 3^a ed., Cengage Learning: Sao Paulo, 2016, vols. 1 e 2; Morrison, R. T.; Boyd, R. N.; Organic Chemistry, 6^th ed., Prentice Hall International, Inc.: Hoboken, 1992; Pine, S. H.; Organic Chemistry, 5^th ed., McGraw-Hill International Edition: Singapore, 1987; Solomons, T. W. G.; Fryhle, C. B.; Química Orgânica, 10^a ed., LTC: Rio de Janeiro, 2012, vols. 1 e 2; Vollard, K. P. C.; Schore, N. E.; Química Orgânica: Estrutura e Funçao, 6^a ed., Bookman: Sao Paulo, 2013.

11. Pauling, L. Sherman, J.; J. Chem. Phys. 1933, 1, 606.

12. Frost, A. A.; Musulin, B.; J. Chem. Phys. 1953, 21, 572.

13. Berson, J. A.; Angew. Chem., Int. Ed. 1969, 8, 781; Berson, J. A.; Chemical Creativity; Wiley-VCH: Weinheim, 1999; Karachalios, A.; Erich Hückel (1896-1980) From Physics to Quantum Chemistry; Springer: New York, 2010.

14. Doering, W. E.; Detert, F. L.; J. Am. Chem. Soc. 1951, 73, 876; Kikuchi, S.; J. Chem. Educ. 1997, 74, 194; Balaban, A. T.; Schleyer, P. v. R.; Rzepa, H. S.; Chem. Rev. 2015, 105, 3436.

15. Nardholm, S.; Bäck, A.; Bacskay, G. B.; J. Chem. Educ. 2007, 84, 1201; Taubmann, G.; J. Chem. Educ. 1992, 69, 96; Vasconcellos, M. L. A. A.; Quim. Nova 2014, 37, 171; Leal, R. C.; Moita Neto, J. M.; Lima, F. C. A.; Feitosa, C. M.; Quim. Nova 2010, 33, 1211; Kutzelnigg, W.; J. Chem. Comp. 2006, 28, 25.

16. Para uma leitura adequada a químicos orgânicos: Gleiter, R.; Haberhauer, G; Aromaticity and Other Conjugation Effects, Wiley-VCH: Weinheim, 2012; Zimmerman, H. E.; Quantum Mechanics for Organic Chemistry, Academic Press: New York, 1975.

17. A topologia deduzida para alguns orbitais moleculares dos polienos cíclicos pelo método alternativo (por exemplo Ψ₅ do benzeno e Ψ₅ do íon ciclopentadienila) nao é rigorosamente a mesma obtida pelos métodos da química-quântica (ver referências 16 e 10) mas as tendências das energias relativas sim. Como o método proposto permite deduzir qualitativamente a diferença de energia entre polienos acíclicos e cíclicos e leva o estudante a compreender a origem desta diferença, nos parece um preço muito pequeno a pagar pelo caráter simples do método e do benefício pedagógico proporcionado.

#Programa de Pós-Graduaçao em Ciências, Energia e Ambiente, Centro Interdisciplinar em Energia e Ambiente, Universidade Federal da Bahia, Campus de Ondina, 40170-115 Salvador - BA, Brasil