JBCS

INTRODUCTION

Use of computational models for prediction of a certain phenomenon is an important stage of the scientific method, since the quantification of variables and the prediction of how the event can be processed are important information that help in the elucidation of the mechanism (detailed steps) by which such phenomenon occurs. The validation of a model or method used in the description and explanation of a phenomenon depends mainly on information and data obtained experimentally, since the model or the method functions as a theoretical representation of a fact / phenomenon.^1,2

An important fact is the role of regulatory agencies in different countries in the production of drugs and food, and in the guidelines for the validation and use of different bioanalytical techniques for this purpose. The authors highlight the similarities and variations of the guidelines for validation of bioanalytical methods issued by the main regulatory agencies in the world (United States Food and Drug Administration - USFDA, European Medical Agency - EMA, Brazilian Agency for National Health Surveillance - ANVISA, and the Ministry of Health, Labour and Welfare - MHLW, Japan) and that the diffusion of these validation regulatory standards assists in the quality of the food and drug production process, resulting in a product with better hygienic-sanitary profiles, stability, resistance to temperature variations and increased expiration date (degradation time) of such product.³

Validation of methods and models has been used in several areas of the knowledge, in special for in silico determinations, and the strategy for such use depends on what the scientist aims to predict, such as example the assessment of the toxicity of nanomaterials using Quantitative Structure-Activity Relationships (QSAR) models, then validated in agreement with the principles of the OECD (Organization for Economic Co-operation and Development) to ensure clarity, consistency and reliability of model forecasts for regulatory purposes.⁴

Paramagnetic NMR techniques and computational modeling approaches for analyses of molecular structures and receptor-ligand complexes have been used as alternatives to reduce the difficulty of obtaining structural data from biological systems because they are complex, dynamic and with high degree of disorder. However, they point out that 3D modeling, validated from paramagnetic NMR experimental data, is an important tool useful for understanding mechanism, recognition and biomolecular function of complex biological systems.⁵

Other different strategies for validation and use of models can be thus cited:

1) Selection of active molecules with potential inhibition of tumors and possible action in the treatment of heart failure with the aid of pharmacophore-based virtual screening, validated from its specificity and sensitivity to active molecules;⁶

2) The obtaining new caffeine analogues molecules with epithelial anticancer activity using molecular docking and thus validated by redocking and low RMSD between the experimental crystallographic pose and the calculated one;⁷

3) Study with QSAR models, built using PLS and PCR, of new molecules derived from artemisinin, validated from the prediction of the biological activity, followed by comparison with experimental data;⁸

4) Validation of the HF/6-31G** method used in the molecular modeling of artemisinin with antimalarial activity, from the correspondence with experimental data of geometric parameters.⁹

We have studied the caffeine molecule and analogues using pharmacophore-based virtual screening and statistical analysis and obtained results indicating the caffeine epithelial anticancer potential.⁷ We will continue here with the search for information that allows the choice of computational method for future studies from the molecular modeling of caffeine and analogues.

In this study, different experimental data of the caffeine molecule were used to evaluate the efficiency of the Hartree-Fock (HF) and Density Functional Theory (DFT/B3LYP) methods, here used with seven different basis sets. The best evaluated method here compared with the experimental data was validated, and it may be indicated to model the caffeine molecule and similar ones to investigate epithelial anticancer activity.

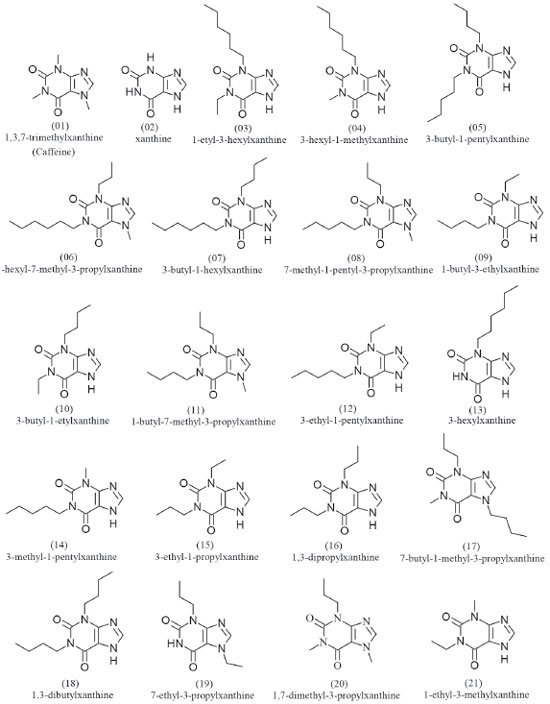
METHODS

Selection of molecules for pharmacophore perception

A set of 19 caffeine analogues with biological activity against epithelial cancer (ICT₅₀ < 0.24 mM) were selected from the literature.¹⁰ This activity corresponds to Epidermal Growth Factor (EGF) prevention in the malignant transformation of epidermal cells from JB6 lineage mice, C141 (JB6 P+) sensitive of developmental, and ICT₅₀ corresponds to inhibition of cell transformation. The most active molecules were selected because the activity is a determining factor in the construction of the pharmacophore.^11,12 The caffeine was inserted in this set because it is the prototype molecule, i.e. the common basis for the studied activity, whereas xanthine is the structural basis for the set of selected molecules. Selection resulted in a total of 21 molecules.

The crystallographic structure of the caffeine was retrieved from the Cambridge Structural Database (CSD, http://webcsd.ccdc.cam.ac.uk/) and the other 20 molecules were drawn using the ChemSketch software.¹³ The HyperChem 7 software¹⁴ was used to pre-optimize the geometry of the molecules, at the MM+ Force Field Molecular Mechanics level.

The pharmacophore was then generated using the PharmaGist¹⁵ web server, adopting the caffeine molecule as pivot (kept frozen). The set of molecules aligned with greater number of ligands and higher score was considered the best candidate for a pharmacophore model.¹⁶

Caffeine molecule optimization using HF and DFT/B3LYP methods

The optimization of the caffeine molecule was performed using the Gaussian 09 software¹⁷ with the HF and DFT/B3LYP methods and the basis sets STO-3G*, 3-21G*, 3-21G**, 6-31G*, 6-31G**, 6-311G* and 6-311G**, totalizing 14 different calculations. The choice of basis sets with polarization function is due to an improved efficiency in the optimization, since the atomic orbitals suffer distortions, or they polarize the molecules formed. Also, possibility of displacement of charges outside the atomic nucleus results in an accumulation of charges in a given region (polarization).¹⁸ Studies suggest that most of calculations using basis sets without polarization function are inadequate choices to reproduce experimental values.^19,20

Thus, theoretical data regarding geometric parameters, heat capacity (at constant pressure), IR, Raman and NMR spectra were here calculated for the caffeine molecule.

Evaluation of methods and basis sets

The Root Mean Square Deviation (RMSD) values observed between experimental caffeine crystallographic data (bond length, bond angle and torsion angle)²¹ and the theoretical ones here calculated using the different methods and basis set were analized. Theoretical errors regrding the experimental values of heat capacity,²² spectroscopic data of IR and Raman,²³ as well as RMSD values regarding to NMR spectroscopic data,²⁴ were also analyzed.

Linear correlation analyses (theoretical × experimental data, theoretical data × RMSD) were carried out for comparison of the methods.²⁵ Classifications (A - D) were assigned to the different methods and basis sets, based on the best matches with the experimental data and as well as correlations, for final classification of each method and basis set regarding the different experimental data.

RESULTS AND DISCUSSION

Pharmacophore model

The pharmacophore model candidate with the highest scoring and highest number of aligned molecules (21 molecules) was selected as the best model. Score and features of the pharmacophore model thus chosen are available in Table 1.

In Figure 1 the final pharmacophore can be visualized. PharmaGist indicates a total of 6 features (or general characteristics - GF) equivalent to different pharmacophoric groups; 6 spatial characteristics (SF) are equivalent to conformation and location in the 3D space of pharmacophoric regions.

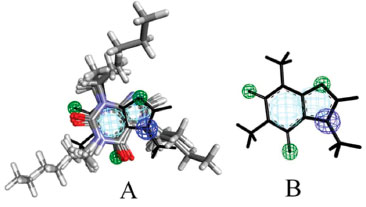Figure 1. Pharmacophore model. A) Multiple alignment and B) Caffeine molecule

The GF and SF characteristics are respectively represented by two aromatic regions (Ar), three hydrogen bonding acceptor regions (Acc) and one cationic atom (Pos). These regions or pharmacophoric groups could be strongly relevant to biological activity against epithelial cancer in this chemotype here investigated. The 21 molecules then selected to build the pharmacophore model can be visualized in Figure 2.

Figure 2. Structures of the molecules used in pharmacophore generation

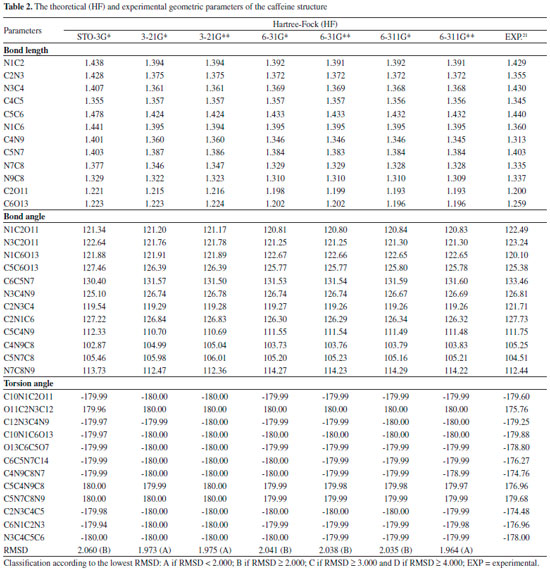
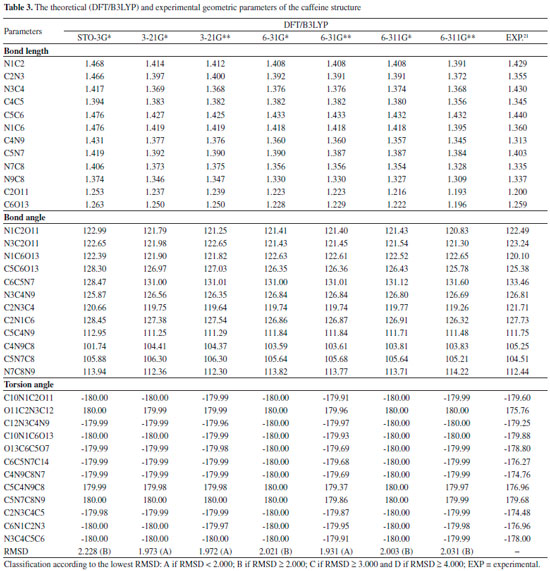
Quantum chemical calculations

Geometric Parameters

With the spatial arrangement accessed from the pharmacophore model here built for caffeine it was possible to calculate bond lengths, bond angles and torsion angles between the atoms of the molecule.

Data on bond lengths, bond angles and torsion angles between the atoms of the caffeine molecule, here calculated using different methods and basis sets, as well as experimental data of crystallography of caffeine are presented in Tables 2 and 3. 2D Structure of caffeine, with its respective numbering is available in Figure 3.

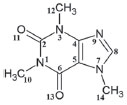Figure 3. Caffeine molecule with numbered atoms

From Tables 2 and 3 it can be inferred that the HF and DFT/B3LYP methods showed good agreement with the experimental data for bond length. The mean of the errors (module values) in relation to the experimental values for HF were: STO-3G* = 0.025; 3-21G* = 0.004; 3-21G* = 0.004; 6-31G* = 0.010; 6-31G** = 0.010; 6-311G* = 0.011; 6-311G** = 0.011. The values for DFT/B3LYP were: STO-3G* = 0.053; 3-21G* = 0.014; 3-21G* = 0.014; 6-31G* = 0.007; 6-31G** = 0.007; 6-311G* = 0.005; 6-311G** = 0.011. The basis set 3-21G*, 3-21G**, 6-31G** e 6-31G** showed the best results for binding length in both HF and DFT/B3LYP, which indicates a better structural representation of the caffeine molecule in these bases in relation to the parameter bond length.

The geometric parameter of bond angle was better represented in the structures calculated by the DFT/B3LYP method, with the STO-3G base set with the lowest value (in module) for error mean (0.048) and with most other bases presenting values for mean error around 0.3. The HF method presented error mean values for all base sets above 0.4, which can also be considered a good result if one evaluates the magnitude of the error that is relatively low.

For the parameter torsion angle all the bases in both the HF and the DFT/B3LYP methods presented mean error values around 1.2 which attests similar structural representativeness for this parameter in both methods in all basis sets.

The DFT/B3LYP method have indicated lower values of RMSD, compared to the experimental data, considering the basis set 3-21G* (RMSD = 1.973), 3-21G** (RMSD = 1.972) and 6-31G** (RMSD = 1.931). Using the Hartree-Fock method, lower RMSD values are obtained for the basis sets 3-21G* (1.973), 3-21G** (1.975) and 6-311** (1.964). These results and the above discussions on the three structural parameters evaluated (Bond Length,Bond Angle, and Torsion Angle) show that the DFT / B3LYP method of general way presented the best results (lower error values) in relation to the experimental data than HF, which resulted in the lower values of RMSD presented by the DFT / B3LYP method. However, the HF method presented low RMSD values in all base sets and can also be considered good results.

Classification of RMSD values within A and B limits (error values lower or around 2.0) allow us to verify that, for the analysis of the caffeine geometry, all the methods and basis set here investigated agree with the experimental data. DFT/B3LYP and HF methods have been used and reported in vast literature for calculation of geometric parameters, also indicating excellent agreement with the experimental data, such as observed in this work. Calculations were performed, for example, with 2,2'-Bithiophene,²⁶ silatran molecules²⁷ and 2-amino-4-Methoxy-6-Methyl-Pyrimidine as well.²⁸

Table 4 shows correlations between the theoretical vs experimental values and between theoretical vs RMSD values for geometric parameter of the caffeine structure. Best correlations with the experimental values were observed for the HF method, indicating classification A (Correlation > 0.70) for most of the basis set used, and B classification (0.50 < correlation < 0.70) for most of the basis set, when comparison was performed with the RMSD values. The DFT/B3LYP method showed low correlations between experimental vs RMSD values, with almost all of the basis sets showing classification D (correlation <0.30). Only the 3-21G* basis set shows classification C for correlation with experimental data.

These correlations express the relationship of the theoretical data obtained with the RMSD values and the experimental geometric parameters values. However, for the study performed here, these results are not sufficient to disqualify the evaluated methods. More experimental data (heat capacity and IR, Raman and NMR spectra) will be compared with theoretical data and discussed in the next sections for better qualification and classification of the methods in evaluation.

Thermochemical parameter - Heat capacity

In Table 5, the different methods and basis set here used for calculation of thermochemical heat capacity as well as the experimental value for caffeine are listed. The Gaussian 09 software¹⁷ returns thermochemical results for the heat capacity, simulating a constant pressure environment, at a temperature of 298.15 Kelvin. The heat capacity is an important parameter for the validation of the computational method to be used in the caffeine molecule, because it can be expressed from contributions of translational, rotational, and vibrational energies, important thermodynamic parameters intrinsically related to the structural geometric parameters.²⁹

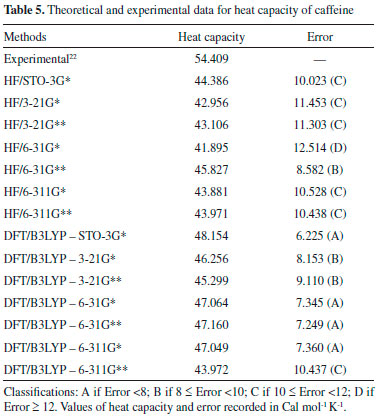
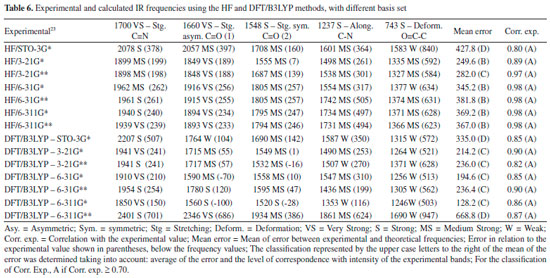
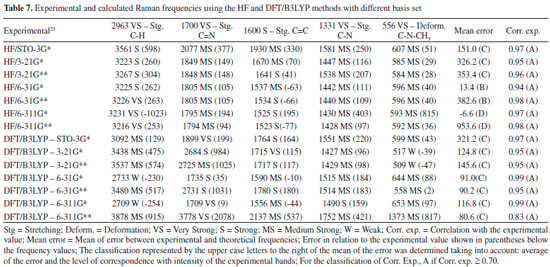
The DFT/B3LYP method indicated better results for calculation of the heat capacity, since it resulted in lower error compared to the experimental value. For this method, the basis set STO-3G* (Error = 6.225), 6-31G** (Error = 7.249), 6-31G* (Error = 7.345) and 6-311G* (Error = 7.360) indicated better agreement or adjust to the experimental values. In these analyses, results obtained using the HF method were all close to the worst value obtained for the DFT/B3LYP method, with error values between 10.023 and 12.514. Due to the lower error values obtained using the DFT/B3LYP method, best classifications were then observed (most of the basis set classified as A - error < 8). The HF method indicated classification C (10 ≤ Error < 12) with most of the basis set used, whereas classification B (error = 8.582) was only indicated for the 6-31G** basis set.

Theoretically (with calculations carried out using the Gaussian 09 software), the heat capacity can be obtained from a partition function that comprises contributions of four different components: translational motion (3/2 R, where R is the gas constant), electronic (null contribution), rotational (3/2 R, similar to translational) and vibrational (3Rf, where f is a function derived by Einstein and improved by Debye, considering the number of oscillating atoms at a given temperature, which contribute to the vibrational energy).²⁹

It can be inferred that calculations for the caffeine molecule using the DFT/B3LYP method indicated better results for these contributions, compared to the HF method. The efficiency of the DFT/B3LYP method for calculation of the heat capacity may be related to the integration of the density functional (configured by the integration of several derivatives of the density functional), step that leads to an increase in the accuracy of the calculation performed^30,31 which does not exist in the HF calculation.

However, the good result obtained using HF/6-31G** (error = 8.582 and classification B) could be due to the presence of the maximum polarization function (** = insertion of polarization functions for the d, p orbitals), which may provide a lowering of the error values for that basis set.^28,32-34

Spectroscopic parameters

The spectroscopic parameters (Infrared, Raman and NMR) are excellent methods for identification of substances and play an important role in the structural characterization of organic molecules such as caffeine.

Infrared and Raman Spectra

Results for the IR and Raman spectra can be seen in Figure 4 and Tables 6 and 7. The error values (in brackets) show how the main bands vary according to the experimental frequencies.

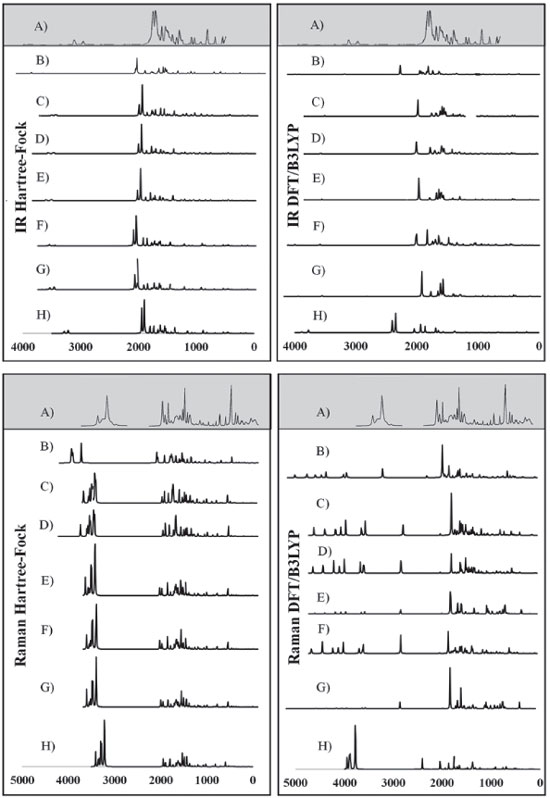Figure 4. Experimental IR and Raman spectra (A),²³ calculated for caffeine using HF and DFT/B3LYP methods with different basis set: (B) STO-3G*; (C) 3-21 G*; (D) 3-21 G**; (E) 6-31G*; (F) 6-31 G**; (G) 6-311G*; (H) 6-311G**

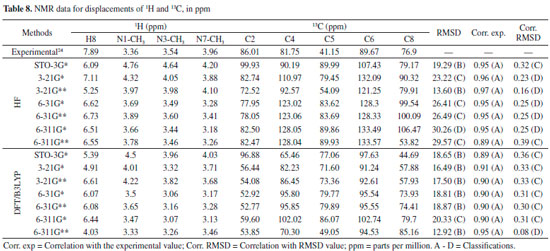
In general, the bases 6-31G * and 6-31G** in both HF and DFT/B3LYP methods showed better agreement with the experimental values in IR and Raman spectra. The HF / 6-31G * method in the Raman spectrum showed lower mean error values for frequencies and good agreement with the intensities of the main experimental bands. he HF / 6-31G** method in the same spectrum showed better correspondence with the intensities of the main experimental bands. Also, in the Raman spectrum, both the 6-31G* and the 6-31G** basis set of the DFT/B3LYP method presented low values of mean of error and good correspondence (being similar) to the intensities of the experimental bands (see Figure 4).

From Figure 4 it can be verified that for IR analysis the HF method in the basis set 6-31G* (E), 6-31G** (F), 6-311G* (G) e 6-311G** (H), although they have a slight shift to the left, has a greater similarity both in the intensities of the bands and in the frequencies with the experimental spectra (A). However, for the same method, the basis set STO-3G (B), 3-21G * (C), HF / 3-21G** (D) showed little similarity in both frequencies and intensity of the bands. Similar observations for Raman spectra data can also be seen in Figure 4. These observations confirm the good match of the spectra calculated by the HF method in the basis set 6-31G* (E), 6-31G** (F), 6-311G* (G) e 6-311G** (H) with the experimental spectra, and less similarity of the spectra in the basis set STO-3G (B), 3-21G* (C), HF/3-21G** (D).

In relation to the IR spectra it can be observed that the experimental data of the C=N bond (1700 VS – Stg), when simultaneously checking the frequency and intensity of the bands, there is a better match with HF/6-31G**, HF/6-311G* e HF/6-311G**. C=O bond (1) (1660 VS – Stg. asym) presented good correspondence with all bases of the HF method except STO-3G*. In C=O bond (2) (1548 S – Stg. sym) all bases in the HF and DFT / B3LYP methods showed similar intensity of the bands and close to the experimental ones, with emphasis on the DFT / B3LYP method with most of the basis set with low value of error compared to experimental frequency. The bonds C-N (1237 S – Along) and O=C-C (743 S – Deform), in general, had better agreement with the basis set of the HF method, mainly in relation to the intensity of the bands with the frequencies showing a sharp shift to the left.

In the Raman spectra, HF/6-31G* e HF/6-31G** presented better agreement with the experimental data in the bonds C-H (2963 VS – Stg), C=N (1700 VS – Stg.), C=C (1600 S – Stg), C-N (1331 VS – Stg) e C-N-CH3 (556 VS – Deform), when analyzed simultaneously the frequencies and intensity of the bands. However, most basis set (both in HF and in DFT/B3LYP methods) presented a reasonable agreement with the experimental spectra data (see tables 6, 7 and Figure 4), since, typically the ab initio harmonic vibrational wave numbers are larger than those obtained experimentally.³⁵

Negative values denote shift of the rightmost frequency values compared to experimental spectra, whereas positive values mean that the shift is more to the left. The positive pattern of the error values indicates that, on average, the calculated IR and Raman spectra are shifted more to the left, in relation to the experimental spectra (see figure 4). In most quantum chemical methods this disagreement can be attributed to the anharmonicity and partially to the general tendency of these methods to overestimate the force constants in the exact equilibrium geometry. Anharmonicity can be large and show important deviations, specifically as in vibrations involving central atoms with isolated pairs and C-H vibrations.

Checking the tables 6, 7 and Figure 4 note the tendency of the minimum basis (STO-3G*, 3-21G* e 3-21G**) lower agreement with the experimental values of frequency and intensity of the bands when compared to the split-valence basis (6-31G*, 6-31G**, 6-311G*, 6-311G**) with better concordances. This trend is in agreement with the one investigated by Stephens and coworkers, which obtained results of frequencies and intensity of the bands closest to the experimental ones with the use of larger basis set.³⁶

Classification assigned to each method was based on the mean error values observed between the frequencies calculated using different methods (and basis sets) and the experimental frequencies values, as well as the correspondence between the intensity of the main bands.

Although none of the methods indicated A (maximum) classification, the HF method showed good agreement with the experimental data for the IR spectra, with most of the basis set with B classification. The HF method also indicated two basis sets (6-31G* and 6-31G**) with B classification for the Raman spectra. The good classification of the HF method is mainly due to the good agreement between the intensities of the theoretical and experimental bands.^23,37

Correlations between theoretical and experimental values indicate results, respectively, between 0.80 and 0.99 for the DFT/B3LYP and HF methods, for both IR and Raman spectroscopic data. These strong correlations obtained signalize that frequencies of the major bands would well correspond to the experimental values if the left of the most displacements (represented by the mean error) were disregarded and the spectra overlapped.

NMR spectra

The chemical shift values for hydrogen and carbon atoms of the caffeine molecule can be seen in table 8. In ¹H, The individual analyzed displacements showed better correspondence with the experimental data in HF/3-21G* for H8, DFT/B3LYP – 6-311G** for N1-CH₃, HF/6-31G* and HF/6-31G** for N3-CH₃ and HF/3-21G* for N7-CH₃. Already for ¹³C the best matches were verified in HF/3-21G*, HF/6-311G* and HF/6-311G** for C2, DFT/B3LYP – 3-21G* for C4, DFT/B3LYP – 6-311G** for C5, DFT/B3LYP – 3-21G* and DFT/B3LYP – 3-21G** for C6 and HF/STO-3G* and DFT/B3LYP – 6-31G** for C8. A general analysis of table 8 allows to infer that the DFT/B3LYP method indicates better agreement with the experimental values for chemical displacement data. However, the data obtained for the HF method also present reasonable agreement with the experimental data. Different from IR and Raman spectra (where the minimum bases showed results with less correspondence with the experimental data), in the calculation of chemical shifts in NMR data, all basis sets presented satisfactory results.

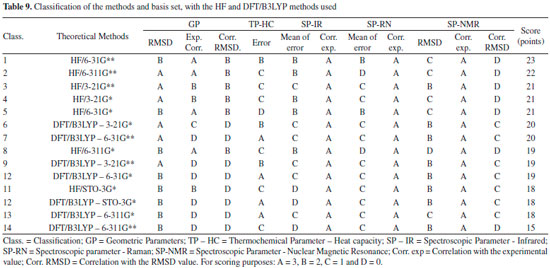
The lower RMSD values and the good classifications (majority with B) of this method confirm such consideration. HF method indicates most of the classifications equal to C, and only the basis set STO-3G* and 3-21G** with classification B. Both methods indicate excellent correlation between theoretical and experimental data for all basis set here evaluated, with A classification in all the cases, which it can be attributed to the low values of RMSD, where the theoretical displacements range from 3.18 to 133.57.

Correlation between the theoretical data and RMSD showed low values in both methods. DFT/B3LYP method showed classifications C for values equal or higher than 0.30, whereas the HF method showed a low correlation with of the RMSD values below 0.30, with classification D.

Good results for NMR data calculated with the DFT/B3LYP method have been also obtained, such as reported in works with 4', 7-dihydroxy-8-prenylflavan,³⁸ as well as 1-methylpyrrolidine-2-one-3-Halo-derivatives.³⁹ Here, the HF method used with basis set 6-31G** has also shown good results for NMR data prediction, with B classification.

Selection of the best computational method

The different experimental data (Geometric parameters, Heat capacity, IR spectra, Raman and NMR) to which the theoretical data using HF and DFT/B3LYP methods were compared and allowed the construction of Table 9.

In this table, the classification data obtained using the HF and DFT/B3LYP methods were organized for each basis set analyzed. In general, the HF method indicated better agreement with the experimental data, since it occupies the top-five positions of the seven possible for this method, with a difference of only two points from the former to the fifth. The best-ranked basis set is the 6-31G** (23 points). The best basis set (3-21G**) for the DFT/B3LYP method reached only the sixth position (20 points). The STO-3G* basis set of both methods were among the worst ranked (18 points), followed by the 6-311G* and 6-311G** of the DFT/B3LYP method, the last two ones of the ranking (18 and 15 points, respectively).

Regards to the caffeine molecule, the 6-31G** basis set, in general, showed better results for each method in comparison to both the STO-3G and 3-21G bases with their respective polarization functions. These data are similar to those reported in the literature,^32,33,40 where the polarization functions (**) in the separate valence basis sets (6-31G and 6-311G) provide more meaningful and accurate results with lower error values, when compared with experimental data.^41-43

The best performance of the HF method in most of our comparisons with the experimental data of the caffeine molecule could be due to the accuracy of the DFT/B3LYP method in performing the calculations be influenced for errors sources that are depending on the integration grid and the number of points used in the numerical integration, where a small integration grid is not recommended for the DFT/B3LYP calculation. Other additional sources of error other than those cited for the DFT/B3LYP method are those similar to the HF method (accuracy of integration and convergence of SCF and CPHF).^30,31,36,44

CONCLUSIONS

Pharmacophore generated from caffeine and analogs with biological epithelial anticancer activity indicates pharmacophoric regions that comprised practically the entire extent of the caffeine molecule, which resulted in the choice of bond lengths, bond angles and torsion angles of the atoms coincident with these regions (see tables 2 and 3).

Both HF and DFT/B3LYP methods had good agreement with the experimental data of geometric parameters of caffeine. In general, the HF method revealed better agreements with the experimental data for both IR and Raman spectra. The DFT/B3LYP method indicated better agreement with experimental data of both heat capacity and NMR spectra.

The general classification of the methods and basis set here used indicated that HF method with the basis set 6-31G** has the best agreement with the experimental datasets evaluated (GP, TP-HC, SP-IR, SP-RN e SP-NMR).

The best rating of HF/6-31G** could be attributed to your excellent individual ratings, mainly because it is the only basis set of the HF method to show B classification for TP-HC and the only one among all basis sets to have most of the classifications in A and B categories, and only one classification in C and D (both in SP-NMR). For comparison purposes, the second best classified method and basis set (HF/6-311G**) indicated two C classifications and two D.

The HF / 6-31G** method that indicated better agreement with the experimental data was properly validated, and it can be used to optimize and obtain theoretical data for the caffeine molecule and similar molecules with epithelial anticancer activity.

ACKNOWLEDGEMENTS

We acknowledge support provided by the Postgraduate Program in Biodiversity and Biotechnology of Amazon (PPG-Bionorte), To the, Paraense Museum Emilio Goeldi (MPEG). Laboratory of Molecular Modeling and Simulation System of Federal Rural University of Amazônia (UFRA-Brazil) and Computational Laboratory of Pharmaceutical Chemistry, School of Pharmaceutical Sciences of Ribeirao Preto, University of Sao Paulo, Ribeirao Preto (USP/RP) and PROPESP/UFPA.

REFERENCES

1. Yang, X. S.; Engineering Mathematics with Examples and Applications, Academic Press: San Diego, 2017.

2. Chicone, C.; An Invitation to Applied Mathematics: Differential Equations, Modeling and Computation, Academic Press: San Diego, 2016.

3. Kadian, N.; Raju, K. S.; Rashid. M.; Malik, M. Y.; Taneja, I.; Wahajuddin, M.; J Pharm. Biomed. Anal. 2016, 126, 83.

4. Puzyn, T.; Jeliazkova, N.; Sarimveis, H.; Marchese, R. R. L.; Lobaskin, V.; Rallo, R.; Richarz, A. N.; Gajewicz, A.; Papadopulos, M. G.; Hastings, J.; Cronin, M. T. D.; Benfenati, E.; Fernández, A.; Food. Chem. Toxicol. 2017, 17, 30556.

5. Pilla, K. B.; Gaalswyk, K.; MacCallum, J. L.; Biochim. Biophys. Acta. 2017, 1865, 1654.

6. Chen, L.; Wang, D.; Cao, Y.; Zhu, Z.; Chai, Y.; Chin. Herb. Med. 2016, 8, 126.

7. Costa, J. S.; Costa, K. S. L.; Cruz, J. V.; Ramos, R. S.; Silva, L. B.; Barros, B. D. S.; H. T. P. C.; Santos, C. B. R.; Macêdo, W. J. C.; Curr. Pharm. Des. 2017, 23, 1.

8. Vieira, J. B.; Braga, F. S.; Lobato, C. C.; Santos, C. F.; Costa, J. S.; Bittencourt, J. A.; Brasil, D. S.; Silva, J. O.; Hage-Melim, L. I.; Macêdo, W. J. C.; Carvalho, J. C. T.; Santos, C. B. R.; Molecules 2014, 19, 10670.

9. Santos, C. B. R.; Vieira, J. B.; Formigosa, A. S.; Costa, E. V. M.; Pinheiro, M. T.; Silva, J. O.; Macêdo, W. J. C.; Carvalho, J. C. T.; J. Comput. Theor. Nanosci. 2014, 11, 553.

10. Rogozin, E. A.; Lee, K. W.; Kang, N. J.; Yu, H.; Nomura, Miyamoto, M.; K. I.; Conney, A. H.; Bode, A. M.; Dong, Z.; Carcinogenesis 2008, 29, 1228.

11. Kandakatla, N.; Ramakrishnan, G.; Adv. Bioinformatics 2014, 812148.

12. Starosyla, S. A.; Volynets, G. P.; Bdzhola, V. G.; Golub, A. G.; Protopopov, M. V.; Yarmoluk, S. M.; Bioorg. Med. Chem. Lett. 2014, 24, 4418.

13. ACD/Chemsketch Freeware, version 12.00: Advanced Chemistry Development, Inc, Toronto, ON, Canada, 2010.

14. ChemPlus, Modular Extensions to HyperChem, Release 6.02. Gainesville: Molecular Modeling for Windows Hyper Inc. 2000.

15. Schneidman-Duhovny, D.; Dror, O.; Inbar, Y.; Nussinov, R.; Wolfson. H. J.; Nucleic Acids Res. 2008, 36, 223.

16. Schneidman-Duhovny, D.; Dror, O.; Inbar, Y.; Nussinov, R.; Wolfson. H. J.; J. Comput. Biol. 2008, 15, 737.

17. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A. Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery Jr., J. A.; Peralta, J. E.; Ogliaro, F.; Bearpark, M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, J. M.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, Ö.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J.; Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009.

18. Santos, C. B. R.; Lobato, C. C.; Vieira, J. B.; Brasil, D. S. B.; Brito, A. U.; Macêdo, W. J. C.; Carvalho, J. C. T.; Pinheiro, J. C.; Comput. Mol. Biosci. 2013, 3, 66.

19. Leach, A. R.; Molecular Modelling: Principles and Applications, Prentice Hall: Englewood Cliffs, 2001.

20. Zuschneid, T.; Fischer, H.; Handel, T.; Albert, K.; Häfelinger, G.; Z. Naturforsch., B: J. Chem. Sci. 2004, 59, 1156.

21. Sutor, D. J.; Acta Crystallogr. 1958, 11, 453.

22. Dong, J. X.; Li, Q.; Tan, Z. C.; Zhang, Z. H.; Liu, Y. J. Chem. Thermodyn. 2007, 39, 108.

23. Gunasekaran, S.; Sankari, G.; Ponnusamy, S.; Spectrochim. Acta, A 2005, 61, 117.

24. Kan, L. S.; Borer, P. N.; Cheng, D. M.; Ts'o, P. P.; Biopolymers 1980, 19, 1641.

25. Anderson, J. E.; Bond, A. M.; Jones, R. D.; O'halloran, R. J.; Electroanal. Chem. 1981, 130, 113.

26. Orti, E.; Viruela, P. M.; Shnchez-Marin, J. C.; Tomás, F.; J. Phys. Chem. 1995, 99, 4955.

27. Csonka, G. I.; Hencsei, P.; Theochem. 1996, 362, 199.

28. Kumar, L.; Chaudhary, J.; J. Appl. Phys. 2017, 9, 30.

29. Atkins, P.; Paula, J.; Physical Chemistry, 10^th ed. rev., Oxford University Press: Oxford, 2014.

30. Becke, A. D.; J. Chem. Phys. 1992, 97, 9173.

31. Perdew, J. P.; Chevary, J. A.; Vosko, S. H.; Jackson, K. A.; Pederson, M. R.; Singh, D. J.; Fiolhais, C.; Phys. Rev. B 1992, 46, 6671.

32. Hariharan, P. C.; Pople. J. A.; Theor. Chim. Acta 1973, 28, 213.

33. Francl, M. M.; Pietro, W. J.; Hehre, W. J.; Binkley, J. S.; Gordon, M. S.; J. Chem. Phys. 1982, 7, 3654.

34. DeTar, D. F.; J. Phys. Chem. A 1998, 102, 5128.

35. Pavel, I.; Szeghalmi, A.; Moigno, D.; Cîntă, S.; Kiefer, W.; Biopolymers 2003, 72, 25.

36. Santos, C. B. R.; Carvalho, J. C. T.; Macêdo, W. J. C.; Rational Design of Antimalarial Drugs, Novas Ediçoes Acadêmicas, 2016, 204.

37. Muthu, S.; Prasath, M.; Paulraj, E. I.; Balaji, R. A.; Spectrochim Acta, A 2014, 120, 185.

38. Alcântara, A. F. C.; Teixeira, A. F.; Silva, I. F.; Quim. Nova 2004, 27, 371.

39. Melo, U. Z.; Silva, R. G. M.; Yamazaki, D. A. S.; Pontes, R. M.; Gauze, G. F.; Rosa, F. A.; Rittner, R.; Basso, E. A.; J Phys. Chem. A 2015 ,119, 2111.

40. Rassolov, V. A.; Ratner, M. A.; Pople, J. A.; Redfern, P. C.; Curtiss, L. A.; J. Comput. Chem. 2001, 22, 976.

41. McLean, A. D.; Chandler, G. S.; J. Chem. Phys. 1980, 72, 5639.

42. Levine, I. N. Q.; Quantum Chemistry. 4^th ed., New York: Prentice-Hall, 1991.

43. Stephens, P. J.; Devlin, F. J.; Ashvar, C. S.; Chabalowski, C. F.; Frisch, M. J.; Faraday Discuss. 1994, 99, 103.

44. Ricca, A. C.; Bauschlicher Jr., W.; J. Phys. Chem. 1995, 99, 9003.