JBCS

INTRODUCTION

"A graph that shows constituents of a molecule and their connectivity is known as molecular graph and such representation is usually referred as topological representation of molecule.¹ Molecular graphs

"are usually characterized by different topological indices for correlation of chemical structure of a molecule with biological, chemical or physical properties. Studies have reported several applications of different topological indices in quantitative structure-activity relationship (QSAR) and quantitative structure-property relationship (QSPR), virtual screening and computational drug designing.^2-7

"So far, many different topological indices have been developed, and most of them are only graph descriptors.^8-18 Only a few indices have shown their correlation with biological, chemical or physical chemical properties of certain molecules.^19-21 For example, Zagreb indices (M₁ & M₂) were first reported by Gutman and Trinajestic for the correlation of chemical structure with ϖ electrons.²² However, later M₁ and M₂ were associated with extent of branching in a molecule. They are described by equation (1) & (2) for a graph G=(V,E), where V to be the vertex set and E to be the edge set of G. The degree d_p of the vertex p is the quantity of edges of G incident with p. The length of a most limited path in a graph G is a distance d(p,q) amongst p and q."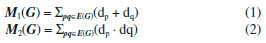

"Another topological index is atom-bound connectivity (ABC) that was introduced by Estrada et al.^23,24 Later, studies have reported its exceptional correlation with thermodynamic properties of organic molecules, specifically with heat of formation of alkanes. This index is characterized by Equation (3) considering the graph similar to Zagreb indices"

"Another molecular descriptor that was correlated with thermodynamic properties is Sankruti index. This index was introduced in 2016 by S. M. Hosamani and it shows considerable correlation with entropy of some organic molecules.²⁵ It is characterized as equation (4) considering the above mentioned graph conditions"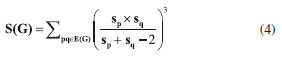

"This study is designed to calculate Zagreb, ABC and Sanskruti indices for two oxides of Cu (CuO & Cu₂O). It will allow us to compare these indices with the experimentally determined entropy, enthalpy and other physical properties of CuO and Cu₂O."

THEORY AND METHODS

Structure of copper (I) oxide (Cu₂O)

Cu₂O is a naturally occurring reddish ore that is mainly used in chemical sensors, solar oriented cells, photo-catalysis and batteries.^26-28 Crystal structure of Cu₂O is composed on small cubic unit cells based on Cu and O atoms (Figure. 1a). Analysis of the crystal lattice showed that each Cu atom is linked with two O atoms; in turn every O atom is connected with four Cu atoms (Figure 1b)"

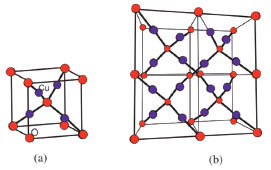Figure 1. Copper(I) oxide . A) Unit cell of . B) Three dimensional crystal lattice of Cu and O are shown in blue and red spheres, respectively

Here, we have considered monolayer of Cu₂O for convenience. To determine the indices for Cu₂O we choose the settings of this graph as; G ≅ Cu₂O[m,n] be the chemical graph of Cu₂O with (m x n) unit cells in the plane. More preciously, m represents the number of unit cells in row and n represents the number of unit cells in column. Also for our convenience we represents Cu₂O[m,n] as a graph G. The Figure 1(b) is representing Cu₂O[2,2]. Also Figure 2 represent one sheet view of Copper(I) oxide Cu₂O[4,4]. Computational analysis showed that the quantity of vertices and edges of Cu₂O[m,n] are 7mn+2m+2n+2 and 8mn, respectively. In Cu₂O[m,n], the number of zero degree vertices is 4, the number of one degree vertices is 4m+4n-4, the number of two degree vertices is 6mn-2m-2n+2 and the number of four degree vertices is mn (Table 1)."

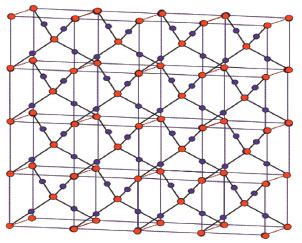Figure 2. One sheet view of copper(I) oxide [4, 4]

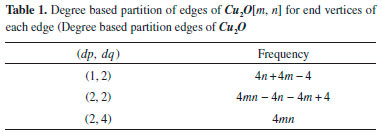
In the next Theorem, we have computed the exact result of first and second Zagreb index for the chemical graph Cu₂O[m, n]."

Theorem 1. "Consider the graph of G ≅ Cu₂O[m,n] with m, n ≥ 1, then its first and second Zagreb index is equal to,"

Proof. "Let G be the crystallographic structure of [m, n].The first Zagreb index is computed as below:"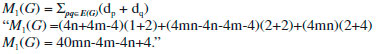

"By using Table 1 and Equation 1 the second Zagreb index are computed as below:"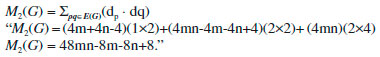

"In the next Theorem, we have computed the exact result of ABC index for the chemical graph Cu₂O[m, n]."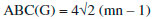

Theorem 2. "Consider the graph of G ≅ Cu₂O[m,n] with m, n ≥ 1, then its ABC index is equal to,"

Proof. "Let G be the chemical graph of Cu₂O[m,n]. Then by using Table 1 and equation (3) the ABC index is computed as below:"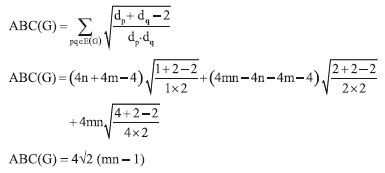

"The Table 2 shows partition of edges of the chemical graph Cu₂O[m,n] depending on the sum of degrees of the neighbouring vertices of end vertices of each edge."

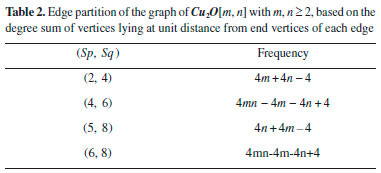
"The next Theorem shows the exact value of Sanskruti index of Cu₂O[m,n]."

Theorem 3. "Consider the graph G ≅ Cu₂O[m,n] with m, n ≥ 2, then its Sanskruti index S(G) is equal"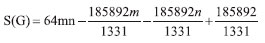

Proof. "Let G be the crystallographic structure of Cu₂O[m,n]. Then by using Table 2 and equation (4) the Sanskruti index S(G) is computed as follows."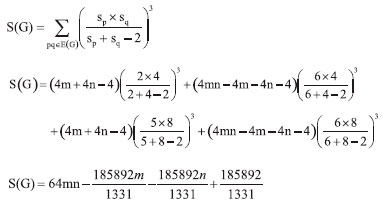

Structure of copper(II) oxide (CuO)

The crystal structure of Copper(II) oxide (CuO) is composed on monoclic unit cells (Figure 3a). Here we have considered monolayer of CuO for convenience. To find the indices we choose the settings of this graph as; let G ≅ CuO[m,n] be the chemical graph of CuO with (m x n) unit cells in the plane. The Figure 3b is representing the lattice of CuO[4,4]. Computational analysis showed that number of vertices and edges of CuO[m,n] are 8mn+2m+2n and 12mn, respectively. In CuO[m,n] the number of one degree vertices are 2n, the number of two degree vertices are 2mn+4m+2n, the number of three degree vertices are 4mn-2n and the number of four degree vertices are 2mn-2m."

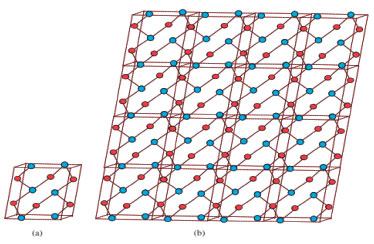Figure 3. Copper (II) oxide CuO: (a) is the unit cell with blue and red circles represents copper and oxygen atom, respectively (b) shows the lattice CuO[4, 4]

In the next Theorem, we have computed the exact value of first and second Zagreb index for the chemical graph CuO[m, n]."

Theorem 4. "Consider the graph of G ∼= CuO[m, n] with m, n ≥ 1, then its first and second Zagreb index is equal to,"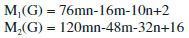

Proof. "Let G be the crystallographic structure of CuO[m, n]. The first Zagreb index is computed as: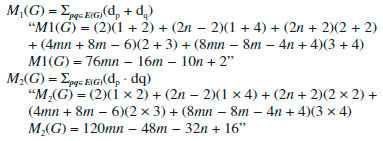

"In the next Theorem, we have computed the exact result of ABC index for the chemical graph CuO[m, n]."

Theorem 5. "Consider the graph of G ∼= CuO[m, n] with m, n ≥ 1, then its ABC index is equal to"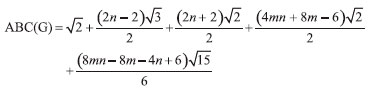

Proof. Let G be the chemical graph of CuO[m, n]. Then by using Table 3 and equation (3) the ABC index is computed as below: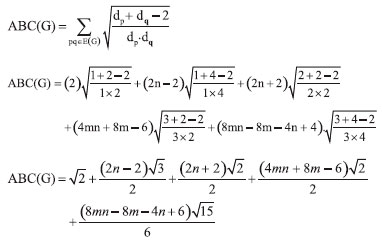

"The Table 4 shows partition of edges of the chemical graph CuO[m, n], which depends on the sum of degrees of the neighboring vertices."

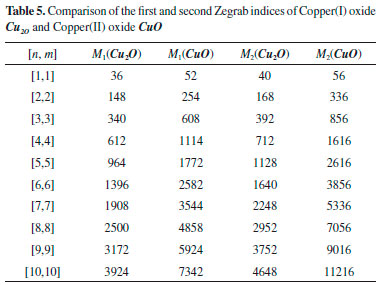
The next Theorem shows the exact value of Sanskruti index of CuO[m, n] .

Theorem 6. "Consider the graph G ∼= CuO[m, n] with m, n ≥ 2, then its Sanskruti index S(G) is equal to:"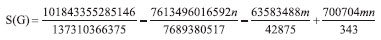

Proof. Let G be the crystallographic structure of CuO[m, n]. Then by using Table 4 and equation (4) the Sanskruti index S(G) is computed as follows:

RESULTS AND DISCUSSIONS

"In this section we have compared the first (M1) and second Zegrab (M2) indices of Copper(I) oxide Cu_2O and Copper(II) oxide CuO which is shown in Table 5. Analysis of the data showed that both the indices are higher in CuO compared to those of . For instance, M1(CuO)/M1() for [1,1] cell is 1.44 and the ratio increases to 1.943 for [7,7] and then it decrease to 1.87 for [10,10] cell. On the other hand, M2(CuO)/M2() for [1,1] is 1.40 and the ratio gradually increases to 2.413 for [10,10] cell."

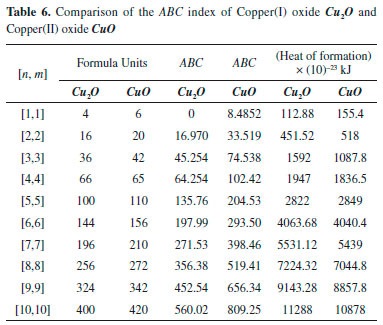
"Comparison of ABC indices for both the oxides of Copper showed higher values for CuO compared to those of (Table 6). For example, ratio of ABC(CuO)/ABC() for [2,2] cell is 1.95 and it decreases to 1.44 for [10,10]. This shows its decreasing trend with the increase of cells."

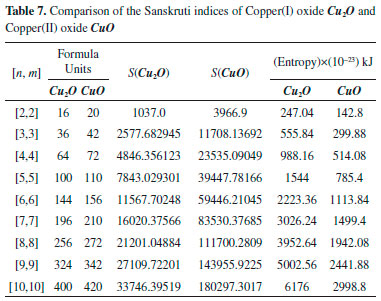
"In the Table 7, we gave a comparison of the Sanskruti indices of Copper(I) oxide Cu_2O and Copper(II) oxide CuO. Analysis of the data showed that host higher Sanskruti index compared to CuO. The S(CuO)/S() for [2,2] is 3.825 and it increases to 5.34 for [10,10]. This shows its increasing trend with the increase of cells."

A topological index is a numerical value that is calculate form molecular graph for explaining the relationship of chemical structure with physiochemical properties. So far, several applications of different indices have been reported for organic molecules, such as entropy and enthalpy determination, chirality identification,⁹ ZE-isomerism¹⁰ and heterosystem studies.¹⁸ The topological indices can be very helpful for crystalline compounds to correlate their structure with physiochemical properties. Therefore, we have determined Zagreb, ABC and Sunskurti indices for Cu₂O and CuO. Additionally, we compared these indices with the physical properties these oxides as described in Pubchem (https://pubchem.ncbi.nlm.nih.gov/)."

"Zagreb indices (M1 & M2) were initially considered for total energy of ϖ-electrons in organic molecules.¹² However, later they were associated with extent of branching in a molecular graph [10,11]. Analyses revealed higher M1 and M2 for CuO compared to those of Cu₂O at any cubic level i.e. at any equal value of (m x n) (Table 5). It suggests more branching in CuO compared to Cu₂O. It may cause more compactCuO (Density: 6.315 g/cm³) structure compared to Cu2O (6.0 g/cm³). Moreover, higher melting point of CuO (1599 K) compared to that of Cu₂O (1505 K) may also be associated to the higher branching."

"ABC indices of Cu₂O and CuO were calculated at different unit cells as shown in Table 6. Analysis of the data showed higher ABC indices for CuO compared to those of Cu₂O (Table 6). Figure 4 shows that ABC indices increase exponentially with number of cells (m x n) for both the oxides of copper. On the other hand, a linear relation of ABC index was observed with formula units (Figure 5). Since, ABC index has previously been linked with the thermodynamic properties" of different alkanes,^7,11 "therefore, we determined the heat of formation per different units cells of both the oxides from the reported real molar enthalpy of formations (Table 6). For example, experimental molar enthalpy for CuO is -156 kJ mol^-1 so for one formula unit it will be -156/6.022x10^-23 kJ. The obtained value then multiplied with the number of formula units present in each cell to get the enthalpy for the cell. Similarly, enthalpy for Cu₂O calculated considering standard molar enthalpy -170 kJ mol^-1 (Table 6). Analysis of the data showed that ABC index is not strongly associated with enthalpy of formation for the oxides of copper as reported in case of alkanes.^6,13" Therefore we determined a mathematical relationship, by using equation generator (http://www.1728.org/threepts.htm), between the ABC indices and the heat of formation of both the oxides of copper as below: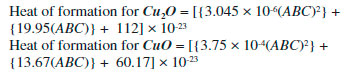

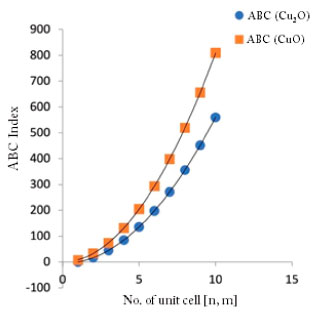Figure 4. ABC indices of Cu₂O and CuO showing exponential increase with number of units cells (at x-axis)

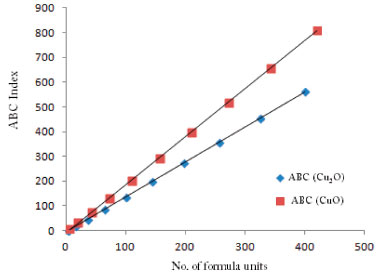Figure 5. ABC indices of Cu₂O and CuO showing linear increase with number of formula units (at x-axis)

These equations can be used for the transformation of ABC indices into the approximate heat of formation of the oxides of Cu at any cubic level.

Figure 6 shows a linear relation of Sanskruti indices with number of formula units and analysis showed higher indices for Cu₂O compared to CuO. Previous studies have shown an association of Sanskruti indices with entropy of octance.¹⁵ Here we calculated the entropy of both the oxides at different cells from the standard molar entropy. For instance, standard molar entropy for CuO is 93 J mol^-1 K^-1 so for one formula unit it will be 93/6.022x10^-23 J K^-1, and for each cell we just multiplied the obtained value with the no. of formula units present in the cell. Similarly entropy for Cu₂O calculated considering standard molar entropy 43 J mol^-1 K^-1 (Table 7). Analysis of the data showed a considerable difference between the Sanskruti indices and entropies for the oxides of Cu (Table 7). Therefore, we determined a mathematical relation for the transformation of Sanskruti indices into approximate entropies of both the oxides of copper as below: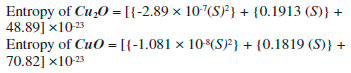

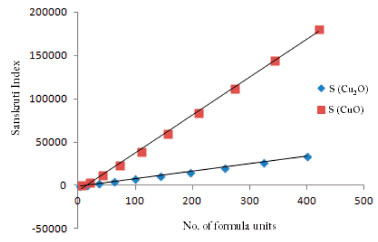Figure 6. Sanskrit indices of Cu₂O and CuO showing linear increase with number of formula units (at x-axis)

CONCLUSIONS

In conclusion, ABC and Sanskuriti indices of Cu₂O and CuO showed considerable difference with the experimentally reported entropy and enthalpy of these oxides. On the other hand, Zagreb index and all these indices showed exponential increase with the number of unit cells. On the other hand, these indices showed a linear behavior with number of formula units, suggesting that we may need a slight transformation of these indices for better explanation of physical properties of crystalline compounds."

ACKNOWLEDGEMENTS

The authors are grateful to the anonymous referees for their valuable comments and suggestions that improved this paper. This research is supported by the Start-up Research Grant 2016 of United Arab Emirates University (UAEU), Al Ain, and United Arab Emirates via Grant No. G00002233 and UPAR Grant of UAEU via Grant No. G00002590.

REFERENCES

1. Babujee, J. B.; Applied Mathematical Sciences 2012, 6, 5383.

2. Baig, A. Q.; Imran, M.; Khalid, W.; Naeem, M.; Can. J. Chem. 2017, 95, 674.

3. Gao, W.; Siddiqui, M. K.; Imran, M.; Jamil, M. K.; Farahani, M. R.; Saudi Pharm. J. 2016, 24, 258.

4. Cotton, F. A.; Wilkinson, G.; Murillo, C. A.; Bochmann, M.; Advanced Inorganic Chemistry, John Wiley and Sons: Hoboken, 1999.

5. Ekimov, E. A.; Sidorov, V. A.; Bauer, E. D.; Melnik, N. N.; Curro, N. J.; Thompson, J. D.; Nature 2004, 428, 5425.

6. Ivanciuc, O.; Curr. Comput. Aided Drug Des. 2013, 9, 153.

7. Soleimani, N.; Nikmehr, M. J.; Tavallaee, H. A.; J. Natl. Sci. Found. Sri Lanka 2015, 43, 127.

8. Gutman, I.; Furtula, B.; MATCH Commun. Math. Comput. Chem. 2012, 68, 131.

9. Gutman, I.; Mathematical Chemistry Monographs No. 1, Kragujevac, 2006.

10. Hu, Y.; Li, X.; Shi, Y.; Xu, T.; Gutman, I.; MATCH Commun. Math. Comput. Chem. 2005, 54, 425.

11. Nikoli, S.; Trinajsti, N.; Toli, I. M. In Complexity in Chemistry; Rouvray, D. H., Bonchev D., eds.; Francis and Taylor: London, 2003, p. 29.

12. Randic, M.; J. Am. Chem. Soc. 1975, 97, 6609.

13. Ramakrishnan, S.; Senbagamalar, J.; Babujee, J. B.; International Journal of Computing Algorithm 2013, 2, 224.

14. Rouvray, D. H.; J. Comput. Chem. 1987, 8, 470.

15. Shegehalli, V. S.; Kanabur, R.; Journal of Mathematics 2016, ID 4341919, doi: 10.1155/2016/4341919. DOI: http://dx.doi.org/10.1155/2016/4341919.

16. Vukicevic, D.; Furtula, B.; J. Math. Chem. 2009, 46, 1369.

17. Wiener, H.; J. Am. Chem. Soc. 1947, 69, 17.

18. Yang, J.; Sun, H.; He, J. L.; Tian, Y.; Chen, C. F. J.; J. Phys.: Condens. Matter 2007, 19, 346.

19. Shao, Z.; Wu, P.; Zhang, X.; Dimitrov, D.; Liu, J.; IEEE Access. 2018, 6, 27604.

20. Shao, Z.; Wu, P.; Gao, Y.; Gutman, I.; Zhang, X.; Appl. Math. and Comp. 2017, 315, 298.

21. Gutman, I.; Das, K. C.; MATCH Commun. Math. Comput. Chem. 2004, 50, 83.

22. Gutman, I.; Trinajst, N.; Chem. Phys. Lett. 1972, 17, 535.

23. Estrada, E.; Torres, L.; Rodriguez, L.; Gutman, I.; Ind. J. Chem. 1998, 37A, 849.

24. Gao, W.; Baig, A. Q.; Khalid, W.; Farahani, M. R.; Maced. J. Chem. Chem. Eng. 2017, 36, 1.

25. Hosamani, S. M.; Journal of Applied Mathematics and Computing 2017, 54, 425

26. Chen, K.; Sun, C.; Song. S.; Xue. D.; Cryst. Eng. Commun. 2014, 16, 52.

27. Yuhas, B. D.; Yang, P.; J. Am. Chem. Soc. 2009, 131, 3756.

28. Zhang, J.; Liu, J.; Peng, Q.; Wang, X.; Li, Y.; Chem. Mater. 2006, 18, 867.