Artigo
| Synthesis, electronic and spectral properties of new 1,3,4-thiadiazole compounds and the spectral analysis of their conformers using density functional theory |
|
Muhammet Serdar ÇavuşI,*; Tuğba ÇelikII
I. Biomedical Engineering Department, Faculty of Engineering and Architecture, Kastamonu University, 37100, Kastamonu, Turkey Recebido em: 10/08/2018 *e-mail: mserdarcavus@kastamonu.edu.tr In this study, new 1,3,4-thiadiazole compounds were synthesised and characterised by FT-IR, 1H-NMR, UV-vis spectroscopy and elemental analysis, Furthermore, the relationship between the electronic and spectral data of the 16 conformers of each compound was investigated by theoretical calculations; the theoretical data were compared with the experimental results. The B3LYP hybrid functional level with a 6-311++g(2d,2p) basis set was used to obtain the ground state geometries, frontier molecular orbital energies, band gap energies and chemical reactivity parameters and to perform a spectral analysis of the compounds. Significant correlations were calculated between the minimum molecular energy and the N-H and C=O vibrational frequencies and the NH proton chemical shifts of the conformers. The charge density on the nitrogen atom and the delocalisation index of the highly polar N-H covalent bond were investigated by quantum theory of atoms in molecules. The effect of conformer structure on the theoretical results and its role in interpreting the experimental data were presented, and it was theoretically shown that the activity degree of the non-aromatic electronegative atoms or groups of atoms in the intramolecular interaction was a very important factor in determining the electronic and spectral properties of each compound. INTRODUCTION Heterocyclic systems containing nitrogen and sulphur atoms have recently become very attractive for therapeutics.1,2 The molecules including the 1,3,4-thiadiazole moiety are used in many applications because they contain two heterocyclic aromatic moieties. Their different derivatives have been used as antimicrobials,3 antifungal,4 antibacterial,5 antileishmanial,6 analgesic, antidepressant,7,8 etc. In this study, 5-[3-phenylypropyl]-N-[2'-methoxycarbonylphenyl]-1,3,4-thiadiazol-2-amine (Compound I) and 5-(1-methyl-2-phenylethenyl)-N-[2'-methoxycarbonylphenyl]-1,3,4-thiadiazol-2-amine (Compound II) were synthesized, and the conformal structures of these compounds were investigated theoretically. The literature contains many reports on the conformational analysis of different molecules, for example, Belaidi et al.9 performed the IR analyses of five conformational structures of butyl methacrylate. Their study focused on the detailed assignment of band intensities and potential energy distribution percentages, and the compatibility between theory and experiment was also examined. The conformational distribution of citronellal by correlating its structure with theoretical chemical shifts based on nuclear magnetic resonance (NMR) data was studied by Nardini et al.10 Okada and Ando11 clarified the relationship between vibrational frequencies of absorption bands in the far-IR region and the local conformations of fully aromatic imides and polyimides. In another study, Bardak et al.12 studied the conformational, interactive, magnetic and electronic properties of isophthalic acid to investigate its effects on human health, toxicology and biodegradability. Ortega et al.13 conducted a comprehensive structural and conformational analysis of the (-) - S-parent as well as an analysis of the electronic structures of different molecular conformations of unnatural species, in an attempt to explain how the conformational stability of the system was controlled by the stereoelectronic effects. Furthermore, density functional theory (DFT) and NMR-based conformational analyses of methyl galactofuranosides were compared by Richards et al.,14 and Galf-specific Karplus-like equations were developed from these conformations. Many experimental studies have been supported by conformational and structural analyses, and structural differences between conformations have been revealed by these analyses. However, conformational analyses have mostly been used to compare experimental and theoretical data and to understand the nature of experimental results.15-23 Here we have considered the question, 'What is the relationship between the electronic and spectral properties of the conformers of a compound, and does the relationship have distinctive characteristics?' We also investigated how molecular conformations affected the minimum molecular energy, frontier molecular orbital (FMO) energies, some electronic parameters such as chemical hardness and electronegativity, and the UV, IR and NMR spectra. Moreover, the importance of choosing appropriate conformers to interpret experimental data was discussed. We also analysed the relation between intramolecular interactions and the minimum energy and showed the influence of intramolecular interactions on the UV, IR and 1H-NMR spectra. The Kohn-Sham DFT24,25 method was used to theoretically investigate the characteristic and spectroscopic properties of the conformers of the synthesised compounds. The molecular structures and FT-IR, UV and 1H-NMR spectra of the conformers were characterised using the B3LYP method with the 6-311++g(2d,2p) basis set. In addition, using the same method, the highest occupied molecular orbital (HOMO), the lowest unoccupied molecular orbital (LUMO) energies, electrostatic potential (ESP) maps and electronic parameters were calculated. Furthermore, quantum theory of atoms in molecules (QTAIM) analysis was performed to determine the intramolecular interactions and any correlations between electron charge distribution, molecular energy and spectral data. An analysis of the data was performed, and the relationship between the electronic and spectral properties of the conformers was studied in detail.
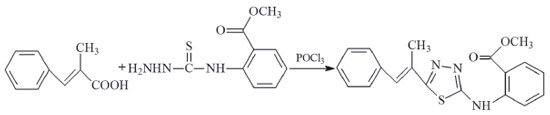
METHODS Experimental process 5-[3-Phenylypropyl]-N-[2'-methoxycarbonylphenyl]-1,3,4-thiadiazol-2-amine (compound I) The synthesis of compound I is shown in Figure 1. In the experimental process, 4-phenylbutyric acid (3.53 g, 10 mmol) and N-(2-methoxycarbonylphenyl)thiosemicarbazide(2.25 g, 10 mmol) were mixed and placed in a refrigerator at 4 °C for 2 h. Subsequently, POCl3 (0.96 mL, 30 mmol) was added dropwise to the cold mixture during stirring. Reflux was continued at 90 °C for 2 h. After the reaction was completed (followed by thin layer chromatography (TLC) by comparing with the raw material), the mixture was cooled to room temperature and added into the stirred ice-cold water. The mixture was then neutralised (pH≈8) using an ammonia solution (10%). The precipitated product was filtered, washed using distilled water and recrystallized from tetrahydrofuran (THF). (Yield: 86%, melting point: 107 °C). Elemental analysis (C19H19N3O2S): theoretical (%): C, 64.57; H, 5.42; N, 11.89; experimental (%): C, 64.63; H, 5.47; N, 12.17.
5-(1-methyl-2-phenylethenyl)-N-[2'-methoxycarbonylphenyl]-1,3,4-thiadiazol-2-amine (compound II) The synthesis route of compound II is presented in Figure 2. 4-phenylbutyric acid (3.51 g, 10 mmol) and N-(2-methoxycarbonylphenyl)thiosemicarbazide(1.67 g, 10.0 mmol) were used as the raw materials instead. The same procedures in the synthesis of compound I were performed. (Yield: 71%, melting point: 197 °C). Elemental analysis (C19H17N3O2S): theoretical (%): C, 64.94; H, 4.88; N, 11.96; experimental (%): C, 64.94; H, 3.85; N, 11.76.
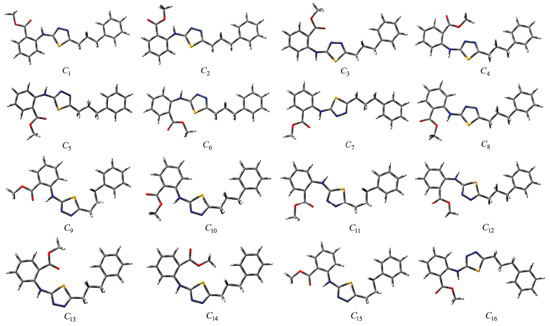
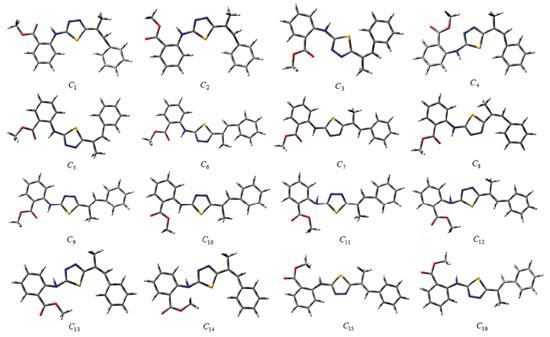
Computational details Although the conformational flexibility and diversity of the synthesised compounds are considerable, 16 initial conformations were selected for each compound (Figures 4 and 5). Kohn-Sham density functional theory (KS-DFT) was employed in the quantum-chemical calculations. No geometric constraints were introduced in the optimisation processes. The conformers were optimised to obtain ground state geometries using the Becke3-Lee-Yang-Parr hybrid exchange-correlation function (B3LYP)26,27 with the 6-311++g(2d,2p) basis set. Furthermore, these methods were also employed for obtaining the optimised molecular conformations and UV, IR and NMR spectra of the conformers. Time-dependent DFT (TD-DFT) was employed to calculate vertical excitation energies. The Self-Consistent Reaction Field (SCRF) method and the Conductor-Polarizable Continuum Model (CPCM) were used for UV spectral analysis in the chloroform phase. IR calculations were also performed in the gas phase, and saddle-point configurations were excluded. In other words, all vibration modes in the calculated IR spectra of the conformers were real, indicating the presence of the local energy minima of the conformers. Moreover, 1H-NMR calculations of the conformers were performed in the dimethyl sulfoxide (DMSO) phase using the same method and basis set.
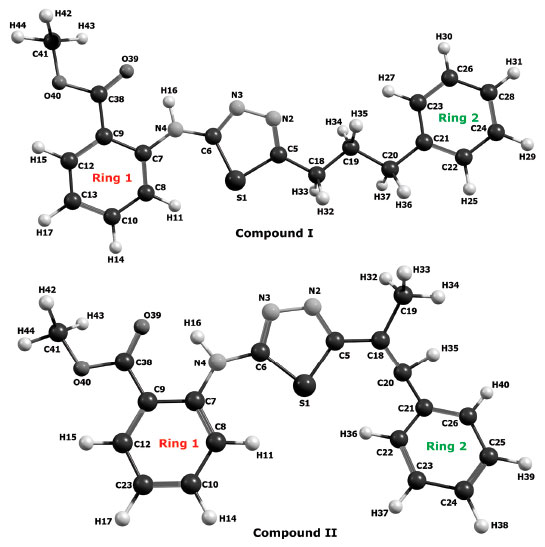 Figure 3. Numbering of the atoms in compounds I and II
The HOMO and LUMO energies (EHOMO and ELUMO) were calculated using the same method and basis set, and the molecular electrostatic potential surfaces were obtained. FMO energy eigenvalues were used to calculate the electronic parameters of the conformers, such as energy gap ΔE, chemical hardness (η) and electronegativity (χ). The correlation between the minimum molecular energy and the electronic parameters of the conformers was investigated. The calculations were performed using the GAUSSIAN 0928 software package program. Bader's theory of atoms in molecules29-31 is a powerful approach for analysing the electron density in a molecule, which is widely used to predict the properties and reactivity of molecules. QTAIM analysis was also performed to determine the intramolecular interactions and to determine the ring-critical points (RCPs) of the charge density distribution and the bond-critical points (BCPs, also called saddle points) of the electron density between two atoms forming a chemical bond. The correlation between conformers and spectral data was investigated by associating BCPs, RCPs, bond paths and ring paths, and using ESP and the HOMO-LUMO energy map. Furthermore, to determine the correlation between electron charge distribution, intramolecular interactions and spectral data, we used the delocalisation index (DI), the average number of electrons localised in an atom (LI) and the percentage of electrons localised on the selected atom ( %L).
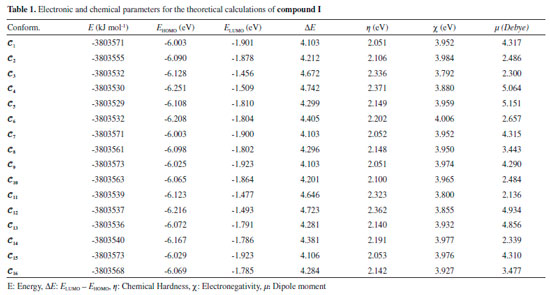
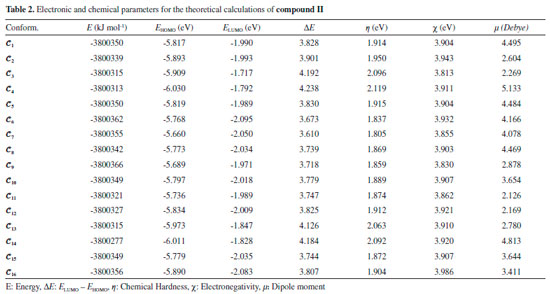
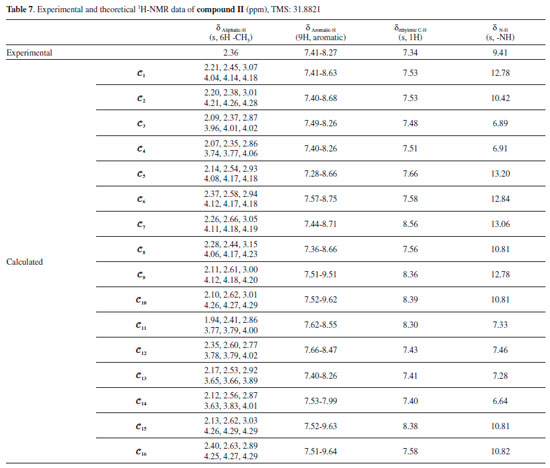
RESULTS AND DISCUSSION The numbers of the atoms in compounds I and II are shown in Figure 3. Although many conformational structures exist, using the dihedral rotors (Dn, n = 1 - 6) shown in Figure 3, only the possible 16 initial conformations of compounds I and II (Figures 4 and 5) with the lowest molecular energy from the obtained structures were considered for theoretical analysis. For structures with similar spatial geometry, as shown in the conformers 𝓒;1, 𝓒;7 and 𝓒;9, 𝓒;15 of compound I and 𝓒;1, 𝓒;5 of compound II, initial geometries were selected to have dihedral angle differences between thiadiazole and aromatic rings, and thus the effects of dihedral angle differences of similar conformer on the optimization results were also examined. As shown in Table 1, the initial geometry of the optimised conformers greatly influenced the minimum molecular energy values (E), HOMO-LUMO eigenvalues, chemical hardness, electronegativity and dipole moments. Although the difference between the calculated minimum molecular energies of the conformers is relatively small, 44 and 89 kJ mol-1 for compounds I and II, respectively, significant differences among other electronic parameters were observed. The calculated minimum molecular energies of the conformer 𝓒;9 of compounds I and II, -3803573 and -3800366 kJ mol-1, respectively, were lower than those of the other conformers. The energies of the conformers whose minimum molecular energies were greater than those of other conformations were calculated as -3803529 kJ mol-1 (𝓒;5) for compound I and -3800277 kJ mol-1 (𝓒;14) for compound II. Differences in the calculated dipole moment values depended on the initial conformations and were observed to be approximately double. For compound I, the dipole moment of the conformers was found to be between 2.136 and 5.151 Debye, and for compound II, it was between 2.126 and 5.133 Debye. Figures 6a and 6b show examples of the HOMO and LUMO energies that were also greatly affected by conformational differences and led to a change in the energy gap ΔE (ΔE = ELUMO - EHOMO). As a result of this situation, many parameters (such as global hardness, global softness and electronegativity) obtained using the HOMO-LUMO values were calculated differently because of the effect of the conformational changes on the HOMO-LUMO energy eigenvalues.
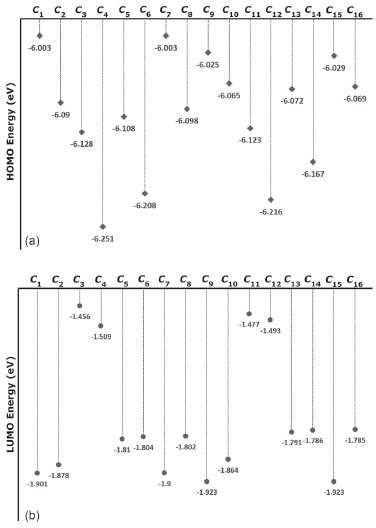 Figure 6. a) HOMO energy eigenvalues of the conformers of compound I. b) LUMO energy eigenvalues of the conformers of compound I
It is well known that electron donating and accepting abilities can be evaluated from the HOMO and LUMO energy eigenvalues. The energy band gap between HOMO and LUMO determines the chemical stability of a molecule. Molecules having small HOMO-LUMO gaps are usually highly active, whereas ones having large gaps are generally stable and tend to be unreactive. In this context, the active or unreactive properties (or different characteristics depending on energy band gap) of a molecule depend on its conformational structure. The conformation of a compound will also affect the interpretation of experimental and theoretical results. In addition, using a reverse approach, the level of reactivity (or unreactivity) of a molecule can also be determined by the molecular conformation, which is achieved by adjusting the experimental process variables such as temperature, pressure, external field and solvent. Furthermore, because the electron density was concentrated around the electronegative atoms, the HOMO-LUMO energy distribution was affected by the geometrical position of electronegative atoms in the compounds. The HOMO-LUMO energy distribution was thus concentrated in the regions where the electron density increased. The HOMO-ESP map for compound I-𝓒;7 in Figure 7 shows that the electron density is concentrated around two nitrogen atoms on the 1,3,4-thiadiazole moiety. In a contrary situation to that of compound I-𝓒;7, compound II-𝓒;14 is an example where the HOMO orbitals are spread over the entire molecule (Figure 7). The minimum molecular energies of the conformers which have HOMO-LUMO orbitals spread more throughout the molecule due to the intramolecular interactions, as in compound II-𝓒;14, were calculated to be larger than those of the other conformers (all HOMO-LUMO and ESP maps are given in Supplementary Material). The intramolecular interactions in the compounds were examined in more detail by the qtaim analysis in Section 3.4. The effect of the interaction between the benzene ring and the methoxy group on the HOMO distributions can be better understood with the help of Supplementary Material.
 Figure 7. HOMO and ESP maps of compounds I-𝓒;7 and II-𝓒;14.
UV analysis of the compounds The UV-visible absorption spectra of 1 x 10-5 mol L-1 solutions of compounds I and II in CHCl3 were recorded between 300 and 700 nm, and their spectral data are summarised in Table 3. The compounds showed two absorption peaks, at 336.75 and 291.75 nm for compound I and at 353.00 and 303.00 nm for compound II. UV-vis absorption bands are thought to originate from π-π* and n-π* electronic transitions in the structures of the compounds. However, the theoretical calculations showed that the UV absorptions of the conformers displayed different characteristics. Figure 8 shows the experimental and calculated UV spectra of six selected conformations for compound I.
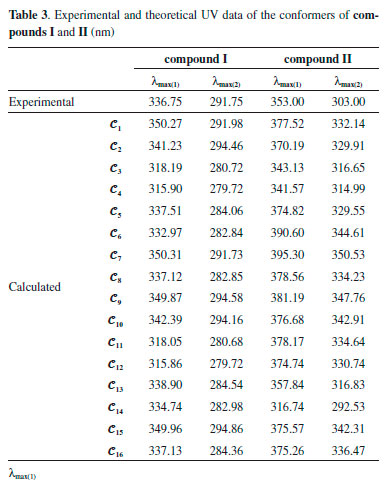
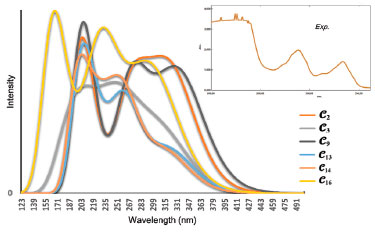 Figure 8. Experimental and calculated UV spectra of the conformers 𝓒;2, 𝓒;3, 𝓒;9, 𝓒;13, 𝓒;14 and 𝓒;16 of compound I
The experimental results and theoretical UV data of the conformers of compounds I and II are given in Table 3. The long wavelength λmax (1) and the short wavelength λmax (2) for the conformers of compound I were calculated to be in the ranges 315.86-350.31 and 279.72-294.86 nm, respectively. The absorption peaks of the long and short wavelengths of the conformers of compound II were in the ranges 316.74-395.30 and 292.53-350.53 nm, respectively. The calculations naturally showed a strong correlation between ΔE and the UV absorption peak values. The Pearson correlation coefficients between ΔE and the UV absorption wavelengths of the conformers of compounds I and II were -0.995 (ΔE vs λmax (1)) and -0.927 (ΔE vs λmax (1)), respectively. Graphs of both the experimental and theoretical UV data of compounds I and II are given in Figures 9a and 9b. The intramolecular interactions differ between conformers, and for this reason, the distribution of the HOMO-LUMO orbitals and the energy gap between them are calculated at different values for each conformer. As shown in Figures 9a and 9b, the long and short wavelength peaks showed a consistent shift across the conformers. The parallel shift in both the long and short wavelength peaks suggests that the computation for a selected conformer is correct, but the fact that the UV calculations seem to be compatible with the experimental data may be misleading and is discussed later in further detail.
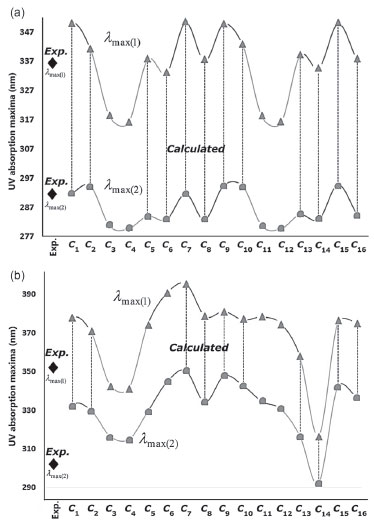 Figure 9. Experimental and theoretical UV data of a) compound I and b) compound II
One distinctive feature of the conformers𝓒;1, 𝓒;7, 𝓒;9 and 𝓒;15 of compound I, which had the lowest molecular energy (E𝓒;7 < E𝓒;9 < E𝓒;15 < E𝓒;7 < E𝓒;1 < ... < E𝓒;16), was that they formed a hydrogen bond between O39 and H16 (see Supplementary Material). Moreover, λmax (1) of these conformers was calculated to be around 350 nm and larger than the other conformers. A similar relation was also observed between 𝓒;2, 𝓒;8, 𝓒;10 and 𝓒;16, wherein the hydrogen (-NH) and oxygen (OCH3) formed a hydrogen bond. These conformers also had lower minimum energies and gave absorption peaks close to the experimental results. Conformers giving low UV absorption peaks were also found to have larger molecular energies than the others. If we summarise the relationship between the molecular energy and UV absorption, although the minimum molecular energies of the conformers having strong interactions (NH->C=O and-NH-OCH3) were calculated to be small, their UV absorption peaks were shifted to longer wavelengths (bathochromic shift). A similar situation was also observed for the conformers of compound II. Figure 10 shows a graphical comparison of the scaled data of ΔE, UV absorption maxima and HOMO and LUMO energies of the conformers of compounds I and II. It was shown that the absorption wavelength peaks were closely related to the E, EHOMO and ELUMO energies as well as to ΔE.
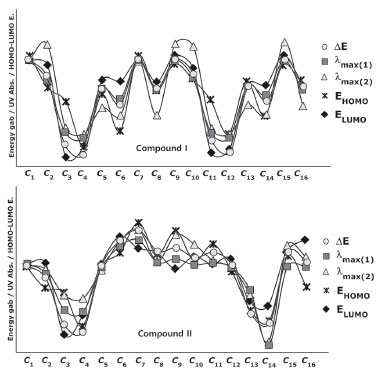 Figure 10. Energy, UV absorption maxima and HOMO and LUMO energies of the conformers of compounds I and II (values are scaled)
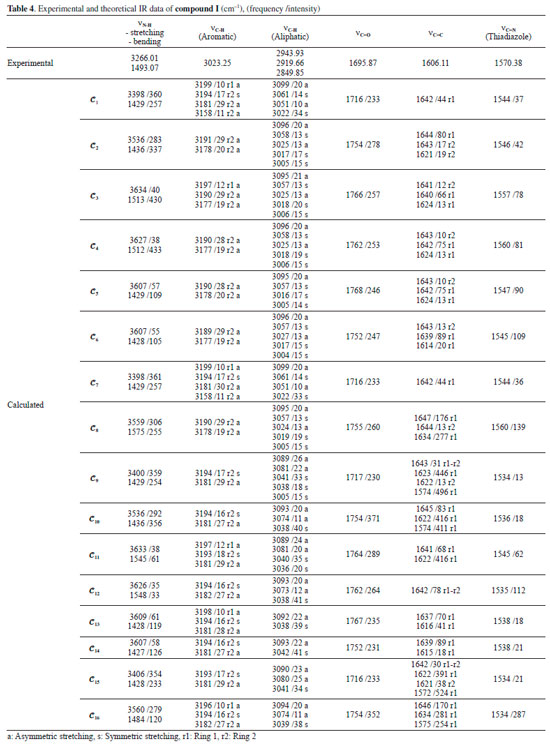
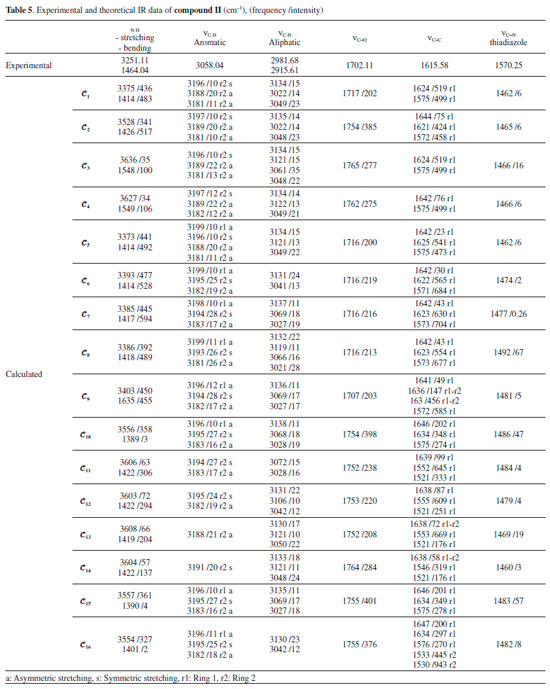
IR analysis of the compounds The IR spectra of the compounds were monitored between 4000 and 200 cm-1 using an Alpha FT-IR spectrometer (Bruker, Germany). The IR absorptions of compounds I and compound II were observed as follows: vibration of N-H groups at 3266.01 and 3251.11 cm-1, stretching vibration of aromatic C-H at 3023.25 and 3058.04 cm-1, stretching vibration of aliphatic C-H at 2943.93-2981.68 cm-1, stretching vibration of C=O at 1695.87 and 1702.11 cm-1, stretching vibration of C=C at 1606.11 and 1615.58 cm-1 and stretching vibration of C=N (thiadiazole) at 1570.38 and 1570.25 cm-1. The experimental and theoretical IR data of compound I and compound II are given in Tables 4 and 5. The experimental IR spectra showed that the observed bands are compatible with the structures of the compounds. Moreover, the effects of molecular conformation on the vibrational frequencies of N-H (stretching and bending), C-H (aromatic and aliphatic), C=O, C=C and C=N were also studied theoretically, and the results were compared with the experimental data. N-H and C=O vibrations gave distinctive peaks, which were investigated to analyse the effects of the conformations on the vibration frequencies. The N-H stretching and bending vibrational frequencies of the conformers of compound I were experimentally found to be 3266.01 and 1493.07 cm-1, respectively. The theoretical results showed that the stretching frequencies were in the range 3398-3634 cm-1 and the N-H bending frequencies were in the range 1427-1575 cm-1. The calculated vibrations of the aromatic C-H peaks were observed in the range 3199-3180 cm-1 and were generally not greatly affected by any conformational changes. Similar situations were also observed for aliphatic C-H (experimentally 2850-2944 cm-1 and theoretically 3004-3099 cm-1) and C=C (experimentally 1606 cm-1 and theoretically 1572-1647 cm-1) vibrations. The vibrational frequencies of the electronegative-atom-bearing groups, O-H and N-H, were more affected by conformational changes.
The N-H vibrational frequencies of compound II were experimentally found to be 3266.01 and 1493.07 cm-1. Theoretical calculations gave stretching and bending frequencies in the range of 3373-3636 and 1389-1635 cm-1, respectively. The aromatic C-H peaks were calculated to be between 3199 and 3181 cm-1, close to the conformers of compound I. The aromatic C-H peaks were not affected much by the molecular conformation or any molecular structural differences. Furthermore, C=C vibrations were also not affected as much by the conformational variations as were the vibration frequencies of O-H and N-H. Aliphatic C-H and C=C vibrations, however, were observed at very low intensities in some conformations such as 𝓒;4 and 𝓒;16 (vibrational intensities below 10 are not given in the table). Similar situations were also observed for the aromatic C-H peaks of the conformers of compounds I and II. The C=O vibration peaks of the conformers of compound II were experimentally found to be 1702.11 cm-1. The theoretical calculations showed that the results were in the range 1716-1765 cm-1 depending on the conformation. It was shown that the C=O vibrations were also affected by the structural differences of the compounds. The experimental and theoretical vibrational frequencies of the conformers of compound II are listed in Table 5. The Pearson correlation coefficients between the N-H stretching and C=O vibration frequencies of the conformers were calculated as R = 0.96 for both compounds I and II. The graphical presentations of the N-H stretching and C=O vibration frequencies of the conformers are given in Figures 11a and 11b. As can be seen, the N-H and C=O vibrations are equally affected by the conformational changes.
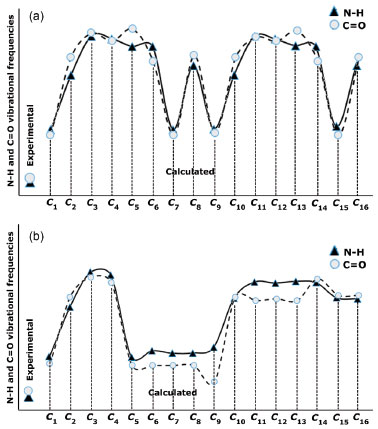 Figure 11. Experimental and theoretical data of the N-H and C=O vibrations of a) compound I and b) compound II (values are scaled)
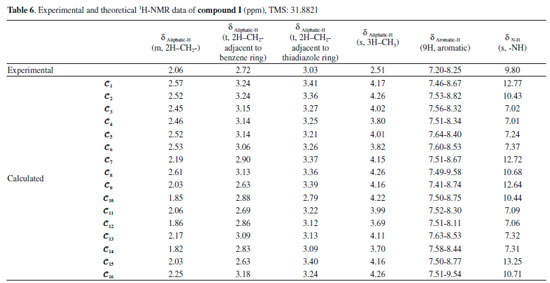
Moreover, it was shown that there was also a relationship between the N-H and C=O vibrational frequencies and the minimum molecular energies of the compounds: The conformers 𝓒;1, 𝓒;7, 𝓒;9 and 𝓒;15 of compound I have lower molecular energies, and the N-H and C=O frequencies of these conformers are also closer to the experimental results. A similar situation applies to the conformers 𝓒;1, 𝓒;5, 𝓒;6, 𝓒;7, 𝓒;8 and 𝓒;9 of compound II. However, although the UV absorption peaks of conformers 𝓒;1, 𝓒;7, 𝓒;9 and 𝓒;15 of compound I are not the most compatible with the experimental data, their vibrational frequencies are more consistent with the experimental results. A similar situation applies to the compatibility of the calculated UV and IR spectra of compound II with the experiments. This uncertainty leads to the next phase of theoretical analysis; the relationship between the spectral and electronic data of the compounds will be examined by 1H-NMR and QTAIM analyses. NMR analysis of the compounds The NMR spectra of all of the compounds were obtained using a Bruker spectrometer (400 MHz) at room temperature in DMSO-d6. All of the 1H-NMR data are listed in Tables 6 and 7. The aliphatic protons of the compounds were observed between 2.06 and 3.03 ppm, the aromatic protons of the compounds were observed between 7.20 and 8.27 ppm, and the NH protons of the compounds were observed between 9.41 and 9.80 ppm. The 1H-NMR spectra show that the observed peaks are compatible with the protons of the compounds.
The NMR spectra give structural information about a compound, and NMR spectroscopy plays an important role in the theoretical analysis of the compounds studied experimentally. It can be observed directly from the 1H-NMR spectra that atoms in a molecule are affected by the intramolecular charge distribution. In this context, the 1H-NMR data of the conformers differed from each other because the distribution of molecular charge density depends on the molecular conformation. The theoretical calculations showed that the chemical shift values, especially for-NH, were more affected by the different conformations than other signals. The -NH chemical shift values for compounds I and II were experimentally found to be 9.80 and 9.41 ppm, respectively. The theoretically obtained values were in the ranges of 7.01-13.25 and 6.64-13.06 ppm for compounds I and II, respectively (Table 6). The -NH chemical shifts of the conformers 𝓒;1, 𝓒;2, 𝓒;7 - 𝓒;10, 𝓒;15 and 𝓒;16 of compound I and 𝓒;1, 𝓒;2, 𝓒;5 - 𝓒;10, 𝓒;15 and 𝓒;16 of compound II were higher than those of the other conformers. In these conformers, the electron density concentrated on the nitrogen atom of the N-H group (see Supplementary A). In other words, the change in the chemical shift of the N-H proton was directly proportional to the electron density on the nitrogen. The minimum and maximum values of the -NH proton chemical shifts of the conformers of compound I were calculated to be 7.01 ppm (𝓒;4) and 13.25 ppm (𝓒;15), respectively. Similarly, for compound II, they were calculated to be 6.89 ppm (𝓒;3) and 13.20 ppm (𝓒;5), respectively (Tables 6 and 7). The correlations between the minimum molecular energies and the -NH chemical shifts of the conformers of compounds I and II are shown graphically by scaling the calculated values (Figure 12). In particular, it was observed that the chemical shift of the -NH proton had a very high correlation with the minimum molecular energies of the conformers. There was a negative correlation between the minimum molecular energy and the -NH chemical shift, and so, the conformers with a low molecular energy exhibited a high chemical shift value. Moreover, Figure 12 also shows that numerical estimates can be made on the minimum molecular energies corresponding to these conformations of the compound by calculating only the -NH chemical shifts of the possible conformations.
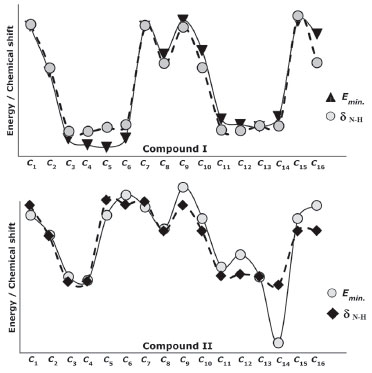 Figure 12. Representation of the correlation between the minimum molecular energies Emin. and the -NH chemical shifts (δN-H) of the conformers of compounds I and II (values are scaled)
As shown in Figures 13a and 13b, the conformers of the compounds can be examined in three groups: the conformers 𝓒;1, 𝓒;7, 𝓒;9 and 𝓒;15, where the calculated ppm values were the highest; the conformers 𝓒;2, 𝓒;8, 𝓒;10 and 𝓒;16, where the ppm values were close to the experimental results; and the conformers 𝓒;3, 𝓒;4, 𝓒;5, 𝓒;6, 𝓒;11, 𝓒;12, 𝓒;13 and 𝓒;14, where the calculated ppm values are lower than the experimental data (for compound I). Similar results were found for the three groups of compound II: 𝓒;1, 𝓒;5, 𝓒;6, 𝓒;7 and 𝓒;9; 𝓒;2, 𝓒;8, 𝓒;10, 𝓒;15 and 𝓒;16; and 𝓒;3, 𝓒;4, 𝓒;11, 𝓒;12, 𝓒;13 and 𝓒;14, respectively. The common feature of the conformers with the highest -NH chemical shift values was the bonding of the H16 protons with the highly electronegative O39 (Supplementary Material). Naturally, this situation resulted from the higher electron density surrounding the N-H bond, and the same applies to compound II. For the conformers of both compounds where the -NH chemical shift values were closer to the experimental results, it was observed that the H16 proton was bound to the oxygen atom of the methoxy group. Although the proton chemical shifts of the conformers 𝓒;2, 𝓒;8, 𝓒;10 and 𝓒;16 (for compound I) and 𝓒;2, 𝓒;8, 𝓒;10 and 𝓒;15 (for compound II) were calculated closer to the experimental results, they were found not to have the lowest molecular energy. In cases where the O40 or methoxy group was bonded to the thiadiazole or benzene ring (see Supplementary Material), the -NH proton chemical shift values were lower than the experimental data, the calculated molecular energies of these conformations were very high, and the theoretical spectroscopic results were farther away from the experimental data.
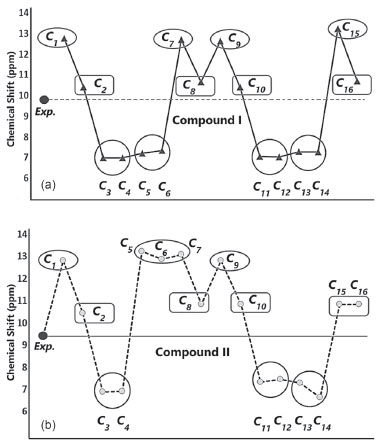 Figure 13. Experimental and theoretical -NH chemical shifts of a) compound I and b) compound II
The analysis of the 1H-NMR data by theoretical calculations plays a more decisive role in the correctness of the selected conformer; that is, we can say that the chemical shifts of protons bound to electronegative atoms are smaller than the experimental ones, indicating that the molecular conformation used in the calculations was the wrong one. Two factors may be responsible for the inconsistencies between experimental and calculated 1H-NMR data. The first is caused by the environment, and the second reason is the intramolecular interactions that are directly related to the conformer structure. Since theoretical calculations were carried out for single molecules, the effects of intermolecular interactions are not observed in the calculation results. In the experimental process, each molecule makes intermolecular interactions as well as intramolecular interactions. Since intermolecular interactions decrease the electron density on hydrogen bonds, the proton chemical shifts are smaller than those obtained in the theoretical calculations, that is, calculated 1H-NMR data is expected to be larger than the experimental data. Considering the correlation between the minimum molecular energies Emin. and -NH chemical shifts, it is seen that the conformers in the ellipse in Figures 13a and 13b are the most suitable conformers for theoretical investigations. QTAIM analysis was also conducted in this study to better illustrate the nature of the relationships between the electronic and spectral data. QTAIM analysis of the compounds The relationship between charge distribution and the minimum molecular energy was investigated by QTAIM analysis. The QTAIM visualisation of compound I-𝓒;9 /𝓒;5 and compound II-𝓒;9 /𝓒;14 is given in Figure 14. Both compounds I-𝓒;9 and II-𝓒;9 had the minimum molecular energy, and compound I-𝓒;5 and compound II-𝓒;14 also had greater molecular energy than those of the other conformers.
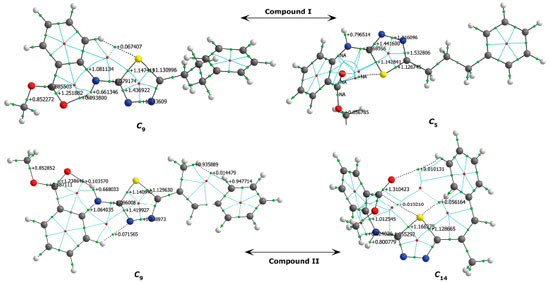 Figure 14. QTAIM visualisation of compound I (𝓒;9, 𝓒;5) and compound II (𝓒;9, 𝓒;14); green points: BCPs, red points: RCPs
As shown in Figure 14, the aromatic rings of compounds I-𝓒;5 and II-𝓒;14 were degenerated because of intramolecular interactions, and the minimum energies of these conformers were calculated to be higher than those of the other conformers. This was also true for the other conformers having higher molecular energy (the conformers whose -NH chemical shift values were lower than the experimental data; see Figures 13a and 13b, and Supplementary Material). In the other word, in the conformers 𝓒;3, 𝓒;4, 𝓒;5, 𝓒;6, 𝓒;11, 𝓒;12, 𝓒;13 and 𝓒;14 of compound I, the O40 and the methoxy group were bound to the thiadiazole or benzene ring by overcoming the electronegative structure (N-H) closest to them. The same was true for the conformers 𝓒;3, 𝓒;4, 𝓒;11, 𝓒;12, 𝓒;13 and 𝓒;14 of compound II. The molecular energies of these conformers were calculated higher and the spectral data were not compatible with the experimental results. Moreover, the conformers having a bond between H16 proton and highly electronegative O39 were more suitable for the theoretical calculation because the electronegative atoms are more inclined to bond and the electron distribution is more regular in the smaller molecular volume. Table 8 summarises the correlation of the electron density distribution on atom N4 and the minimum energy, IR and 1H-NMR data. The delocalisation index (DI) between N4 and H16, the average number of electrons localised on atom N4 (LI) and the percentage of electrons localised on atom N4 (%L) were calculated and showed that the charge distribution of the N-H bond was strongly related to all of the spectral and electronic data (Table 8 and Figure 15).
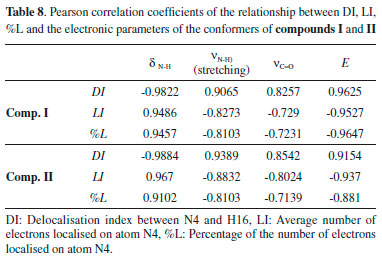
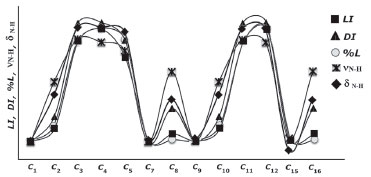 Figure 15. Representation of the correlation between the LI, DI, %L-N4, ν(N-H) and δ(N-H) of the conformers of compound I (values are scaled)
The electronic properties of the N-H covalent bond played an important role in determining both the molecular energy and the spectral properties of the compounds. In particular, the correlation between the DI of the N-H bond and the molecular energies of the compounds was very high (R > 0.96). Since the interaction of the N-H bond with the atoms or group of atoms in the local environment determines the DI, the molecular energies of the compounds, in cases where delocalisation was high, were calculated to be lower. It is also clear that the delocalisation between N and H is effective in determining the spectral properties of the compound. These results showed that, in the geometric optimisation process, the choice of the initial geometry that had the highest delocalisation on the electronegative atoms is very important both in terms of calculation time and the accuracy of the calculation processes, and such a selection will also allow for more accurate interpretation of spectral data. The QTAIM analysis revealed that the initial geometry of the optimisation process should be selected by considering the positions of the electronegative atoms and the probability of bonding with nearby atoms or groups of atoms. In other words, the molecular energies of the conformers, in which electronegative atoms can degenerate the symmetry of the molecular charge distribution by bonding to atoms or groups of atoms at distant locations, are more likely to be highly calculated and give distant results than the experimental data. Furthermore, the minimum molecular energy is directly dependent on electron delocalisation, and Figure 15 clearly shows the relationship between the N-H delocalisation and the minimum molecular energy and spectral data of the compound.
CONCLUSION A molecule can be studied theoretically by considering a number of initial conformations. In this study, the effects of the possible conformational structures of two compounds on the theoretical results were investigated using DFT. It was demonstrated that the choice of optimised starting geometries of the compounds was important in assessing the theoretical results and in supporting the experimental data. The electronic, IR, UV and 1H-NMR data of 16 conformers of compounds I and II were theoretically analysed. Tips for the selection of the geometry of the initial conformation of a molecule are presented. A strong correlation was observed between the electronic data and the observed UV absorption wavelengths, non-aromatic IR vibration frequencies and non-aromatic proton chemical shifts of the conformers. How the intramolecular interactions affected the calculation results was also revealed. The importance of choose of initial conformation of a molecule for optimisation by considering intramolecular interactions was also demonstrated. The role of electronegative atoms or groups in the intramolecular interaction was shown to be more dominant. This study shows that the compatibility of the results obtained from the theoretical calculations with the experimental data does not indicate that the selected conformation is the most accurate. In addition, there may be more than one conformer which is compatible with the experimental data, and the electronic data of these conformers have different values. This may cause problems, especially in the interpretation of the calculated electronic data. In the spectral data analysis of the conformers, the -NH proton chemical shift had a high correlation with the N-H vibration frequency. A weak correlation between the electronic and spectral data of the conformers was generally observed for conformations where the aromatic structures contributed greatly to the intramolecular interaction. It was observed that conformers whose proton chemical shifts are larger than those of the experimental data were more suitable for theoretical analyses supporting and interpreting experiments. Furthermore, it was shown that the minimum molecular energies of structures where the optimisations of molecules approximated a planar geometry might not be the smallest. Careful use of the commands forcing the molecule into a planar symmetry during optimisation was therefore emphasised. Finally, some clues on how the initial conformation of the compound should be chosen in the most accurate way were determined.
REFERENCES 1. Balaji, K.; Bhatt, P.; Mallika, D.; Jha, A.; Int. J. Pharm. Pharm. Sci. 2015, 7, 145. 2. Gür, M.; Şener, N.; Anadolu University Journal of Science and Technology A: Applied Sciences and Engineering 2017, 18, 939. 3. Foroumadi, A.; Soltani, F.; Moshafi, M. H.; Ashraf, A. R., II Farmaco 2003, 58, 1023. 4. Pinaki S. B.; Song Y.; Linhong J.; Guang-Fang Xu; Qian-Zhu Li; Deyu Hu; Baoan S.; Fang L.; Cai-Jun C.; Bioorganic Med. Chem. 2007, 15, 3981. 5. Gür, M.; Şener, N.; Muğlu, H.; Çavuş, M. S.; Özkan, O. E.; Kandemirli, F.; Şener, İ.; J. Mol. Struct. 2017, 1139, 111. 6. Poorrajab, F.; Ardestani, S. K.; Emani, S.; Behrouzi F. M.; Shafiee, A.; Foroumadi, A.; Eur. J. Med. Chem. 2009, 44, 1758. 7. Hafez, H. N.; Hegab, M.I.; Ahmed, F. I. S.; El-Gazzar A. B. A.; Bioorganic Med. Chem 2008, 18, 4538. 8. Gür, M.; Şener, N.; Kaştaş, A. Ç.; Özkan, O. E.; Muğlu, H.; Elmaswari, M. A.; J. Heterocycl. Chem. 2017, 54, 3578. 9. Belaidi, O.; Bouchaour, T.; Maschk, U.; Int. J. Chem. Anal. Sci. 2013, 4, 185. 10. Viviani, N.; Luis, G. D.; Vinicius, P.; Gil, V. J. S.; J. Mol. Struct. 2018, 1157, 401. 11. Tomohiro, O.; Shinji, A.; Polymer 2016, 86, 83. 12. Bardak, F.; Karaca, C.; Bilgili, S.; Atac, A.; Mavis, T.; Asiri, A. M.; Karabacak, M.; Kose, E.; Spectrochim. Acta, Part A 2016, 165, 33. 13. Ortega, P. G. R.; Montejo, M.; Márquez, F.; González, J. J. L.; J. Mol. Graphics Modell. 2015, 60, 169. 14. Richards, M. R.; Bai Y.; Lowary, T. L.; Carbohydr. Res. 2013, 374, 103. 15. Alcântara, A. F. C.; Teixeira, A. F.; Silva, I. F.; Almeida, W. B.; Piló-Veloso, D.; Quim. Nova 2004, 27, 371. 16. Cisneros-García, Z. N.; Nieto-Delgado, P. G.; Rodríguez-Zavala, J. G.; Dyes Pigm. 2015, 121, 188. 17. Medina, J. J. M.; Ferrer, E. G.; Williams, P. A. M.; Okulik, N. B.; J. Mol. Graphics Modell. 2017, 76, 181. 18. Arjunan, V.; Santhanam, R.; Rani, T.; Rosi, H.; Mohan, S.; Spectrochim. Acta, Part A 2013, 104, 182. 19. Oliveira, D. M.; Mussel, W. N.; Duarte, L. P.; Silva, G. D. F.; Duarte, H. A.; Gomes, E. C. L.; Guimaraes, L.; Filho, S. A. V., Quim. Nova 2012, 35, 1916. 20. Sienkiewicz-Gromiuk, J.; Spectrochim. Acta, Part A 2018, 189, 116. 21. Domingos, S. R.; Perez, C.; Medcraft, C.; Pinacho, P.; Schnell, M.; Phys. Chem. Chem. Phys, 2016, 18, 16682. 22. Bell, A.; Singer, J.; Desmond, D.; Mahassneh, O.; Wijngaarden, J.; J. Mol. Spectrosc. 2017, 331, 53. 23. Chashmniam, S.; Tafazzoli, M.; J. Mol. Struct. 2017, 1148, 73. 24. Hohenberg, P.; Kohn, W.; Phys. Rev. 1964, 136, B864. 25. Kohn, W.; Sham, L.; Phys. Rev. 1965, 140, A1133. 26. Becke, A. D.; J. Chem. Phys. 1993, 98, 1372. 27. Lee, C.; Yang, W.; Parr, R. G.; Phys. Rev. B 1988, 37, 785. 28. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Petersson, G. A.; Nakatsuji, H.; Li, X.; Caricato, M.; Marenich, A. V.; Bloino, J.; Janesko, B. G.; Gomperts, R.; Mennucci, B.; Hratchian, H. P.; Ortiz, J. V.; Izmaylov, A. F.; Sonnenberg, J. L.; Williams-Young, D.; Ding, F.; Lipparini, F.; Egidi, F.; Goings, J.; Peng, B.; Petrone, A.; Henderson, T.; Ranasinghe, D.; Zakrzewski, V. G.; Gao, J.; Rega, N.; Zheng, G.; Liang, W.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Throssell, K.; Montgomery, J. A., Jr.; Peralta, J. E.; Ogliaro, F.; Bearpark, M. J.; Heyd, J. J.; Brothers, E. N.; Kudin, K. N.; Staroverov, V. N.; Keith, T. A.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A. P.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Millam, J. M.; Klene, M.; Adamo, C.; Cammi, R.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Farkas, O.; Foresman, J. B.; Fox, D. J.; Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010. 29. Bader, R. W. F.; Atoms in Molecules. A Quantum Theory, Calendon Press: Oxford, 1990. 30. Bader, R. F. W.; Acc. Chem. Res. 1985, 18, 9. 31. Bader, R. F. W.; Chem. Rev. 1991, 91, 893. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access