JBCS

INTRODUCTION

In 1931, Pauling¹ and Slater² originated independently the concept of taking linear combinations of 2s and 2p wave functions to build four new orthogonal wave functions, or valences. Pauling refers to this process in methane as ‘s-p quantization’.³ For example, methane has H-C-H bond angle ~109.5°. How do we achieve such a bond angle when the s and p atomic orbitals are not mutually oriented at this angle? The quantization approach was to invoke a tetrahedral geometry of carbon in CH₄ involving combinations of s and p orbitals; orbitals with directionality would presumably provide stronger bonds. In 1932, Hultgren included ‘s-p-d quantization’ to describe equivalent bonds for elements in the long periods of the periodic chart.⁴

The term ‘hybrid atomic orbitals’ and the related process ‘hybridization’ were introduced by Mulliken⁵ and Van Vleck⁶ before being accepted by the entire scientific community. To achieve orbitals with an appropriate directionality, mixtures of atomic orbitals on the same atom are formed through hybridization. For a carbon atom, there are thus three principal hybrid combinations - commonly denoted sp, sp² and sp³; one or other combination is invoked to describe a linear, trigonal planar or tetrahedral geometry, respectively, of a central atom. Penney extended this system to ethyne using bond energies to justify the sp hybridization with 180° bond angles.⁷ Furthermore, in 1934, Penney provided the first illustration of the hybrid orbital structure of ethane and ethene; ‘Penney’s model’ is sometimes used to describe ‘ideal’ 109.5° angles for ethane and the 120° angles provided by sp² hybrids in ethene.⁸ By 1935, Van Vleck had reviewed the ‘quantum theory of valence’ to include most concepts of hybridization that are common in contemporary chemistry.⁹

The use and reliability of hybrid atomic orbitals (which we abbreviate as HAO) has since become challenged. We divide our critique into two parts; the present analysis arose from our endeavor to answer these two relevant scientific questions. In Part 1, does this concept of HAO from the 1930s have mathematical and logical bases? In Part 2, what are the practical problems with this concept as a pedagogical model and how can we overcome these challenges? In this article, we present modern calculations about hybrid atomic orbitals, we provide irrefutable evidence, based on Schrödinger’s time-independent equation for the hydrogen atom, that HAO lack justification, and we list six logical errors and a further critique of the hybridization model.

MATHEMATICAL NATURE OF HYBRID ATOMIC ORBITALS

We here focus our attention on the purported tetrahedral and trigonal hybrid functions of carbon atoms because these are the forms most commonly invoked in organic chemistry, but our analysis and conclusions are applicable equally to other HAO. Digonal or sp hybrids might seem to be an exception, but they are anyhow superfluous.

For the purpose of his introduction of hybrid functions, Pauling¹ simply proffered these functions that depend on only angular variables θ and ϕ within the system of spherical polar coordinates r, θ, ϕ. He presented the following (one-electron) amplitude functions for unspecified “normal atoms”, with justification of neither a source of these functions nor their applicability to any particular “normal atom”, and represented the standardized eigenfunctions in terms of only their angular parts.¹⁰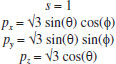

According to the direct solution (in SI units with conventional symbols, including µ as the reduced mass of the atomic system) of Schrödinger’s temporally independent equation for an atom of atomic number Z having only one electron, the exact definitions of the pertinent amplitude functions ψ_k,l,m(r,θ,ϕ) follow (we retain the relation to Pauling’s nomenclature above; quantum numbers radial k, azimuthal l and equatorial m derive from the three coordinates r,θ,ϕ respectively, with energy quantum number n = k + l + 1 for this system of coordinates).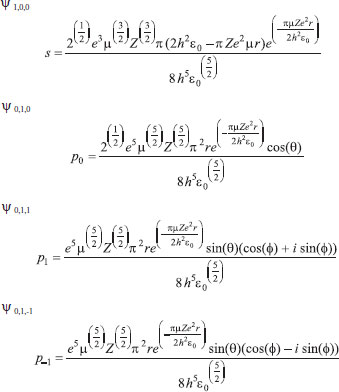

The latter two formulae that contain i = √−1 are complex, containing real and imaginary parts. On taking a sum p_x = (p₁ + p_-1)/√2, we obtain a purely real quantity,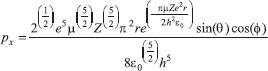

whereas a corresponding difference p_y = (p₁ − p_-1)/√2 yields a purely imaginary quantity,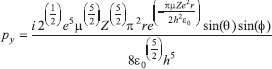

with p_z = p₀, also purely real.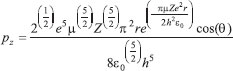

According to the latter three expressions, on removing their common factors the remaining parts depending on angular variables θ and ϕ are, including s for completeness in the comparison,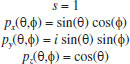

which are the same as Pauling's formulae apart from numerical factors and, particularly notably, the presence of i in p_y. Our formulae above pertain explicitly to the one-electron atom, whereas Pauling made no such association with any atom. Although an exponential factor,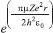

is common to all four original functions, the remaining part of the radial dependence with associated constants is not; instead of just radial distance r in the other three formulae, in s there appears,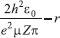

of which the former term is 2 a₀/Z in terms of Bohr radius a₀.

We proceed to assess the disparities between Pauling's definitions in the set stated above and the expressions in our set obtained directly from the solution of Schrödinger's equation for an atom with one electron. The angular parts of p_x and p_z agree exactly between the two sets, but the angular part of p_y must contain i. Pauling claimed to distinguish correctly the radial parts as R_n0(r) for s and R_n1(r) for his three p_x, p_y, p_z, although he provided neither justification nor evidence of this claim. Without the radial part, the mathematical relation of angular wave functions to the overall ψ is limited.¹¹

According to his definitions of s, p_x, p_y, p_z, Pauling defined four purported tetrahedral hybrid functions, which he subsequently named sp³ orbitals.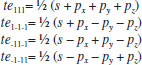

Functions s and p, in common with all ψ_klm(r, θ, ϕ), have infinite extent in all directions in coordinate space, except that p functions, and others with k or l > 0, have zero value on nodal planes or surfaces separating regions of positive phase from those of negative phase. Like these functions s and p, the hybrid functions have nodal surfaces between regions of positive and negative phase, and they retain formally an infinite extent. For the purpose of attributing an explicit shape to any such function, we might specify a magnitude of its amplitude that is a small fraction of the maximum amplitude at any point in space, and then form a surface of that constant function to be viewed in Cartesian coordinates x,y,z. Whereas that surface for function s becomes hence spherically symmetric, the surfaces for functions p_x, p_y and p_z are cylindrically symmetric about the indicated Cartesian axes. In contrast, tetrahedral hybrid functions te have surfaces cylindrically symmetric about one or other axis that is a body diagonal between opposite corners of a cube of which the origin of coordinates is at its center; functions te have this directional quality whether or not they contain s, but with systematic s content the amplitude is more concentrated along the body diagonal axis on one side of the origin than on the other. The objective of Pauling's construction of these tetrahedral hybrid functions was to obtain a resemblance to the structure of methane: with the atomic nucleus of carbon at the center of a cube, the hydrogen nuclei lie at alternate corners of that cube; the hybrid functions that clearly originate as hydrogen functions might then serve as bond orbitals - more accurately, bond basis functions.

With the same definitions of s, p_x, p_y, p_z, one can form these combinations,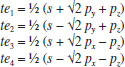

of which the surfaces of the orbitals, according to the same criteria as before, have exactly the same shape, size and directed orientations as the previous tetrahedral hybrid functions; these functions can be legitimately called sp² hybrids because in each case they contain one s and two p functions. The number of such sets of equivalent combinations of s and p functions with the same geometric properties is uncountable;¹² any particular choice of such a set is entirely arbitrary.¹³

For trigonally directed hybrid atomic orbitals (tr_i), the following combinations are possible: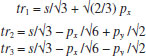

These three hybrid functions, of which tr₁ has s and notably only one p function, have their centers within plane xy containing the nucleus (trigonal sp² hybrids); with p_z = p₀ as above as a fourth function, we then have the above three functions that can make three bonds that are symmetric with respect to that plane.

In Figure 1 appear accurate plots of sp³ , sp² and sp hybrid orbitals generated with a computer. Although these orbitals are generated as purely real (i.e. after removal of √−1) linear combinations of solutions of the Schrödinger equation for the hydrogen atom in spherical polar coordinates, the software (Maple) has transformed the functions into Cartesian coordinates for conventional viewing. In a) the lobes are axially symmetric about a body diagonal of a cube with the atomic nucleus at its center; in b) the lobes are axially symmetric about axis x; in c) the lobes are axially symmetric about axis z, consistent with conventional depictions of these orbitals. In all cases the overall shape is roughly spherical, consistent with a lack of angular dependence of the coulombic attraction between electron and atomic nucleus; a paraboloidal nodal surface exists between the lobe of positive phase (blue) and the lobe of negative phase (red). The small lobe is in each case discernible to have a relative volume decreasing in the order sp³ > sp² > sp.

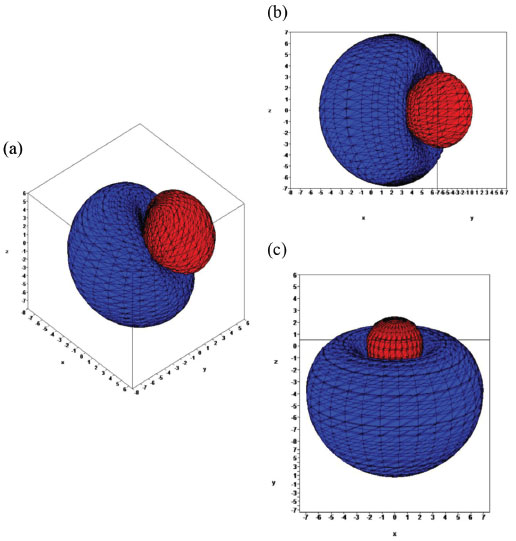Figure 1. Quantitatively accurate plots of hybrid atomic orbitals: a) sp³, b) sp², c) sp; each surface of constant ψ is chosen such that ψ² at that magnitude contains 0.99 of the total electronic density. The scale of each axis in expressed in unit 10⁻¹⁰ m

GENERAL CRITIQUE BASED ON FIRST PRINCIPLES

Many chemists and material scientists use these HAO for a qualitative description of geometric structure and bonding characteristics of molecules of various chemical compounds. The fact that HAO are irrelevant in these cases but that the usage continues indicates the difficulty in eliminating obsolete concepts.

Tetrahedral and trigonal hybrid orbitals are open to severe criticism, of which six instances follow.

1. The formation of four real tetrahedral HAO using linear combinations of real and imaginary parts in spherical polar coordinates is mathematically impossible and logically unsound. In discarding √−1 from p_y above, there is a callous disregard for the inalienable properties of complex numbers and complex functions. Orbitals p_x, p_y, p_z can never occur together; whenever p_z is rotated to become p_x or p_y, the remaining two transform into an orthogonal complex couple. The premise that couple p_x and p_y as real functions is equivalent to a complex couple containing e^±iϕ is false.¹⁴

2. The combinations of HAO in various sets such as the set described as sp³ were devised to generate tetrahedrally oriented hybrid functions; their subsequent use to explain a tetrahedral structure of methane is manifestly a circular argument. Explicitly, stating that methane has a tetrahedral structure because of sp³ hybridization is equivalent to stating that methane has a tetrahedral structure because it has a tetrahedral structure. This circular argument has been pointed out long ago. In 1957, the admonition that "the description (hybrid orbitals) should not be regarded as the cause of the molecule being tetrahedral" was first published.¹⁵ Gillespie later commented "In other words, sp³ hybridization is postulated because CH4 is tetrahedral and then sp³ hybridization is given as the explanation for the tetrahedral shape of the methane molecule!"¹⁶

3. Although Pauling emphasized the value of sp³ hybrid functions to explain the structure of methane, quantitative calculations that he also reported indicated that such sp³ hybrids account for only 60 per cent of the energy of the electronic structure; he declared that other configurations such as s²p² contribute significantly to that structure.¹⁰ Pauling's recognition of a significant contribution of a s²p² configuration is inconsistent with his original assumption of twoelectron bonds, because only the two p² orbitals of carbon are available to make four bonds with the four electrons from the hydrogen atoms. Moreover, in 1958, he included 2 % d orbital and 2 % f orbital character in the tetrahedral orbitals.¹⁷ Subsequent Hartree-Fock computations assigned a value of s^1.5p^2.5 to the electronic structure of methane.¹⁸ To attribute the structure of methane to sp³ tetrahedral hybrid atomic orbitals (neglecting an alternative description, above, as sp² tetrahedral hybridization) is hence at least an exaggeration and a grossly misleading simplification.

4. Trigonal hybrid functions (to which reference is sometimes made as sp² but which are distinct from the tetrahedrally oriented sp² hybrid functions specified above) suffer from the same unjustified discard of √−1 as a coefficient of p_y. In contrast, another hybrid function known as sp or digonal constitutes a legitimate linear combination of real functions in spherical polar coordinates, but functions having exactly the same geometric properties arise directly in Schrödinger's own solution of his equation for the hydrogen atom in paraboloidal coordinates;¹⁹ there is no necessity for such an arbitrary linear combination to generate the desired shape.

5. If one undertakes a molecular-orbital calculation for CH₄ according to a standard quantum-chemical procedure (with a typical computer program for quantum chemistry) at a common level of theory, i.e. parameterization, with a basis set comprising only four 1s functions on H, and on C (implicitly involving only 2s and 2p functions) one or other of these forms,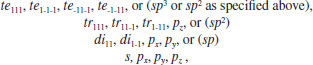

one obtains exactly the same structure of CH₄ and the same energy,²⁰ also with modern valence-bond calculations. There is neither a necessity for, nor an advantage to, the use of hybrid functions within such a basis set; whereas, in the original and primitive valence-bond theory, there was a necessity to impose a set of hybrid atomic functions that yielded the corresponding structure, neither the molecular-orbital procedure nor the modern valence-bond procedure involves such a constraint. (One must distinguish between orbitals and members of a basis set.)

6. Those solutions of Schrödinger's equation in spherical polar coordinates as presented above, and which were obviously Pauling's inspiration for s-p hybrids, are applicable to only an atomic system with rigorously spherical symmetry; their direct use as orbitals for an atom in the vicinity of another atom is inadmissible. Ellipsoidal, also known as prolate spheroidal, orbitals have two centers; the corresponding coordinates are applicable to a hydrogen atom in a diatomic context, as Teller recognized in 1930.²¹

PREVIOUS CRITIQUE OF HYBRID ATOMIC ORBITALS

During 1955-1956, a thesis criticizing the hybridization model "hybridisation...is consequently shown to be of no physical meaning" was censored and papers based on this work rejected (Pritchard²² recently chronicled this censorship). Edmiston and coworkers showed that the removal of hybridization does not affect their calculational results²³ and suggested about hybrids that "chemists have played fast and loose with many qualitative quantum-chemical concepts".²⁴ Gil provided an entire section of his book on the use and misuse of the hybrid orbital concept "... no geometric parameter nor any other molecular property can be explained by invoking hybrid orbitals".²⁵ Boeyens in 2008 presented arguments illuminating the glaring defects of "hybridization, an artificial simulation without scientific foundation".²⁶ Common to all these criticisms is the refusal of much of the chemistry community to acknowledge the existence of alternative perspectives; an impartial review of this subject is lacking.

We recall some pertinent quotations from the literature. In Coulson's Valence, McWeeny wrote "hybridization is not a physical effect but a feature of [a] theoretical description", and "It would be quite wrong to say that, for example, CH₄ was tetrahedral because the carbon atom was sp³ hybridized. The equilibrium geometry of a molecule depends on energy and energy only".²⁷ In a collection of papers to mark the anniversary of Pauling's paper about hybrids, Cook agreed that "hybridization cannot explain the shapes of molecules", but his contention that hybridization is not arbitrary fails to take into account the practical formation of tetrahedral hybrid functions from sp³ or sp² combinations, as delineated above, or indeed innumerable other.²⁸ "The idea of sp³ hybridization is therefore as ludicrous as perpetual motion",¹⁴ but Boeyens failed to understand the significance of the existence of multiple systems of coordinates in which Schrödinger's equation for the hydrogen atom is amenable to a separation of the spatial variables.²⁹

DISTINCTION BETWEEN HYBRID ATOMIC ORBITALS AND OTHER HYBRIDS

We seek to distinguish clearly between the HAO used in the teaching of general and organic chemistry and the other uses of 'hybrid orbitals' in modern chemistry, in which these orbitals might be implemented within basis sets for these calculations. Whether such basis sets for the calculations comprise atomic orbitals or their combinations in hybrid orbitals as presented above, such functions are artifacts of those particular calculations, and have no meaning outside those contexts. Orbitals are the exact algebraic solutions of the Schrödinger's equation for an atom with one electron, i.e. the result or output of such a calculation, whereas a basis set that might consist of orbitals on other atomic centers serves as input for an approximate calculation of observable properties of a molecule. Whether such a calculation is of type molecular orbital or valence bond is immaterial. The words 'hybrid' and 'hybridization' are used for mathematical procedures that are optional for both valence-bond³⁰ and molecular-orbital³¹ calculations of electronic structure, but with a meaning different from 'hybrid' and 'hybridization' in HAO; these other definitions or applications of hybrids are neither discussed nor applied in teaching organic chemistry. Our discussion, and objections, involve the qualitative explanation of chemical phenomena, especially the shapes or general structural properties of organic molecules, in terms of HAO. We have no quarrel with the use of quantum-chemical calculations of molecular structure, which we on occasion perform for various purposes; whether a so-called orbital as a member of a basis set that might be applied in these calculations is canonical or orthogonal or corresponds to a particular energy is entirely irrelevant and superfluous for the purpose that evidently pervades every textbook of organic chemistry.

It would be unwise to remove all use of 'hybrids' or 'hybridization' from chemistry; 'hybridization' used in modern calculations is different and much more rigorously defined. For instance, in their work Foster and Weinhold used rigorous algorithms of the natural-bond-orbital (NBO) method to derive natural hybrid orbitals (NHO) that describe the electronic density based on calculated wave functions,³² but has no relation mathematically with HAO applied in qualitative explanations of the structure of organic molecules. The hybridization concept in modern quantum chemistry does not employ the 'primitive' HAO model. HAO should not be defined as, or conflated with, localized orbitals.

CONCLUSION

In this article, we seek to convince readers, based on mathematical and logical arguments, that, for the teaching of organic chemistry, hybridization is an obsolete concept; the pioneers (e.g. Slater, Pauling, Penney, Van Vleck) who originated the concept could not imagine the overwhelming evidence provided by the experimental data and computers that we have today. A model is useful as long as it gives satisfactory answers to the questions posed at a certain time; when it can no longer fulfill this role, it should be modified or discarded. We have demonstrated that HAO clearly lack mathematical support; based on that fallacy of HAO, we contend that HAO should be retired from the teaching of organic chemistry. The fact that we can eliminate superseded theories in chemistry shows the maturity of the science -- a continuation of their use shows stagnation. The elimination of HAO from the teaching of organic chemistry is thus a positive advancement for the development of future chemists. In Part 2, we continue this argument based on the use of HAO in organic chemistry and a pedagogical model for the future without HAO.

ACKNOWLEDGMENTS

El Centro de Investigaciones en Productos Naturales (CIPRONA) and la Escuela de Química, Universidad de Costa Rica provided support. We thank many professors and students at UCR for helpful discussion.

REFERENCES

1. Pauling, L.; J. Am. Chem. Soc. 1931, 53, 1367.

2. Slater, J. C.; Phys. Rev. 1931, 38, 1109; Slater, J. C.; Phys. Rev. 1931, 37, 481; Slater, J. C.; Phys. Rev. 1932, 41, 255.

3. Pauling, L.; Phys. Rev. 1931, 37,1185.

4. Hultgren, R.; Phys. Rev. 1932, 40, 891.

5. Mulliken, R. S.; Chem. Rev. 1931, 9, 347.

6. Van Vleck, J. H.; J. Chem. Phys. 1934, 2, 20; Van Vleck, J. H.; J. Chem. Phys. 1933, 1, 177; Van Vleck, J. H.; J. Chem. Phys. 1933, 1, 219.

7. Penney, W. G.; Trans. Faraday Soc. 1935, 31, 734.

8. Penney, W. G.; Proc. R. Soc. Lond. A 1934, 144, 166.

9. Van Vleck, J. H.; Sherman, A.; Rev. Mod. Phys. 1935, 7, 167.

10. Pauling, L.; The Nature of the Chemical Bond and the Structure of Molecules and Crystals: an Introduction to Modern Structural Chemistry; Cornell University Press: Ithaca, NY, USA, 1960, pp 120.

11. Rhile, I. J.; J. Chem. Educ. 2015, 92, 1973.

12. Hsu, C.-Y.; Orchin, M.; J. Chem. Educ. 1973, 50, 114.

13. Lewars, E. G.; Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics; Springer International Publishing: 2016, pp 121-123.

14. Boeyens, J. C. A.; Models, Mysteries and the Magic of Molecules; Springer: Dordrecht, 2008, pp. 447-475.

15. Dickens, P. G.; Linnett, J. W.; Q. Rev., Chem. Soc. 1957, 11, 291.

16. Gillespie, R.; Chem. Can. 1976, 23.

17. Pauling, L.; Proc. Natl. Acad. Sci. U. S. A. 1958, 44, 211.

18. Clementi, E.; Popkie, H.; J. Am. Chem. Soc. 1972, 94, 4057.

19. Schrödinger, E.; Ann. Phys. 1926, 80, 437.

20. Ogilvie, J. F.; J. Chem. Educ. 1990, 67, 280.

21. Teller, E.; Z. Phys. 1930, 61, 458.

22. Pritchard, H. O.; J. Chem. Educ. 2012, 89, 301.

23. Jarvie, J.; Willson, W.; Doolittle, J.; Edmiston, C.; J. Chem. Phys. 1973, 59, 3020.

24. Edmiston, C.; J. Chem. Educ. 1992, 69, 600.

25. Gil, V. M. S.; Orbitals in Chemistry: a Modern Guide for Students; Cambridge University Press: Cambridge, UK, 2000, pp 201-204.

26. Boeyens, J. C. A.; Chemistry From First Principles; Springer Science & Business Media: 2008, pp 62.

27. McWeeny, R.; Coulson, C. A.; Coulson’s Valence; Oxford University Press: Oxford, UK, 1979.

28. Cook, D. B.; J. Mol. Struct. 1988, 169, 79.

29. Kalnins, E. G.; Miller, Jr, W.; Winternitz, P.; SIAM J. Appl. Math. 1976, 30, 630.

30. Shaik, S.; Danovich, D.; Hiberty, P. C.; Comput. Theor. Chem. 2017, 1116, 242.

31. Cohen, I.; Del Bene, J.; J. Chem. Educ. 1969, 46, 487.

32. Foster, J. P.; Weinhold, F.; J. Am. Chem. Soc. 1980, 102, 7211.