JBCS

INTRODUÇÃO

Aspectos da vida do Prof. Stammreich e do seu trabalho na Universidade de São Paulo têm sido apresentados em textos anteriores.^1-3 O leitor prontamente assimila que o Prof. Stammreich, além de introduzir a espectroscopia Raman no Brasil, teve contribuições fundamentais para ampliação do escopo de aplicação da técnica, em particular ao construir lâmpadas de hélio para excitação dos espectros. Amostras que absorviam a mais usual radiação de arcos de mercúrio ou eram fotossensíveis passaram a ser estudadas por espectroscopia Raman com excitação no amarelo ou vermelho. O Prof. Stammreich resume alguns dos avanços técnicos (espectrógrafos com redes de difração, fontes de luz para excitação, métodos fotográficos para detecção) em um artigo de 1956.⁴

A presente revisão está direcionada para os resultados efetivamente alcançados pelo grupo do Prof. Stammreich. Neste artigo pretendemos transmitir ao leitor o contexto científico e as conclusões alcançadas pelo grupo do Prof. Stammreich com o uso da espectroscopia Raman. Os aspectos experimentais de preparação de amostras e obtenção dos espectros Raman não serão comentados nesta revisão. Concentraremos a discussão no ponto central de cada artigo de tal forma a destacar a questão científica pendente no momento e, portanto, a principal conclusão do artigo. Cerca de vinte e cinco artigos publicados pelo Prof. Stammreich serão revistos, ou seja, aproximadamente metade do número obtido numa consulta a um serviço de indexação de publicações científicas. Os artigos a serem revistos compreendem o período 1955–1969, mas a discussão não seguirá ordem cronológica. Os artigos foram alocados em quatro grupos em função do tipo de composto: carbonil-metais; halogênios e inter-halogênios; compostos de halogênio; oxoânions.

CARBONIL-METAIS

A determinação da estrutura do pentacarbonilferro(0), Fe(CO)₅, por espectroscopia de absorção no infravermelho (IR) era ambígua ao final da década de 1950. Atribuição do espectro IR levou às proposições de pirâmide tetragonal⁵ (C_4v) ou bipirâmide trigonal⁶ (D_3h). A Figura 1 mostra estruturas esquemáticas para cada um desses dois grupos de ponto e o número de modos normais de cada espécie de simetria. A partir das atividades no IR e Raman indicadas na Figura 1, fica claro que espectroscopia Raman complementaria a atribuição do espectro vibracional e discriminaria a estrutura correta entre C_4v ou D_3h. Nesse sentido, a possibilidade do grupo do Prof. Stammreich de excitar o espectro Raman com radiações de He (667,8 nm e 706,5 nm) foi fundamental porque Fe(CO)₅ é colorido e fotosensível.⁷ A atribuição do espectro Raman indicou três modos atribuídos como estiramentos C–O (2 A₁' e 1 E'), três dobramentos de ângulo C–Fe–C (2 E' e 1 E") e sete modos de estiramento Fe–C ou dobramento de ângulo Fe–C–O (2 A₁', 3 E' e 2 E"). Portanto, ao comparar o número de modos normais de cada espécie de simetria e as correspondents atividades Raman, concluiu-se que a estrutura de Fe(CO)₅ é a bipirâmide trigonal (D_3h).⁷ Uma ambiguidade análoga foi a motivação de um artigo póstumo de 1970⁸ sobre a estrutura do íon pentacianidoniquelato(II) em solução aquosa. Stammreich e colaboradores⁸ propuseram que a estrutura de [Ni(CN)₅]^3- é bipirâmide trigonal (D_3h) a partir da atribuição do espectro Raman. Devemos notar, no entanto, que Griffith e Lane⁹ propuseram poucos anos depois que a estrutura de [Ni(CN)₅]^3- é pirâmide tetragonal (C_4v) a partir do espectro Raman da solução aquosa.

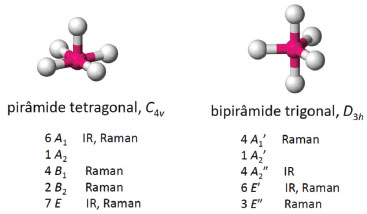Figura 1. Ambiguidade das estruturas de Fe(CO)₅ propostas a partir da atribuição de espectros IR: pirâmide tetragonal⁵ (C_4v) ou bipirâmide trigonal⁶ (D_3h). As estruturas esquemáticas mostram cada ligante carbonil como uma esfera branca. O número de modos normais de cada espécie de simetria e atividades IR e Raman estão indicados para cada estrutura

A esperada estrutura tetraédrica dos ânions [Co(CO)]₄^- e [Fe(CO)]₄^2- foi confirmada pelos espectros Raman obtidos no grupo do Prof. Stammreich.¹⁰ A questão não trivial abordada nesse trabalho foi a estrutura do derivado [HFe(CO)]₄^-. Espectro IR de HCo(CO)₄ sugeria que a simetria T_d era mantida,¹¹ i.e. posição do hidrogênio desconhecida, mas dublete de bandas do modo de estiramento do ligante carbonil indicava que o hidrogênio estava ligado a um carbonil, ou seja, simetria C_3v. No entanto, o espectro IR não indicava a presença de um modo de estiramento OH.¹¹ Edgell et al.^12,13 propuseram um modelo de ponte para HCo(CO)₄ a partir do espectro IR e de cálculo de orbitais moleculares. Nesse modelo (ver Figura 2) o hidrogênio está ligado a três carbonilas e ao metal numa estrutura de simetria C_3v.

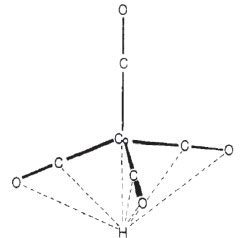Figura 2. O modelo com simetria C_3v proposto por Edgell et al.^12,13 para HCo(CO)₄. Reproduzido com permissão de Edgell, W. F.; Magee, C.; Gallup, G.; J. Am. Chem. Soc. 1956, 78, 4185. Copyright 1956 American Chemical Society

A redução da simetria implica em desdobramento das vibrações triplamente degeneradas do grupo de ponto T_d em vibrações das espécies de simetria A₁ e E do grupo C_3v, mas este efeito não foi observado por Edgell et al.¹² no espectro IR de HCo(CO)₄. Ao comparar os espectros Raman de [Fe(CO)]₄^2- e [HFe(CO)]₄^-, Stammreich et al.¹⁰ comprovaram que os modos F₂ do tetraedro regular em [Fe(CO)]₄^2- eram, de fato, desdobrados em [HFe(CO)]₄^-. A Tabela 1 mostra as frequências vibracionais dos modos relevantes reportadas no artigo de Stammreich et al.¹⁰

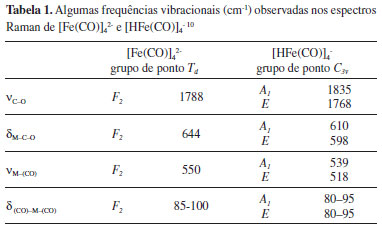
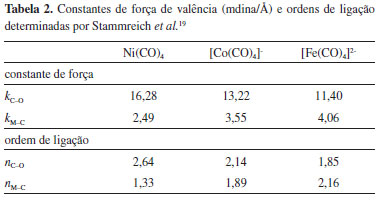
A indicação de estrutura C_3v para [HFe(CO)]₄^- está citada na terceira edição do clássico livro de Linus Pauling (página 334).¹⁴ É curioso notar que Pauling cita o trabalho do Stammreich como sendo espectro infravermelho em vez de espectro Raman. O erro decorre do fato que no livro, o qual é do mesmo ano que o artigo do Stammreich (1960),¹⁰ Pauling faz referência ao estudo de HCo(CO)₄ publicado por Cotton¹⁵ em que o autor menciona uma comunicação particular do Prof. Stammreich (sem explicitar que se tratava de espectroscopia Raman) sobre o desdobramento dos modos ao passar de [Fe(CO)]₄^2- para [HFe(CO)]₄^-. Finalmente, mencionamos que Stammreich et al.¹⁰ consideraram que não estava clara a qual banda Raman atribuir a vibração esperada envolvendo hidrogênio e metal em [HFe(CO)]₄^-. No ano seguinte, Edgell e Summit¹⁶ analisaram o espectro IR de HCo(CO)₄ em fase gasosa e atribuíram o estiramento ν(Co–H) à banda em 1934 cm^-1. Difração de elétron em fase gasosa confirmou a simetria C_3v de HCo(CO)₄, sendo o comprimento da ligação r_Co–H = 1.556 Å.¹⁷

Os estudos de carbonil-metais por espectroscopia Raman inserem-se no contexto científico mais amplo da natureza da ligação química com caráter parcial de ligação dupla. Pauling, no capítulo dedicado ao tema (ver capítulo 9 da ref. 14), considera como exemplo, entre outros sistemas, a distância relativamente pequena r_Ni–C = 1,82 Å do complexo tetraédrico Ni(CO)₄ como manifestação do caráter duplo parcial da ligação Ni–C e das estruturas de ressonância. Comprimento de ligação é inversamente proporcional à ordem de ligação (por exemplo, ver Figura 7.3 da ref. 14) e à constante de força do modelo do oscilador harmônico (a chamada regra de Badger).¹⁸ Na relação direta entre ordem de ligação e constante de força reside a motivação da análise de modos normais realizada pelo grupo do Prof. Stammreich para a sequência Ni(CO)₄, [Co(CO)₄]^- e [Fe(CO)₄]^2-. Stammreich et al.¹⁹ consideram a distribuição eletrônica desses complexos de acordo com os conceitos comumente encontrados em livros-textos atuais:²⁰ ligação σ envolvendo doação de elétron do ligante para o metal e retrodoação de elétron d do metal para orbital π anti-ligante do carbonil. Assim, Stammreich et al.¹⁹ argumentam que na sequência de compostos isoeletrônicos Ni(CO)₄, [Co(CO)₄]^- e [Fe(CO)₄]^2-, as ordens das ligações M–C e C–O, estimadas a partir das respectivas constantes de força, devem variar de forma complementar, i.e. a ordem da ligação M–C aumenta a expensas da C–O.

A partir de um campo de força de valência, Stammreich et al.¹⁹ determinaram as constantes de força, algumas delas aqui reproduzidas na Tabela 2. Note a ordem decrescente de k_C–O, enquanto que crescente de k_M–C, ao longo da sequência Ni(CO)₄, [Co(CO)₄]^- e [Fe(CO)₄]^2-. As tendências opostas de k_C–O e k_M–C indicam a conjugação na estrutura eletrônica. As ordens de ligação mostradas na Tabela 2,¹⁹ considerando monóxido de carbono (k_CO = 18,53 mdina/ Å; n_CO = 3) como referência, indicam o caráter parcial de ligações múltiplas e a tendência inversa de diminuição de n_C–O concomitante ao aumento de n_M–C. Note que a soma de n_C–O e n_M–C é aproximadamente quatro conforme a ordem de ligação total.

Espectroscopia IR indicou²¹ que as estruturas de carbonil-metais polinucleares, tais como as estudadas por Stammreich et al.,²² Cd[Co(CO)₄]₂ e Hg[Co(CO)₄]₂, envolviam ligação entre os metais. A evidência nesse sentido é a frequência do modo de estiramento ν(CO) ser observada acima de 2000 cm^-1,²¹ i.e. sem o CO em ponte entre dois centros metálicos. A Figura 3 mostra esquemas de estruturas em duas conformações, alternada (D_3d) e eclipsada (D_3h), sendo que o espectro IR de Hg[Co(CO)₄]₂ em solução de n-heptano indicou a estrutura alternada.²¹ No entanto, a evidência mais direta da ligação metal–metal, ou seja, uma banda de baixa frequência correspondente ao modo de estiramento, não é facilmente acessível por espectroscopia IR. Os espectros Raman obtidos por Stammreich et al.²² confirmaram a ausência de CO em ponte e a estrutura alternada (D_3d). O resultado mais importante do estudo foi a identificação do modo de estiramento metal–metal como uma banda Raman intensa, fina e polarizada. Os estiramentos ν(Cd–Co) e ν(Hg–Co) de Cd[Co(CO)₄]₂ e Hg[Co(CO)₄]₂ em solventes orgânicos foram observados em 152 e 161 cm^-1, respectivamente.²²

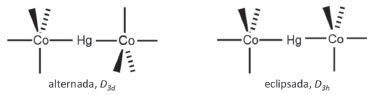Figura 3. Esquema das estruturas de Hg[Co(CO)₄]₂ nas conformações alternada (grupo de ponto D_3d) e eclipsada (grupo de ponto D_3h)

O espectro IR de [(C₅H₅)Fe(CO)₂]₂ apresenta bandas de absorção em ∼800 cm^-1 e em 1950–2060 cm^-1 correspondentes aos estiramentos das carbonilas em ponte e terminais, respectivamente.²³ A estrutura mostrada na Figura 4 corresponde à fase cristalina determinada por difração de raios-X. Uma vez que essa estrutura possui um centro de inversão, então, é válida a chamada regra de exclusão, ou seja, não há vibração ativa em comum, entre ambas as espectroscopias IR e Raman. No entanto, no caso de [(C₅H₅)Fe(CO)₂]₂ em solução, Cotton, Stammreich e Wilkinson²³ observaram várias coincidências de bandas nos espectros IR e Raman na região dos estiramentos das carbonilas. A interpretação dada na ref. 23, embora de forma não categórica, foi que ocorre uma mudança estrutural na passagem do sólido para a solução e que existe mais de uma espécie em solução. De fato, estudo posterior de espectroscopias RMN e IR em função da temperatura caracterizaram a termodinâmica e cinética da conversão entre diferentes isômeros (ver a Figura 3 da ref. 24).

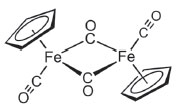Figura 4. Estrutura de di-μ-carbonil-bis[carbonil(ciclopentadienil)ferro], [(C₅H₅)Fe(CO)₂]₂

HALOGÊNIOS E INTER-HALOGÊNIOS

A técnica de excitação na região do vermelho é particularmente apropriada para obtenção do espectro Raman do vapor marrom de Br₂. Stammreich²⁵ obteve o espectro Raman de Br₂(g) a 85 ºC e 900 mmHg usando a radiação 587,56 nm de uma lâmpada de He e tempo de exposição de 15 horas. O espectro Raman de Br₂(g) reproduzido na Figura 5 mostra, além da transição fundamental em 316,8 cm^-1, também a primeira e segunda harmônicas em 631,1 e 944,5 cm^-1. Esse resultado foi "inesperado", nas palavras do próprio Stammreich, pois "harmônicas nunca haviam sido observadas em espectros Raman de moléculas diatômicas".²⁵

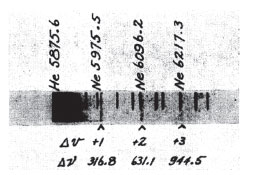Figura 5. Espectro Raman de Br₂(g) obtido por Stammreich.²⁵ Reproduzido de Stammreich, H.; Phys. Rev. 1950, 78, 79, com permissão da APS

Observação de harmônicas relativamente intensas seria hoje explicada simplesmente como resultado do efeito Raman ressonante. No entanto, espectroscopia Raman ressonante não era uma área de pesquisa estabelecida em 1950, embora sabido teoricamente que o espectro Raman seria intensificado se a energia de excitação coincidisse com uma transição eletrônica da molécula. Por outro lado, Barrow²⁶ mostrou que as linhas observadas por Stammreich²⁵ no "espectro Raman" do Br₂(g) correspondiam, em verdade, ao espectro de fluorescência devido à transição eletrônica B(³Π_0u⁺) ← X(¹Σ_g⁺) envolvendo os estados vibracionais v' = 13 e v" = 2, 3, 4 e 5. Assim, o artigo do Prof. Stammreich desencadeia uma discussão ainda mais fundamental, a saber, a distinção entre Raman e fluorescência quando o espectro é excitado em condição de ressonância. Kiefer e Schrötter²⁷ mostraram que espectros de fluorescência e Raman ressonante de Br₂(g) são observados simultaneamente se a linha de excitação é 694,3 nm, mas apenas espectro Raman ressonante se excitado com 488,0 nm. Holzer et al.²⁸ resumiram a questão ao comparar os espectros de diferentes gases (Cl₂, Br₂, I₂, BrCl, ICl, IBr) excitados com as várias linhas de um laser de íon argônio: espectro Raman ressonante é obtido quando a energia de excitação é maior do que o limite de convergência da transição B(³Π_0u⁺) ← X(¹Σ_g⁺), enquanto que fluorescência ressonante se a energia de excitação está dentro da estrutura rovibracional da banda de absorção.

Várias propostas têm sido feitas para separar os termos atribuídos à Raman ressonante e fluorescência ressonante nas equações obtidas por teoria de perturbação da mecânica quântica para a interação radiação–molécula. A abordagem mais adequada da questão é pelo formalismo do tempo da espectroscopia, o qual mostra, no entanto, que a separação entre fluorescência e Raman ressonante não é formalmente válida sob um ponto de vista teórico matematicamente rigoroso.²⁹ Por outro lado, é mais fácil distinguir entre fluorescência e Raman ressonante sob o ponto de vista experimental, por exemplo, diferenças em largura de banda, razão de despolarização e dependência com a pressão.^28,30

A característica distintiva ainda mais evidente é que, se forem usadas diferentes radiações de excitação, a linha Raman manterá a mesma diferença de energia em relação à excitação. Nesse sentido, Stammreich e Forneris³¹ registraram o espectro Raman do bromo líquido usando simultaneamente sete radiações de uma lâmpada de argônio. A Figura 6 reproduz os espectros Raman de Br₂(l), a partir dos quais a frequência da transição fundamental é 306,1 ± 0,6 cm^-1. O espectro Raman de Br₂(l) não exibe harmônicas, assim Stammreich e Forneris³¹ reconhecem que no caso de Br₂(g) do artigo anterior²⁵ não se tratava de espectro Raman. Recentemente, um estudo detalhado do espectro Raman de bromo líquido identificou até trinta harmônicas quando excitado com a radiação 405 nm de um laser de diodo.³²

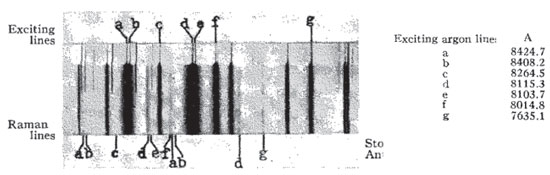Figura 6. Espectro Raman de bromo líquido obtido por Stammreich e Forneris.³¹ Reproduzido de Stammreich, H.; Forneris, R.; J. Chem. Phys. 1954, 22, 1624, com permissão da AIP

Os espectros Raman de moléculas diatômicas de halogênios e inter-halogênios permitiriam obter as constantes vibracionais de uma forma mais direta do que as reportadas a partir da análise da estrutura da banda do espectro eletrônico. Por exemplo, o valor tabelado por Herzberg³³ para BrCl é ω = 430 cm^-1. Stammreich e Forneris³⁴ obtiveram ω = 428 ± 2 cm^-1 a partir do espectro Raman de BrCl em solução de CCl₄. No caso de cloro líquido, Stammreich e Forneris³⁵ obtiveram o espectro Raman com alta resolução, sendo que linhas Raman foram atribuídas aos diferentes isótopos e transições fundamental e harmônica. A frequência harmônica e a constante de anarmonicidade resultantes, por exemplo, para ³⁵Cl₂, são ω_e = 562,3 cm^-1 e _ex_e = 2,7 cm^-1.³⁵ As constantes de anarmonicidade obtidas a partir do espectro Raman são consideravelmente menores do que aquelas obtidas a partir do espectro eletrônico: Herzberg³⁶ reporta para ³⁵Cl₂ os valores ω_e = 564,9 cm^-1 e _ex_e = 4,0 cm^-1. Stammreich e Forneris³⁵ argumentam que a análise usual da progressão vibracional, bem conhecida em livros-texto de Físico-Química (gráfico de Birge-Sponer),³⁷ depende da expressão para os termos vibracionais, G(v) = (v+½)ω_e – (v+½)²ω_ex_e, ser estritamente válida mesmo para números quânticos elevados. Por isso que Stammreich e Forneris³⁵ consideram que as constantes de anarmonicidade corretas são as resultantes dos espectros Raman. De fato, uma consulta a um banco de dados atual (NIST, National Institute of Standards and Technology)³⁸ indica os seguintes valores para ³⁵Cl₂: ω_e = 559,7 cm^-1 e _ex_e = 2,67 cm^-1.

Stammreich e Forneris³¹ já salientam o efeito de fase condensada na frequência vibracional de Br₂(l), pois a mesma é cerca de 10 cm^-1 menor do que Br₂(g). Na segunda parte do artigo sobre moléculas diatômicas de halogênios e inter-halogênios, Stammreich et al.³⁹ compararam as frequências vibracionais de várias diatômicas (Cl₂, F₂, Br₂, I₂, ClF, BrCl, ICl, BrF, IF, IBr) em gás, líquido e solução em diferentes solventes. A comparação entre diatômicas homo- e heteronucleares teve a intenção de discriminar os efeitos das forças intermoleculares de dispersão de London e a presença adicional de momento de dipolo no caso das heteronucleares. A partir do conjunto de dados de frequências vibracionais, Stammreich et al.³⁹ concluíram que o principal efeito das forças intermoleculares sobre a frequência vibracional nesse grupo de moléculas é devido à polarizabilidade das mesmas, sendo menos importante o efeito da polaridade da ligação nos inter-halogênios.

Stammreich e Forneris⁴⁰ analisaram os espectros Raman de moléculas AB₄ que possuem uma estrutura de quadrado planar (D_4h) em vez da simetria tetraédrica mais usual. No capítulo dedicado às ligações químicas envolvendo orbitais d, Pauling apresenta os quatro orbitais híbridos sp²d que apontam ao longo dos vértices de um quadrado (ver pag. 153 da Ref. [14]). Stammreich e Forneris⁴⁰ partem dessa consideração para estudar os espectros Raman de (ICl₄)^-, (AuCl₄)^-, (AuBr₄)^- e (PtCl₄)^2-. Esses complexos são quadrados planares de acordo com dados de difração de raios-x, mas não havia um estudo por espectroscopia Raman, além de ser difícil estudá-los por espectroscopia IR por causa das frequências vibracionais baixas. Os espectros Raman dos quatro complexos apresentaram, de fato, as três frequências ativas no Raman esperadas pela simetria D_4h: estiramento simétrico (A_1g), estiramento anti-simétrico (B_2g) e dobramento de ângulo no plano (B_1g).⁴⁰

No caso do íon poli-halogênio (ICl₄)^-, Stammreich e Forneris⁴⁰ fazem notar que a simetria D_4h decorre da hibridização sp³d², a qual resulta em seis orbitais ao longo de um octaedro, sendo que dois pares de elétron não compartilhados ocupam as direções dos ápices do octaedro. Isso estava de acordo com considerações de Linus Pauling na segunda edição do seu livro (1944), em que íons poli-halogênios são incluídos na lista de exemplos (ver pág. 111 da ref. 41). No entanto, medidas de frequências de ressonância de quadrupolo nuclear realizadas por Cornwell e Yamasaki^42,43 em sais de (ICl₂)^- e (ICl₄)^- indicaram que a participação de orbitais d na ligação química é menor do que antecipado. Em vez de ligações essencialmente covalentes entre orbitais σ do cloro e híbridos sp³d² (octaedro) ou sp³d (bipirâmide trigonal) do iodo, foi proposto que a representação mais adequada da ligação química envolveria híbridos de ressonância entre estruturas do tipo ^-[Cl ^... I – Cl] ↔ [Cl – I ^... Cl]^-.^42,43

Isto motiva a análise de coordenadas normais realizada por Stammreich et al.:⁴⁴ obter indícios sobre a natureza da ligação química a partir das constantes de força dos íons poli-halogênios. As frequências vibracionais dos modos de estiramento simétrico ν₁ e antissimétrico ν₃ observadas, respectivamente, nos espectros Raman e infravermelho dos íons triatômicos (ICl₂)^-, (BrCl₂)^- e (Br₃)^- prontamente permitem obter as constantes de força do estiramento X–Y, f_r, e a constante de interação entre as ligações adjacentes, f_rr, de um campo de força de valência.⁴⁵ Stammreich et al.⁴⁴ encontraram que f_r é significativamente menor nos íons triatômicos do que na molécula diatômica correspondente. Por exemplo, f_r em (ICl₂)^- é 1.00 mdina/Å, a ser comparado com 2.38 mdina/Å em ICl. Além disso, as constantes de interação f_rr são relativamente grandes nos íons poli-halogênios: f_rr = 0.36 mdina/Å em (ICl₂)^-, enquanto que o usual, e.g. CO₂, é f_rr apenas ca. 10% de f_r. Os valores pequenos de f_r, concomitante com valores grandes de f_rr, levaram Stammreich et al.⁴⁴ a concordarem com a descrição proposta para a ligação química em termos de orbitais p e ressonância do tipo ^-[Cl ^... I – Cl] ↔ [Cl – I ^... Cl]^-.

Bell e Longuet-Higgins⁴⁶ apresentaram um estudo muito detalhado sobre a análise de coordenadas normais de moléculas X₂Y₆ com simetria correspondente ao grupo de ponto D_2h. A estrutura em questão é mostrada no painel esquerdo da Figura 7, sendo que os sistemas representativos abordados por Bell e Longuet-Higgins⁴⁶ foram diborano, B₂H₆, e haletos de alumínio, e.g. Al₂Cl₆. Stammreich e Kawano⁴⁷ estudaram o espectro Raman de I₂Cl₆, o qual é também de simetria D_2h, mas com estrutura planar conforme ilustrado no painel direito da Figura 7. A estrutura cristalina de I₂Cl₆ já tinha sido determinada por difração de raios-X,⁴⁸ mas não havia um estudo do espectro vibracional de uma molécula do tipo X₂Y₆ planar. Stammreich e Kawano⁴⁷ atribuíram todas as nove vibrações ativas Raman esperadas para I₂Cl₆ de acordo com o grupo de ponto D_2h: 4 A_g, 1 B_1g, 1 B_2g e 3 B_3g. Destaque para as vibrações com contribuição de estiramentos I–Cl: quando envolve as ligações dos átomos de cloro em ponte entre os átomos de iodo é de frequência menor (ν₈ (B_3g) 106,2 cm^-1) do que as vibrações envolvendo ligações I–Cl das extremidades (ν₁ (A_g) 312,1 cm^-1 e ν₇ (B_3g) 342,9 cm^-1).⁴⁷ Essa diferença de frequências vibracionais entre ligações I–Cl em ponte e na extremidade é consistente com as distâncias de ligação obtidas por difração de raios-X,⁴⁸ respectivamente, 2,68 e 2,39 Å.

Figura 7. Estruturas de moléculas X₂Y₆ com simetria D_2h

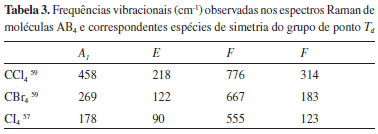
COMPOSTOS DE HALOGÊNIOS

Stammreich obteve espectros Raman de diversos compostos de halogênios, sendo que análise de coordenadas normais foi realizada para vários sistemas e em alguns havia ambiguidade entre diferentes estruturas possíveis.

A estrutura de dicloreto de enxôfre, SCl₂, tinha sido determinada por difração de elétrons: d_S–Cl = 1.99 Å, = 101º.⁴⁹ Stammreich et al.⁵⁰ registraram o espectro Raman de SCl₂ líquido e, a partir das frequências observadas (208 cm^-1 (A₁), 514 cm^-1 (A₁) e 535 cm^-1 (B₂)), calcularam as constantes de força considerando um campo de força de valência. A constante de força de estiramento da ligação, k_S-Cl = 2,58 × 10⁵ dina cm^-1, foi usada para estimar a distância da ligação, r_S-Cl, a partir da conhecida regra de Badger que relaciona k e r.¹⁸ O valor r_S-Cl = 2,02 Å estimado a partir do espectro Raman concorda com o valor determinado por difração de elétrons.⁵⁰

A estrutura de cloreto de cromilo, CrO₂Cl₂, também foi determinada no estudo de difração de elétrons,⁴⁹ o qual indicou que CrO₂Cl₂ pertence ao grupo de ponto C_2v. Durante o andamento do estudo de CrO₂Cl₂ por espectroscopia Raman no grupo do Prof. Stammreich, o espectro infravermelho desse composto foi publicado por Hobbs.⁵¹ Quatro frequências fundamentais foram observadas no espectro infravermelho de CrO₂Cl₂, sendo que oito modos são ativos infravermelho. No caso do espectro Raman, Stammreich et al.⁵² atribuíram as noves frequências fundamentais esperadas para CrO₂Cl₂ de acordo com o grupo de ponto C_2v: 4 A₁ + 1 A₂ + 2 B₁ + 2 B₂. A análise de coordenadas normais realizada com um campo de força quadrático resultou em frequências calculadas em excelente concordância com as experimentais. Assim como em vários sistemas discutidos nas seções anteriores, o escopo mais amplo da análise de coordenadas normais era obter inferência sobre a natureza da ligação química ao comparar com moléculas análogas. Por exemplo, a frequência vibracional 984 cm^-1 atribuída ao estiramento Cr–O em CrO₂Cl₂ é maior do que em sistemas com estruturas de ressonância, tais como [CrO₄]^2- (859 cm^-1) e [Cr₂O₇]^2- (904 cm^-1) que foram objetos de estudos anteriores no próprio grupo do Prof. Stammreich e que serão comentados na próxima seção.^53,54 A ordem de ligação maior de Cr–O em CrO₂Cl₂ resulta na frequência de estiramento maior em comparação com a mesma ligação nos oxoânions.⁵²

Análise de coordenadas normais para moléculas AB₃, grupo de ponto C_3v, foi realizada para vários trihaletos:⁵⁵ PF₃, PCl₃, PBr₃, AsF₃, AsCl₃, SbCl₃ e BiCl₃. O campo de força usado na análise incluiu quatro constantes de força para o estiramento da ligação, dobramento de ângulo e para as correlações entre ligações e entre ângulos. Stammreich et al.⁵⁶ consideraram os derivados iodeto: PI₃ e AsI₃. A obtenção dos espectros Raman desses derivados é difícil pela cor vermelha dos compostos, sendo usada, então, a radiação 667,82 nm do He. A análise por espectroscopia de absorção no infravermelho também é difícil devido às frequências vibracionais baixas. Por exemplo, as frequências vibracionais observadas no espectro Raman de AsI₃ diluído em solventes orgânicos são 216 cm^-1 (A₁), 94 cm^-1 (A₁), 221 cm^-1 (E) e 70 cm^-1 (E).⁵⁶ As frequências vibracionais calculadas concordam com as frequências experimentais mesmo se as constantes de força de interação são ignoradas no campo de força proposto para moléculas AB₃.⁵⁶

Stammreich et al. trabalharam com outros derivados de iodo cuja análise vibracional era conhecida para moléculas análogas: tetraiodeto de carbono (CI₄)⁵⁷ e iodofórmio (CHI₃).⁵⁸ Simanouti⁵⁹ fez a análise de coordenadas normais considerando o campo de força Urey-Bradley para moléculas tetraédricas AB₄, inclusive CCl₄ e CBr₄. A Tabela 3 compara as frequências vibracionais dessas moléculas com as observadas por Stammreich et al.⁵⁷ no espectro Raman de CI₄. Como esperado, a constante de força de estiramento da ligação C–X diminui na sequência CCl₄, CBr₄ e CI₄, respectivamente, 1,76, 1,43 e 1,12 × 10⁵ dina/cm. No entanto, a constante de força do dobramento de ângulo em CI₄ (0,094 × 10⁵ dina/cm) é maior que em CCl₄ e CBr₄, respectivamente, 0,080 e 0,045 × 10⁵ dina/cm. Stammreich et al.⁵⁷ atribuíram esse fato ao volume atômico grande dos átomos de iodo em CI₄. No caso do iodofórmio, a análise detalhada do espectro infravermelho foi publicada por Hexter e Cheung⁶⁰ no mesmo ano do artigo de Stammreich e Forneris⁵⁸ sobre o espectro Raman de CHI₃. De fato, os autores compartilharam seus resultados antes da publicação no Oxford Meeting 1955 do European Molecular Spectroscopy Group.⁵⁸ O estudo por espectroscopia infravermelho considerou monocristal de CHI₃,⁶⁰ enquanto que o estudo por espectroscopia Raman considerou CHI₃ em solução em diversos solventes orgânicos.⁵⁸ Excelente concordância foi obtida entre as frequências vibracionais dos espectros IR e Raman de CHI₃.

Outros estudos de compostos de halogênios tiveram a geometria da molécula como questão principal. Espectros Raman⁶¹ e infravermelho⁶² de cloreto de tionilo, SOCl₂, reportados na primeira metade da década de 1950 tinham confirmado que a estrutura não é planar C_2v, mas sim piramidal C_s. No caso C_2v são esperadas 3 A₁ + 2 B₁ + B₂ vibrações, enquanto que no caso C_s são esperadas 4 A' + 2 A" vibrações. Todos esses modos são ativos no Raman e IR, mas medidas de polarização das bandas Raman permitem discriminar entre as geometrias planar e piramidal, pois são polarizadas as bandas correspondentes aos três modos A₁ ou quatro modos A'. Stammreich et al.⁶³ registraram o espectro Raman do correspondente derivado brometo, SOBr₂. As medidas de polarização das bandas Raman confirmaram que a estrutura de SOBr₂ também é piramidal, C_s.⁶³

A determinação da estrutura da molécula P₂I₄ é mais complicada devido às várias conformações possíveis. A Figura 8 mostra possíveis estruturas de P₂I₄ com os respectivos grupos de ponto e as atividades dos modos no IR e Raman. Em um estudo por espectroscopia infravermelho, Cowley e Cohen propuseram que a estrutura de P₂I₄ é trans (C_2h) no estado sólido e "provavelmente" gauche (C₂) em solução em CS₂.⁶⁴ O uso combinado das espectroscopias IR e Raman por Stammreich et al.⁶⁵ indicou, no entanto, a estrutura trans (C_2h) para P₂I₄ em ambos os estados sólido e solução. Todas as vibrações esperadas para o grupo de ponto C_2h foram identificadas, A_g: 316, 303, 114 e 78; A_u: 327, 90 e 51; B_g: 330 e 95; B_u: 313, 109 e 65 cm^-1 (valores em solução).⁶⁵

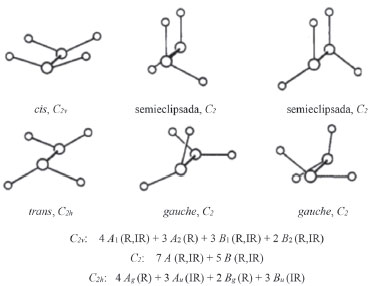Figura 8. Estruturas possíveis para a molécula P₂I₄, respectivos grupos de ponto e atividades das vibrações no infravermelho e no Raman⁶⁴

Diferentes estruturas também poderiam ser propostas para os complexos de iodeto de bismuto.⁶⁶ No caso de (BiI₄)^-, se a estrutura fosse tetraedro (T_d) ou quadrado planar (D_4h), o espectro Raman seria relativamente simples com apenas quatro ou três bandas, respectivamente. A complexidade do espectro Raman em solução de acetona (bandas em 141, 129, 107, 80 e 53 cm^-1) indicou que a geometria de (BiI₄)^- corresponde ao grupo de ponto C_2v numa estrutura de bipirâmide trigonal, ou seja, análoga à estrutura mostrada na Figura 1, mas com uma posição equatorial ocupada pelo par isolado de elétrons. No caso de (BiI₆)^3-, as frequências observadas (130, 110 e 55 cm^-1) são consistentes com uma estrutura de octaedro.⁶⁶

OXOÂNIONS

As frequências vibracionais do ânion cromato, [CrO₄]^2-, estavam estabelecidas pelos espectros Raman reportados por Venkateswaran.⁶⁷ No entanto, Stammreich et al.⁵³ notaram que as frequências atribuídas aos modos de dobramento de ângulo eram muito altas e, por consequência, a respectiva constante de força. Nesse sentido, Stammreich et al.⁵³ obtiveram o espectro Raman da solução aquosa de K₂CrO₄ usando a radiação 587,56 nm do He para excitação do espectro. As frequências vibracionais obtidas por Venkateswaran⁶⁷ e Stammreich et al.⁵³ são comparadas na Tabela 4. Stammreich et al.⁵³ interpretaram que o valor elevado das frequências dos modos ν₂ e ν₄ no artigo de Venkateswaran⁶⁷ era devido ao fato de linhas de referência do espectro de comparação para as medidas de comprimento de onda terem sido identificadas como sendo linhas Raman da amostra. A partir das frequências corrigidas, Stammreich et al.⁵³ determinaram a constante de força para o dobramento de ângulo consideravelmente menor que o valor encontrado por Venkateswaran,⁶⁷ respectivamente, 0,61 e 1,00 mdina/Å. É interessante notar que Venkateswaran e Sundaram,⁶⁸ em um artigo posterior, calcularam constantes de força para várias moléculas tetraédricas, inclusive [CrO₄]^2-, para o qual consideraram as novas frequências vibracionais corrigidas. Vários artigos do Prof. Stammreich são usados como referências de frequências vibracionais no conhecido livro do Nakamoto.^69,70 Os valores citados por Nakamoto (ver tabela 2.6e, pag. 202 da Ref. [69]) para [CrO₄]^2- também estão na Tabela 4, mas referem-se ao artigo de Malchus e Jansen.⁷¹ As diferenças em frequências vibracionais deve-se ao fato de Malchus e Jansen⁷¹ considerarem cromato de tetrametilamônio no estado sólido. Em solução aquosa, Kiefer e Bernstein⁷² reportam, de fato, frequências vibracionais de [CrO₄]^2- consistentes com os valores obtidos por Stammreich et al.⁵³

A atribuição dos espectros Raman e infravermelho do ânion dicromato, [Cr₂O₇]^2-, realizada por Stammreich et al.⁵⁴ considerou um modelo separando as vibrações em dois tipos. Ao visualizar a estrutura molecular como O₃Cr–O–CrO₃, o oxigênio central e os átomos de cromo (Cr–O–Cr) definem uma simetria local C_2v, enquanto que cada extremidade (O₃Cr–O') possui simetria local C_3v. As frequências observadas em 220, 558 e 772 cm^-1 no espectro Raman da solução aquosa foram atribuídas às vibrações da parte central, respectivamente, δ(CrOCr), ν_s(CrOCr) e ν_as(CrOCr). As frequências dos grupos das extremidades são 365, 904 e 946 cm^-1, atribuídas às vibrações δ(CrO₃), ν_s(CrO₃) e ν_as(CrO₃), respectivamente. Nesse modelo, a constante de força da ligação central, f_Cr–O' = 3,27 mdina/Å, é consideravelmente menor que da ligação da extremidade, f_C–O = 6,07 mdina/Å.⁵⁴ Por outro lado, Abbas e Davidson⁷³ reavaliaram a frequência do modo de dobramento de ângulo δ(CrOCr), o qual foi atribuído à frequência 89 cm^-1 observada no espectro Raman da solução aquosa. Cálculo recente das frequências vibracionais por método de química quântica computacional resultou em 117 cm^-1 com 90% de distribuição de energia potencial no modo δ(CrOCr).⁷⁴ O cálculo de química quântica confirma que a magnitude de f_Cr–O' é aproximadamente metade de f_Cr–O.

Finalmente mencionamos os trabalhos sobre os derivados de halogênio de oxoânions: [CrO₃Cl]^{- 75} e [CrO₃F]^-.⁷⁶ As frequências observadas nos espectros Raman e infravermelho, assim como a polarização das bandas Raman, indicam que a simetria de [CrO₃Cl]^- corresponde ao grupo de ponto C_3v. As constantes de força foram obtidas por análise de coordenadas normais considerando um campo de força de valência para o íon [CrO₃Cl]^-. Isso permitiu comparar as constantes de força de [CrO₃Cl]^- com as correspondentes determinadas nos trabalhos anteriores sobre [CrO₄]^2-,⁵³ [Cr₂O₇]^{2- 54} e CrO₂Cl₂.⁵² A constante de força da ligação Cr–O aumenta na sequência de compostos [CrO₄]^2- < [Cr₂O₇]^2- < [CrO₃Cl]^- < CrO₂Cl₂ e, consequentemente, aumenta também a ordem da ligação Cr–O. Os cálculos de química quântica realizados por Bell e Dines⁷⁴ para diferentes oxoânions de cromo e seus derivados halogênios confirmam essa tendência, inclusive mostrando uma correlação linear entre a constante de força e o comprimento da ligação Cr–O de forma análoga à regra de Badger. No caso de [CrO₃F]^-,⁷⁶ um ponto interessante é a identificação de uma atribuição errada feita por Dupuis⁷⁷ no espectro infravermelho desse íon. Stammreich et al.⁷⁶ notaram que bandas em 481 e 740 cm^-1 apareciam no espectro infravermelho devido à impureza [SiF₆]^2- quando a amostra de KCrO₃F em emulsão de nujol era preparada em contato com materiais de vidro ou cerâmica. O destaque na análise de coordenadas normais é que a distribuição de energia potencial dos modos ν₂ e ν₃, atribuídos ao estiramento Cr–X e ao dobramento dos ângulos O–Cr–O e O–Cr–X, respectivamente, indica que a mistura entre os modos é maior em [CrO₃Cl]^- do que em [CrO₃F]^-. Os resultados de Stammreich et al. para [CrO₃Cl]^{- 75} e [CrO₃F]^{- 76} foram comparados com os cálculos de frequências vibracionais e constantes de força por métodos modernos de química quântica computacional.⁷⁴

AGRADECIMENTOS

O autor agradece à FAPESP (2016/21070-5) e ao CNPq pelo suporte financeiro.

REFERÊNCIAS

1. Sala, O.; Kawano, Y.; Santos, P. S.; Temperini, M. L. A.; Quim. Nova 1983, 7, 320.

2. Sala, O.; Fundamentos da espectroscopia Raman e no infravermelho, 2ª ed., Editora UNESP: São Paulo, 2008, pag. 16-17.

3. Laboratório de Espectroscopia Molecular: http://lem.iq.usp.br, acessada em setembro 2019.

4. Stammreich, H.; Spectrochim. Acta 1956, 8, 41.

5. Odwyer, M. F.; J. Mol. Spec. 1958, 2, 144.

6. Pistorius, C.; Haarhoff, P. C.; J. Chem. Phys. 1959, 31, 1439.

7. Stammreich, H.; Sala, O.; Tavares, Y.; J. Chem. Phys. 1959, 30, 856.

8. Spragg, R. A.; Stammreich, H.; Kawano, Y.; J. Mol. Struct. 1970, 5, 359.

9. Griffith, W. P.; Lane, J. R.; J. Chem. Soc. - Dalton Trans. 1972, 158.

10. Stammreich, H.; Kawai, K.; Tavares, Y.; Krumholz, P.; Behmoiras, J.; Bril, S.; J. Chem. Phys. 1960, 32, 1482.

11. Friedel, R. A.; Wender, I.; Shufler, S. L.; Sternberg, H. W.; J. Am. Chem. Soc. 1955, 77, 3951.

12. Edgell, W. F.; Magee, C.; Gallup, G.; J. Am. Chem. Soc. 1956, 78, 4185.

13. Edgell, W. F.; Gallup, G.; J. Am. Chem. Soc. 1956, 78, 4188.

14. Pauling, L.; The Nature of the Chemical Bond, 3^rd ed., Cornell University Press: Ithaca, 1960.

15. Cotton, F. A.; J. Am. Chem. Soc. 1958, 80, 4425.

16. Edgell, W. F.; Summitt, R.; J. Am. Chem. Soc. 1961, 83, 1772.

17. McNeill, E. A.; Scholer, F. R.; J. Am. Chem. Soc. 1977, 99, 6243.

18. Badger, R. M.; J. Chem. Phys. 1934, 2.

19. Stammreich, H.; Kawai, K.; Sala, O.; J. Chem. Phys. 1961, 35, 2168.

20. Atkins, P. W.; Overton, T. L.; Rourke, J. P.; Weller, M. T.; Armstrong, F. A.; Shriver and Atkins' Inorganic Chemistry, 5^th ed., W. H. Freeman and Company: New York, 2010, p. 541.

21. Bor, G.; Marko, L.; Spectrochim. Acta 1960, 16, 1105.

22. Stammreich, H.; Kawai, K.; Krumholz, P.; Sala, O.; J. Chem. Phys. 1961, 35, 2175.

23. Cotton, F. A.; Stammreich, H.; Wilkinson, G.; J. Inorg. Nucl. Chem. 1959, 9, 3.

24. Bullitt, J. G.; Cotton, F. A.; Marks, T. J.; Inorg. Chem. 1972, 11, 671.

25. Stammreich, H.; Phys. Rev. 1950, 78, 79.

26. Barrow, R. F.; J. Chem. Phys. 1954, 22, 1775.

27. Kiefer, W.; Schrotter, H. W.; J. Chem. Phys. 1970, 53, 1612.

28. Holzer, W.; Murphy, W. F.; Bernstein, H. J.; J. Chem. Phys. 1970, 52, 399.

29. Lee, D.; Albrecht, A. C.; Adv. Infrared Raman Spectrosc. 1985, 12, 179.

30. Ziegler, L. D.; Acc. Chem. Res. 1994, 27, 1.

31. Stammreich, H.; Forneris, R.; J. Chem. Phys. 1954, 22, 1624.

32. Branigan, E. T.; van Staveren, M. N.; Apkarian, V. A.; J. Chem. Phys. 2010, 132, 044503.

33. Herzberg, G.; Molecular Spectra and Molecular Structure. I. Spectra of diatomic molecules, 2^nd ed., D. van Nostrand Company: Princeton, 1950, p. 512.

34. Stammreich, H.; Forneris, R.; J. Chem. Phys. 1953, 21, 944.

35. Stammreich, H.; Forneris, R.; Spectrochim. Acta 1961, 17, 775.

36. Herzberg, G.; Molecular Spectra and Molecular Structure. I. Spectra of diatomic molecules, 2^nd ed., D. van Nostrand Company: Princeton, 1950, p. 519.

37. McQuarrie, D. A.; Simon, J. D.; Physical Chemistry - A Molecular Approach, University Science Books: Sausalito, 1997, p. 539.

38. http://webbook.nist.gov/chemistry/, acessada em setembro 2019.

39. Stammreich, H.; Forneris, R.; Tavares, Y.; Spectrochim. Acta 1961, 17, 1173.

40. Stammreich, H.; Forneris, R.; Spectrochim. Acta 1960, 16, 363.

41. Pauling, L.; The Nature of the Chemical Bond, 2^a ed., Cornell University Press: Ithaca, 1944.

42. Yamasaki, R. S.; Cornwell, C. D.; J. Chem. Phys. 1959, 30, 1265.

43. Cornwell, C. D.; Yamasaki, R. S.; J. Chem. Phys. 1957, 27, 1060.

44. Person, W. B.; Fordemwalt, J. N.; Stammreich, H.; Forneris, R.; Anderson, G. R.; J. Chem. Phys. 1961, 35, 908.

45. Herzberg, G.; Infrared and Raman spectra of poliatomic molecules, D. van Nostrand Company: Princeton, 1945, p. 187.

46. Bell, R. P.; Longuet-Higgins, H. C.; Proc. R. Soc. London, Ser. A 1945, 183, 357.

47. Stammreich, H.; Kawano, Y.; Spectrochim. Acta, Part A 1968, A 24, 899.

48. Boswijk, K. H.; Wiebenga, E. H.; Acta Crystallogr. 1954, 7, 417.

49. Palmer, K. J.; J. Am. Chem. Soc. 1938, 60, 2360.

50. Stammreich, H.; Forneris, R.; Sone, K.; J. Chem. Phys. 1955, 23, 972.

51. Hobbs, W. E.; J. Chem. Phys. 1958, 28, 1220.

52. Stammreich, H.; Kawai, K.; Tavares, Y.; Spectrochim. Acta 1959, 15, 438.

53. Stammreich, H.; Bassi, D.; Sala, O.; Spectrochim. Acta 1958, 12, 403.

54. Stammreich, H.; Bassi, D.; Sala, O.; Siebert, H.; Spectrochim. Acta 1958, 13, 192.

55. Howard, J. B.; Wilson, E. B.; J. Chem. Phys. 1934, 2, 630.

56. Stammreich, H.; Forneris, R.; Tavares, Y.; J. Chem. Phys. 1956, 25, 580.

57. Stammreich, H.; Tavares, Y.; Bassi, D.; Spectrochim. Acta 1961, 17, 661.

58. Stammreich, H.; Forneris, R.; Spectrochim. Acta 1956, 8, 52.

59. Simanouti, T.; J. Chem. Phys. 1949, 17, 245.

60. Hexter, R. M.; Cheung, H.; J. Chem. Phys. 1956, 24, 1186.

61. McDowell, C. A.; Trans. Faraday Soc. 1953, 49, 371.

62. Martz, D. E.; Lagemann, R. T.; J. Chem. Phys. 1954, 22, 1193.

63. Stammreich, H.; Forneris, R.; Tavares, Y.; J. Chem. Phys. 1956, 25, 1277.

64. Cowley, A. H.; Cohen, S. T.; Inorg. Chem. 1965, 4, 1200.

65. Frankiss, S. G.; Miller, F. A.; Stammreich, H.; Sans, T. T.; Spectrochim. Acta, Part A 1967, A 23, 543.

66. Spragg, R. A.; Stammreich, H.; Kawano, Y.; J. Mol. Struct. 1969, 3, 305.

67. Venkateswaran, C. S.; Proc. Indian Acad. Sci. 1938, 7, 144.

68. Venkateswarlu, K.; Sundaram, S.; J. Chem. Phys. 1955, 23, 2365.

69. Nakamoto, K.; Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part A: Theory and Applications in Inorg. Chem., 6^th ed., John Wiley & Sons: Hoboken, 2009.

70. Nakamoto, K.; Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part B: Applications in Coordination, Organometallic, and BioInorg. Chem., 6^th ed., John Wiley & Sons: Hoboken, 2009.

71. Malchus, M.; Jansen, M.; Z. Naturforsch., B 1998, 53, 704.

72. Kiefer, W.; Bernstein, H. J.; Mol. Phys. 1972, 23, 835.

73. Abbas, M. H.; Davidson, G.; Spectrochim. Acta, Part A 1994, 50, 1153.

74. Bell, S.; Dines, T. J.; J. Phys. Chem. A 2000, 104, 11403.

75. Stammreich, H.; Sala, O.; Kawai, K.; Spectrochim. Acta 1961, 17, 226.

76. Stammreich, H.; Sala, O.; Bassi, D.; Spectrochim. Acta 1963, 19, 593.

77. Dupuis, T.; C. R. Acad. Sci. 1958, 246, 3332.

FAPESP contribuiu para custear a publicação deste artigo