JBCS

INTRODUÇÃO

A Química de Coordenação se destaca como sendo uma das mais importantes áreas da Química Inorgânica. A possibilidade da existência de diferentes estados de oxidação estáveis para um mesmo átomo, as diversas geometrias possíveis para os complexos, e a possibilidade da existência de diferentes multiplicidades de spin para complexos envolvendo os mesmos íons metálicos, por exemplo, mostram a diversidade que envolve a química dos metais de transição. Por conta dessas características, essa área de estudo se difere significativamente da química dos elementos representativos.

Quando se pretende avaliar a abordagem dos conteúdos apresentados nas disciplinas de Química Inorgânica oferecidas nos cursos de Graduação em Química e áreas afins, nota-se uma forte mudança no que diz respeito ao modo como estes conteúdos eram apresentados e como isso é feito hoje em dia. Ao olhar-se, por exemplo, para a literatura de Química Geral nos anos 60 e 70, observa-se que esse tópico era exposto de forma bastante superficial, se restringindo à nomenclatura e à aplicação da teoria de ligação de valência, abordando, de forma básica, a geometria dos Compostos de Coordenação.^1,2 Modelos mais robustos, do ponto de vista teórico, que explicavam outras propriedades, só eram apresentados, via de regra, em disciplinas de Química Inorgânica mais avançadas no curso, utilizando principalmente o clássico livro "Basic Inorganic Chemistry", de autoria dos professores Cotton e Wilkinson.³ A partir de meados dos anos 90, as principais obras de Química Geral ^4-9 já discutiam o conteúdo de Química de Coordenação utilizando a Teoria do Campo Cristalino, explorando conceitos como geometria, isomeria, cor e propriedades magnéticas. Entretanto, a introdução dessa abordagem logo no primeiro período da graduação, já na disciplina de Química Geral, seria de fundamental importância não só para o futuro aprofundamento desse conteúdo nas disciplinas de Química Inorgânica, mas também para a compreensão do que é tratado nas disciplinas iniciais, por exemplo, de Química Analítica, em que a avaliação qualitativa de uma amostra advém, irremediavelmente, das observações das mudanças de cores em reações que envolvem substituição de ligantes, originando diferentes Compostos de Coordenação.

Dentro ainda da Química de Coordenação, há um grande número de assuntos a serem discutidos que são abordados, em maior ou menor grau, em função do local onde a disciplina é ministrada. Entretanto, há assuntos que praticamente não são tratados nos cursos de graduação, principalmente em função de não serem descritos nos principais livros de Química Inorgânica utilizados nas mais conceituadas Intituições de ensino superior. Nesse ponto, chama-se a atenção para o fenômeno conhecido como "Spin Crossover" (SCO) ou "Transição de Spin", que é praticamente ignorado pelos livros de Química Inorgânica mais utilizados no mundo.^10-14 A excessão a este quadro é o livro "Principles of Inorganic Chemistry", editado em 2015.¹⁵ Esse fenômeno consiste na possibilidade dos íons metálicos da primeira série de transição, com configuração eletrônica de d⁴ a d⁷, em seus estados fundamentais, formarem complexos que sofrem uma alteração em sua multiplicidade (Alto Spin → Baixo Spin ou Baixo Spin → Alto Spin) quando estimulados por fatores externos, tais como: variação de temperatura, de pressão, e irradiação de luz.

Esse fenômeno foi primeiramente observado por Cambi e colaboradores¹⁶ em 1931, os quais descobriram esse comportamento anômalo no complexo tris(N,N-dialquilditiocarbamato)-ferro-(III). Os estados de spin desse complexo eram sensíveis à natureza de seus ligantes axiais. Após o desenvolvimento da Teoria do Campo Ligante, tornou-se evidente que o equilíbrio poderia existir entre os dois estados de diferentes multiplicidades. Na década de 1960, o primeiro complexo de Co-(II) que apresentava SCO foi relatado.¹⁷ Medidas magnéticas e estudos espectroscópicos de Mössbauer estabeleceram a natureza da transição de spin em complexos de ferro (II).¹⁸ A partir disso, a compreensão desse fenômeno aumentou, levando, posteriormente, à observação da aplicação de complexos que realizam Spin Crossover como "switches" moleculares e em displays eletrônicos e óticos.¹⁹

Entretanto, a determinação e a previsão da existência desse fenômeno, observado em alguns compostos de coordenação, não é óbvia, dependendo fundamentalmente da diferença de energia do complexo em seus dois estados de multiplicidade possíveis. Assim, o uso de métodos computacionais para a determinação da variação (GAP) entre os dois possíveis estados de multiplicidade (Alto e Baixo Spin), é uma ferramenta extremamente útil na previsão desse efeito. Além disto, a utilização de métodos computacionais acaba sendo muito importante quando se leva em conta o tempo gasto para a comprovação da existência experimental do SCO. Desta forma, o uso destes métodos pode ser uma boa estratégia para se apresentar o fenômeno do Spin Crossover como parte do conteúdo nas matérias dos cursos de graduação, mostrando a sinergia e a importância que a Química Computacional apresenta no entendimento de uma Química Inorgânica Moderna.

O uso de métodos computacionais para a compreensão da reatividade de compostos de coordenação só se popularizou neste século devido ao enorme avanço da capacidade computacional e do desenvolvimento de softwares que continham metodologias de cálculo passíveis de serem aplicadas na Química de Coordenação. Inicialmente, essas aplicações se deram através do desenvolvimento de campos de força específicos para alguns íons metálicos.^20,21 Posteriormente, o desenvolvimento de programas de Orbital Molecular a nível semiempírico foram utilizados ²² e, finalmente, a Teoria do Funcional de Densidade (DFT)^23-25 surgiu e desde então, dominou o cenário no uso de métodos computacionais aplicados à Compostos de Coordenação. A DFT associa uma alta qualidade nos resultados obtidos com um menor custo computacional, sendo, efetivamente, a melhor opção para o estudo de sistemas que envolvem metais de transição.^26,27

Assim, neste trabalho, foram realizados cálculos utilizando a DFT, com o funcional B3LYP e a função de base LanL2DZ ²⁸ a fim de avaliar a possibilidade de previsão do efeito do SCO teoricamente, permitindo que esta metodologia seja aplicada no direcionamento de experimentos que tenham como objetivo a obtenção de sistemas que apresentem SCO. Para tal, escolheu-se sistemas de ferro em que classicamente se apresentam SCO e sistemas que não apresentam SCO, a fim de poder constatar a reprodutibilidade do método utilizado.

METODOLOGIA

Os cálculos da energia, para os diferentes complexos estudados neste trabalho, simulando uma configuração de Alto e Baixo Spin, foram realizados no programa Gaussian 09 utilizando a Teoria do Funcional de Densidade (DFT) com o funcional B3LYP, escolhido por apresentar bons resultados em cálculos envolvendo complexos, e a função de base LanL2DZ, escolhida por ser uma boa descritora de moléculas envolvendo metais de transição. Calculou-se a diferença de energia entre os dois estados com as duas multiplicidades possíveis (GAP Alto Spin - Baixo Spin) dos complexos estudados. Posteriormente, foi utilizado o efeito do solvente nos mesmos complexos, através do uso do Modelo de Polarização Contínua (PCM) com o objetivo de averiguar se as energias relativas, entre os dois estados de diferentes multiplicidades, se mantinham com a simulação do solvente.

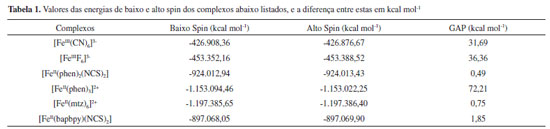
RESULTADOS E DISCUSSÃO

Com o objetivo de validar essa metodologia computacional para prever a ocorrência de SCO, e sabendo-se que a literatura aponta para a diferença de energia entre os estados de Alto Spin e Baixo Spin dentro de um intervalo de 0,7 kcal mol^-1 até 6,7 kcal mol^-1, ²⁷ foram realizados os cálculos de otimização da geometria de complexos padrões dos quais se tinha o conhecimento prévio da possibilidade de apresentar, ou não, a propriedade de SCO.

Os resultados obtidos para as otimizações realizadas em fase gasosa são apresentados na Tabela 1. Em todos os cálculos, as estruturas não apresentaram frequências vibracionais imaginárias, indicando serem pontos de mínimo. As representações das estruturas otimizadas são apresentadas na Figura 1.

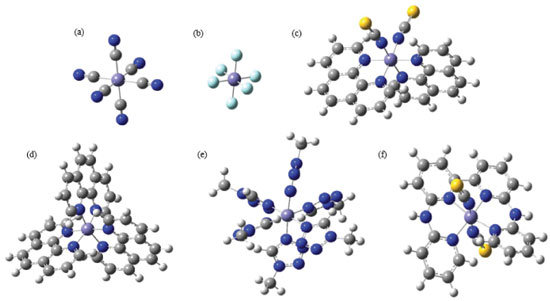Figura 1. Representação das geometrias otimizadas, em fase gasosa, dos complexos: (a) [Fe(CN)₆]^-3; (b) [FeF₆]^-3; (c) Fe(Phen)₂(NCS)₂ onde phen = 1,10-fenantrolina; (d) [Fe(Phen)₃]²⁺; (e) [Fe(mtz)₆]²⁺ onde mtz = 1-metil-1,2,3,4-tetrazol; (f) [Fe(bapbpy)(NCS)₂] onde bapbpy=6,6-bis(amino-2-piridina)-2,2-bipiridina

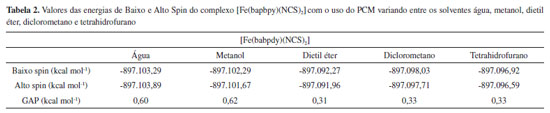
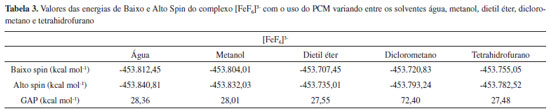
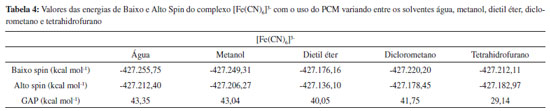
Os complexos [FeF₆]^3- (Alto Spin), [Fe(CN)₆]^3- (Baixo Spin) e [Fe(phen)₃]²⁺ (Baixo Spin) são bem conhecidos por serem estáveis em apenas uma única multiplicidade, devido à força de seus ligantes. Os demais complexos apresentados na Tabela 1, contudo, realizam SCO.^15-18

Ao analisar os dados da Tabela 1, observou-se que, no caso dos complexos que não realizam SCO, o GAP calculado foi grande (da ordem de 30 kcal mol^-1 e 70 kcal mol^-1), ou seja, muito acima do limite indicado pela literatura. No caso dos complexos que realizam SCO, seus GAPs foram pequenos e se encaixaram dentro do intervalo mencionado anteriormente de até 6,7 kcal mol^-1. Em um aspecto geral, nota-se que, em todos os casos em que o complexo não realiza SCO, o GAP apresentou um valor extremamente alto, independente do complexo ser de alto ou de baixo spin, enquanto que, para todos os complexos que realizam SCO, o GAP estava contido dentro do intervalo da literatura.

Acrescendo a esses dados, testou-se o efeito do solvente nos resultados obtidos utilizando o Modelo de Polarização Contínua (PCM). Empregou-se os complexos previamente utilizados, Fe(bapbpy)(NCS)₂, [FeF₆]^3- e [Fe(CN)₆]^3-, para realizar os cálculos. A metodologia anterior foi repetida, com o acréscimo do PCM, escolhendo solventes com polaridades variadas. Os dados obtidos são apresentados nas Tabelas 2, 3 e 4.

A partir dos resultados obtidos, simulando o uso de solvente, observa-se que a utilização do PCM com a metodologia aplicada apresenta resultados positivos para a previsão da ocorrência de SCO em complexos que, de fato, realizam essa interconversão entre seus estados de diferentes multiplicidades e negativo para os que não a realizam. Os valores observados na Tabela 2 são menores do que o intervalo apresentado na literatura. Contudo, comprova-se, com os cálculos anteriores e com os dados das Tabelas 3 e 4 que, no caso do complexo não realizar SCO, os valores para o GAP são de uma magnitude bem mais alta que a do intervalo esperado quando o complexo realiza a transição de spin.

Ao comparar os valores obtidos ao se considerar o sistema em fase gasosa ou simular a presença de solvente, observa-se que, em ambos os casos, os dados indicaram ocorrência de SCO corretamente.

Dessa forma, comprovamos a eficácia dessa metodologia em prever quando um complexo pode realizar SCO através dos cálculos de energia, entre as diferentes configurações de multiplicidade dos complexos utilizando a DFT, com a função de base LanL2DZ e o funcional B3LYP.

Como já abordado anteriormente, o SCO é um assunto muito pouco explorado nos principais livros de Química Inorgânica, sendo, portanto, praticamente não mencionado ou estudado em aulas de Graduação ou Pós-Graduação. Portanto, além de poder ser utilizada para auxiliar na previsão da ocorrência de complexos que podem apresentar SCO, a metodologia descrita pode ser empregada para apresentar o assunto de SCO em aulas de Graduação e Pós-Graduação, para aprofundar o conteúdo de Compostos de Coordenação, visto que é um método simples e de baixo custo para obter os resultados, sendo suficientemente precisos.

CONCLUSÃO

A partir dos resultados obtidos, conclui-se que o uso da Teoria do Funcional de Densidade com o funcional B3LYP e a função de base LanL2DZ é adequada para se utilizar nos cálculos computacionais com o objetivo de verificar se um complexo pode realizar SCO ou não. Essa metodologia, além de sua importância na compreensão dessa propriedade, pode ser utilizada como ferramenta de ensino em aulas de Graduação e/ou Pós-Graduação para explorar o SCO no estudo de Compostos de Coordenação, visto que livros de Química Inorgânica somente abordam superficialmente esse fenômeno.

AGRADECIMENTOS

Os autores agradecem à Fundação de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ), ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), a Coordenadoria de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) e a Bolsa PIBID/CNPq de Karina de Carvalho Pougy.

REFERÊNCIAS

1. Quagliano, J.V.; Vallarino.L.M.; Química, 3ª ed., Guanabara Dois: Rio de Janeiro, 1979.

2. Spratley, R.D.; Pimentel, G.C.; Química um tratamento moderno, 1ª ed, Edgard Blucher: São Paulo, 1974.

3. Cotton, F.A.; Wilkinson, G.; Química Inorgânica, 2ª ed, Livros Técnicos e Científicos: Rio de Janeiro, 1978.

4. Loretta J.; Atkins P.; Chemistry, Molecules, Matter and Changes, 4^th ed., Freeman: New York, 1999.

5. Kotz, J. C.; Treiche, P. Jr; Quimica e Reações Químicas, 4ª ed., Livros Técnicos e Científicos: Rio de Janeiro, 2002.

6. Brown, T. L.; Lemay, H. E.; Bursten, B. E.; Química: A Ciência Central, 9ª ed., Pearson: São Paulo, 2005.

7. Chang, R.; Química Geral: Conceitos Essenciais, 5ª ed., McGraw-Hill: São Paulo, 2007.

8. Tro, N. J.; Química: Uma Abordagem Molecular, 1ª ed., LTC: Rio de Janeiro, 2016.

9. Brady, J. E.; Russel, J. W.; Holu, J. R.; Química: A matéria e suas transformações, LTC: Rio de Janeiro, 2002.

10. Atkins, P. W.; Overton, T. L.; Rourke, J. P.; Weller, M. T.; Armstrong, F. A.; Inorganic Chemistry, 5^th ed., Oxford: New York, 2010.

11. Huheey, J. E.; Keiter, E. A.; Keiter, R. L.; Inorganic Chemistry: Principles of Structure and Reactivity, 4^th ed., Pearson: New York, 1993.

12. Miessler, G. L.; Fischer, P. J.; Tarr, D. A.; Inorganic Chemistry, 5^th ed., Pearson: New York, 2014.

13. Housecroft, C. E.; Sharpe, A. G.; Inorganic Chemistry, 4^th ed., Pearson: London, 2012.

14. Wulfsberg, G.; Inorganic Chemistry, 1^st ed., University Science Books: California, 2000.

15. Pfenning, B.W.; Principles of Inorganic Chemistry, 1^st ed., Wiley: New York, 2015.

16. Cambi, L.; Szego, L.; Ber. Dtsch. Chem. Ges. 1931, 64, 2591.

17. Stoufer, R. C.; Busch, D. H.; Hadley, W. B.; J. Am. Chem. Soc. 1961, 83, 3732.

18. Koenig, E.; Madeja, K.; Inorg. Chem. 1967, 6, 48.

19. Shatruk, M.; Avendano, C.; Dunbar, K. R.; Prog. Inorg. Chem. 2009, 56, 155.

20. Herrera, J. O. M.; Tese de Doutorado, Universidade Estadual de Campinas, Brasil, 1988.

21. Comba, P.; Hambley, T. W.; Matin, B.; Molecular Modeling of Inorganic Compounds, 3^rd ed., VHC: New York, 2009.

22. Cundari, T. R.; Deng, J.; J. Chem. Inf. Comput. Sci. 1999, 39, 376.

23. Kohn, W.; Sham, L. J.; Phys. Rev. 1965, 140, 1133.

24. Sham, L.J.; Kohn, W.; Phys. Rev. 1966, 145, 561.

25. Custódio, R.; Morgon, N.; Química Nova 1995, 18, 44.

26. McGrady,J.E. Em Computational Inorganic and Bioinorganic Chemistry Solomons, E. I.; Scott, R. A.; King, R. B. eds.; John Wiley & Sons: West Sussex, 2009.

27. Hay, P. J.; Wadt, W. R.; J. Chem. Phys. 1985, 82, 270.

28. Ashley, D. C.; Jakubikova, E.; Coordination Chemistry Reviews 2017, 337, 97.