Artigo
|
|
| Análise gráfica do desempenho de métodos computacionais no estudo de propriedades termoquímicas Graphical analysis of the computational methods performance in the study of thermochemical properties |
|
Leonardo Viana das Chagas Lima; Nelson Henrique Morgon*
Instituto de Química, Universidade Estadual de Campinas, 13083-861 Campinas - SP, Brazil Recebido em 12/09/2019 *e-mail: nhmorgon@unicamp.br In this manuscript we have evaluated the computational methods performance in the calculation of thermochemical properties using graphical analysis. The analysis was carried out in a set of 74 organic molecules considering the following thermochemical proper- ties: standard enthalpy of formation, ionization energy and electron and proton affinities. The evaluated methodologies were: G3, G3MP2, G3B3, G3MP2B3, G4 and G4MP2, and the exchange-correlation func- tionals: SOGGA11, RevTPSS, B3LYP, PBE0, B98, M06-2X, BMK and HSE06. Larger basis function sets (G3LargeXP) were employed with these functionals. It was observed that Gaussian-4 theory using reduced order perturbation theory (G4MP2) offered the best relationships between accuracy and computational cost. INTRODUÇÃO A previsão de propriedades termoquímicas atualmente dispõe de uma grande variedade de metodologias teóricas. Desde métodos que utilizam tratamento rigoroso, a um custo computacional elevado, e deste modo restrito apenas a sistemas com alguns poucos átomos,1 até outras abordagens menos rigorosas, onde correções empíricas são adicionadas, mas que permitem o cálculo em sistemas moleculares maiores.2 A questão computacional tem sido muitas vezes contornada através de tratamentos aditivos, os quais corrigem tanto efeitos de correlação eletrônica quanto da completeza dos conjuntos de funções de base.3,4 Em muitas situações, mesmo cálculos simples de funcional de densidade com conjuntos de funções correlacionadas têm tido sucesso na estimativa de propriedades termoquímicas.5 Os tratamentos aditivos, ou métodos compostos, são de fato os que têm atraído maior atenção, por apresentarem precisão de ordem química (≈ 1 kcal mol−1), a um custo computacional moderado. Tais métodos surgiram a partir da década de 1980,6 utilizando como estratégia principal a combinação (tipicamente linear) de etapas de cálculos individuais: otimização de geometria, convergência de conjunto de bases e inclusão de correlação eletrônica.7 A característica mais importante desses métodos é a obtenção de energias eletrônicas precisas a partir da adição de termos de energia oriundos de cálculos mais simples e do uso de extrapolação de conjuntos de funções base. Essa sequência ou "etapas" envolve cálculos pouco custosos computacionalmente,6,8 ou seja, a obtenção de uma energia eletrônica mais precisa na geometria de equilíbrio é feita pela soma das contribuições das diferentes etapas, realizadas em diferentes métodos (ab initio e/ou de funcional de densidade) com conjuntos de bases específicos.6 Além dos termos oriundos dos cálculos de energia, pode-se adicionar parâmetros empíricos que incluem efeitos relativísticos, correlação adicional entre outros efeitos. Isso possibilita a correção de eventuais deficiências do método.8 Essa combinação de níveis de cálculos permite a determinação de propriedades atômicas e moleculares com baixo custo computacional, quando comparados com cálculos únicos em métodos de alto nível com conjuntos de bases extensos, e com exatidão próxima a esses. Atualmente existem diversos métodos compostos,9-11 destacando-se: • Teorias Gaussian-n (n = 1, 2, 3, 4);2,12-14 • Abordagem composta de correlação consistente (ccCA);15 • Método de conjunto de base completo (CBS);16 • Abordagem da análise do ponto focal (FPA);17 • Método de correlação de múltiplos coeficientes (MCCMs);18 • Abordagem HEAT19 e • Teorias Weizmann-n (n = 1, 2, 3, 4).1,20-22 As teorias Gaussian-n são os métodos mais populares utilizados, e assim, como o método CBS e as teorias Weizmann-n, estão implementadas no pacote de programas Gaussian.23 No entanto, essas duas últimas possuem custos computacionais substancialmente superiores. Existem variações das teorias G3 e G4, as quais consistem em modificações em etapas realizadas a fim de melhorar a aplicabilidade em sistemas com muitos átomos. Elas consideram o uso de teorias da perturbação Møller-Plesset (G3MP2 e G4MP2),24 de estruturas e frequências vibracionais do funcional híbrido B3LYP (G3B3 e G3MP2B3)25 ou pseudopotencial.26,27 De um modo geral, os métodos compostos podem ser usados em estudos de mecanismos de reação, cálculo de propriedades relacionadas às energias de ativação e constantes de equilíbrio.6 Neste trabalho, propomos um método gráfico na análise do desempenho computacional de vários métodos teóricos utilizados no cálculo de propriedades termoquímicas. Foram selecionadas um conjunto de moléculas orgânicas e avaliadas as metodologias baseadas nas Teorias Gaussian-n, e métodos da Teoria do Funcional de Densidade (Density Functional Theory, DFT), considerando-se diferentes funcionais de troca-correlação.
METODOLOGIA COMPUTACIONAL O estudo dos desempenhos computacional e dos cálculos das propriedades termoquímicas foi feito utilizando-se quatorze métodos. As propriedades termoquímicas selecionadas foram: entalpia padrão de formação (ΔƒHo), energia de ionização (EI), afinidade eletrônica (AE) e por próton (AP). Em Morgon e colaboradores estão descritas as maneiras de se calcular essas propriedades termoquímicas.6,8,9,26,28 Foram avaliados métodos associados à teoria Gaussian-3 (G3)13 e suas variações G3MP2,24 G3B325 e G3MP2B3,25 além da teoria Gaussian-4 (G4)14 e sua variação G4MP2.29 Os estudos considerando-se a DFT foram feitos para os funcionais de troca-correlação das classes GGA puro (SOGGA11),30 meta-GGA puro (RevTPSS),31 GGA híbrido (B3LYP,32 PBE033 e B98,34 meta-GGA híbrido (M06-2X35 e BMK36) e range-separated híbrido (HSE06).37 Nesse último conjunto empregou-se as funções de base G3LargeXP,14 conjunto de base presente na teoria G4. O uso desse conjunto de base permite a obtenção de funções de onda de qualidade e apropriadas na descrição das propriedades consideradas. Os cálculos foram feitos para um conjunto composto por 74 moléculas orgânicas (conjunto principal) representadas na Figura 1.
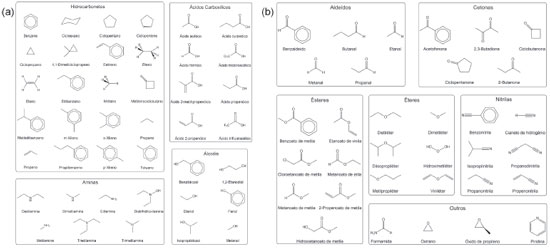 Figura 1. Conjunto de moléculas orgânicas utilizadas no estudo dos desempenhos computacional e metodológico
Os ΔƒHo teóricos foram obtidos a uma temperatura de 298,15 K e pressão de 1 bar (pressão padrão) para as moléculas do conjunto principal. As EIs foram calculadas para um subconjunto de 25 moléculas descritas na Figura 2. Utilizou-se estados eletrônicos com multiplicidade de spin 2 (dubletos) para os cátions.
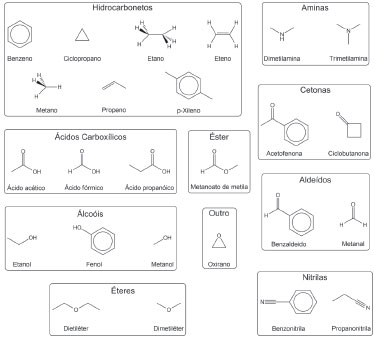 Figura 2. Conjunto de moléculas orgânicas utilizadas no cálculo de energia de ionização
As AEs foram calculadas para um subconjunto composto por 16 moléculas representadas na Figura 3. Utilizou-se estados eletrônicos com multiplicidade de spin 2 (dubletos) para os ânions.
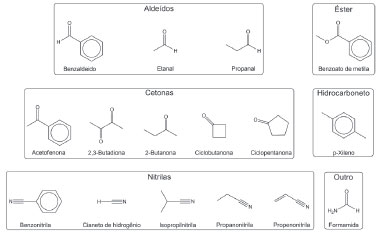 Figura 3. Conjunto de moléculas orgânicas utilizadas no cálculo de afinidade eletrônica
As APs foram calculadas a 298,15 K e 1 bar para os ânions equivalentes de um subconjunto do conjunto principal composto por 12 espécies. Os ânions presentes nas reações químicas de protonação são dados na Figura 4.
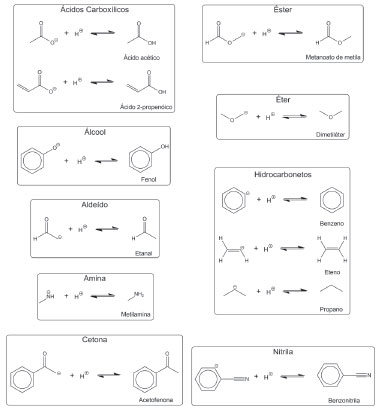 Figura 4. Reações utilizadas no cálculo de afinidade por próton dos ânions indicados
Todos os valores experimentais das afinidades por próton foram retirados do NIST Chemistry WebBook,38 bem como os dados das entalpias padrões de formação, exceto os casos descritos a seguir. Para a molécula de hidroximetiléter utilizou- se dados do The NBS Chemical Thermodynamic Properties,39 para as moléculas de eteno e metano da JANAF Thermochemical Tables,40 para as moléculas de ácido acético, ácido fórmico, benzeno, ciclopropano, dimetilamina, dimetiléter, etilamina, etanol, metilamina, metanoato de metila, oxirano, propano, propeno e trimetilamina dados da Thermochemical Data of Organic Compounds,41 e para a molécula de metanol de Curtiss et. al.42 Os tempos de processamento foram obtidos de cálculos realizados no ambiente IBM P750 do CENAPAD-SP, composto de 4 processadores Power7/8 Cores (3,55 GHz, 32 cores), 128 GB de memória RAM, 2 discos SAS 300GB 10K e desempenho teórico de 908,8 GFlops. Todos os cálculos foram realizados com o pacote de programas Gaussian 09,23 em fase gasosa, utilizando-se métodos spin-restricted para os sistemas de camada fechada e spin-unrestricted para os de camada aberta. A fim de manter a homogeneidade dos resultados, todos os parâmetros dos cálculos DFT foram aqueles de default do programa Gaussian 09. Para análise do desempenho dos métodos (exatidão e custo computacional) foram determinados os erros médios (Mean Signed Error - MSE), os desvios quadráticos médios (Root Mean Square Deviation - RMSD) e os tempos de processamento (TCPU) médios (TM) para cada um dos métodos teóricos e propriedades termoquímicas avaliados. O erro médio de cada um dos métodos é definido pela Eq. 1: 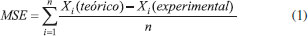 em que o termo Xi é o valor da propriedade em análise e n o número de moléculas utilizadas no estudo dessa propriedade. O desvio RMS de cada um dos métodos é definido pela Eq. 2: 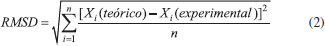 em que o termo Xi é o valor da propriedade em análise e n o número de moléculas utilizadas no estudo dessa propriedade. Em estatística, o erro médio associado a uma medida quantifica a média dos erros em relação a um referencial. Já o desvio quadrático médio é usado para aferir a qualidade do ajuste de um modelo através da raiz do erro médio quadrático. São duas das métricas mais comuns utilizadas para medir a precisão para variáveis contínuas. E tanto RMSE quanto MSE são comumente empregados em estudos de avaliação de modelos. Willmott e Matsuura43 têm sugerido que o RMSE não é um bom indicador do desempenho médio de um determinado modelo, sendo um falso indicador de erro médio, e assim a MSE seria uma melhor métrica para esse fim. O tempo médio de CPU de cada um dos métodos é definido pela Eq. 3:  em que o termo TCPU é o tempo de processamento e n o número de moléculas utilizadas no estudo da propriedade. Para a avaliação do desempenho dos métodos na determinação das quatro propriedades termoquímicas simultaneamente, propôs-se a definição de três novas variáveis a partir das outras apresentadas nas avaliações individuais: 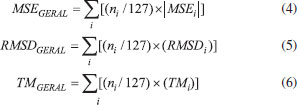 As novas variáveis consistem em combinações lineares cujos coeficientes são proporcionais às quantidades de moléculas nos conjuntos de cada propriedade. O índice i se refere às diferentes propriedades termoquímicas avaliadas, ni é o número de moléculas em cada caso (127 corresponde à soma dos quatro casos) e |MSEi|, RMSDi e TMi são os valores das variáveis da análise estatística individual. As variáveis MSEGERAL (kcal/mol), RMSDGERAL (kcal/mol) e TMGERAL (min) possuem diferentes unidades dimensionais, portanto, visando a consideração em igualdade dessas propriedades na análise de desempenho, propôs-se o escalonamento dessas variáveis, gerando outras três variáveis: 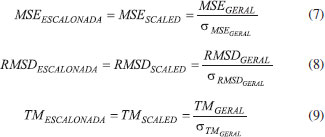 onde os termos XGERAL são os valores da variável X geral para o método em questão e os termos σX correspondem aos desvios padrão da mesma variável X geral. O escalonamento proposto gera variáveis adimensionais e com variância unitária, possibilitando a consideração dessas em igualdade de condições. O Método Gráfico A fim de se estabelecer uma maneira unívoca e simples de determinação do método com o desempenho mais vantajoso no balanço entre exatidão (MSE e RMSD) e custo computacional (TM), considera-se as variáveis (MSESCALED, RMSDSCALED, TM SCALED) formando um espaço cartesiano (x, y, z), faz-se transformação dessas coordenadas em coordenadas esféricas através das Eqs. 10 a 12: 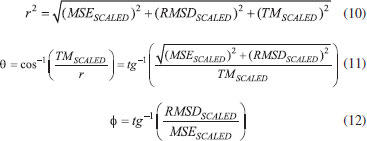 A Figura 5 apresenta a representação gráfica das novas variáveis r, θ e Φ em relação às coordenadas cartesianas (MSESCALED, RMSDSCALED, TMSCALED).
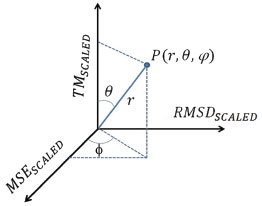 Figura 5. Representação gráfica das variáveis r, θ e Φ no espaço cartesiano definido (MSESCALED, RMSDSCALED, TMSCALED).
A variável r apresenta uma relação simétrica entre as variáveis escalonadas e consiste na norma do vetor que liga a origem dos eixos ao ponto e por isso foi utilizada como índice do desempenho geral dos métodos teóricos. As variáveis θ e Φ revelam características dos desempenhos dos métodos.
RESULTADOS E DISCUSSÃO A comparação entre os valores calculados e experimentais das entalpias padrões de formação permitiu a determinação de TM (Figura 6a) e MSE e RSMD (Figura 6b) de cada um dos métodos na previsão dessa propriedade.
Os maiores tempos médios foram observados para os métodos G3 e G4, enquanto as variações G3MP2, G3MP2B3 e G4MP2 obtiveram os menores valores. Os funcionais de troca e correlação apresentaram tempos intermediários, entre os quais o menor foi obtido pelo funcional revTPSS e o maior pelo HSE06. Os funcionais B3LYP, B98 e M06-2X mostraram a tendência de superestimar os valores das entalpias padrões de formação, enquanto nos demais métodos teóricos observa-se a tendência de subestimar os resultados. Os métodos compostos apresentaram os menores MSE (em módulo), destacando-se os métodos G4 e G4MP2, bem como os menores RMSD, com destaque para os métodos G4 e G3B3. Entre os funcionais de troca e correlação, o menor MSE (em módulo) foi observado para SOGGA11 e o menor RMSD para M06-2X. Os resultados dos tempos e erros associados às energias de ionização para a moléculas consideradas ((Figura 2) estão nas Figuras 7a e 7b. O maior tempo foi observado para o método G4, enquanto que, novamente, as variações G3MP2, G3MP2B3 e G4MP2 apresentaram os menores tempos médios. Para os funcionais de troca e correlação foram observados tempos intermediários novamente, com o menor para B3LYP e o maior para o funcional revTPSS. Os métodos compostos apresentaram a tendência de superestimar os valores da propriedade enquanto os funcionais tenderam a subestimar os resultados. Os métodos compostos apresentaram em geral os menores MSE (em módulo) e RMSD, com destaque para G4 e G4MP2. Destaca-se também o funcional M06-2X, com MSE (em módulo) inferior aos métodos G3 e G3MP2 e o quarto menor RMSD.
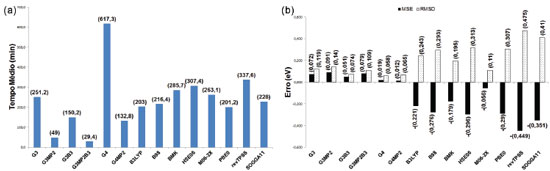 Figura 7. Análise dos resultados dos cálculos de energia de ionização para o sub- conjunto de 25 moléculas)
Os resultados dos cálculos das afinidades eletrônicas (em fase gasosa) do sub- conjunto contendo 16 das moléculas (Figura 3) que permitem a análise dos 14 métodos teóricos e comparação entre os valores calculados e experimentais dos TM e MSE e RSMD, são dados nas Figuras. 8a e 8b, respectivamente. O maior tempo foi observado para o funcional SOGGA11, seguido pelos métodos compostos G4 e G3. Nova- mente G3MP2, G3MP2B3 e G4MP2 apresentaram os menores tempos médios. Para os demais funcionais de troca e correlação e métodos compostos foram observados tempos intermediários. Todos os métodos apresentaram a tendência de subestimar os resultados. Os funcionais de troca e correlação apresentaram os menores MSE (em módulo), bem como os menores RMSD, com destaque para o funcional SOGGA11. O desempenho inferior dos métodos compostos nessa propriedade pode ser resultado de geometrias com qualidade inferior, pois as bases utilizadas na obtenção de geometrias nesses métodos não possuem funções difusas, as quais são importantes no tratamento de ânions, no entanto, mais investigação é necessária para comprovar essa hipótese.
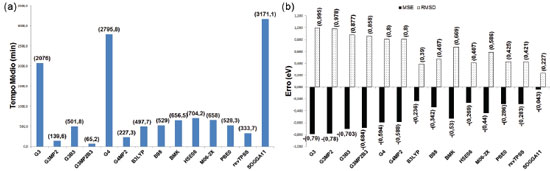 Figura 8. Resultados dos cálculos associados à afinidade eletrônica do subconjunto contendo 16 moléculas
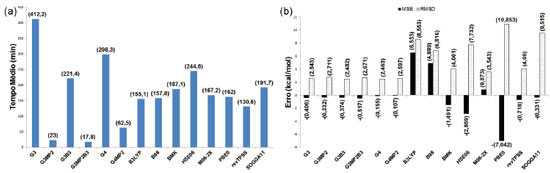
As afinidades por próton (fase gasosa, 298,15 K e 1 bar) das 12 moléculas (Figura 4) foram calculadas com os 14 métodos teóricos avaliados nesse estudo. Na Figura 9a estão os resultados dos TM para cada desses 14 métodos. Os valores de MSE e RSMD, também associados a esses métodos na previsão de AP, podem ser vistos na Figura 9b. Os maiores tempos médios foram observados para o método com- posto G4, seguido do funcional SOGGA11. G3MP2 e G3MP2B3 apresentaram os menores tempos médios, enquanto para os demais foram observados tempos intermediários. Os métodos compostos G3, G3MP2 e G3B3 apresentaram a tendência de superestimar os valores da afinidade por próton, enquanto os demais métodos demonstraram a tendência de subestimar os resultados. O método composto G3MP2 apresentou o menor MSE (em módulo), seguido por B98, BMK e G3B3. O maior RMSD foi obtido para os funcionais SOGGA11, enquanto os demais apresentaram valores próximos entre si.
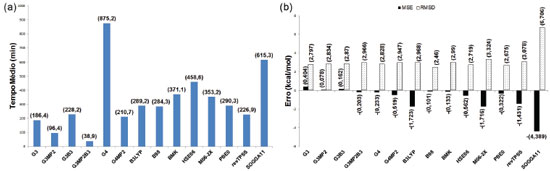 Figura 9. Tempos e erros dos diferentes métodos no cálculo de afinidade por próton do subconjunto contendo 12 moléculas
A Tabela 1 apresenta os resultados das variáveis gerais, em ordem numérica crescente. Ela sumariza o desempenho dos métodos na previsão das propriedades termoquímicas estudadas. Observa-se nessa tabela casos interessantes como os resultados obtidos por G4, que obteve um excelente desempenho no quesito exatidão, com o segundo melhor MSEGERAL e o melhor RMSDGERAL, porém com o maior custo computacional observado. Esse comportamento pode ser explicado com base na estrutura da Teoria G4, que inclui métodos de alto custo computacional, como MP4 e CCSD(T), e uso de bases extensas, como aug-cc-pVQZ, aug-cc- pV5Z e G3LargeXP, gerando um tratamento mais refinado da estrutura eletrônica ao mesmo tempo que eleva o custo computacional. Os métodos G3MP2B3 e G3MP2 apresentaram baixos custos computacionais, no entanto, com valores de erros intermediários assim como o G3, que, porém, obteve um custo computacional alto. Essa diferença nos custos computacionais se deve ao fato de os métodos G3MP2B3 e G3MP2 substituírem os cálculos MP4 encontrados no método G3, por cálculos MP2, reduzindo o custo computacional. Os resultados de MSEGERAL e RMSDGERAL dos métodos G3 e G3MP2 foram muito próximos, indicando que a retirada dos cálculos MP4 foi vantajosa. O método G3MP2B3 apresentou resultados superiores de MSEGERAL e RMSDGERAL em relação aos outros dois e isso pode ser atribuído ao uso de geometrias e frequências vibracionais no nível B3LYP. O caso do funcional SOGGA11 ilustra a importância da consideração do desvio quadrático médio (RMSD) além do erro médio (MSE). Esse método obteve o quarto melhor MSEGERAL, indicando a princípio ser um método com boa exatidão, no entanto, julgando-se apenas pelo RMSDGERAL, ele se mostra um método com baixo desempenho no quesito erro. Um baixo MSE juntamente com um alto RMSD é um forte indício da ocorrência de cancelamento de erros, já que os resíduos [Xi(teórico) −Xi(experimental)], são elevados ao quadrado no RMSD (Eq. 2), fazendo com que os erros sejam sempre somados. Ou seja, de um modo geral, todas as propriedades termoquímicas estudadas são obtidas a partir de diferenças de energias. Assim, eventuais deficiências na descrição de um dado sistema podem levar a erros. No entanto, tais deficiências podem ser compensadas a partir do cálculo das diferenças comentadas acima. Para o funcional M06-2X obteve-se um bom desempenho (exatidão e custo computacional), com os terceiros melhores MSEGERAL e RMSDGERAL a um custo computacional intermediário. O funcional HSE06 foi o método mais consistente, obtendo a mesma posição nas três variáveis gerais, embora não sendo colocações de destaque. O método G4MP2 apresentou um desempenho equilibrado, com o melhor MSEGERAL, segundo RMSDGERAL e o terceiro TMGERAL. Sua exatidão nos resultados (MSE e RMSD) foi similar à do método G4. Isso indica não haver prejuízo na substituição das teorias de perturbação de Møller-Plesset de quarta ordem por de segunda ordem. No entanto, com o método G4MP2 observa-se uma redução significativa (approx 6.5 vezes) no custo computacional se comparado ao método G4. O escalonamento das variáveis gerias tornou-as adimensionais, permitindo assim, uma avaliação quantitativa, simétrica e simultânea das três.
A Tabela 2 apresenta os valores escalonados das variáveis, em ordem numérica crescente, para os diferentes métodos avaliados. Como no escalonamento as variáveis foram divididas por um fator constante, as ordens dos métodos não sofreram alterações. A representação gráfica desses resultados por ser vista na Figura 10.
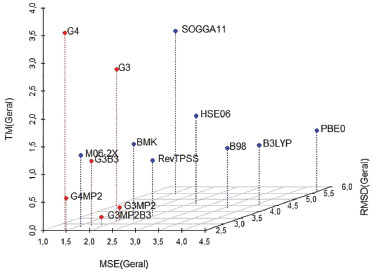 Figura 10. Representação gráfica do desempenho dos métodos no espaço cartesiano (MSESCALED, RMSDSCALED, TMSCALED)
Um ponto na origem de um espaço cartesiano é aquele com coordenadas (0,0,0), ou do ponto de vista desse estudo, é o método perfeito, com exatidão absoluta (MSESCALED e RMSDSCALED = 0) e sem custo computacional (TMSCALED = 0). A transformação das coordenadas cartesianas em coordenadas esféricas gerou uma variável que indica a distância do ponto é origem do sistema de coordenadas, r, que foi então utilizada como único índice de desempenho dos métodos teóricos. Na Tabela 3 tem-se os valores da coordenada esférica r, em ordem numérica crescente, para todos os métodos estudados. E na Figura 11 tem-se a representação da coordenada esférica r para os métodos que obtiveram os melhores desempenhos.
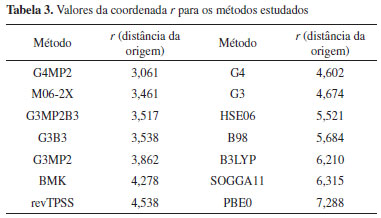
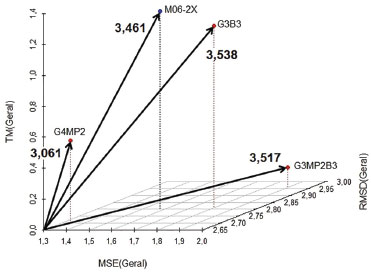 Figura 11. Representação do componente r para os métodos com melhores desempenhos
A Tabela 3 e a Figura 11 permitem concluir que o método G4MP2 apresenta a maior eficiência entre exatidão e custo computacional, sendo então o método com o melhor desempenho obtido nesse estudo. A análise das coordenadas θ e Φ possibilita evidenciar características do desempenho dos métodos, provendo assim, uma ferramenta para diferenciar métodos com relações exatidão/custo computacional (estabelecida pela coordenada r na Eq. 10) similares, gerando informações adicionais para a classificação dos desempenhos de métodos. Para as análises foram utilizadas as formulações das Eqs. 11 e 12 que envolvem a função trigonométrica arco tangente. Como as variáveis MSESCALED, RMSDSCALED e TMSCALED apresentam apenas valores positivos (Eq. 1 a 9), as coordenadas θ e Φ assumem valores de 0° a 90°, região em que o valor de um ângulo é diretamente proporcional ao valor de sua respectiva tangente, a qual varia de 0 a +∞ nesse intervalo. Tabela 4 foram apresentados os valores da coordenada θ juntamente com os de r, MSESCALED, RMSDSCALED e TMSCALED para os métodos avaliados. Métodos com valores da coordenada r similares podem ser diferenciados pela análise da coordenada θ com base nas considerações feitas anteriormente e das seguintes relações entre a coordenada θ e as variáveis escalonadas (Eq. 11). 
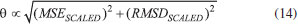 Os métodos G3MP2B3 e G3B3 apresentaram r próximos, porém se diferenciam nos valores de θ, indicando que os valores similares foram obtidos com características de desempenho distintas. O valor da coordenada para o método G3MP2B3 foi cerca de 17° superior em relação ao do G3B3, isso revela que o valor de r para G3MP2B3 foi obtido por uma "estratégia" com erros maiores, no entanto a um custo computacional menor em comparação com o outro método. Essa é exatamente a estratégia proposta pelos autores dos métodos G3B3 e G3MP2B3.25 Os métodos G4 e G3 também apresentaram r semelhantes com valores de θ distintos. O método G3 obteve, em relação ao G4, erros maiores a um custo computacional menor, gerando assim o valor superior de θ. O perfil do desempenho dos métodos B3LYP e SOGGA11 também foram distintos apesar dos valores próximos de r, com o B3LYP, no geral, apresentando erros maiores com, no entanto, um custo computacional menor. Na Tabela 5 estão os valores da coordenada f juntamente com os de r, MSESCALED e RMSDSCALED para os métodos avaliados. Com base nesses resultados, as seguintes relações entre a coordenada Φ e as variáveis escalonadas podem ser observadas (Eq. 12): 
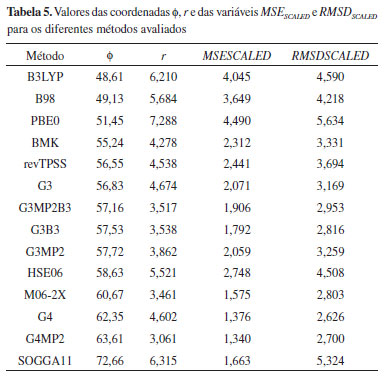
A coordenada Φ pode ser usada como um indício de ocorrência de cancelamento de erros, pois quando RMSDSCALED >> MSESCALED, o método apresenta um valor grande de Φ, como foi o caso do método SOGGA11, o qual apresentou um valor de Φ consideravelmente superior aos demais.
CONCLUSÕES O estudo dos métodos teóricos em relação aos cálculos de entalpias padrões de formação e de energias de ionização revelou um melhor desempenho na previsão das propriedades pelas das Teorias Gaussian-n com representantes apresentando os menores erros médios em módulo (G4 e G4MP2), os menores desvios quadráticos médios. Em relação às afinidades eletrônicas, na qual todos os métodos mostraram a tendência de subestimar os valores, os funcionais de troca e correlação revelaram um melhor desempenho na previsão dessa propriedade, apresentando os menores MSE (em módulo) e RMSD para os funcionais SOGGA11 e B3LYP. Na previsão das afinidades por próton, em geral, os desempenhos foram similares, com o menor MSE (em módulo) para G3MP2 e o menor RMSD para B98. Os menores custos computacionais foram obtidos pelos métodos G3MP2 e G3MP2B3 nos cálculos de todas as propriedades termoquímicas. A análise geral de desempenho dos métodos teóricos revelou diferentes comportamentos. A Teoria Gaussian-4 obteve a melhor performance em relação à exatidão, porém com o maior custo computacional. O funcional SOGGA11 revelou a importância da consideração do MSE e RMSD, apresentando o quarto melhor MSEGERAL aliado ao segundo pior RMSDGERAL, indicando possivelmente cancelamento de erros. Os métodos G3MP2B3, G3B3 e G3 apresentaram erros (MSEGERAL e RMSDGERAL) intermediários, porém a custos computacionais baixos para os dois primeiros casos e alto para o último. O funcional M06-2X e o método G4MP2 apresentaram valores pequenos de MSE (1,575 e 1,340) e RMSD (2,803 e 2,700) e os menores valores de TM (1,280 e 0,536), ou seja, boa exatidão a um baixo custo computacional. Sendo o segundo, por essa análise, o de melhor desempenho geral. A avaliação da performance dos métodos pelo procedimento das variáveis escalonadas seguidas pela transformação de coordenadas (cartesianas para esféricas) permitiu a análise simultânea de todas as propriedades termoquímicas, além da união simétrica de todas as variáveis de desempenho em uma simples variável, r, escolhida como a representação quantitativa do desempenho. Através do Método de Análise de Desempenho, nota-se que o método G4MP2 obteve o menor valor para a variável r (3,061), provando ser o método, para o universo específico considerado, com a melhor relação entre exatidão (MSE e RMSD) e custo computacional (TM). Vale destacar também o funcional M06-2X, com o segundo melhor r, superando várias Teorias Gaussian-n. As coordenas θ e Φ permitiram diferenciar características no desempenho de métodos com valores próximos de r, gerando assim mais informações úteis para es- colha de métodos mais adequados. A coordenada θ mostrou que apesar de valores de r bem próximos, os métodos G3MP2B3 e G3B3 apresentaram comportamentos distintos, com o primeiro fornecendo resultados menos precisos a um custo computacional menor em relação ao segundo. O mesmo caso se seguiu para os pares G3 e G4, além de B3LYP e SOGGA11. A coordenada Φ é um indicativo da ocorrência de cancelamento de erros quanto apresenta um valor grande, como foi o caso do funcional SOGGA11.
AGRADECIMENTOS Os autores gostariam de agradecer às agências de fomento CNPq (303581/2018-2) e FAPESP (2013/08293-7 e 2019/12294-5), bem como ao Instituto de Química da Unicamp.
REFERÊNCIAS 1. Martin, J. M. L.; de Oliveira, G.; J. Chem. Phys. 1999, 111, 1843. 2. Pople, J. A.; Head-Gordon, M.; Fox, D. J.; Raghavachari, K.; Curtiss, L. A.; J. Chem. Phys. 1989, 90, 5622. 3. Ledo, J. M.; Flores, H.; Freitas, V. L.; Solano-Altamirano, J.; Hernández- Pérez, J. M.; da Silva, M. D. R.; Camarillo, E. A.; J. Chem. Thermodyn. 2019, 133, 93. 4. Rogers, D. W.; Zavitsas, A. A.; Rogers-Bennett, L. K.; J. Mol. Model. 2019, 25, 233. 5. Jiang, W.; Laury, M. L.; Powell, M.; Wilson, A. K.; J. Chem. Theory Comput. 2012, 8, 4102. 6. Lima, J. C. B.; Morgon, N. H.; Quim. Nova 2010, 33, 195. 7. Friesner, R.; Proc. Natl. Acad. Sci. USA 2005, 102, 6648. 8. Heerdt, G.; Morgon, N. H.; J. Braz. Chem. Soc. 2012, 23, 1741. 9. Heerdt, G.; Morgon, N. H.; Quim. Nova 2011, 34, 868. 10. Helgaker, T.; Klopper, W.; Tew, D. P.; Mol. Phys 2008, 106, 2107. 11. Rocha, C. M. R.; Pereira, D. H.; Morgon, N. H.; Custódio, R.; J. Chem. Phys. 2013, 139, 184108. 12. Curtiss, L. A.; Raghavachari, K.; Trucks, G. W.; Pople, J. A.; J. Chem. Phys. 1991, 94, 7221. 13. Curtiss, L. A.; Raghavachari, K.; Redfern, P. C.; Rassolov, V.; Pople, J. A.; J. Chem. Phys. 1998, 109, 7764. 14. Curtiss, L. A.; Redfern, P. C.; Raghavachari, K.; J. Chem. Phys. 2007, 126, 084108. 15. DeYonker, N. J.; Cundari, T. R.; Wilson, A. K.; J. Chem. Phys. 2006, 124, 114104. 16. Petersson, G. A.; Al-Laham, M. A.; J. Chem. Phys. 1991, 94, 6081. 17. East, A. L. L.; Allen, W. D.; J. Chem. Phys. 1993, 99, 4638. 18. Fast, P. L.; Sánchez, M. L.; Truhlar, D. G.; Chem. Phys. Lett. 1999, 306, 407. 19. Tajti, A.; Szalay, P. G.; Császár, A. G.; Kállay, M.; Gauss, J.; Valeev, E. F.; Flowers, B. A.; Vázquez, J.; Stanton, J. F.; J. Chem. Phys. 2004, 121, 11599. 20. Boese, A. D.; Oren, M.; Atasoylu, O.; Martin, J. M. L.; Kállay, M.; Gauss, J.; J. Chem. Phys. 2004, 120, 4129. 21. Karton, A.; Rabinovich, E.; Martin, J. M. L.; Ruscic, B.; J. Chem. Phys. 2006, 125, 144108. 22. Karton, A.; Taylor, P. R.; Martin, J. M. L.; J. Chem. Phys. 2007, 127, 064104. 23. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, J. A.; Peralta Jr., J. E.; Ogliaro, F.; Bearpark, M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V. N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, J. M.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, ?.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J. "Gaussian 09 Revision D.01", Gaussian Inc. Wallingford CT, 2013. 24. Curtiss, L. A.; Raghavachari, K.; Redfern, P. C.; Rassolov, V.; Pople, J. A.; J. Chem. Phys. 1999, 110, 4703. 25. Baboul, A. G.; Curtiss, L. A.; Redfern, P. C.; J. Chem. Phys. 1999, 110, 7650. 26. Pereira, D. H.; Rocha, C. M. R.; Morgon, N. H.; Custodio, R.; J. Mol. Model. 2015, 21. 27. Caldeira, M. T.; Custodio, R.; J. Mol. Model. 2019, 25, 28. Heerdt, G.; Pereira, D. H.; Custodio, R.; Morgon, N. H.; Comput. Theor. Chem. 2015, 1067, 84. 29. Curtiss, L. A.; Redfern, P. C.; Raghavachari, K.; J. Chem. Phys. 2007, 127, 124105. 30. Peverati, R.; Zhao, Y.; Truhlar, D. G.; J. Phys. Chem. Lett. 2011, 2, 1991. 31. Perdew, J. P.; Ruzsinszky, A.; Csonka, G. I.; Constantin, L. A.; Sun, J.; J. Phys. Chem. Lett. 2009, 103, 026403. 32. Becke, A. D.; J. Chem. Phys. 1993, 98, 5648. 33. Adamo, C.; Barone, V.; J. Chem. Phys. 1999, 110, 6158. 34. Schmider, H. L.; Becke, A. D.; J. Chem. Phys. 1998, 108, 9624. 35. Zhao, Y.; Truhlar, D. G.; Theor. Chem. Acc. 2008, 120, 215. 36. Boese, A. D.; Martin, J. M. L.; J. Chem. Phys. 2004, 121, 3405. 37. Heyd, J.; Scuseria, G.; J. Chem. Phys. 2004, 121, 1187. 38. Linstrom, P. J.; Mallard, W. G.; NIST Chemistry WebBook - NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, 2014 http://webbook.nist.gov. 39. Wagman, D. D.; Evans, W. H.; Parker, V. B.; Schumm, R. H.; Halo w, I.; Bailey, S. M.; Churney, K. L.; Nuttall, R. L.; J. Phys. Chem. Ref. Data 1982, 11, 1. 40. Chase, M. W.; Davies, J. R.; Downey, J. R.; Frurip, D. J.; McDonald, R. A.; Syverud, A. N.; J. Phys. Chem. Ref. Data 1985, 14, 1. 41. Pedley, J. B.; Naylor, R. D.; Kirby, S. P.; Thermochemical Data of Organic Compounds; 2 ed.; Chapman and Hall: New York, 1986. 42. Curtiss, L. A.; Raghavachari, K.; Redfern, P. C.; Pople, J. A.; J. Chem. Phys. 1997, 106, 1063. 43. Willmott, C.; Matsuura, K.; Clim. Res. 2005, 30, 79. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access