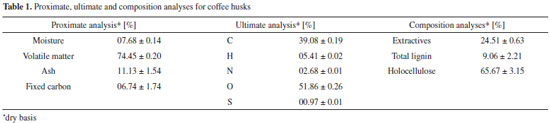
Artigo
| Kinetic parameters study for the slow pyrolysis of coffee residues based on thermogravimetric analysis |
|
Fernando L. TibolaI; Tiago J. P. de OliveiraII; Daniel A. CerqueiraIII,*; Carlos H. AtaídeIV; Cássia R. CardosoV
I. Departamento de Engenharia Química, Universidade Federal do Triângulo Mineiro, 38064-200 Uberaba - MG, Brasil Recebido em 29/10/2019 *e-mail: daniel.cerqueira@uftm.edu.br Thermal decomposition of coffee husks was investigated by thermogravimetric analyses. The proximate, ultimate and composition analyses were performed. Thermogravimetric tests were realized, the material was heated to 1173 K using five heating rates: 5, 10, 15, 20, 25 K min-1. The kinetic parameters were estimated using the methods of Kissinger-Akahira-Sunose and Friedman, the distributed activation energy model and the independent parallel reactions model. The isoconversional models of Kissinger-Akahira-Sunose and Friedman showed the dependence between determined values of activation energy and mass conversion, the activation energy values varied from 1437.39 to 199.22 kJ mol-1 for Kissinger-Akahira-Sunose and from 127.81 to 230.35 kJ mol-1 for Friedman model. The values of activation energy were determined for Miura-Maki method; varying from 137.39 to 199.22 kJ mol-1. The model of parallel and independent reactions showed the presence of six different reactions (with activation energy values varying from 42.0 to 214.2 kJ mol-1) occurring during coffee husks pyrolysis, indicating a complex reaction. Currently, works regarding the determination of kinetic parameters for coffee husks pyrolysis are not common. The present work is the first report using the model of parallel and independent reactions to estimate kinetic parameters for pyrolysis of coffee husks, a residue widely generated worldwide. INTRODUCTION Lignocellulosic biomass is a resource for renewable electricity, thermal energy, biofuels, and chemicals.1 According to the International Coffee Organization, coffee is widely produced worldwide, and it is considered as the second largest traded commodity in the world. Coffee plants are cultivated in 98% of the world countries. The global coffee production in 2016/2017 was approximately 150 million 60-kg bags and Brazil is the largest producer.2 Considering high coffee production, there is a large generation of coffee husks, which disposal has become a matter of increasing concern. Coffee residue is characterized chemically by a high content of carbon, as various agricultural wastes used as biomass fuels.3 Pyrolysis is characterized by the thermal degradation of the solid biomass, which can be carried out in the total absence of an oxidizing agent or in such an amount that the gasification does not occur extensively. The pyrolysis process can produce oil, charcoal and gases for energy uses.4 The main product obtained by the fast pyrolysis of biomass, bio-oil, is a renewable fuel that can be used to produce value-added chemical compounds.5 Bio-oil presents higher energetic density, when compared to biomass. The oil production can reduce transport and handling costs.6 Several reactions occur during the fast pyrolysis of heterogeneous biomass due to the heterogeneous composition of these materials. These reactions are influenced by various process conditions, such as heating rate, temperature, pressure, residence time, particle size. Knowledge about the kinetic of biomass decomposition is important for the process understanding and for comparison between different biomass decomposition. Modeling of lignocellulosic biomass pyrolysis processes can be used to determine their key operating and design parameters.1 To estimate the kinetic parameters of pyrolysis process, thermogravimetric analyses can be used. This technique enables the description and interpretation of the phenomena of biomass decomposition.7,8 However, thermogravimetry presents relatively low heating rates when compared to the fast pyrolysis process. It is known that experimental techniques employing high heating rates cannot guarantee efficiency for temperature measurements.9 Moreover, small samples at low heating rates ensure the absence of heat and mass transport limitations, and a kinetically controlled regime. High heating rates or high initial masses can lead to thermal lag, resulting in a low value for apparent activation energy.10 Numerous kinetic models have been developed, such as single-step global reaction model, multiple step model, semi-global model, and distributed activation energy model (DAEM).11 The decomposition of agricultural residues is a complex process due to the presence of a set of chemical reactions and physical processes and it is more reliable to evaluate the thermal data using multiple kinetic methods together with results comparison.12 Single-step global reaction model or isoconversional models consider that biomass pyrolysis is frequently described as a homogeneous single reaction of solids being converted into volatiles and char, resulting in a linear regression for the estimation of the activation energy values for the studied biomass, considering a unit-order reaction. According to Miura and Maki,13 the straight lines resulting from isoconversional models for different conversions must be parallel, since the models consider the occurrence of a single chemical reaction. Linear relationships for different conversions that are not parallel indicate that the biomass degradation involves more than one reaction, and the presence of different constituents in a heterogeneous biomass was considered in DAEM, for unit-order reactions. Regarding heterogeneous biomass, derivative mass loss curves from thermogravimetric data frequently contain shoulders and/or tailing, which indicate the occurrence of more than one reaction and that biomass consists of components with different reactivity.14 Biomass pyrolysis can be affected by changes in reaction geometry and by interfacial diffusion of reactants and products. However, pyrolytic decompositions of biomass can also be described by independent parallel reactions, considering the presence of pseudo-components, each one with its characteristic reaction parameters.15 The slow pyrolysis of biomass has been studied and discussion concerning the use of different kinetic models have been developed.16-18 A review on the pyrolysis of beech and pine woods was performed and thermogravimetric data was studied considering isoconversional models and the parallel and independent reaction model for three pseudo-components; cellulose, hemicelluloses and lignin. The consideration of first order reaction of isoconversional models produced unreliable results, particularly an underestimation of the activation energy of lignin pyrolysis. The independent parallel reaction model with nth order reactions suggested a more effective representation for the pyrolysis of heterogeneous biomass.16 Hu et al. used the one-step reaction model and the parallel and independent reactions model for the determination of parameters for the slow pyrolysis of lignocellulosic biomass (pine wood, rice husk and bamboo). The authors addressed that for one-step models the values of activation energy are conversion dependent, observing large variations to the mean value of the parameter; they also considered that the parallel and independent reaction model fitted well the experimental data.17 Chen et al. studied the pyrolysis of coffee industrial residue using thermogravimetric data with different heating rates. The kinetics of the pyrolysis reaction was analyzed using the distributed activation energy model (Miura-Maki), indicating activation energy values with reliable determination coefficients for linear regressions.19 Thermogravimetric studies, for pyrolysis processes, are essential for the knowledge of kinetic behavior, hence to reactor design and process control.20 The focus of the present work is the investigation concerning the determination of kinetic parameters for the slow pyrolysis of coffee husks, using different kinetic models, comparing the obtained results and discussing the model characteristics for the studied biomass. Currently, works regarding the pyrolysis behavior of coffee residues3 and the determination of kinetic parameters for the pyrolysis of coffee residues using isoconversional and distributed activation energy models are available in literature,19,21 but an investigation concerning the parallel and independent reaction model is not available for coffee husks. Thus, this is the first work using this model for the determination of kinetic parameters for pyrolysis of coffee husks, a residue widely generated worldwide.
MATERIAL AND METHODS Material The studied coffee husks were obtained in São Sebastião farm, Pedrinópolis-Minas Gerais, Brazil. The husks were ground in a knife mill and were kept in an oven at 353 K, during approximately 48 h, for drying and sterilization. The husks were sifted through an 80-mesh sieve, presenting true density 1.5700 ± 0.0032 g cm-3, determined by five measurements of helium gas pycnometer, Accupyc 1331, Micromeritics. Particles smaller than 80 mesh sieve were chosen for thermogravimetric analyses, in order to minimize the effects of heat transfer.22 The thermogravimetric tests were performed without pretreatment such as washing or extraction. The proximate analysis of coffee husks (particles smaller than 80 mesh sieve) was carried out according to ASTM E871 method. The ultimate analysis was performed in a PerkinElmer® 2400 Series II CHNS/O Elemental Analyzer according to D3176 ASTM method. The extractives content was ascertained by the method of extraction with alcohol-toluene and following the standard of TAPPI-Technical Association of the Pulp and Paper Industry,23 substituting the mixture ethanol/benzene by the mixture ethanol/toluene. The insoluble lignin content was determined by the modified Klason method, according to the procedure proposed by Gomide and Demuner.24 The soluble lignin content was obtained according to the methodology suggested by Goldschimid.25 The content of structural polysaccharides, holocellulose, was calculated by subtracting the percentages of total lignin and extractives from 100%. The analyses were performed in triplicate. Table 1 presents the results of these analyses. Details of the biomass characterization are presented in a previous work of the research group.26
Thermogravimetric analyses Thermogravimetric analyses (TGA) were performed in a SHIMADZU Simultaneous TGA/DTA Analyzer model DTG-60H. No isothermal measurements were taken using nitrogen purge gas at a flow rate of 20 mL min-1. Samples of approximately 6 mg were used in TGA tests and aiming at minimizing the effect of samples heterogeneity, each experiment was performed three times. The material was heated to 373 K at a heating rate of 50 K min-1 (the maximum operating rate of the equipment), and held at that temperature for 30 min, aiming the biomass drying. After drying, the material was heated to 1173 K to evaluate its thermal behavior. Five heating rates were used: 5, 10, 15, 20 and 25 K min-1. Weight and time/temperature data were recorded using TGA software, resulting in thermogravimetric (TG) and derivative thermogravimetric (DTG) curves; TG curves presents weight loss data and DTG curves presents the derivative values for TG. Data on the first 30 min of reaction were not processed, so mass variations due to water losses were not considered. The mentioned procedure is the same used in previous work.27 Models and equations Kinetic parameters were inferred by different estimation methods: the classical methods of Kissinger-Akahira-Sunose (KAS) and Friedman; the distributed activation energy model (DAEM) and the independent parallel reactions model (IPRM). The purpose of the work was to investigate the influence of the model in the determined values of kinetic parameters, discussing the main characteristics of the considered mathematical models. Single reaction step models Isoconversional methods of KAS and Friedman were used. These models consider that biomass pyrolysis is described as a homogeneous single reaction of solids being converted into volatiles and char by a unit-order reaction. Isoconversional models are calculated using several heating rates and for some mass conversions, resulting in values for activation energy for each conversion.7 According to the models, the thermal decomposition of the biomass can be described by Eq. (1) which represents the conversion rate:  where X is the mass conversion, the reaction parameter k(T) is described by the Arrhenius equation, and ƒ(X) is a function of the conversion. The mass conversion can be calculated by Eq. (2) and Arrhenius equation is presented in Eq. (3). 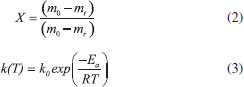 where m0 is the initial mass, mt is the mass at time t, and mr is the residual mass. k0 is the pre exponential factor of Arrhenius, Ea is the activation energy, R is the ideal gas constant, T is temperature. Considering a model for n-order reaction, as described by Eq. (4).  Combining equations (1), (2), (3) and (4), there is Eq. (5), which shows that the pyrolytic conversion depends on material conversion and temperature.28 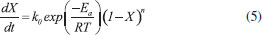 Several methods to determine the activation energy (Ea) and the pre-exponential factor (k0) are available in the literature. The advantage of isoconversional methods is that the previous knowledge of the reaction mechanism for biomass thermal degradation is unnecessary for the estimation of Ea values.15,29,30 The following models presented by Equations (6) and (7) were obtained by solving Eq. (5); using linearization and adoption of values for conversion. Eq. (6) and (7) present Kissinger-Akahira-Sunose model and Friedman model, respectively, where β is the heating rate, ƒ(X) and g(X) are conversion functions. 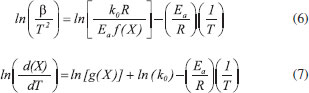 Distributed activation energy model The straight lines resulting from isoconversional models for different conversions must be parallel, since the models consider the occurrence of a single chemical reaction. Linear relationships for different conversions that are not parallel indicate that the biomass degradation involves more than one reaction.13 In view of the above, the method for the DAEM was considered.31 This model has been widely used to describe complex reactions such as biomass pyrolysis. The model considers that an infinite number of reactions occur simultaneously during the pyrolysis process, and these reactions are considered irreversible, parallel and unitorder. The model considers that there is an activation energy value for each reaction temperature at a constant heating rate, as well as a distribution function ƒ(Ea) of activation energy values that vary with temperature. Further details about this model are available in literature.13 The DAEM used here considers that there is one activation energy value for a given temperature and heating rate. The Miura-Maki method is represented by Eq. (8): 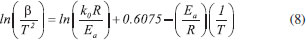 Thus, considering the linear equations for different conversion values, where T is the temperature for a given conversion; it is possible to determine the values of Ea and k0. The distribution function, f(Ea), can be estimated from experimental data without considering a Gaussian distribution.31 The distributed activation energy curve is determined from experimental data using Eq. (9), which considers that at a given temperature, a single reaction occurs with a specific activation energy value:  Therefore, f(Ea) is given by differentiation, considering the relationship between conversion and activation energy, and is presented in Eq. (10):  Independent parallel reactions model DTG curves for heterogeneous biomass frequently contain shoulders and/or tailing, which indicate the occurrence of more than one reaction and that biomass consists of components with different reactivity.14 Biomass pyrolysis can be classified as a heterogeneous chemical reaction and can be affected by changes in reaction geometry and by interfacial diffusion of reactants and products. However, pyrolytic decompositions of biomass are described considering independent parallel reactions, considering the presence of pseudo-components. Biomass is essentially composed of cellulose, hemicelluloses and lignin. Other components such as sugars, pectin, oxalates, carbonates and sulfates are also present in smaller amounts.32 Considering the same definition of conversion by Eq. (2), the rate of conversion of each pseudo-component (hemicelluloses, cellulose, lignin and others) can be written as follows:33  where Xi is the conversion value for pseudo-component i, ki is the rate constant for pseudo-component i, and ni is the reaction order for this pseudo-component i. The rate constant for a pseudo-component i is described by the Arrhenius equation:  Regarding the nonlinear calculation for the independent parallel reactions model, the overall rate of reaction is the linear combination of the rates of partial reactions considering the mass fraction of each pseudo-component, ci. Mass loss as a function of time is calculated by the following relationship, where m is the number of pseudo-components. 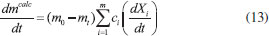 The unknown parameters of the model are determined from an evaluation of the experimental data by nonlinear least squares fitting (on the DTG curve), which minimizes the summation: 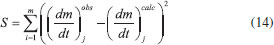 The subscript j refers to the data points used, (dm/dt)obs represents the experimentally observed values, and (dm/dt)calc indicates the values calculated by Eq. (13) with a given set of parameters. The numerical calculations were performed using Scilab software (version 5.7.2). Considering the models of peak deconvolution, some studies evaluate the kinetics of lignocellulosic biomass considering experiments at one heating rate.20 Branca et al. commented that the use of a single heating rate can generate very inconsistent Arrhenius parameters presenting strong dependence on the selected kinetic model.34 The use of different heating rates can reduce the mentioned effect.16
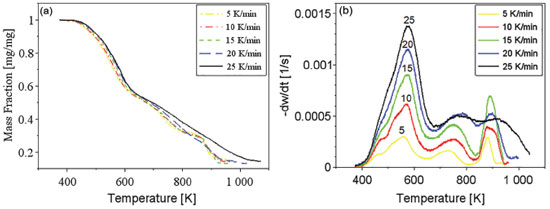
RESULTS AND DISCUSSION The performed TG analyses presented good reproducibility considering triplicates for each heating rate, what prevents the influence of biomass heterogeneity in the determination of kinetic parameters. Data obtained experimentally by the thermogravimetric analysis generated the following mass loss (TG) and mass loss derivative curves (DTG) presented in Figures 1(a) and 1(b), respectively. In Figure 1(b) the curves represent the derivative of mass fraction (w) related to time.
The mass loss curves in Figure 1(a) shift to the right when increasing the heating rates, indicating higher values of initial decomposition temperature. Slower heating rates result in longer residence times of volatiles inside the biomass particles and the reactor, favoring secondary reactions such as cracking, repolymerization and recondensation.21 The DTG curves in Figure 1(b) shows a first large peak with shoulders corresponding to the biopolymers decomposition: hemicelluloses, cellulose and lignin21 since the temperature ranges for the decomposition of these materials are referred as 400-600 K for hemicelluloses, 500-660 K for cellulose 500-1000 K for lignin;27,33 and two more peaks, which can be attributed to primary materials that react at higher temperatures and/or secondary reactions from products of the first pyrolysis processes. It can be also observed in Figure 1(b) that for higher heating rates, there are increases in rates of mass loss. These changes can be attributed to larger differences between the temperature of the furnace and that of the sample, which increase with heating rate.35 According to Li et al., this can be explained by the higher availability of energy provided by the increase in the heating rate, which accelerates the heat transfer process.36 This higher availability of energy induces the overlapping of peaks for higher heating rates, due to the occurrence of simultaneous reactions that used to happen separately at lower heating rates. Although that happens throughout the studied temperature interval, it can be specially noticed for the mass loss events occurring around 900 K. The estimated parameters are activation energy and the pre-exponential factor of Arrhenius, which represent the energy required for a reaction to start and how quickly it occurs, respectively. The lower the activation energy and the higher the Arrhenius pre-exponential factor, the faster the reaction will occur.37 Single reaction step models The global reaction models used to evaluate the data were those of Kissinger-Akahira-Sunose (KAS) and Friedman. Figures 2(a) and 2(b) present the regression results for the respective models.
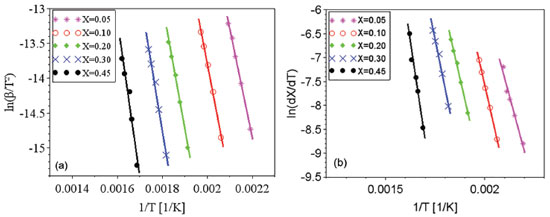 Figure 2. Linear relations for the estimative of activation energy values for coffee husks: (a) Kissinger-Akahira-Sunose methodology (b) Friedman methodology
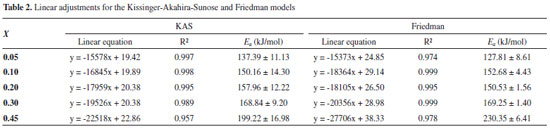
The regressions obtained for each conversion value with determination coefficient and activation energy value are presented in Table 2.
For the KAS and Friedman models, five conversion values were adopted: 0.05; 0.1; 0.2; 0.3; and 0.45. The highest conversion value used in the estimates was 0.45, considering that for conversions above 0.45 the values of R2 were lower than 0.95. The isoconversional models consider the occurrence of a first order reaction of a homogeneous material, what differs from the composition of the studied biomass. The decomposition of original components of biomass occur for low conversion values, while secondary reactions are expected to happen for higher conversion values. Previous works commented about the possibility of the occurrence of secondary reactions for higher values of conversion and/or the occurrence of more complex reaction mechanisms, which might not be represented by the proposed models.38 Considering isoconversional models, the limitation of Ea estimative regarding high values of conversion is commonly mentioned in literature.27,38-42 The fit quality is commonly evaluated by R2 and values higher than 0.95 were considered for trustful estimation of Ea, as commented by previous works.17,19 The isoconversional models of KAS and Friedman showed the dependence between Ea values and mass conversion, what was also observed previously. The complexity of biomass reaction and these variations are caused by the mechanism changes occurring during the degradation of a heterogeneous material, these changes are complex to be determined.17,39 Hu and colleagues used the global model of Friedman to determine the values of activation energy for pine wood, rice husk and bamboo. The mean apparent activation energy in conversion ranges between 0.05 and 0.80 for pine wood, rice husk and bamboo were respectively 164.04, 193.72 and 179.78 kJ mol-1.17 The values for activation energy were also calculated for different wood types by KAS method, considering conversion values from 0.1 to 0.9, the values varied from 127.1 to 350 kJ mol-1. The authors registered the great dependence between estimated values of activation energy and the studied conversions.16 The Friedman model was used by Cai and colleagues aiming the estimation of activation energy values for corn stalk pyrolysis. The results have shown that the activation energies of corn stalk pyrolysis vary from 148 to 473 kJ mol-1 when the conversion ranges from 0.05 to 0.85.1 Regarding the isoconversional models, when the straight lines produced by regressions are parallel, it is considered that the model is adequate to represent the experimental data. However, parallel regression was not observed for coffee husks, what is presented in Figures 2(a) and 2(b). The higher the temperature, the more significant the occurrence of secondary reactions due to the increasing presence of primary products from reactions of natural biomass components. The nonparallelism can be attributed to the decomposition of the primary reaction products, modifying the reaction mechanism.38 The consideration of first order kinetic models can lead to erroneous kinetic parameters, particularly leading to an underestimation of the activation energy of lignin pyrolysis.10 Distributed activation energy model The DAEM proposed by Miura and Maki13 was also used to estimate the values of activation energy for coffee husks. Figure 3 shows the linear regression for the estimation of Ea and k0 values.
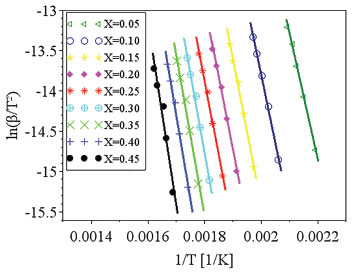 Figure 3. Linear regressions for Miura-Maki method
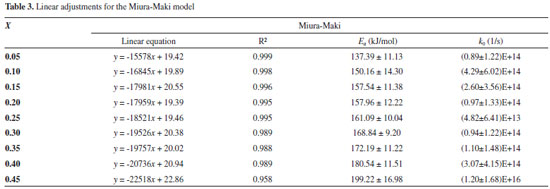
Table 3 lists some of the values of Ea and k0, which were calculated for each conversion value based on the linear regressions.
The distributive activation energy models commonly consider a Gaussian distribution of activation energy, which may not be adequate to represent the decomposition of a multicomponent biomass. The Miura-Maki model allows the estimative of the distributed activation energy curve without an initial assumption of its function format.43 The limitation of the Miura-Maki method for the study of biomass pyrolysis is the consideration of unit-order for the various simultaneous reactions and the DAEM has been widely used in the determination of kinetic parameters of biomass.44 Activation energy values were calculated for conversion values of up to 0.45, while values of R2 lower than 0.95 were obtained for higher conversion values. These results indicate that for the higher conversion values, the reaction mechanisms may not be represented by the DAEM model; what can be attributed to the occurrence of secondary reactions for higher temperatures, or the occurrence of reactions with orders distinct from unitary value, what is expected for a heterogeneous material. Considering the observed results, it might be inferred that reaction orders for high conversions, with the presence of primary reactional products, may differ greatly in relation to the unitary value.38 The curve of the distributed activation energy was calculated but did not present a valid representation for the pyrolysis reaction. The values of the distributive function were negative for conversions above 0.40. This behavior indicates that the experimental data do not fit well the studied model. As mentioned in previous works, the curve of the distributed activation energy was supposed to be obtained by numerical differentiating the X versus Ea relationship. However, sometimes for heterogeneous materials Ea varies with X dramatically, implying restrictions to the calculation of derivatives of the X versus Ea relationship.45 The results of the present work suggest the occurrence of these mentioned variations. Lignocellulosic biomass consists of three major components (cellulose, hemicelluloses, and lignin), besides smaller quantities of extractives and inorganics salts.27 Cellulose, hemicelluloses, and lignin are all long-chain biopolymers.45 Chen and colleagues studied the pyrolysis of coffee industrial residue using thermogravimetric data of different heating rates. The kinetics of the pyrolysis reaction was analyzed using the distributive activation energy model, and it indicated that activation energy values changed from 163.42 to 239.49 kJ mol-1. The curve of distributive activation energy function was not presented.19 Considering DAEM results, the values of k0 changed with the activation energy values at different mass conversion, as reported by Chen and colleagues.19 Sonobe and Worasuwannarak have used DAEM to study the pyrolysis of several agricultural residues (rice straw, rice husk, corncob and cellulose) and determined activation energy values from 120 to 250 kJ mol-1. The distributive curves of activation energy were presented for the studied materials. The values of activation energy determined by the present work are close to values for other agricultural residues.46 Cai and colleagues studied the DAEM and presented a review on the use of the kinetic model. The work commented that there are different reactions involved in the thermal decomposition of cellulose, hemicelluloses and lignin; what indicates the model limitations for the description of the pyrolysis of heterogeneous materials considering a single reaction description. The mentioned work comments that the presence of different components is shown by DTG curves with different peaks or shoulders and that for distributive activation energy function, sometimes, X varies with Ea dramatically, which makes it difficult to calculate the derivative curve.45 The Miura-Maki method is widely used for the estimation of kinetic parameters for biomass pyrolysis.19,38,46 The model presents easy calculation but is limited by the consideration of unit-order reactions. For the present work, the values of activation energy were determined, but the function of distributive activation energy could not be obtained. The results indicate that for biomass with several peaks in DTG the Miura-Maki method may not be successful for the estimation of the function of distributive activation energy. Independent parallel reactions model Regarding the heterogeneity of biomass composition, the model of independent parallel reactions allowed the estimation of parameters considering the presence of six different reactions during the biomass pyrolysis. The IPRM was studied for each heating rate. The adjustment for the TG and DTG curves at the rate of 10 K min-1 are shown in Figures 4(a) and 4(b). The adjustment for the TG and DTG curves at the rate of 20 K min-1 are shown in Figures 5(a) and 5(b).
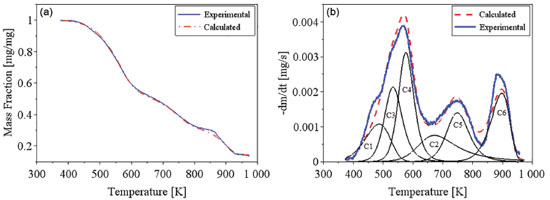 Figure 4. Experimental and calculated data for TG (a) and DTG (b) curves for coffee husks at a heating rate of 10 K/min, for independent parallel reactions model
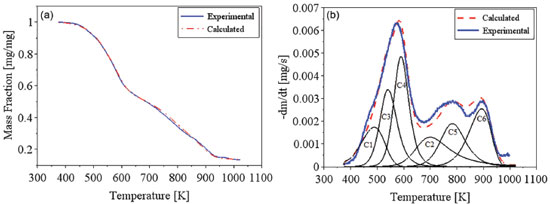 Figure 5. Experimental and calculated data for TG (a) and DTG (b) curves for coffee husks at a heating rate of 20 K/min, for independent parallel reactions model
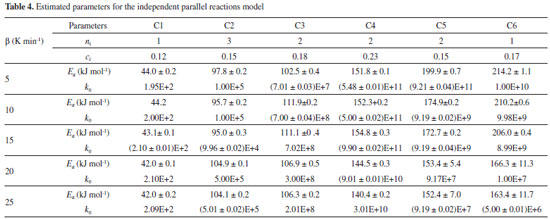
The DTG curves shows some peaks and/or shoulders, indicating that the studied biomass presents different components and that there are different pyrolysis kinetics occurring during the pyrolysis reaction. The complex shape of DTG curve was registered in previous studies considering thermogravimetric data for coffee residues.3,18,20 The modeling of the DTG curve at 10 K min-1 was calculated for six pseudo-components, and the presence of these distinct reaction can be observed in Figure 4(b). For the highest rates, as 20 K min-1, the six peaks are not so evident, what can be explained by their overlapping caused by the faster heat transfer processes. The main components of each identified reaction can be estimated by the temperature ranges in which the decomposition occurs. For the first peak (C1) the major component is considered as extractives, which are low molecular weight substances, the common extractives for lignocellulosic biomass are resins, fats, fatty acids, waxes, sterols, lignans and sugars.10 The major decomposition of extractives was considered at low temperatures, between 400 K and 550 K. The second peak (C2) is mainly attributed to lignin that decomposes over a wide temperature range, between 500 K and 1000 K. The third peak (C3) is probably due to the major decomposition of hemicelluloses, which occurs in this temperature range, 400-600 K. The fourth peak is considered for the decomposition of cellulose, which mainly occurs between 500 and 660 K.27,33 Holocellulose is mainly composed of cellulose and hemicelluloses, other polysaccharides present in lignocellulosic biomass are pectin, a polymer of units of galacturonic acid (hexose) with dispersed units of rhamnose, galactose or arabinose.10 Probably, some extractives and pectin contents also decompose during the C2, C3 and C4 reactions. The other two peaks (C5 and C6) exhibit decomposition at high temperatures, and can be attributed to inorganic salts, as well as oxalates, carbonates, sulfides, chlorates and sulfates; and to fractions of lignin and secondary pyrolysis products that degrades at higher temperatures.35,47 The dependence between the investigated parameters was noted for the IPRM. The calculated curve can fit the model by adopting different combinations of activation energy values and Arrhenius pre-exponential factor. Thus, it is up to the user of the algorithm to define the range of parameter that will be investigated for each pseudo-component. For this work, the estimated values were investigated based on previous literature and on research group experience.16,27,34,38,48 Table 4 shows the estimated parameters for the parallel and independent reactions model and Table 5 presents the respective adjustments.
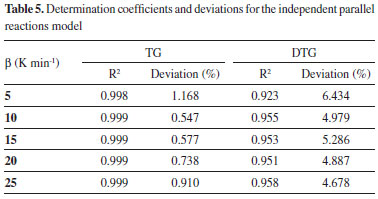
A review on the pyrolysis of beech and pine woods was carried out and the thermogravimetric data was studied considering isoconversional models and the parallel and independent reaction model for three pseudo-components; cellulose, hemicelluloses and lignin. The activation energy values reported were around 200 kJ mol-1 for the reaction with cellulose as main component, 150 kJ mol-1 for the reaction containing hemicelluloses and less than 100 kJ mol-1 for the reaction with major mass fraction of lignin.16 The mentioned authors considered that first order reaction produced unreliable results, and that three independent parallel reaction model with nth order reactions was more effective representing the pyrolysis of heterogeneous biomass. The independent parallel reaction model was used by the present research group to estimate parameters for the pyrolysis of tobacco residue and sorghum bagasse. The pyrolysis of tobacco residue was described by six different reactions: (1) sugars, nicotine; (2) lignin; (3) cellulose; (4) hemicelluloses; (5) and (6) oxalates, carbonates, sulfides, calcium, potassium and magnesium salts, inorganic phosphates, chlorides and sulfates, besides silica. The values of activation energy varied from values 39.7 to 272.0 kJ mol-1. The pyrolysis of sorghum bagasse was described by five reactions: (1) sugars and pectin; (2) hemicelluloses; (3) cellulose; (4) lignin; (5) oxalates, carbonates and sulfides. The values of activation energy varied from 35.7 to 220.0 kJ mol-1.27 It can be observed that the values obtained in the present work are similar to the values found in the literature, especially considering the different constitution of the materials. The modeling of the pyrolytic kinetics of the coffee husks proved to be a complex process, and six different decomposition reactions were identified. In general, small variations in the activation energy were verified for the investigated heating rates, which indicates the efficiency calculation for the pyrolytic reactions considering the values estimated by the model. Considering the mass loss data, the comparison between the experimental and calculated curves showed a determination coefficient of 0.99 and low deviation values. Considering the mass loss derivative curves, the values of R2 were around 0.95 and the values of deviations around 5.3%. These values represent a good fit and the lower adjustment quality observed for the mass loss derivative curve can be justified by the evident representation of different reactions attributed to distinct peaks and a complex curve for the simultaneous reactions. Considerations on the studied models In the view of the above, the isoconversional and Miura-Maki models provide an initial estimate, however, they are limited by the representation of a pyrolytic reaction of heterogeneous biomass, considering unit-order reactions. The determined values of activation energy for these models indicate the decomposition of the most abundant components; cellulose, hemicelluloses and lignin; but do not indicate the influence of components with higher activation energy values, which decomposes at higher temperature rates. For isoconversional models it was noted a strong dependence between activation energy values and biomass conversion, what indicates inadequacy between experimental data and the studied model. The function of distributive activation energy for Miura-Maki method could not be determined, indicating that for biomass with several peaks in DTG the Miura-Maki method is not successful for the estimation of the function of distributive activation energy. However, the method is extensively used and reported as an efficient estimation for kinetic parameters of biomass which have smaller numbers of pseudo-components representing the DTG curve. The model of parallel and independent reactions considered several reactions with different orders, what enabled the representation of a complex pyrolytic reaction and indicated the presence of six different reactions occurring during coffee husks pyrolysis, which is one of the probable reasons for the inadequacies observed in the resolution of the other studied models.
CONCLUSIONS Regarding the determination of kinetic parameters for the pyrolysis of coffee residues, the isoconversional models of KAS and Friedman showed the dependence between Ea values and mass conversion. The mentioned dependence can be attributed to the material heterogeneity and to the reaction orders of biomass components differing from unitary values. The activation energy values varied from 137.39 to 199.22 kJ mol-1 for Kissinger-Akahira-Sunose model and from 127.81 to 230.35 kJ mol-1 for Friedman model. The values of activation energy were determined for Miura-Maki method; varying from 137.39 to 199.22 kJ mol-1; but the function of distributive activation energy could not be determined. The obtained results indicated the dramatic variation of Ea with X, implying restrictions to the calculation of derivative curves for the function obtainment. The main reason for the calculation restrictions is the consideration of unitary reaction orders. The resolution of IPRM considered the presence of six different reactions (with distinct orders and activation energy values varying from 42.0 to 214.2 kJ mol-1) occurring during the biomass pyrolysis, highlighting the material heterogeneity, which is one of the probable reasons for the inadequacies observed in the resolution of the other studied models. The experimental data presented good adjustments for the studied models (considering lower conversion values for isoconversional and distributive activation energy models), due to the high values of correlation coefficients and the low values of deviation.
ACKNOWLEDGMENTS This work was financially supported by FAPEMIG (Fundação de Amparo à Pesquisa de Minas Gerais) [grant numbers APQ-02058-14; APQ-00652-18].
REFERENCES 1. Cai, J.; Xu, D.; Dong, Z.; Yu, X.; Yang, Y.; Banks, S. W.; Bridgwater, A. V.; Renewable Sustainable Energy Rev. 2018, 82, 2705. 2. ICO International Coffee Organization, available at http://www.ico.org/documents/cy2017-18/annual-review-website-e.pdf, accessed on March 2020. 3. Chaiklangmuang, S.; Kurosawa, K.; Li, L.; Morishita, K.; Takarada, T.; J. Energy Inst. 2015, 88, 323. 4. Klass, D. L.; Biomass for renewable energy. fuels. and chemicals, 1st ed., Academic Press: Cambridge, 1998. 5. Czernik, S.; Bridwater, A. V.; Energy Fuels 2004, 18, 590. 6. Badger, P. C.; Fransham, P.; Biomass Bioenergy 2006, 30, 321. 7. Slopiecka, K.; Bartocci, P.; Fantozzi, V.; Appl. Energy 2012, 97, 491. 8. Sfakiotakis, S.; Vamvuka, D.; J. Energy Inst. 2018, 91, 951. 9. Várhegyi, G.; Czégény, Z.; Jakab, E.; Mcadam, K.; Liu, C.; J. Anal. Appl. Pyrolysis 2009, 86, 310. 10. Anca-Couce, A.; Prog. Energy Combust. Sci. 2020, 53, 41. 11. Soria-Verdugo, A.; Garcia-Hernando, N.; Garcia-Gutierrez, L. M.; Ruiz-Rivas, U.; Energy Convers. Manage. 2013, 65, 239. 12. Ren, X.; Chen, J.; Li, G.; Wang, Y.; Lang, X.; Fan, S.; Bioresour. Technol. 2018, 261, 403. 13. Miura, K.; Maki, T.; Energy Fuels 1998, 12, 864. 14. Hu, S.; Jess, A.; Xu, M.; Fuel 2007, 86, 2778. 15. White, J. E.; Catallo, W. J.; Legendre, B. L.; J. Anal. Appl. Pyrolysis 2011, 91, 1. 16. Anca-Couce, A.; Berger, A.; Zobel, N.; Fuel 2014, 123, 230. 17. Hu, M.; Chen, Z.; Wang, S.; Guo, D.; Ma, C.; Zhou, Y.; Chen, J.; Laghari, M.; Fazal, S.; Xiao, B.; Zhang, B.; Ma, S.; Energy Convers. Manage. 2016, 118, 1. 18. Mishra, R. K.; Mohanty, K.; Bioresour. Technol. 2018, 251, 63. 19. Chen, N.; Ren, J.; Ye, Z.; Xu, Q.; Liu, J.; Sun, S.; Bioresour. Technol. 2016, 221, 534. 20. Órfão, J. J. M.; Antunes, F. J. A.; Figueiredo, J. L.; Fuel 1999, 78, 349. 21. Fermoso, J.; Masek, O.; J. Anal. Appl. Pyrolysis 2018, 130, 358. 22. Samolada, M. C.; Vasalos, I. A.; Fuel 1991, 70, 883. 23. TAPPI; Solvent Extractives of Wood and Pulp, T 204 cm-97, 2007, p. 12. 24. Gomide, J. L.; Demuner, B.; Papel 1986, 47, 36. 25. Sarkanen, K. V.; Ludwig, C. H.; Lignins: occurrence, formation, structure and reactions, John Wiley & Sons, Inc.: New York, 1971. 26. Tibola, F. L.; de Oliveira, T. J. P.; Carvalho, W. S.; Ataíde, C. H.; Cardoso, C. R.; Mater. Sci. Forum 2017, 899, 130. 27. Cardoso, C. R.; Miranda, M. R.; Santos, K. G.; Ataíde, C. H.; J. Anal. Appl. Pyrolysis 2011, 92, 392. 28. Antal, M. J.; Várhegyi, G.; Jakab, E.; Ind. Eng. Chem. Res. 1998, 37, 1267. 29. Ozawa, T.; Bull. Chem. Soc. Jpn. 1965, 38, 1881. 30. Starink, M. J.; Thermochim. Acta 1998, 228, 97. 31. Vand, V.; Proc. Phys. Soc. 1943, 55, 222. 32. Vassilev, S. V.; Baxter, D.; Andersen, L. K.; Vassileva, C. G.; Fuel 2010, 89, 913. 33. Vamvuka, D.; Kakaras, E.; Kastanaki, E.; Grammelis, P.; Fuel 2003, 82, 1949. 34. Branca, C.; Albano, A.; Di Blasi, C.; Thermochim. Acta 2005, 429, 133. 35. Uzun, B. B.; Yaman, E.; J. Energy Inst. 2017, 90, 825. 36. Li, H.; Li, L.; Zhang, R.; Tong, D.; Hu, C.; J. Energy Chem. 2014, 23, 732. 37. Luangkiattikhun, P.; Tangsathitkulchai, C.; Tangsathitkulchai, M.; Bioresour. Technol. 2008, 99, 986. 38. Simão, B. L.; Santana Júnior, J. A.; Chagas, B. M. E.; Cardoso, C. R.; Ataíde, C. H.; Algal Res. 2018, 32, 221. 39. Vyazovkin, S.; Burnham, A. K.; Criado, J. M.; Pérez-maqueda, L. A.; Popescu, C.; Sbirrazzuoli, N.; Thermochim. Acta 2011, 520, 1. 40. Dong, Z.; Cai, J.; J. Energy Inst. 2018, 91, 513. 41. Mallick, D.; Kumar, M.; Mahanta, P.; Moholkar, V. S.; Bioresour. Technol. 2018, 261, 294. 42. Hilten, R.; Vandenbrink, J. P.; Paterson, A. H.; Feltus, F. A.; Das, K. C.; Thermochim. Acta 2014, 577, 46. 43. Miura, K.; Energy Fuels 1995, 9, 302. 44. Wang, K.; Brown, R. C.; Homsy, S.; Martinez, L.; Sidhu, S. S.; Bioresour. Technol. 2013, 127, 494. 45. Cai, J.; Wu, W.; Liu, R.; Renewable Sustainable Energy Rev. 2014, 36, 236. 46. Sonobe, T.; Worasuwannarak, N.; Fuel 2008, 87, 414. 47. Bokelman, G. H.; Ryan, W. S.; Beiträge zur Tabakforschung International 1985, 13, 29. 48. Amutio, M.; Lopez, G.; Alvarez, J.; Moreira, R.; Duarte, G.; Nunes, J.; Olazar, M.; Bilbao, J.; Chem. Eng. Res. Des. 2013, 91, 2682. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access