Educação
|
|
| Implementação do campo de força ClayFF no GROMACS: uma aplicação em estrutura de caulinita Implementation of the ClayFF force field in GROMACS: an application in kaolinite structure |
|
Eric Mochiutti*; Rodrigo Luiz da C. Sehwartz; João Pedro O. Lima; Arthur Lobato S. Carvalho; Roberto de F. Neves; Davi do Socorro B. Brasil; Marlice C. Martellia
Faculdade de Engenharia Química, Universidade Federal do Pará, 66075-110 Belém - PA, Brasil Recebido em 16/11/2019 *e-mail: mochiuttieric@gmail.com Molecular dynamics techniques are increasingly being used for material science studies, being a theoretical approach based on molecular mechanics studies. GROMACS is a free software that allows the development of simulations of various types of molecules, from biological molecules to inorganic structures associated with the area of materials, requiring the system parameterization according to the force fields used in the simulation. ClayFF is a force field used for crystalline clay structures and has been applied in several articles published in scientific journals. The objective of this work was to present a didactic approach to the implementation of ClayFF in GROMACS and the force field was used to simulate a kaolinite structure as an example, demonstrating the implementation for students and researchers in the field. INTRODUÇÃO No âmbito do conhecimento da química, existem os mais diversos campos de estudos. Dentre os quais, o ramo da química computacional destaca-se por uma evolução significativa. A dinâmica molecular aplicada através de simulações computacionais caracteriza-se como uma importante ferramenta para a compreensão das propriedades de um sistema de moléculas, em relação as estruturas e interações microscópicas. Inicialmente, a dinâmica molecular fora utilizada para entender o comportamento de sistemas de macromoléculas biológicas.1 Com o objetivo de ampliar a abrangência de utilização da dinâmica molecular para outros tipos de estruturas, não somente biológicas, foi gerada a necessidade de novos campos de forças, que descrevessem, de forma satisfatória, o comportamento de diversas estruturas em um sistema dinâmico. Um exemplo de outros tipos de estruturas a serem estudados, são as dos argilominerais. A vasta gama presente de materiais argilosos e o fato de existirem os mais diversos estudos com estes, demonstra por si só a importância da obtenção de conhecimento da estrutura interna e das propriedades destes materiais, assim como dos processos envolvidos, quando estes interagem com diferentes estruturas. Estudos experimentais como o de Monteiro e Santana,2 que mostram a avaliação do caráter adsortivo da caulinita pura com íons de chumbo, complementado com trabalhos de dinâmica molecular que fornecem uma visão microscópica de como a adsorção ocorre nos sítios da caulinita, como o realizado por Li et al.,3 que pelas técnicas computacionais mostram que a adsorção desse metal foi fundamentalmente promovida pelos defeitos da estrutura (defect sites) sendo as quantidades adsorvidas aprimoradas pelo tamanho crescente dos defeitos. Outro exemplo são estudos experimentais que demonstram a comparação de características adsortivas de caulinitas puras e caulinitas que passaram pelo processo de intercalação,4 ou os combinados entre a parte computacional e experimental, como o processo de intercalação com acetato de potássio, estudado por Cheng et al.,5 em que por dinâmica molecular indica que os íons de acetato e de potássio se distribuem entre as camadas tetraédrica e octaédrica da caulinita, sendo que os ânions de acetato formam pontes de hidrogênios fortemente ligadas à parte octaédrica da estrutura da caulinita. Destaca-se o fato de haver um aumento nas propriedades adsortivas da caulinita após o processo de intercalação, denotando um avanço relacionado a materiais argilosos, em que diversas pesquisas tanto pelo método de simulação por dinâmica molecular quanto por métodos experimentais, avaliaram o processo de intercalação, assim como o de adsorção. Neste contexto, uma comparação dos dados obtidos pela simulação com os resultados experimentais pode levar ao entendimento das interações microscópicas, ressaltando que os trabalhos de dinâmica molecular citados utilizaram campos de força para estruturas inorgânicas e sendo o ClayFF específico para a simulação de estruturas cristalinas de argilas. Através da utilização de dados encontrados na literatura, contendo equações e os parâmetros do campo de força, é possível a implementação deste em diferentes softwares de simulação computacional, podendo assim, estender a metodologia para diversas aplicações e, por conseguinte, ampliar à abrangência deste ramo do conhecimento. Com a implementação do campo de força, torna-se viável os seguintes resultados para estruturas de materiais argilosos: o desvio médio quadrático da raiz (RMSD), a flutuação quadrática média da raiz (RMSF), raio de giro (RG) e a densidade da célula unitária. Representando estes, respectivamente, as modificações nas posições dos átomos no decorrer do tempo de simulação (RMSD); a rigidez do arranjo estudado, denotando a flexibilidade de pontos específicos deste no transcorrer do tempo (RMSF); a compactação da conformação estudada (RG) e as densidades da estrutura cristalina nos eixos x, y e z. Além destes, pode-se também analisar as pontes de hidrogênio (H-Bond) formadas entre agrupamentos de doadores e aceitadores, presentes no sistema estudado.6 Esses são apenas alguns resultados que podem ser obtidos com cálculos de dinâmica molecular. Com intuito de facilitar ainda mais a aplicação desta metodologia de implementação de novos campos de forças para dinâmica molecular, utiliza-se o software de livre acesso GROMACS, onde pode-se simular uma ampla faixa de moléculas e estruturas, desde materiais biológicos até estruturas inorgânicas, em que são adicionados parâmetros para que o programa possa ler os dados de forma automática. Outra vantagem encontra-se no fato de este software ser gratuito e de fácil acesso, podendo assim atingir os mais diversos leitores. De maneira geral, é de suma importância a divulgação da simulação computacional na formação de novos alunos, devido ao fator da interconectividade entre as áreas da química, onde um ramo do conhecimento pode suprir a carência de outro, fazendo com que resultados obtidos através de experimentos sejam complementados por meio da simulação computacional. Considerando também devido ao aumento da capacidade de processamento dos computadores fazendo com que sistemas cada vez mais complexos possam ser simulados, tornando-se mais comum em pesquisas científicas. Neste contexto, a metodologia de implementação usada nesse artigo pode servir como base em uma disciplina de dinâmica molecular para alunos interessados nas pesquisas de materiais argilosos. Para isso usou-se o exemplo didático em uma estrutura de caulinita, a qual é amplamente conhecida e estudada no campo de ciências dos materiais.
DINÂMICA MOLECULAR As simulações computacionais são uma importante ferramenta para compreender as propriedades de um conjunto de moléculas em termos de sua estrutura e interações microscópicas.7 Entretanto, ainda que as propriedades de uma molécula isolada possam estar bem definidas, assim como as leis que regem os processos elementares das interações entre as mesmas, realizar a análise de um sistema contendo várias moléculas pode ser uma tarefa árdua.8 Desta forma, devido aos avanços envolvendo a construção de modelos moleculares, é possível realizar tal tarefa com o emprego da dinâmica molecular.9 A dinâmica molecular é fundamentada nos princípios da mecânica clássica.10 Neste sentido, dentre as formas de solucionar as equações de Newton presente nos processos de simulação, o algoritmo de Verlet e suas variantes são os mais utilizados, devido às suas reversibilidades no tempo (time-reversible) e por serem simpléticos.11,12 O método de Verlet é o mais eficiente para resolver equações diferenciais sem solução analítica originárias de um sistema de equações Newtoniano, próprio para mecânica molecular clássica.13,14 O algoritmo ainda pode receber modificações conforme o sistema analisado e a capacidade computacional disponível. Na dinâmica molecular, campos de força representam um conjunto de funções e parametrização que denotam aspectos do comportamento da estrutura em questão, sendo esse comportamento caracterizado por propriedades moleculares como comprimento de ligações, torção e deformação de diedros, entre outras. Essas características são descritas em forma de interações entre átomos (provenientes de ligações ou atrações intermoleculares).15 Esses potenciais são construídos conforme a natureza dos componentes da estrutura, isto é, a abordagem do sistema define o tipo de campo de força que será utilizado. Os campos de força utilizados durante as simulações são uma combinação dos termos de Leonnard-Jones e de Coulomb, que são responsáveis por realizar cálculos de energia e de força para um sistema.12,16 Muitos potenciais interatômicos foram propostos com o objetivo de descrever a interação entre átomos ao longo dos tempos. Nesse contexto, o potencial de Lennard-Jones (L-J ou 12-6) vem sendo aplicado aos campos de força para realizar as aproximações envolvendo as interações de Van der Waals.17 As equações que definem o potencial de Lennard-Jones18 podem ser descritas em sua forma comum ou em termos de sigma, como mostrado pelas Equações 1 e 2, respectivamente, enquanto a forma representada pela Equação 3 é utilizada por softwares como o GROMACS.19 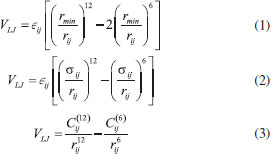 onde ∈ij é definido como a profundidade do potencial, σij é a distância na qual o potencial entre as partículas é nulo, rij é a distância entre as partículas i e j, rmin é a distância na qual o potencial é mínimo.12,20,21 Para haver a determinação dos parâmetros de repulsão (1/r)12 e dispersão (1/r)6 do potencial de Lennard-Jones, aplicam-se as denominadas regras de combinações, as quais podem ser divididas em dois grupos: (i) regras baseadas em médias geométricas de ε e σ, além da regra de Lorentz-Berthelot e (ii) regras mais específicas como de Halgren e Fender-Halsey.22,23 Nesse sentido, as Equações 4, 5, 6 e 7 representam as regras de combinação envolvendo médias geométricas de Cij(6) e Cij(12) e a regra de Lorentz-Berthelot,24,25 respectivamente, enquanto as Equações 8 e 9 representam a regra de combinação considerando a média geométrica de ∈ e σ. Em softwares como o GROMACS, também é denotado que: (i) Vii = Ci(6) [kJ mol-1 nm6] e Wii = Ci(12) [kJ mol-1 nm6] para as Equações 4 e 5 e (ii) Vii = σi [nm] e Wii = ∈i [kJ mol-1] para as Equações 6, 7, 8 e 9. 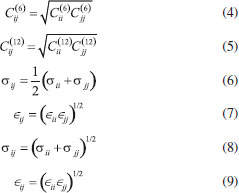 A energia de Coulomb é representada pela Equação 10, em que a energia da interação é inversamente proporcional à distância de separação rij. 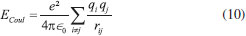 onde qi e qj são as cargas total ou parcial da partícula, é a carga do elétron e é a permissividade dielétrica do vácuo (8,85419 × 10-12 F m-1).9 Ademais, a classificação dos campos de força é feita em dois grupos: bonded e nonbonded. O primeiro grupo é empregado com o intuito de analisar o alongamento das ligações, os ângulos de ligação e a rotação dos diedros, enquanto que o segundo grupo visa obter informações referentes à eletrostática, dispersão e a exclusão de Pauli das moléculas.12,16,26 Os termos do campo de força bonded podem ser descritos por diferentes equações dependendo da descrição da dinâmica das moléculas ligadas. Para o alongamento das ligações pode-se adotar um comportamento potencial harmônico simples como na Equação 11, potencial de Morse pela Equação 12, ou potencial cúbico pela Equação 13, entre outras possibilidades.13 Em que i e j representam os átomos ligados em uma ligação covalente, kijb, Dij, kijcubic são constantes, bij representa comprimento de ligação no equilíbrio e rij o comprimento da ligação. 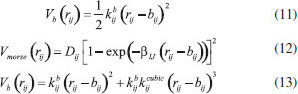 Da mesma forma, para a curvatura da ligação, que forma um ângulo, tem como possibilidades ângulos baseados no potencial harmônico, como mostrado na Equação 14 ou ângulos baseados em cossenos pela Equação 15. E por fim, a rotação dos diedros, que podem ser divididos em dois tipos: próprios ou impróprios. As notações i, j, k representam a sequência de átomos ligados covalentemente.13 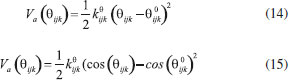 Em que, kθijk é uma constante, θ0ijk e θijk são respectivamente o ângulo de equilíbrio e o ângulo formado pelos átomos i, j, k.
GROMACS A origem do software GROMACS vem dos anos de 1980 na Universidade de Groningen (Holanda), onde um grupo liderado por Berendsen e Van Gusteren lançou a primeira versão do software.27 No período em questão, havia a necessidade de criar e aprimorar métodos para simulação de dinâmica molecular. O GROMACS, sendo um software livre, demonstra possuir uma vasta biblioteca e gama de programas, os quais propiciam uma ampla versatilidade para o mesmo.28,29 A princípio, o objetivo de aplicação deste software foi para moléculas biológicas contendo interações complexas entre ligações. Entretanto, o fato de ter implementado cálculos de interações externas as ligações, faz com que o GROMACS possua uma grande efetividade para simulações com os mais variados tipos de moléculas. Isto acontece devido a fácil aplicabilidade de diversos campos de forças diferentes.30,31 Uma das principais ideias do GROMACS é o desenvolvimento de maior eficiência possível da simulação, através da paralelização computacional, o qual otimiza o processamento de dados mediante a distribuição de funções nos múltiplos núcleos de um processador.19,32
CAMPO DE FORÇA ESPECÍFICO PARA ARGILAS O campo de força ClayFF é ideal para realizar a dinâmica molecular de um sistema formado por uma estrutura cristalina interagindo com moléculas de água ou hidroxilas. Campos de força mais generalistas têm dificuldade em simular a movimentação atômica dentro da célula unitária. Dessa forma, esses campos geralmente consideram a estrutura como "rígida", onde o bloco cristalino somente se move por inteiro durante a simulação, não permitindo uma análise mais precisa de energia e momento, entre os átomos isolados.33 As aplicações desse campo na área de modelagem molecular e ciência dos materiais são inúmeras, como no estudo de Pouvreau et al.,34 que faz uma análise das estruturas de brucita e gibbsita hidratadas e propõe um novo tipo de abordagem para ligações metal-O-H no campo de força. Ou ainda, no modelo de Sosso et al.,35 que utilizou dessa parametrização para analisar a nucleação de gelo na superfície hidroxilada de uma caulinita e o formato que as moléculas de água assumem neste processo. Embora o objetivo inicial desse campo de força fosse analisar estruturas cristalinas hidratadas, sistemas mais complexos podem tê-lo como base. Estudos realizados por Abramov e Iglauer36 analisaram um sistema de quartzo alquilado implementando o ClayFF para a estrutura mineral e o campo de força DREIDING para o componente orgânico do modelo. Assim, mesclando esses potenciais, obtêm-se resultados mais precisos. O ClayFF tem como base uma descrição iônica (nonbonded) para interações entre metal e oxigênio e modelo SPC (Single Point Charge) para interações de O-H e O-O (bonded).37 Dito isso, o conjunto de energias de interação átomo-átomo é descrito pela Equação 16: 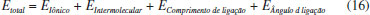 onde os termos do lado direito da Equação 16 significam, respectivamente: energia de interação eletrostática (metal-O), potencial de interações intermoleculares e energias relacionadas ao alongamento e ao ângulo de ligação covalente. As equações referentes a cada tipo de energia que relacionam parâmetros de distância interatômica, constantes universais, parâmetros empíricos e cargas parciais dos átomos constam em Cygan et al.33 O campo de força ClayFF utiliza de cargas parciais dos átomos para as interações de Coulomb, devido a carga total no campo de força introduzir uma forte influência estabilizadora na interação, enquanto as cargas parciais mostram um comportamento mais suave, permitindo mais flexibilidade e movimento. Ou seja, o modelo com cargas completas terá contribuições de Coulomb artificialmente grandes que influenciam fortemente a estrutura entre camadas, dinâmica de argilas e a adsorção de espécies na superfície.33 Cygan et al.33 apresentam ainda valores de parâmetros necessários para estabelecer esses cálculos de energia, sendo divididos em parâmetros nonbonded, obtidos a partir da teoria de determinação de campo de Lennard-Jones (1924), com o devido tratamento matemático para metais, oxigênio e hidrogênio, além de valores para íons em ambiente aquoso compatíveis com o tipo de água utilizada (SPC), obtidos em outras literaturas, e parâmetros bonded, estipulados após um processo iterativo das equações relacionadas às energias de ligação covalente utilizando valores empíricos de equilíbrio de comprimento e ângulo de ligação. A utilização de um campo de força específico como o ClayFF depende do entendimento de como cada átomo será reconhecido dentro do sistema. Para isso, a Tabela 1 expõe a nomenclatura de algumas espécies utilizadas para o campo, além das informações de carga e parâmetros empíricos a serem aplicados nas equações de energia para nonbonded.
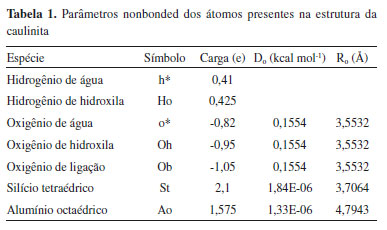
Os parâmetros empíricos Do e Ro são termos que representam, respectivamente, energia e distância entre os átomos que participam da interação. Como a tabela indica esses valores para cada tipo de átomo, ao analisar a ligação, esses parâmetros são submetidos a uma média aritmética ou geométrica, como indicado nas Equações 17 e 18 a seguir: 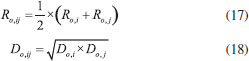 onde i e j representam a qual átomo o parâmetro se refere e ij ao valor resultante da interação. Para as equações de energia de ligação (bonded) para comprimento e ângulo, os parâmetros são dispostos nas Tabelas 2 e 3:
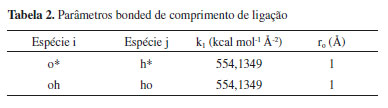

Onde j é o átomo central e i e k estão nas extremidades da sequência. ro e θo representam, respectivamente, comprimento e ângulo de equilíbrio de ligação e k é a constante de força, que serão aplicadas nas Equações 19 e 20. Essas equações são baseadas no potencial harmônico simples para o alongamento de ligação e ângulos de ligação.33 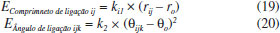
CAULINITA Os principais componentes das argilas são os silicatos hidratados de alumínio, ferro e magnésio. Sabe-se que argilas são compostas por argilominerais, sendo estas partículas cristalinas de tamanho estritamente pequeno, possuindo uma faixa granulométrica específica. Sendo assim, as argilas podem ser compostas exclusivamente de um argilomineral ou por uma mistura de diferentes argilominerais, dentre os quais, para este trabalho, se evidenciará a caulinita.38 A caulinita é um mineral originário de solos desenvolvidos em cinzas vulcânicas ou solos tropicais. É considerada como um mineral de fase estável na natureza, o qual possui composição química Al2Si2O5(OH)4. A caulinita possui uma formação lenta, em solos que possuem uma boa drenagem e os líquidos possuem uma baixa concentração iônica. Estes fatores são determinantes para o crescimento lento e com baixo grau de desordem da estrutura lamelar da caulinita. A caulinita é encontrada na natureza com baixa granulometria (inferior a 2 µm), sendo um filossilicato de coloração normalmente branca.39 A Figura 1 denota através da utilização do MEV (Microscopia Eletrônica de Varredura) a morfologia da caulinita, onde pode-se constatar as lamelas formadas.
 Figura 1. Microscopia Eletrônica de Varredura da caulinita
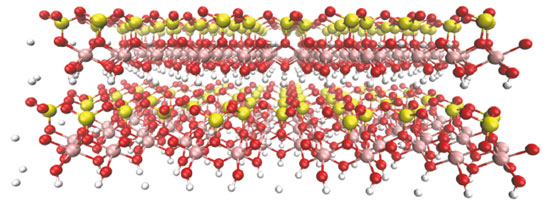
A caulinita é formata através do empilhamento de dois tipos de folhas diferentes, uma octaédrica e outra tetraédrica, onde a folha tetraédrica é composta de SiO4, enquanto a folha octaédrica é composta de Al2(OH)6. A construção das camadas se dá de forma com que uma folha tetraédrica se combine com uma folha octaédrica (empilhamento regular 1:1). A composição percentual de uma célula unitária de caulinita se dá por: 46,54% de SiO2; 39,50% de Al2O3; 13,96% de H2O.38 A estrutura da caulinita é contínua no decorrer dos eixos a e b, e encontram-se empilhadas ao longo do eixo c, possuindo estrutura cristalográfica triclínica. Os valores para os parâmetros de rede descritos por Newnham e Brindley40 estão dispostos na Tabela 4.
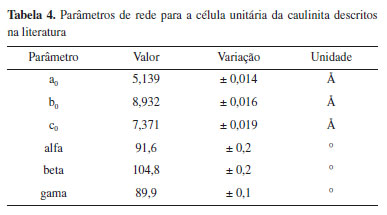
Outra grande importância do trabalho de Newnham e Brindley40 foi o cálculo da distância interplanar basal da caulinita, isto é, a distância entre as camadas basais (001), o qual pode se denominar também como a espessura de uma célula unitária para a outra durante o empilhamento ao longo do eixo c. Para isto, a Equação 21, disposta a seguir, denota a metodologia utilizada para calcular a distância interplanar, bem como o valor encontrado. 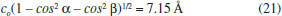 A Figura 2 disposta a seguir destaca os planos basais (001), (010) e (100) para as células unitárias e para as super células construídas.
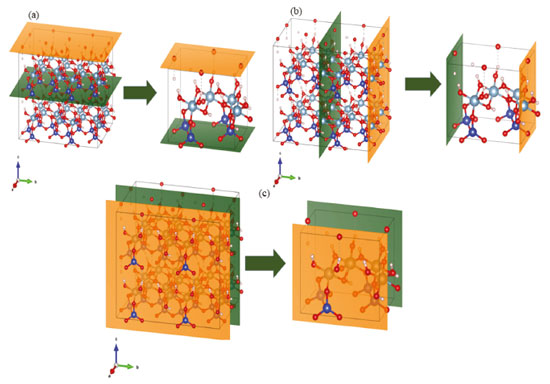 Figura 2. Planos basais de uma estrutura 2x2x2 e a célula unitária da caulinita (a) plano basal (001); (b) plano basal (010); (c) plano basal (100) Figura 3.
Através da utilização do método de difração de raios X (DRX) com ânodo de cobre, pode-se constatar, através do ângulo de difração do raio incidente, a distância interplanar do cristal de caulinita.41 A Figura 3 denota a análise de DRX para uma amostra de caulinita estudada.
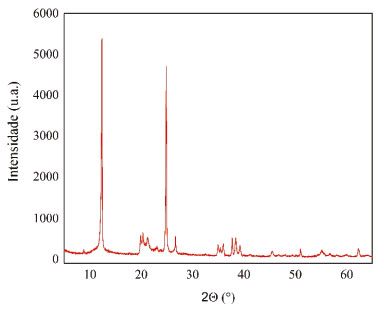 Figura 3. DRX, pelo método do pó e com ânodo de Cu, de uma amostra de caulinita da região amazônica
Através das análises do DRX, pode-se destacar o grupo de três picos pequenos encontrados na região de 19° à 23°, a qual se localiza entre os dois picos de maior intensidade, onde estes demonstram uma amostra de caulinita "bem cristalizada", de mesmo modo que, pode-se encontrar no banco de dados uma ficha com código de referência 83-0971 de caulinita,42 compatível com os picos presentes na amostra estudada, onde nesta encontra-se determinados os parâmetros de rede da célula unitária, bem como a densidade de 2,61 g cm-3, fatores que serão importantes para futuras comparações com resultados obtidos na simulação.
METODOLOGIA DE IMPLEMENTAÇÃO DO CLAYFF NO GROMACS Para facilitar o entendimento da parametrização, o fluxograma presente na Figura 4 representa as etapas do processo de implementação no GROMACS. As extensões de cada arquivo citado abaixo serão abordadas mais adiante.
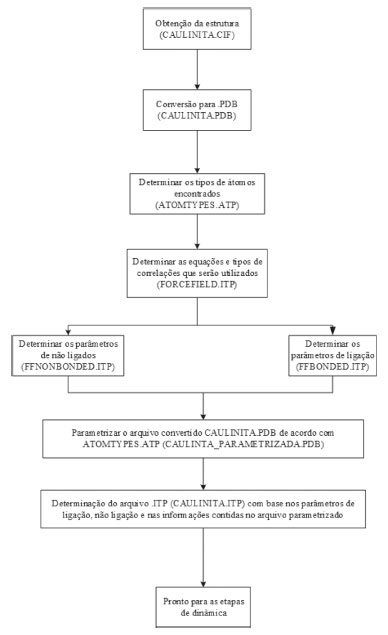 Figura 4. Fluxograma de implementação do ClayFF no GROMACS
Obtenção da estrutura cristalina da caulinita O arquivo da estrutura da caulinita, baseado no trabalho de Bish,42 foi obtido do banco de dados American Mineralogist Crystal Structure Database. O formato do arquivo baixado foi Arquivo de Informações Cristalográficas (.cif). Entretanto, o software GROMACS não suporta esse tipo de arquivo. Com o auxílio do software livre Avogadro ou Open Babel é possível converter esse arquivo para Banco de Dados de Proteínas (.pdb). É importante ressaltar que o arquivo no formato .pdb é baseado na leitura pela numeração da coluna, encontrada nos exemplos a seguir entre parênteses: número de identificação do átomo (7-11), nome de identificação do tipo de átomo (13-16), nome do resíduo (18-20), numeração do resíduo (23-26), posição no eixo X (31-38), posição no eixo Y (39-46), posição no eixo Z (47-54), elemento químico (77-78), entre outras informações contidas nesse formato de arquivo. Nessa etapa devem ser alterados os parâmetros de rede da caulinita, de acordo com os resultados experimentais da estrutura a ser estudada. Para o nosso exemplo os parâmetros estão apresentados na Tabela 5, informados na parte superior do arquivo .pdb pelo cabeçalho CRYST1 (Material Suplementar, Figura 1S).
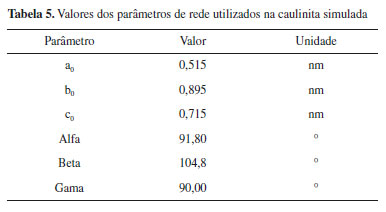
Determinação dos tipos de átomos encontrados e parametrização do arquivo .pdb da caulinita Após a obtenção da estrutura, é necessário nomear os átomos conforme descritos no campo de força e parametrizar os valores de acordo com as funções selecionadas no software. Para isso, primeiramente deve-se identificar os tipos de átomos presentes na estrutura pela Tabela 1. A caulinita é composta por átomos de silício, alumínio, hidrogênio, oxigênio.38,39,41 Os átomos de silício são classificados como silícios tetraédricos (st), os de alumínio octaedros (ao), os hidrogênios pertencem ao grupo hidroxila (ho), e os oxigênios em dois grupos, de ligação/ponte (ob) e de hidroxilas (oh). Com estas informações, pode-se então montar o arquivo atomtypes.atp (atomtype parameter) ao campo de força. Na Figura 5 encontra-se os tipos de átomos encontrados na caulinita.
 Figura 5. Arquivo para os tipos de átomos da caulinita, após o símbolo ";" representa um comentário na linguagem da programação (atomtypes.atp)
Para os átomos de oxigênio é recomendado expandir a caixa de simulação, devido a se tratar de uma célula unitária e que a simulação é realizada conforme as condições periódicas de contorno. Assim, alguns átomos, aparentemente, não possuirão ligações até que ocorra a repetição das células unitárias. Deste modo, os átomos de oxigênio ligados ao de hidrogênios, pertencem ao grupo "oh", enquanto os outros oxigênios, ao grupo "ob". Na Figura 6 pode-se ver a nomenclatura dos átomos com base no arquivo atomtypes.atp.
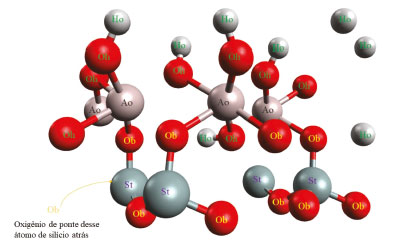 Figura 6. Nomenclatura dos átomos da caulinita em uma célula unitária, com base no arquivo atomtypes.atp criado anteriormente
A partir dessas informações utilizou-se o arquivo convertido da caulinita (.pdb) e parametrizou-se o mesmo em relação ao arquivo de tipo de átomos (.atp), diferenciando átomos iguais por índices após a nomenclatura do átomo. A parametrização citada nesse tópico é apresentada na Figura 1S. Determinação das equações e tipos de correlações do campo de força e parâmetros ligados e não-ligados Para o arquivo dos parâmetros do campo de força, baseando-se no campo de força para argilas, é necessário selecionar o Potencial de Lennard-Jones para átomos não-ligados (representado pela função 1 no software), além da regra de combinação de Lorentz-Berthelot (representado pela função 2 no software)43 e geração de pares, além da inclusão dos parâmetros de ligações e de não-ligados. Na Figura 7 encontra-se o arquivo de inclusão de topologia (.itp) com as funções selecionadas para o campo de força (forcefield.itp).
 Figura 7. Arquivo com as equações do campo de força e a inclusão dos parâmetros bonded e nonbonded descritos posteriormente (forcefield.itp)
Após a indicação das Equações que serão utilizadas nos cálculos de dinâmica molecular, pode-se montar o arquivo de parâmetros de força dos átomos ligados e não-ligados. Para os parâmetros não-ligados é necessário, primeiramente, indicar pela diretiva [atomtypes], e em seguida converter a Equação 1 para Equação 2, para obter-se parâmetros e da Equação de Potencial de Lennard-Jones que serão usados nos cálculos. Na Tabela 1 são fornecidos os valores de D0 (kcal mol-1) e R0 (Å), os valores de D0 precisam ser convertidos para kJ, para adequar-se ao parâmetro épsilon da Equação 1 e os valores de R0 devem ser primeiramente convertidos para nanômetros e em seguida aplicado a Equação 22 para ser convertido para o parâmetro sigma presente na Equação 1:  Organizando o arquivo de parâmetros de força não-ligados (ffnonbonded.itp), e indicando que se trata de um átomo pela sigla "A", encontram-se na Figura 8 os parâmetros de campo de força não-ligados.
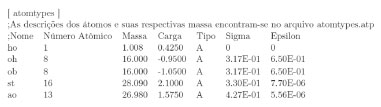 Figura 8. Arquivo com os parâmetros do campo de força não-ligados (ffnonbonded. itp)
Para a implementação dos parâmetros de ligação presentes na Tabela 2, é necessário a diretiva [bondtypes], e indicar a função com valor 1.43 É necessário converter os valores da distância da Tabela 2 para nanômetros (nm) e da constante de energia para a unidade de joule (J), além de multiplicar por dois, devido os valores presentes na Tabela 2 serem a média aritmética. O arquivo dos parâmetros de ligação pode ser visto na Figura 9.
 Figura 9. Arquivo com os parâmetros de ligação da hidroxila (ffbonded.itp)
Caso seja necessário adicionar água ao sistema, íons ou outras moléculas, deve-se adicionar os modelos em arquivos .itp de campo de força e parâmetros ligados e não-ligados na pasta do campo de força (Clayff.ff). Determinação do arquivo de topologia da caulinita (caulinita.itp) Nessa etapa é necessária a criação de um arquivo caulinita.itp e que o mesmo esteja conforme as etapas anteriores, ou seja, com a mesma nomenclatura, numeração do arquivo caulinita.pdb e os parâmetros dos arquivos de ligação e não-ligados, conforme mostrado nas Figuras 1S e 2S do material suplementar. Uma dica importante é manter parametrizada a célula unitária, pois para sistemas com replicação dessas células é necessário apenas o comando de replicação genconf do próprio software GROMACS. Na parte inferior do arquivo .itp da caulinita, as ligações são entre os átomos de ho-oh, e constar a numeração de identificação, tanto a função, quanto os parâmetros já apresentados no arquivo ffbonded.itp, encontrados na Figura 3S no material suplementar. Após essas etapas, o sistema está pronto para simular uma dinâmica molecular. Dinâmica molecular da caulinita No modelo descrito por este artigo, a dinâmica foi realizada com o campo de força ClayFF, específico para argilas, replicando-se a célula unitária em 8x4x4, obtendo o total de 128 células unitárias, contendo condições periódicas de contorno nos eixos XYZ, presente na Figura 10.
Inicialmente um cálculo de minimização foi feito a partir do algoritmo steepest descent com um total de 50000 passos, com tolerância de 0.01 kJ mol-1 nm-1. Após a minimização foi realizado o equilíbrio em duas etapas: a primeira usando o conjunto NVT (número de mols, temperatura e volume constantes) e outra utilizando o conjunto NPT (número de mols, temperatura e pressão constantes). Por fim, a dinâmica molecular foi executada. Essa simulação foi efetuada com 5000000 passos para um tempo de 10 ns (nanosegundos), baseando-se no algoritmo de integração Leap-Frog, algoritmo LINCS para a restrição do comprimento de todas as ligações com condições periódicas de contorno em 3 dimensões. Foi especificado também o método de cálculo de interações a longa distância, sendo esse o PME (Particle Mesh Ewald) com uma restrição de 1,4 nm de alcance eletrostático e de Van der Waals. O controle de pressão foi efeito a partir de um barostato de Parrinello-Rahman, em uma escala isotrópica, com pressão de referência de 1 bar. A dinâmica foi executada com temperatura 298,15 K com um termostato de V-rescale. Com isso foi possível obter resultados de Energia Cinética, Potencial e Total (Figuras 4S, 5S, 6S presentes no material suplementar). É possível também observar a variação da densidade nos três eixos X, Y e Z, presentes na Figura 11, comparando isso com os planos cristalográficos da Figura 2.
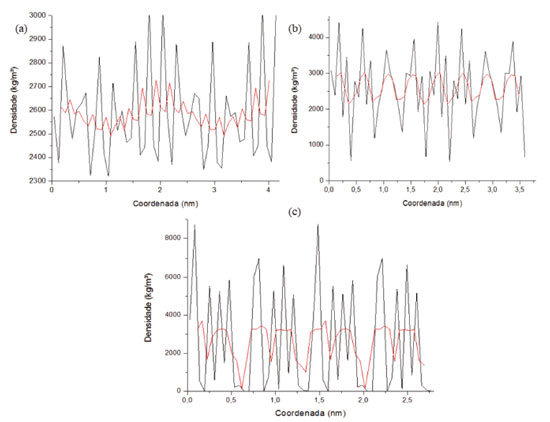 Figura 11. (a) Densidade em relação ao eixo X da caulinita (b); densidade em relação ao eixo Y da caulinita; (c) densidade em relação ao eixo Z da caulinita
Através da análise da Figura 11, pode-se identificar uma ampla faixa de variação nas densidades nos eixos XYZ. Esta variação se dá principalmente devido aos espaços intermoleculares (lacunas) presentes no decorrer da estrutura. Além disso, para a densidade no decorrer do eixo Z, pode-se destacar também momentos em que o valor da densidade é zero, isto ocorre devido aos espaços interplanares. Determina-se então, mediante aos resultados da simulação, um valor médio da densidade combinada para os eixos XYZ de aproximadamente 2700 ± 100 kg m-3 (2,7 g cm-3), o qual condiz com a ficha obtida através da análise do DRX disposto na Figura 3.42 Na Figura 12 podemos analisar os resultados de desvio médio quadrático da raiz (RMSD) e flutuação quadrada média da raiz (RMSF) da estrutura cristalina da caulinita.
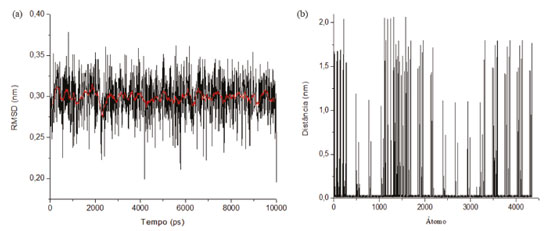 Figura 12. (a) Desvio médio quadrático da raiz (RMSD) da estrutura cristalina da caulinita; (b) flutuação quadrada média da raiz (RMSF) da estrutura cristalina da caulinita
O RMSD indica o quanto a estrutura de interesse se modifica ao longo de uma simulação em relação à estrutura de partida, uma consideração importante quando são realizadas análises de RMSD, a qual se refere ao fato de que esta análise oferece uma medida média de um conjunto de átomos selecionados para a análise. A linha vermelha representa a média dos pontos, obtendo um valor entorno de 0,3 nm. Se todos os átomos de um sistema são considerados, como no exemplo acima, os valores observados trazem consigo influências de diferentes regiões. Então, para isso é necessária uma análise de RMSF para determinar quais regiões/átomos estão apresentando maior flutuação, ou seja, movimentação. Com os resultados apresentados é possível observar que os maiores picos de movimentação estão relacionados aos átomos do grupo hidroxila na caulinita, entretanto os picos dos outros átomos presentes apresentam de maneira pontual também grandes flutuações.
CONSIDERAÇÕES FINAIS Cálculos de dinâmica molecular resultam em diversas propriedades dos sistemas simulados, além das citadas. Alguns dos resultados que podem ser obtidos são: quantidade de pontes de hidrogênio (H-Bond) entre a caulinita e outra molécula inserida no sistema; função radial de distribuição de pares (RDF); potencial de campo; viscosidade; energia livre de superfície, porém deve-se buscar os resultados relevantes para o fenômeno de interesse. Uma das limitações do campo de força, na forma feita nesse artigo, é que a estrutura na caixa de simulação não apresenta as bordas da caulinita para estudos de adsorção, no entanto, adicionando-se parâmetros é possível simular o efeito de borda, conforme realizado no estudo de Zeitler et al.44 Um dos recursos de cálculo que pode ser adicionado no GROMACS é a extensão do PLUMED, que permite métodos de cálculos de energia livre, como a meta-dinâmica, ou seja, qualquer um destes recursos permite adicionar novas aplicações, adaptando o campo de força, conforme artigos encontrados na literatura ou com extensões online. O desenvolvimento de artigos e materiais didáticos que possam auxiliar estudantes e pesquisadores da área de química computacional é de extrema importância, tendo em vista que permite a familiarização dos mesmos com as ferramentas disponíveis para o estudo e implementação dos seus respectivos alvos de pesquisa. Logo, baseando-se nesse artigo, os interessados podem implementar o campo de força ClayFF e utilizar como referência o exemplo da caulinita para aplicação em outras estruturas cristalinas de argilas, além de ser um ponto inicial para estudos mais complexos envolvendo esses tipos de estruturas.
MATERIAL SUPLEMENTAR Os arquivos caulinita.pdb e caulinita.itp e suas indicações de formas de parametrização das células unitárias e gráficos de energias total, cinética e potencial estão disponíveis em http://quimicanova.sbq.org.br, na forma de arquivo PDF, com acesso livre.
REFERÊNCIAS 1. Namba, A. M.; da Silva, V. B.; da Silva, C. H. T. P.; Eclet. Quim. 2008, 33, 13. 2. Monteiro, E. P.; Santana, G. P.; Revista Eletrônica de Materiais e Processos 2009, 4, 48. 3. Li, X.; Li, H.; Yang, G.; Sci. Rep. 2015, 5, 28. 4. Oliveira, S. P.; Silva, W. L. L.; Viana, R. R.; Cerâmica 2013, 59, 338. 5. Cheng, H.; Zhang, S.; Liu, Q.; Li, X.; Frost, R. L.; Appl. Clay Sci. 2015, 116-117, 273. 6. Lemkul, J.; Living J. Comp. Mol. Sci. 2019, 1, 5068. 7. Attig, N.; Binder, K.; Grubmüller, H.; Kremer, K., eds.; Computational Soft Matter: From Synthetic Polymers to Proteins; NIC-Directors, 2004. 8. Alder, B. J.; Wainwright, T. E.; J. Chem. Phys. 1959, 31, 459. 9. Heinecke, A.; Eckhardt, W.; Horsch, M.; Bungartz, H.-J.; Supercomputing for Molecular Dynamics Simulations; Springer, 2015. 10. Rapaport, D. C.; The art of molecular dynamics simulation; Cambridge University Press: Cambridge, 2004. 11. Barbatti, M.; Ruckenbauer, M.; Plasser, F.; Pittner, J.; Granucci, G.; Persico, M.; Lischka, H.; Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 4, 26. 12. Deuflhard, P.; Hermans, J.; Leimkuhler, B.; Mark, A. E.; Reich, S.; Skeel, R. D.; eds.; 2nd International Symposium on Algorithms for Macromolecular Modelling; Berlin, Alemanha, 1998. 13. Schlick, T.; Molecular Modelling and Simulation: An Interdisciplinary Guide; Springer: New York, 2010. 14. Grubmüller, H.; Heller, H.; Windemuth, A.; Schulten, K.; Mol. Simul. 1991, 6, 121. 15. Verli, H., ed.; Bioinformática: da biologia à flexibilidade molecular; Sociedade Brasileira de Bioquímica e Biologia Molecular (SBBq): São Paulo, 2014. 16. Hospital, A.; Goñi, J. R.; Orozco, M.; Gelpí, J. L.; Adv. Appl. Bioinf. Chem. 2015, 8, 37. 17. Yu, N.; Polycarpou, A. A.; J. Colloid Interface Sci. 2004, 278, 428. 18. Lennard-Jones, J. E.; Proc. Phys. Soc. 1931, 43, 461. 19. Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E.; J. Chem. Theory Comput. 2008, 4, 435. 20. Kittel, C.; Introduction to solid state physics; Wiley: New York, 1976. 21. Griebel, M.; Knapek, S.; Zumbusch, G.; Numerical simulation in molecular dynamics; Springer: Berlin, 2007. 22. Schnabel, T.; Vrabec, J.; Hasse, H.; J. Mol. Liq. 2007, 135, 170. 23. Nikitin, A.; Milchevskiy, Y.; Lyubartsev, A.; J. Phys. Chem. B 2015, 119, 14563. 24. Lorentz, H. A.; Ann. Phys. 1881, 248, 127. 25. Berthelot, D.; Comptes Rendus 1898, 126, 1703. 26. Guvench, O.; MacKerell, A. D.; Methods in Molecular Biology; Humana Press, 2008. 27. Berendsen, H. J. C.; van der Spoel, D.; van Drunen, R.; Comput. Phys. Commun. 1995, 91, 43. 28. Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M. R.; Smith, J. C.; Kasson, P. M.; van der Spoel, D.; Hess, B.; Lindahl, E.; Bioinformatics 2013, 29, 845. 29. Markidis, S.; Laure, E.; Solving Software Challenges for Exascale; Markidis, S.; Laure, E., eds.; Springer International Publishing: Cham, 2015. 30. Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A. E.; Berendsen, H. J. C.; J. Comput. Chem. 2005, 26, 1701. 31. Lindahl, E.; Hess, B.; van der Spoel, D.; J. Mol. Model. 2001, 7, 306. 32. Abraham, M. J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J. C.; Hess, B.; Lindah, E.; SoftwareX 2015, 1-2, 19. 33. Cygan, R. T.; Liang, J. J.; Kalinichev, A. G.; J. Phys. Chem. B 2004, 108, 1255. 34. Pouvreau, M.; Greathouse, J. A.; Cygan, R. T.; Kalinichev, A. G.; J. Phys. Chem. C 2017, 121, 14757. 35. Sosso, G. C.; Tribello, G. A.; Zen, A.; Pedevilla, P.; Michaelides, A.; J. Chem. Phys. 2016, 145, 211927. 36. Abramov, A.; Iglauer, S.; Langmuir 2019, 35, 5746. 37. Berendsen, H. J. C.; Postma, J. P. M.; van Gunsteren, W. F.; Hermans, J.; Intermolecular forces; Springer: New York, 1981. 38. Santos, P. S.; Santos, H. S.; Ciência e tecnologia de argilas; E. Blucher: São Paulo, 1989. 39. Meunier, A.; Clays; Springer-Verlag: Berlin/Heidelberg, 2005. 40. Newnham, R. E.; Brindley, G. W.; Acta Crystallogr. 1956, 9, 759. 41. Sachan, A.; Penumadu, D.; Geotechnical and Geological Engineering 2007, 25, 603. 42. Bish, D. L.; Clays Clay Min. 1993, 41, 738. 43. Abraham, M. J.; Van Der Spoel, D.; Lindahl, E.; Hess, B.; the GROMACS development team, GROMACS User Manual, version 5.0.4, 2014. 44. Zeitler, T. R.; Greathouse, J. A.; Cygan, R. T.; Fredrich, J. T.; Jerauld, G. R.; J. Phys. Chem. C 2017, 121, 22787. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access