JBCS

INTRODUÇÃO

Nanopartículas metálicas apresentam propriedades ópticas que podem ser utilizadas para diferentes aplicações que vão desde a construção de dispositivos de sensoriamento de espécies químicas,^1-3 dispositivos fotovoltaicos,^4-8 até a mediação ou indução de reações químicas de moléculas em superfície.^9-16 O ponto fundamental para qualquer destas aplicações é a excitação de modos coerentes de oscilação dos elétrons de superfície destas nanoestruturas, conhecidos como plasmon de superfície.^17-19 Desta forma, seja qual for a aplicação desejada, é fundamental o entendimento das características ópticas ou espectroscópicas de nanopartículas que suportam a excitação de plasmon de superfície.

Devido a grande versatilidade de aplicações e interdisciplinaridade na área, acreditamos que a melhor maneira de abordar diferentes aspectos do tema é através de uma revisão em duas partes, sendo a primeira o presente artigo, que trata dos aspectos fundamentais da excitação plasmônica, sendo mais centrada nas propriedades dos nanomateriais. Na segunda parte, são tratadas as interações entre moléculas e nanomateriais sob um aspecto mais molecular e baseado em conceitos de química de coordenação, com a apresentação de aplicações em sensoriamento e construção de catalisadores.

Neste sentido, este trabalho de revisão tem como objetivo explorar a espectroscopia de nanopartículas metálicas de diferentes tamanhos, formas, estados de agregação e dispersas em diferentes meios químicos. Daremos ênfase aos efeitos de todas estas variáveis sobre o comprimento de onda da radiação em que se observa a excitação plasmônica. Em paralelo a esta descrição será feita análise dos mecanismos de relaxação do plasmon de superfície, indicando as contribuições que estão relacionadas às diferentes aplicações como sensoriamento ou indução de reações químicas. Além desta análise mecanística, são discutidos efeitos locais da excitação plasmônica: amplificação da temperatura e da intensidade da radiação eletromagnética nas vizinhanças das nanopartículas. Tais efeitos locais estão relacionados a aplicações biomédicas e espectroscópicas, respectivamente. Como exemplificação destes efeitos locais será discutida a intensificação do espectro Raman de moléculas na superfície de nanopartículas (SERS, "surface-enhanced Raman scattering").

Os dois termos abordados neste trabalho, plasmon de superfície e SERS, têm sido explorados em um número cada vez crescente de trabalhos em química presentes na literatura, tanto teóricos como experimentais. No sentido de abordar o tema com um apelo mais fundamental, optou-se neste trabalho por apresentar, majoritariamente, dados provenientes de simulações computacionais, que são baseados em eletrodinâmica clássica.^20,21 Embora esta abordagem numérica seja escolhida aqui, conexões com experimentos serão constantemente apresentadas. Algumas das simulações apresentadas foram realizadas apenas para este trabalho para melhor exemplificar as discussões realizadas. Nestes casos foram utilizados exemplos que estão bem estabelecidos na literatura e que, portanto, encontram excelente acordo com diversas publicações.

PLASMON DE SUPERFÍCIE. UMA ANÁLISE DA ESPECTROSCOPIA ELETRÔNICA DE NANOPARTÍCULAS METÁLICAS

A interação entre radiação eletromagnética na região do ultravioleta-visível (UV-Vis) e nanopartículas metálicas ocorre principalmente através do acoplamento entre os elétrons de valência do metal e o campo elétrico da radiação. Tal interação pode ser caracterizada através de uma polarização da densidade eletrônica da nanopartícula. A Figura 1 apresenta de forma esquemática este processo.

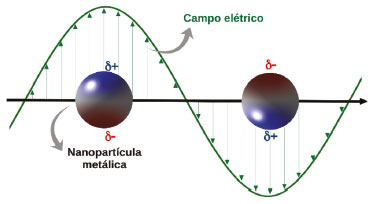Figura 1. Perturbação da densidade eletrônica de uma nanoesfera provocada pela interação com o campo elétrico da radiação excitante. Adaptado com permissão da ref. 22. Copyright 2020 American Chemical Society

Na situação descrita acima, há uma força de restauração (F_rest) entre os íons da rede cristalina do material e os elétrons no sentido de restauração da posição de equilíbrio. Uma vez que o campo elétrico da radiação excitante oscila com o tempo, a perturbação da nuvem eletrônica é periódica, assim como a força de restauração, de tal forma que os elétrons do metal oscilam com a mesma frequência da radiação incidente.

Para uma determinada frequência de excitação, a interação com a densidade eletrônica leva a uma máxima polarização, associada ao movimento coerente dos elétrons de superfície do metal, estado que é conhecido pelo termo plasmon de superfície localizado (as oscilações são confinadas à superfície da nanopartícula, ao contrário do caso de materiais estendidos, em que se observa propagação).^17,18 A excitação ressonante do plasmon de superfície confere diversas características para nanomateriais, principalmente os metálicos. Por exemplo, enquanto dispersões coloidais de nanoesferas de Au de 40 nm de diâmetro em água apresentam coloração avermelhada, dispersões de nanoesferas de Ag com as mesmas dimensões apresentam coloração amarelada.

A frequência da radiação necessária para excitar os modos plasmônicos em um nanomaterial metálico depende de aspectos como composição química (do metal e do meio em que este se encontra), tamanho e forma da nanopartícula.²² Tal dependência pode ser amplamente explorada através de simulações computacionais, como será mostrado neste trabalho com alguns exemplos. Porém, é possível criar um modelo simples para prever qualitativamente as tendências a serem observadas para a frequência de ressonância de plasmon de superfície. Tal modelo assume a lei de Coulomb para representar a força de restauração, que também pode ser descrita pela lei de Hooke (comumente empregada no contexto de espectroscopia vibracional):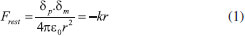

onde δ_p e δ_m são, respectivamente, as densidades de carga positiva e negativa associadas a polarização da nuvem eletrônica devido a excitação plasmônica. é a constante de força associada a restauração, que guarda informações sobre a frequência do processo ressonante: , com m representando a massa do elétron e Ω_plasmon a frequência de ressonância do plasmon de superfície. representa a magnitude de separação entre as densidades de carga positiva e negativa. A Eq. 1 pode, portanto, ser utilizada para investigar as dependências da frequência associada ao plasmon de superfície para diferentes nanomateriais:

A Eq. 2 indica uma dependência qualitativa da frequência de ressonância do plasmon de superfície com a polarização no material devido ao campo elétrico da radiação, representada pelas densidades de carga. Além disso, nota-se uma dependência com aspectos geométricos (r) da nanopartícula, os quais definem a magnitude de separação de cargas.

Uma maneira de se caracterizar a frequência de ressonância do plasmon de superfície é através de medidas de espectroscopia eletrônica, utilizando radiação excitante na região do UV-Vis, por exemplo. Neste caso, a análise de nanopartículas metálicas suspensas em um solvente envolve a atenuação da intensidade do feixe de luz em função do comprimento de onda incidente. Dois principais motivos podem ser utilizados como argumentação para esta afirmação:

i) cargas aceleradas (elétrons) levam ao espalhamento de radiação, processo que ocorre em todas as direções, ou seja, parte da radiação incidente é espalhada pela nanopartícula, indicando diminuição da intensidade inicial do feixe ao longo da direção de propagação;

ii) a nanopartícula pode absorver energia. Neste caso não há radiação eletromagnética sendo emitida em todas as direções do espaço, e consequentemente ocorre diminuição da intensidade da radiação ao longo da direção de propagação. Um exemplo de processo de absorção é a excitação de transições eletrônicas interbandas no metal.^17,18

Estes dois processos, absorção e espalhamento (cuja soma é conhecida como extinção), definem as características espectrais de nanopartículas metálicas e podem ocorrer em uma ampla faixa do espectro UV-Vis. Como será discutido a seguir, a excitação plasmônica leva tanto a absorção quanto ao espalhamento de radiação e, portanto, as medidas de espectros de extinção na região do UV-Vis são ferramentas essenciais na caracterização da sua frequência de ressonância.

A ocorrência do espalhamento de radiação é uma via de relaxação do plasmon de superfície.¹⁸ Neste caso, diz-se que a relaxação é radiativa. Por outro lado, o plasmon de superfície pode relaxar por via não-radiativa, ou seja, sem liberação de fótons. Neste caso, diremos que a radiação foi absorvida. Uma maneira de ocorrer tal relaxação é através da transferência ressonante de energia (plasmon) para excitações entre níveis eletrônicos do metal.^23-29

A medida dos processos de absorção, espalhamento e extinção nas simulações é feita através do cálculo de suas seções de choque, que são medidas relacionadas a probabilidade de ocorrência do fenômeno. Por exemplo, a seção de choque de espalhamento é calculada a partir da relação entre a potência da luz espalhada e a intensidade da luz incidente e tem unidade SI de m².¹⁸ Estas simulações são altamente eficientes em descrever as respostas ópticas de nanopartículas metálicas. Um exemplo bastante interessante é o trabalho de Amendola e Meneghetti, resumido na Figura 2, que apresenta comparações entre espectros de extinção experimental (linha preta) de nanoesferas de Au (AuNSs) em água e obtido por simulações computacionais.³⁰ Neste exemplo observa-se excelente ajuste entre os dados experimentais e de simulação quando os autores consideram dispersão de tamanhos nas nanopartículas (inserto, linha vermelha), cuja distribuição apresenta elevada concordância com aquela obtida por microscopia eletrônica (histograma). A Figura 2 sugere a possibilidade de se utilizar estas simulações como ferramentas para investigar a resposta plasmônica de nanopartículas, bem como avaliar efeitos geométricos como tamanho e forma, que são apresentados mais adiante neste trabalho.

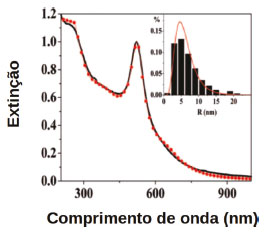Figura 2. Comparação entre espectros de extinção de nanoesferas de Au experimental (linha preta) e obtido por simulações computacionais baseadas em eletrodinâmica clássica (vermelho). A correlação com o dado experimental é feita através da inclusão de dispersão de tamanhos (inserto, vermelho), que descreve muito bem as distribuições de tamanhos das nanopartículas (histograma preto) nos experimentos obtidas por análises de microscopia eletrônica. Reproduzido e adaptado com permissão da ref. 30. Copyright 2020 American Chemical Society

As simulações por eletrodinâmica clássica são baseadas na resolução das equações de Maxwell sujeitas a condições de contorno.^19-21,31 Para este objetivo, existem diferentes metodologias que podem ser do tipo analítica ou numérica. Para o caso de nanopartículas esféricas estas equações apresentam solução exata, conhecida como teoria de Mie.^19-21,31 Para outras geometrias as soluções são numéricas e podem ser obtidas por diferentes métodos de resolução, como o FDTD ("finite-difference time-domain"),^18-21 DDA ("discrete dipole approximation"),^20,32-34 FEM ("finite element method")^20,35 ou BEM ("boundary element method"),^36,37 para citar alguns. Em todos os casos são investigados os efeitos da incidência de um campo eletromagnético sobre um objeto de determinada forma, tamanho e composição química. O campo elétrico (E) incidente provoca uma polarização da densidade eletrônica do objeto, que pode ser descrita por:^18,19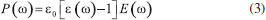

onde ε₀ é a permissividade elétrica no vácuo e ε(Ω) = n(Ω)² é a função dielétrica do metal (equivalente ao índice de refração ao quadrado), parâmetro que é utilizado para caracterizar as respostas ópticas dos elétrons nos diferentes materiais. Para o caso de metais, esta resposta é basicamente devido aos elétrons de valência e pode ser computada de forma aproximada pelo modelo clássico de Drude, onde se considera um gás de elétrons com movimento amortecido pela interação com a rede de íons positivos.^18,19,38 Este efeito de amortecimento na resposta aparece na parte imaginária da função dielétrica. A Figura 3 apresenta a parte real (A) e imaginária (C), considerando o modelo de Drude para alguns metais, mostrando que a função dielétrica apresenta alta dependência com o comprimento de onda da radiação incidente.

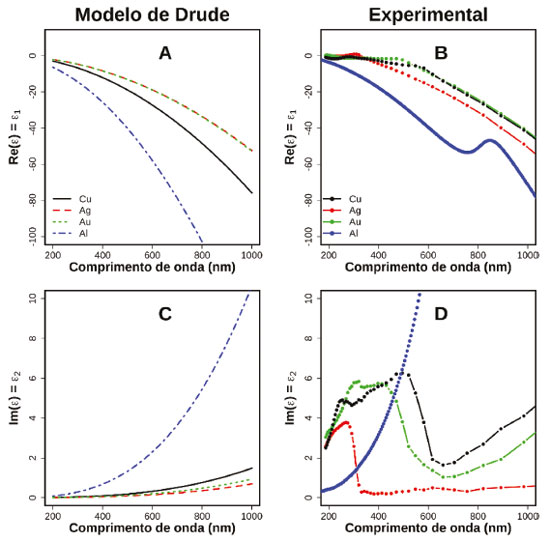Figura 3. Comparação entre modelo de Drude e dados experimentais para as partes real (A e B) e imaginária (C e D) da função dielétrica de Cu (preto), Ag (vermelho), Au (verde) e Al (azul). O resultado do modelo de Drude considera parâmetros como densidade de elétrons e tempo médio de colisão, que são tabelados.³⁸ Os dados experimentais para Au, Ag e Cu foram extraídas da compilação de Johnson e Christy, enquanto os dados de Al foram obtidos do trabalho de McPeak et al.³⁹ Funções dielétricas de diferentes materiais podem ser consultados na referência 40

Na Figura 3 também são apresentadas as partes real e imaginária medidas experimentalmente para os metais selecionados. Existe um bom acordo qualitativo entre o dado experimental e o modelo de Drude, principalmente para a parte real, indicando que a resposta (polarização) de nanopartículas metálicas na região do visível pode ser bem descrita classicamente, motivo para o sucesso dos métodos clássicos de simulação indicados acima. A grande diferença entre os dados experimentais e os do modelo de Drude está na parte imaginária, principalmente para Au e Cu, que apresenta grande contribuição na região abaixo de 600 nm, proveniente de transições interbandas nestes metais.^18,19,38 A presença destas transições afeta a resposta plasmônica destes materiais, como será discutido neste trabalho e, portanto, devem ser consideradas nas simulações computacionais, como aquelas apresentadas na Figura 2. Na maioria dos casos apresentados na literatura e também neste trabalho, as simulações são realizadas utilizando dados experimentais para a função dielétrica.

Uma aproximação comumente empregada para a obtenção do espectro de extinção de nanopartículas é a chamada aproximação quasi-estática,^20,41-43 válida para partículas esféricas de dimensões muito menores que o comprimento de onda da radiação excitante. Para este caso, a seção de choque de extinção pode ser escrita como:²²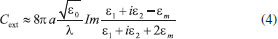

sendo a o raio da nanopartícula, λ o comprimento de onda da radiação e ε_m a função dielétrica do meio em que a partícula está dispersa. ε₁ e ε₂ representam a parte real e imaginária da função dielétrica do metal, respectivamente. Im representa parte imaginária da função que o sucede.

A parte real da função dielétrica está relacionada à capacidade de polarização da nuvem eletrônica do metal pela radiação incidente (tanto maior quanto mais negativo ε₁), enquanto ε₂ mede a contribuição de processos contrários ao movimento dos elétrons frente ao campo, tais como espalhamento elétron-elétron, interações elétron-rede cristalina e transições interbandas.^18,31 De modo geral, pode-se considerar que quanto maior o valor de ε₂, maior é o amortecimento do plasmon de superfície.

Uma importante característica da Eq. 4 é a possibilidade de verificar diretamente a dependência do espectro de extinção com a composição química da nanopartícula, bem como do meio em que a mesma se encontra. Em particular, nota-se que a seção de choque de extinção atinge valores mais elevados quando:

As expressões acima definem a chamada condição de ressonância para o plasmon de superfície na aproximação quasi-estática e serão utilizadas nas discussões a seguir em conjunto com o modelo mais simples (porém mais geral) da Eq. 2.

Dependência do plasmon de superfície com a composição química da nanopartícula e do meio

A Figura 4A reproduz os valores da parte real da função dielétrica de diferentes metais em função do comprimento de onda da radiação eletromagnética. Na figura também é apresentado o valor da função dielétrica da água (assumida aqui como constante e igual a 1,77⁴⁴) multiplicada por -2 (linha tracejada). Para o caso de nanopartículas suspensas em água, a Eq. 5 sugere que a ressonância plasmônica deve ocorrer em comprimentos de onda que satisfazem ε₁ = -2ε_água. Se para estes comprimentos de onda a parte imaginária da função dielétrica destes metais assume valores pequenos (Eq. 6, situação de pouco amortecimento), deve-se observar alta extinção de radiação devido ao plasmon. Na Figura 4B a parte imaginária da função dielétrica é apresentada para os diferentes metais em comprimentos de onda selecionados.

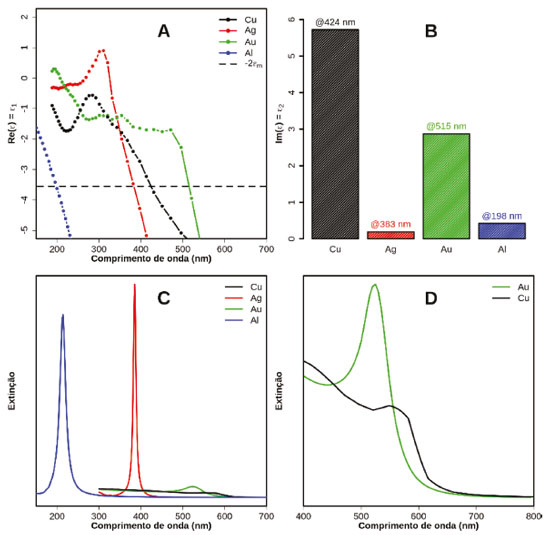Figura 4. (A) Parte real da função dielétrica de alguns metais selecionados. A linha tracejada horizontal representa a condição imposta pela Eq. 5 considerando-se água como ambiente químico em torno da nanopartícula (constante dielétrica igual a 1,77⁴⁴). (B) Valores da parte imaginária da constante dielétrica nos comprimentos de onda em que a Eq. 5 é respeitada. (C) Espectros de extinção simulados para nanoesferas de 10 nm de diâmetro para metais selecionados. (D) Ampliação dos espectros de extinção para as nanoesferas de Au e Cu

A condição de ressonância descrita por Eq.5 e Eq.6 é observada para nanoesferas de Ag e Al de 10 nm de diâmetro, cujos espectros de extinção (Figura 5C) apresentam bandas centradas em comprimentos de onda para os quais ε₁ = -2ε_água. Note que a frequência de ressonância de plasmon de superfície para o Al é maior que para a Ag. Apesar de numericamente consistente com as observações, este modelo torna difícil a interpretação física para este resultado, o que pode ser feito mais facilmente no contexto da Eq. 2: Al apresenta maior capacidade de polarização de sua nuvem eletrônica do que Ag em toda a região espectral analisada, como evidenciado pelos valores mais negativos de . Isto ocorre devido a maior densidade de elétrons livres no Al que na Ag.³⁸ Esta maior polarização leva a uma maior força de restauração e, portanto, maior frequência associada ao movimento dos elétrons.

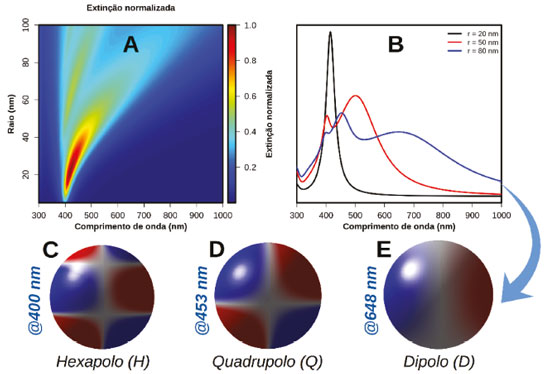Figura 5. (A) Espectros de extinção simulados de nanoesferas de Ag de diferentes tamanhos. Os valores das seções de choque de extinção foram normalizados pelo valor de máximo na sequência de espectros. (B) Apresentação em detalhe dos espectros para nanoesferas de Ag de raio 20, 50 e 80 nm. A nanopartícula de raio 80 nm apresenta três bandas plasmônicas, para as quais as densidades de carga na ressonância estão apresentadas em (C), (D) e (E)

No caso de Au e Cu, nos comprimentos de onda em que a condição ε₁ = -2ε_água é satisfeita, a parte imaginária (Figura 4B) apresenta valores consideravelmente maiores que os observados para Ag e Al, principalmente devido à existência de transições interbandas nestes metais.^17-19,31 Este maior amortecimento à dinâmica de movimentação dos elétrons acaba modificando a condição de ressonância nestes metais. Com isto, podem ser observados dois efeitos importantes nos espectros de extinção de Au e Cu em relação aos outros metais:

a) A ressonância é observada em comprimentos de onda maiores que os previstos pela relação ε₁ = -2ε_água, especialmente para o caso do Cu.

b) Como a parte imaginária da função dielétrica é maior, a ressonância plasmônica é altamente amortecida nestes metais, i.e., a relaxação é mais rápida, o que leva a uma maior largura de banda e menor intensidade nos espectros de extinção.^31,45-49

A análise acima pode levar a uma interpretação inicial de que Al e Ag são metais muito mais apropriados que Au e Cu para aplicações baseadas na excitação do plasmon de superfície. Porém, há de se considerar que os espectros de extinção da Figura 5 foram simulados para nanopartículas esféricas pequenas (em relação ao comprimento de onda da radiação incidente). Como será discutido neste trabalho, a ressonância plasmônica é dependente da forma e do tamanho das nanopartículas. Para comprimentos de onda maiores, a parte imaginária das funções dielétricas de Au e Cu ficam mais próximas daquela para Ag¹⁸ e, portanto, nestes casos deve-se esperar uma melhor resposta plasmônica para aqueles metais. Além disso, devemos considerar que, além das propriedades ópticas, um fator importante para aplicação de nanomateriais plasmônicos é a síntese das nanopartículas com forma e tamanho controlados.^50,51 A estabilidade química do Au (e em menor grau da Ag) permite uma maior facilidade na produção de materiais para diversas aplicações. Isto faz com que Ag e Au estejam entre os sistemas plasmônicos mais investigados e, por este motivo, serão os metais citados neste trabalho. Há de se destacar, porém, exemplos de investigações experimentais das propriedades plasmônicas de metais como Al.^52-54

Uma aplicação imediata da aproximação quasi-estática é a possibilidade de avaliar a dependência da ressonância plasmônica com a mudança do meio em que a nanopartícula se encontra. Neste caso, a mudança do ambiente químico leva a uma alteração no comprimento de onda em que a condição ε₁ = -2ε_m é obedecida. A dependência da função dielétrica com o comprimento de onda apresentada na Figura 4A indica que o aumento da constante dielétrica do meio (aumento do índice de refração) leva a um deslocamento da condição de ressonância para maiores comprimentos de onda. Esta dependência indica, por exemplo, que a ressonância plasmônica é sensível às modificações químicas na superfície das nanopartículas devido a adsorção de moléculas. Esta característica permite a construção de dispositivos de sensoriamento altamente sensíveis e com elevada especificidade. Por exemplo, é possível desenvolver sensores de uma certa proteína que interage especificamente a um ligante ancorado nas nanopartículas. Em trabalho de revisão recente, Santos et al.¹ apresentaram diversas plataformas para uma importante aplicação envolvendo nanomateriais plasmônicos: o sensoriamento de espécies de interesse bioquímico.^2-3,53-57

Efeito do tamanho

As discussões acima levaram em consideração partículas com dimensões muito menores que o comprimento de onda da radiação eletromagnética na região UV-Vis. Porém, comumente são empregadas nas diversas aplicações nanopartículas com formas e tamanhos variados. A Figura 5A apresenta espectros de extinção para nanoesferas de Ag com tamanhos variados. A escala de cores nesta figura indica os valores da seção de choque de extinção (apresentada, por simplificação, em escala normalizada pelo valor de máximo no conjunto de dados). O aumento do tamanho da nanopartícula leva a um deslocamento da condição de ressonância para comprimentos de onda maiores. Este resultado observado nas simulações pode ser interpretado no contexto da Eq. 2, em que o aumento nas dimensões da nanopartícula (r) leva a uma menor força de restauração e, consequentemente a uma menor frequência (maior comprimento de onda) de ressonância. Além do deslocamento da banda plasmônica com o aumento das dimensões das nanopartículas, também pode ser observado um alargamento a meia altura, como indicado na Figura 5B, que apresenta três espectros extraídos da Figura 5A. A largura da banda de uma ressonância está associada ao tempo de vida do plasmon de superfície. Quanto menor o tempo de vida, ou seja, quanto mais rápida a relaxação plasmônica, maior a largura de banda.^19,46 A observação acima, portanto, indica que o aumento do tamanho das nanopartículas acelera a relaxação do plasmon de superfície. Como discutido anteriormente, as possibilidades de relaxação são por absorção e espalhamento de radiação. O aumento no tamanho das nanopartículas leva a um aumento mais expressivo da contribuição via espalhamento de radiação, o que é conhecido pelo termo em inglês "radiative damping".^{17,18,27,31,45-49} Esta análise é discutida na próxima sub-seção (Extinção, espalhamento e absorção).

Outro fato interessante da dependência dos espectros de extinção com o tamanho é a observação de múltiplas ressonâncias para o caso de nanopartículas maiores. A Figura 5B permite observar 3 bandas para o caso de nanoesferas de 80 nm de raio em comprimentos de onda 400, 453 e 648 nm. Estas bandas estão relacionadas a diferentes modos plasmônicos na nanopartícula. Nas Figuras 5C, 5D e 5E são apresentadas as densidades de carga na superfície desta nanoesfera para cada um destes comprimentos de onda de ressonância. Nesta representação, a escala de cores indica densidades de carga negativa (vermelho) e positiva (azul), o que é bastante útil para a atribuição dos modos plasmônicos. São observadas distribuições de carga do tipo dipolar (D, 648 nm), quadrupolar (Q, 453 nm) e hexapolar (H, 400 nm), que apresentam progressivamente menor separação entre as densidades de carga. Destas distribuições, a dipolar é a menos energética e a única observada para nanopartículas menores, como as de raio 20 nm. Os dados de simulação mostram que quanto maior a ordem do multipolo, maior a frequência de ressonância do plasmon de superfície, fato que está associado à menor separação de cargas nestes modos (r na Eq. 2). Em Au e Cu, devido a grande contribuição de transições interbandas na região de maior energia na região UV-Vis, modos de maior ordem como Q e H são dificilmente observados (mais detalhes apresentados a seguir).

Extinção, espalhamento e absorção

Nesta seção será discutida a composição do espectro de extinção de nanopartículas em termos de espalhamento e absorção. Embora estes parâmetros possam ser obtidos diretamente das simulações computacionais, existe também a possibilidade de extrair tais informações experimentalmente. Por exemplo, os espectros de espalhamento e de extinção de nanopartículas podem ser obtidos utilizando espectroscopia de campo escuro ("dark-field").^35,58-65 Neste tipo de medida, um arranjo óptico de lentes e condensadoras permitem, por exemplo, a detecção apenas da luz espalhada pelas nanopartículas.⁶⁶ Diferenças entre a intensidade de extinção e espalhamento, por fim, permitem a obtenção do espectro de absorção.

A Figura 6 apresenta as componentes de absorção e espalhamento nos espectros de extinção de nanopartículas de Ag (A e C) e Au (B e D) de diferentes tamanhos.

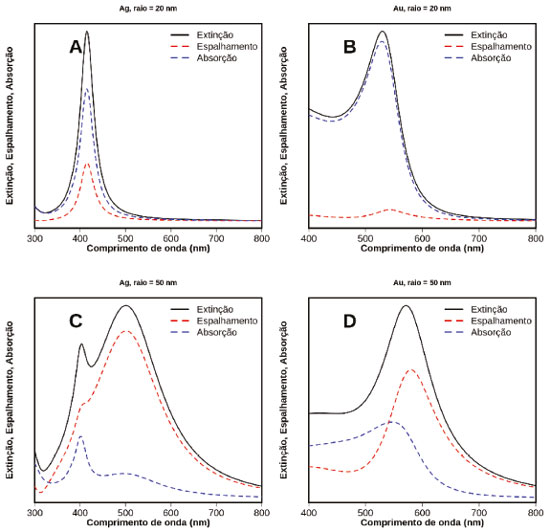Figura 6. Espectros de extinção (preto, linha cheia), absorção (azul, tracejado) e espalhamento (vermelho, tracejado) para nanoesferas de Ag (A e C) e Au (B e D) de 20 nm e 50 nm de raio

Os exemplos selecionados mostram que, independentemente do metal, nanopartículas pequenas (por exemplo, 20 nm de raio) têm como principal contribuição para a extinção de radiação o fenômeno de absorção. Isto significa que a principal via de relaxação do plasmon de superfície é não-radiativa. Situação contrária é observada para o caso de nanopartículas maiores, em que há uma maior contribuição devido a relaxação radiativa, isto é, com espalhamento de radiação. De forma semelhante, observa-se que em materiais que suportam a excitação de modos multipolares, há um domínio da via não-radiativa para modos de maior ordem (quadrupolo, hexapolo, etc.), como pode ser observado na Figura 6C.

Os casos de nanoesfera de Au nas Figuras 6B e 6D merecem destaque. Em primeiro lugar, não se observam os modos multipolares nestes sistemas como no caso da Ag. Isto ocorre devido ao grande amortecimento provocado pelas transições eletrônicas interbandas no Au. Além disso, observa-se uma assimetria no perfil observado para o espectro de espalhamento, cuja origem também está associada ao efeito de transições interbandas. A presença de tais transições acaba diminuindo a eficiência de espalhamento de radiação em menores comprimentos de onda. O efeito deste amortecimento inclusive desloca o comprimento de onda em que é observado o máximo de espalhamento nos dois casos (Figuras 6B e 6D).⁶⁷

A análise espectroscópica acima tem grande relevância pois define as diferentes aplicações destes materiais. A radiação espalhada por nanomateriais pode ser utilizada, por exemplo, como sonda da presença de moléculas sobre a superfície das nanopartículas. Neste caso, o perfil de espalhamento (ressonância) será dependente da natureza e concentração das espécies adsorvidas. Além disso, análise de espectros de espalhamento permite investigar interações envolvendo as nanopartículas que não são facilmente detectadas na análise de espectros de extinção. Por exemplo, a excitação de plasmon de superfície pode levar a interferências destrutivas envolvendo o acoplamento entre modos plasmônicos, conhecidas como ressonâncias de Fano, discutida mais adiante.^68-76 Nordlander et al. demonstraram que a existência destas interferências destrutivas em nanocubos de Ag podem ser excelentes estratégias para a construção de sensores químicos altamente sensíveis.⁷⁶

As perdas por absorção, por outro lado, estão atualmente sendo amplamente investigadas em aplicações envolvendo reações químicas mediadas por plasmon ("plasmon mediated chemical reactions", PMCRs).^{12,16,19,71,72} Neste caso, acredita-se que a própria relaxação não-radiativa pode levar a transferência de elétrons (ou buracos) para moléculas adsorvidas na superfície da nanopartícula, induzindo reações químicas.^9-16

A transferência de energia associada ao plasmon para elétrons próximos ao nível de Fermi cria uma maior distribuição de pares elétron-buraco com energias acima da condição de equilíbrio e, por isto, são chamados pelo termo em inglês "hot carriers" (HCs).^23,25,54 Com o avanço da relaxação, há uma termalização dos elétrons através de colisões elétron-elétron e também elétron-fônon, que culmina no aumento da temperatura da rede cristalina e, consequentemente, transferência de calor para a vizinhança (aumento local de temperatura).^77-83

Baffou et al. investigaram o processo de conversão térmica de energia e o aumento da temperatura local em torno das nanopartículas,^80,81,84-86 o que permite aplicações particularmente interessantes em fototermia, em que a nanopartícula, quando adsorvida em um tecido celular cancerígeno, pode levar à morte celular devido ao aquecimento local após iluminação, contribuindo para a destruição de tumores.⁸⁷ Neste sentido, alguns autores investigaram a eficiência para conversão térmica da energia associada ao plasmon de superfície para diferentes formas de nanopartículas, como nanobastões.⁸⁸

Além das aplicações em fototermia, pode-se argumentar que o aumento da temperatura também é um fator importante para favorecer o aumento da velocidade de reações químicas na superfície de nanopartículas.^77,82,89,90 Contudo, mais recentemente, atenção especial tem sido dada para a investigação do efeito dos HCs para induzir ou mediar reações químicas via transferência de carga. Há indícios experimentais e teóricos que sugerem grande envolvimento de HCs nestes processos químicos de superfície.^15,16,25,91 Neste caso, HCs podem ser transferidos para moléculas adsorvidas antes mesmo da relaxação térmica na nanopartícula. Há diferentes evidências que apontam para reações redox de moléculas adsorvidas nas nanopartículas metálicas, que dão suporte para estas interpretações. Um exemplo clássico é a dimerização via oxidação do 4-aminobenzenotiol (4-ABT) induzida pela excitação do plasmon de superfície, a qual pode ser acompanhada pelas mudanças nos espectros vibracionais das moléculas adsorvidas.⁹

A investigação do principal mecanismo associado a reações químicas na superfície de nanopartículas (térmico ou transferência de HCs) ainda é tema de debate, mas sem dúvida, o conhecimento das principais vias de relaxação em uma determinada nanoestrutura é ponto fundamental para qualquer argumentação.

As propriedades discutidas acima são comumente chamadas de propriedades de campo distante, pois estão associadas a medidas da radiação espalhada e detectada distante da nanopartícula.¹⁸ Como será mostrado neste trabalho, a excitação plasmônica também leva a propriedades locais que podem ser sondadas utilizando moléculas adsorvidas na superfície. Uma destas propriedades locais já foi discutida, que é o aumento da temperatura em torno das nanopartículas. Outra propriedade local é o aumento de campo elétrico nas vizinhanças das nanopartículas, o que pode ser usado para a amplificação de processos espectroscópicos de moléculas em superfície, como é o caso do efeito SERS. A obtenção de espectros SERS pode ser utilizada, por exemplo, para a construção de sensores altamente eficientes. Além disso, as evoluções espectrais no SERS podem ser utilizadas para avaliar a evolução de PMCRs.

A concentração local de campo elétrico também está relacionada a amplificação de propriedades catalíticas de semicondutores, como por exemplo TiO₂, em sistemas híbridos de semicondutores/nanopartículas.^92-95 Nestes sistemas, o aumento da intensidade local da luz na superfície dos semicondutores permite um aumento na taxa de geração de pares elétron-buraco no semicondutor e consequente aumento das propriedades catalíticas do mesmo.

Efeito da forma das nanopartículas

As discussões feitas acima foram todas focadas na geometria esférica. Além da dependência com o tamanho das nanopartículas, há também forte dependência da ressonância plasmônica com a forma. Existe um elevado número de metodologias sintéticas que permitem obtenção de nanopartículas com diferentes morfologias com respostas plasmônicas diferenciadas.^96-100 Neste sentido podem ser citadas as geometrias de nanobastões,^{50,88,101,102} nanodiscos,^54,103,104 nanoprismas,^46,105,106 bipirâmides,^107-109 nanocubos,^76,110-115 nanopartículas na forma de nanocamadas ("nanoshells"),^116-119 nanopartículas caroço@casca envolvendo diferentes metais,^120-123 etc. A revisão destas formas é por si um trabalho de revisão, que deve passar por um grande número de trabalhos altamente relevantes como os já citados. Com o objetivo de se fazer uma descrição mais geral da espectroscopia de nanopartículas em termos dos diferentes modos (dipolo, quadrupolo, etc.) e modulação espectral das ressonâncias, neste trabalho serão discutidas apenas algumas das estruturas mais simples, como nanobastões, nanoprismas e nanocubos. Esta abordagem é utilizada apenas com caráter de indicar alguns dos efeitos da forma sobre os modos plasmônicos discutidos para as nanoesferas.

Nanobastões

Na Figura 7 são apresentados espectros de extinção simulados pelo método BEM para nanobastões de Au (AuNRs). A escolha do metal se deve ao fato de que a maior parte das sínteses deste tipo de estrutura são para Au. AuNRs são comumente empregados em diferentes aplicações relacionadas às suas propriedades ópticas. A geometria desta estrutura permite a excitação de dois modos plasmônicos associados à excitação ao longo e perpendicular ao eixo principal do bastão (direção do comprimento L do bastão), os quais são usualmente chamados de longitudinal e transversal, respectivamente.

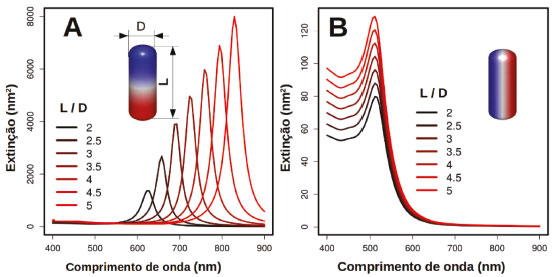Figura 7. (A e B) Espectros de nanobastões de Au (AuNRs) de diferentes razões de aspecto (L/D) que variam de 2 a 5, conforme as cores nas figuras. Em todos os casos D =10 nm. Em (A) a polarização do campo elétrico da radiação incidente é paralela ao eixo principal (direção do comprimento L na figura) do nanobastão, enquanto em (B) é perpendicular. Nas figuras são apresentadas as distribuições de carga calculadas nos comprimentos de onda associados aos modos plasmônicos

Os espectros apresentados nas Figuras 7A e 7B foram obtidos através de excitação com campo elétrico da radiação excitante paralelo e perpendicular ao eixo principal dos AuNRs, respectivamente. As diferentes cores nas figuras correspondem aos resultados para bastões de diferentes razões de aspecto (relação entre comprimento e largura). A ausência de modos quadrupolares nos espectros na Figura 7 está principalmente relacionada ao fato do metal considerado ser Au. Nota-se nas figuras que o modo transversal apresenta comprimentos de onda de ressonância menores do que aqueles associados ao modo longitudinal, o que está diretamente associado à menor dimensão da estrutura nesta direção. Além disso, observa-se dependência com a razão de aspecto (L/D) dos AuNRs, principalmente para o modo longitudinal, com elevado caráter modular da ressonância plasmônica para este tipo de estrutura.

Nanoprismas

Na Figura 8A são apresentados espectros de extinção simulados pelo método DDA para AgNTs com diferentes estruturas criadas pelo corte das pontas ("snip" como chamados pelos autores).²² Em sínteses desta morfologia, misturas destas estruturas podem ser obtidas e, portanto, é fundamental avaliar os efeitos deste tipo de alteração sobre os espectros de extinção.

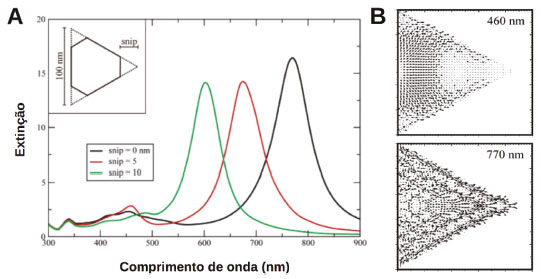Figura 8. (A) Espectros de extinção simulados pelo método DDA para nanoprismas triangulares de Ag com diferentes estruturas criadas pelo corte das pontas ("snip"). (B) Distribuições dos momentos de dipolo para os modos em 460 e 770 nm na estrutura sem corte. Reproduzido e adaptado com permissão da ref. 22. Copyright 2020 American Chemical Society

A Figura 8B faz uma representação gráfica da polarização na nanopartícula para o caso da estrutura sem corte (linha preta na Figura 8A) nos comprimentos de onda 770 e 460 nm, que revelam modos do tipo dipolar e quadrupolar, respectivamente. A observação de modos de maior ordem neste tipo de estrutura está relacionada ao tamanho (100 nm) e à composição química (Ag). Fato interessante dos resultados apresentados é a alta variação do comprimento de ressonância, sobretudo para o modo dipolar, com a alteração na estrutura dos AgNTs. Veja, por exemplo, que um corte de apenas 5 nm em uma estrutura de 100 nm leva alterações espectrais significativas. Portanto, em sínteses deste tipo de estrutura, a dispersão de estruturas e tamanhos pode levar a observação de espectros experimentais com ressonâncias altamente alargadas. Grasseschi et al. investigaram por microscopia hiperespectral os espectros de espalhamento deste tipo de estrutura e análises de deconvolução espectral permitiram a identificação de populações distintas de nanopartículas, contendo contribuições nos espectros de prismas triangulares e hexagonais com as pontas cortadas.^124,125

Nanocubos

A Figura 9 apresenta outro exemplo do efeito da forma sobre os espectros de nanopartículas metálicas. Os resultados reportados por Pellarin et al. são de simulações dos espectros de extinção, absorção e espalhamento para nanocubos de Ag (AgNCs) de 50 nm.¹¹⁵

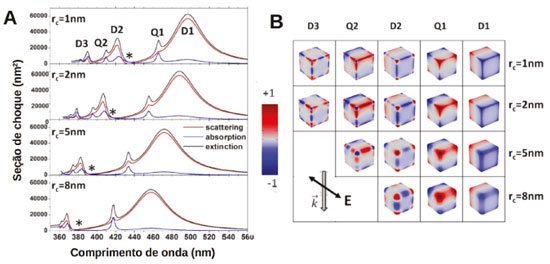Figura 9. (A) Espectros de extinção (preto), absorção (azul) e espalhamento (vermelho) simulados pelo método FEM para AgNCs de 50 nm com diferentes graus de arredondamento introduzidos pela substituição das arestas e vértices por cilindros e esferas de raio r_c. (B) Distribuições de carga para os modos observados para os AgNCs. Reproduzido e adaptado com permissão da ref. 115. Copyright 2020 American Chemical Society

Os dados apresentados na Figura 9 são para AgNCs com diferentes estruturas relacionadas ao grau de arredondamento das arestas e vértices. Estas estruturas são geradas a partir do nanocubo perfeito através da substituição dos vértices e arestas por esferas e cilindros com raio r_c. Para o AgNC com r_c de 1 nm, são observados mais modos que no caso de esferas de mesmo tamanho. A Figura 9B apresenta as distribuições de carga para os modos observados nos espectros. Os modos descritos por D1, D2 e D3 são atribuídos a modos do tipo dipolar, enquanto os modos Q1 e Q2 apresentam distribuição antissimétrica de cargas associadas a distribuições do tipo quadrupolares. Estas características destacam os nanocubos das nanoesferas que apresentam apenas um modo dipolar e um quadrupolar. O grau de arredondamento dos AgNCs altera profundamente os comprimentos de onda de ressonância. Os espectros de AgNCs mais arredondados se aproximam mais daqueles observados para AgNSs.

Os exemplos de efeito de forma sobre a resposta plasmônica de nanopartículas apresentados acima indicam a possibilidade de se efetuar um ajuste fino da ressonância plasmônica com a alteração de aspectos geométricos das nanopartículas, como, por exemplo, a razão de aspectos de nanobastões ou o controle sobre o grau de arredondamento de nanocubos. Este ajuste fino pressupõe um controle sobre a forma (e tamanho) de nanopartículas sintetizadas para uma determinada aplicação, o que é uma grande barreira experimental, já que diversos fatores podem levar a caminhos reacionais diferentes na síntese, tais como tipo de redutor e estabilizante utilizados, a velocidade de adição de reagentes e a temperatura reacional, para citar alguns. Recentemente, Xia et al.⁵¹ apresentaram uma perspectiva a respeito destes efeitos visando maior controle sobre forma e tamanho de nanopartículas.

Acoplamento entre nanopartículas metálicas

Além das características associadas as ressonâncias para nanopartículas individuais descritas acima, interações entre nanopartículas são fundamentais para aplicações envolvendo nanomateriais plasmônicos. Por simplicidade descreveremos tais interações para o caso de dímeros de nanoesferas de Ag. As ideias desenvolvidas podem ser transferidas para sistemas com maior número de partículas bem como contendo estruturas de formas diferentes da esférica.

A Figura 10 apresenta os espectros de extinção em função da distância de separação (g) entre as superfícies de nanoesferas de Ag de 25 nm de raio para duas polarizações da radiação excitante: paralela (Figura 10B) e perpendicular (Figura 10C) ao eixo que conecta as partículas, conforme indica o esquema da Figura 10A. Os perfis espectrais observados para grandes valores de g (por exemplo, g = 50 nm) são muito próximos aos de nanopartículas individuais, independente da polarização da radiação incidente, indicando que a excitação plasmônica de uma partícula tem pouca influência de partículas vizinhas mais distantes. Para polarização paralela ao eixo de separação interpartículas, observa-se que a diminuição da distância de separação leva a um deslocamento da banda plasmônica para maiores comprimentos de onda. Além disso, em pequenas separações pode ser observado um conjunto maior de bandas no espectro. Contudo, para polarização perpendicular ao eixo interpartículas, não são observadas diferenças expressivas com relação ao espectro de extinção de nanoesferas individuais, mostrando que nesta configuração de iluminação a ressonância de uma nanopartícula não é afetada de forma significativa pela presença da nanopartícula vizinha.

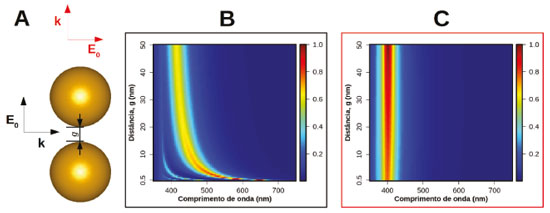Figura 10. A) Modelo para sondar o acoplamento óptico entre nanoesferas de Ag. As diferentes configurações neste sistema modelo são descritas pela separação entre superfícies das nanopartículas, g, e direção do campo elétrico relativo ao eixo de separação interpartículas. B) e C) apresentam os espectros de extinção para diferentes espaçamentos g para campo elétrico incidente paralelo e perpendicular, respectivamente, ao eixo que conecta as das partículas

No caso de nanobastões alinhados de forma paralela entre si, esta última geometria de iluminação permite observar deslocamentos das bandas plasmônicas para menores comprimentos de onda, devido a interferências eletromagnéticas.^68,127 Um exemplo é apresentado na Figura 11, que apresenta imagens de microscopia eletrônica (A) e de campo escuro (B) de uma amostra de nanobastões de Au depositados sobre Si.¹²⁶ Os espectros de espalhamento na Figura 11A mostram diferentes perfis espectrais relacionados com diferentes geometrias de interação entre os nanobastões, como indicado nas Figuras 11D-11G.

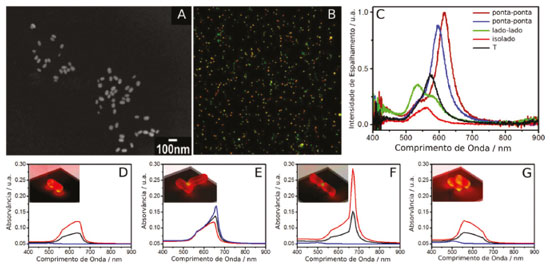Figura 11. Caracterização morfológica e óptica de nanobastões de ouro. (A) Imagem de microscopia eletrônica de varredura. (B) Imagem de microscopia óptica de campo escuro. (C) Espectros de espalhamento Rayleigh de nanobastões de ouro em pontos contendo dímeros com diferentes orientações. (D-G) Espectros teóricos calculados para um único nanobastão e dímeros com diferentes orientações conforme mostrado nas figuras em destaque. A absorvância média (curva preta) e para um campo elétrico perpendicular (curva azul) e paralelo (curva vermelha) são mostradas. Reproduzida com permissão da ref. 126. Copyright 2020 American Chemical Society

As alterações espectrais observadas na Figura 10B podem ser entendidas de forma semelhante ao formalismo de orbitais moleculares, em que as funções de onda que descrevem a dinâmica eletrônica (plasmon) podem interferir em fase (formando um estado ligante) ou fora de fase (formando um estado antiligante). Esta ideia (comumente chamada pelo termo inglês "plasmon hybridization") está representada de forma esquemática na Figura 12A para o caso do acoplamento entre os modos dipolares de duas nanoesferas quando a polarização é paralela ao eixo de separação entre as partículas (Figura 10B). Nesta figura as setas são representações gráficas das polarizações da nuvem eletrônica em cada nanopartícula devido a excitação do plasmon de superfície. De forma semelhante, pode-se esperar interações deste tipo para polarização perpendicular ao eixo de separação entre as partículas (Figura 10C), embora neste caso as energias dos modos ligante e antiligante devam ser próximas daquela para a nanopartícula individual (Figura 10C). Da mesma forma, o modelo pode ser aplicado a modos de maior ordem, como quadrupolares.

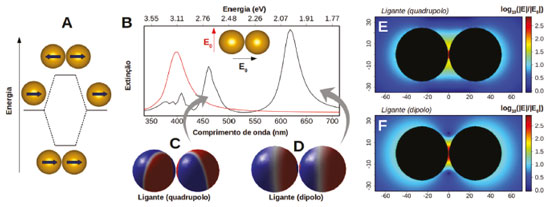Figura 12. A) Esquema para representar o acoplamento entre os modos plasmônicos em uma nanopartícula, no caso o modo dipolar por simplicidade. De forma semelhante a um diagrama de orbitais moleculares, a interação em fase entre os modos plasmônicos leva a criação de um modo plasmônico de menor energia (ligante), enquanto que a interação fora de fase das ondas plasmônicas cria um modo (antiligante) de maior energia. B) Espectros de extinção de um dímero de nanoesferas de Ag de 25 nm de raio e separação g = 1 nm para duas polarizações da radiação excitante (paralela e perpendicular ao eixo interpartículas). C) Representação, por meio das densidades de carga, dos modos associados de menor energia observados no espectro com acoplamento entre os plasmons de superfície. E) e F) são mapas (em escala logarítmica) da relação entre o campo elétrico local e o campo elétrico da radiação excitante para os dois modos em (C) e (D), respectivamente

A Figura 12B apresenta os espectros de extinção para as duas polarizações da Figura 10A para o caso de g = 1 nm, em que se observa no espectro com polarização paralela ao eixo interpartículas duas bandas bem definidas que são deslocadas para maiores comprimentos de onda (menores energias) em relação a banda das nanoesferas individuais (próximo a 400 nm). As Figuras 12C e 12D apresentam as distribuições de carga para estas bandas, indicando que se tratam de interações em fase (estado ligante) entre modos plasmônicos de cada uma das nanoesferas. O modo de menor energia corresponde ao acoplamento entre modos dipolares, enquanto que o de maior energia tem contribuição de modos quadrupolares.

Uma característica interessante sobre os dados apresentados na Figura 12B é que os modos antiligantes não são ativos para nenhuma das configurações de excitação analisadas. De fato, o modo antiligante apresentado no esquema da Figura 12A não é ativo para a excitação óptica, isto é, usando luz. Porém, é possível excitar tais modos com a utilização de feixe de elétrons como sonda. Tal técnica, conhecida como espectroscopia de perda de energia de elétrons ("electron energy loss spectroscopy", EELS), utiliza um microscópio eletrônico de altas resoluções espacial e energética para excitar transições entre níveis de energia no sistema estudado. Recentemente, a técnica EELS tem sido apresentada como uma ferramenta bastante poderosa para mapear os modos plasmônicos de nanoestruturas.^37,128-131 Alguns princípios e ideias deste tipo de espectroscopia são apresentados neste trabalho.

As Figuras 12E e 12F apresentam mapas bidimensionais de log₁₀(|E|/|E₀|) para os dois modos ligantes da Figura 12B, onde |E| e |E₀| representam os módulos do campo elétrico local (em torno da nanoestrutura) e da radiação incidente, respectivamente. As figuras mostram que a excitação destes modos plasmônicos leva a um aumento bastante expressivo (em relação à radiação incidente) do campo elétrico em torno das nanopartículas, especialmente na região interpartículas, em que se nota amplificações de campo superiores a duas ordens de grandeza. Tais regiões de intensa localização de campo elétrico são comumente conhecidas pelo termo "hot spots" (HSs) e estão por trás de parte significativa das aplicações envolvendo nanopartículas plasmônicas em química, particularmente, as envolvendo dispositivos de sensoriamento e espectroscopias intensificadas, como o SERS.

Deve-se destacar que o aumento local de campo elétrico é ainda mais importante em sistemas formados por nanopartículas com pontas, tais como nanobastões ou nanoprismas triangulares. Nestes casos, há uma considerável localização das intensificações nas pontas.²²

ESPECTROSCOPIA DE PERDA DE ENERGIA DE ELÉTRONS (EELS) APLICADA A NANOMATERIAIS PLASMÔNICOS

Embora o mecanismo de interação entre os modos plasmônicos proposto na Figura 12A indique a existência de modos do tipo antiligante, a excitação por luz apenas nos permite observar modos ligantes. A pertinência de tal modelo de interação necessita de um método de excitação que permita observar tais modos antiligantes. Uma maneira de se fazer isso é através da excitação via elétrons acelerados, como aqueles em microscópios eletrônicos de alta resolução. Em sistemas como esse, é possível realizar espectroscopias em que a excitação é feita a partir da extração de energia do feixe de elétrons acelerados. A análise da energia perdida pelo feixe permite montar uma figura de probabilidade de perda de energia (Γ_EELS) em função da energia perdida, que contém informações espectrais a respeito do sistema de estudo. Tal técnica é conhecida como EELS. Uma vez que a fonte de excitação é diferente, as regras de seleção no EELS não necessariamente seguem as mesmas regras observadas em espectroscopia por excitação óptica e, portanto, excitações que são proibidas em um tipo de espectroscopia podem ser permitidas na outra. Nos últimos anos vários estudos têm demonstrado a utilização de EELS como uma ferramenta extremamente versátil para a investigação de sistemas plasmônicos, uma vez que permite aliar em uma mesma investigação resoluções espectral e espacial, esta última graças a utilização do microscópio eletrônico.^37,128-132

A Figura 13 apresenta resultados obtidos por Quillin et al.¹³³ de simulação e experimentais de EELS para dímeros de AgNSs. Nestas simulações a probabilidade de um elétron com velocidade (v) perder energia ħΩ para o sistema, ou seja Γ_EELS(ħΩ) , pode ser calculada através de:¹³¹

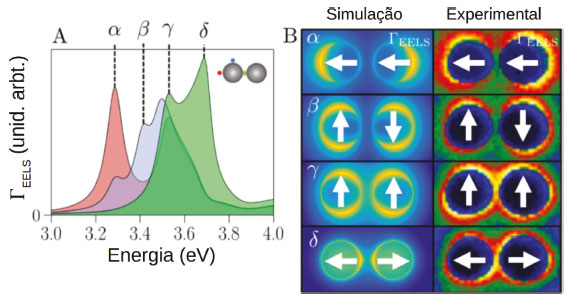Figura 13. (A) Espectros EELS simulados para incidência de feixe de elétrons em diferentes posições (inserto na figura). (B) Mapa da probabilidade de perda de energia para os modos indicados por α, β, γ e δ. As imagens simuladas são comparadas com imagens experimentais. Reproduzido e adaptado com permissão da ref. 133. Copyright 2020 American Chemical Society

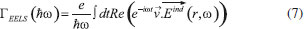onde Re representa parte real de uma função e é o campo elétrico induzido no material pelo feixe de elétrons na posição e com frequência angular Ω.

A Figura 13A apresenta espectros EELS para um dímero de AgNSs com separação entre as superfícies de 5 nm.¹³³ Os dados são apresentados para diferentes posições de incidência do feixe de elétrons como indicado de forma esquemática na figura e mostram a possibilidade de sondagem de diferentes modos plasmônicos com variação da posição do feixe. Isto se deve ao fato de que a polarização da densidade eletrônica na nanopartícula é criada pelo campo elétrico associado aos elétrons, cuja distribuição espacial é do tipo radial.^128,131 Este perfil espacial do campo elétrico permite não apenas a excitação de modos ligantes (α e γ), mas também de modos antiligantes (β e δ), cuja seleção é feita apenas com a modificação da posição do feixe. A Figura 13B apresenta a distribuição espacial de Γ_EELS para cada um dos modos observados nos espectros. Esta figura é particularmente interessante, pois indica as regiões de incidência do feixe de elétrons que apresentam maior probabilidade de excitação para um determinado modo. Observa-se, por exemplo, que a excitação de modos antiligantes tem maior probabilidade de ocorrer quando o feixe está próximo da região entre as duas partículas. A correlação com o dado experimental corrobora o modelo da Figura 12A e mostra o poder da técnica EELS e das simulações computacionais baseadas na eletrodinâmica clássica para a investigação espectroscópica de nanomateriais plasmônicos. Uma desvantagem deste tipo de técnica é a necessidade de instrumentos de espectroscopia de altas resoluções espacial e espectral, muito mais caros do que aqueles utilizados em espectroscopia óptica.

O EFEITO SERS E AS PROPRIEDADES DE CAMPO PRÓXIMO

As Figuras 12E e 12F mostram que a magnitude do campo elétrico em torno da nanopartícula é profundamente alterada pela excitação ressonante do plasmon de superfície. O aumento da magnitude do campo elétrico local contribui para o aumento das intensidades de sinais espectroscópicos de moléculas adsorvidas (ou próximas) à superfície das nanopartículas, sobretudo nos HSs.^18,134 Um exemplo de espectroscopia intensificada pela excitação do plasmon de superfície é o SERS, que será utilizada neste trabalho como exemplo para explorar a relação entre as propriedades locais resultantes da excitação plasmônica e a amplificação de sinais espectroscópicos.^{18,35,41,62,68,107,135-141} A abordagem apresentada aqui é focada exclusivamente nas propriedades plasmônicas das nanopartículas. Para mais detalhes sobre o efeito SERS em língua portuguesa, recomenda-se a leitura do trabalho de Faria et al., que apresentam uma perspectiva histórica do efeito e indicam algumas aplicações.¹⁴²

A medida da magnitude de intensificação no efeito SERS é tipicamente conhecida por fator de intensificação (F), que é formalmente definido como a relação entre as intensidades para uma única molécula nos espectros SERS (I^sm_SERS) e Raman (I^sm_Raman):¹⁴³

Na prática, estimativas de performance de um determinado substrato SERS (material utilizado para obtenção dos espectros) são realizadas levando-se em consideração estimativas do número de moléculas (N) contribuindo para o sinal SERS e Raman, ou seja:^143-145

onde I_SERS e I_Raman são as intensidades SERS e Raman geradas por N_SERS e N_Raman moléculas, respectivamente. Neste tipo de abordagem (Eq. 9) para caracterização da performance de um substrato SERS, a dificuldade está sempre na estimativa do número de moléculas contribuindo para o sinal, o que, dependendo das aproximações utilizadas, pode levar a uma variabilidade de resultados. Portanto, tal tipo de estimativa deve ser realizada com considerável rigor experimental e cautela.

Neste ponto, torna-se fundamental a correlação entre estas estimativas de performance de uma determinada amostra com as características associadas a excitação do plasmon de superfície, o que permite uma melhor compreensão do fenômeno, bem como a otimização das intensificações SERS. O valor de I^sm_SERS é dependente da posição onde a molécula se encontra na superfície da nanopartícula, já que a intensificação do campo elétrico apresenta elevada dependência espacial, como demonstrado nas Figuras 12E e 12F. De fato, pode-se mostrar que o fator de intensificação SERS, devido a contribuição eletromagnética associada a intensificação plasmônica, pode ser descrito em termos do aumento do campo elétrico local na frequência da radiação incidente (Ω₀) e da radiação espalhada (Ω_esp) no espectro Raman:¹⁴⁶

A aproximação (E⁴) na Eq. 10 se justifica pelo fato de que as diferenças entre as frequências das radiações incidentes e espalhadas inelasticamente são pequenas. Uma vez que o efeito SERS está relacionado a excitação do plasmon de superfície, os fatores de intensificação dependem das características das nanopartículas (composição química, tamanho, forma estado de agregação) e também da radiação utilizada para a obtenção dos espectros SERS. A Figura 14 resume algumas destas dependências para o caso de dímeros de AgNSs em água. As simulações na figura foram realizadas através da teoria de Mie generalizada.^65,141

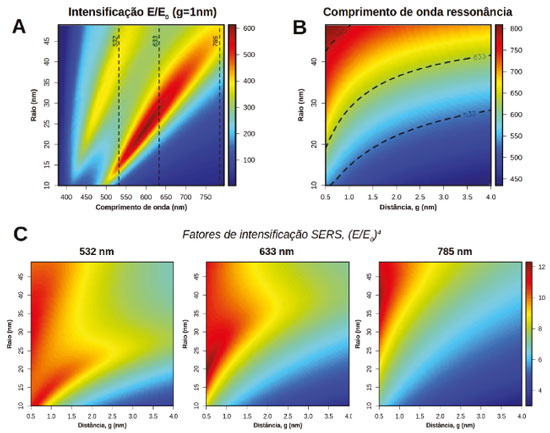Figura 14. (A) Perfil de intensificação do campo elétrico local em função com comprimento de onda no HS de dímeros de AgNSs de diferentes raios. (B) Mapa dos comprimentos de onda de ressonância para o modo plasmônico de menor energia no dímero em função dos parâmetros raio das nanopartículas e distância entre as superfícies, g. Reproduzida com permissão da ref. 141. Copyright 2020 American Chemical Society. (C) Mapas de fatores de intensificação SERS para três comprimentos de onda de radiação incidente: 532, 633 e 785 nm

A Figura 14A apresenta os valores da intensificação local do campo elétrico (E/E₀) no centro do HS para AgNs separadas por uma distância entre as superfícies (g na Figura 10) de 1 nm. Os resultados são apresentados em função do comprimento de onda da radiação incidente e do raio das AgNSs formando os dímeros.

A exemplo do que é observado Figura 10 (espectros de extinção), para cada tamanho na Figura 14A são observadas duas bandas no perfil de intensificação do campo elétrico que apresentam deslocamento para maiores comprimentos com o aumento do tamanho das AgNSs. Maiores intensificações são observadas para o caso do acoplamento entre os modos dipolares (ressonância em maior comprimento de onda) do que no caso de acoplamento envolvendo modos de maior ordem (menor comprimento de onda). Além da dependência das ressonâncias nos perfis de intensificação com o tamanho das nanopartículas, há dependência com a distância de separação entre as superfícies (g). Esta dependência é apresentada na Figura 14B que contém um mapa dos comprimentos de onda de ressonância para o modo de menor energia em função dos parâmetros raio e distância g.

Nas Figuras 14A e 14B são indicados por linhas tracejadas três comprimentos de onda tipicamente utilizados para obtenção de espectros Raman (SERS): 532, 633 e 785 nm. Os dados mostram que diferentes configurações de tamanho e distância entre partículas apresentam plasmon de superfície que estão mais em ressonância com um destes comprimentos de onda e, portanto, devem apresentar performances diferenciadas em função da radiação incidente. A Figura 14C apresenta o mapa dos fatores de intensificação SERS (Eq. 10) para os três comprimentos de onda destacados. De forma geral, maiores intensificações SERS são observadas para menores valores de g (por exemplo 1 nm, que será tomado como referência no que segue), situação que leva a uma grande concentração de campo no HS. A utilização de radiação laser em 785 nm leva a maiores intensificações SERS para nanopartículas maiores (raios entre 40 e 45 nm), já que esta radiação está em ressonância com a excitação plasmônica para estas configurações de tamanho e valores de g. Para laser em 633 nm, por outro lado, são observadas maiores intensificações para nanopartículas menores, por exemplo, com raios entre 20 e 25 nm. Dentre os três exemplos, esta radiação é a que leva às maiores intensificações SERS no caso de dímeros de AgNSs. Por fim, para radiação em 532 nm são observadas altas intensificações SERS tanto para partículas pequenas (raios 10 e 20 nm), quanto para partículas maiores (raios entre 30 e 45 nm). No primeiro caso (partículas pequenas), esta radiação excitante em 532 nm está em ressonância com plasmon de superfície associado ao acoplamento entre modos dipolares, enquanto que para partículas maiores a ressonância ocorre com o acoplamento envolvendo modos de maior ordem (quadrupolo veja Figura 14A).

A Figura 15 apresenta os perfis de intensificação SERS em função do comprimento de onda da radiação incidente para o caso de dímeros de nanoesferas de Ag (AgNSs) e Au (AuNSs) em água.

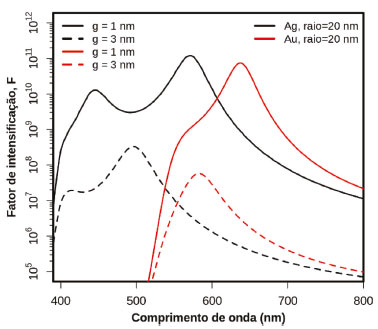Figura 15. Simulação dos perfis de intensificação SERS em função do comprimento de onda da radiação incidente para dímeros de AgNSs (preto) e AuNSs (vermelho). Duas separações entre as superfícies das nanoesferas são consideradas: g = 1 nm (linhas cheias) e g = 3 nm (linhas tracejadas)

Em ambos os casos da Figura 15, o raio das esferas corresponde a 20 nm. Duas configurações de dímeros em termos da distância entre superfícies foram consideradas: g = 1 nm e g = 3 nm. As diferenças entre as propriedades ópticas de Au e Ag (Figura 3) se manifestam nas intensificações SERS de diferentes formas: i) dímeros de AuNSs apresentam grandes intensificações SERS para comprimentos de onda maiores que no caso de dímeros de AgNSs; ii) modos de maior ordem (por exemplo quadrupolo) não apresentam grandes contribuições para dímeros de AuNSs; iii) nestes exemplos, as intensificações SERS para dímeros de AuNSs são menores que as envolvendo AgNSs, sobretudo para g = 3 nm.

As três observações acima estão relacionadas às diferenças na parte imaginária da função dielétrica para Au e Ag. As observações i e ii já foram discutidas no contexto dos espectros de extinção de partículas individuais (Figuras 4 e 6). O resultado novo em relação às discussões realizadas até o momento é a observação iii. Para o caso de g = 3 nm ambos os dímeros apresentam ressonância abaixo de 600 nm. Nesta faixa espectral, a parte imaginária da função dielétrica do Au é maior que da Ag (Figura 3D) e, portanto, a resposta plasmônica apresenta maior amortecimento no Au. Este efeito acaba influenciando nos valores de intensificação do campo elétrico local e, consequentemente, nas intensificações SERS, como observado pelos resultados indicados pelas linhas tracejadas. A diminuição no valor de g para 1 nm leva a uma condição de ressonância no dímero de AuNSs para comprimentos de onda acima de 600 nm, condição em que as respostas ópticas de Au e Ag se assemelham e isto se manifesta nos valores de intensificação SERS observados (linhas cheias) para os dímeros. Os resultados das Figuras 14 e 15 indicam como o entendimento das propriedades plasmônicas de nanopartículas podem guiar a síntese de nanopartículas (agregados) voltados para uma determinada aplicação.

Finalmente, na Figura 16B é apresentado um exemplo para o efeito da forma de nanopartículas sobre os fatores de intensificação SERS. Neste caso em particular é apresentada a comparação entre dímeros de AuNSs (vermelho) e de nanoelipsóides de Au (AuNEs, preto).¹⁴⁷ A resposta plasmônica de AuNEs é semelhante ao observado para AuNRs, com a observação de modos transversais e longitudinais.¹⁸

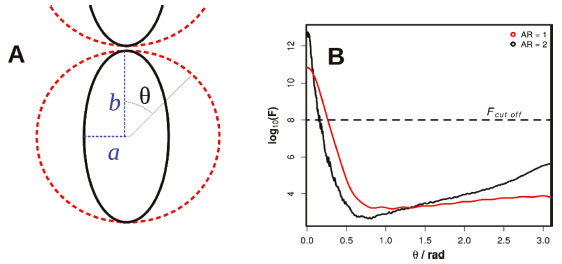Figura 16. (A) Representações esquemáticas de nanopartículas de diferentes razões de aspecto formando dímeros: nanoelipsóides (preto) com razão de aspecto AR=b/a=1 e nanoesferas (vermelho) com AR=1. O ângulo θ é utilizado para ambas estruturas para indicar a variação espacial dos fatores de intensificação SERS a partir dos HSs (θ = 0 rad). (B) Dependência espacial dos fatores de intensificação para dímeros de nanoelipsóides (preto) e nanoesferas (vermelho) de Au. As AuNSs apresentam raio de 20 nm e os parâmetros a e b foram escolhidos para apresentar o mesmo volume que as AuNSs. Reproduzido da ref. 147

Nos exemplos da Figura 16 a distância entre as superfícies considerada é de 1 nm. O dímero de AuNSs é o mesmo que na Figura 15 (linha cheia). Os parâmetros a e b que descrevem a razão de aspecto dos AuNEs (Figura 16A) foram escolhidos de tal maneira que a nanopartícula tenha o mesmo volume que a AuNS, com restrição de razão de aspecto (b/a) igual a 2. A Figura 16A mostra de forma qualitativa (e fora de escala) as duas estruturas consideradas.

Os fatores de intensificação SERS em função do ângulo θ (definido na figura) foram calculados nos comprimentos de onda de ressonância (633 nm e 674 nm para os dímeros de AuNSs e AuNEs, respectivamente). A presença de pontas no dímero de AuNEs (AR=2) leva a maiores fatores de intensificação SERS no centro do HS (θ = 0) que no dímero de AuNSs. Além disso, F apresenta um decaimento mais intenso com a variação de θ (veja, por exemplo, a variação entre o valor de máximo e F=10⁸ como referência). Embora, a discussão realizada acima tenha focado no caso de nanoelipsóides, estas observações de altas intensificações extremamente localizadas nas pontas são também observadas para outras geometrias como nanoprismas triangulares ou nanobastões, por exemplo, indicando sistemas que permitem elevadas intensificações SERS.

Os exemplos das Figuras 14-16 mostram que a presença de HSs levam a intensificações do espectro Raman de um analito de interesse em várias ordens de magnitude, o que permite a detecção de moléculas a baixas concentrações, inclusive em regime de detecção de uma molécula.^{134,136,138-140,148-153} Contudo, estas altas intensificações ficam localizadas em pequenas regiões da superfície, o que contribui para observação de intensas flutuações de intensidades SERS de analitos a baixas concentrações.^{134,141,148,154,155}

INTERFERÊNCIAS ELETROMAGNÉTICAS E RESSONÂNCIA DE FANO

Um aspecto importante a ser considerado na análise das propriedades espectroscópicas e de campo próximo de nanopartículas é que, nas aplicações destes materiais, estas nanopartículas são normalmente depositadas sobre uma superfície que atua como suporte, que pode ser um sólido dielétrico (por exemplo Si) ou metálico. Nesta seção consideramos o efeito do suporte sobre as respostas plasmônicas de nanoestruturas. Aproveitamos este sistema para introduzir efeitos resultantes de interferências eletromagnéticas, em especial a chamada ressonância de Fano.

A Figura 17 apresenta um exemplo do acoplamento entre um AuNR e o material suporte pela excitação do modo longitudinal no AuNR. A distribuição de carga do tipo dipolar resultante da excitação plasmônica no AuNR leva a uma imagem especular na superfície do material suporte (Figura 17A). Tal interação é comumente chamada de dipolo-imagem.¹⁵⁶ Esta interação altera a resposta espectroscópica da nanopartícula. A Figura 17B apresenta cálculos para os espectros de absorção e espalhamento de um AuNR sobre um cilindro de Au que simula o material suporte. A aproximação entre menor a distância entre a nanopartícula e o suporte desloca a ressonância plasmônica do AuNR para maiores comprimentos de onda. Este efeito de deslocamento também ocorre para agregados de nanopartículas. Portanto, em aplicações que envolvem nanopartículas suportadas, deve ser dada atenção ao efeito do suporte sobre a condição de ressonância. O sinal alargado observado nos espectros de absorção e espalhamento na região de maiores comprimentos de onda (800 nm) é devido ao cilindro de Au. Uma vez que o dipolo (no AuNR) e a imagem (no suporte) estão fora de fase, pode-se esperar interferência destrutiva entre estes dipolos. Esta interferência se manifesta nos espectros de espalhamento, em que se observa decréscimo da intensidade exatamente no comprimento de onda de ressonância.

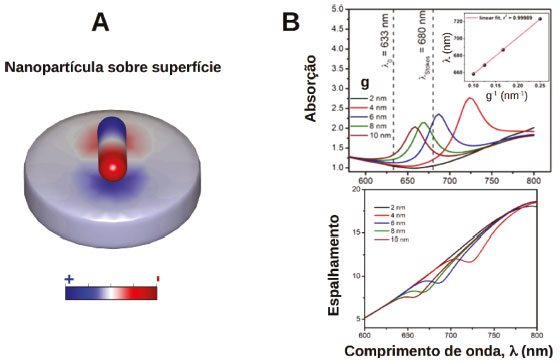Figura 17. (A) Esquema ilustrativo da distribuição para um AuNR sobre a superfície de um material suporte. A excitação do modo longitudinal do AuNR leva a criação de uma distribuição de carga espelhada na superfície do suporte. (B) Efeito da alteração da distância (g) entre a superfície de um AuNR (AR=3) e do suporte (superfície de Au) sobre os espectros de absorção e espalhamento. Reproduzida com permissão da ref. 156. Copyright 2020 American Chemical Society

A Figura 18 apresenta outro exemplo do efeito do suporte sobre a resposta plasmônica de uma nanopartícula, neste caso nanocubos de Ag de 60 nm, apresentado por Zhang et al.⁷⁶ Na Figura 18A é apresentada uma comparação entre os espectros de espalhamento de um AgNC em vácuo (preto) e de um AgNC sobre vidro (vermelho), também em vácuo. Além do deslocamento da resposta plasmônica para maiores comprimentos de onda, nota-se que a presença da superfície leva a um aumento da intensidade do modo quadrupolar do nanocubo (indicado por II na figura), bem como assimetria na forma da banda para maiores comprimentos de onda. Este perfil assimétrico e a alteração de intensidade relativa são típicos da chamada ressonância de Fano,^{70,71,73-76,115,119,129} que surge da interferência destrutiva entre modos plasmônicos claros (alta intensidade de espalhamento) e escuros (baixa intensidade de espalhamento). Neste exemplo, a interferência ocorre entre o modo dipolar e o modo quadrupolar do nanocubo induzida pela presença da superfície. A superfície atua não só por meio de interações dipolo-imagem, mas também leva a uma quebra de simetria permitindo a mistura entre modos plasmônicos que apresentem sobreposição espectral.

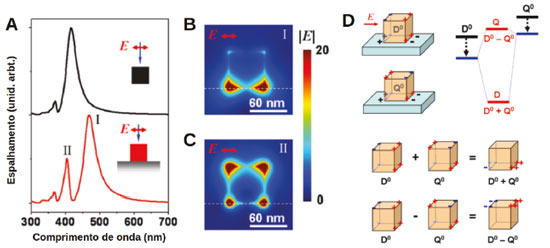Figura 18. (A) Espectros de absorção de nanocubos de Ag de 60 nm em ar (preto) e depositado sobre vido (vermelho). (B) e (C) apresenta mapas de intensificação de campo elétrico para os modos indicados por I e II, respectivamente, em (A). (D) modelo para interação em fase e fora de fase para os modos dipolar e quadrupolar. Reproduzida com permissão da ref. 76. Copyright 2020 American Chemical Society

A Figura 18D mostra de forma qualitativa esta interação entre modos dipolares e quadrupolares através de interferências construtiva (modo ligante) e destrutiva (anti-ligante). Nas Figuras 18B e 18C são apresentados mapas de distribuição de campo elétrico para cada um dos modos. Nota-se que a ressonância de Fano altera de forma significativa esta distribuição, sendo notável a maior intensificação de campo nas faces próxima (Figura 18B) e distante (Figura 18C) do material suporte, o que pode contribuir para respostas diferenciadas na detecção espectroscópica de moléculas em solução, por exemplo.

O exemplo da Figura 18 é emblemático quanto ao poder das simulações computacionais para a previsão e design de materiais com respostas diferenciadas. Esta previsão teórica de 2011 foi confirmada experimentalmente em 2013 por Nicoletti et al. utilizando a técnica EELS.¹⁵⁷

Estas interferências associadas a ressonância de Fano podem ser observadas também em agregados de nanopartículas com diferentes formas como esférica, cúbica ou de nanobastões. Baldwin et al. mostraram evidências de assinaturas térmicas associadas a relaxação plasmônica com contribuições da ressonância de Fano.¹⁵⁸ Fan et al. também observaram assinaturas no espectro SERS referentes a tais ressonâncias.¹⁵⁹ Recentemente, mostramos indícios destes efeitos em agregados de nanocubos aparecendo nos espectros SERS.⁶⁹ Simulações computacionais também sugerem, no caso de ressonâncias de Fano em agregados de nanobastões, a possibilidade de ampliação da área efetiva de HSs sobre a superfície das nanopartículas.⁶⁸ Portanto, estas interferências podem ser alternativas altamente viáveis para as modificações das propriedades plasmônicas de nanoestruturas.

CONCLUSÕES

Nanomateriais plasmônicos apresentam diversas aplicações em química, que dependem das características associadas à excitação e relaxação plasmônica. O entendimento destas características é fundamental para o desenho inteligente de materiais voltados a uma determinada aplicação. Neste trabalho, portanto, foi realizada tal investigação das propriedades plasmônicas de nanomateriais de diferentes formas, composição química, tamanho e ambiente químico em que estão dispersas. A análise das propriedades locais resultantes da excitação plasmônica permitiu a fundamentação do efeito SERS, em que foi dada ênfase apenas a contribuição oriunda do plasmon de superfície. Neste caso, foram discutidos os efeitos associados ao tamanho, forma e composição química de nanopartículas. A análise das propriedades de nanopartículas em superfície e os efeitos de interferências eletromagnéticas também foram brevemente explorados e apresentam-se como alternativas que permitem maior grau de modulação sobre as propriedades de nanomateriais plasmônicos. A fundamentação apresentada aqui serve como base para a exploração de diferentes nanomateriais plasmônicos, através da análise de suas propriedades espectroscópicas e do efeito SERS, para a construção de sensores altamente sensíveis, estudo de interação de moléculas com superfícies metálicas e mediação de reações químicas em superfície.

AGRADECIMENTOS

Agradecemos o apoio financeiro da FAPESP (2016/21070-5), CNPq (408985/2016-0), FAPERJ (26/211.281/2019) e Petrobras (2017/00367-2). Este trabalho foi financiado em parte pela CAPES-código 001.

REFERÊNCIAS

1. Santos, J.; Santos, M.; Thesing, A.; Tavares, F.; Griep, J.; Rodrigues, M.; Quim. Nova 2016, 39, 1098.

2. Peixoto, L. P. F.; Santos, J. F. L.; Andrade, G. F. S.; Quim. Nova 2019, 42, 1044.

3. Brolo, A.; Nat. Photonics 2012, 6, 709.

4. Carretero-Palacios, S.; Jiménez-Solano, A.; Míguez, H.; ACS Energy Lett. 2016, 1, 323.

5. Tsakalakos, L.; Nanotechnology for Photovoltaics, CRC Press: Boca Raton, 2010.

6. Ferry, V. E.; Munday, J. N.; Atwater, H. A.; Adv. Mater. 2010, 22, 4794.

7. De Souza, M. L.; Corio, P.; Brolo, A. G.; Phys. Chem. Chem. Phys. 2012, 14, 15722.

8. Higgins, M.; Ely, F.; Nome, R. C.; Nome, R. A.; dos Santos, D. P.; Choi, H.; Nam, S.; Quevedo-Lopez, M.; J. Appl. Phys. 2018, 124, 065306.

9. Zhan, C.; Chen, X.; Huang, Y.; Wu, D.; Tian, Z.; Acc. Chem. Res. 2019, 52, 2784.

10. Cortés, E.; Adv. Opt. Mater. 2017, 5, 1700191.

11. Kumari, G.; Zhang, X.; Devasia, D.; Heo, J.; Jain, P. K.; ACS Nano 2018, 12, 8330.

12. Shaik, F.; Peer, I.; Jain, P. K.; Amirav, L.; Nano Lett. 2018, 18, 4370.

13. Gargiulo, J.; Berté, R.; Li, Y.; Maier, S. A.; Cortés, E.; Acc. Chem. Res. 2019, 52, 2525.

14. Zhang, Z.; Zhang, C.; Zheng, H.; Xu, H.; Acc. Chem. Res. 2019, 52, 2506.

15. Mukherjee, S.; Libisch, F.; Large, N.; Neumann, O.; Brown, L. V.; Cheng, J.; Lassiter, J. B.; Carter, E. A.; Nordlander, P.; Halas, N. J.; Nano Lett. 2013, 13, 240.

16. Zhang, Y.; He, S.; Guo, W.; Hu, Y.; Huang, J.; Mulcahy, J. R.; Wei, W. D.; Chem. Rev. 2018, 118, 2927.

17. Shahbazyan, T. V.; Stockman, M. I.; Plasmonics: Theory and Applications, vol. 15; Shahbazyan, T. V.; Stockman, M. I., eds.; Springer Netherlands: Dordrecht, 2013.

18. Ru, E. C. L.; Etchegoin, P. G.; Principles of Surface-Enhanced Raman Spectroscopy and Related Plasmonic Effects, Elsevier: Amsterdam, 2008.

19. Quinten, M.; Optical Properties of Nanoparticle Systems, Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2011.

20. Zhao, J.; Pinchuk, A. O.; McMahon, J. M.; Li, S.; Ausman, L. K.; Atkinson, A. L.; Schatz, G. C.; Acc. Chem. Res. 2008, 41, 1710.

21. Kahnert, F. M.; J. Quant. Spectrosc. Radiat. Transfer 2003, 79-80, 775.

22. Kelly, K. L.; Coronado, E.; Zhao, L. L.; Schatz, G. C.; J. Phys. Chem. B 2003, 107, 668.

23. Brongersma, M. L.; Halas, N. J.; Nordlander, P.; Nat. Nanotechnol. 2015, 10, 25.

24. Besteiro, L. V.; Govorov, A. O.; J. Phys. Chem. C 2016, 120, 19329.

25. Zhang, H.; Govorov, A. O.; J. Phys. Chem. C 2014, 118, 7606.

26. Sundararaman, R.; Narang, P.; Jermyn, A. S.; Goddard III, W. A.; Atwater, H. A.; Nat. Commun. 2014, 5, 5788.

27. Brown, A. M.; Sundararaman, R.; Narang, P.; Goddard, W. A.; Atwater, H. A.; ACS Nano 2016, 10, 957.

28. Seemala, B.; Therrien, A. J.; Lou, M.; Li, K.; Finzel, J. P.; Qi, J.; Nordlander, P.; Christopher, P.; ACS Energy Lett. 2019, 4, 1803.

29. Hartland, G. V.; Besteiro, L. V.; Johns, P.; Govorov, A. O.; ACS Energy Lett. 2017, 2, 1641.

30. Amendola, V.; Meneghetti, M.; J. Phys. Chem. C 2009, 113, 4277.

31. Kreibig, U.; Vollmer, M.; Optical Properties of Metal Clusters, vol. 25; Springer Berlin Heidelberg: Berlin, Heidelberg, 1995.

32. Yurkin, M. A.; Hoekstra, A. G.; J. Quant. Spectrosc. Radiat. Transfer 2007, 106, 558.

33. Yang, W.; Schatz, G. C.; Van Duyne, R. P.; J. Chem. Phys. 1995, 103, 869.

34. Felidj, N.; Aubard, J.; Levi, G.; J. Chem. Phys. 1999, 111, 1195.

35. Wustholz, K. L.; Henry, A.-I.; McMahon, J. M.; Freeman, R. G.; Valley, N.; Piotti, M. E.; Natan, M. J.; Schatz, G. C.; Van Duyne, R. P.; J. Am. Chem. Soc. 2010, 132, 10903.

36. Hohenester, U.; Trügler, A.; Comput. Phys. Commun. 2012, 183, 370.

37. Hohenester, U.; Comput. Phys. Commun. 2014, 185, 1177.

38. Ashcroft, N. W.; Mermin, N. D.; Física do estado sólido; Cengage Learning: Stamford, 2011.

39. McPeak, K. M.; Jayanti, S. V.; Kress, S. J. P.; Meyer, S.; Iotti, S.; Rossinelli, A.; Norris, D. J.; ACS Photonics 2015, 2, 326.

40. Polyanskiy, M. N.; Refractive index database; https://refractiveindex.info, accessed in August 2020.

41. Dal Forno, S.; Ranno, L.; Lischner, J.; J. Phys. Chem. C 2018, 122, 8517.

42. Schatz, G. C.; Young, M. A.; Van Duyne, R. P. In Surface-Enhanced Raman Scattering. Topics in Applied Physics; Kneipp, K.; Moskovits, M.; Kneipp, H., eds.; Springer: Berlin, 2006, pp. 19-45.

43. Lermé, J.; J. Phys. Chem. C 2011, 115, 14098.

44. Hale, G. M.; Querry, M. R.; Appl. Opt. 1973, 12, 555.

45. Chen, H.-Y.; He, C.-L.; Wang, C.-Y.; Lin, M.-H.; Mitsui, D.; Eguchi, M.; Teranishi, T.; Gwo, S.; ACS Nano 2011, 5, 8223.

46. Blaber, M. G.; Henry, A.-I.; Bingham, J. M.; Schatz, G. C.; Van Duyne, R. P.; J. Phys. Chem. C 2012, 116, 393.

47. Hartland, G. V.; Chem. Rev. 2011, 111, 3858.

48. Berciaud, S.; Cognet, L.; Tamarat, P.; Lounis, B.; Nano Lett. 2005, 5, 515.

49. Pazos-Perez, N.; Garcia De Abajo, F. J.; Fery, A.; Alvarez-Puebla, R. A.; Langmuir 2012, 28, 8909.

50. Ye, X.; Jin, L.; Caglayan, H.; Chen, J.; Xing, G.; Zheng, C.; Doan-Nguyen, V.; Kang, Y.; Engheta, N.; Kagan, C. R.; Murray, C. B.; ACS Nano 2012, 6, 2804.

51. Xia, Y.; Xia, X.; Peng, H.-C.; J. Am. Chem. Soc. 2015, 137, 7947.

52. Knight, M. W.; King, N. S.; Liu, L.; Everitt, H. O.; Nordlander, P.; Halas, N. J.; ACS Nano 2014, 8, 834.

53. Swearer, D. F.; Leary, R. K.; Newell, R.; Yazdi, S.; Robatjazi, H.; Zhang, Y.; Renard, D.; Nordlander, P.; Midgley, P. A.; Halas, N. J.; Ringe, E.; ACS Nano 2017, 11, 10281.

54. Zhang, C.; Zhao, H.; Zhou, L.; Schlather, A. E.; Dong, L.; McClain, M. J.; Swearer, D. F.; Nordlander, P.; Halas, N. J.; Nano Lett. 2016, 16, 6677.

55. Henry, A. I.; Sharma, B.; Cardinal, M. F.; Kurouski, D.; Van Duyne, R. P.; Anal. Chem. 2016, 88, 6638.

56. Fan, M.; Thompson, M.; Andrade, M. L.; Brolo, A. G.; Anal. Chem. 2010, 82, 6350.

57. Maisonneuve, M.; Valsecchi, C.; Wang, C.; Brolo, A. G.; Meunier, M.; Biosens. Bioelectron. 2015, 63, 80.

58. Pereira, M. L. O.; Grasseschi, D.; Toma, H. E.; Energy Fuels 2017, 32, 2673.

59. Toma, H. E.; Shinohara, J. S.; Grasseschi, D. In Nanoscale Imaging, Sensing, and Actuation for Biomedical Applications XII; Cartwright, A. N.; Nicolau, D. V., eds.; SPIE: Bellingham, 2015, vol. 9337, p. 933702.

60. Grasseschi, D.; Parussulo, A. L. A.; Zamarion, V. M.; Guimarães, R. R.; Araki, K.; Toma, H. E.; RSC Adv. 2013, 3, 24465.

61. Grasseschi, D.; Parussulo, A. L. A.; Zamarion, V. M.; Guimarães, R. R.; Araki, K.; Toma, H. E.; J. Raman Spectrosc. 2014, 45, 758.

62. Fairbairn, N.; Christofidou, A.; Kanaras, A. G.; Newman, T. A.; Muskens, O. L.; Phys. Chem. Chem. Phys. 2013, 15, 4163.

63. Santos, J. J.; Ivanov, E.; dos Santos, D. P.; Toma, H. E.; Corio, P.; ChemPhysChem 2016, 17, 463.

64. Joplin, A.; Jebeli, S. A. H.; Sung, E.; Diemler, N.; Straney, P. J.; Yorulmaz, M.; Chang, W.-S.; Millstone, J. E.; Link, S.; ACS Nano 2017, 11, 12346.

65. Henry, A.-I.; Bingham, J. M.; Ringe, E.; Marks, L. D.; Schatz, G. C.; Van Duyne, R. P.; J. Phys. Chem. C 2011, 115, 9291.

66. Itoh, T.; Yamamoto, Y. S.; Okamoto, T.; Phys. Rev. B 2019, 99, 235409.

67. Zuloaga, J.; Nordlander, P.; Nano Lett. 2011, 11, 1280.

68. Souza, K. S.; Teixeira-Neto, E.; Temperini, M. L. A.; dos Santos, D. P.; J. Braz. Chem. Soc. 2019, 30, 2624.

69. Santinom, A.; da Silva, M. A.; Villa, J. E. L.; Poppi, R. J.; Mazali, I. O.; dos Santos, D. P.; Vib. Spectrosc. 2018, 99, 34.

70. Ci, X.; Wu, B.; Song, M.; Liu, Y.; Chen, G.; Wu, E.; Zeng, H.; Appl. Phys. A 2014, 117, 955.

71. Rahmani, M.; Luk'yanchuk, B.; Hong, M.; Laser Photonics Rev. 2013, 7, 329.

72. Zhou, F.; Li, Z.; Liu, Y.; Xia, Y.; J. Phys. Chem. C 2008, 112, 20233.

73. Lovera, A.; Gallinet, B.; Nordlander, P.; Martin, O. J. F.; ACS Nano 2013, 7, 4527.

74. Luk'yanchuk, B.; Zheludev, N. I.; Maier, S. A.; Halas, N. J.; Nordlander, P.; Giessen, H.; Chong, C. T.; Nat. Mater. 2010, 9, 707.

75. Li, G.; Li, Q.; Xu, L.; Wu, L.; Plasmonics 2015, 10, 1401.

76. Zhang, S.; Bao, K.; Halas, N. J.; Xu, H.; Nordlander, P.; Nano Lett. 2011, 11, 1657.

77. Jain, P. K.; J. Phys. Chem. C 2019, 123, 24347.

78. Kim, Y.; Smith, J. G.; Jain, P. K.; Nat. Chem. 2018, 10, 763.

79. Ferbonink, G. F.; Spada, E. R.; dos Santos, D. P.; Sartorelli, M. L.; Nome, R. A.; J. Braz. Chem. Soc. 2016, 27, 423.

80. Baffou, G.; Quidant, R.; Laser Photonics Rev. 2013, 7, 171.

81. Baffou, G.; Quidant, R.; Girard, C.; Appl. Phys. Lett. 2009, 94, 153109.

82. Golubev, A. A.; Khlebtsov, B. N.; Rodriguez, R. D.; Chen, Y.; Zahn, D. R. T.; J. Phys. Chem. C 2018, 122, 5657.

83. Govorov, A. O.; Richardson, H. H.; Nano Today 2007, 2, 30.

84. Baffou, G.; Quidant, R.; Chem. Soc. Rev. 2014, 43, 3898.

85. Baffou, G.; Quidant, R.; García De Abajo, F. J.; ACS Nano 2010, 4, 709.

86. Lalisse, A.; Tessier, G.; Plain, J.; Baffou, G.; J. Phys. Chem. C 2015, 119, 25518.

87. Sotiriou, G. A.; Starsich, F.; Dasargyri, A.; Wurnig, M. C.; Krumeich, F.; Boss, A.; Leroux, J. C.; Pratsinis, S. E.; Adv. Funct. Mater. 2014, 24, 2818.

88. MacKey, M. A.; Ali, M. R. K.; Austin, L. A.; Near, R. D.; El-Sayed, M. A.; J. Phys. Chem. B 2014, 118, 1319.

89. Sarhan, R. M.; Koopman, W.; Schuetz, R.; Schmid, T.; Liebig, F.; Koetz, J.; Bargheer, M.; Sci. Rep. 2019, 9, 3060.

90. Zhang, X.; Li, X.; Reish, M. E.; Zhang, D.; Su, N. Q.; Gutiérrez, Y.; Moreno, F.; Yang, W.; Everitt, H. O.; Liu, J.; Nano Lett. 2018, 18, 1714.

91. Pensa, E.; Gargiulo, J.; Lauri, A.; Schlücker, S.; Cortés, E.; Maier, S. A.; Nano Lett. 2019, 19, 1867.

92. Zhang, J.; Jin, X.; Morales-Guzman, P. I.; Yu, X.; Liu, H.; Zhang, H.; Razzari, L.; Claverie, J. P.; ACS Nano 2016, 10, 4496.

93. de Souza, M. L.; dos Santos, D. P.; Corio, P.; RSC Adv. 2018, 8, 28753.

94. de Souza, M. L.; Corio, P.; Appl. Catal., B 2013, 136-137, 325.

95. De Souza, M. L.; Tristão, D. C.; Corio, P.; RSC Adv. 2014, 4, 23351.

96. Rodrigues, T. S.; Zhao, M.; Yang, T.; Gilroy, K. D.; da Silva, A. G. M.; Camargo, P. H. C.; Xia, Y.; Chem. - Eur. J. 2018, 24, 16944.

97. Lohse, S. E.; Burrows, N. D.; Scarabelli, L.; Liz-Marzán, L. M.; Murphy, C. J.; Chem. Mater. 2014, 26, 34.

98. Grzelczak, M.; Pérez-Juste, J.; Mulvaney, P.; Liz-Marzán, L. M.; Chem. Soc. Rev. 2008, 37, 1783.

99. Personick, M. L.; Mirkin, C. A.; J. Am. Chem. Soc. 2013, 135, 18238.

100. Grasseschi, D.; Pereira, M. L. O.; Shinohara, J. S.; Toma, H. E.; J. Nanoparticle Res. 2018, 20, 35.

101. Nikoobakht, B.; El-Sayed, M. A.; Chem. Mater. 2003, 15, 1957.

102. Brioude, A.; Jiang, X. C.; Pileni, M. P.; J. Phys. Chem. B 2005, 109, 13138.

103. Langhammer, C.; Schwind, M.; Kasemo, B.; Zorić, I.; Nano Lett. 2008, 8, 1461.

104. Zorić, I.; Zäch, M.; Kasemo, B.; Langhammer, C.; ACS Nano 2011, 5, 2535.

105. Jin, R.; Cao, Y.; Mirkin, C. A.; Kelly, K. L.; Schatz, G. C.; Zheng, J. G.; Science (80-. ) 2001, 294, 1901.

106. Yang, P.; Portalès, H.; Pileni, M. P.; J. Phys. Chem. C 2009, 113, 11597.

107. Le Ru, E. C.; Grand, J.; Sow, I.; Somerville, W. R. C.; Etchegoin, P. G.; Treguer-Delapierre, M.; Charron, G.; Félidj, N.; Lévi, G.; Aubard, J.; Nano Lett. 2011, 11, 5013.

108. Guffey, M. J.; Miller, R. L.; Gray, S. K.; Scherer, N. F.; Nano Lett. 2011, 11, 4058.

109. Ringe, E.; Zhang, J.; Langille, M. R.; Mirkin, C. A.; Marks, L. D.; Van Duyne, R. P.; Nanotechnology 2012, 23, 444005.

110. Im, S. H.; Lee, Y. T.; Wiley, B.; Xia, Y.; Angew. Chem., Int. Ed. Engl. 2005, 44, 2154.

111. Hooshmand, N.; O'Neil, D.; Asiri, A. M.; El-Sayed, M.; J. Phys. Chem. A 2014, 118, 8338.

112. Mazzucco, S.; Geuquet, N.; Ye, J.; Stéphan, O.; Van Roy, W.; Van Dorpe, P.; Henrard, L.; Kociak, M.; Nano Lett. 2012, 12, 1288.

113. McMahon, J. M.; Wang, Y.; Sherry, L. J.; Van Duyne, R. P.; Marks, L. D.; Gray, S. K.; Schatz, G. C.; J. Phys. Chem. C 2009, 113, 2731.

114. Zhou, S.; Li, J.; Gilroy, K. D.; Tao, J.; Zhu, C.; Yang, X.; Sun, X.; Xia, Y.; ACS Nano 2016, 10, 9861.

115. Pellarin, M.; Ramade, J.; Rye, J. M.; Bonnet, C.; Broyer, M.; Lebeault, M. A.; Lermé, J.; Marguet, S.; Navarro, J. R. G.; Cottancin, E.; ACS Nano 2016, 10, 11266.

116. Lindquist, N. C.; de Albuquerque, C. D. L.; Sobral-Filho, R. G.; Paci, I.; Brolo, A. G.; Nat. Nanotechnol. 2019, 14, 981.

117. Hao, E.; Li, S.; Bailey, R. C.; Zou, S.; Schatz, G. C.; Hupp, J. T.; J. Phys. Chem. B 2004, 108, 1224.

118. Prodan, E.; Radloff, C.; Halas, N. J.; Nordlander, P.; Science 2003, 302, 419.

119. Mukherjee, S.; Sobhani, H.; Lassiter, J. B.; Bardhan, R.; Nordlander, P.; Halas, N. J.; Nano Lett. 2010, 10, 2694.

120. Fu, Q.; Zhang, D. G.; Yi, M. F.; Wang, X. X.; Chen, Y. K.; Wang, P.; Ming, H.; J. Opt. 2012, 14, 085001.

121. Pastorello, M.; Sigoli, F. A.; dos Santos, D. P.; Mazali, I. O.; Spectrochim. Acta, Part A 2020, 231, 118113.

122. Tebbe, M.; Kuttner, C.; Mayer, M.; Maennel, M.; Pazos-Perez, N.; König, T. A. F.; Fery, A.; J. Phys. Chem. C 2015, 119, 9513.

123. Goris, B.; Guzzinati, G.; Fernández-López, C.; Pérez-Juste, J.; Liz-Marzán, L. M.; Trügler, A.; Hohenester, U.; Verbeeck, J.; Bals, S.; Van Tendeloo, G.; J. Phys. Chem. C 2014, 118, 15356.

124. Grasseschi, D.; Lima, F. S.; Chaimovich, H.; Toma, H. E.; 2016, arXiv:1607.00530.

125. Grasseschi, D.; Lima, F. S.; Nakamura, M.; Toma, H. E.; Micron 2015, 69, 15.

126. Vianna, P. G.; Grasseschi, D.; Costa, G. K. B.; Carvalho, I. C. S.; Domingues, S. H.; Fontana, J.; De Matos, C. J. S.; ACS Photonics 2016, 3, 1027.

127. Lee, A.; Ahmed, A.; dos Santos, D. P.; Coombs, N.; Park, J. I.; Gordon, R.; Brolo, A. G.; Kumacheva, E.; J. Phys. Chem. C 2012, 116, 5538.

128. Mirsaleh-Kohan, N.; Iberi, V.; Simmons, P. D.; Bigelow, N. W.; Vaschillo, A.; Rowland, M. M.; Best, M. D.; Pennycook, S. J.; Masiello, D. J.; Guiton, B. S.; Camden, J. P.; J. Phys. Chem. Lett. 2012, 3, 2303.

129. Bigelow, N. W.; Vaschillo, A.; Camden, J. P.; Masiello, D. J.; ACS Nano 2013, 7, 4511.

130. Hohenester, U.; Ditlbacher, H.; Krenn, J. R.; Phys. Rev. Lett. 2009, 103, 106801.

131. Wu, Y.; Li, G.; Camden, J. P.; Chem. Rev. 2018, 118, 2994.

132. García De Abajo, F. J.; Rev. Mod. Phys. 2010, 82, 209.

133. Quillin, S. C.; Cherqui, C.; Montoni, N. P.; Li, G.; Camden, J. P.; Masiello, D. J.; J. Phys. Chem. C 2016, 120, 20852.

134. Santos, D.; Temperini, M.; Brolo, A. In Introduction to Plasmonics: Advances and Applications; Szunerits, S.; Boukherroub, R., eds.; Pan Stanford: New York, 2015, pp. 275-317.

135. Lin, K.-Q.; Yi, J.; Hu, S.; Liu, B.-J.; Liu, J.-Y.; Wang, X.; Ren, B.; J. Phys. Chem. C 2016, 120, 20806.

136. Le Ru, E. C.; Etchegoin, P. G.; Meyer, M.; J. Chem. Phys. 2006, 125, 204701.

137. Kiefl, E. J.; Kiefl, R. F.; dos Santos, D. P.; Brolo, A. G.; J. Phys. Chem. C 2017, 121, 25487.

138. dos Santos, D. P.; Temperini, M. L. A.; Brolo, A. G.; J. Am. Chem. Soc. 2012, 134, 13492.

139. dos Santos, D. P.; Temperini, M. L. A.; Brolo, A. G.; J. Phys. Chem. C 2016, 120, 20877.

140. Etchegoin, P. G.; Le Ru, E. C.; Phys. Chem. Chem. Phys. 2008, 10, 6079.

141. dos Santos, D. P.; J. Phys. Chem. C 2020, 124, 6811.

142. de Faria, D. L. A.; Temperini, M. L. A.; Sala, O.; Quim. Nova 1999, 22, 541.

143. Le Ru, E. C.; Blackie, E.; Meyer, M.; Etchegoin, P. G.; J. Phys. Chem. C 2007, 111, 13794.

144. Batista, E.; dos Santos, D.; Andrade, G. S.; Sant'Ana, A.; Brolo, A.; Temperini, M. A.; J. Nanosci. Nanotechnol. 2009, 9, 3233.

145. Rodrigues, D. C.; de Souza, M. L.; Souza, K. S.; dos Santos, D. P.; Andrade, G. F. S.; Temperini, M. L. A.; Phys. Chem. Chem. Phys. 2015, 17, 21294.

146. Le Ru, E. C.; Etchegoin, P. G.; Chem. Phys. Lett. 2006, 423, 63.

147. dos Santos, D. V. N. ; dos Santos, D. P.; Quim. Nova 2019, 42, 1029.

148. dos Santos, D. P.; Temperini, M. L. A.; Brolo, A. G.; Acc. Chem. Res. 2019, 52, 456.

149. Zrimsek, A. B.; Wong, N. L.; Van Duyne, R. P.; J. Phys. Chem. C 2016, 120, 5133.

150. Kleinman, S. L.; Ringe, E.; Valley, N.; Wustholz, K. L.; Phillips, E.; Scheidt, K. A.; Schatz, G. C.; Van Duyne, R. P.; J. Am. Chem. Soc. 2011, 133, 4115.

151. Nie, S.; Science 1997, 275, 1102.

152. Etchegoin, P. G.; Meyer, M.; Blackie, E.; Le Ru, E. C.; Anal. Chem. 2007, 79, 8411.

153. Dieringer, J. A.; Lettan, R. B.; Scheidt, K. A.; Van Duyne, R. P.; J. Am. Chem. Soc. 2007, 129, 16249.

154. Wang, Z.; Rothberg, L. J.; J. Phys. Chem. B 2005, 109, 3387.

155. dos Santos, D. P.; Andrade, G. F. S.; Brolo, A. G.; Temperini, M. L. A.; Chem. Commun. 2011, 47, 7158.

156. Souza, K. S.; dos Santos, D. P.; Andrade, G. F. S.; Pereira, M. B.; Teixeira-Neto, E.; Temperini, M. L. A.; J. Phys. Chem. C 2017, 121, 20937.

157. Nicoletti, O.; de la Peña, F.; Leary, R. K.; Holland, D. J.; Ducati, C.; Midgley, P. A.; Nature 2013, 502, 80.

158. Baldwin, C. L.; Bigelow, N. W.; Masiello, D. J.; J. Phys. Chem. Lett. 2014, 5, 1347.

159. Fan, J. A.; Wu, C.; Bao, K.; Bao, J.; Bardhan, R.; Halas, N. J.; Manoharan, V. N.; Nordlander, P.; Shvets, G.; Capasso, F.; Science 2010, 328, 1135.