Educação
|
|
| Introdução às redes neurais para regressões não-lineares: ajuste de superfícies de energia potencial Introduction to neural networks for non-linear regressions: potential energy surface fitting |
|
Eduardo D. Vicentini; Antonio G. Sampaio de Oliveira-Filho* Departamento de Química, Faculdade de Filosofia Ciências e Letras de Ribeirão Preto, Universidade de São Paulo, 14040-900 Ribeirão Preto - SP, Brasil Recebido em 02/07/2020 *e-mail: antoniogsof@ffcrp.usp.br The present work demonstrates how neural networks are used to do non-linear regressions. The technique is presented in a simple and didactic manner and applied to fit potential energy surfaces for the FeC molecule and for the reaction H + H2. It shows how to do the fitting for single- and multi-variable system providing examples and code that can be easily extended to many problems in chemistry. All the code used to perform the fitting and generate the results is available as a Jupyter Notebook, which can be used without neither installation nor configuration INTRODUÇÃO Redes neurais são um subgrupo de algoritmos de aprendizagem de máquina, que foi idealizado em 19431 e, em 1959 já tinha sua primeira aplicação em um filtro para eliminar ecos em linhas telefônicas, denominado MADALINE.2 As aplicações tiveram uma grande pausa até o sucesso moderno, resultado da evolução dos hardwares e, também, do desenvolvimento dos algoritmos. Com isso, as aplicações de redes neurais chegaram, inclusive, a jogar jogos complexos como o go e ser campeão mundial,3 analisar rostos e identificar a pessoa,4 analisar e copiar voz,5 entre outras aplicações que não seriam possíveis de implementar com programação comum, por causa da complexidade da solução direta do problema. Em química, não foi diferente e diversas aplicações foram feitas, como a de Schütt et al., 6 que desenvolveu um framework baseado em redes neurais profundas que calcula uma função de onda aproximada em uma base local de orbitais atômicos para poder retirar todas as outras informações do estado fundamental eletrônico de um sistema molecular, na tentativa de unificar o aprendizado de máquina com os sistemas quânticos. Segler e Waller desenvolveram um sistema de redes neurais para previsão de retrossíntese e de reação.7 As aplicações são extensas e demonstram que é uma técnica importante para o pesquisador da área.8-15 Além das aplicações para resolver problemas muito complexos, as redes neurais podem ser utilizadas em ajuste de função para dados na forma de um conjunto de variáveis independentes para calcular uma outra dependente. Elas são adequadas porque são compostas de funções contínuas que podem ser usadas para ajustar qualquer forma funcional com precisão arbitrária16,17 e, por serem amplamente utilizadas, o nível de abstração adquirido permite o uso de modo que possa tratá-las como uma caixa preta, sem a necessidade de conhecimento sobre a implementação dela. Além disso, não é necessário o conhecimento prévio de qual forma funcional os dados que se deseja ajustar obedecem. Essa flexibilidade fez com que ajuste de superfície de energia potencial (SEP) fosse amplamente feito com redes neurais feed-foward.18-26 O conceito de SEP tem origem aproximação Born-Oppenheimer, que permite descrever a energia para um estado eletrônico como função de 3N -6 variáveis para N > 2, que são as coordenadas internas para os graus de liberdade nucleares, com N sendo o número de átomos no sistema. Para o caso de diatômicas, há apenas um grau de liberdade. A SEP é um caso interessante em que não há uma forma funcional que descreva todos os casos possíveis, apesar de existirem determinações de funções empíricas que, com o ajuste de alguns parâmetros, obtém-se uma função para o sistema.27 Ao utilizar redes neurais para tanto, retira-se o problema de funções que não possam representar determinadas características da SEP e diminui a interferência humana no ajuste. Neste artigo, será utilizado o problema de ajuste de uma função para a SEP para criar um guia de como realizar um ajuste simples utilizando redes neurais feed-foward em uma abordagem de caixa preta, como implementado no pacote scikit-learn para Python 3.28 Será feito um ajuste para a SEP da diatômica FeC e para a SEP da reação H + H2. Dessa forma, terá um exemplo de um ajuste não linear e multivariável, que é facilmente extensível para outros casos em que se deseja fazer um ajuste. O artigo será acompanhado, também, de um Jupyter Notebook, contendo todo o código necessário para gerar os dados apresentados, auxiliando na compreensão do trabalho e na aplicação em outros problemas de regressão. Esse formato, utilizado com sucesso em trabalhos anteriores,29 é especialmente conveniente para distribuir e executar códigos Python devido a existência de ferramentas como o Google Colaboratory30 que não exigem configuração ou instalação. Com isso, pretende-se criar uma introdução mais compreensiva para comunidade química do uso de redes neurais.
FUNDAMENTOS TEÓRICOS O algoritmo de redes neurais utilizado nesse artigo é de aprendizado supervisionado. Isso significa que, para realizar o ajuste, é necessário fornecer tanto os valores da variável independente quanto os da variável alvo, que são chamados de conjunto de treino. Então, para, por exemplo, ajustar uma função de uma SEP que relacione a energia em função das coordenadas do sistema, as variáveis independentes são as coordenadas do sistema e a variável alvo é a energia. Também, é um algoritmo de regressão por perceptron em multicamada. O perceptron é uma unidade de decisão binária. Se combinado em uma rede de perceptron e, após o ajuste dos seus parâmetros, seria possível utilizar em um aparelho que teria a capacidade de reconhecer padrões. Logo, aparentemente, ele poderia compreender, o que dá origem ao seu nome (do inglês, perceive). 31,32 A rede de perceptrons é o que historicamente deu origem às redes neurais, pela semelhança no seu comportamento, tanto no uso de operadores lógicos, quanto no comportamento binário em que, se a variável de entrada assumir um valor maior que um limite predefinido, o perceptron produz como valor de saída um. Ao contrário, o valor produzido é zero. Isso seria semelhante a um neurônio disparar após haver uma mudança no potencial elétrico dentro da célula.31 Matematicamente, a unidade perceptron é representada pela equação 1, que recebe um valor de entrada x, e tem como parâmetros os valores de w e de b, que são, respectivamente, o peso dado ao valor de entrada e o negativo do valor limiar da unidade.
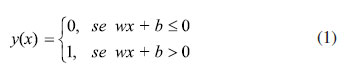
Esse comportamento binário, descrito para a rede de perceptrons, claramente seria útil apenas para tarefas de classificação. Para ser um algoritmo de regressão, há apenas uma transformação do y de uma variável discreta para uma variável contínua. Assim, o parâmetro b perde o sentido de um valor limiar para ser encarado como um parâmetro linear da equação, que é, agora, chamado de viés. Por fim, a característica não linear do ajuste vem da aplicação de uma função de ativação que recebe, como argumento, a função anterior. A representação de cada unidade é dada por:

Ser multicamada significa que terá uma ou mais camadas de unidades entre os dados de entrada e os de saída, chamadas de camadas escondidas. As unidades de todas essas camadas são os neurônios. A representação da estrutura para uma rede que siga essa descrição está na Figura 1.
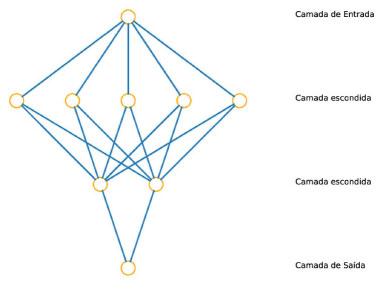 Figura 1. Representação da estrutura de uma rede neural. Os círculos laranjas representam as unidades e as linhas azuis representam a distribuição dos resultados matemáticos gerados pelos neurônios e enviados à próxima camada
Os parâmetros de cada unidade dessa rede serão variados de forma a minimizar a função de perda, equação 3, que é dependente do erro quadrático médio entre os dados de saída calculados, Ê, e os fornecidos como alvo, E, que são vetores com o número de pontos igual ao utilizado para o treino da rede, Nα, e um fator de regularização, o L2, definido na equação 4. Os termos que compõem a equação 4 são o parâmetro a, o número de neurônios, Ni, e os pesos de cada neurônio i, wi. O fator L2 permite uma regularização maior ao direcionar os pesos o mais perto possível de zero, podendo-se controlar a influência da regularização na determinação dos parâmetros e no desempenho do modelo, pelo valor do a. Na prática, esse parâmetro pode reduzir a importância de cada valor individual dos dados de entrada, privilegiando a suavidade do modelo final, podendo levar a underfitting, se muito grande, e overfitting, se muito pequeno. Overfitting acontece se o modelo previsto se ajusta aos dados fornecidos, porém, ao fazer previsões para pontos, fora do conjunto de treinamento, tem erros grandes.33 Underfitting é o efeito contrário.
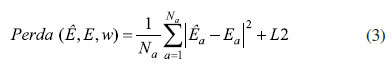

A função de ativação utilizada nas unidades das camadas escondidas será a tangente hiperbólica. Essa função tem os seus limites de ±∞ iguais a ±1 As unidades das camadas escondidas são definidas da seguinte forma:
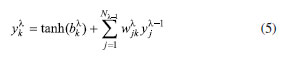
Em que Nl1 é o número de neurônios na camada l - 1 e j é um neurônio da camada l - 1. O parâmetro é o peso da conexão do neurônio k da camada l com o neurônio j da camada l -1 e é o viés do neurônio k da camada l, sendo ambos determinados durante o processo de treinamento da rede neural por uma regressão não linear. Vale notar que, para a camada de saída, é utilizada a função identidade no lugar da tangente hiperbólica, para fornecer um valor escalar que não esteja entre -1 e 1 e, para a camada de entrada, são utilizados os dados como fornecido pelo usuário. Existem vários parâmetros a serem definidos em uma rede neural que podem levar a resultados melhores ou piores, mas apenas alguns serão destacados. Para uma explicação mais ampla, referências específicas são recomendadas ao leitor.34-37 Um dos parâmetros a ser definido é o tamanho da rede neural. Uma técnica para determinar a quantidade de camadas e o número de neurônios nas camadas é começar com uma camada escondida do tamanho da camada de entrada e, a partir disso, construir redes neurais maiores,31 considerando que, ao aumentar, o custo computacional também cresce, assim como a possibilidade de overfitting. O processo de minimização da função de perda parte de um valor inicial para, a partir desse valor, seguir na direção do gradiente da função de perda, equação 3. A construção da rede precisa ser feita com valores iniciais para os pesos e vieses. A escolha desses parâmetros iniciais, a priori, não tem um valor preferido. Então, a escolha deles é gerada de forma randômica. O grande problema é que a otimização desses parâmetros acontece de forma não linear, não tendo apenas um mínimo. Portanto, ela pode parar em mínimos locais, o que faz a escolha desses parâmetros iniciais influenciar no resultado final. Então, para escolher os parâmetros iniciais, é feita uma amostragem pela variação do estado randômico e, após a otimização das redes neurais, seleciona-se o que produzir o menor erro, por exemplo. Na Tabela 1, estão reunidos alguns passos que foram aqui citados, para auxiliar o leitor em aplicações mais simples e fornecer uma ideia geral do procedimento.
Resumindo, para um ajuste utilizando as redes neurais, o usuário precisará fornecer um conjunto que contenha os valores para as variáveis independentes da função e o valor da variável dependente produzido por esse conjunto. Também, o usuário precisará definir a função de ativação por ele desejada. Para o caso de ajustes lineares, ele deve se utilizar da identidade. No caso de ajustes não-lineares, recomenda-se o uso da tangente hiperbólica. Após, ele precisará definir o número de neurônios, o que poderá ser feito aumentando-se o número de neurônios na rede, evitando que ocorra overfitting. O usuário precisará escolher o parâmetro de regularização, que deve ser um valor que capture o comportamento do seu conjunto de treino, mas, também, que evite o overfitting. Por fim, é recomendado que se teste uma gama de valores para o estado randômico.
DISCUSSÃO FeC Determinaremos a curva de energia potencial eletrônica para o FeC utilizando redes neurais feed-forward com treino supervisionado e, como função de ativação, a tangente hiperbólica, conforme implementado no pacote scikit-learn. O erro quadrático médio será usado para analisar o erro do ajuste. Com essas funções, calcularemos as constantes espectroscópicas, a distância internuclear de equilíbrio, a energia de dissociação e a frequência vibracional harmônica. Isso será feito para validar o ajuste nas regiões entre pontos. Para obter a distância internuclear de equilíbrio, teremos que encontrar a distância que tem como imagem o mínimo de energia potencial eletrônica para a molécula FeC. A energia de dissociação é calculada por meio da diferença entre a energia dos átomos dissociados e da energia na distância internuclear de equilíbrio. A frequência de vibração harmônica pode ser calculada a partir da equação 6. A constante de vibração harmônica, k, é obtida da segunda derivada do potencial na distância de equilíbrio.38 Os outros termos que compõem a equação são μ, que é a massa reduzida, e c, que é a velocidade da luz.

Para ajustar uma função, precisa-se, primeiramente, calcular os pontos que servirão como conjunto de treino. Portanto, por meio de métodos de estrutura eletrônica, mais especificamente o nível teórico B3LYP/def2-TZVP39-41 utilizando o programa ORCA 4.1,42 são calculados os valores de energia potencial eletrônica para 50 distâncias internucleares entre 1,00 e 4,50 Å, igualmente espaçadas.43 Com essas distâncias e as energias calculadas para elas, tem-se todas as informações necessárias para ajustar a rede neural. As distâncias antes de serem usadas na camada de entrada serão transformadas em coordenadas de Morse, da seguinte forma:

Em que g é escolhido como 1 Å. Isso ajuda no ajuste pois é uma forma funcional que a rede terá que seguir, em que o valor dela se aproxima de zero quando a distância vai ao infinito, um comportamento esperado para a energia de interação. Seria possível o ajuste sem utilizar a coordenada de Morse, porém, seria de menor qualidade e, com isso, introduz-se a ideia de criação de características, que é importante em aplicações mais avançadas de redes neurais.44-46 As energias serão os alvos calculados na camada de saída. Portanto, a função ajustada mapeia os valores de energia em função das distâncias internucleares. O ajuste segue, depois de carregadas as informações em matrizes NumPy (numpy.array),47 com uma expansão de muitos corpos, equação 8, com termos de um corpo e de dois corpos, sendo, respectivamente, as energias dos átomos Fe e O e a energia da diatômica FeC relativa à energia dos átomos que a compõe. Isso diminui o erro do ajuste pois a parte que será ajustada, ou seja, a que é dependente de pelo menos uma variável, terá uma contribuição energética menor, diminuindo a influência do erro do ajuste no potencial total.
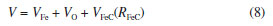
As redes neurais têm o ajuste com menores erros ao serem feitas para valores com média zero e variância um. Então, esses valores são escalados da seguinte forma:

em que,
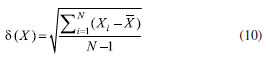
No caso, X são os valores passados às camadas de entrada e de saída e -X é a média dos N valores. Para ajustar a rede neural, existe uma série de parâmetros que precisam ser escolhidos. Definimos que vamos utilizar a tangente hiperbólica nas camadas escondidas, que terão duas camadas com cinco e dois neurônios. Para minimizar a função perda, o método BFGS de baixa memória (lbfgs),48-50 a tolerância e o número máximo de iterações são também escolhidos previamente para valores que produzem bons resultados. Um parâmetro importante é o estado randômico de inicialização dos parâmetros, já que esse é um ajuste não linear com diversos mínimos locais. É feita uma estrutura de repetição, procurando-se o conjunto de valores iniciais que produz menor erro quadrático médio, dentro de 100 tentativas. Por ser um conjunto de dados pequenos e uma rede simples, essas 100 tentativas levam algo em torno de 20 segundos para terminar. Por fim, também escolhemos o parâmetro a, da regularização L2, como 10-2. Ao final desse passo, a função final é obtida, pronta para o uso. Os parâmetros utilizados no ajuste estão reunidos na Tabela 1. Esses valores não são os únicos a produzir um ajuste adequado. Pode-se fazer um teste variando o número de neurônios na rede. Uma sugestão seria experimentar com três neurônios na primeira camada e dois na segunda. Ao utilizar essa função para construir a curva de energia potencial, por meio do pacote matplotlib,51 juntamente aos pontos de estrutura eletrônica, a Figura 2 é produzida.
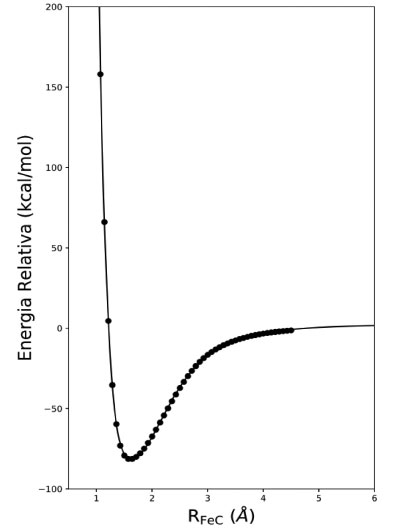 Figura 2. Curva de energia potencial para a diatômica FeC, ajustada utilizando redes neurais. A curva sólida é referente à energia prevista pela rede neural, enquanto os pontos são aqueles calculados pelo método de estrutura eletrônica no nível teórico B3LYP/def2-TZVP
Com a função da energia potencial eletrônica já calculada, podemos utilizá-la para calcular as constantes espectroscópicas. Para encontrar a distância de equilíbrio, utilizamos a função minimize do pacote SciPy,52 que vai calcular o mínimo local da função. Com isso, além da distância de equilíbrio, temos a energia para essa distância. Ao calcular a diferença das energias dos átomos com a energia mínima da molécula, temos a energia de dissociação, De. Por fim, para calcular a frequência vibracional harmônica, calculamos, primeiramente, a constante pela segunda derivada na distância de equilíbrio. Com ela, aplicamos na equação 6 e obtemos a frequência we. Na Tabela 2, estão reunidos os valores para o ajuste e para o nível teórico. Ao se comparar, percebe-se que o ajuste adicionou pouco erro em todos os cálculos de constantes. Se comparada, a energia de dissociação só tem uma diferença de 0,3 kcal/mol, valor muito pequeno, considerando a escala dos valores do problema. A distância de equilíbrio tem um pequeno desvio de 0,022 Å, o que é muito pouco. O desvio da frequência de vibracional harmônica ficou em 4 cm-1. Combinando essa análise com a raiz do erro quadrático médio, de 0,60 kcal/mol, verifica-se o ajuste como sendo adequado.

H + H2 H + H2 é a mais simples reação envolvendo três átomos e, por isso, é amplamente estudada para servir como modelo teórico para testes de novos métodos.53-57 Essa reação tem a descrição completa em um sistema de três coordenadas e, assim, é adicionada complexidade em relação ao sistema de diatômicas. Para o ajuste da SEP reativa do H + H2, há uma grande sobreposição nas técnicas utilizadas para o FeC. Continuamos utilizando a maioria dos parâmetros para a regressão, havendo apenas duas mudanças. Primeiramente, a quantidade de neurônios muda de duas camadas escondidas com cinco e dois neurônios para vinte e dez neurônios. Assim, a função tem uma maior flexibilidade, exigida para um ajuste de maior dimensão. Também, é mudado o parâmetro de regularização para 10-4, obtendo-se um ajuste mais preciso. Os parâmetros utilizados no ajuste estão reunidos na Tabela 3. Vale notar, assim como no primeiro ajuste, esse não é o único conjunto de parâmetros que produz um ajuste adequado e, portanto, convida-se o leitor a experimentar outras configurações da rede.
Como no caso do FeC, são necessários os pontos de energia para cada configuração nuclear, para o ajuste da função, ou seja, o conjunto de treino. Portanto, utilizou-se o potencial ajustado no nível teórico CCI/CBS de Peterson et al.58 como substituto dos pontos de estrutura eletrônica e foram calculados 1711 pontos distribuídos de forma a se ter pontos por toda a superfície reativa da aproximação linear, levando em conta a simetria dela. Isso quer dizer que ao descrever a aproximação de um dos átomos da reação aos outros dois, estamos descrevendo o que aconteceria a qualquer uma das três possíveis combinações desses três átomos, com essa descrição. Uma nova técnica de transformação dos dados da camada de entrada foi usada. Foram empregados os polinômios permutacionalmente invariantes (PIP), de forma a se conseguir, com menos dados, representar uma maior parte do potencial e conseguir adicionar a invariância na energia, dado à permutação de átomos idênticos. É uma técnica de combinação de monômios, de forma que se produza uma base invariante sobre permutação. A explicação sobre ela está fora do escopo desse artigo, mas é recomendado ao leitor uma ampla bibliografia desenvolvida por Bowman et al.21,59,60 As camadas de entrada serão da seguinte forma:
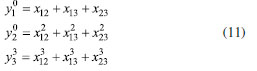
Em que xij é a coordenada de Morse para a distância entre os átomos i e j. Essa é a forma do polinômio por ser o caso de três átomos iguais, assim como acontece na reação estudada, H + H2. Para validar o ajuste iremos utilizar, juntamente ao erro quadrático médio, uma comparação entre os gráficos da SEP para o potencial original com o ajustado pela rede neural. Esse gráfico é um corte da superfície total feito para a aproximação linear do átomo de hidrogênio da molécula de hidrogênio. O gráfico tem, em suas coordenadas, as distâncias entre dois dos três hidrogênios e a energia é representada por projeções de curvas isopotenciais em sua superfície. O ajuste teve um erro quadrático médio de 0,076 kcal/mol. O erro é bastante pequeno pois o interesse era em ajustar apenas uma parte da SEP, a referente à aproximação linear de um átomo de hidrogênio à diatômica de hidrogênio e, com a simetria adicionada pelos PIP, a região que precisa ser amostrada é bem pequena. Ao se comparar o gráfico produzido pela rede neural, Figura 3, com o do potencial original,58 é verificável a semelhança entre os dois, sendo outra evidência de o ajuste ter sido conduzido adequadamente.
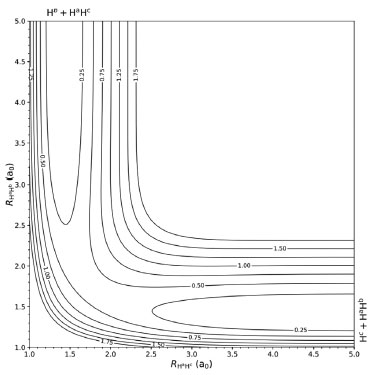 Figura 3. SEP da reação Hc + HªHb → Hb + HªHc colinear, ajustada pela rede neural, em coordenadas internas (RHª Hc, RHª Hb). As curvas isopotenciais são de 0,25 eV. As distâncias, nos dois eixos, estão em a0
CONSIDERAÇÕES FINAIS As redes neurais podem ser aplicadas à regressão e à classificação, o que pode ajudar qualquer pesquisador na análise de seus resultados. Comparada aos métodos tradicionais, ela traz a vantagem de ajustar uma função genérica, podendo se ajustar a qualquer função contínua e, por ser amplamente empregada, alcançou um nível alto de abstração e, para aplicações mais simples, pode ser utilizada sendo encarada como uma caixa preta. Apesar disso, não é um conhecimento difundido na comunidade química brasileira. Nesse estudo, foi realizado ajuste de funções para a superfície de energia potencial para o FeC e para a reação H + H2. Os ajustes foram feitos de forma bastante simples e, com pouca variação, podem ser estendidos a uma variedade de casos. Então, com esse estudo, espera-se criar mais que uma introdução ao assunto para a comunidade e servir, também, como uma amostra do potencial da técnica para incentivar sua exploração.
MATERIAL SUPLEMENTAR O código comentado, descrevendo os processos envolvidos para produzir os resultados descritos aqui está disponível em http://quimicanova.sbq.org.br/ e no website GitHub em https://github.com/eduardo-vicentini/artigoQN_data/blob/master/artigoQN.ipynb, como um Jupyter Notebook, com acesso livre.
AGRADECIMENTOS Os autores agradecem à FAPESP, processos #2015/11714-0 e #2020/08553-2, e ao CNPq, processo #306830/2018-3. E. D. Vicentini agradece à CAPES pela bolsa concedida.
REFERÊNCIAS 1. McCulloch, W. S. ; Pitts, W. ; Bull. Math. Biophys. 1943, 5, 115. 2. https://cs.stanford.edu/people/eroberts/courses/soco/projects/neural-networks/History/history1.html acessada em setembro 2020. 3. Silver, D. ; Huang, A. ; Maddison, C. J. ; Guez, A. ; Sifre, L. ; Van Den Driessche, G. ; Schrittwieser, J. ; Antonoglou, I. ; Panneershelvam, V. ; Lanctot, M. ; Nature 2016, 529, 484. 4. Sun, Y. ; Liang, D. ; Wang, X. ; Tang, X. ; arXiv preprint arXiv:1502.00873 2015. 5. Hinton, G. ; Deng, L. ; Yu, D. ; Dahl, G. E. ; Mohamed, A. -r. ; Jaitly, N. ; Senior, A. ; Vanhoucke, V. ; Nguyen, P. ; Sainath, T. N. ; IEEE Signal Process. Mag. 2012, 29, 82. 6. Schütt, K. T. ; Gastegger, M. ; Tkatchenko, A. ; Müller, K. R. ; Maurer, R. J. ; Nat. Commun. 2019, 10, 1. 7. Segler, M. H. S. ; Waller, M. P. ; Chem - Eur. J. 2017, 23, 5966. 8. Mardt, A. ; Pasquali, L. ; Wu, H. ; Noé, F. ; Nat. Commun. 2018, 9, 5. 9. Balabin, R. M. ; Lomakina, E. I. ; J. Chem. Phys. 2009, 131, 074104. 10. Lemes, M. R. ; Dal Pino Júnior, A. ; Quim. Nova 2008, 31, 1141. 11. Zen, R. ; My, L. ; Tan, R. ; Hébert, F. ; Gattobigio, M. ; Miniatura, C. ; Poletti, D. ; Bressan, S. ; Phys. Rev. E 2020, 101, 053301. 12. Su, S. ; Yang, Y. ; Gan, H. ; Zheng, S. ; Gu, F. ; Zhao, C. ; Xu, J. ; J. Chem. Inf. Model. 2020, 60, 1165. 13. Li, X. ; Sanderson, A. R. ; Allen, S. S. ; Lahr, R. H. ; Analyst 2020, 145, 1511. 14. Bort, W. ; Baskin, I. I. ; Sidorov, P. ; Marcou, G. ; Horvath, D. ; Madzhidov, T. ; Varnek, A. ; Gimadiev, T. ; Nugmanov, R. ; Mukanov, A. ; ChemRxiv 2020. 15. Manzhos, S. ; Machine Learning: Science and Technology 2020, 1, 013002. 16. Attali, J. -G. ; Pagès, G. ; Neural Networks 1997, 10, 1069. 17. Schäfer, A. M. ; Zimmermann, H. -G. ; Int. J. Neural Syst. 2007, 17, 253. 18. Manzhos, S. ; Dawes, R. ; Carrington, T. ; Int. J. Quantum Chem. 2015, 115, 1012. 19. Li, J. ; Jiang, B. ; Guo, H. ; J. Chem. Phys. 2013, 139, 204103. 20. Jiang, B. ; Li, J. ; Guo, H. ; Int. Rev. Phys. Chem. 2016, 35, 479. 21. Jiang, B. ; Guo, H. ; J. Chem. Phys. 2013, 139, 054112. 22. Lu, X. ; Meng, Q. ; Wang, X. ; Fu, B. ; Zhang, D. H. ; J. Chem. Phys. 2018, 149, 174303. 23. Handley, C. M. ; Popelier, P. L. ; J. Phys. Chem. A 2010, 114, 3371. 24. Behler, J. ; Phys. Chem. Chem. Phys. 2011, 13, 17930. 25. Yuan, M. ; Li, W. ; Yuan, J. ; Chen, M. ; Int. J. Quantum Chem. 2018, 118, e25493. 26. Wang, S. ; He, D. ; Li, W. ; Chen, M. ; RSC Adv. 2017, 7, 35648. 27. Le Roy, R. J. ; Pashov, A. ; J. Quant. Spectrosc. Radiat. Transfer 2017, 186, 210. 28. Pedregosa, F. ; Varoquaux, G. ; Gramfort, A. ; Michel, V. ; Thirion, B. ; Grisel, O. ; Blondel, M. ; Prettenhofer, P. ; Weiss, R. ; Dubourg, V. ; Vanderplas, J. ; Passos, A. ; Cournapeau, D. ; Brucher, M. ; Perrot, M. ; Duchesnay, É. ; Journal of Machine Learning Research 2011, 12, 2825. 29. De Oliveira Filho, A. G. ; De Lima Batista, A. P. ; Quim. Nova 2016, 39, 118. 30. Google Colaboratory, disponível em https://colab.research.google.com/, acessada em setembro 2020. 31. Fiesler, E. ; Beale, R. ; Handbook of neural computation Oxford University Press, Inc. : Oxford, 1997. 32. Rosenblatt, F. ; Principles of Neurodynamics, Spartan: Washington, D. C. , 1962. 33. Andreas, M. C. ; Guido, S. ; Introduction to Machine Learning with Python: A Guide for Data Scientists, O'Reilly: Beijing, 2016. 34. Géron, A. ; Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems O'Reilly Media: Sebastopol, 2019. 35. Ba, J. ; Caruana, R. ; Neural Information Processing Systems 2014, 2654. 36. Hunter, D. ; Yu, H. ; Pukish, III, M. S. ; Kolbusz, J. ; Wilamowski, B. M. ; IEEE Trans. Ind. Electron. 2012, 8, 228. 37. Bebis, G. ; Georgiopoulos, M. ; IEEE Potentials 1994, 13, 27. 38. Sala, O. ; Quim. Nova 2008, 31, 914. 39. Becke, A. D. ; J. Chem. Phys. 1993, 98, 5648. 40. Stephens, P. J. ; Devlin, F. J. ; Chabalowski, C. F. ; Frisch, M. J. ; J. Phys. Chem. 1994, 98, 11623. 41. Weigend, F. ; Ahlrichs, R. ; Phys. Chem. Chem. Phys. 2005, 7, 3297. 42. Neese, F. ; WIREs Comput. Mol. Sci. 2017. 43. Vicentini, E. D. ; Dissertação de Mestrado, Universidade de São Paulo, Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto, Brasil, 2019. 44. Garla, V. N. ; Brandt, C. ; J. Biomed. Inform. 2012, 45, 992. 45. Cormack, G. V. ; Hidalgo, J. M. G. ; Sánz, E. P. ; Proceedings of the 30th annual international ACM SIGIR conference on Research and development in information retrieval, Amsterdam, 2007. 46. Yu, H. -F. ; Lo, H. -Y. ; Hsieh, H. -P. ; Lou, J. -K. ; McKenzie, T. G. ; Chou, J. -W. ; Chung, P. -H. ; Ho, C. -H. ; Chang, C. -F. ; Wei, Y. -H. ; Weng, J. -Y. ; Yan, E. -S. ; Chang, C. -W. ; Kuo, T. -T. ; Lo, Y. -C. ; Chang, P. T. ; Po, C. ; Wang, C. -Y. ; Huang, Y. -H. ; Hung, C. -W. ; Ruan, Y. -X. ; Lin, Y. -S. ; Lin, S. -D. ; Lin, H. -T. ; Lin, C. -J. ; JMLR Workshop and Conference Proceedings 2010, 1, 1. 47. Walt, S. van der; Colbert, S. C. ; Varoquaux, G. ; Comput. Sci. Eng. 2011, 13, 22. 48. Byrd, R. H; Lu, P. ; Nocedal, J. ; Zhu, C. ; SIAM J. Sci. Comput. 1995, 16, 5. 49. Zhu, C. ; Byrd, R. H; Lu, P. ; Nocedal, J. ; ACM Trans. Math. Software 1997, 23, 4. 50. Morales, J. L. ; Nocedal, J. ; ACM Trans. Math. Software 2011, 38, 1. 51. Hunter, J. D. ; Comput. Sci. Eng. 2007, 9, 90. 52. Virtanen, P. ; Gommers, R. ; Oliphant, E. , T. ; Haberland, M. ; Reddy, T. ; Cournapeau, D. ; Burovski, E. ; Peterson, P. ; Weckesser, W. ; Bright, J. ; Walt, d. , v. , J. , S. ; Brett, M. ; Wilson, J. ; Millman, J. , K. ; Mayorov, N. ; Nelson, J. , R. , A. ; Jones, E. ; Kern, R. ; Larson, E. ; Carey, J. , C. ; Polat, İ. ; Feng, Y. ; Moore, W. , E. ; VanderPlas, J. ; Laxalde, D. ; Perktold, J. ; Cimrman, R. ; Henriksen, I. ; Quintero, A. , . . , E. ; Harris, R. , C. ; Archibald, M. , A. ; Ribeiro, H. , A. ; Pedregosa, F. ; Mulbregt, v. , P. ; Vijaykumar, A. ; Bardelli, P. , A. ; Rothberg, A. ; Hilboll, A. ; Kloeckner, A. ; Scopatz, A. ; Lee, A. ; Rokem, A. ; Woods, N. , C. ; Fulton, C. ; Masson, C. ; Häggström, C. ; Fitzgerald, C. ; Nicholson, A. , D. ; Hagen, R. , D. ; Pasechnik, V. , D. ; Olivetti, E. ; Martin, E. ; Wieser, E. ; Silva, F. ; Lenders, F. ; Wilhelm, F. ; Young, G. ; Price, A. , G. ; Ingold, G. ; Allen, E. , G. ; Lee, R. , G. ; Audren, H. ; Probst, I. ; Dietrich, P. , J. ; Silterra, J. ; Webber, T. , J. ; Slavič, J. ; Nothman, J. ; Buchner, J. ; Kulick, J. ; Schönberger, L. , J. ; Cardoso, M. , d. , V. , J. ; Reimer, J. ; Harrington, J. ; Rodríguez, C. , L. , J. ; -Iglesias, N. , J. ; Kuczynski, J. ; Tritz, K. ; Thoma, M. ; Newville, M. ; Kümmerer, M. ; Bolingbroke, M. ; Tartre, M. ; Pak, M. ; Smith, J. , N. ; Nowaczyk, N. ; Shebanov, N. ; Pavlyk, O. ; Brodtkorb, A. , P. ; Lee, P. ; McGibbon, T. , R. ; Feldbauer, R. ; Lewis, S. ; Tygier, S. ; Sievert, S. ; Vigna, S. ; Peterson, S. ; More, S. ; Pudlik, T. ; Oshima, T. ; Pingel, J. , T. ; Robitaille, P. , T. ; Spura, T. ; Jones, R. , T. ; Cera, T. ; Leslie, T. ; Zito, T. ; Krauss, T. ; Upadhyay, U. ; Halchenko, O. , Y. ; Vázquez-Baeza, Y. ; Nat. Methods 2020, 17, 261. 53. Peterson, K. A. ; Woon, D. E. ; Dunning Jr, T. H. ; J. Chem. Phys. 1994, 100, 7410. 54. Mayne, H. R. ; Poirier, R. ; Polanyi, J. ; J. Chem. Phys. 1984, 80, 4025. 55. Partridge, H. ; Bauschlicher Jr, C. W. ; Stallcop, J. R. ; Levin, E. ; J. Chem. Phys. 1993, 99, 5951. 56. Garashchuk, S. ; Tannor, D. ; Chem. Phys. Lett. 1996, 262, 477. 57. Chapman, S. ; Garrett, B. C. ; Miller, W. H. ; J. Chem. Phys. 1975, 63, 2710. 58. Mielke, S. L. ; Garrett, B. C. ; Peterson, K. A. ; J. Chem. Phys. 2002, 116, 4142. 59. Xie, Z. ; Bowman, J. M. ; J. Chem. Theory Comput. 2010, 6, 26. 60. Braams, B. J. ; Bowman, J. M. ; Int. Rev. Phys. Chem. 2009, 28, 577. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






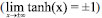 e é simétrica na origem, produzindo resultados que têm mais chance de estarem com média próxima a zero e, como elas funcionam como dado de entrada para a próxima camada, é melhor que estejam dessa forma, pois foi empiricamente mostrado que isso é uma característica dos dados de entrada que ajuda na precisão do ajuste.33
e é simétrica na origem, produzindo resultados que têm mais chance de estarem com média próxima a zero e, como elas funcionam como dado de entrada para a próxima camada, é melhor que estejam dessa forma, pois foi empiricamente mostrado que isso é uma característica dos dados de entrada que ajuda na precisão do ajuste.33
