JBCS

INTRODUÇÃO

As duas técnicas de Ressonância Magnética Nuclear (RMN) mais conhecidas na academia e na indústria são a RMN de imagens, denominada de Magnetic Resonance Imaging, muito conhecida nas áreas de radiologia para exames médicos, e a segunda técnica mais popular é a RMN de alta resolução, high-resolution NMR, amplamente utilizada em centrais de análise químicas na caracterização de estruturas químicas.^1-3

A RMN de baixo campo ou também denominada de RMN no domínio do tempo (RMN-DT)^4,5 é uma técnica baseada nos mesmos princípios físicos fundamentais das citadas acima, porém, com instrumentação mais simples e magnetos permanentes, não necessitando de manutenção com líquidos criogênicos. Assim, os espectrômetros de RMN-DT apresentam dimensões consideravelmente reduzidas, resultando em equipamentos leves e de bancada. Essas características tornam a RMN-DT uma ferramenta de custo reduzido e muito versátil, que vem sendo cada vez mais utilizada na indústria e na pesquisa.^5-9

Essa simplificação na instrumentação vem com algumas desvantagens, pois ao reduzir a homogeneidade e intensidade do campo magnético externo () aplicado na amostra, perde-se resolução e sensibilidade, portanto, a RMN-DT não tem resolução para determinar o mesmo tipo de informação à nível molecular que os RMN de alta resolução. Apesar disso, uma série de parâmetros físico-químicos podem ser estudados com esses espectrômetros.

A ilustração da Figura 1, compara espectrômetros de RMN de alta resolução (HR-NMR), do inglês high-resolution Nuclear Magnetic Resonance, com um espectrômetro de RMN de baixa resolução (RMN-DT),⁴ do inglês time-domain Nuclear Magnetic Resonance (TD-NMR), cuja resolução espectral é insuficiente para identificação de grupos químicos do sistema em estudo, de modo que, por exemplo, em uma amostra de etanol pura, nenhuma multiplicidade para sinais dos ¹H pode ser definida. Dessa forma, técnicas de baixa resolução são principalmente exploradas com base nas análises dos sinais no domínio do tempo, especialmente por métodos de relaxometria.

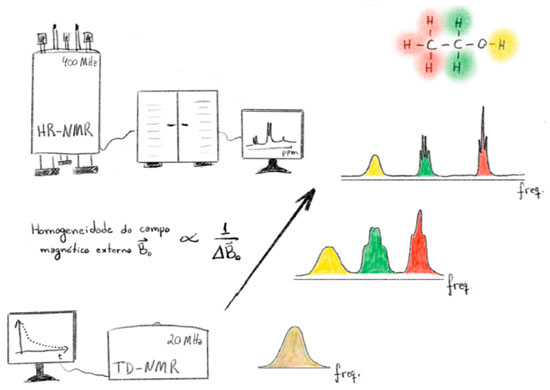Figura 1. Ilustração comparando um espectrômetro de RMN de alta resolução (HR-NMR) com um de baixa resolução (TD-NMR). No equipamento HR-NMR a homogeneidade do campo magnético externo ( 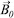) é alta, pois a variação do campo aplicado na amostra é pequena (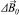 ~ 0), assim podemos obter informação à nível molecular nos espectros, por exemplo identificando os três grupos químicos CH₃, CH₂ e OH no espectro do etanol. Em sistemas magnéticos com ímãs permanentes, de baixa homogeneidade de campo magnético externo, temos 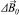> 0, não apresentando resolução no domínio da frequência para identificação dos grupos químicos. A definição de 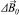pode ser consultada na referência T.B. Moraes9. Nos espectrômetros de RMN-DT, métodos de relaxometria são empregados e permitem o estudo de diferentes parâmetros físico-químicos

Ao analisar sinais de ¹H de uma amostra complexa em espectrômetros de RMN-DT, como por exemplo um pedaço de carne com fibras e gordura, o sinal obtido será formado pela contribuição de todos os spins nucleares dos diferentes ¹H presentes na amostra, que estão em diferentes ambientes químicos, com diferentes mobilidades, de modo que todos esses fatores vão influenciar na curva de relaxação resultante, e portanto é esperada a observação de vários tempos de relaxação longitudinal (T₁) e transversal (T₂) para essa amostra.

Nosso enfoque aqui não é discutir os métodos de relaxometria, os quais podem ser consultados nas referências,^5-9 mas discutir o processamento dos sinais obtidos por sequências de pulsos tais como Carr-Purcell-Meiboom-Gill (CPMG), Inversão Recuperação (IR), Saturação Recuperação (SR), Continuous Wave Free Precession (CWFP),^10,11 entre outras, que resultam em curvas de caráter multi-exponencial, depedentes dos tempos de relaxação T₁ e/ou T₂.

A determinação da contribuição de cada uma dessas componentes presentes no sinal experimental não é trivial, pois trata-se de um problema inverso com sinais ruídosos, matematicamente denominados de 'mal-posto' ou 'mal colocados'.^12-14 Uma consequência importante de um problema matemático inverso mal-posto, é que uma pequena variação nos seus valores de entrada pode resultar em uma solução final significativamente diferente, de modo que a inversão de um sinal admite multiplas soluções, sendo necessárias a utilização de métodos matemáticos sofisticados de regularização para seu processamento.^15-18

Vale aqui destacar o paralelo da Tranformada Inversa de Laplace (ILT) com a Transformada de Fourier (TF), utilizada na análise dos sinais FID (free induction decay) em espectrômetros de alta resolução. A TF é um problema matemático direto bem-posto, possuindo solução exata e única, portanto tendo comportamento estável, diferente se sua prima ILT.¹

A Figura 2 ilustra a problemática envolvida na solução de um problema inverso mal-posto típico na RMN-DT, como é o caso da análise multi-exponencial de sinais CPMG. É comum ao realizar o ajuste (fitting) desse sinal experimental - por exemplo, usando equações com duas ou com três componentes exponenciais - em ambos os casos obtermos um ajuste ótimo dos dados, e nessa situação fica a dúvida ao analista: qual dos dois processamentos descreve melhor o sistema em análise?

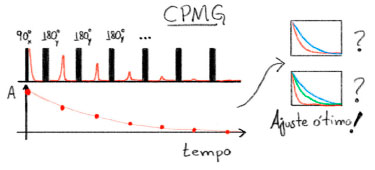Figura 2. Sequência de pulsos CPMG representando os ecos formados em vermelho. As amplitudes dos ecos formam a curva de decaimento T₂ do experimento (pontos vermelhos), que é então análisada com métodos de ajuste (fitting) do sinal ou através da Transformada Inversa de Laplace (ILT). Em algumas situações o ajuste ótimo dos dados pode ser obtido com diferentes números de exponenciais e valores de T₂ e amplitude, sendo ambas as respostas soluções matemática do problema, uma vez que se trata de um problema matemático mal-posto, que admite mais de uma solução

Físicamente é esperado que apenas uma das respostas possíveis seja a correta, pois podemos saber a priori que o sistema tem apenas duas componentes (por exemplo, saber que temos exatamente apenas dois tamanhos de poros, ou duas componentes químicas, etc) e, portanto, o ajuste com três exponencias foi uma solução matematicamente válida para os dados obtidos, porém, incorreta na interpretação física do sistema.

Assim, a questão fundamental aqui é que a forma como foram adquiridos os sinais experimentais, nos coloca nesta situação matemática mal-posta, que admite mais de uma solução, em que é necessário algum conhecimento extra sobre o sistema em análise para melhor determinar se, por exemplo, é esperada a solução com duas ou três componentes.

Os métodos de matemáticos de regularização, introduzem conhecimentos prévios na análise do sinal, como por exemplo, sabemos que os tempos de relaxação não devem ter valores negativos na RMN, então aceitam apenas soluções não-negativas; sabemos também que nas extremidades (tempos de relaxação muito curto e muito longo) não devem ser encontradas soluções; outra informação que assumimos verdadeira é que a distribuição de tempos de relaxação deve ter uma forma contínua, não sendo esperado encontrarmos distribuições descontínuas de tempos de relaxação, entre outras informações que podem ser assumidas na procura da solução mais realista.

Transformada Inversa de Laplace

Em muitas análises de dados de RMN-DT é suficiente a utilização de ajustes (fitting) mono-exponencial, bi-exponenciais ou tri-exponenciais, porém, geralmente na análise de amostras mais complexas, esses ajustes podem não descrever bem o sistema em observação, pois quando temos uma larga distribuição de valores de tempos de relaxação, esses métodos de ajuste não conseguem capturar corretamente cada contribuição.

Nessas situações, é vantajoso realizarmos a inversão dos dados experimentais através do processamento popularmente conhecido como "Transformada Inversa de Laplace", do inglês Inverse Laplace Transform (ILT),^13,14 que consegue obter curvas contínuas de distribuição dos tempos de relaxação T₁, T₂, ou de coeficientes de difusão, tamanho de poros etc (Figura 3).

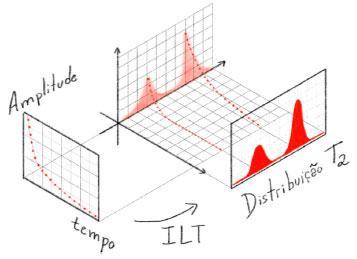Figura 3. Ilustração representando o processamento da Transformada Inversa de Laplace (ILT). Na esquerda o sinal do tipo CPMG é representado pelo gráfico das amplitudes dos ecos em função do tempo. Processando esse sinal com a ILT, obtemos o gráfico na direita, que representa a distribuição de tempos de relaxação T₂. A informação das posições dos picos de T₂ e das áreas dos picos refletem propriedades do material em análise, como distribuição de poros, teor de água/óleo, proporção carne/gordura, entre outros

Diversos softwares realizam esse processamento, alguns com acesso gratuito e outros sendo apenas fornecidos com as licenças pelas empresas fabricantes dos espectrômetros, cada qual com diferentes caraterísticas de processamento. Muitos algoritmos se propõem a resolver esse problema inverso mal-posto, como o CONTIN (CONTINuous distribution),¹⁸ o UpenWin (Uniform PENalty),^19,20 Butler-Reeds-Dawson (BRD),²¹ Decomposição em Valores Singulares truncado (TSVD),¹³ NNLS (non-negative least squares),¹⁷ PDCO (Primal-Dual interior method),²² entre muitos outros.

Nosso objetivo aqui é discutir os conceitos teóricos fundamentais e distribuir na comunidade de RMN brasileira um código de simples utilização, gratituto para pesquisa e ensino, desenvolvido para realização da ILT de sinais de RMN-DT na plataforma do software Origin Lab²³ e do Matlab, que são softwares muito utilizados pela nossa comunidade, visando o processamento de experimentos do tipo CPMG, Inversão Recuperação, Saturação Recuperação, entre outros.

Nas próximas seções apresentamos inicialmente uma descrição matemática do processamento realizado. A seguir são apresentados alguns resultados obtidos com sinais simulados e experimentais, e por fim dedicamos uma seção para detalhar o procedimento para utilização do programa desenvolvido. Um vídeo com explicação sobre instalação e utilização do código pode ser encontrado no link: https://youtu.be/aobB016VhXs ou requisitado no e-mail tiagobuemoraes@gmail.com

Problema Inverso na RMN-DT

Muitos problemas na física são descritos por equações diferenciais cuja solução é um sinal, s(t), que decai exponencialmente com o tempo, do tipo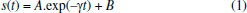

em que A é a amplitude do sinal, B é uma constante que determina a linha de base e γ sua constante de decaimento. O inverso desse fator, T = 1/γ, tem unidade de tempo e é denominado constante de tempo do decaimento.

Dentro do contexto da RMN-DT, tipicamente encontramos experimentos que resultam em sinais que decaem ou crescem exponencialmente no tempo, em que a constante de tempo que determina a taxa desse processo é dada pelos tempos de relaxação T₁ e/ou T₂. Um exemplo dessa situação é numa aquisição de um experimento CPMG, onde o sinal, s(t), começa com amplitude A, decai para zero (B=0) e apresenta tempo de relaxação T₂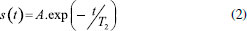

Um ajuste mono-exponecial dos dados obtidos nessa situação é suficiente para fornecer as constantes T₂, a amplitude A do sinal, e o offset B, caso esse último esteja diferente de zero.

Em amostras mais complexas, com vários tempos de relaxação, o sinal CPMG será composto pela somatória dessas componentes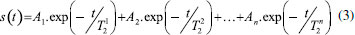

em que A₁ é a amplitude do grupo de spins com tempo de relaxação T₂¹, A₂ é a amplitude do grupo de spins com taxa de relaxação T₂², etc. Vale destacar que as amplitudes A_n desses sinais estão diretamente relacionadas com a quantidade de spins, naquele grupo, que apresentam aquele repectivo tempo de relaxação T₂ⁿ.

Na análise de sinais com apenas duas ou três componentes exponenciais, muitas vezes é suficiente realizamos simplesmente o ajuste (fitting) com uma função bi-expoencial ou tri-exponencial, como a equação 3, e assim determinar essas amplitudes A_n e tempos de relaxação T₂ⁿ.

Em sistemas mais complexos com larga distribuição de tempos de relaxação, como por exemplo, uma rocha porosa saturada com água e óleo, apenas a determinação de duas ou três componentes de amplitude A_n e tempos de relaxação T_n, pode não ser suficiente para caracterização do sistema, uma vez que não temos valores de amplitude e tempos de relaxação singulares (picos estreitos), mas o que temos é uma distribuição larga de tempos de relaxação, que vão corresponder à uma distribuição larga de tamanhos de poros na rocha, e quantidade de água e óleo presente.

A Figura 3 resume de maneira ilustrativa o objetivo do procedimento matemático realizado pela Transformada Inversa de Laplace. Na esquerda vemos um sinal do tipo CPMG, representado pelo gráfico das amplitudes dos ecos em função do tempo, que ao ser processado com a ILT resulta no gráfico na direita, revelando o espectro da distribuição de tempos de relaxação T₂.

Dessa forma, o processamento com a ILT revela a contribuição de diferentes grupos de spins do sistema em análise, onde os dois picos ilustrados na distribuição de T₂ podem por exemplo representar: óleo e água presentes em um grão de milho; ou fibras da carne e gordura presentes em um bife; ou dois grupos de tamanhos de poros em rochas, etc.

A distribuição obtida no processamento com a ILT pode advir de uma curva de Inversão Recuperação (T₁), Saturação Recuperação (T₁), CPMG (T₂), Difusão, entre outros experimentos, onde o que muda no processamento é a equação (kernel) utilizada na transformação, como será discutido na próxima seção.

Descrição matemática da ILT

A literatura apresenta diversos métodos matemáticos para realização da inversão desses sinais de RMN-DT, denominados genericamente de ILT pela comunidade científica de RMN. Vale destacar que a "Transformada Inversa de Laplace" aqui tratada é diferente do procedimento de mesmo nome encontrado em livros de Física Matemática.²⁴ Apesar de o nome estar formalmente incorreto no nosso contexto, a origem da utilização desse termo pela comunidade de RMN está relacionada com uma analogia com o procedimento da Transformada de Fourier Inversa. Maiores detalhes dessa história podem ser encontrados no trabalho de Fordham e colaboradores.¹³

No contexto da RMN-DT, na maioria das sequências de pulsos utilizadas, os sinais adquiridos apresentam caráter de crescimento ou decaimento exponencial e/ou gaussiano, que carregam informações, por exemplo dos tempos de relaxação ou coeficientes de difusão, onde o processamento matemático de inversão é realizado para obter as distribuições com a contribuição de cada componente. Assim, o que denominamos ILT é um caso particular de um problema mais geral de inversão das equações Integrais de Fredholm,^14,15,20 que podem ser escritas da forma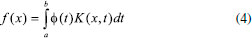

em que K(x,t) é a função kernel do sistema e a função φ(t) representa a função a ser determinada a partir da curva dos dados experimentais f(x).

No caso de um sinal experimental proveniente de uma sequência de pulsos CPMG, o sinal de entrada, c(t), é dado da forma c(t) = c(0)exp(-t/T₂), onde c é o sinal experimental, t é a variável de tempo do sinal adquirido, e T₂ o tempo de relaxação. Para uma amostra composta por k tempos de relaxação, temos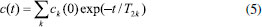

em que k denota o número de componentes presente na amostra.

Nas amostras reais, não temos valores singulares de tempos de relaxação, mas temos uma distribuição contínua de tempos de relaxação, assim podemos escrever o sinal como sendo dado pela integral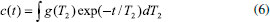

em que a função g(T₂) representa a distribuição dos tempos T₂, fornecendo as amplitudes de cada componente infinitesimal dT₂.

O propósito da Transformada Inversa de Laplace é obter a distribuição de amplitudes g(T₂), a partir do dado experimental c(t). Sabemos que para um sinal CPMG experimental, Figura 3, um conjunto de dados n é adquirido no intervalo de tempo t, com a presença do ruído experimental (ε_n), ou seja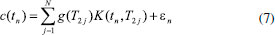

em que K é a equação kernel dessa somatória. Para um experimento CPMG o kernel deve ser definido como sendo composto por exponenciais decrescentes, veja equação 9. A inversão desse problema pode ser obtida através da minimização dos erros quadráticos, dada por

em que F(t) é a função que melhor descreve os dados experimentais c(t). Esse problema de minimização não é trivial, pois trata-se de um problema matemático mal-posto.^14,15 As propriedades e dificuldades desse tipo de problema inverso mal-posto é muito bem aprofundada por A. Istratov numa análise geral dos fenômenos físicos que envolvem análises expoenciais.¹²

Diversos métodos de regularização podem ser utilizados para obtenção das soluções das Integrais de Fredholm, apresentando diferentes características de estabilidade e confiabilidade. Fisicamente em nossos experimentos de RMN-DT é razoável esperar que nossa solução seja uma distribuição contínua da distribuição de tempos de relaxação, sem a existência de picos delta, pontos descontínuos ou valores negativos de amplitude na distribuição, Figura 3. Essas informações podem ser introduzidas no algoritmo do programa através de um termo que suaviza a distribuição e impõe resultados não-negativos, como se propõe o método NNLS (non-negative last square). Essa regularização da solução impõe resultados com distribuições mais estáveis e contínuas, e o termo de regularização (α) é responsável pela suavização dessa solução.

Diferentes valores de regularização α podem obter ajustes ótimos da curva, resultando em distribuições com certa variação. A definição de qual distribuição que representa melhor o sistema físico não é trivial e, portanto, apresenta certa subjetividade uma vez que o ajuste tem forte dependência com a razão sinal/ruído dos dados, pois trata-se de um problema matemático mal-posto que aceita multiplas soluções. Diversos métodos são utilizados e vêm sendo propostos para a otimização da escolha do parâmetro de regularização α.^25-27 Aqui nesse algoritmo apresentado, não implementamos nenhum dos métodos de otimização do parâmetro α, ficando a cargo do analista sua escolha, baseado no conhecimento extra que possa ter do seu material em estudo.

O código apresentado na próxima seção utiliza o método da Regularização de Tikhonov¹⁵ com decomposição de valores singulares assumindo a não-negatividade da resposta, também denominado de NNLS (non-negative last square), amplamente utilizado pela comunidade de RMN.²⁰ Além disso, o programa foi desenvolvido para trabalhar dentro da plataforma do software Origin Lab 9,²³ pois o mesmo já apresenta uma vasta oferta de ferramentas para análise de sinais, e é amplamente utilizado pela comunidade de RMN, não apresentando o processamento ILT dentro de suas funções padrões.

IMPLEMENTAÇÃO DA REGULARIZAÇÃO DE TIKHONOV NO SOFTWARE ORIGIN LAB

O programa desenvolvido foi implementando na plataforma do Origin Lab 9, para as equações (kernels) de experimentos do tipo Carr-Purcell-Meiboom-Gill (CPMG), Inversão Recuperação (IR) e Saturação Recuperação (SR), com as seguintes equações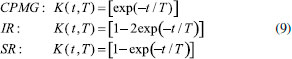

Após instalado o código, deve-se abrir o sinal a ser processado no Origin Lab, que tipicamente são duas colunas, uma de tempo e outra das amplitudes, como mostram as Figuras 4 a) e 4 b). Ao executar o comando "ilt" na linha de comando (command window) do Origin Lab, abre-se uma interface gráfica, apresentada na Figura 4c), na qual se deve fornecer os parâmetros de entrada (inputs) para o processamento do sinal. Na interface define-se o kernel do sinal experimental (função que representa a dependência esperada do sinal para uma dada sequência de pulsos), o parâmetro de regularização (α), a região da solução requerida entre Starting T value e Ending T value, o número total de pontos na distribuição resultante e o valor mínimo do valores singulares.

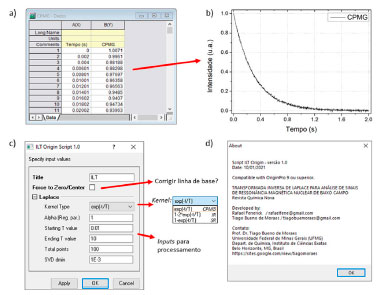Figura 4. A entrada do código são duas colunas: a primeira o eixo do tempo e a segunda as amplitudes c(t). Ao digitar "ilt" no command window, surge a interface gráfica no Origin Lab para entrar com os parâmetros de processamento do sinal

Após o processamento é gerada uma nova planilha (workbook), Figura 5 a), contendo na aba Result duas colunas, uma é o eixo dos tempos T e a outra com as amplitudes g(T) da ILT; na aba Fitting, apresenta a coluna do sinal corrigido e do ajuste (fitting) resultante; na aba Singular Values os valores singulares; e na aba Inputs os parâmetros utilizados no processamento.

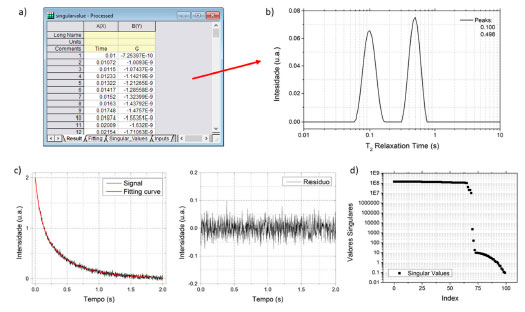Figura 5. Após processamento pelo programa "ilt" é gerada uma nova planilha com duas colunas, uma o eixo dos tempos T e outra com as amplitudes g(T) da ILT. São geradas também quatro figuras onde a) apresenta a distribuição de tempos de relaxação obtida já com eixo na escala logarítmica, b) a comparação entre o sinal de entrada e o fitting resultante (curva em vermelho) e o resíduo e c) os valores singulares resultantes da decomposição SVD

Além do workbook, o processamento gera quatro figuras, apresentadas nas Figuras 5 b)-d). Na Figura 5 b) apresenta-se a distribuição de tempos de relaxação obtidos, já com o eixo x em escala logarítmica; Figura 5 c) a comparação entre o sinal de entrada, o ajuste (fitting) resultante e o resíduo; e Figura 5 d) os valores singulares resultante da decomposição SVD.

Detalhes de como instalar o código, e da utilização são apresentados no vídeo que pode ser encontrado no site: https://sites.google.com/view/tiagomoraes ou pelo e-mail tiagobuemoraes@gmail.com.

RESULTADOS E DISCUSSÃO

Para certificarmos o correto funcionamento do código desenvolvido, realizamos uma série de processamentos com sinais simulados e experimentais, em diversas condições para os experimentos do tipo CPMG, IR, e SR. Nas próximas seções apresentamos alguns desses resultados, evidenciando as principais caracteristicas do programa frente aos diversos sinais e parâmetros de processamento.

Parâmetro de regularização alpha (α)

A Figura 6 apresenta o efeito do parâmetro de regularização α na distribuição de tempos de relaxação T₂ obtida após ILT de um sinal CPMG simulado bi-exponencial com tempos de relaxação de 0,1 s e 0,5 s. Como esperado, observa-se que para α maior, a distribuição se torna mais larga e de menor amplitude, mantendo a área total dos picos.

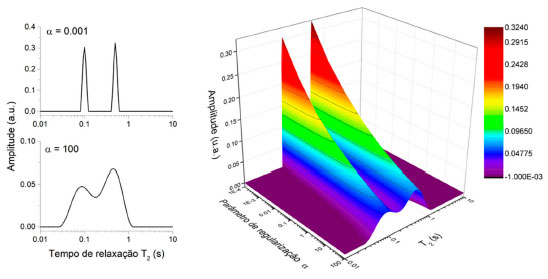Figura 6. Efeito do parâmetro de regularização (α) nos resultados obtidos para a distribuição de tempos de relaxação. Conforme maior o valor de α, mais larga se torna a distribuição

Diversos métodos para otimização do parâmetro α são encontrados na literatura. Em cada situação a resolução obtida e a largura das linhas mudam, ocorrendo situações onde a escolha do parâmetro α se torna subjetiva. Sinais com baixa razão sinal-ruído (s/r) apresentam esses problemas na escolha do parâmetro de regularização, sendo essas questões muito exploradas em diversos artigos recentes,^25-30 que buscam calcular a otimização do parâmetro (α) e mostram que a resolução é fortemente dependente da relação sinal-ruído, dentre outros fatores.

Demonstração com sinais simulados e experimentais

Uma vez que sinais puramente mono-exponenciais ou bi-exponenciais são raros em sistemas físicos reais, uma simulação mais realista pode ser feita gerando uma larga distribuição de picos gaussianos-logarítmica como apresentados na Figura 7, nas linhas pretas (dist). Após geradas as distribuições apresentadas, elas foram integradas para considerar a contribuição de cada tempo de relaxação no sinal no domínio do tempo, possibilitando assim gerar um sinal simulado CPMG de uma distribuição de tempos de relaxação previamente conhecida. Em seguida, os sinais gerados foram processados com a ILT, gerando as distribuições em vermelho (ILT) na Figura 7. Comparando as distribuições esperadas (dist) com as distribuições obtidas (ILT), vemos a excelente concordância.

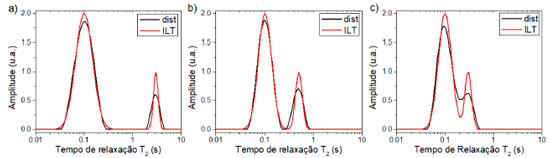Figura 7. Comparação da distribuição de tempos de relaxação utilizada para gerar sinal CPMG simulado (dist) em comparação com o sinal obtido (ILT) após processamento com a ILT do correspondente sinal no domínio do tempo em três situações diferentes. Em a) respectivamente picos nas posições 0,1 e 3 segundos. Em b) picos nas posições 0,1 e 0,5 segundos. Em c) nas posições 0,1 e 0,3 segundos

Na Figura 8 apresentamos um resumo da comparação de sinais simulados com os kernels de três experimentos: a) CPMG, b) Inversão Recuperação, c) Saturação Recuperação com diferentes tempos de relaxação. Nas Figuras 8 a)-c) são mostrados os sinais no domínio do tempo, e nas Figuras 8 d)-f) as respecticas distribuições de tempos de relaxação obtida em cada processamento, todos utilizando α = 0,1 e 100 pontos. Todos resultados apresentaram ótima concordância com as distribuições usadas na simulação dos sinais.

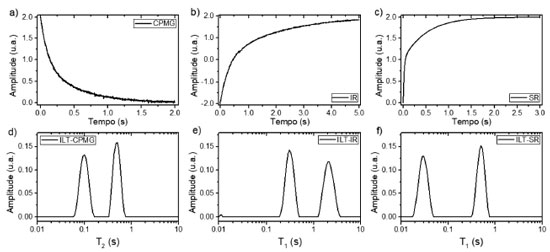Figura 8. Sinais simulados para os núcleos (kernel) de experimentos a) CPMG, b) Inversão Recuperação e c) Saturação Recuperação, todos com duas componentes de relaxação de mesma amplitude, centradas nos tempos CPMG (0,1 s e 0,5 s), IR (0,3 s e 2 s) e SR (0,03 s e 0,5 s). Em d), e) e f) são apresentados os respectivos resultados obtidos após processamento com o programa ILT

Na Figura 9 são apresentados sinais CPMG experimentais de uma amostra de cimento asfáltico de petróleo (CAP) adquiridos no espectrômetro Minispec ND mq20, Bruker, equipado com um magneto permanente de 0,47 Tesla (19,9 MHz) e sonda de 10 mm. As medidas foram realizadas em treze temperaturas diferentes, entre 30 °C e 150 °C, pelo sistema de controle BVT 3000. A sequência de pulsos utilizada foi CPMG, com τ = 0,1 ms e 10.000 ecos. O processamento ILT utilizou 100 pontos e α = 1.

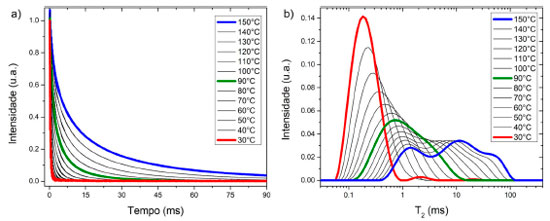Figura 9. a) Medidas CPMG de uma mistura de cimento asfáltico de petróleo em função da temperatura, em b) são apresentadas as respectivas distribuições de tempos de relaxação obtidas. Nota-se que em baixa temperatura, o aglomerado é um sistema rígido único com curto tempo de relaxação (~0,2 ms), e conforme sobe a temperatura, seus diferentes componentes ganham mobilidade, evidenciando três grupos com mobilidades distintas em 1 ms, 10 ms e 60 ms

INSTALAÇÃO E DISTRIBUIÇÃO DO PROGRAMA

Os requisitos básicos para instalação do programa são:

1) Ter o software Origin Lab 9 ou superior instalado no computador;

2) Realizar o download do arquivo "ILT Origin Script" v.1 no endereço: https://sites.google.com/view/tiagomoraes ou pelo e-mail tiagobuemoraes@gmail.com;

3) O programa desenvolvido é distribuido gratuitamente para utilização no ensino e pesquisa, apenas requisitamos os devidos créditos e citação à este artigo quando utilizado.

4) Outras dúvidas e sugestões podem ser encaminhadas para o e-mail: tiagobuemoraes@gmail.com

Algumas caracteristicas do código desenvolvido são:

i) Fácil instalação e manuseio. Uma vez instalado em um computador que possua o software do Origin Lab, sua utilização é realizada simplesmente chamando a função com o comando "ilt" na linha de comando (command window);

ii) Interface gráfica amigável, apresentando janelas, botões e menus autoexplicativos, o que permite seu uso sem necessidade de conhecimento de programação; e em conjunto com todas as ferramentas disponíveis no software Origin Lab;

Alguns aspectos práticos devem ser reforçados para a correta análise do processamento ILT, veja Figura 10:

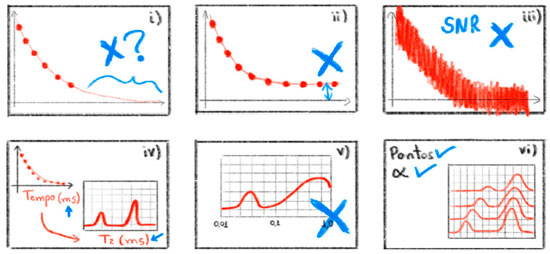Figura 10. Ilustração com detalhes que devem ser observados durante o processamento de sinais com a ILT

i) O sinal com decaimento/crescimento exponencial deve ser medido completamente, com uma linha de base longa o suficiente. Descontinuidades nos pontos iniciais ou um degrau na linha de base final, resultará em picos artificiais no espectro resultante da ILT;

ii) Picos artificias podem surgir de um pequeno deslocamento da linha de base (offset), para corrigir isso temos a opção "Force to zero/center" na interface gráfica;

iii) A distribuição obtida na ILT é fortemente dependente da relação sinal-ruído dos dados adquiridos, ou seja, sinais ruídosos vão resultar em distribuições pouco confiáveis;

iv) A distribuição obtida na ILT apresentará a mesma unidade de tempo que o sinal de entrada. Recomendamos utilizar os tempos no sinal de entrada em segundos, pois tipicamente os tempos de relaxação vão estar entre 0,001 s até 10 s;

v) O janela da distribuição ILT (Starting T value e Ending T value) e número de pontos (~100) devem ser corretamente escolhidos, pois se for muito curta ou longa vão gerar distribuições com picos artificiais e distorcidos;

vi) Para estudos comparando sinais, é recomendado sempre utilizar os mesmo parâmetros na aquisição dos sinais experimentais e também os mesmo parâmetros no processamento na ILT, como o número de pontos (~100), o parâmetro α, e os valores de Starting T value e Ending T value.

CONCLUSÕES

Neste trabalho apresentamos os conceitos fundamentais relacionados a Transformada Inversa de Laplace e desenvolvemos um código para execução desse processamento no software Origin Lab 9 ou versão superior, denominado "ILT Origin Script " v.1, de distribuição gratuita para utilização em pequisa e ensino, que possibilita a execução do método non-negative last square com regularização de Tikhonov, de sinais de Ressonância Magnética Nuclear no domínio do tempo.

Os resultados e discussões demonstram a correta determinação da distribuição dos tempos de relaxação com sinais simulados e experimentais, correspondendo aos resultados obtidos com outros softwares de processamento. Sendo assim, este é mais um código disponível para utilização. Versões atualizadas do código apresentado poderão ser solicitadas ao autor pelo e-mail: tiagobuemoraes@gmail.com

AGRADECIMENTOS

Agradeço as sugestões e contribuições no desenvolvimento dos códigos deste trabalho à Rafael Fenerick e Eduardo Ribeiro de Azevedo.

REFERÊNCIAS

1. Gerothanassis, P. I.; Troganis, A.; Exarchou, V.; Barbarossou, K.; Chem. Educ. Res. Pract. 2002, 3, 229.

2. Levitt, M. H.; Spin dynamics: basics of nuclear magnetic resonance, John Wiley & Sons: Chichester, 2001.

3. Gil, V. M. S.; Geraldes, C. F. G. C.; Ressonância magnética nuclear: fundamentos, métodos e aplicações, Fundação Calouste Gulbekian: Lisboa, 1987.

4. Nomes comuns na literatura são: Time domain - NMR (TD-NMR), Low-Field NMR (LF-NMR) e Low Resolution NMR (LR-NMR).

5. Colnago, L. A.; Wiesman, Z.; Pages, G.; Musse, M.; Monaretto, T.; Windt, C. W.; Rondeau-Mouro, C.; J. Magn. Reson. 2021, 323, 106899.

6. Zalesskiy, S. S.; Danieli, E.; Bluemich, B.; Ananikov, V. P.; Chem. Rev. 2014, 114, 5641.

7. Blumich, B.; TrAC, Trends Anal. Chem. 2016, 83, 2.

8. Song, Y. Q.; J. Magn. Reson. 2013, 229, 12.

9. Moraes, T. B.; Colnago, L. A.; Quim. Nova 2014, 37, 1410.

10. Moraes, T. B.; Monaretto, T.; Colnago, L. A.; J. Magn. Reson. 2016, 270, 1.

11. Moraes, T. B.; Monaretto, T.; Colnago, L. A.; Appl. Sci. 2019, 9, 1312.

12. Istratov, A. A.; Vyvenko, O. F.; Rev. Sci. Instrum. 1999, 70, 1233.

13. Fordham, E. J.; Venkataramanan, L.; Mitchell, J.; Valori, A.; Journal for the Basic Principles of Diffusion Theory, Experiment and Application 2017, 29, 1.

14. Venkataramanan, L.; Song, Y.; Hurlimann, M.; IEEE Trans. Signal Process 2002, 50, 1017.

15. Tikhonov, A. N.; Dokl. Akad. Nauk SSSR 1963, 151, 501.

16. Twomey, S.; Journal of the ACM 1963, 10, 97.

17. Lawson, C. L.; Hanson, R. J.; In Solving Least Squares Problems, Philadelphia SIAM: Philadelphia, 1974, Cap. 26

18. Provencher, S. W.; Comput. Phys. Commun. 1982, 27, 229.

19. Borgia, G. C.; Brown, R. J. S.; Fantazzini, P.; J. Magn. Reson. 1998, 132, 65.

20. Bortolotti, V.; Brizi, L.; Fantazzini, P.; Landi, G.; Zama, F.; SoftwareX 2019, 100302.

21. Butler, J. P.; Reeds, J. A.; Dawson, S. V.; SIAM J. Numer. Anal. 1981, 18, 381.

22. Berman, P.; Levi, O.; Parmet, Y.; Saunders, M.; Wiesman, Z.; Concepts Magn. Reson., Part A 2013, 42, 72.

23. Origin Lab; version 9.4, OriginLab Corporation, Northampton, MA, USA, 2017.

24. Arfken, G. B.; Weber, H. J., Mathematical Methods for Physicists, 4^th ed., Academic Press: San Diego, 1995.

25. Hansen, P. C.; SIAM Rev. 1992, 34, 561.

26. Song, Y. Q.; J. Magn. Reson. 2007, 25, 445.

27. Gruber, F. K.; Venkataramanan, L.; Habashy, T. M.; Singer, P. M.; Freed, D. E.; J. Magn. Reson. 2013, 228, 95.

28. Song, Y. Q.; Venkataramanan, L.; Burcaw, L.; J. Chem. Phys. 2005, 122, 104104.

29. Prange, M.; Song, Y. Q.; J. Magn. Reson. 2009, 196, 54.

30. Campisi-Pinto, S.; Levi, O.; Benson, D.; Cohen, M.; Resende, M. T.; Saunders, M.; Linder, C.; Wiesman, Z.; Appl. Magn. Reson. 2018, 49, 1129.