Nota Técnica
|
|
| Gurupi isotherms plot (GIP): uma ferramenta com interface gráfica intuitiva e gratuita como alternativa para o cálculo de parâmetros de isoterma de adsorção Gurupi isotherms plot (GIP): a tool with intuitive and free graphic interface as an alternative for the calculation of adsorption isotherma parameters |
|
Douglas A. CastroI; Mateus P. S. MilhomemI; Douglas H. PereiraI,*; Paulo V. B. LealII
I. Departamento de Ciências Exatas e Biotecnológicas, Universidade Federal do Tocantins, 77410-530 Gurupi - TO, Brasil Recebido em 08/02/2021 *e-mail: doug@uft.edu.br Gurupi Isotherms Plot (GIP) is a new software and has been developed to facilitate the study of absorptive processes. The adsorption isotherm parameters are determined by the GIP in a non-linearized way, and the current version is implemented to determine the parameters of Langmuir, Freundlich, Dubinin-Radushkevich, coefficient of determination (R2) and average relative error (ARE). In order to facilitate the access and use of the program, a friendly graphical interface has been developed with a response time in seconds. It should also be noted that is a free software. The program was tested with different sets of absorptive data and showed an excellent correlation with the literature data proving its performance. INTRODUÇÃO A escassez da água resultante do crescimento econômico e populacional é considerada como uma das ameaças mais importantes para a sociedade humana. Dentro das próximas décadas a água pode tornar-se o recurso mais estratégico, especialmente em regiões áridas e semi-áridas do mundo.1 Desse modo, alternativas que promovam a sustentabilidade no uso da água, tais como, educação ambiental e tratamento de efluentes devem ser sempre planejadas. A tecnologia de adsorção tem sido considerada como um dos processos mais eficientes e econômicos para a remoção de poluentes de correntes aquosas. O processo de adsorção é superior a muitos outros processos de tratamento em virtude do seu baixo custo e limite de operação.2 A dinâmica dos processos de adsorção de espécies químicas em solução em materiais sólidos, como minerais de argila, depende da distribuição destas espécies entre as fases sólidas e líquidas. O equilíbrio de adsorção é avaliado a partir das isotermas de adsorção que são representadas pelas concentrações das espécies químicas nas fases sólidas em relação às das fases líquidas.3 A determinação de isotermas de adsorção é uma ferramenta usada para caracterizar adsorventes. No entanto, a interpretação correta das isotermas requer a avaliação de alguns fatores, tais como: tamanho dos poros, propriedades do adsorvato e sua afinindade com o adsorvente, entre outros.4 Nesse contexto, a modelagem é importante para auxiliar na interpretação de resultados experimentais e útil para a determinação de propriedades.5 Diversos modelos isotérmicos foram desenvolvidos, cada um com características próprias, o que os tornam singulares na descrição de determinados sistemas de adsorção. Dentre os mais utilizados, para avaliação da adsorção química, destacam-se os modelos isotérmicos de Langmuir,6,7 Freundlich,8 Dubinin-Radushkevich,9 dentre outros. O modelo de isoterma de Langmuir é frequentemente usado para descrever as isotermas de equilíbrio de adsorção em superfícies homogêneas. Originalmente, a isoterma de Langmuir foi descrita para avaliar à adsorção de gases sobre sólidos. Entretanto, o modelo de isoterma também pode ser aplicado a distribuição de equilíbrio de adsorvato entre as fases líquida e sólida.10 O processo de adsorção em que uma superfície adsorvente heterogênea está envolvida na distribuição do adsorvato é explicado pelo modelo de Freundlich.11 Desse modo, a isoterma de Freundlich propõe uma equação empírica que assume que a superfície do adsorvente é heterogênea e com sítios de adsorção em diferentes níveis de energia.12 A equação de Dubinin-Radushkevich (DR) é amplamente utilizada para a descrição da adsorção em materiais microporosos. A equação é de origem semiempírica e baseia-se nos pressupostos de uma variação na energia potencial entre as fases dessorvidas e adsorvidas e uma energia característica de um dado sólido. Essa equação proporciona um comportamento macroscópico de carga de adsorção para uma dada pressão.13 A isoterma de Dubinin-Radushkevich é útil para a estimativa da energia aparente e as características de adsorção.14 Investigações computacionais podem ser entendidas como um instrumento preditivo para a orientação de análises experimentais bem como auxílio na compreensão de resultados com o intuito de alcançar maior eficiência além de interpretar vários aspectos de um processo.15 De modo a minimizar os esforços necessários para se realizar ensaios de adsorção, a utilização de ferramentas computacionais que possibilitam não somente a redução do tempo empregado como o aumento da praticidade no tratamento e análise de dados são de suma importância.16,17 Nesse contexto, o presente trabalho tem como objetivo a proposição de um software para tratamento de dados de análises de isoterma de adsorção, denominado Gurupi Isotherms Plot (GIP), com intuito de disponibilizar, de forma gratuita, uma ferramenta computacional com interface gráfica intuitiva e amigável. Nessa primeira versão do software é possível calcular as isotermas a partir dos modelos de Langmuir, Freundlich e Dubinin - Raduskevich de forma rápida, simples e eficiente.
PARTE EXPERIMENTAL Desenvolvimento do software O software GIP foi inicialmente desenvolvido para três modelos isotérmicos: Langmuir,6,7 Freundlich8 e Dubinin-Radushkevich9 descritos pelas equações (1) - (3). São elas: 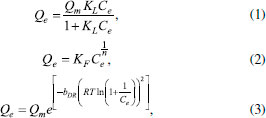 em que Qe é a quantidade de adsorvato adsorvido por unidade de massa do adsorvente, Qm é a quantidade de adsorvato adsorvido, Ce é a concentração do adsorvato no equilíbrio, R a constante dos gases, T a temperatura, KL é a constante de Langmuir, KF a constante de Freundlich, n representa a intensidade de adsorção e bDR é a constante de Dubinin-Radushkevich. Para ajustar os dados obtidos experimentalmente, a saber Qe e Ce, busca-se minimizar a soma das distâncias entre amostras e isotermas. Em outras palavras, busca-se determinar, por exemplo Qm e KL, para o modelo isotérmico de Langmuir, de modo a minimizar a soma dos quadrados dos erros de aproximação entre os valores tabelados (experimentais) e a isoterma. Analogamente, obtém-se os coeficientes para os demais modelos isotérmicos. Para tal, utilizou-se o método dos quadrados mínimos, de forma a obter as equações (4) - (6), dadas por: 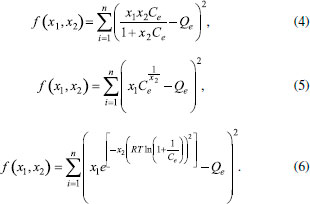 Para obter os pontos de mínimo das equações (4) - (6), calculou-se as derivadas parciais em relação a cada uma das variáveis, igualando cada uma delas a zero Não é o caso do GIP mas, cabe mencionar que em algumas análises de modelos isotérmicos são considerados os dados linearizados uma vez que, a regressão linear é, de fato, mais fácil de usar e interpretar, mas em contraponto pode não fornecer bons ajustes. Mesmo que a regressão linear possa modelar diferentes curvas, pode ocorrer de não se enquadrar de forma adequada a curva específica do diagrama de dispersão. O emprego de regressão não-linear, apesar de mais trabalhoso, pode fornecer resultados de ajustes mais precisos. Desse modo o software foi desenvolvido levando em consideração dados não-lineares por serem mais adequados e precisos para análise de modelos isotérmicos. As resoluções dos sistemas não-lineares foram realizadas pelo uso do método de Newton e os parâmetros de interesse para cada isoterma determinados. De fato, para que haja convergência do método iterativo para a solução do problema de minimização do resíduo é necessário que este se inicie das bacias de atração corretas. Visando amplo uso dessa ferramenta computacional, com base na matriz utilizada e fornecida pelo usuário, são estimadas as regiões de interesse para se buscar os coeficientes das isotermas. Por se tratar de uma região grande, é feita uma partição do domínio em subretângulos e cada vértice é usado como aproximação inicial para o método iterativo. Atingido o critério de parada, por exemplo uma quantidade máxima de iterações, o resultado é comparado com o obtido anteriormente para saber quais coeficientes manter. Uma das comparações é a imagem das equações (4)-(6) nos pontos candidatos a mínimo da função. Inicialmente, a implementação numérica do algoritmo, necessária para resolver numericamente os sistemas não lineares, foi realizada em linguagem C, com o software Dev-C++.18 A implementação numérica para os testes estatísticos, coeficiente de determinação, R2, e erro relativo médio, ERM, junto ao algoritmo, foi realizada com a utilização das equações (7) - (8), dadas por 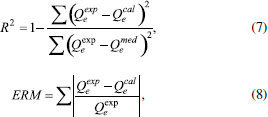 em que Após os testes de funcionalidade o código foi reescrito em linguagem Java, através da IDE Apache Netbeans.19 Essa escolha facilitou o desenvolvimento da interface. O software foi depositado para registro junto ao INPI pela Universidade Federal do Tocantins (UFT) e com a finalização dos trâmites do processo, o mesmo estará disponível, de forma gratuita, na página do programa de Pós-Graduação em Química da UFT, www.uft.edu.br/ppgq.
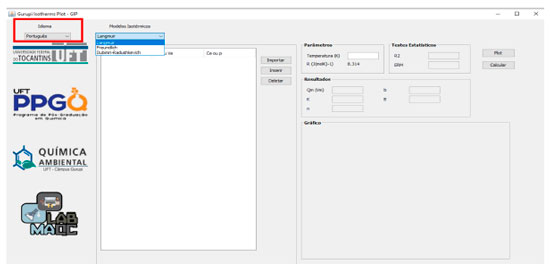
RESULTADOS E DISCUSSÃO O programa e suas funcionalidades O programa GIP foi desenvolvido para ser um software de interface amigável, de fácil uso no que diz respeito a determinação dos coeficientes das isotermas de adsorção. O usuário deve fornecer apenas, por exemplo, os dados experimentais de Qe e Ce, no caso das isotermas de Langmuir e Freundlich. Já no caso de usar a isoterma de Dubinin-Raduskevich deve-se ainda fornecer a temperatura em Kelvin. Na versão apresentada estão implementados três modelos isotérmicos para a escolha do usuário: Langmuir, Freundlich e Dubinin-Radushkevich. A Figura 1 apresenta a interface do programa. Pode-se observar que o programa possui a opção de Idioma, permitindo ao usuário escolher entre o uso em Português, Inglês ou Espanhol. Ao lado da caixa de idiomas é possível observar uma caixa de diálogo denominada Modelos Isotérmicos com a lista dos modelos implementados e disponíveis para a escolha do usuário.
Os dados experimentais para serem inseridos são: a quantidade de adsorvato adsorvido por unidade de massa do adsorvente Qe e a concentração do adsorvato no equilíbrio Ce. A medida que os valores escolhidos são inseridos no campo Dados, o número de amostras (N. Amostras) vai se modificando. O programa também pode ser utilizado para gás, inserindo as variáveis de quantidade de adsorvato adsorvido por unidade de volume do adsorvente Ve ao invés de Qe e pressão do adsorvato no equilíbrio p ao invés de Ce. Os dados determinados experimentalmente podem ser inseridos manualmente no programa com o botão Inserir ou importados de uma planilha em .xlsx com a opção de Importar. Para usar a funcionalidade de importação de documento, é necessário que haja uma planilha previamente preenchida (apenas com números) de modo que na primeira coluna vão os valores de Ce e na segunda coluna os valores de Qe. É importante destacar que as casas decimais devem ser separadas por ponto e não por vírgula e que os modelos isotérmicos foram implementados considerando o Sistema Internacional (SI). Nessa versão, ao pressionar o botão Plot tem-se o gráfico apenas com os dados amostrais. Para o usuário obter os valores dos coeficientes que fazem com que a isoterma melhor ajuste aos dados experimentais, é necessário que seja pressionado o botão Calcular. Assim, além dos coeficientes ainda é gerado o gráfico que apresenta os dados experimentais, a isoterma selecionada para análise e os erros. Seleção feita no campo Modelos isotérmicos. A Figura 2 apresenta um exemplo prático do programa funcionando.
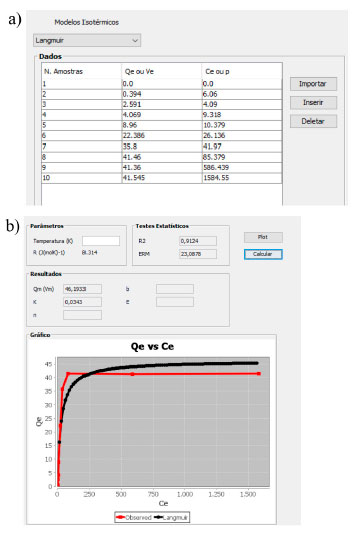 Figura 2. a) Parâmetros encontrados experimentalmente e adicionados no GIP; b) resultados obtidos após a execução do programa
Outra funcionalidade do programa pode ser encontrada com um clique no botão direito sobre o gráfico. Com esse comando o usuário tem acesso a opções para edição do mesmo, dentre elas: copiar, salvar como, imprimir, ampliar ou reduzir eixos e escala automática, como representado na Figura 3a. Nesse contexto, o software permite que o usuário analise regiões específicas de interesse como região de baixo grau de ocupação dos sítios, Figura 3b, além de alteração de cores do plano de fundo do gráfico, conforme a Figura 3c.
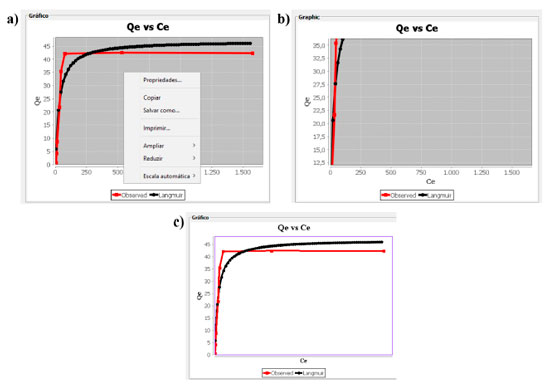 Figura 3. a) Propriedades dos gráficos gerados pelo GIP; b) imagem de uma região de baixo grau de ocupação dos sítios e c) gráfico com cores e alteradas
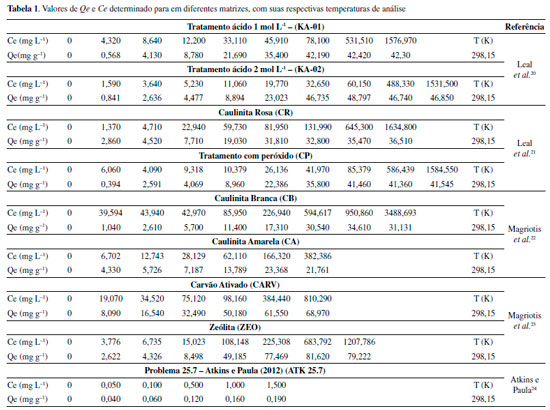
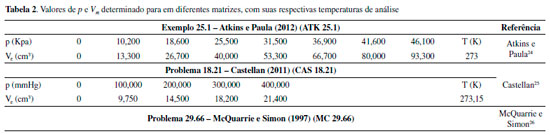
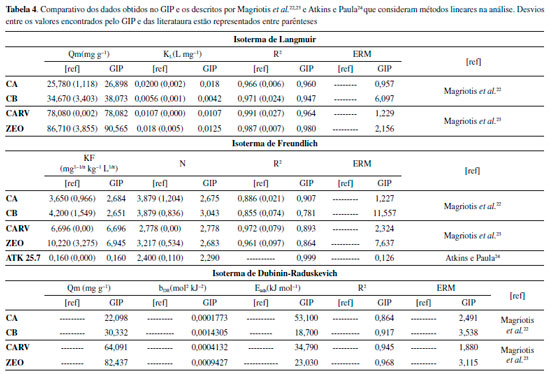
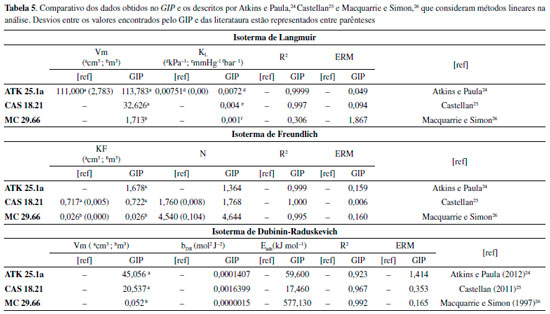
Performace e validação do software Para verificar a precisão do software, confiabilidade e a performance, diversos testes foram realizados, com dados obtidos de diferentes literaturas disponíveis. Foram consideradas tanto adsorção de líquidos quanto gás. O comparativo ocorreu com as seguintes referências: Leal et al.,20,21 que utlizaram métodos não lineares para a análise dos modelos isotérmicos, Magriotis et al.22 e Magriotis et al.,23 que utilizaram métodos lineares para a análise dos modelos isotérmicos e com exemplos de livros-texto utilizados na área, tais como: Atkins e Paula,24 Castellan25 e McQuarrie e Simon26 que também utilizaram métodos lineares para a análise dos modelos isotérmicos. O adsorvente utilizado nas literaturas Leal et al.20,21 foi a caulinita rosa, obtida na cidade de Ijaci - MG, tratada com ácido em diferentes concentrações e peróxido de hidrogênio, respectivamente. No caso de Magriotis et al.,22 as caulinitas: rosa, branca e amarela, obtidas na cidade de Ijaci - MG, que receberam essa nomenclatura pela coloração. Já no trabalho de Magriotis et al.,23 foram utilizados como adsorvente, a caulinita rosa, carvão ativado comercial (Marca Cromoline) e uma zeólita desenvolvida pelo grupo. No caso da comparação com os livros didáticos, foi considerado somente o desenvolvimento dos exercícios. Desse modo, a nomenclatura utilizada nas tabelas se deu a partir dos adsorventes, no caso das referências dos artigos: caulinita rosa (CR), caulinita amarela (CA), caulinita branca (CB), caulinita tratada com peróxido de hidrogênio (CP), caulinita tratada com ácido 1 mol L-1 (KA-01), caulinita tratada com ácido 2 mol L-1 (KA-02), carvão ativado (CARV) e zeólita (ZEO). Para os exercícios dos livros a nomenclatura utilizada nas tabelas se deu pela abreviação dos nomes dos autores e número do exercício: Atkins (ATK - 25.1, ATK - 25.7), Castellan (CAS - 18.21) e McQuarrie (MC - 29.66). As Tabelas 1 e 2 apresentan as matrizes de dados usadas.
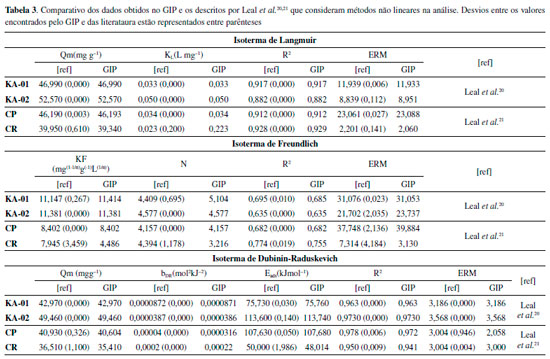
A escolha do conjunto de dados considerou alguns pontos importantes: o primeiro foi a utilização de dados publicados em artigos de um grupo de pesquisa que atua na área. O segundo foi a comparação com livros textos que são utilizados no meio acadêmico e que apresentam dados amostrais para a fase líquida e para a fase gasosa, auxiliando na validação do software em diferentes fases. Outro ponto a considerar é que o conjunto de dados proposto nos exercícios dos livros em conjunto com o software GIP pode ser utilizado também de forma didática por professores nas disciplinas em que os modelos isotérmicos são estudados. Cabe destacar que a utilização das matrizes em questão teve por finalidade avaliar a eficiência e confiabilidade do software, com o intuito de validar o programa, por meio de comparação com dados existentes na literatura e não efetuar uma análise sobre os ajustes dos dados aos modelos isotérmicos dos autores. Os dados das Tabelas 1 e 2 foram inseridos no software GIP e foram calculados os parâmetros para as isotermas de Langmuir, Freundlich, Dubinin-Radushkevich, R2 e ERM. Para avaliar a precisão do GIP, foram avaliado os desvios entres os valores das literaturas e os encontrado pelo software, equação (9), dada por: 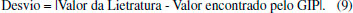 Performace do GIP em comparação com resultados não linearizados Os resultados encontrados para o software GIP, levando em consideração a comparação com dados não linearizados, estão representados na Tabela 3. Os valores entre parênteses são os desvios encontrados conforme a equação 9. Ao avaliar o comparativo com os resultados não linearizados, Tabela 03, foi possível observar que os resultados do GIP apresentaram boa correlação com os valores da literatura. Os resultados dos desvios aproximaram-se de zero para a maioria dos resultados analisados. Desse modo, foi possível observar que o GIP apresentou boa precisão quando comparado a dados não linearizados.
Performace do GIP em comparação com resultados linearizados em fase líquida Os resultados encontrados para o software GIP em comparação com os dados linearizados estão representados na Tabela 4.
O comparativo com os parâmetros linearizados em fase líquida, Tabela 4, apresentam um maior desvio entre os valores (ref - GIP) em relação ao comparativo com os dados não linearizados. Porém esse fato pode ser justificado pela diferença de métodos empregados para a obtenção dos parâmetros, uma vez que, o software considera métodos não linearizados. No entanto, é possível observar a precisão do software em relação aos melhores ajustes dos modelos isotérmicos descritos nas referências. Performace do GIP em comparação com resultados linearizados em fase gasosa Para a fase gasosa foram avaliados três matrizes e os resultados estão representados na Tabela 5.
Foi possível observar, na análise de matrizes com adsorvatos gasosos que o GIP respondeu com precisão aos resultados dos exemplos/problemas. Os desvios observados podem estar relacionados as diferenças no método de análise, uma vez que as referências nesse caso consideraram métodos linearizados para a análise enquanto o software utiliza métodos não linearizados. A comparação é válida pois, apesar da diferença dos métodos, foi possível observar que a tendência de ajuste ao melhor modelo isotérmico, proposto por tais literaturas, foi seguida. Nesse contexto, é possível destacar o problema proposto por Castellan.25 No problema, o autor propõe um conjunto de dados que se ajusta perfeitamente ao modelo de Freundlich. Esse fato foi facilmente detectado, com o auxílio do GIP, a partir da análise de R2 que foi igual a 1,00 e de um erro relativo médio muito baixo (0,006), além dos gráficos experimental e calculado que foram análogos. No intuito de verificar o ajuste dos dados aos outros modelos implementados, foi possível confirmar o melhor ajuste para a isoterma de Frendlich, conforme proposto pelo exercício. A Figura 4 apresenta o resultado obtido no GIP do problema para a isoterma de Freundlich.
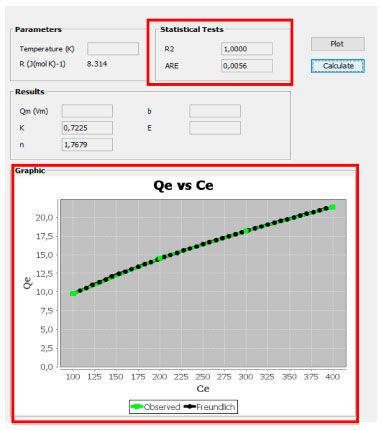 Figura 4. Resultado obtido do programa Gurupi Isotherms Plot para o problema proposto por Castellan25
Performace geral do GIP De maneira geral os resultados obtidos pelo GIP comprovam a eficiência do método empregado no software para os parâmetros das isotermas analisadas, seja para os parâmetros linearizados como os não linearizados e para as fases líquida ou gasosa. A Figura 5 mostra a dispersão dos desvios encontrados (Tabela 3-5) e, como observado, a maior parte dos desvios se encontra próximo de zero.
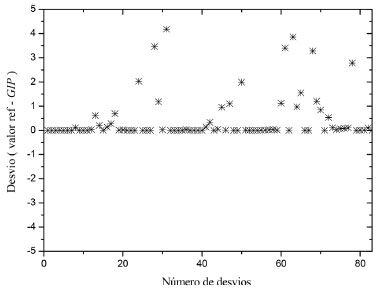 Figura 5. Gráfico dos desvios calculados entre os valores das referências e os valores do GIP
A obtenção dos valores de R2 e de erro relativo médio (ARE) foram outros critérios importantes para a comparação dos resultados do software com algumas das referências. Em especial aquelas que consideram esses fatores em suas análises. Cabe destacar que o cálculo é realizado em poucos segundos após o início mostrando assim um bom desempenho em termos de velocidade.
CONCLUSÕES O presente trabalho apresentou o software GIP, que permite calcular parâmetros das isotermas de Langmuir, Freundlich, Dubinin-Radushkevich. A partir do teste do programa, com dados obtidos da literatura, foi possível observar uma excelente precisão do software. Os parâmetros de coeficiente de determinação (R2) e erro relativo médio (ERM) também estão implementados no programa, permitindo, assim, que o usuário já tenha dados estatísticos para seus resultados. O software é livre, apresenta um interface de fácil uso e uma resposta rápida (na casa de segundos). Desse modo, o Gurupi Isotherms Plot apresenta-se como uma alternativa gratuita, rápida e eficiente para auxiliar alunos e pesquisadores em estudos de processos adsortivos.
AGRADECIMENTOS O presente trabalho foi realizado com apoio da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Código de Financiamento 001. Douglas Henrique Pereira agradece a Pró-Reitoria de Pesquisa, Pós-Graduação e Inovação (PROPESQ) e a Universidade Federal do Tocantins (UFT) pelo aporte financeiro (Edital Nº29 /2020).
REFERÊNCIAS 1. Gohari, A.; Eslamian, S.; Mirchi, A.; Abedi-Koupaei, J.; Bavani, A.; Madani, K.; J. Hydrol. 2013, 491, 23. 2. Poonkuzhali, K.; Rajeswari, V.; Saravanakumar, T.; Viswanathamurthi, P.; Park, S.M.; Govarthanan, M.; Sathishkumar, P.; J. Hazard. Mater. 2014, 272, 89. 3. Tavares, L. C.; Lemos, V. P.; Pinheiro, M. H. T.; Filho, H. A. D.; Fernandes, K. G.; Cerâmica 2013, 59, 640. 4. Kwiatkowski, M.; Duda, J. T.; Duda, J. M.; Colloids Surf., A 2014, 457, 449. 5. Knani, S.; Aouaini, F.; Bahloul, N.; Khalfaoui, M.; Hachicha, M.A.; Lamine, A. B.; Physica A: Statistical Mechanics and its applications 2014, 400, 57. 6. Langmuir, I.; J. Am. Chem. Soc. 1916, 38, 2221. 7. Langmuir, I.; J. Am. Chem. Soc. 1918, 40, 1361. 8. Freundlich, H.; Trans. Faraday Soc. 1932, 28, 195. 9. Dubinin, M. M.; Chem. Rev. 1960, 60, 235. 10. Massoumi, A.; Ghaemy, M.; Carbohydr. Polym. 2014, 108, 206. 11. Rout, P.R.; Bhunia, P.; Dash, R. R.; J. Environ. Chem. Eng. 2014, 2, 1331. 12. Luna, M. D. G.; Flores, E. D.; Genuino, D. A. D.; Futalan, C. M.; Meng-Wei, W.; J. Taiwan Inst. Chem. Eng. 2013, 44, 646. 13. Nguyen, C.; Do, D. D.; Carbon 2001, 39, 1327. 14. Rangabhashiyam, S.; Anu, N.; Nandagopal, M. S. G.; Selvaraju, N.; J. Environ. Chem. Eng. 2014, 2, 398. 15. Deka, B. C.; Bhattacharyya, P. K.; Comput. Theor. Chem. 2015, 1051, 35. 16. Boulinguiez, B.; Cloirec, P. L.; Wolbert, D.; Langmuir 2008, 24, 6420. 17. Foo, K.; Hameed, B.; Chem. Eng. J. 2010, 156, 2. 18. https://sourceforge.net/projects/orwelldevcpp/, acessada em março 2021. 19. www.netbeans.org, acessada em março 2021. 20. Leal, P. V. B.; Magriotis, Z. M.; Sales, P. F.; Papini, R. M.; Viana, P. R. M.; J. Environ. Manage. 2017, 197, 393. 21. Leal, P. V. B.; Magriotis, Z. M.; Sales, P. F.; Papini, R. M.; Viana, P. R. M.; Matéria 2019, 24. 22. Magriotis, Z. M.; Leal, P. V. B.; Sales, P. F.; Papini, R. M.; Viana, P. R. M.; J. Hazard. Mater. 2010, 184, 465. 23. Magriotis, Z. M.; Leal, P. V. B.; Sales, P. F.; Papini, R. M.; Viana, P. R. M.; Arroyo, P. A.; Appl. Clay Sci. 2014, 91-92, 55. 24. Atkins, P.; Paula, J.; Físico-química, 8I ed.; LTC: Rio de Janeiro, 2012. 25. Castellan, G.; Fundamentos de Físico-química, LTC: Rio de Janeiro, 2011. 26. McQuarrie, D. A.; Simon, J. D.; Physical Chemistry: A molecular approach, University Science Books: Sausalito, 1997. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






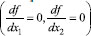 . Isso gera um sistema não-linear para cada uma das isotermas.
. Isso gera um sistema não-linear para cada uma das isotermas.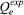 é a quantidade de adsorvato obtida experimentalmente,
é a quantidade de adsorvato obtida experimentalmente, 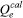 é a quantidade de adsorvato adsorvida obtida através do cálculo das equações isotérmicas (após a obtenção dos parâmetros desejados) e
é a quantidade de adsorvato adsorvida obtida através do cálculo das equações isotérmicas (após a obtenção dos parâmetros desejados) e 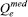 é a quantidade média de adsorvato adsorvida obtida experimentalmente.
é a quantidade média de adsorvato adsorvida obtida experimentalmente.