Artigo
| Detailed evaluation of pervaporation modeling to obtaining anhydrous ethanol |
|
Camila Cavalcanti; Wagner Ramos; Romildo Brito; Karoline Brito*
Universidade Federal de Campina Grande, 58429-900 Campina Grande - PB, Brasil Recebido em: 02/09/2021 *e-mail: karoline.dantas@ufcg.edu.br Pervaporation requires operation at mild temperatures and provides low energy consumption, which makes this technology economically attractive. However, pervaporation is not yet a widespread process in the industry. One of the justifications is the complexity in the quantification of variables related to the membrane in the most diverse conditions. This factor results in the absence of generic models in the simulation software. This work aims at the rigorous phenomenological modeling of a pervaporation process using a polyetherimide membrane intended for the dehydration of ethanol. The model was developed on the Aspen Custom ModelerTM platform. Two approaches were implemented and compared: PERKAT and PERVAP models, being the last one the best model. The main variables of the process were evaluated. It was possible to verify the capacity of separation of the pervaporation module in breaking the barriers of the azeotrope, reaching a product with a high level of purity in ethanol, and recovery of up to 99.8%. In addition, the generic PERVAP model was exported to Aspen PlusTM and a cascade pervaporation unit was simulated. The specific energy consumption was calculated and compared to that of traditional separation processes. A 70% reduction was obtained compared to the most economical distillation configuration. INTRODUCTION The ethanol/water mixture forms a minimum boiling azeotrope with 95.6 by mass% of ethanol. Currently, the most used processes to separate this mixture are extractive and azeotropic distillations. However, both require high-energy consumption and azeotropic distillation uses solvents with a high level of toxicity. In this sense, pervaporation appears as a technology to overcome these disadvantages. Kober1 was the first one to use the term "pervaporation". For decades, it was considered merely a laboratory technique due to its low selectivity, low permeate flow and high cost. A few years later, the asymmetric membranes developed by Loeb and Sourirajan2 obtained a promising product flow, which stimulated developments in the area. Only in 1983, GFT Membrane Systems built the first pilot-scale unit for ethanol production.3 In 1988, GTF also designed the first industrial-scale plant in France.4 Pervaporation (PV) is a separation consisted by the partial vaporization of a liquid mixture through a membrane.5 It is mainly used to separate mixtures with special thermodynamic characteristics, such as mixtures that present azeotrope or pinch point.6 The membrane is a physical barrier that separates the feed into permeate and retentate streams. The driving force is the gradient in chemical potential, corresponding to the concentration difference between the two sides of a membrane.3 Figure 1 illustrates a simplified PV module. The feed corresponds to a liquid solution at low temperature and atmospheric pressure. The permeate is constituted by the fraction of permeate flux that is vaporized, which is immediately removed from the module by vacuum or entrained gas. The permeate flux is rich in the component with the highest degree of affinity with membrane. The retentate flux is concentrated in the compounds with less affinity with membrane. The temperature of the retentate is lower than the feed temperature. This decrease occurs because of the permeate evaporation, which loses latent heat. This reducing in temperature limits the size of PV module.
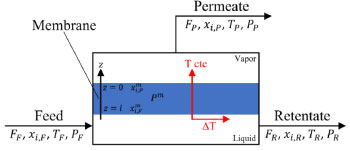 Figure 1. Simplified pervaporation module
The advantage of the PV process is the fact that membranes operate at low temperatures and demand only the replacement of lost latent heat during phase change. On the other hand, the limitations are the production capacity and installation costs. Rigorous phenomenological models of the pervaporation process are not easily found in commercial simulators. Aspen PlusTM, for example, uses general models like SEP and SEP2. These models combine feed streams and separate the resulting stream, according to the specifications supplied by the user. In addition, these models do not include the energy balance. It is usual to find studies like the one by Servel et al.7 and Babaie et al.,8 in which simple separators are used to represent a PV module. These models have limited application, as they do not take account the influence of relevant factors, such as composition and feed temperature. The scarcity of rigorous models to represent PV processes has motivated worldwide research. Boutikos et al.9 proposed models from experimental data for the dehydration of aqueous n-butanol solutions. Constantino et al.10 studied multicomponent mixtures for the compounds involved in the esterification reaction of acrylic acid with n-butanol. The authors evaluated the influence of permeation flux, selectivity, separation factor, effect of temperature and feed composition. Toth and Mizsey11 investigated the separation of methanol/water via organophilic membranes. The authors simulated the PV process and compared the results considering the transport coefficient constant12 and varying with the feed concentration.13 They concluded that the latter approach is more suitable to represent the PV process. Mafi et al.14 studied the ethanol purification by using a hydrophobic membrane. The authors used a constant diffusion coefficient and concluded that the feed concentration has a strong influence on temperature. Ashraf et al.15 proposed a one-dimensional model for the dehydration of 1-butanol. The authors considered permeation as a function of concentration and included a relationship to evaluate the temperature effect. Pereira et al.16 developed and compared the mathematical models for a batch pervaporation and a continuous pervaporation membrane reactor, being the last one the most attractive configuration for the synthesis of ethyl lactate. Qiu et al.17 evaluated the effects of mass transfer in ethanol purification using PDMS membranes and measured the effects of convection and diffusion using the solution-diffusion model. More recently, Soares et al.18 analyzed the flow pattern in a PV module using computational fluid dynamics. PV has also been applied in processes intensification, which is the case of the simulated moving bed membrane reactor;19 it combines in the same equipment the pervaporation membranes and the moving bed reactors, continuous countercurrent chromatographic separation with chemical reaction.20 Silva et al.,21 Pereira et al.22 and Constantino et al.23 evaluated this configuration in the production of 1,1-diethoxyethane, 1,1-dibutoxyethane and butyl acrylate, respectively. All the authors found improvements in the productivity. This work aims to implement a pervaporation unit using the Aspen Custom ModelerTM (ACM) tool, from AspenTechTM. ACM is a platform with object-oriented language, and is capable of creating, editing, and reusing customized models of processes that are unusual or absent in conventional simulator libraries. The developed module aims the ethanol/water separation, due to its economic relevance, that has resulted in US$ 89.1 billion in 2019.24 Polymeric membranes of polyetherimide - or PEI - were considered. They have been used in PV processes for alcohol dehydration since the 90's. They are hydrophilic (water selective) and have an asymmetric structure, composed of a thin dense skin layer and a finger-like porous sublayer.25 The modeling presented in this work considers that the mass transfer inside the membrane is based on the solution-diffusion model. Two models were considered: the first determines the solute transport parameter in the membrane from the regression of experimental data; the second measures the diffusion coefficient using the free volume theory. The two approaches were compared to the experimental data available in literature. The selectivity, feed temperature, pressure on the permeate side and fraction of recovered ethanol were evaluated. The model with the highest accuracy was exported to the Aspen PlusTM software library and a cascade pervaporation unit was simulated. The specific energy consumption was calculated and compared to traditional distillation systems. As modeling the pervaporation is still a challenge, the published papers has considered few aspects at a time. Dong et al.26 proposed a model based on experimental data, Wang et al.27 evaluated the energy savings of hybrid processes and Vatankhah et al.28 carried out the validation and study of the effect of certain variables. The present work contributes to the available literature as a complete evaluation in a general scope of the pervaporation process is done: modeling of a rigorous model, validation against experimental data, investigation of the main variables, inclusion of developed model in a commercial simulator and comparison with models found in the literature. Also, the cascade configuration of pervaporation process using the polyetherimide membrane to separate water from ethanol was not found in literature.
NOMENCLATURE

CASE STUDY The system under evaluation is a mixture of ethanol (i) / water (j). The hydrophilic polymeric membrane is used - polyetherimide (Ultem 1000, from General Electric Co.). The PV module aims to remove water from a concentrated stream of alcohol. The experimental data used for validation and comparison were:29 feed is 40 °C and 1 atm and the permeate is under vacuum of 0.133 kPa. The input information for the model is: flowrate, composition, temperature and pressure of the feed stream, and pressure on the permeate side. In addition to the PERVAP model, the thickness of the membrane was also specified.
STEADY STATE MODELING Hypotheses The following premises were assumed to be true: The above assumptions are based on the work of Servel et al.6 and Schiffmann and Repke30 and did not significantly affect the results of the analysis. Mass balance The overall mass balance for a PV module, is:  If the feed is known and the permeate is determined using the solution-diffusion model, the flowrate FF can be calculated. From the individual mass balance, mass composition of the retentate is calculated: 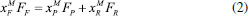 The fraction of ethanol recovered in the PV corresponds to the ratio between the molar flow of ethanol in the retentate and in the feed.  Energy balance From the energy balance: 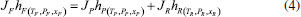 To solve the energy balance is considered that:6 Once flows and enthalpies are calculated, temperatures can be determined. Mass transfer The solution-diffusion model is the most widely used to describe permeation through membranes.31 The mechanism is divided into three stages: sorption; diffusion and desorption. According to the Fick's law, the steady state diffusive flow of component i (ethanol) through the membrane with l thickness is:  where Dim is the diffusion coefficient of the membrane and Cim is the concentration of component i on the membrane surface. This study evaluated two approaches to determine the mass transfer. The first one uses the PERKAT model,32 which encompasses all parameters related to membrane morphology and interaction with solute in a single variable. The second approach uses the PERVAP model,33 which determines the diffusion coefficient through the theory of free volume and reduces the need for experimental information. The two models were developed based on Figure 1, which presents an illustrative scheme of the main parameters of mass transfer in a PV membrane. PERKAT model The permeate flow is related to the gradient of chemical potential: 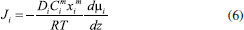 The chemical potential is a function of the composition inside the membrane and the pressure variation across it: 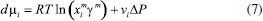 Since Pm is the pressure at different points in membrane, a linear decay is assumed: 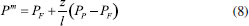 To calculate the composition on the feed side of the membrane ( x i , F m ), it was considered the liquid phase in equilibrium. So, the chemical potential on fluid can be considered equal to the chemical potential on the membrane surface ( μ i , F = μ i , F m ). Thus, a relationship can be obtained between the feed composition and the activity coefficients of the pure component (γi) and the membrane (γm). The same considerations were made for the permeate side, assuming equilibrium in the vapor phase ( μ i , P = μ i , P m ). Finally, the permeate flow is: 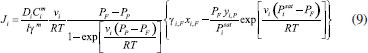 where the vapor fraction in the permeate stream (yi,P) must be collected from experiments, while the feed fraction is known. The term (DiCim/lγm) is known as a transport parameter, and includes the variables related to the morphological and kinetic characteristics related to the membrane permeability. This parameter was considered constant. Selectivity The separation factor, or selectivity, quantifies the ability to transport a particular specie:  PERVAP model The PERVAP model expresses the chemical potential in terms of concentration and includes selectivity in Fick's Law. In this case, it is not necessary to use experimental data. In this model, the permeate flow is: 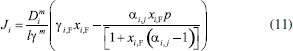 where Dim is the diffusion coefficient, γm is the membrane activity coefficient, which is responsible for quantifying the affinity between the membrane with a certain component, and p = Pp/Pisat is the relative pressure on the permeate side. In this approach, Eq.(10) and (11) are solved simultaneously. The vapor and liquid phases were considered to be in equilibrium ( μ i , F = μ i , F m and μ i , P = μ i , P m ). Determination of the diffusion coefficient The diffusion coefficient calculates the dependence between temperature, concentration and molar mass in polymeric systems and measures the resistance to mass transfer of each component. This coefficient is calculated according to the free volume theory:34,35 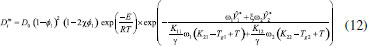 where D0 is the pre-exponential factor; E is the critical energy needed for a diffusant to overcome neighboring attractive forces; γ is an overlap factor, accounting for the fact that more than one molecule may access the same free volume; V ^ i is the critical local hole free volume required for a diffusive jump of component i; ωi is the mass fraction of i; ξ is the constant that expresses the ratio between the molar volume of the solvent and polymer jump unit; K11 and K21 are free volume parameters for the solvent; K12 and K22 are the parameters for the polymer; φ1 is the volume fraction of the solvent; χ is the solvent/polymer binary iteration parameter; Tgi is the glass transition temperature of component i. Many published papers in the literature are based on this theory. Mafi et al.14 developed a hydrophobic pervaporation model for the removal of ethanol from aqueous solutions. The authors satisfactorily predicted permeate flows and selectivity and determined the effects of feed concentration and temperature on system performance. In this way, it was possible to determine the operating conditions. Darvishi et al.36 developed a predictive model for removing styrene from wastewater in petrochemicals. The authors compared the free volume theory by Vrentas and Duda,34,35 and another theory proposed by Fujita.37 After verification with experimental data, the theory of Vrentas and Duda,34,35 presented higher representativeness of the results. However, the authors concluded that accuracy of both methodologies decreases with the increasing in feed concentration. Model parameters The ethanol/water chemical system has polar components, no electrolytes, with an operating pressure less than 10 bar. For this reason, the Nonrandom Two-Liquid (NRTL) thermodynamic model is indicated to calculate the activity coefficients.38 The vapor pressure and molar volume of components on the feed side were determined from the extended Antoine equation and the modified Rackett equation, respectively. The data used for the free volume parameters of ethanol/water mixture are presented in Table 1. Table 2 presents data for the polymer.
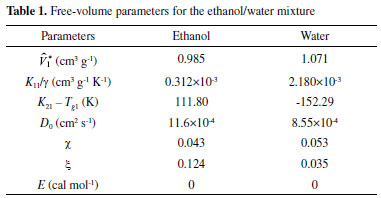

The specific free volume (V^i) was estimated using atomic constants according to Sugden.39 The binary iteration parameter (χ) was calculated using the Lee and Danner group contribution method. Data of the free volume parameters for the polymer were extracted from literature,40 and are a function of the viscosity and temperature of the pure polymer. Infinite dilution was assumed for both components. For the PERVAP model, it is necessary to specify the membrane thickness (l) equal to 160 µm.29 Numerical solution and optimization The algorithm for the solution of all equations was developed in Aspen Custom Modeler and is shown in Figure 2. The system of non-linear equations was solved using the Newton Mixed method. This algorithm uses the pure Newton method in the initialization and steady state steps and Fast Newton in the dynamic steps.
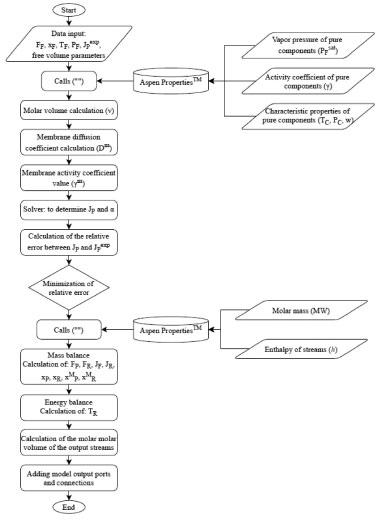 Figure 2. Algorithm in Aspen Custom Modeler
The transport parameter (related to the PERKAT model), and the membrane activity coefficient (related to the PERVAP model) were determined by minimizing the relative error (Eq. (13)) between the experimental data and those obtained by the respective models for the permeate flow: 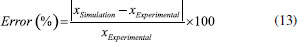 The minimum of each objective function was determined using the Nelder-Mead method (Simplex). Aspen PlusTM simulation A cascaded PV unit consists of a sequence of PV modules in series, interspersed by heat exchangers. In order to condense the permeate stream, a heat exchanger and a vacuum pump are required, as shown in Figure 3. Aspen PlusTM was used to model this process. The auxiliary equipment was modeled using the simulator library. Only the membrane was represented by the model developed in the Aspen Custom ModelerTM. In this case, the model that obtained the best results was generalized and exported to Aspen PlusTM.
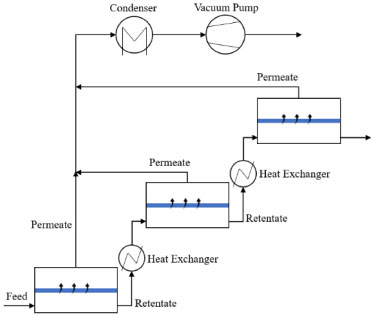 Figure 3. Cascading pervaporation process
In order to compare the developed model with other processes for obtaining anhydrous ethanol, flow and composition information for the inlet stream were collected from the study by Brito et al..41 For membrane operation, temperature and pressure data were based on Qariouh et al..29 All the required information is shown in Table 3. The ethanol specification in product stream is 99.99 wt %.

The temperature of the retentate (TR) is determined based on the consideration made by Servel et al.6 A temperature difference between the feed and product stream of 20 °C was assumed (ΔT = TF - TR), in order to achieve a minimum permeation rate in each PV module. The configuration of PV cascade was developed to optimize the relation between the area and energy consumption of the membrane. To obtain the optimum configuration of the cascade PV process, the number of modules was calculated though the algorithm presented in Figure 4. This procedure was done just using Excel calculations.
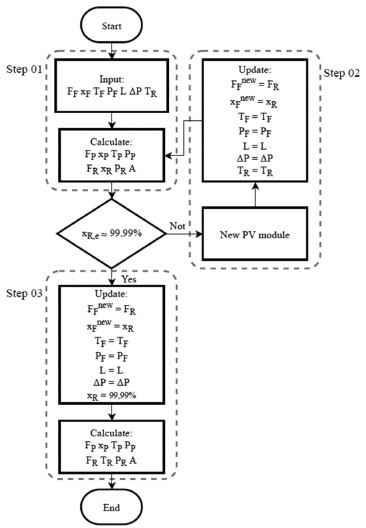 Figure 4. Algorithm to determine the area of each PV module in the cascade configuration
The input condition is the fresh feed. Initially (step 1) the model calculates the area of the PV module in order to reach the required temperature difference specified by retentate Servel,6 and determines the output composition of this module (xre). If the retentate composition is lower than 99.99 wt%, go to step 2; if else go to step 3. In step 2, a new module is added to the process. The retentate stream of the previous module is updated as the feed of the actual module. Every time step 2 is executed, a new module is added to the process; this is done until the composition of the retentate stream is sufficiently close to the required specification. The step 3 is executed only in the last module, when the purity is reached, the area of the last module is obtained and, the temperature of the retentate stream is calculated. The area of each module is required as specification of the PV block in Aspen PlusTM. If the feed stream is 1 atm and the permeate is 0.133 kPa,29 the pressure drop between the feed side and the permeate stream is 101.192 kPa. The heaters were included to reestablish the temperature and pressure of feed stream (40 °C and 1 atm, respectively). The condenser was specified for the same pressure as the permeate stream (0.133 kPa) and a vapor fraction equal to zero. A discharge pressure of 1 atm was set in the vacuum pump. Specific energy consumption Specific energy consumption (SEC) is an energy indicator that relates the total amount of energy required by a process to produce a unit of mass or mole within specifications, as shown in Eq. (14):  where Q corresponds to the sum of the energy required by the heat exchangers, condenser, and vacuum pump. These values were obtained from Aspen PlusTM simulation. The SEC was used to compare the pervaporation process with the extractive distillation process by Brito et al.41 and Tututi-Avila. et al.42
RESULTS AND DISCUSSION Model validation The key parameters for the characterization of the membrane are responsible for the way that diffusion of each component will occur. The transport parameter (DiCim/lγm) and the membrane activity coefficient (γm) refer to the PERKAT model and PERVAP, respectively. These parameters were determined through the optimization between the results of each model and the experimental data. Table 4 presents the obtained results, as well as the values of the diffusion coefficient used in the PERVAP model.
Figure 5 shows the comparison between the flow of each component in permeate stream the experimental data of Qariouh et al..29 The blue line refers to water flows in permeate (indicated by the left-hand y-axis); black refers to ethanol flows (right-hand y-axis). For the PERKAT model, the absolute error for ethanol and water flows is 14.36% and 27.96%, respectively. For the PERVAP model, these deviations are 10.75% and 5.43%. Therefore, the PERVAP model (more rigorous) represented the data trend with more accuracy.
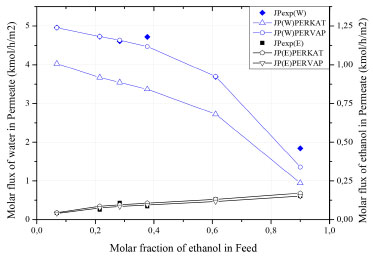 Figure 5. Permeate flow as a function of the ethanol composition in the feed
The water flow in the permeate is always preponderant to that of ethanol flow, as the membrane is hydrophilic (selective to water). On the other hand, when the composition approaches the azeotropic point, the difference between flows is substantially reduced. This behavior suggests the occurrence of coupled transport of both components, caused by strong interactions with the membrane. As observed by Valentinyi et al.,43 there is a strong coupling between the organic and water flows. As the PERVAP model presented the best fit to the experimental data, it was assumed that it describes the real behavior of the process. In this case, PERVAP will be used for subsequent analyzes. Selectivity The solution-diffusion model indicates that selectivity during pervaporation is governed by the sorption and diffusion rates of the elements of the mixture.29 Therefore, the selectivity of water over ethanol () measures how much difficulty is the permeation of ethanol in relation to water. According to Figure 6, the increasing of ethanol composition in feed stream is directly proportional to the separation factor, presenting an almost linear behavior.
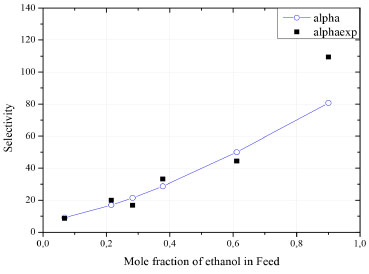 Figure 6. Effect of the feed composition in selectivity () of the PEI membrane
Figure 5 and Figure 6 indicates that the increasing of ethanol molar fraction in feed stream causes a considerable reduction in water flow on permeate stream, while the ethanol flow slightly increases. This behavior is a consequence of the increasing in membrane selectivity for ethanol. In this regard: (1) at low and moderate concentrations of ethanol, water molecules have higher mobility within the membrane, due to their smaller molecular size; (2) high concentrations shift the concentration gradient, which impacts the activity coefficient and favors the permeation of the undesired component. It is important to highlight that, even so, the membrane remains preferentially selective to water in the entire concentration range. Influence of pressure on the permeate side The solution-diffusion model indicates that the pressure reduction on the permeate side favors diffusion through the membrane. This behavior is explained by the formation of a concentration gradient between the sides, which results in the shift of the chemical potential (the driving force of the process). A sensitivity analysis of pressure was carried out to verify this effect, as shown in Figure 7.
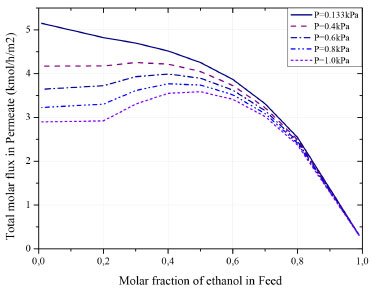 Figure 7. Influence of pressure on flow in the permeate side
The pressure has a significant effect in solutions with a low concentration of ethanol (below 60%). In regions with a high ethanol concentration, the pressure effect is insignificant. This behavior indicates that the coupling flows have a predominant effect in this range. In this case, water permeation is hampered due to the increasing of ethanol fraction on feed, as presented in Figure 5. Another phenomenon can be observed in ethanol concentrations below 20% and at higher pressures on the permeate side. It is known that two factors promote the gradient of chemical potential: the difference in concentration and pressure between the faces of the membrane. In this context, in a permeate pressure greater than 0.4 kPa (lower pressure gradient), this factor is no longer preponderant over the permeate flow. In turn, it is up to the concentration of the feed to reach the minimum gradient necessary to promote the permeation increasing. Influence of the feed flow The feed flow is a variable usually used to control the product composition. Its influence on ethanol purity in the retentate stream is evaluated in Figure 8. The increase in feed flow results in a product stream with a lower degree of purity. As the membrane has a fixed rate of permeation per square meter, the increasing in feed will only serve to decrease the concentration of the product stream.
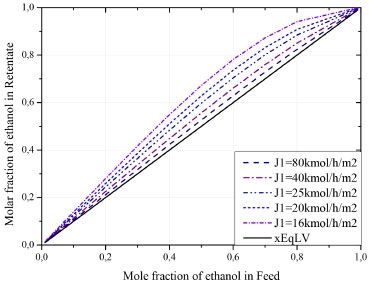 Figure 8. Influence of feed flow on ethanol purity in the retentate stream
Figure 8 can also be interpreted as an x-y diagram, where the black line indicates the equilibrium composition. In this system there is no limitation in the separation along the entire feed range. In conventional distillations, a binary azeotrope is formed, around 89 mol% of ethanol. Figure 9 shows the ethanol recovery in the retentate stream when the feed flow is varied. In case of lower ethanol concentrations in feed, the membrane presents lower efficiency for ethanol recovery. This recovery can be improved by increasing the initial flow. It is important to highlight that the recovered fraction, even in the weakest performance, is higher than 93%. For high concentrations of ethanol in feed, this value can be between 98.9 and 99.8% (molar).
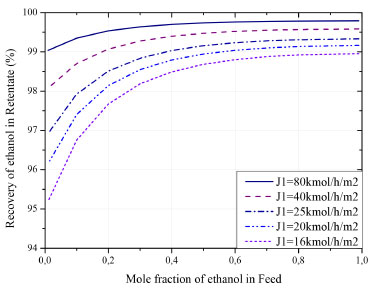 Figure 9. Ethanol recovery as a function of flow and composition in the feed
PERVAP model in Aspen PlusTM To simulate the complete pervaporation unit, the PERVAP model was exported to Aspen PlusTM through a .dll available in its library. Figure 10 shows the simulated flowsheet.
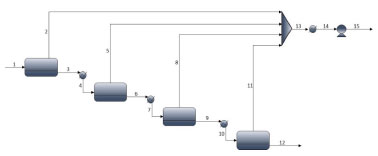 Figure 10. Flowsheet of pervaporation in Aspen PlusTM
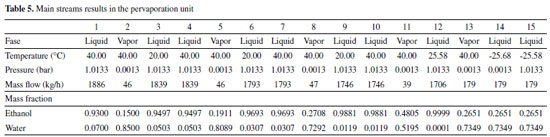
The feed flowrate is 1886 kg/h and is consisted of 93% and 7% by mass of ethanol and water, respectively. The main results obtained for each stream are shown in Table 5. It was considered a specification of 99.99% by mass of ethanol in the product stream of the last module (12). The final permeate stream (15) reached 73.49% by mass of water.
The calculated cross-sectional areas for modules PV1, PV2, PV3 and PV4 were 1.097 m2, 1.331 m2, 1.845 m2 and 2.625 m2, respectively. The inclusion of a new module in process results in an increasing in ethanol composition of the output, which justifies the progressive increasing in the area of module. As noted earlier, the increasing in ethanol composition in feed possibly favors the occurrence of coupled transport of the undesired component; on the other hand, the total permeate flow per square meter of membrane decreases. The decreasing in flow reduces the amount of lost latent heat, which results in a usage of a larger membrane area for a fixed amount of heat (ΔT = 20 °C). According to Table 5, the feed flow decreases along the modules. This decrease favors obtaining a product with high purity. The fraction of ethanol recovered by streams 3, 6, 9 and 12 is 99.60%, 99.49%, 99.27% and 98.90% respectively. Once again, the reduction in flow affects the percentage of ethanol recovered. The fraction recovered from the overall process was 97.29%. Specific energy consumption In case of cascade PV, considering a feed of 1886 kg/h, 37.05 kmol/h of ethanol at 99.97% molar were produced. The total energy consumption was 194.197 kWh. Table 6 compares the SEC obtained by the cascade pervaporation unit (PVC) to conventional (CS) and thermally coupled (TCS) extractive distillation,42 and to extractive distillation with (CS+) and without thermal integration (CS-), and thermally coupled with (TCS+) and without (TCS-) thermal integration.41
The PVC configuration presented the lower SEC; heat should be supplied to the replacement of the lost latent heat, due evaporation of the permeate amount. In mass basis, SEC of PVC is equal to 0.1138 kWh/kg. This value is compared with PV process from literature (ethanol/water system), as shown in Table 7.
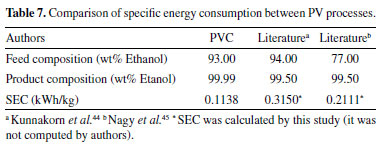
It was not found in literature the cascade configuration of pervaporation process using the polyetherimide membrane to separate water from ethanol. The PVC was compared with the papers by Kunnakorn et al.44 and Nagy et al.,45 who used single pervaporation module, and present disadvantages since the module area is increased until the specifications product is reached. Larger areas require larger permeate flows, which results in heat latent loss, lower temperature of downstream retentate, and progressive reduction in permeation rate of the membrane. In the cascade configuration, a minimum rate of permeation was estabilished (through ΔTmodule = 20 °C). Hence, the make-up of heat latent is done in the end of each section. In this way, the membranes operate in an optimum range of their conditions, which explains the lower SEC. Even so, only the SEC should not be considered in isolation. Costs related to investment, operation and maintenance are crucial factors for the definition of new projects. Viability varies according to the type of component to be separated, as well as the used membrane. Model limitations The developed model is rigorous when compared to some studies in the literature, such as those by Khazaei et al.7 and Babaie et al..8 However, the model has some limitations, which should be investigated in the future:
Still, this model can do a quick and robust assessment of the membrane's permeation capacity. It is suitable for a quick comparison of different system configurations and a rough estimate of energy demand and installation costs.
CONCLUSIONS The phenomenological modeling of the pervaporation process, using a polyetherimide membrane to separate the azeotropic ethanol/water mixture, was implemented in the Aspen Custom ModelerTM software. Two approaches were investigated: PERKAT and PERVAP. The models were compared with data from the literature, and PERVAP resulted in the highest representativeness. These results confirm the importance of including the variables that correlate the morphological characteristics of the membrane in the modeling of the process. It was found that the increase in the concentration of ethanol in the feed promotes the occurrence of coupled transport of the undesired component through the membrane, affecting the permeation of water. The pressure reduction on the permeate side favors the diffusion phenomena, due to the intensification of chemical potential gradient between the faces of the membrane. However, it has a predominant effect on ethanol concentrations below 60% in the feed. On the other hand, for pressures above 0.4kPa, a minimum concentration gradient is necessary to promote the increasing in permeation. Pervaporation avoided the azeotrope formation, making it possible to achieve high purity content. Increasing the feed flow with constant composition results in a less concentrated product. On the other hand, it favors the recovery rate of ethanol, which varied between 93.0 and 99.8% on a molar basis. The simulation of complete cascading pervaporation unit shows that the increase in the cross-sectional area of the membrane for each module added to the system is related to the increase in feed composition, which reduces the permeation rate per square meter of membrane. It was also found that the reduction of the total feed flow in each module favors the obtaining of a product with high purity, although the fraction of ethanol recovered is reduced throughout the modules. The specific energy consumption of the PVC configuration was the lowest when compared with other distillation processes and also with single PV modules.
ACKNOWLEDGMENTS The authors would like to thank the Paraíba Research Support Foundation (FAPESQ) for the financial support of this work.
REFERENCES 1. Kober, P. A.; J. Am. Chem. Soc. 1917, 39, 944. 2. Loeb, S.; Sourirajan, S.; Adv. Chem. ACS 1963, 38, 117. 3. Tsuru, T.; Wang, J.; In Kirk-Othmer Encyclopedia of Chemical Technology; John Wiley & Sons, Inc.: Hoboken, 2013; pp. 1. 4. Alvarez, M. E. T.; Tese de Doutorado, Univerisdade Estadual de Campinas, Brasil, 2005. 5. Smitha, B.; Suhanya, D.; Sridhar, S.; Ramakrishna, M.; J. Memb. Sci. 2004, 241, 1. 6. Servel, C.; Roizard, D.; Favre, E.; Horbez, D.; Ind. Eng. Chem. Res. 2014, 53, 7768. 7. Khazaei, A.; Mohebbi, V.; Behbahani, R. M.; Ahmad Ramazani, S. A.; Chemical Engineering and Processing: Process Intensification 2018, 128, 46. 8. Babaie, O.; Nasr Esfahany, M.; Chemical Engineering and Processing: Process Intensification 2020, 151, 107910. 9. Boutikos, P.; Pereira, C. S. M.; Silva, V. M. T. M.; Rodrigues, A. E.; Sep. Purif. Technol. 2014, 127, 18. 10. Constantino, D. S. M.; Faria, R. P. V.; Ribeiro, A. M.; Loureiro, J. M.; Rodrigues, A. E.; Ind. Eng. Chem. Res. 2017, 56, 13064. 11. Toth, A. J.; Mizsey, P.; Chem. Eng. Res. Des. 2015, 98, 123. 12. Lovasz, A.; Mizsey, P.; Fonyo, Z.; Chem. Eng. J. 2007, 133, 219. 13. Valentínyi, N.; Cséfalvay, E.; Mizsey, P.; Chem. Eng. Res. Des. 2013, 91, 174. 14. Mafi, A.; Raisi, A.; Hatam, M.; Aroujalian, A.; J. Memb. Sci. 2012, 423-424, 175. 15. Ashraf, M. T.; Schmidt, J. E.; Kujawa, J.; Kujawski, W.; Arafat, H. A.; Sep. Purif. Technol. 2017, 174, 502. 16. Pereira, C. S. M.; Silva, V. M. T. M.; Pinho, S. P.; Rodrigues, A. E.; J. Memb. Sci. 2010, 361, 43. 17. Qiu, B.; Wang, Y.; Fan, S.; Liu, J.; Jian, S.; Qin, Y.; Xiao, Z.; Tang, X.; Wang, W.; Sep. Purif. Technol. 2019, 220, 276. 18. Soares, L. S.; Vieira, A. C. F.; Fidler, F.; Fritz, A. R. M.; Di Luccio, M.; Sep. Purif. Technol. 2020, 232, 115968. 19. Silva, V. M. T. M.; Pereira, C. S. M.; Rodrigues, A. E.; PT WO Pat. 2010/116335 2009. 20. Pereira, C. S. M.; Rodrigues, A. E.; Catal. Today 2013, 218-219, 148. 21. Silva, V. M. T. M.; Pereira, C. S. M.; Rodrigues, A. E.; AIChE J. 2010, 57, 1840. 22. Pereira, C. S. M.; Silva, V. M. T. M.; Rodrigues, A. E.; Ind. Eng. Chem. Res. 2012, 51, 8928. 23. Constantino, D. S. M.; Faria, R. P. V.; Ribeiro, A. M.; Rodrigues, A. E.; Ind. Eng. Chem. Res. 2020, 59, 2817. 24. Ethanol Market Size, available at https://www.grandviewresearch.com/industry-analysis/ethanol-market accessed at October 2021. 25. Kim, S. G.; Lee, K. H.; Curr. Appl. Phys. 2009, 9, e51. 26. Dong, G.; Nagasawa, H.; Yu, L.; Wang, Q.; Yamamoto, K.; Ohshita, J.; Kanezashi, M.; Tsuru, T.; J. Memb. Sci. 2020, 610, 118284. 27. Wang, C.; Zhang, Z.; Zhang, X.; Gao, J.; Stewart, B.; Sep. Purif. Technol. 2019, 221, 1. 28. Vatankhah, F.; Moheb, A.; Mehrabani-Zeinabad, A.; J. Memb. Sci. 2021, 618, 118717. 29. Qariouh, H.; Schué, R.; Schué, F.; Bailly, C.; Polym. Int. 1999, 48, 171. 30. Schiffmann, P.; Repke, J. U.; Chem. Eng. Technol. 2015, 38, 879. 31. Wijmans; J. G.; Baker; R. W. In Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., eds.; John Wiley & Sons, Ltd.: Hoboken, 2006; pp. 159. 32. Alvarez, M. E. T.; Martini, R. F.; Wolf-Maciel, M. R.; Comput. Aided Chem. Eng. 2001, 9, 567. 33. M. E. T. Alvarez, E. B. Moraes, W. A. Araujo, R. Maciel Filho, M. R. W.-M.; J. Appl. Polym. Sci. 2007, 107, 2256. 34. Vrentas, J. S.; Duda, J. L.; J Polym Sci Polym Phys Ed 1977, 15, 403. 35. Vrentas, J. S.; Duda, J. L.; AIChE J. 1979, 25, 1. 36. Darvishi, A.; Aroujalian, A.; Keshavarz Moraveji, M.; Pazuki, G.; RSC Adv. 2016, 6, 15327. 37. Fujita, H.; Fortschr. Hochpolym.-Forsch. 1961, 3, 1. 38. Carlson, E. C.; Chem. Eng. Prog. 1996, 35. 39. Haward, R. N.; J. Macromol. Sci. 1970, C4, 191. 40. Bretas, R. E. S.; Collias, D.; Baird, D. G.; Polym. Eng. Sci. 1994, 34, 1492. 41. Brito, K. D.; Cordeiro, G. M.; Figueirêdo, M. F.; Vasconcelos, L. G. S.; Brito, R. P.; Comput. Chem. Eng. 2016, 93, 185. 42. Tututi-Avila, S.; Jiménez-Gutiérrez, A.; Hahn, J.; Chemical Engineering and Processing: Process Intensification 2014, 82, 88. 43. Valentinyi, N.; Andre, A.; Haaz, E.; Fozer, D.; Toth, A. J.; Nagy, T.; Mizsey, P.; Sep. Sci. Technol. 2020, 55, 601. 44. Kunnakorn, D.; Rirksomboon, T.; Siemanond, K.; Aungkavattana, P.; Kuanchertchoo, N.; Chuntanalerg, P.; Hemra, K.; Kulprathipanja, S.; James, R. B.; Wongkasemjit, S.; Renew. Energy 2013, 51, 310. 45. Nagy, E.; Mizsey, P.; Hancsók, J.; Boldyryev, S.; Varbanov, P.; Chemical Engineering and Processing: Process Intensification 2015, 98, 86. |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access