Revisão
|
|
| Quimiometria III - revisitando a análise exploratória dos dados multivariados Chemometrics III - revisiting the exploratory analysis of multivariate data |
|
Márcia Miguel Castro Ferreira*
Laboratório de Quimiometria Teórica e Aplicada, Instituto de Química, Universidade Estadual de Campinas, 13083-970 Campinas - SP, Brasil Recebido em: 15/03/2022 *e-mail: mmcf@unicamp.br In this work, three methods for pattern recognition, used as exploratory data analysis, are revisited. A brief review of principal component analysis, PCA, an unsupervised method, is provided. Next, the Mahalanobis distance and the confidence ellipses usually drawn around the scores samples are discussed. Fisher's canonical variate analysis (a supervised methodology) is the second method revisited in this work. The third exploratory data analysis methodology addressed is ANOVA-PCA, which uses the analysis of variance to separate variations into main effects, interaction and noise followed by principal component analysis. Unlike the other two, ANOVA-PCA was proposed recently and is still not yet explored in all its capabilities. One advantage of this method is the possibility to calculate the variance of each of the effects involved in the experimental design. The mathematical bases of the three methods are discussed as well as examples are presented. INTRODUÇÃO O parque instrumental da Química sofreu grandes mudanças nos últimos 50 anos, decorrentes do avanço tecnológico. Os métodos espectroscópicos e cromatográficos passaram por uma revolução com o desenvolvimento dos detectores com arranjo de diodos, dos métodos hifenados bem como dos instrumentos portáteis de baixo custo. Simultaneamente, a área computacional que compreende hardware e software também passou por mudanças radicais que afetaram o mundo como um todo. As máquinas de grande porte (supercomputadores) foram miniaturizadas dando lugar aos microcomputadores e em um curto intervalo de tempo os equipamentos de laboratório foram interfaciados aos microcomputadores. Com isso uma instrumentação sofisticada se tornou de uso disseminado e passou a fazer parte das análises de rotina tanto nos laboratórios como em campo. Decorrente desses avanços, a complexidade dos problemas que puderam ser tratados aumentou exponencialmente. Outro fato importante que ocorreu também na década de 70 foi o surgimento e desenvolvimento da Quimiometria, como consequência natural do avanço tecnológico e da necessidade de desenvolver métodos apropriados para lidar com toda a massa de informação digital adquirida1 (cromatogramas, espectros, etc.) para cada amostra (objeto, indivíduo). A Quimiometria nasceu no início da década de 1970 com as tentativas de resolver problemas de classificação, que na época eram designados como "reconhecimento de padrões na Química". Dois nomes devem ser citados nesse contexto: Bruce Kowalski2 dos Estados Unidos (1944 - 2012) e Svante Wold3 da Suécia (1941 - 2022), que são conhecidos como os seus fundadores. O papel da Quimiometria foi crucial para a Química Analítica nas décadas de 80 e 90, quando surgiram os métodos multivariados de calibração (regressão) e os métodos multimodos. Entretanto, a área de reconhecimento de padrões foi a que mais se desenvolveu nos últimos quinze anos em que o principal objetivo não é fazer a determinação quantitativa de um composto de interesse com acurácia, mas, detectar falhas em processos industriais, determinar a origem ou autenticação de produtos industrializados, identificar metabólitos marcadores na medicina, dentre outros. Este trabalho pretende expor uma revisão de alguns métodos de análise exploratória dos dados assim como algumas de suas aplicações. O objetivo nesses casos é explorar os dados na busca por tendências que possam estar mascaradas e visualizá-las em duas ou três dimensões sem a preocupação de construir modelos preditivos. Serão discutidos a análise de componentes principais (PCA - principal component analysis) e ANOVA-PCA, que são dois métodos não supervisionados de reconhecimento de padrões e a análise de variáveis canônicas de Fisher, CVA (canonical variate analysis), que também é considerado um método exploratório mesmo sendo supervisionado. Esse é o terceiro trabalho da série Quimiometria. O primeiro artigo4 introduziu os conceitos da calibração multivariada na forma de um tutorial utilizando o software MATLAB onde estão discutidos os métodos de regressão por componentes principais (PCR - principal component regression) e regressão por quadrados mínimos parciais (PLS - partial least squares). Nesse mesmo artigo foi também apresentada a análise de componentes principais. O segundo trabalho, Quimiometria II,5 abordou a área de planejamentos experimentais, (DOE - design of experiments) sendo então discutidos vários tipos de planejamentos em forma de tutorial, neste caso fazendo uso das planilhas eletrônicas do Excel.
ANÁLISE DE COMPONENTES PRINCIPAIS PCA é certamente o método de análise multivariada mais conhecido e utilizado e também o primeiro contato de estudantes na área de Quimiometria.4,6-8 Karl Pearson9 propôs esse método em 1901, mas o tratamento formal é devido ao trabalho de Hotelling10 na década de 1930. Esse é um método de projeção e que ao mesmo tempo faz a compressão dos dados. A Figura 1 nos ajuda a compreender esses conceitos.
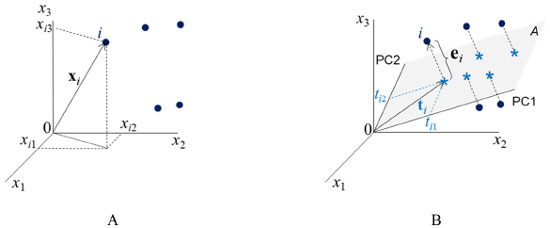 Figura 1. A) Coordenadas (xi1, xi2, xi3) da amostra i no espaço tridimensional. B) Representação gráfica da projeção dessa mesma amostra no subespaço A gerado pelas duas componentes principais, PC1 e PC2. ti é o vetor de escores definido no plano das PC; ti1 e ti2 são as coordenadas (os escores) de i nesse plano e ei é o vetor de resíduos, ortogonal ao plano A
Os círculos cheios nas Figuras 1A e 1B representam algumas das amostras de um conjunto de dados contendo I amostras para o qual foram medidas três propriedades (x1, x2 e x3). A amostra i destacada na Figura 1A tem coordenadas xi1, xi2 e xi3 no espaço original, de dimensão 3. Ao fazer a análise de componentes principais, dois novos eixos, PC1 e PC2, cujas direções indicam a máxima dispersão dos dados, foram definidos gerando o subespaço A de dimensão 2, como indicado na Figura 1B. As amostras são então projetadas nesse plano e obtém-se as estrelas. As coordenadas da amostra i no plano A são os seus escores, ti1 e ti2. A distância ortogonal ao plano entre o círculo e a estrela é o resíduo que representa a informação eliminada resultante da análise de componentes principais. Ao definir o subespaço e efetuar a projeção das amostras no plano A, a dimensionalidade dos dados é reduzida de três para dois. Por esse motivo diz-se que esse é um método de projeção e também de compressão. Do ponto de vista matemático, a expressão 1 descreve uma matriz de dados X de dimensões (I×3) onde cada linha se refere a uma amostra (objeto, indivíduo). Nas colunas estão as três propriedades x1, x2 e x3, medidas.  O vetor linha, xiT ((•)T indica a transposta de um vetor ou matriz) se refere à amostra i e seus elementos são os valores das três propriedades xi1, xi2 e xi3 medidas para descrever essa amostra (veja Figura 1A). Cada vetor coluna xj se refere a uma variável, ou seja, a uma medida realizada para todas as amostras. A análise de componentes principais resulta de uma transformação linear na matriz X representada pela expressão 2  em que T, L e E são as matrizes de escores, pesos e resíduos, respectivamente, e A é a dimensão do subespaço, i.e., o número de componentes principais retidas na decomposição de X, que no caso da Figura 1B é igual a 2. L é a matriz de pesos, cujos elementos indicam o quanto cada variável original contribuiu para gerar as PC (o novo sistema de eixos). Por exemplo, a variável x1 contribuiu com l11, a variável x2 com l21 e x3 com l31 para formar a primeira componente principal. O vetor de pesos da primeira componente principal e a matriz de pesos para as duas PC estão indicados a seguir (expressão 3). 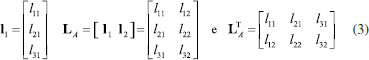 A matriz T contém os escores, i. e., as coordenadas das amostras no novo sistema de eixos. Associando à Figura 1B, ti é o vetor de escores da amostra i, que tem dois elementos: tiT = [ti1 ti2], um na primeira e outro na segunda componente principal. A matriz de resíduos, E, é constituída de vetores linha (que para a amostra i é um vetor com três coordenadas, eiT = [ei1 ei2 ei3]) ortogonais ao subespaço A e contém toda a informação que foi considerada como sendo irrelevante. A matriz de resíduos é nula quando não há compressão dos dados, i. e., quando A = 3. Considerando ainda os dados da expressão 1, o procedimento de obtenção das PC também pode ser representado pelo Esquema 1 em que todas as matrizes indicadas têm dimensões (I×3). A matriz X foi decomposta em três matrizes, cada uma sendo o produto de dois vetores, t 1 l 1 T , t l 2 e t 3 l 3 T . As informações descritas em PC1 "não se misturam", i. e., não se correlacionam com as de PC2, PC3 e assim por diante. A informação relevante dos dados está nas duas primeiras componentes principais, X ^ A , que é a matriz de dados reconstruída com apenas essas duas PC. A terceira componente principal descreve os resíduos.
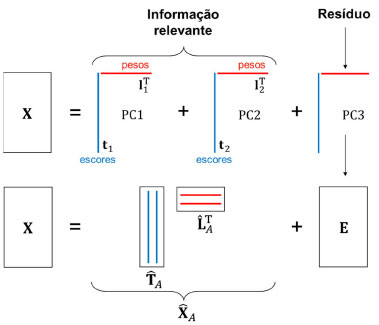 Esquema 1. Representação esquemática da decomposição da matriz X (I×3) da expressão 1 em duas componentes principais e a matriz de resíduos
Generalizando para J variáveis, A essa altura torna-se claro ao leitor que, a análise de componentes principais é baseada exclusivamente nas informações contidas na matriz de dados, sem assumir nenhuma forma paramétrica para a distribuição da população. Os métodos mais comuns para o cálculo dos escores e os pesos utilizam: 1) o algoritmo NIPALS (Non Linear Iterative Partial Least-Squares); 2) a diagonalização da matriz de variância-covariância ou; 3) a decomposição por valores singulares, SVD. O algoritmo NIPALS11 foi o primeiro método proposto para esse fim.7 Ele calcula as componentes principais uma a uma. O processo é iterativo e inicia-se com a matriz de dados devidamente pré-processada, X0. Como o objetivo no caso é definir vetores que descrevam a máxima variância dos dados, é natural selecionar a coluna de X0 que tenha a maior variância como escore inicial, t0. O quadro a seguir descreve a sequência de passos da primeira iteração.

Esse procedimento é repetido até que a diferença entre as variâncias de duas iterações sucessivas (o valor de delta) esteja dentro da tolerância especificada, como, por exemplo, 10-8. Então, se delta ≤ 10-8, o critério de convergência foi satisfeito, o processo iterativo está encerrado e o vetor de pesos da primeira componente principal, l1, e o primeiro vetor de escores, t1, já estão calculados. A contribuição dessa componente principal, t1l1T, é então subtraída de X0, (X1 = X0 - t1l1T), e os cálculos são repetidos para a próxima componente principal iniciando com X1. O outro método de se calcular os pesos e escores das componentes principais faz uso da diagonalização da matriz de variância-covariância, que explica a dispersão dos dados ao redor do seu centroide. Ela tem dimensões (J×J) e se encontra definida na expressão 4. Os vetores de pesos são calculados resolvendo a equação 5 de autovalores, na qual Ia são os autovetores e λa os respectivos autovalores para 1 ≤ a ≤ A e I é a matriz identidade. 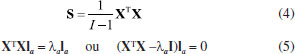 Os autovalores, λa são todos não negativos (positivos ou iguais a zero) e indicam as variâncias dos dados originais descritas pelas respectivas componentes principais. Eles são determinados em ordem decrescente, (λ1 ≥ λ2 ≥ . ≥ λA), de modo que cada componente principal maximiza a variância que não foi descrita pelas anteriores. Esses autovalores compõem a matriz diagonal Λ. Os autovetores la são os vetores de pesos que indicam as direções das componentes principais, i. e., as de máxima variância. Eles são ortogonais e normalizados (laTlb = 1 para a = b e laTlb - para a ≠ b). Uma vez que os novos eixos foram definidos, os escores são determinados através de uma transformação linear, TA = XLA, em que cada amostra é projetada no espaço gerado pelas componentes principais. A quantidade de informação descrita por uma única componente principal pode ser descrita pela porcentagem de variância explicada.7 Não havendo compressão dos dados, ao se fazer A = K, em que K é o mínimo entre I e J, normalmente representado como K = min{I, J}, os resíduos são iguais a zero e a soma de todos os autovalores da matriz de dados pré-processada é igual ao traço, Tr (soma dos elementos da diagonal), da matriz (XT X), i. e.,  Uma vez definido o número de componentes principais suficiente para a descrição do problema em estudo (a dimensão intrínseca ou o posto químico), pode-se calcular a porcentagem de variância acumulada pelas A componentes (% Varacumulada) usando a expressão 7. 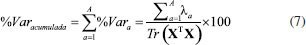 O método de decomposição por valores singulares,7 SVD, é um dos mais importantes na álgebra linear, e se constitui na técnica mais acurada e estável para o cálculo dos escores e dos pesos. A matriz de dados X é decomposta nas três matrizes: U, S e V, de tal modo que X pode ser escrita como o produto indicado na expressão 8.  As matrizes U e V são quadradas ((I×I) e (J×J), respectivamente) e ortonormais, i.e., as colunas de U e de V são ortogonais entre si e normalizadas: U UT = UT U = I, a matriz identidade de dimensões (I×I) e V VT = VT V = I de dimensões (J×J). A matriz S é retangular (I×J) com todos os elementos fora da diagonal iguais a zero. Os elementos da diagonal de S são chamados de valores singulares, saa, e eles estão sempre ordenados em ordem decrescente. O autovalor da matriz de variância-covariância, λa, é igual ao quadrado do respectivo valor singular, λa = (saa)2. Nessa decomposição, a matriz V é igual à matriz de pesos, L, e a matriz de escores é o produto T = US. Para exemplificar o procedimento descrito acima será analisado um conjunto de dados de amostras do Instituto Chinês de chá.12 Três categorias de chá foram consideradas: o verde, o oolong e o preto. Eles diferem entre si no processamento das folhas frescas, sendo que o chá oolong é uma categoria intermediária entre o verde e o preto. O objetivo desse exemplo era investigar a relação entre a qualidade do chá e a sua composição química. Duas variedades de cada uma das três categorias foram estudadas: K e F do chá preto; C e H do verde e S e T do oolong. Quanto ao parâmetro de qualidade, as amostras de cada variedade foram testadas por um painel de provadores segundo o atributo sensorial do sabor e então rotuladas com um índice numérico (1, 2, 3, ⋯) que aumenta à medida que decresce a qualidade. Em outras palavras, ao chá de melhor qualidade de uma dada variedade foi atribuído o índice igual a 1. Para a composição química, foram determinados os teores de celulose (11,42 ± 0,97), hemicelulose (8,98 ± 3,56), lignina (7,34 ± 2,68), polifenóis(22,73 ± 2,89), cafeína(3,64 ± 0,60) e aminoácidos(3,31 ± 0,92); todos medidos em% peso /% peso matéria seca. A matriz de dados consiste de 31 amostras (linhas) e seis variáveis para a composição química (colunas), X = (31×6). Como os teores médios e os desvios padrões dos constituintes analisados são bem distintos, sugere-se que os dados sejam autoescalados7 ponderando com maior peso as variáveis com menor desvio padrão e vice-versa. Esse procedimento é aplicado às colunas de X para que todas as variáveis tenham o mesmo grau de importância na análise dos dados. Os gráficos de escores e de pesos obtidos ao se aplicar a análise de componentes principais se encontram na Figura 2.
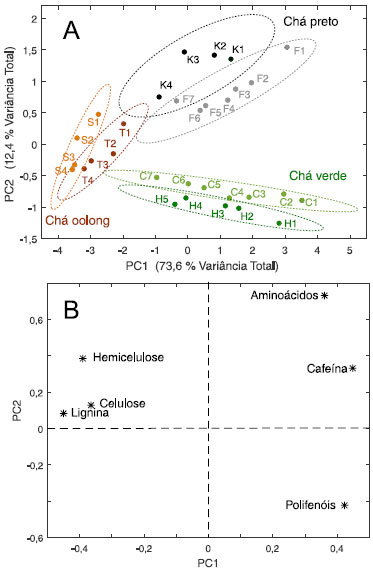 Figura 2. Gráfico de escores (A) e de pesos (B) de PC1×PC2 das três categorias de chá chinês estudadas sendo que K e F são duas variedades de chá preto, C e H as variedades de chá verde e S e T são as duas variedades de chá oolong. Os índices nos rótulos das amostras indicam a qualidade do chá. O índice 1 foi dado ao chá de melhor qualidade de uma dada variedade
A variância descrita pelas duas primeiras componentes principais corresponde a 86% da variância total, sendo 73,6% em PC1 e 12,4% em PC2. As três categorias de chás (preto, verde e oolong) estão bem discriminadas (Figura 2A). Observa-se também uma discriminação razoável entre as duas variedades de cada categoria. Para todas elas, a qualidade aumenta gradativamente quando se desloca da esquerda para a direita no gráfico de escores. Portanto, PC1 descreve a qualidade do chá. O gráfico de pesos (Figura 2B) explica as tendências observadas no gráfico de escores. À medida que os escores aumentam em PC1, os teores de fibras tendem a diminuir e os teores de aminoácidos, polifenóis e cafeína tendem a aumentar. As amostras das duas variedades de chá oolong apresentam em média maiores teores de fibras em comparação com as demais categorias. Consequentemente estão mais à esquerda no gráfico de escores. A segunda componente principal está relacionada às categorias (Figura 2A). Com escores negativos em PC2 estão as variedades de chá verde e com escores positivos as de chá preto. Os chás verdes tendem a ter maiores teores de polifenóis (Figura 2B) enquanto que chás pretos apresentam os maiores teores de aminoácidos. As variedades de chá estão circundadas por elipses que não foram traçadas livremente, mas utilizando distâncias estatísticas (distâncias adimensionais e invariantes com respeito à escala) associadas a um limite de confiança definido a priori. Com 95% de confiança, as duas variedades de chá verde estão bem discriminadas. Uma amostra da variedade F de chá preto (F7) está na região de sobreposição entre os dois grupos dessa categoria. O mesmo ocorre para duas amostras da variedade S de chá oolong (S3 e S4). É importante que os usuários de Quimiometria tenham uma compreensão de como essas curvas são traçadas. A seguir será feita uma breve discussão a respeito das elipses de confiança, iniciando pela distância Euclidiana, que é a medida mais intuitiva e a mais utilizada nas situações diárias. A distância Euclideana entre os dois pontos A = (xa1, xa2) e B = (xb1, xb2) no espaço bidimensional pode ser calculada usando o teorema de Pitágoras como indicado na expressão 9. 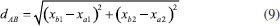 A representação geométrica é a reta que une A e B na Figura 3.
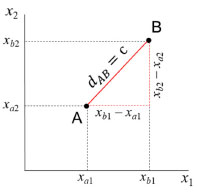 Figura 3. Distância Euclidiana entre os pontos A com coordenadas (xa1, xa2) e B (xb1, xb2) no espaço bidimensional
Generalizando para o espaço multidimensional RJ em que xaj e xbj são os valores numéricos da j-ésima coordenada de A e B, respectivamente, a distância é dada pela expressão 10. 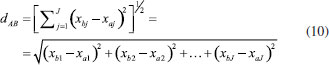 A distância Euclideana também pode ser escrita na forma de produto interno de acordo com a expressão 11 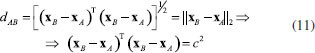 em que xA e xB são dois vetores (J×1) e c é o raio de uma hiperesfera no espaço de dimensão J ou um círculo no espaço bidimensional. Todos os objetos que se encontram no círculo de raio igual a c da Figura 4 são equidistantes de B.
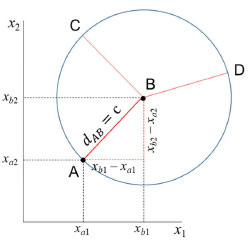 Figura 4. Distâncias dAB = dCB = dDB = c. Todos os objetos equidistantes de B a uma distância igual a c, estão no círculo
A distância Euclideana não é adequada em muitas análises estatísticas uma vez que ela varia com a mudança de escala. Em várias situações é desejável ponderar as variáveis que possuem variâncias distintas, como no caso do exemplo do chá chinês em que as variáveis foram autoescaladas. A distância de Mahalanobis, DAB é uma distância estatística ou generalizada que foi introduzida pelo matemático indiano Prasanta Mahalanobis em 1936.13 Ela tem em conta a variância de cada variável e também a associação entre elas. Para uma única variável x1, DAB é a distância Euclideana usual ponderada pelo desvio padrão (expressão 12). 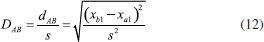 No caso de duas variáveis, x1 e x2, com variâncias distintas é razoável ponderar com maior peso a variável com menor dispersão e vice-versa, dividindo ambas pelo seu desvio padrão (expressão 13).  Esse procedimento equivale a autoescalar os dados, fazendo com que as variáveis tenham pesos semelhantes na análise de dados multivariados. Na expressão 13, não foi considerada a correlação entre as variáveis (r12 = 0), i.e., as variáveis são independentes e a matriz de correlação é diagonal. Ao invés de um círculo, a figura formada pelos pontos que estão a uma distância c de Mahalanobis ao ponto B é uma elipse, como exemplificado na Figura 5.
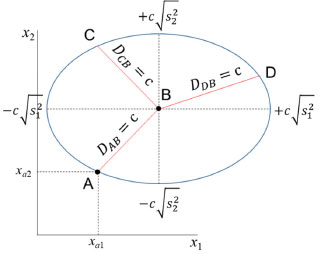 Figura 5. Distâncias DAB = DCB = DDB = c. Todos os objetos equidistantes de B (centroide) a uma distância igual a c, estão na elipse de eixos ±c 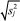 para j = 1, 2 para j = 1, 2
Quando a variabilidade para variáveis distintas é diferente e ao mesmo tempo elas estão correlacionadas com um coeficiente de correlação de Pearson igual a r12, a distância de Mahalanobis é acrescida de mais um termo (expressão 14). 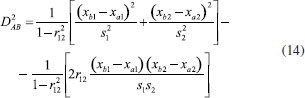 Assim como a distância Euclidiana (expressão 11), a distância de Mahalanobis também é descrita na forma de um produto interno de vetores como mostrado na expressão 15 ((•)-1 indica a inversa de uma matriz). 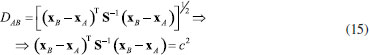 Nessa expressão, S-1 é a inversa da matriz de variância-covariância já definida anteriormente (expressão 4). De maneira semelhante ao caso anterior, os objetos que estão equidistantes de B segundo a distância de Mahalanobis com correlação também formam uma elipse, todavia com os eixos rotacionados (Figura 6).
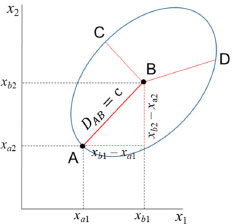 Figura 6. Todos os objetos equidistantes de B a uma distância igual a c, estão na elipse
A distância de Mahalanobis pode ser calculada usando as variáveis originais como na expressão 15 ou os escores quando for feita a análise de componentes principais. O fato interessante é que os resultados em ambos os casos são idênticos.7 Essa é a grande vantagem de se fazer uso de uma distância estatística. A distância de Mahalanobis da amostra i ao centro do conjunto de dados em função dos escores se encontra na expressão 16. 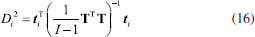 Como TTT é a matriz de autovalores Λ, (TTT = (US)T(US) = STUTUS = STS = Λ), a expressão 16 pode ser expandida produzindo a expressão17 que é a equação de um elipsoide 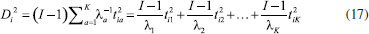 Os raios dos eixos principais da elipse de distância constante da origem para duas variáveis (K = 2) são dados na expressão 18. 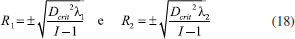 Se a variância é conhecida e os objetos seguem uma distribuição normal, a distância de Mahalanobis segue uma distribuição χK2 com K graus de liberdade. Por exemplo, para dois graus de liberdade no nível de confiança α = 0,05, o valor tabelado de χ20,05,2 = 5,99 é a distância crítica nesse nível de confiança, Dcrit2(α). Substituindo Dcrit na expressão 18, determina-se a elipse de distância constante no nível de confiança α. Amostras para as quais Di < Dcrit(α) se encontram no interior da elipse. Assim foram traçadas as elipses da Figura 2, que envolvem as variedades das três categorias de chá chinês. Se a variância não é conhecida, usa-se a distância de T2 de Hotteling, que é proporcional à distância de Mahalanobis e segue uma distribuição F. Concluindo, a análise de componentes principais é o método mais acurado para representar um conjunto de dados em um espaço de dimensão menor uma vez que os objetos são projetados em direções de variância máxima (as componentes principais, PC). No entanto, não há como captar a causa da variância, mas é possível descrevê-la da maneira mais eficiente possível. A Figura 7 apresenta um exemplo simples em que é visível que os objetos das duas populações podem ser separados. Na Figura 7A, a direção de máxima variância (PC1) é a reta que passa entre os dois grupos. Ao projetar os objetos nessa direção, vê-se que os dois grupos estão totalmente misturados. Essa não é uma orientação adequada para discriminá-los pois não descreve a variância exclusiva de nenhum dos grupos. Por outro lado, na Figura 7B a direção apresentada é a que melhor discrimina os objetos das duas populações. Ao projetá-los nessa direção, verifica-se que os dois grupos são totalmente distintos.
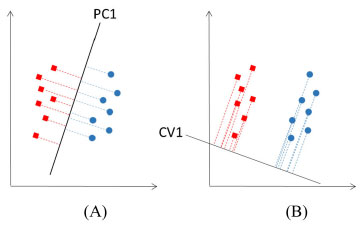 Figura 7. Dois grupos de objetos de diferentes populações. (A) Escores dos objetos na primeira componente principal (PC1) mostrando que essa direção não separa os dois grupos. (B) projeção dos objetos na primeira variável canônica (CV1), a reta que melhor discrimina os dois grupos
A seguir será introduzida a análise canônica de Fisher, que também é um método de análise exploratória no qual a separação de grupos pré-definidos, como os da Figura 7, é enfatizada.
ANÁLISE DE VARIÁVEIS CANÔNICAS DE FISHER, CVA A análise de variáveis canônicas de Fisher, CVA (Canonical Variate Analysis), foi proposta pelo estatístico e biólogo inglês Ronald Fisher em 1936.14 A ideia de Fisher foi transformar as observações multivariadas de diferentes grupos de amostras, representadas na matriz X, definindo novas variáveis designadas de variáveis canônicas de tal modo que a separação entre os grupos fosse maximizada. Deve-se salientar que a atribuição das amostras a diferentes grupos torna o método supervisionado. Tal como no método PCA, essa é uma técnica exploratória de projeção e que permite a redução da dimensionalidade de dados. Ela também usa as informações contidas na matriz X de dados sem assumir nenhuma forma paramétrica para a distribuição das populações ou dos grupos envolvidos. As variáveis canônicas são ordenadas em termos da sua importância, que neste caso não é a variância explicada (Figura 7A), mas a separação em grupos previamente definidos (Figura 7B). As variáveis canônicas mais importantes são usadas para obter uma representação gráfica dos objetos. Em geral, duas ou três dimensões são suficientes para se ter uma boa discriminação visual. Dois fatores são determinantes na separação dos grupos: 1) a distância entre eles e 2) o quão compacto eles são. Para contemplar esses dois fatores, Fisher se baseou na matriz da soma total de quadrados e produtos cruzados, SStotal, que será definida a seguir. Essa matriz descreve a dispersão global dos dados e pode ser particionada, de modo semelhante à análise de variância, na soma de duas matrizes, sendo que uma delas descreve a dispersão dentro dos grupos e a outra, a distância entre os grupos. As variáveis canônicas são derivadas dessas duas matrizes, como sendo as melhores combinações das variáveis originais que maximizam a razão da distância entre os grupos e a variância dentro dos grupos. Do ponto de vista matemático considera-se que X é uma matriz de dados de dimensões (I×J) em que os I objetos estão distribuídos em G grupos de diferentes populações e designados como g1, g2, ..., gG. O grupo 1 é constituído de I1 objetos pertencentes à população g1, o grupo 2 contém os I2 objetos que pertencem ao grupo g2 e assim por diante tal que I1+ I2+ ... + IG = I. A matriz da soma total de quadrados e produtos, SStotal, que descreve a variância global dos dados, está definida na expressão 19 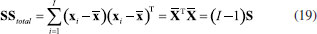 em que 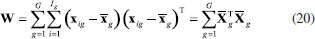 Nessa expressão, o vetor A soma de quadrados e produtos entre os grupos é representada pela matriz B que está definida na expressão 21. 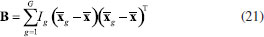 A matriz B fornece uma medida da distância entre os grupos, que é dada pela distância da média de cada grupo à média global. Uma característica importante dessa matriz é que ela é de posto (G - 1), independente do número de variáveis e, como consequência, somente (G - 1) variáreis canônicas serão diferentes de zero. Uma vez que as matrizes W e B são conhecidas, a soma total de quadrados e produtos, SStotal, pode ser escrita como uma somatória de todos os grupos como indicado na expressão 22. 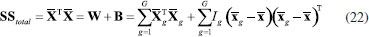 Segundo Fisher, a melhor descrição dos dados é aquela derivada da razão entre o "quadrado da distância entre as médias e a variância dentro dos grupos". O objetivo é encontrar a direção que maximiza a separação entre os grupos e isso equivale a encontrar a direção no espaço multivariado para a qual a diferença entre as médias dos grupos é a maior possível, comparada à variabilidade dentro dos grupos. É natural então propor que a razão da variabilidade "entre" versus a variabilidade "dentro" dos grupos seja maximizada. Esse é um método de análise exploratória que, de modo muito semelhante ao das componentes principais, define combinações lineares ótimas das variáveis originais. Algebricamente, procuramos uma transformação linear que maximize o produto W-1B, de modo semelhante à expressão 5, sob a condição de que a inversa de W existe.  Resolvendo a equação de autovalores, são encontrados os autovetores a e os respectivos escalares, λ, que são os autovalores. Esses novos eixos são designados vetores canônicos ou variáveis canônicas, CV. As primeiras variáveis canônicas são úteis para condensar a diferença entre os grupos. Uma vez que os vetores canônicos foram determinados, as coordenadas y de todos os objetos no novo sistema de eixos, designadas como "escores canônicos", devem ser calculadas conforme o Esquema 2, que é uma transformação linear onde se projeta cada amostra nas variáveis canônicas. A relação entre os diferentes grupos pode ser visualizada por meio dos gráficos de escores canônicos, em dimensões bem menores. Já foi comentado que CVA é uma técnica supervisionada, mas não de classificação, pois pela própria concepção do método não existe uma regra de classificação.
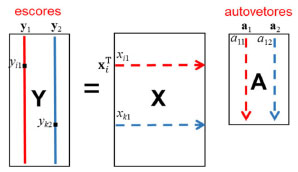 Esquema 2. Representação esquemática da determinação dos escores canônicos, y, no espaço gerado pelos autovetores (variáveis canônicas CV1 e CV2) para um conjunto de três grupos. é o escore da amostra i na primeira variável canônica e é o escore da amostra k na segunda variável canônica
As variáveis canônicas e as componentes principais apresentam várias características em comum, mas são métodos totalmente distintos. Em ambas, foram aplicadas transformações lineares gerando novas variáveis, que são combinações lineares das variáveis originais. Além disso, as variáveis canônicas, são extraídas em ordem de importância, assim como as PC. Uma das diferenças entre os dois métodos está na maneira de se obter as combinações lineares. A análise de componentes principais se baseia no critério de máxima variância. As combinações lineares das variáveis originais são obtidas de modo a maximizar a variância explicada; a primeira PC tem a direção que maximiza a informação contida nos dados, que não é necessariamente a direção que melhor separa os grupos (veja Figura 7A). Se eles são discriminados, é uma questão acidental e não conceitual. O termo "acidental" está sendo utilizado aqui apenas para enfatizar a diferença entre PCA e CVA. Se na análise de componentes principais, os objetos se agrupam, conclui-se que a informação majoritária contida nas variáveis medidas para cada objeto está relacionada com as diferenças entre os grupos. Por outro lado, a análise canônica se baseia no critério de máxima verossimilhança (maximiza o produto W-1B). As combinações lineares das variáveis originais que dão origem às variáveis canônicas são aquelas que maximizam a separação dos grupos previamente definidos sendo que a direção da primeira variável canônica é aquela que melhor separa tais grupos (veja Figura 7B). Outra diferença entre os dois métodos e que deve ser mencionada é que os vetores canônicos não são ortogonais como os vetores peso. Os escores calculados em ambos os métodos são não correlacionados, mas as direções das variáveis canônicas não são ortogonais. As variáveis canônicas são obtidas efetuando-se rotações nos eixos originais que também mudam as orientações relativas entre eles. Para exemplificar a análise canônica, utilizaremos o mesmo conjunto de dados que Ronald Fisher utilizou para estabelecer um critério de separação de três espécies de flores de íris.15 Esses dados consistem de 150 flores de íris de três espécies diferentes (Iris setosa, Iris versicolor e Iris virginica), para as quais foram medidas 4 propriedades (o comprimento e a largura das sépalas e das pétalas, em centímetros). Os dados originais são apresentados na Figura 8 na forma de gráficos bivariados, sendo 50 flores de cada espécie.
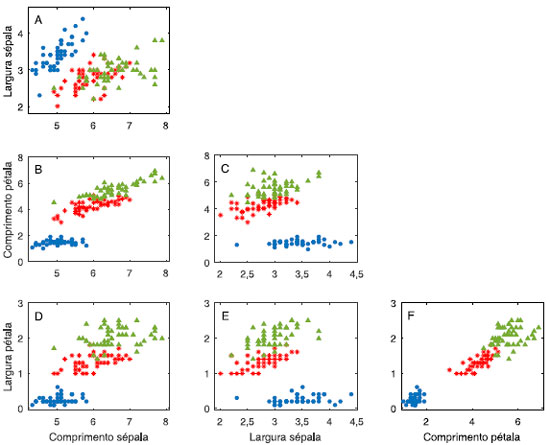 Figura 8. Gráficos bivariados das medidas realizadas nas flores de íris em centímetros. Íris setosa (●); Íris versicolor (*) e Íris virgínica (▲)
Explorando a Figura 8, o gráfico bivariado 8F, que considera o comprimento versus a largura das pétalas mostra que há uma correlação positiva entre essas duas variáveis. Verifica-se também que as flores da espécie setosa (●) formam um grupo compacto à parte das restantes, pois suas pétalas se caracterizam por terem comprimento e largura menores. Essas propriedades nas flores da espécie versicolor (*) são intermediárias e as flores da espécie Íris virgínica (▲) são as que apresentam, no geral, pétalas com maiores comprimento e largura. Essa é uma indicação de que tanto o comprimento quanto a largura da pétala contribuem para discriminá-las. De um modo geral, todas as variáveis contribuem para a discriminação dos grupos. A seguir, será aplicada a análise canônica de Fisher aos dados autoescalados. Foram calculadas as matrizes das somas de quadrados e produtos SStotal, W e B, todas elas de dimensões (4×4). As variáveis canônicas que são os autovetores da matriz produto W-1B foram calculadas resolvendo-se a equação de autovalores 23. Como são três grupos de flores, G = 3, apenas duas variáveis canônicas serão diferentes de zero. Uma vez encontrados os vetores canônicos, os escores foram calculados projetando cada uma das amostras nessas duas direções. A Figura 9 apresenta visualmente os resultados dos escores obtidos para essas duas variáveis canônicas, CV1 e CV2 sendo que a primeira variável canônica é que está associada à discriminação das três populações.
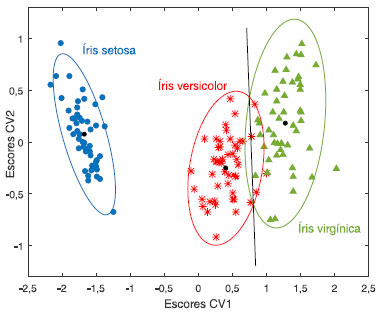 Figura 9. Gráfico dos scores canônicos de CV1 versus CV2 das três espécies de flores. Os dados da matriz X(150×4) foram autoescalados. Os pontos pretos indicam o centroide de cada grupo. As elipses ao redor das amostras foram traçadas com 95% de confiança
Apenas a título de visualização, assumiu-se que cada grupo apresenta uma distribuição normal para traçar as elipses no nível de confiança α = 0,05 e cuja origem é o centroide da respectiva espécie de flor. A reta que passa pela interseção das duas elipses justapostas (quando as distribuições têm a mesma probabilidade), foi inserida para tornar mais clara a eficiência do método de Fisher. A análise de componentes principais foi aplicada a esse mesmo conjunto de dados autoescalados com a finalidade de comparar os dois métodos e o gráfico de escores obtido para as duas primeiras PC se encontra na Figura 10. De modo semelhante à análise canônica assumiu-se que os dados seguem uma distribuição normal e as elipses foram traçadas com 95% de confiança para comparar os resultados com aqueles da Figura 9.
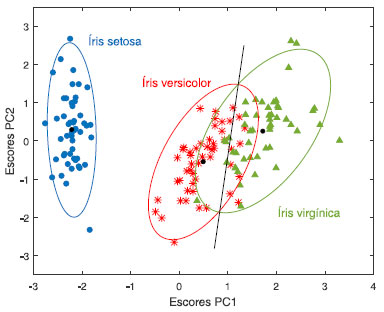 Figura 10. Gráfico de escores das componentes principais PC1 versus PC2 das três espécies de flor. Os dados da matriz X(150×4) foram previamente autoescalados. Os pontos pretos indicam os centroides de cada classe. As elipses foram traçadas no nível de confiança α = 0,05
É visível que os escores das duas primeiras componentes principais da análise PCA e as duas primeiras variáveis canônicas da análise CVA apresentam características semelhantes. Pode-se concluir que, nesse caso, as informações contidas nas quatro medidas experimentais estão intimamente relacionadas com as diferenças nas espécies de flor, o que pode ser confirmado pelos gráficos bivariados da Figura 8. Todavia, a análise canônica é mais eficiente para discriminar as espécies de íris uma vez que a redução de dimensionalidade foi feita maximizando-se a discriminação entre as espécies e não a variância explicada. Nesse momento, é importante enfatizar que para aplicar a análise canônica é necessário calcular a inversa da matriz W. Esse é um problema bem conhecido por quem trabalha com matrizes nas quais o número de variáveis é maior que o número de amostras. A matriz é singular provocando uma instabilidade na determinação da sua inversa. Duas soluções possíveis para esse problema seriam fazer uma seleção de variáveis ou usar um método de compressão dos dados que retenha o máximo da informação original e o mais óbvio nesse caso é a análise de componentes principais. A dimensionalidade dos dados é reduzida através da análise de componentes principais o que permite a aplicação da análise canônica restrita ao subespaço gerado pelas PC. No próximo exemplo, a análise de variáveis canônicas será aplicada a um conjunto de dados originados da análise dos compostos voláteis de quatro culturas de fungos in vitro.16 Esses fungos (Alternaria alternata, Colletotrichum gloeosporioides, Fusarium solani e Lasiodiplodia theobromae) se desenvolvem com frequencia no mamão e podem causar grandes perdas na pós-colheita. Os isolados de fungos foram ativados em meio batata dextrose-ágar e os compostos voláteis foram extraídos por microextração em fase sólida (SPME - solid-phase micro-extraction) e analisados por cromatografia gasosa acoplada com espectrometria de massa (GC-MS gas chromatography coupled with mass spectrometry). As análises de cada espécie de fungo foram realizadas por 4 dias consecutivos a partir do dia da inoculação, sendo que em cada dia foram executados cinco experimentos (cinco inoculados de uma mesma espécie de fungo). Os perfis cromatográficos originais foram organizados em formato de matriz X (80 × 3141), onde cada inoculado representa uma amostra. As regiões inicial e final dos cromatogramas, antes de 3,68 e após 28,14 min, foram removidas da matriz de dados por caracterizarem ruído experimental. Além disso, um pico intenso e amplo presente em alguns dos cromatogramas no tempo de retenção de 6,3-7,4 min (oriundo de algum volátil presente no ambiente laboratorial) foi substituído pela média da linha de base dessa mesma região. Cada perfil cromatográfico foi normalizado pela norma 1
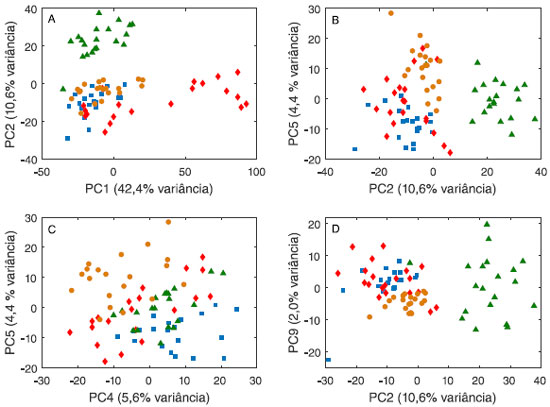 Figura 11. Gráficos de escores da análise de componentes principais dos compostos voléteis de quatro espécies de fungos: Alternaria alternata (■), Colletotrichum gloeosporioides (●), Fusarium solani (♦) e Lasiodiplodia theobromae (▲). As amostras foram normalizadas pela norma 1 e os dados foram autoescalados
Ao fazer a análise de componentes principais, constatou-se que a partir de 9PC (que descrevem 82,5% da informação dos dados originais) não havia nenhuma tendência de separação das espécies de fungo. Selecionou-se então 9 PC e a análise canônica de Fisher foi aplicada à matriz de escores T9 (80 × 9). Como são quatro espécies de fungos, três variáveis canônicas serão diferentes de zero, i.e., a melhor separação entre os grupos ocorre com 3 CV. A Figura 12 apresenta o gráfico de escores das duas primeiras variáveis canônicas e a composição (os pesos) de cada uma delas. Espera-se que as componentes principais que mais contribuam para a discriminação das espécies sejam aquelas com maiores pesos em CV1 e CV2: PC2, com pesos negativo em CV1 e positivo em CV2, é importante para a discriminação da espécie de fungo Lasiodiplodia; PC4, PC6 e/ou PC9 (com pesos positivos em CV1 e CV2) contribuem para a discriminação da espécie Alternaria enquanto que CV5 (pesos negativos em CV1 e CV2) é importante para a discriminação da espécie Colletotrichum. Quanto à espécie Fusarium, espera-se que PC1 com pesos positivo CV1 e negativo em CV2, tenha uma contribuição na discriminação dessa espécie.
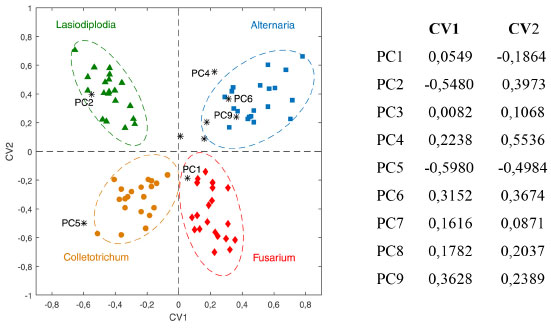 Figura 12. Escores canônicos CV1 × CV2 e as contribuições de cada componente principal na definição das variáveis canônicas CV1 e CV2. As elipses foram traçadas ao redor de cada espécie de fungo no nível de confiança α = 0,05
O objetivo nesse estudo não é detectar os prováveis voláteis marcadores de cada espécie de fungo, mas mostrar a superioridade da análise canônica de Fisher comparada à análise de componentes principais em separar amostras similares. Concluindo, ambos, PCA e CVA são métodos de análise exploratória baseados na compressão dos dados. A análise de componentes principais é um método não supervisionado, que não faz uso da informação a respeito dos grupos para otimizar a separação dos mesmos. Por outro lado, a análise de variáveis canônicas de Fisher, apesar de ser uma técnica supervisionada uma vez que faz uso da identificação de grupos a priori, não é de classificação pois não existe uma regra explícita para classificar objetos. Todavia, é comum definir uma regra ad hoc e utilizá-la como método de classificação.
ANÁLISE ANOVA-PCA A análise de ANOVA-PCA também é um método de análise exploratória e que foi introduzido em 2005 por Peter Harrington.17 Nesse método, a análise de variância ANOVA é combinada com a análise de componentes principais, PCA. De modo semelhante ao método CVA, a matriz de dados X é particionada em submatrizes com a diferença que nesse caso a partição é sequencial e de acordo com um planejamento experimental sendo que as submatrizes correspondem aos fatores, interações e à matriz de erros. Os fatores são caracterizados por níveis e através da ANOVA é possível testar se a resposta é significativamente diferente para os diferentes níveis de cada fator. Após a partição, a matriz de erros é adicionada à cada matriz de fatores e finalmente aplica-se a análise de componentes principais. O Esquema 3A apresenta um fluxograma da partição sequencial da matriz X nas matrizes que descrevem as fontes de variação (média, fator 1, ...) e o erro puro. Na primeira etapa do processo, a matriz X é centrada na média: calcula-se a média de cada coluna de X, forma-se uma matriz de médias que é então subtraída de X produzindo X ¯ . No Esquema 3, o primeiro fator tem três níveis e são feitas três sub-matrizes de médias, uma para cada um deles. A matriz resultante é subtraída de X ¯ de onde se obtém a matriz XF1 que será utilizada para o cálculo do fator seguinte, XF2 (com 8 níveis), e assim por diante até que ao final reste a matriz de erro residual, Xerro, que, em princípio deve descrever o erro experimental. O Esquema 3B mostra as matrizes resultantes da partição de X enquanto o Esquema 3C indica a adição dos erros residuais a cada fator para que então seja aplicada a análise de componentes principais. O método de ANOVA-PCA está baseado na hipótese de que se um fator é uma fonte dominante de variação comparada ao erro residual, então essa variação estará caracterizada em PC1 e a segunda PC reflete, principalmente, variações aleatórias. Como nos outros métodos apresentados nesse trabalho, a distância de Mahalanobis (ou T2 de Hotteling) é usada para gerar limites com 95% de confiança ao redor das amostras de cada nível de um dado fator.
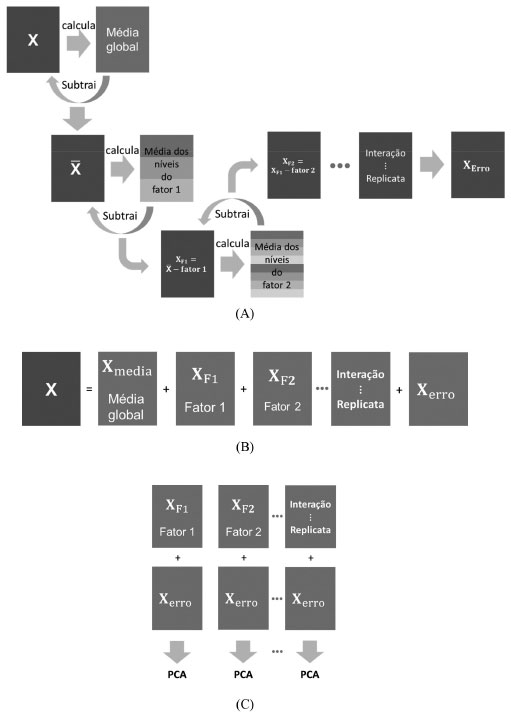 Esquema 3. Partição da matriz de dados X em matrizes de mesmas dimensões e que descrevem os fatores, interações, replicatas e o erro puro. A) Construção das matrizes de fatores, interação e erro puro. Nesse esquema, o fator F1 tem três níveis e o fator F2 tem oito. B) Resultado da partição sequencial de X em que a soma de todas as contribuições é igual à matriz original. C) A matriz de erros residuais (Xerro do esquema 3B) é adicionada às contribuições de X para a aplicação da análise de componentes principais
Todo esse procedimento pode ser representado e executado de maneira simples e elegante, lembrando-se que as matrizes de fatores seguem o modelo linear geral GLM18 (General Linear nodel), que é utilizado pelos químicos na construção das superfícies de resposta de planejamentos fatoriais. Essa metodologia permite reescrever os modelos de ANOVA na forma de uma regressão linear múltipla como indicado na expressão 24  em que X (I×J) é a matriz de dados, F (I×p) é a matriz de planejamento codificada em que p é o número de parâmetros no modelo, B (p×J) é a matriz dos coeficientes de regressão e E é a matriz de resíduos. A matriz F, em geral, não é quadrada e os coeficientes de regressão devem ser estimados pelo método clássico de quadrados mínimos de acordo com a expressão 25.  Uma vez estimados os coeficientes de regressão, pode-se calcular diretamente a matriz de resíduos usando a expressão 26.  Para um planejamento fatorial balanceado, isto é, quando o número de ensaios é o mesmo para todos os tratamentos, as matrizes dos fatores e interações são ortogonais entre si. Essas matrizes, X ¯ ; XF1; XF2; ., são facilmente construídas fazendo o produto dos sub-blocos FF* e BF* das matrizes F e B, correspondentes ao fator F conforme indicado na expressão 27  A essas matrizes são incorporados os resíduos, XF1 + XErro; XF2 + XErro; . e, finalmente, aplica-se a análise de componentes principais aos fatores individuais (Esquema 3C). Assumindo que há apenas dois fatores envolvidos e a interação entre eles, então, de acordo com o Esquema 3B, a matriz X é particionada como X = XMedia + XF1 + XF2 + XF1F2 + XErro. É importante ressaltar que essa decomposição também particiona a soma dos quadrados dos elementos de X na soma dos quadrados dos fatores como indicado na expressão 28 onde ||·||2 indica o quadrado da norma de Frobenius (soma dos quadrados dos elementos da matriz). Essas somas quadráticas podem ser usadas para quantificar a porcentagem de variação explicada pelos fatores e interação. Por exemplo, para o fator 1, a porcentagem explicada é dada pela expressão 29. 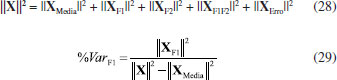 Quando há ensaios a mais ou a menos nos diferentes tratamentos, o planejamento deixa de ser balanceado, fazendo com que as matrizes dos fatores e interações não sejam ortogonais entre si e a soma das porcentagens de variação explicadas pelos fatores e interação pode não ser igual a 100%. Na literatura encontram-se ainda poucas aplicações desse método, mas é possível citar estudos de proteômica / metabolômica para a detecção de biomarcadores,16,19-23 estudos de estabilidade de materiais de referência,24,25 a análise de variância dos diferentes fatores26 e análise discriminante.27 Será apresentado a seguir um exemplo para ilustrar o funcionamento do método. O conjunto de dados escolhidos foi extraído de um estudo acelerado de shelf-life.28 Nesse estudo, o produto preparado foi submetido a três condições de estocagem. As análises químicas e sensoriais foram realizadas com frequência predefinida. As amostras são concentrados de tomate com 18 NTSS (Natural Tomato Soluble Solids) e foram preparadas na indústria. A seguir foram estocadas a 8 °C, 25 °C e 35 °C, em três estufas com controle de temperatura, mantendo-se a variação máxima em cada câmara de ± 1 °C. As avaliações foram feitas no instante inicial (t = 0) e após 1, 2, 3, 4, 6, 8, 10, 13, 18, 22, 24 e 30 meses. Quatro parâmetros instrumentais foram monitorados: os teores de licopeno, β-caroteno, vitamina C e a cor (delta E), bem como oito atributos sensoriais: cor visual, sabores doce, salgado e azedo, consistência e sabores de tomate verde, amargo e passado. O planejamento proposto para esse estudo se encontra na Figura 13 onde estão envolvidos dois fatores: o da temperatura com 3 níveis e o do tempo com 13 níveis. Os símbolos ● nessa figura indicam as 4 análises químicas e as 8 sensoriais realizadas nos meses indicados para os produtos acondicionados nas três temperaturas.
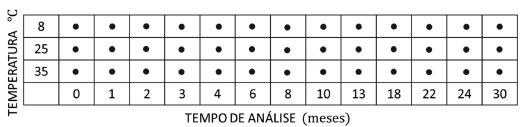 Figura 13. Planejamento proposto para o estudo dos efeitos da temperatura e do tempo em polpas de tomate. O símbolo ● indica as avaliações químicas e sensoriais feitas no produto acondicionado em uma dada temperatura nos tempos predefinidos
A matriz de dados X tem dimensões (39×12), sendo (13×12) para cada temperatura. Nesse exemplo serão considerados esses dois fatores e a interação entre eles. A matriz de planejamento codificada, F = [1 FTemp Ftempo FTemp×tempo], tem dimensões (39×39) sendo que a primeira coluna de "uns" é usada para o cálculo da média e FTemp×tempo é a interação entre os dois fatores. A Figura 14 contém a matriz de planejamento codificada para os dois fatores, [1 FTemp. Ftempo]. Essa forma de planejamento18 é bastante utilizada na indústria e designada como "codificação de soma zero" (sum coding) quando se impõe a restrição de que a soma de cada coluna deve ser zero. Cada linha da matriz codifica os níveis dos fatores (13 linhas para cada uma das temperaturas) e cada fator com n níveis é codificado com (n - 1) colunas (duas colunas para o fator temperatura e 12 para o fator tempo). Os primeiros (n - 1) níveis são codificados com zeros e uns e o último nível é codificado com -1. Por exemplo, os níveis da temperatura são codificados como [1 0], [0 1] e [-1 -1] para todos os níveis do fator tempo. A matriz codificada da interação temperatura×tempo (39×24) não está incluída nessa figura, mas pode ser facilmente calculada multiplicando elemento a elemento cada uma das colunas de FTemp pelas colunas de Ftempo.
 Figura 14. Matriz de planejamento F para o cálculo da média e dos dois fatores, F1 da temperatura com três níveis e F2 do tempo com 13 níveis
As matrizes B (39×12) dos coeficientes, de resíduos XErro e dos fatores e interação FTemp., Ftempo e FTemp×tempo foram calculadas usando as expressões 25, 26 e 27, respectivamente. Foi feita a análise ANOVA e as variâncias percentuais explicadas pelos fatores temperatura e tempo, interação e resíduo foram calculadas usando a expressão 29 e são, respectivamente, 44,17%, 31,05%, 24,78% e < 0,001% (a variância percentual do erro é praticamente nula). Os dados foram escalados pelo desvio-padrão uma vez que há variáveis com diferentes unidades. Os resíduos foram incorporados a cada fator e interação (Esquema 3C) e a análise de componentes principais foi aplicada separadamente às matrizes resultantes. O primeiro fator investigado foi o tempo. O estudo foi conduzido por 30 meses e foram feitas 13 avaliações nos concentrados de tomate acondicionados nas três temperaturas durante esse período. O gráfico de escores de PC1 × PC2 e os pesos de PC1 estão na Figura 15. Os 13 níveis do fator tempo estão bem discriminados ao longo de PC1 (74,45% da variância), indicando que esse fator é significativo comparado ao erro residual. Para cada nível há três medidas correspondentes às três temperaturas de estocagem. Os pesos descrevem a tendência de degradação do produto ao longo do tempo. Os teores de carotenoides e vitamina C, os sabores doce e azedo, bem como a consistência são elevados no período inicial (pesos negativos), quando os escores são altamente negativos em PC1. Concomitantemente, as cores visual e instrumental (Delta E), e o sabor amargo são menos intensos. À medida que o tempo passa, o produto é gradativamente degradado e ao final (escores positivos em PC1), os carotenoides e a vitamina C apresentam níveis baixos. Além disso, a consistência do concentrado e os sabores doce e azedo diminuíram, o concentrado se tornou mais escuro, mais amargo e ligeiramente salgado.
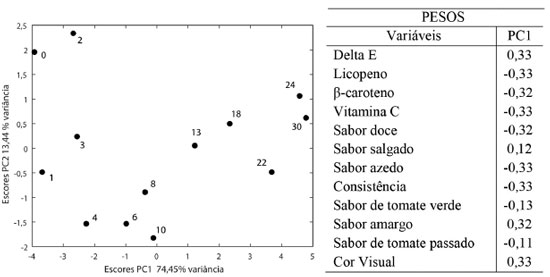 Figura 15. Resultados dos escores de PC1×PC2 obtidos da ANOVA-PCA para o fator tempo e os pesos de PC1. Os índices indicam o tempo (meses) em que as análises químicas e sensoriais foram realizadas a 8 °C, 25 °C e 35 °C
Para o fator temperatura, os escores obtidos estão na Figura 16 juntamente com os pesos em PC1 uma vez que essa é a componente que descreve a máxima variância desse fator (86,37%). Os três níveis de temperatura (do mercado consumidor a 25 °C; abaixo e acima dessa temperatura, a 8 °C e 35 °C, respectivamente) estão bem separados ao longo de PC1 mostrando que o fator temperatura também é significativo comparado ao erro residual.
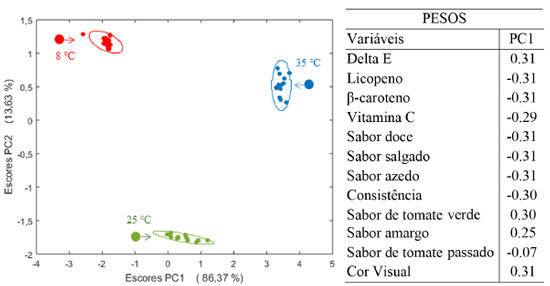 Figura 16. Resultados dos escores de PC1×PC2 obtidos da ANOVA-PCA para o fator temperatura e uma ampliação de cada nível com as respectivas elipses traçadas no nível de confiança α = 0,05. À direita estão os pesos da primeira componente principal
A ampliação dos escores e as elipses traçadas no nível de 95% de confiança foram incluídas para que se possa visualizar a distribuição das amostras. A variação nos escores das medidas realizadas em amostras mantidas na câmara fria (negativos em PC1) é menor uma vez que, excetuando uma amostra que se encontra fora da elipse, todas as outras formam um grupo compacto, indicando que a degradação do produto foi reduzida nessa temperatura. Já a 25 °C bem como a 35 °C as elipses de confiança são maiores e as amostras se encontram dispersas dentro das mesmas confirmando a tendência de degradação do produto. Os pesos indicam que amostras acondicionadas a 8 °C por 30 meses (com escores negativos) mantém altos teores de carotenoides, vitamina C, os sabores (excetuando os sabores amargo e de tomate verde) e as cores instrumental e visual menos intensas. Já as amostras acondicionadas em 35 °C apresentam escores positivos causados pelo decréscimo na concentração de carotenoides e vitamina C, bem como nos sabores doce, azedo, salgado e na consistência. Concomitantemente, há um acréscimo na cor e nos sabores amargo e de tomate verde. Observa-se que o produto estocado a 25 °C, com escores próximos de zero em PC1, sofre degradação menos drástica ao longo dos 30 meses. Comparando os dois fatores tempo e temperatura, observa-se que o sabor de tomate passado tem pesos próximos de zero e, portanto, manteve-se ao longo do tempo e não sofreu influência das temperaturas de estocagem. O sabor salgado e de tomate verde que praticamente não contribuíram com o fator tempo, são mais sensíveis ao efeito da temperatura. A interação temperatura × tempo também foi analisada. De acordo com o planejamento proposto na Figura 14, a interação ocorre entre os tempos finais (iniciais) das amostras acondicionadas a 8 °C e aquelas dos tempos iniciais (finais) acondicionadas a 35 °C. Além disso, entre as amostras finais e iniciais estocadas a 25 °C. A Figura 17 apresenta o gráfico de escores onde é visível que não existe uma discriminação dos grupos e conclui-se que a interação temperatura × tempo não é significativa.
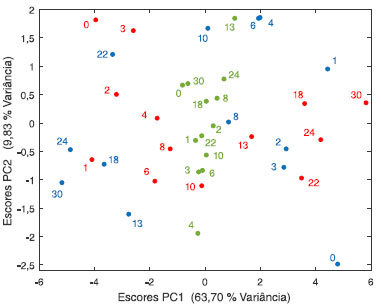 Figura 17. Resultados dos escores de PC1×PC2 obtidos da ANOVA-PCA para o fator de interação temperatura × tempo. Os índices indicam o tempo em que as análises experimentais e sensoriais foram realizadas. a 8°C (●), 25°C, (●) e 35 °C (●)
Com esse exemplo, ficou clara a vantagem do método, uma vez que possibilita extrair informações dos fatores e interações separadamente. Verificou-se que a interação entre os dois fatores não foi significativa. Em particular, foi através dessa análise que se pôde inferir que os sabores salgado e de tomate verde não sofreram alterações significativas ao longo do tempo, mas foram sensíveis à temperatura de estocagem.
CONCLUSÕES O objetivo deste trabalho foi discutir três métodos de análise exploratória de dados. A análise de componentes principais que é um método não supervisionado, a análise de variáveis canônicas de Fisher que é um método supervisionado e a análise ANOVA-PCA. As variáveis canônicas são vetores análogos aos pesos das componentes principais. Os pesos em PCA indicam direções de máxima variância, enquanto as variáveis canônicas indicam direções em que as diferenças entre os grupos são maximizadas em relação às variações dentro dos grupos. A análise canônica de Fisher pode ser aplicada aos dados instrumentais de grande porte desde que se aplique um método de compressão como a análise componentes principais a priori. Pela própria concepção, o método CVA é superior à PCA ao agrupar amostras com características similares. Por fim, foi introduzida a análise de variância combinada com PCA: ANOVA-PCA. Um diferencial desse método é a possibilidade de determinar a variação descrita pelos fatores em questão e de discutir cada um deles individualmente. Esse é um método com grandes potenciais, mas ainda pouco utilizado na literatura. ANOVA-PCA é uma ferramenta indicada para estudos que utilizam planejamentos multifatoriais, como é o caso das áreas de "ômicas", em que permite uma interpretação mais adequada dos resultados experimentais. MATERIAL SUPLEMENTAR No material suplementar disponível em http://quimicanova.sbq.org.br na forma de arquivo PDF, com acesso livre, estão os comandos na linguagem do MATLAB para a construção das elipses de confiança no plano; os comandos (também na linguagem do MATLAB) para representar graficamente os escores e pesos em um único gráfico, denominado na literatura de biplot; a matriz de planejamento F e os comandos para o cálculo das matrizes de interação FTemp×tempo e dos coeficientes B para o exemplo de ANOVA-PCA; a matriz FTF que mostra a ortogonalidade das matrizes de fatores e interação.
AGRADECIMENTOS A autora agradece ao Conselho Nacional de Desenvolvimento Científico e Tecnológico, CNPq, pela bolsa de professor pesquisador.
REFERÊNCIAS 1. S. Wold; Chemometr. Intell. Lab. Syst. 1995, 30, 109. [Crossref] 2. Wold, S. Em 40 Years of Chemometrics - From Bruce Kowalski to the Future; Lavine, B. K., Brown, S. D., Booksh, K. S., eds; ACS Symposium Series; American Chemical Society: Washington, DC, 2015, cap.1. [Crossref] 3. Davies, A. N.; Spectroscopy Europe 2022, 34, 27. 4. Ferreira, M. M. C.; Antunes, A. M.; Melo, M. S.; Volpe, P. L. O.; Quim. Nova 1999, 22, 724. 5. Teófilo, R. F.; Ferreira, M. M. C. Quim. Nova 2006, 29, 338. 6. Jolliffe, I.; Journal of Multivariate Analysis 2022, 188, [Crossref] 7. Ferreira, M. M. C.; Quimiometria: Conceitos, Métodos e Aplicações, Ed. UNICAMP: Campinas, 2015. 8. Ferreira, M. M. C.; J. Braz. Chem. Soc. 2002, 13, 742. [Crossref] 9. Pearson, K.; Phil. Mag. 1901, 2, 559. 10. Hotelling, H.; J. Edu. Psychol. 1933, 24, 417; 498. 11. Geladi, P.; Kowalski, B. R.; Anal. Chim. Acta 1986, 185, 1. [Crossref] 12. Liu, X; Van Espen, P.; Adam, F.; Anal. Chim. Acta 1987, 200, 421. [Crossref] 13. Mahalanobis, P. C.; Proceedings of the National Institute of Sciences of India 1936, 2, 49. 14. Fisher, R. A.; Ann. Eug. 1936, 7, 179. 15. https://archive.ics.uci.edu/ml/machine-learning-databases/íris, acessada em maio 2022. 16. Terra, L. R.; Queiroz, S. C. N.; Terao, D.; Ferreira, M. M. C.; J. Chemom. 2020, 34, e3244. [Crossref4] 17. Harrington, P. D. B.; Vieira, N. E.; Espinoza, J.; Nien, J. K.; Romero, R.; Yergey, A. L.; Anal. Chim. Acta 2005, 544, 118. [Crossref] 18. Thiel. M.; Feraud, B.; Govaerts, B.; J Chemom. 2017, 31, e2895. [Crossref] 19. Bonnefoy, C.; Fildier, A.; Buleté, A.; Bordes, C.; Garric, J.; Vulliet, E.; Talanta 2019, 202, 221. [Crossref] 20. Lemaire-Chamley, M.; Mounet, F.; Deborde, C.; Maucourt, M.; Jacob, D.; Moing, A.; Metabolites 2019, 9, 93. [Crossref] 21. Fritzsch, R.; Donaldson, P. M.; Greetham, G. M.; Towrie, M.; Parker, A. W.; Baker, M. J.; Hunt, N. T.; Anal. Chem. 2018, 90, 2732. [Crossref] 22. Sun, J.; Zhang M.; Kubzdela, N.; Luo, Y.; Harnly, J. M.; Chen, P.; Journal of Analysis and Testing 2018, 2, 312. 23. Geurts, B. P.; Neerincx, A. H.; Samuel Bertrand, S.; Leemans, M. A. A. P.; Postma, G. J.; Wolfender, Jean-Luc; Cristescu, S. M.; Buydens, L. M. C.; Jansen, J. J.; Anal. Chim. Acta 2017, 963, 1. [Crossref] 24. dos Santos, L. O.; dos Santos, A. M. P.; Ferreira, M. M. C.; Ferreira, S. L. C.; Nepomuceno, A. F. S. F.; Food Chem. 2022, 367, 130748. [Crossref] 25. Sarembaud, J.; Pinto, R.; Rutledge, D. N.; Feinberg, M.; Anal. Chim. Acta 2007, 603, 147. [Crossref] 26. Harnly, J. M.; Pastor-Corrales, M. A.; Luthria, D. L.; J. Agric. Food Chem. 2009, 57, 8705. [Crossref] 27. Pinto, R. C.; Bosc, V.; Noçairi, H.; Barros; A. S.; Rutledge, D. N.; Anal. Chim. Acta 2008, 629, 47. [Crossref] 28. Pedro, A. M. K.; Ferreira, M. M. C.; J. Chemom. 2006, 20, 76. [Crossref] |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






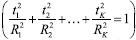 com raios R1, R2, ..., RK., onde K é o número de autovalores calculados, (veja a expressão 6).
com raios R1, R2, ..., RK., onde K é o número de autovalores calculados, (veja a expressão 6). g (J×1) é o centroide do g-ésimo grupo cujos elementos são as médias das colunas da matriz Xg de dimensões (Ig×J).
g (J×1) é o centroide do g-ésimo grupo cujos elementos são as médias das colunas da matriz Xg de dimensões (Ig×J).