JBCS

INTRODUÇÃO

O desenvolvimento da instrumentação analítica, impulsionado pela eletrônica do microcomputador a partir da década de 1970, aumentou a quantidade dos resultados gerados durante uma análise química. Nesse sentido, houve a necessidade do avanço de métodos de estatísticas multivariadas que possibilitam a interpretação destes resultados de forma conjunta, extraindo o máximo de informação com o menor número de experimentos possível. Esse avanço tecnológico e científico permitiu a criação de uma nova subárea da química, a quimiometria. Embora a quimiometria tenha crescido voltada à química analítica, outras áreas da química e da indústria têm usufruído de métodos quimiométricos para resolução de problemas.^1,2

Os planejamentos fatoriais é a frente de estudo da quimiometria mais difundida e aplicada no meio acadêmico e, mesmo assim, o ensino da quimiometria nos cursos de química das Instituições de Ensino Superior Brasileiras ainda é pequeno, onde em muitos casos é restrito a pós-graduação.^3,4 Uma das explicações para esse fato está na falta de domínio de programas computacionais, muitas vezes complicados, e professores com formação na área.³ Diante disso, surge uma pergunta importante: Por que estudar o planejamento fatorial?

Planejar inicialmente um experimento químico é de suma importância para obter resultados que representem de forma eficaz seu sistema de estudo. Em outras palavras, saber se uma variável A ou B influencia ou não nos resultados de um experimento é importante para entender os processos que estão sendo monitorados, maximizando os ganhos de um determinado sistema. Dessa forma, os planejamentos fatoriais são usados para extrair o máximo de informação com o menor número de experimentos possível, sem prejudicar ou encobrir efeitos e interações importantes entre as variáveis de um sistema, facilitando assim o entendimento do resultado final de um experimento.^1,5,6

A seleção do tipo de planejamento fatorial a ser utilizado é uma parte importante de um planejamento experimental, que depende do objetivo do pesquisador e da etapa na qual o projeto se encontra.^7,8 Para um estudo inicial com o objetivo de triagem das variáveis e identificação daquelas que possuem maior influência na resposta, deve-se empregar planejamentos fatoriais completos,^8-11 fracionários^12,13 ou saturados.⁵ Após essa etapa, são indicados planejamentos fatoriais que se baseiam na metodologia de superfície de resposta, como o planejamento composto central (CCD) e Doehlert,^9,14,15 usados para a otimização multivariada das variáveis independentes que influenciam nas respostas.^5,14,16 Na literatura há muitos trabalhos publicados empregando os planejamentos fatoriais completos, CCD e Doehlert.^{7,8,10,14,17,18} Para conhecimento do leitor há alguns tutoriais didáticos que facilitam o aprendizado dos planejamentos fatoriais completos^1,15,19 e fracionários.²⁰ Entretanto, como o planejamento fatorial fracionário ainda é pouco abordado na literatura, seria enriquecedor propor um experimento simples e fácil de ser reproduzido para facilitar o entendimento deste tipo de planejamento, a fim de torná-lo mais acessível no meio acadêmico.

A extração da cafeína (1,3,7-trimetilxantina) foi o experimento escolhido para a aplicação do planejamento fatorial fracionário, visto que a partir deste experimento é possível avaliar as variáveis mais significativas para a extração da cafeína usando uma máquina de café expresso. Sabe-se que a concentração da cafeína é um dos principais parâmetros de qualidade do café e pode ser afetada por diferentes variáveis durante a preparação desta bebida: variedade do café, preparação dos grãos, temperatura da água, pressão relativa, grau de moagem e a compactação do café.²¹ Portanto, o objetivo deste trabalho foi empregar o planejamento fatorial fracionário para avaliar as variáveis que mais contribuem para a extração da cafeína do café. Vale ressaltar que este experimento permeia por diferentes temas ensinados na disciplina de Química Analítica (curva analítica, espectrofotometria UV-Vis e extração líquido-líquido), possibilitando o ensino de quimiometria de uma forma mais descontraída.

Planejamento fatorial fracionário

O número de ensaios no planejamento fatorial completo (2^k) aumenta proporcionalmente com o número de variáveis (definidos também como fatores, k) necessárias para realização de um planejamento experimental. Para um número de variáveis k maior ou igual a 5, há um aumento considerável na quantidade de experimentos realizados, além de maior tempo para realização de todos os ensaios e o maior custo com reagentes e amostra. Entretanto, uma parte das interações entre as variáveis (isso é, as interações de maior ordem) têm alta probabilidade de serem consideradas não significativas para o resultado, o que torna possível obter os resultados necessários para a análise estatística apenas com uma fração do ensaio total.^5,22

O método de planejamento que utiliza apenas uma fração dos ensaios é denominado na literatura como fatorial fracionário (2^k-b), sendo k o número de variáveis estudadas e b o tamanho da fração aplicada. Esse planejamento é utilizado principalmente quando as variáveis estudadas são muitas e se tem pouca informação sobre o sistema. Dessa forma, o planejamento fatorial fracionário funciona como uma triagem das variáveis que realmente são significativas, que posteriormente poderão ser usadas em um planejamento de otimização (superfície de resposta). A estratégia do planejamento fatorial fracionário consiste em considerar os efeitos (também chamados de contrastes) das interações de maiores ordens (ou seja, interações entre duas ou mais variáveis) como pouco ou não significativos. Dessa forma, os efeitos dessas interações de maiores ordens (com baixas significâncias) são misturados com os efeitos de variáveis ou de interações significativas, gerando um valor de contraste para essas variáveis ou interações misturadas o que é chamado de "confundimento". Essa mistura dos efeitos de interações não significativos com os efeitos das variáveis ou interações significativas permite a realização apenas de uma fração dos experimentos sem perdas significativas para o resultado.^3,5

A escolha do tamanho da fração (parâmetro b do planejamento 2^k-b), corresponde ao valor da proporção que se pretende reduzir, ou seja, o número total de experimentos executados para transformar um planejamento fatorial completo em um planejamento fracionário. Entretanto, um valor alto de b pode resultar em uma perda de informação do sistema, impactando nas respostas e no número de experimentos que devem ser executados.

Para exemplificar, quando se avalia a influência de cinco fatores (variáveis) diferentes em dois níveis, um alto e outro baixo, na resposta de um planejamento fatorial completo (2⁵) é necessário a realização de 32 experimentos. Esse número grande de experimentos pode dificultar a execução do planejamento. Dessa forma, faz-se necessário diminuir esse número de ensaios pela metade (obtendo resultados semelhantes) e, portanto, emprega-se um planejamento fracionário (2^5-1), totalizando 16 experimentos. Nesse planejamento (2^5-1), a estratégia adotada é misturar os efeitos principais com os efeitos das interações de grau quatro, enquanto as interações dos efeitos de grau dois são misturadas com os de grau três (veja Figura 1). O resultado obtido é um planejamento com 16 experimentos com a mesma capacidade de realizar o estudo de triagem de variáveis.^5,15 Vale ressaltar que se fosse aplicada um b = 2 (2^5-2), resultaria em um planejamento com somente 8 experimentos, que apesar da possibilidade de ser realizado, é insuficiente para representar de forma satisfatória a variabilidade das 5 variáveis avaliadas, isso é, há uma perda considerável de informação para o sistema. A Figura 1 apresenta um infográfico com a estratégia adotada para transformar um planejamento fatorial completo 2⁵ em um fracionário 2^5-1.

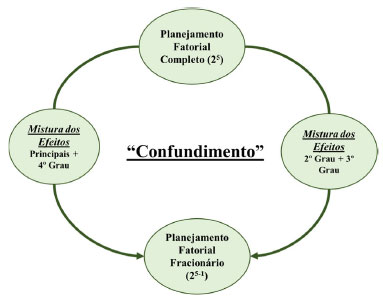Figura 1. Infográfico da estratégia adotada no planejamento fatorial fracionário

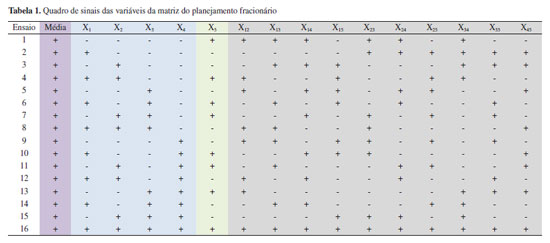
Nos planejamentos completos são avaliadas as respostas de todos os efeitos (principais e interações). Nos planejamentos saturados ou Plackett-Burman são avaliadas as respostas somente dos efeitos principais e no planejamento fatorial fracionário é estimado somente os efeitos (contrastes) que apresentam a possibilidade de influenciar na resposta.¹⁵ A Matriz X do planejamento é o conjunto de sinais algébricos que identificam o nível de cada variável e todas as combinações de interações possíveis para o cálculo de todos os efeitos.^5,15 No planejamento fatorial fracionário 2^5-1 os efeitos das interações de terceira (X_ijk) e quarta (X_ijkl) ordem não aparecem na Matriz X, visto que estes efeitos de maiores ordens são confundidos com outros efeitos principais e de 2ª ordem. Dessa forma, os efeitos das interações de 4ª ordem (X₁₂₃₄ X₁₂₃₅ X₁₂₄₅ X₁₃₄₅ X₂₃₄₅) são misturados com os efeitos principais (X₅, X₄, X₃, X₂ e X₁), respectivamente. Já os efeitos de 2ª ordem (X_12; X_13; X_14; X_15; X_23; X_24; X_25; X_34; X_35; X_45;) são misturados com os efeitos de 3ª ordem (X_345; X_245; X_235; X_234; X_145; X_135; X_134; X_125; X_124; X₁₂₃), respectivamente. A Figura 2 apresenta as misturas (chamados também de confundimentos) dos efeitos num planejamento fatorial fracionário 2^5-1.

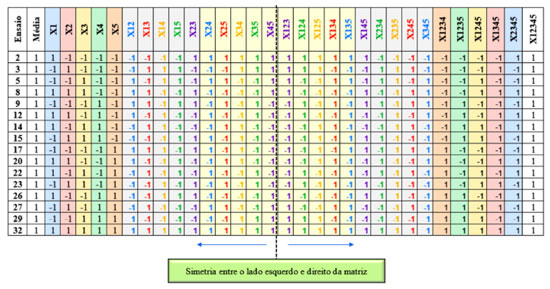Figura 2. Confundimentos dos efeitos das interações de quarta ordem (X1234 X1235 X1245 X1345 X2345) com os efeitos principais (X5, X4, X3, X2 e X1), respectivamente; e dos efeitos de segunda ordem (X12; X13; X14; X15; X23; X24; X25; X34; X35; X45;) com os efeitos de terceira ordem (X345; X245; X235; X234; X145; X135; X134; X125; X124; X123), respectivamente

A Figura 2 foi apresentada somente com o intuito de demonstrar que no planejamento 2^5-1 há o confundimento dos efeitos. Entretanto, essa não é a matriz usada para construir o planejamento fatorial fracionário 2^5-1, conforme será mencionado mais adiante. Os sinais das colunas do lado esquerdo da matriz são os mesmos que os do lado direito e, por isso, dizemos que o efeito referente a cada uma dessas variáveis ou interações estão confundidos. Para facilitar a visualização das colunas da matriz correspondentes aos efeitos confundidos foram coloridas com as mesmas cores. Dessa forma, pode-se afirmar que o efeito da interação de 4ª ordem (X₁₂₃₄) está misturado com o efeito principal (X₅), por exemplo. A Figura 1S (Material suplementar) apresenta as informações que foram usadas para chegar na matriz simétrica (Figura 2) do planejamento fatorial fracionário 2^5-1.

Uma maneira simples de obter os efeitos que estão confundidos no planejamento fatorial fracionário é usar a relação geradora I (coluna representada por todos os sinais +1, ou seja, a média - Figura 2) e a partir dela obter os efeitos que são confundidos (Eq. 1).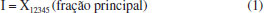

Multiplicando ambos os lados da Eq. 1 por X₁, tem-se (Eq. 2).

Quando multiplicamos duas colunas iguais o resultado será sempre um vetor unitário, assim, podemos eliminá-lo da equação (Eq. 3).

Portanto, o efeito da variável X₁ está misturado (confundido) com o efeito da interação X₂₃₄₅ (efeitos que estão confundidos são chamados de pares associados, ou aliases). No entanto, por uma questão hierárquica, é muito mais comum que efeitos principais sejam mais importantes do que os de ordens mais altas. Assim, ao assumir que os efeitos de ordens mais altas têm pouco ou nenhuma significância, então pode-se concluir que um efeito grande de X₁ seja exclusivamente desse efeito principal.

Como construir uma matriz de um planejamento fatorial fracionário?

O resultado da mistura desses efeitos principais ou interações com efeitos de maiores ordens gera a matriz do planejamento fracionário 2^5-1 (Tabela 1). Dessa forma, a construção da Matriz X do planejamento fatorial fracionário (2^5-1) é realizada seguindo os seguintes passos:

Passo 1: Construir a coluna da média com nível alto (+ 1) para todos os 16 ensaios (coluna colorida em roxo na Tabela 1).

Passo 2: Construção de um planejamento completo 2⁴ para os fatores principais (variáveis) X₁, X₂, X₃ e X₄ (coluna colorida em azul na Tabela 1). Os níveis da coluna X₁ se revezam entre o nível baixo (-1) e nível alto (+1), seguido pelo revezamento dois a dois (-1-1+1+1), quatro a quatro (-1-1-1-1+1+1+1+1) e oito a oito (-1-1-1-1-1-1-1-1+1+1+1+1+1+1+1+1) para as colunas X₂, X₃ e X₄, respectivamente.

Passo 3: Atribuir à coluna X₅ o resultado do produto dos níveis das 4 variáveis principais (X₁, X₂, X₃ e X₄) de cada ensaio (Eq. 4) (coluna colorida em verde na Tabela 1).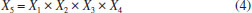

Passo 4: Atribuir às colunas dos fatores de 2ª ordem (X₁₂; X₁₃; X₁₄; X₁₅; X₂₃; X₂₄; X₂₅; X₃₄; X₃₅ e X₄₅) (coluna colorida em cinza na Tabela 1) o resultado do produto dos seus respectivos efeitos principais em cada ensaio (Eq. 5).¹⁵

sendo i e j os índices das variáveis usadas no planejamento (1, 2, 3, 4 e 5).

Observe que foram usados somente as variáveis principais e as interações de 2ª ordem para construir a matriz do planejamento 2^5-1, visto que os efeitos das interações de maiores ordem (3ª e 4ª) estão misturadas com estes efeitos principais e de 2ª ordem (Figura 1). Vale ressaltar que ao construir a matriz do planejamento fracionário 2^5-1 há uma perda de informação sobre as respostas dos experimentos. Entretanto, essa perda de informação não é expressiva, pois a confusão causada entre os efeitos principais e os efeitos de interações tem como objetivo dar importância somente aos efeitos significativos que serão avaliados pelo gráfico de pareto e pelo gráfico de probabilidade normal, conforme será visto nos resultados e discussão.¹⁵

Observe que os ensaios 2, 3, 5, 8, 9, 12, 14 e 15 da Tabela 1 correspondem aos mesmos ensaios da Figura 2, se considerar somente as variáveis principais (exceto para variável 5) e interações de 2ª ordem. Os ensaios faltantes (1, 4, 6, 7, 10, 11, 13 e 16) são os ensaios presentes na matriz alternativa (Figura 1S).

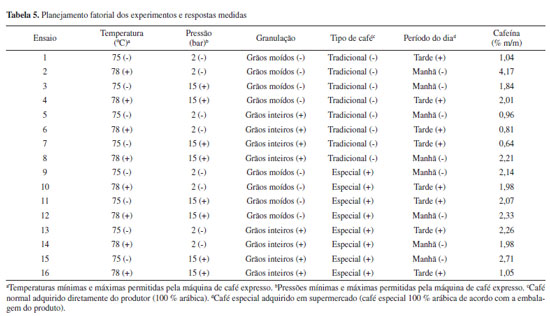
PARTE EXPERIMENTAL

Materiais e reagentes

Os frascos e vidrarias empregados nas análises foram lavados com Extran MA 02 Neutro 5% v v^-1 (Merck, Alemanha) e água deionizada antes das análises. Diclorometano P.A. ACS (Vetec, Brasil) foi usado para a extração da cafeína dos cafés. A água deionizada (condutividade ≤ 5,0 µS cm^-1) foi preparada por um deionizador (Permution^®, modelo 1800 Evolution, BR). As soluções-padrão usadas para construção da curva analítica foram preparadas após diluições sucessivas da solução estoque de 100 mg L^-1 de Cafeína (Sigma-Aldrich, BR). As diluições foram executadas em balões volumétricos de 25 mL e completadas até o ponto de aferição com diclorometano P.A (Vetec, Brasil).

Amostras e equipamentos

Foram usados cafés especiais e tradicionais torrados e moídos e em grãos adquiridos em supermercados brasileiros. Uma cafeteira multipressão de 2 bar e 15 bar com reservatório de água de 950 ml (Três Corações, G1 lov, Brasil) foi usada para o preparo do café. Já para a análise da cafeína foi empregado um espectrofotômetro de absorção molecular UV/Vis (BioMate 3S, Thermo Fisher Scientific, EUA).

Planejamento experimental

Os cafés foram extraídos usando a máquina de café expresso, variando a temperatura (X₁), pressão (X₂), granulação (X₃), tipo de café (X₄) e período do dia (X₅). As variáveis X₁, X₂, X₃, X₄ e X₅ foram estudadas usando o planejamento fatorial fracionário com dois níveis (2^5-1), a fim de verificar a significância dessas variáveis na obtenção da máxima extração de cafeína das bebidas de café preparadas na máquina de café expresso. A Tabela 2 apresenta as 5 variáveis e os dois níveis estudados, gerando 16 experimentos. Para evitar resultados tendenciosos, os 16 experimentos foram realizados de forma aleatória.

Preparo dos cafés usando a máquina de café expresso

Cada uma das 16 cápsulas de café expresso (Figura 3) foram abertas nas laterais com auxílio de um estilete, esvaziadas e limpas, de acordo com a metodologia empregada por Querubina et al.²³ Os grãos foram macerados e pesados (1,0000 g) em uma balança analítica (Shimadzu, AY220). Todas as cápsulas contendo o café (moídos ou em grãos inteiros) foram devidamente fechadas utilizando cola para material plástico e fita adesiva, e foram envoltas em papel alumínio (Figura 3). A máquina de café expresso foi configurada, variando as condições de temperatura e pressão, seguindo as instruções do manual antes de cada um dos experimentos. O volume de 100 mL de água deionizada foi fixo em todos os 16 experimentos para extração da cafeína das amostras de café.

Figura 3. Procedimento de preparo das cápsulas com as amostras de café: 1: abertura da cápsula com estilete; 2: a cápsula foi esvaziada e limpa; 3: a amostra do café foi adicionada à cápsula limpa; 4: fechamento da cápsula com cola e fita adesiva; 5: cápsula envolta em papel alumínio

Extração e análise da cafeína

A extração da cafeína foi realizada a partir da metodologia de Belay et al. ²⁴ Após a extração, os extratos foram diluídos (1:25) em água deionizada e adicionados 25 mL de diclorometano (CH₂Cl₂). A mistura foi agitada a 300 rpm durante 5 minutos em agitador magnético. Após o repouso, houve a separação das fases aquosas e orgânica (contendo a cafeína) (Figura 4). Após isso, foram realizadas duas extrações líquido-líquido da amostra usando um funil de separação. A cafeína contida na fase orgânica foi analisada por espectrofotometria de absorção molecular no comprimento de onda máximo de 275 nm.

Figura 4. (a) Extrato em agitação magnética durante a extração líquido-líquido da cafeína; (b) separação das fases

Características de desempenho para o procedimento analítico

Para a construção da curva analítica da cafeína, foi preparada inicialmente uma solução estoque de padrão de cafeína (Sigma-Aldrich, Brasil) com 100 mg L^-1, obtendo soluções-padrão nas concentrações de 0, 1, 2, 4, 6, e 8 mg L^-1, usando o solvente diclorometano. As soluções-padrão foram preparadas em duplicatas e analisadas por um espectrofotômetro UV/Vis (275 nm). Além disso, o limite de detecção (LD) e o limite de quantificação (LQ) foram calculados de acordo com a International Union of Pure and Applied Chemistry (IUPAC): o LD foi calculado como sendo três vezes o desvio-padrão do intercepto (s) dividido pela inclinação da curva analítica (m), ou seja, 3s/m, enquanto o LQ foi calculado como sendo 10 vezes o desvio-padrão do intercepto (s) dividido pela inclinação da curva analítica (m), ou seja, 10s/m.^25,26

RESULTADOS E DISCUSSÃO

Avaliação do desempenho analítico para determinação da cafeína

A Tabela 3 apresenta os parâmetros de desempenho alcançados para a determinação da cafeína nas amostras de café por espectrofotometria UV-Vis.

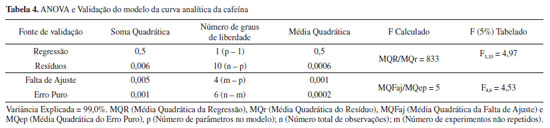
Os teores de cafeína nos 16 experimentos (Tabela 5) apresentaram-se maiores que o LQ para a cafeína, indicando que a determinação da cafeína nas amostras de café foi realizada com precisão e exatidão aceitáveis. Além disso, foi empregada a análise da variância (ANOVA) para avaliar a regressão e falta de ajuste da curva analítica (Tabela 4).

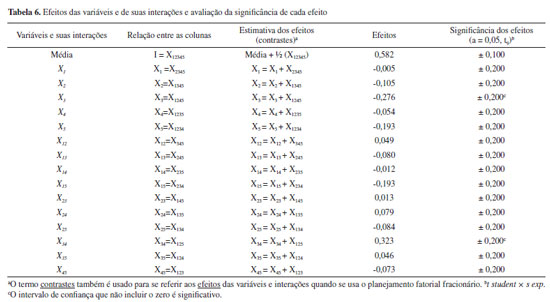
A linearidade da curva analítica da cafeína foi expressa usando o coeficiente de determinação (r² = 0,990), indicando uma ótima relação linear (r² próximo a 1). No entanto, para validação de procedimentos analíticos é recomendado que a linearidade seja avaliada por métodos estatísticos de análise de variância (ANOVA).²⁷ O Teste F foi aplicado para verificar a significância da regressão, uma vez que um F_calculado maior que o F_tabelado indica uma regressão linear adequada e, consequentemente, um modelo matemático que represente satisfatoriamente o experimento. O modelo apresenta um F_calculado (833) maior que o F_{1,10 (tabelado)} (4,97) indicando uma regressão linear ideal. Além disso, o modelo apresentou um F_calculado (5) próximo ao F_{4,6 (tabelado)} (4,53), indicando que não há evidência de grande falta de ajuste no modelo. Desse modo, pode se considerar, com 95% de confiança, que a curva analítica está significantemente correta e bem ajustada para a quantificação da cafeína e que a hipótese da linearidade não pode ser descartada para a curva analítica construída (ou seja, a hipótese nula não pode ser rejeitada).

Avaliação das variáveis usadas no planejamento fatorial fracionário 2^5-1

A partir do planejamento fatorial fracionário de resolução V (2^5-1) foi realizada uma avaliação das cinco variáveis usadas para a extração de cafeína usando a máquina de café expresso. O planejamento fatorial fracionário executado neste trabalho e as concentrações de cafeína (% m/m) extraídas na máquina de café expresso são apresentados na Tabela 5. A Tabela 5 foi construída com base na Matriz X do planejamento fracionário 2^5-1 (Tabela 1) e apresenta as cinco variáveis e os dois níveis estudados, gerando 16 experimentos.

A partir das respostas (concentração de cafeína % m/m) geradas no planejamento fatorial fracionário foram calculados todos os efeitos e sua significância. Vale destacar que a extração líquido-líquido da cafeína dos cafés moídos empregando o diclorometano como solvente extrator, apresenta uma eficiência de extração de 98 - 99 % de acordo com a literatura.^24,28-30 Além disso, de acordo com a Resolução CNNPA nº12/1978, os cafés devem conter pelo menos 0,7% m/m de cafeína.³¹ Em todos os experimentos realizados obteve-se um teor de cafeína maior que 0,7% m/m. Vale destacar que o teor de cafeína obtido em todos os ensaios está em conformidade aos encontrados na literatura.^32-35

Cálculo dos efeitos

Para o cálculo dos efeitos de cada variável e dos efeitos das suas interações foi necessário transpor a Matriz X (Tabela 1) e multiplicá-la pelo vetor y (respostas da concentração de cafeína apresentadas na Tabela 5). Após isso, a multiplicação (X^t ×y ) foi dividida pela metade do número de experimentos diferentes executados, obtendo os valores dos efeitos das variáveis e de suas interações (Eq. 6) (Tabela 6). Os efeitos se referem a diferença entre duas médias, a média do nível superior menos a média do nível inferior. Como a metade dos experimentos é realizada em cada nível, os valores dos efeitos são divididos pela metade do número de ensaios realizados.

O efeito da média é obtido dividindo a multiplicação (X^t × Y) pelo número total de experimentos, obtendo assim o efeito global médio (Eq. 7).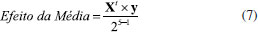

A seguir, será calculado o efeito da variável temperatura usando o Excel para demonstrar como é feito. A planilha eletrônica do Google (Google sheets) também pode ser usada para cálculo dos efeitos.

Passo 1: Transpor a Matriz X

É necessário que seja construída a Matriz X^t que pode ser obtida copiando toda a Matriz X e, posteriormente, colando especial de forma transposta (T).

Passo 2: Multiplicação (X^t × y)

Na célula do Excel que desejar, coloque o sinal de igual e selecione a função matemática de multiplicação de matrizes (= MATRIZ.MULT). Em seguida, selecione as células que apresentem os códigos -1 e +1 e que correspondem à variável temperatura na matriz transposta (X^t).

Passo 3: Cálculo do efeito

Aperte a tecla ponto e vírgula (;) e selecione agora as células com todas as respostas do vetor y. Feche o parêntese e dividida por oito.

O mesmo procedimento pode ser realizado para calcular os outros coeficientes de contraste. Vale destacar que para cálculo do contraste global médio, o valor final deve ser dividido por dezesseis.

Cálculo da significância de cada efeito

A estimativa da incerteza para cada efeito deve ser analisada com 95% de confiança por meio das interações dos efeitos de maior ordem (X₁₂, X₁₃, X₁₄, X₁₅, X₂₃, X₂₄, X₂₅, X₃₄, X₃₅, X₄₅), considerando um grau de liberdade para cada um desses efeitos, totalizando 10 graus de liberdade (t student = 2,228). Entretanto, o efeito X₃₄ apresentou um valor bem alto se comparado aos demais efeitos das interações (Tabela 6). Dessa forma, a estimativa da incerteza foi calculada somente com as 9 interações dos efeitos de maior ordem (X₁₂, X₁₃, X₁₄, X₁₅, X₂₃, X₂₄, X₂₅, X₃₅, X₄₅), considerando um grau de liberdade para cada um desses efeitos, totalizando 9 graus de liberdade (t student = 2,262).

A significância dos efeitos foi calculada a partir da multiplicação do t student, 2,262 (95 % de confiança) pela estimativa do erro padrão do efeito (Tabela 6).

A seguir, será apresentado os passos para calcular a estimativa da incerteza dos efeitos das variáveis.

Passo 1: Elevar ao quadrado todos os efeitos das interações, isso é, obter a variância de cada efeito (Eq. 8).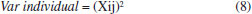

em que ij são os números referentes as interações X₁₂, X₁₃, X₁₄, X₁₅, X₂₃, X₂₄, X₂₅, X₃₅, X₄₅.

Passo 2: Obter a média de todos os efeitos elevados ao quadrado para estimar a variância conjunta (Eq. 9).

Passo 3: Obter a estimativa do erro padrão do efeito (Eq. 10).

Passo 4: Obter a significância dos efeitos (estimativa da incerteza dos efeitos) a partir da multiplicação do t student, 2,262 (95 % de confiança, 9 graus de liberdade) pela estimativa do erro padrão do efeito (Eq. 11).

Avaliação dos efeitos pelo gráfico de pareto

Espera-se que as interações dos efeitos de maior ordem sejam não significativas (exceto o X₃₄), visto que eles foram usados para calcular a significância dos efeitos. A Figura 5 apresenta os efeitos significativos das variáveis estudadas. Observa-se que somente a variável X₃ (granulação) e a interação da variável X₃ com a variável X₄ (ou seja, X₃₄) foram significativas.

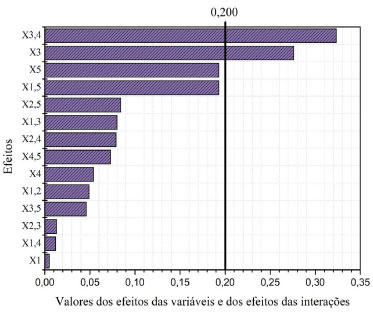Figura 5. Representação gráfica da significância das variáveis estudadas e de suas interações

O efeito da variável X₃ (granulação) foi o único efeito principal significativo, pois o intervalo de confiança não inclui o zero, ou seja, - 0,276 ± 0,200. Além disso, o gráfico de pareto (Figura 5) indica que os efeitos são significativos quando ultrapassam a linha preta, isso é, t student × s exp (que neste experimento foi igual a 0,200). Dessa forma, somente os efeitos X₃ e X₃₄ foram significativos.

A variável granulação influência negativamente na extração da cafeína usando a máquina de café expresso. Quando não há interação desta variável com as demais variáveis avaliadas, pode-se assumir que o valor negativo deste efeito (- 0,276) indica que há uma diminuição da extração da cafeína em 0,276 % m/m em média ao passar do nível -1 (grãos moídos) para o nível +1 (grãos inteiros). O efeito de X₃ está confundido com a o efeito da interação de maior ordem X₁₂₄₅ (Figura 2), porém é mais comum que o efeito principal (X₃) seja mais importante do que o de ordem mais alta (X₁₂₄₅), conforme já discutido.

É de se esperar que o aumento da superfície de contato permita uma maior extração de cafeína, visto que a interação do solvente com as pequenas partículas do café moído é mais efetiva que nos grãos inteiros. De acordo com a literatura, o grau de extração de sólidos e compostos solúveis é inversamente proporcional ao tamanho da partícula.³⁶ Além disso, a torra e moagem do café pode ser levada em conta já que gera diferentes microestruturas e o tamanho de partícula modificam o resultado da extração.^21,36,37

O efeito da interação (X₃₄) das variáveis X₃ (granulação) e X₄ (tipo de café) apresentou-se bem significativo. A interação entre essas duas variáveis (X₃₄) é a diferença entre o efeito médio da variável X₃ (granulação) com o tipo de café tradicional e o tipo de café especial. O efeito da interação permite o aumento da extração de cafeína em 0,323% m/m. Desta forma, os efeitos de interação caracterizam o sinergismo entre as duas variáveis (X₃ e X₄), de tal forma que o efeito principal dessas variáveis não deve ser interpretado individualmente, visto que há interação entre elas.

A variável X₁ (temperatura) não foi significativa neste experimento devido a pequena variação de temperatura permitida pela máquina de café expresso (ΔT = 3 ºC). Sabe-se que a temperatura afeta fortemente a extração da cafeína presente no café, entretanto, nesse experimento essa variável foi considerada não significativa devido aos níveis - 1 (75 ºC) e +1 (78 ºC) serem muito próximos. Caso a máquina de café permitisse uma variação da temperatura mais acentuada, possivelmente a variável X₁ afetaria significativamente a extração da cafeína.³⁸

A variável X₂ (pressão) também se apresentou não significativa para extração da cafeína. É importante destacar que a variação da pressão na máquina de café expresso é escolhida de acordo com o tipo de bebida a ser preparada. Dessa forma, o manual de instruções do equipamento orienta que para a preparação de cafés expressos sejam utilizados 50 mL de água a 15 bar. Já para o preparo das bebidas denominadas cafés filtrados devem-se utilizar 100 mL de água, a 2 bar. Entretanto, nos experimentos realizados foram utilizados sempre um volume fixo de 100 mL de água para o preparo das bebidas (independente da pressão utilizada). Nesse sentido, ao utilizar a pressão de 15 bar foi necessário realizar a extração duas vezes, totalizando 100 mL. Mesmo empregando 2 extrações ao usar a pressão de 15 bar (para obter 100 mL da bebida), não houve diferença significativa se comparado à pressão de 2 bar. Era de se esperar uma maior extração da cafeína a uma maior pressão, entretanto, a pressão máxima exercida pela máquina não se mostrou significativa para a extração da cafeína.

A Variável X₄ (tipo de café) foi não significativa, indicando que não há uma variação significativa no teor de cafeína extraída (% m/m) nos dois tipos de cafés estudados (tradicional e especial). Ambos os cafés utilizados neste estudo foram 100% arábica, o que pode justificar os teores de cafeína semelhantes para os dois tipos de cafés. Caso esse experimento fosse realizado usando cafés arábica versus conilon, a variável "tipo de café" poderia apresentar-se significativa, devido ao maior teor de cafeína nos cafés da espécie conilon. Os cafés da espécie conilon apresentam um teor de cafeína 50% maior que as espécies arábicas.³⁹

A Variável X₅ apresentou uma baixa significância para a extração da cafeína. Como a temperatura do laboratório onde se realizou os experimentos foi mantida fixa a 22 ºC durante os períodos da manhã e da tarde, era de se esperar que essa variável fosse não significativa, conforme foi obtido nos resultados deste estudo.

Dessa forma, após avaliar todos os efeitos é possível propor uma equação que represente o modelo do planejamento fatorial fracionário realizado (Eq. 12).

As variáveis X₃ e X₃₄, destacado em negrito, dentre as 15 variáveis avaliadas pelo gráfico de pareto são as únicas consideradas significativas e, portanto, as que devem constar no modelo que represente o planejamento fracionário. Os parâmetros do modelo linear b₀ e b_x foram determinados pela resolução de uma única equação matricial (Eq. 13). A resolução dessa equação consiste na multiplicação matricial da matriz (X^tX)^-1 pela matriz (X^ty) para estimar os coeficientes b da equação linear.⁵ O procedimento para multiplicação matricial no Excel é o mesmo usado no passo 2 do cálculo significância dos efeitos já supracitado.

Avaliação dos efeitos pelo gráfico normal

Além da avaliação dos efeitos pelo gráfico de pareto apresentado na secção anterior (considerando a significância dos efeitos, isto é, t student × s exp), o gráfico normal é uma ferramenta com base na noção de probabilidade acumulada que pode ser usada como uma alternativa para distinguir os valores que realmente correspondem aos efeitos e são significativos, dos que são apenas ruídos.⁵ Dessa forma, obtêm-se um gráfico de probabilidade cumulativa nos quais os pontos centrais se ajustam a uma reta que cruza a probabilidade acumulada de 50%, aproximadamente, sobre o ponto zero das abscissas. Se os experimentos do planejamento foram executados de forma aleatória, os efeitos calculados a partir dos resultados devem apresentar uma população normal a ser representada por um gráfico normal (Figura 6). A forma detalhada para a construção do gráfico normal pode ser encontrada na literatura.⁵ A Tabela 7 apresenta os efeitos calculados para o planejamento fracionário 2^5-1 e os valores de probabilidade acumulada (z).

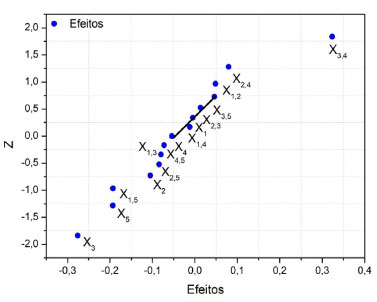Figura 6. Gráfico normal dos contrastes do planejamento fracionário 25-1

O gráfico normal foi obtido plotando os valores dos efeitos versus os valores de probabilidade acumulada (z), ambos em ordem crescente (Figura 6).

Os efeitos não significativos devem se ajustar a uma distribuição normal centrada em zero. Já os efeitos significativos devem se afastar dessa distribuição normal. Dessa forma, os efeitos que se ajustam próximo ao ponto zero das abscissas (probabilidade acumulada de 50%) são considerados não significativos. Em contrapartida, os efeitos X₃ e X₃₄ estão mais afastados do ponto zero das abscissas e, portanto, são considerados significativos, corroborando com a avaliação apresentada no gráfico de pareto.

Vale destacar que nos planejamentos fracionários não são realizadas duplicatas, uma vez que isso forneceria mais experimentos, o que contradiz a redução proposta nos planejamentos fracionários. Entretanto, alguns trabalhos têm empregado uma triplicata em um ponto central para estimar a significância de cada efeito.²⁰

Sendo assim, como normalmente não há duplicatas ou repetição nos pontos centrais ao usar os planejamentos fracionários, deve-se estimar a significância dos efeitos usando as interações de maiores ordens (conforme foi apresentado na secção para obtenção do gráfico de pareto) ou empregar o gráfico de probabilidade normal para avaliar a significância dos efeitos.

CONCLUSÕES

A aplicação do planejamento fatorial fracionário no experimento permitiu executar a triagem de variáveis experimentais que mais contribuíram para a extração da cafeína, sendo elas a granulação do grão do café (X₃) e a sua interação com o tipo de café aplicado (X_3,4). Era de se esperar uma maior extração da cafeína a uma maior pressão e temperatura exercida pela máquina de café expresso. Entretanto, a variação da temperatura (Δt) e pressão (Δp) ofertada por essa classe de equipamento para uso doméstico não se mostrou significativa para a extração da cafeína. O experimento desenvolvido apresentou potencial para o ensino do planejamento fracionário e disseminação da quimiometria no ambiente acadêmico, visto a facilidade de reproduzi-lo em laboratórios de ensino. O simples manuseio da máquina de café expresso, do espectrofotômetro UV-Vis e fácil preparo das cápsulas de café permitem que os discentes sejam capazes de aplicar o planejamento fracionário para extração de cafeína de uma forma descontraída, facilitando o aprendizado nas aulas de quimiometria e química analítica no nível superior e na pós-graduação.

MATERIAL SUPLEMENTAR

As Matrizes X, X^t e a planilha com todos os cálculos realizados nesse artigo estão disponíveis em http://quimicanova.sbq.org.br, na forma de arquivo PDF e Excel, com acesso livre.

AGRADECIMENTOS

Os autores Gabriel Rocha Figueira Caldeira e Murilo de Oliveira Souza agradecem ao Instituto Federal de Educação, Ciência e Tecnologia Fluminense Campus Itaperuna-RJ pela bolsa PIBIC_IFF (Edital 226/2021).

Os autores agradecem às agências de fomento CAPES, CNPq e FAPERJ; ao Programa de Pós-Graduação em Ciências Naturais (UENF); aos grupos de pesquisa LAQUA (Laboratório de Análises Químicas e Agroambientais- IFF) e GPQA (Grupo de Pesquisa em Química Ambiental-UENF).

REFERÊNCIAS

1. Breitkreitz, M. C.; De Souza, A. M.; Poppi, R. J.; Quim. Nova 2014, 37, 564. [Crossref]

2. Otto, M.; Chemometrics, 3^rd ed.; John Wiley & Sons: Weinheim, Germany, 2016.

3. Valderrama, L.; Março, P. H.; III Conferencia Latinoamericana del International, History and Philosophy of Science Teaching Group IHPST-LA, 2014, 17-19.

4. Barros Neto, B. de; Scarminio, I. S.; Bruns, R. E.; Quim. Nova 2006, 29, 1401. [Crossref]

5. Barros Neto, B.; Scarminio, I. S.; Bruns, R. E.; Como fazer experimentos : pesquisa e desenvolvimento na ciência e na indústria, Bookman: São Paulo, 2010.

6. IUPAC - chemometrics (CT06948), disponível em https://goldbook.iupac.org/terms/view/CT06948, acessada agosto 2022.

7. Vanini, G.; Souza, M. O.; Carneiro, M. T. W. D.; Filgueiras, P. R.; Bruns, R. E.; Romão, W.; Microchem. J. 2015, 120, 58. [Crossref]

8. Ferreira, R. S.; Nunes, C. R. O.; Souza, M. O.; Canela, M. C.; J. Braz. Chem. Soc. 2021, 32, 618. [Crossref]

9. Souza, M. O.; Da Silva, F. L. F.; Matos, W. O.; Ferreira, R. Q.; Rev. Virtual Quim. 2017, 9, 1658. [Crossref]

10. Luiza Fernandes Seares, A.; de Oliveira Souza, M.; Lionel-Mateus, V.; De Almeida, C. M. S.; Microchem. J. 2021, 163, 105917. [Crossref]

11. de Oliveira Pinheiro Ramos, A. C.; Caldeira, G. R. F.; de Oliveira Nunes, C. R.; da Silva Terra, W.; de Oliveira Souza, M.; Braz. J. Anal. Chem. 2020, 7, 31. [Crossref]

12. Colombo, Renata; Yariwake, Janete H.; Lanza, M. R. V.; Quim. Nova 2014, 37, 535. [Crossref]

13. Silveira, G.; Tarley, Ć. R. T.; Quim. Nova 2008, 31, 1653. [Crossref]

14. Souza, M. de O.; Rainha, K. P.; Castro, E. V. R.; Carneiro, M. T. W. D.; Ferreira, R. de Q.; Quim. Nova 2015, 38, 980. [Crossref]

15. Teófilo, R. F.; Ferreira, M. M. C.; Quim. Nova 2006, 29, 338. [Crossref]

16. Plackett, R.L; Burman, J. P.; Biometrika Trust. 1946, 33, 305.

17. Ruschel, C. F. C.; Ferrão, M. F.; Dos Santos, F. P.; Samios, D.; Quim. Nova 2016, 39, 267. [Crossref]

18. Sá, I. P.; Santos, L. N.; Erik, G. P.; Lima, D. D. C.; Alan, F.; Amorim, C.; Quim. Nova 2019, 42, 10. [Crossref]

19. De MacEdo Guedes, T. L.; De Lima Soares, M. S.; Das Neves, L. S.; De Lima, K. M. G.; Quim. Nova 2013, 36, 480. [Crossref]

20. Pereira, F. M. V.; Pereira-Filho, E. R.; Quim. Nova 2018, 41, 1061. [Crossref]

21. Severini, C.; Derossi, A.; Fiore, A. G.; De Pilli, T.; Alessandrino, O.; Del Mastro, A.; J. Sci. Food Agric. 2016, 96, 3023. [Crossref]

22. Greco, J. A. S.; Tese de Doutorado, Universidade de São Paulo, Brasil, 2004.

23. de Sousa Querubina, A.; Andreoli Coser, M.; Ruggeri Waldman, W.; Quim. Nova Esc. 2016, 38, 269. [Crossref]

24. Belay, A.; Ture, K.; Redi, M.; Asfaw, A.; Food Chem. 2008, 108, 310. [Crossref]

25. Thompson, M.; Ellison, S. L. R.; Wood, R.; Pure Appl. Chem. 2002, 74, 835. [Crossref]

26. Ribani, M.; Grespan Bottoli, C. B.; Collins, C. H.; Fontes Jardim, I. C. S.; Costa Melo, L. F.; Quim. Nova 2004, 27, 771. [Crossref]

27. Souza, M. D. O.; Sánchez, B.; Fuentes, M.; Gilaranz, J.; Canela, M. C.; Anal. Methods 2020, 12, 5247. [Crossref]

28. Mariano, R. S.; Trabalho de Conclusão de Curso, Universidade Técnológica Federal do Paraná, Brasil, 2018.

29. Espinoza-Pérez, J. D.; Vargas, A.; Robles-Olvera, V. J.; Rodríguez-Jimenes, G. C.; García-Alvarado, M. A.; J. Food Eng. 2007, 81, 72. [Crossref]

30. García Martínez, E.; Fuentes López, A.; Fernández Segovia, I.; Extracción y cuantificación de cafeína mediante espectroscopía UV-Visible en café, té y cacao, 2018, disponível em https://riunet.upv.es/bitstream/handle/10251/104055/Garc%C3%ADa%3BFuentes%3BFern%C3%A1ndez%20-%20Extracci%C3%B3n%20y%20cuantificaci%C3%B3n%20de%20cafe%C3%ADna%20mediante%20espectroscop%C3%ADa%20UV-Visi....pdf, acessado em agosto 2022.

31. Brasil; Ministério da Saúde- Resolução CNNPA N^o 12, de 1978, disponível em https://bvsms.saude.gov.br/bvs/saudelegis/anvisa/2003/res0899_29_05_2003.html, acessado em agosto 2022.

32. Lim, L. T.; Zwicker, M.; Wang, X.; Coffee: One of the most consumed beverages in the world, 3^a ed.; Elsevier: Amsterdam, 2019; Vol. 4. [Crossref]

33. Jeon, J. S.; Kim, H. T.; Jeong, I. H.; Hong, S. R.; Oh, M. S.; Yoon, M. H.; Shim, J. H.; Jeong, J. H.; Abd El-Aty, A. M.; J. Adv. Res. 2019, 17, 85. [Crossref]

34. Jeon, J. S.; Kim, H. T.; Jeong, I. H.; Hong, S. R.; Oh, M. S.; Park, K. H.; Shim, J. H.; Abd El-Aty, A. M.; J. Chromatogr. B 2017, 1064, 115. [Crossref]

35. Alcantara, G. M. R. N.; Dresch, D.; R. Melchert, W.; Food Chem. 2021, 360, 130088. [Crossref]

36. Andueza, S.; Paz De Peña, M.; Cid, C.; J. Agric. Food Chem. 2003, 51, 7034. [Crossref]

37. Bell, L. N.; Wetzel, C. R.; Grand, A. N.; Food Res. Int. 1996, 29, 785. [Crossref]

38. Albanese, D.; Di Matteo, M.; Poiana, M.; Spagnamusso, S.; Food Res. Int. 2009, 42, 727. [Crossref]

39. Agnoletti, B. Z.; Oliveira, E. C. da S.; Pinheiro, P. F.; Saraiva, S. H.; Rev. Virtual Quim. 2019, 11, 785. [Crossref]