Artigo
| Formaldehyde analysis by SPME on-fiber derivatization: a study of the kinetic models of adsorption for divinylbenzene |
|
Stefano DugheriI,*; Giovanni CappelliII; Niccolò FanfaniIII; Jacopo CeccarelliII; Lucia TrevisaniII; Marco SartiIV; Donato SquillaciII; Elisabetta BucalettiII; Riccardo GoriV; Nicola MucciII; Giulio ArcangeliII
I. Industrial Hygiene and Toxicology Laboratory, University Hospital Careggi, 50139 Florence, Italy Recebido em 28/11/2022 *e-mail: stefano.dugheri@unifi.it Solid-phase microextraction (SPME) via on-fiber derivatization with O-(2,3,4,5,6-pentafluorobenzyl)-hydroxylamine (PFBHA) and gas chromatographic determination is considered a technique of choice in many analytical fields for formaldehyde (FA) monitoring. Vapor phase adsorption models of experimentally loaded PFBHA on porous divinylbenzene (DVB) SPME were investigated at 60 ºC, 35 cm s-1 of air velocity, in a 1-64 min range: with the fiber completely exposed, loaded PFBHA was about 276 µg. Among the models tested, i.e. heat transfer, pseudo-second-order (PSO), Elovich, intra-particle diffusion, extra-particle diffusion and Langmuir, PFBHA adsorption was best fit by the PSO model, showing agreement with experimental data (272 µg). The sampling rate of FA in our conditions, obtained with a permeation tube system, was in agreement with literature (17.4 and 18.3 mL min-1, respectively). Thus, an overall standardization of the sampling phase is presented, leaving the sampling time as the most crucial parameter to be set for future applications. INTRODUCTION Formaldehyde (FA) is an organic compound that, at room temperature and standard atmospheric pressure, occurs in the form of a colourless, pungent, and irritating gas, extremely volatile and highly soluble in water.1 It is a natural product in many living systems, in the environment, in some foods, and in the organism of mammals, including humans, as a product of oxidative metabolism. The global FA market size is expected to reach 12.21 billion United States (US) dollars by 2028, and it is estimated to expand at a compound annual growth rate (CAGR) of 5.7%, from 2021 to 2028.2 The growth can be attributed to the increasing construction activities worldwide and the manufacturing of disinfectants, vaccines, and personal care products, including mouthwash and toothpaste, due to its antibacterial attributes.3,4 In 2020, the urea-FA derivatives segment held the largest revenue share of over 35%, owing to its extensive usage in several end-use applications, including textiles, foundry sand, paper, electrical appliances, agriculture, and wood glue.5-9 The melamine-FA derivatives segment is anticipated to register the fastest revenue-based CAGR of 6.2% from 2021 to 2028 due to its properties such as moisture resistance, thermal stability, scratch resistance, flame retardant, strength, and hardness.2 FA is not only a ubiquitous environmental chemical, but it is also classified as a human carcinogen.10 The carcinogenicity of FA and the derivation of a safe occupational exposure limit have been the subject of documentation by several scientific expert panels.11 Currently, there are substantial differences among associations' guidelines concerning FA occupational exposure, not only in terms of parts per million limits but also regarding which value has to be applied.12 Recent trends in global food production, processing, distribution, and preparation are creating an increasing demand for food safety research to ensure a safer global food supply, and among these, great attention has been paid to volatile toxic aldehydes such as FA.13 The concern enlarged to several industrial sectors as well, such as cosmetics,14 wood,15 diesel engines,16 and building materials.17 Many analytical methods for determining airborne FA values have been developed. The present validated methods for detecting gaseous FA by gas chromatography (GC) or liquid chromatography (LC) are based on either active or passive sampling: the former using 2,4-dinitrophenylhydrazine (DNPH) and the latter using O-(2,3,4,5,6-pentafluorobenzyl)-hydroxylamine (PFBHA) as the reagent, both on a filter and a solid sorbent.18 Over the last ten years, miniaturization has attracted much attention and has driven solvent and sample savings, sample enrichment, rapid sample preparation, and easier automation. Moreover, miniaturization and automatization are crucial in the development of green analytical methods, and the solid-phase microextraction (SPME) has proved to be the most applied and versatile technique.19,20 SPME, patented in 1989,21 is a non-exhaustive sampling technique that integrates sampling, extraction, concentration, and sample introduction into a single step, and is considered one of the major advances that shaped 20th century analytical chemistry: it is mainly used as a passive sampler, either exposing it in the headspace (HS) of the sample or dipping it in said solution, without need of pumping stages.22-29 To deal with two of the major issues of SPME, specifically, the brittleness of the SPME device and full automation of SPME-based procedures, Chromline (Prato, Italy), in collaboration with Supelco (Bellefonte, USA), developed the SPME Fast Fit Assembly (FFA-SPME) in 2009, enabling the completely automated exchange of SPME fibers.30 In 2015, StableFlex and Nitinol-core were proposed by Supelco to obtain better physical stability instead of traditional fused silica-core,31 while in 2019, Supelco proposed the Smart SPME technology, consisting of a chip containing usage history and parameters of the fiber. To date, polydimethylsiloxane (PDMS) is one of the most widely used commercially available coatings for microextraction techniques (METs) to sample volatile analytes,32 due to its easy extraction process control and the absence of competition between the analytes during absorption. The solid, porous coating, such as divinylbenzene (DVB) and carboxen® (CAR) showed a higher sensitivity than PDMS in volatile organic compounds' adsorption.25 The main difference between CAR and DVB is the much higher percentage of micropores in the former: the latter is primarily mesoporous, allowing rapidly reaching an adsorption equilibrium. In the case of DVB, it is generally understood that π–π interactions with the benzenic cycle of DVB enhance the adsorption of molecules containing aromatic cycles, such as PFBHA.33 For this reason, commercially available METs using DVB as the adsorbent were developed, such as Thin Film-SPME, HiSorb (Markes International Ltd), SPME-Arrow (Restek Corporation), NeedleTrap (PAS Technologies), and µSPEed® (EPREP PTY LTD, Oakleigh, Australia). In SPME technique, the use of porous coatings results in a high sampling rate (SR);23 moreover, the quantity of adsorbent phase is significantly lower than conventional sampling systems. For this reason, a crucial aspect of using SPME technique by on-fiber derivatization23 is to quantify the maximum amount of derivatizing reagent that can be doped onto the fiber on a single run: this aspect enables to customize fundamental analytical parameters, such as fiber loading time, derivatizing reagent concentration, and FA sampling time. By doing so, the setup of the method can be adjusted to guarantee a complete and representative monitoring of the FA present, simultaneously maintaining a high throughput. Moreover, the range of loadable analyte can be defined to know in advance whether the use of SPME is adequate to the concentration scenario presented, resulting in savings of both money and time. The present study aims to define the better experimental conditions to maximize PFBHA fiber loading on a DVB PDMS SPME fiber; later on, the maximum quantity of derivatizing reagent loaded is predicted using various adsorption models present in literature, which represent a valid tool for data modelization, and confronted to the results obtained to verify the accordance. A heat transfer model, a pseudo-second order (PSO) kinetic model, a Langmuir isotherm adsorption model and a Elovich model are presented and applied to investigate classical isotherm utility to define capacity parameters for PFBHA loading. Furthermore, intraparticle- and extraparticle- diffusion (IPD and EPD, respectively) are tested to get a better understanding of the limiting factors impacting the adsorption process, to get a comprehensive view of the fiber behaviour. Lastly, the system is tested to examine the influence of the experimental setup on the sampling rate. The results suggest essential considerations for the subsequent FA chemisorption on the functionalized fiber, not only giving a clear prediction of the SPME system performance, but also allowing a restricted number of experimental tests to be conducted, limiting costs and enhancing the greenness of the method.
EXPERIMENTAL Chemicals and reagents O-(2,3,4,5,6-Pentafluorobenzyl)-hydroxylamine hydrochloride (PFBHA·HCl) (98% purity, CAS 57981-02-9), methanol (≥ 99.8% purity, CAS 67-56-1), and n-hexane (≥ 99% purity, CAS 110-54-3) were purchased from Sigma-Aldrich (Saint Louis, MO, USA). Formaldehyde O-(pentafluorobenzyl)oxime (FA-oxime) (≥ 98% purity, CAS 86356-73-2) and PDMS/DVB 65-µm FFA-SPME fibers with 23 gauge needle (Cat. No. FFA57293-U) were purchased from GiottoBiotech (Sesto Fiorentino, Italy) and Chromline (Prato, Italy), respectively. MilliQ water 18 MΩ cm (mQ) and PURE UV3 - 4-Stage UV Water Purification System, used to further purify the ultrapure water and eliminate aldehydes, were obtained from Millipore (Darmstadt, Germany) and Pure n Natural Systems, Inc. (Steamwood, IL, USA), respectively. Helium (99.999%) as GC carrier gas was obtained from Air Liquid (Paris, France). For automation of the SPME on-fiber PFBHA derivatization, HeadSpace screw-top 20-mL glass vials (HSV) (Part No. 5188-2753) and Hdsp cap 18 mm magnetic PTFE/Sil (Part No. 5188-2759) were purchased from Agilent Technologies (Santa Clara, CA, USA). PFBHA on-fiber derivatization routine Automated SPME on-fiber derivatization was performed at 60 ºC by using a 50 mg mL-1 PFBHA ultrapure water solution (1 mL) in the HS of the 20-mL HSV, exposing the SPME fiber for various times (i.e., 1, 2, 4, 7.5, 12, 16, 32 and 64 min), previous solution equilibrium to 5 min under vigorous stirring. Five repetitions for each curve level were performed. The whole procedure was achieved using a CTC PAL3 System xyz Autosampler (CTC Analytics AG, Zwingen, Switzerland) equipped with HeatEx Stirrer, Liquid Syringe Tool (CTC Analytics AG, Zwingen, Switzerland), and Multi Fiber eXchange (MFX) system (Chromline, Prato, Italy), to guarantee an automated routine between the exchange of FFA-SPME fiber and the 10 µL syringe (26 gauge). The fiber was used without any issue for the entirety of the experimental procedure, confirming the number of cycles perfomed per fiber obtained in our previous work, around 150.34 The absolute quantity of PFBHA in the HS of the vial was evaluated through automated direct injection of the gas phase with a gas-tight syringe, performing ten repetitions on likewise solutions after equilibrium. The nominal quantity was calculated on a regression curve obtained by injection in GC of PFBHA methanol solutions (20-300 µg). Permeation tube apparatus for the generation of FA gaseous standard mixtures A calibration gas generator with a temperature controlling system, set at 60 ºC (Sonimix 6000C1, LNI Swissgas, Versoix, Switzerland), was employed to generate FA atmospheres at constant concentrations, using multiple permeation tubes filled with paraformaldehyde (Fine Metrology, Italy), obtaining gaseous standard atmospheres of FA with permeation rate in a 48-3000 ng min-1 (± 5% at 60 ºC) range: the desired volumetric concentration was established or changed by simply varying the inert carrier gas flow from 0.5 to 5 L min-1. The effect of air velocity on the SPME was tested with a glass cylinder connected to the exposure chamber. The glass cylinder (internal diameter of 2 cm) with a plug for the introduction of the SPME fiber allows obtaining the linear air speed dividing the airflow (mL s-1) by the cross-sectional area (cm2), as shown in the Results and Discussion section.25 The gas concentration generated from the permeation system with different dilution gas flows can be represented by Equation 1:  where [FAair] is the concentration of the FA in the air (µg L-1), Fair-1 is the airflow (L min-1), W/T is the permeation rate (PR) (ng min-1) given by W, the FA weight loss (ng) and T, the measurement interval (min). The FA dynamic generation system was tested with ProCeas® formaldehyde analyzer (AP2E, Aix-en-Provence, France), an online, instantaneous, pre-calibrated monitoring device to check the quantity of generated aldehyde. Furthermore, the gaseous FA generated was tested by DNPH independent method.35 GC setting for FA-oxime analysis For GC analysis of the FA-oxime, the method by Dugheri et al.34 was used. Varian CP3800 GC system was coupled with a Varian Saturn 2200 Ion-Trap as the detector (scan mode, 45-300 m/z, EI energy 70 eV). The 1079 injector port (SCION Instruments, Amundsenweg, The Netherlands) was equipped with 0.75 mm internal diameter liner. The chromatographic column was DB 35-MS-UI GC Column (Agilent J&W, Part No. 122-38-32UI), and the GC oven settings were: 50 ºC (1 min) and then increased by 10 ºC min-1 to 260 ºC. Helium, as the carrier gas, was used and set at 1.2 mL min-1. Online, full automation of the procedure was achieved using the autosampler described above equipped with MFX system and Liquid Syringe Tool. The latter was used to inject 1 µL of FA-oxime hexane standard solutions, and a curve was constructed to obtain nominal quantities. The chromatogram obtained for FA-oxime and PFBHA is reported in Figure 1S of the Supplementary Material.
RESULTS AND DISCUSSION Theoretical SR of porous coating used for SPME fiber completely exposed from the needle For a cylindrical open tube, the SR is defined for the analyte in air through Fick's first law of diffusion, as shown in Equation 2: 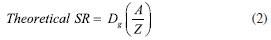 where Z is the effective diffusion path length (cm), A is the cross-sectional area of the sampling surface (cm2), and Dg is the FA diffusion coefficient in the air (cm2 s-1): Equation 2 provides a constant SR once the molecule, i.e. Dg, and the sampler features, i.e. A and Z, are defined. Dg depends on the molecular weight of the target analyte and temperature. Various models using different predictive variables are suggested to calculate the Dg of FA.36-41 Dg can be obtained from many chemical property's handbooks. US Environmental Protection Agency (EPA) developed a user-friendly online diffusion coefficient calculator.42 This online tool uses Fuller-Schettler-Giddings (FSG), FSG-LeBas, and Wilke and Lee models to estimate the Dg for a chemical based on its molecular structure and boiling point.43 The three models give very close values of Dg for FA, and the average Dg, equal to 0.177 cm2 s-1, was used. The same approach was used for further calculation concerning PFBHA with the average Dg (0.0664 cm2 s-1). With SPME fiber completely exposed is not possible to define Z. So, to calculate theoretical SR using a porous coating, the theory of heat transfer is applied,44 expressed as a function of the quantity of heat that passes through the walls of the tube during a given time (t), defined by Equation 3: 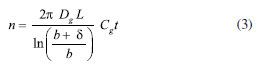 where b represents the radius of the fiber (i.e., 0.013 cm for 65 µm PDMS/DVB), Cg is the nominal concentration of PFBHA (µg mL-1), δ is the thickness of the boundary layer (cm) and t is the loading time (min); this formulation is similar to Equation 2, where Z is replaced by δ. The factors which most affect δ are the linear velocity and temperature of the air, the radius of the SPME fiber, and Dg. The transfer is considered to occur according to conventional principles, but as far as the transfer of the analyte inside the film is concerned, it occurs by diffusion.25 Therefore, the real thickness of δ can be obtained by the laws which rule heat transfer, using the model suggested by Nernst, in which the matrix inside the film is within a coating25 (Equation 4):  where Re (the Reynolds number) is defined as 2ubv-1 (where u is the linear air speed (cm s-1), v the air viscosity, 0.014607 cm2 s-1), and Sc (Schmidt's number) is expressed as vDg-1. Theoretically, linear air speeds higher than 10 cm s-1 yield a δ value closer to zero, so that the effect of the boundary layer becomes negligible and can be considered constant, nullifying Equation 3; moreover, mass transfer results are overestimated.25 Figure 1(1) shows the regression line obtained using heat transfer theory; a linear velocity of 10 cm s-1 was used, with a nominal value of PFBHA concentration in the HS of 30 µg mL-1. The model predicts a linear increase in the adsorbed PFBHA with time without reaching a plateau. However, the number of active sites available for adsorption on the fiber is finite, pointing out a clear limitation when predicting the saturation of the derivatizing reagent loaded.
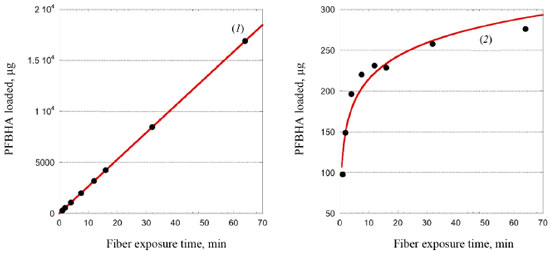 Figure 1. Predicted PFBHA loaded on SPME fiber by heat transfer theory (1) and experimental PFBHA loaded (2)
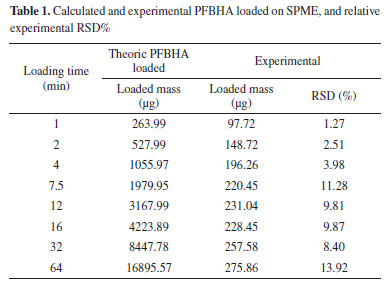
Figure 1(2) shows the experimental quantities of PFBHA loaded on the fiber as described in the Experimental section; moreover, Table 1 reports both the calculated and experimental loaded PFBHA, with the calculated relative standard deviation percentage (RSD%). The results are significantly different since the air velocity under vigorous stirring, measured in fivefold by GrayWolf's telescoping hotwire anemometer (Graywolf Sensing Solutions, Ireland), resulted in being around 35 cm s-1, with a RSD% of 0.83%, confirming that more specific adsorption models are required to predict the fiber behaviour: at this value, heat transfer theory would violate its limit of application, overestimating the sampled derivatizing reagent even more. Despite considering the setup investigated as a dynamic emitter is not proper, the stirring makes the system more similar to that condition compared to a static one; that is the main reason for the lack of agreement with the application of heat transfer theory in our previous work.34 We observed no significant differences in the concentration of PFBHA in the HS after the 64 min derivatization cycle, i.e., 30 µg mL-1; we can conclude that the stirring permits considering the concentration as a constant, balancing the depletion due to the adsorption on the fiber. This aspect will be helpful in the following application of adsorption models, reducing the variables and allowing a more straightforward data elaboration.
SPME fiber carry-over When using SPME, general drawbacks reducing the performance of the technique are present; one of the most important is fiber brittleness, which can be overcome using commercially available alternatives, such as SPME arrow. Conversely, when using SPME technique in gas chromatographic analysis, more specific problems may occur: among them, carry-over represents an important issue to be addressed, since it impacts the linearity of the response and the LOQ.45,46 It is well known that enhancing the desorption time and the injector temperature can indeed minimize this effect, yet impacting fiber lifetime due to increased coating degradation phenomena (e.g. phase bleeding).47-49 For this reason, SPME fiber carry-over was addressed by sampling and analyzing a known FA atmosphere (1 mg m-3) using derivatized fibers (PFBHA loaded in the 1-64 min time range, as described in the derivatization routine), followed by a second run without performing any preconditioning or bake. In particular, FA-oxime desorption time was investigated at 250 ºC (operating injector temperature) for 1, 3, 5 and 10 min. We observed a total desorption of the analyte for every time setting with no memory effects. Similarly, the derivatized SPME fiber provided negligible carry-over results in the whole range of loaded PFBHA, even before analyte reaction. The results obtained confirmed the suitability of the desorption time chosen, i.e. 1 min. Adsorption kinetic models The complex nature of SPME fibers as sorbent systems requires to consider various limiting factors, to better understand its behaviour in terms of capacity. Different adsorption models are taken into account and applied to experimental data: PSO model, Elovich model, IPD, EPD and Langmuir isotherm model are here presented and their results confronted. Since its introduction in 1996 by Ho et al.,50 several works have used the PSO approach to describe the adsorption process, in order to calculate the adsorption rate constants and to model experimental data. The PSO model and the integrated formulation are reported in Equation 5 and Equation 6, respectively: 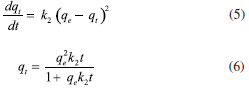 where qe represents the adsorption capacity at equilibrium (µg L-1), k2 is the pseudo-second rate order constant (g µg-1 min-1), t is the adsorption time (min), and qt represents the adsorbed amount of analyte at a given time t (µg L-1). However, calculating the model parameters from Equation 6 can be quite trivial; therefore, it is convenient to convert it into a linear form, as reported in Equation 7:51  Nonetheless, the linearization introduces propagated errors in the evaluation of the model parameters: for this reason, both formulations were applied.52-55 Using the experimental values of qt, converted in absolute PFBHA quantities, the best fitting curve was constructed to extrapolate k2 and qe (converted in µg, also for later applied models), as shown in Figure 2: the parameters derived from software elaboration, including R2, adjusted R2 and qe, are reported in Table 2. The linearized model and the residual plots for both formulations are available in Supplementary Material (Figures 2S-4S). It can be observed that the quantity of loaded PFBHA tends towards a plateau past 32 min, reaching about 276 µg at 64 min; on the contrary, the calculated amount equals 273 ± 5 µg.
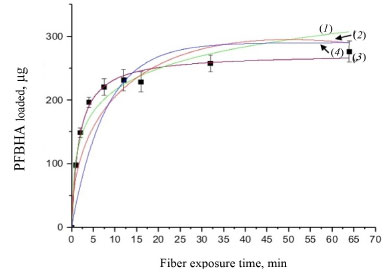 Figure 2. Elovich model (1), IPD model (2), PSO model (3), and EPD model (4)
Moreover, the Elovich adsorption model was applied:56 the model and the integrated formulations are reported in Equations 8 and 9, respectively: 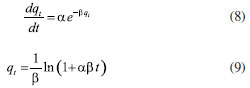 where α is the initial adsorption rate (µg g-1 min-1), and β is the Elovich desorption constant (g µg-1). The speed of equilibrium approaching for adsorption processes is based on β, as stated by Wu et al:57 we found a low desorption constant from fiber surface (i.e. 0.02 g µg-1), nonetheless the model does not instantly reach an equilibrium state. In particular, the authors suggest the use of a parameter called "approaching equilibrium factor", i.e. RE, to characterize the curvature of the regression: it is defined as β-1qref-1, where qref represents the absorbate concentration at the longest operating time (µg g-1). The value obtained, i.e. 0.18, confirms the mild curvature of the regression: as shown in Figure 2, this model does not properly fit our data, since the experimental trend towards a plateau appears more rapid; software parameters for the Elovich model, in particular R2 and adjusted R2, are reported in Table 2, while the residual plot is available in Supplementary Material (Figure 5S) We then considered IPD and EPD models, since their application permit to gather more informations, combined with isotherm kinetic models: diffusion can indeed represent a possible limit to particle adsorption on a porous system. The formulations used for IPD, as presented by Boyd and Reichenberg, are reported in Equations 10 and 11:58,59  where B, defined as Diπ2r-2, is a constant composed of the diffusion coefficient and geometrical factors (r is the radius of the adsorbent particle), F is the fractional uptake, defined as qt qe-1, and n is a constant. The curve obtained does not fit properly experimental data, and therefore it is possible to conclude that IPD is not the only limiting factor to the adsorption process, as previously suggested by Xiaoxia et al.60 and Al-Muhtaseb et al.61 Therefore, EPD model was also applied, to investigate possible adsorption limitation by diffusion through the boundary layer surrounding the sorbent.62 Equation 12, as presented by Boyd et al., was applied:58  where R, defined as 3Di r0-1Δr0-1k-1, is a constant depending of diffusion coefficient, partition coefficient k and geometrical factors; in particular, Δr0 represents the thickness of the boundary layer surrounding the fiber and r0 is the radius of the spherical adsorbent particle. R2, adjusted R2 and qe for IPD and EPD are reported in Table 2. As shown in Figure 2, also EPD does not provide a proper data fitting, as the regression curve appears similar to IPD: nonetheless, the quantity of equilibrium PFBHA loaded, i.e. 290 µg, differs slightly from the experimental value. This could be due to the major influence of EPD to the adsorption process when compared to IPD; however, in-depth studies should be perfomed to understand this divergence. The residual plots for IPD and EPD are presented in Figures 6S and 7S, respectively, of the Supplementary Material. From the tests performed, PSO appears to be the best adsorption model to converge in the entire time frame: as a general consideration, the results obtained thus far suggest that there is no single limiting factor to the adsorption process when it comes to predict the behaviour of the SPME fiber as sorbent. Despite the extremely good convergence of the PSO model with experimental data, we tested the model far from equilibrium. This needs to be addressed since a good fitting in a large window of time exposure could be biased and not represent the system investigated properly: as indicated by Guo and Wang,52 the PSO model can be applied successfully when three conditions are respected. The first one is that the initial concentration of the adsorbate is low: among the various literature works reported, none reports the application to DVB-coated SPME fibers exposed to the HS of a PFBHA ultrapure water solution.51 Hence, we confronted the average value obtained, as described in the Experimental section, verifying concentration of similar orders of magnitude, i.e., tens of µg mL-1 against our 30 µg mL-1.51 As for time, since adsorption is strictly dependent on the viscosity of the system, working in a gas phase (i.e., this work) requires shorter loading and equilibrium times confronted with liquid phase interactions.63 The second condition to be respected is the adsorption process, which should be far from equilibrium. Simonin64 indicated that the percentual fractional uptake shall not exceed 85%: this condition is essential to prevent bias in applying the PSO model. Hence, we restricted the range of SPME exposure up to 16 min, which was calculated to be a fractional uptake of about 83%. Lastly, the adsorbent material must present a large number of active sites for the uptake of the target compound. BET calculations performed by Supelco, demonstrated a DVB area per mass unit (grams of adsorbent phase) of 750 m2 g-1, with a density of 0.36 g mL-1 and a porosity of 0.11, 0.85, and 0.58 mL g-1 for micro-, meso- and macro-pores, respectively.65 In our condition, the amount of DVB allows to consider the kinetic dominated by the adsorption on the active sites. We therefore moved on to restrict the PSO elaboration up to 16 min to eliminate any possible bias in the application of the model: Figure 3 shows the fitting obtained and Table 3 reports the calculated parameters, while Figure 8S of the Supplementary Material reports the linearized version. The regression predicts a qe value coherent with the experimental load of PFBHA, i.e. 272 µg, even with data in a time range far from equilibrium; the residual sum of squares confirms a good agreement of the restricted model with the experimental values observed. The residual plots for both restricted-range formulations are available in Supplementary Material (Figures 9S and 10S).
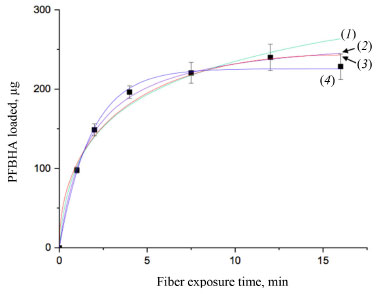 Figure 3. Elovich model (1), PSO model (2), IPD model (3) and EPD model (4)
The restriction in the time range was also investigated using Elovich, IPD and EPD models, presented in Figure 3 and Table 3: despite the lack of agreement with the complete data set, the quantity of loaded PFBHA at the equilibrium stage tend to the experimental value for IPD, i.e. 254.45 ± 18.40 µg; moreover, the fit obtained is very similar to the PSO curve, suggesting an influence in the adsorption process. Theorically, plotting Equation 11, i.e. Bt, against time should provide a straight line passing through axis origin, in case of adsorption limited by IPD only; as shown in Figure 11S of the Supplementary Material this is not the case, therefore suggesting that IPD is not the only limiting factor to the adsorption process. On the contrary, EPD-predicted derivatizing reagent loaded slightly deviates from the real amount when compared to the full time range: further inquiries would be necessary to understand this behaviour. Lastly, Elovich model does not provide an acceptable fit, with calculated RE value of 0.22; it is evident that the mild curvature of the regression is maintained despite the restricted time range. The residual plot for Elovich, IPD and EPD models are reported in Figures 12S-14S of the Supplementary Material. From the elaborations presented, it is clear that PSO still represents the best model to describe SPME fiber behaviour in our conditions. Azizian66 demonstrated that PSO represents a simplification of Langmuir isotherm adsorption model when the adsorbate concentration is low; since we observed a good prediction using PSO, we tested the latter to verify the results achieved. The formulation adopted for the Langmuir model is expressed in Equation 13: 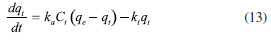 where ka represents the adsorption rate constant (L µg-1 min-1), Ct represents the adsorbate concentration at a certain time (µg L-1), and kd is the desorption rate constant (min-1). The equation would require an initial condition based on programming software, making it difficult to be applied: considering Ct constant, as observed in this work, permitted to perform an easier data elaboration. Table 3 reports the parameters obtained from the fit, shown in Figure 4: the model is able to predict the value of PFBHA loaded at equilibrium in good accordance with experimental data, despite the restricted time range investigated. The correlation appears slightly worse than other models tested, yet the agreement with our results confirms the feasibility when it comes to predicting the adsorbed PFBHA at equilibrium stages. The residual plot for Langmuir isotherm is available in Supplementary Material (Figure 15S).
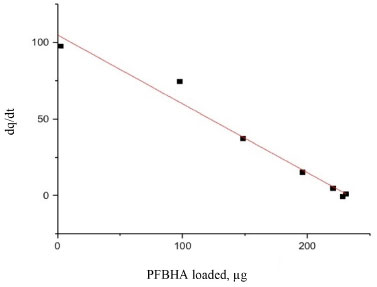 Figure 4. Langmuir isotherm model for PFBHA loading in the unbiased
The convergence of investigated models, in particular PSO, IPD and Langmuir isotherm, confirms the adsorption at homogenous sites with uniform energy levels: the direct consequence is that the adsorption forms a monolayer of PFBHA on the surface of the fiber. Moreover, the missing convergence of Elovich fitting reinforce this aspect, since previous studies suggested it to be more suitable for heterogeneous sorbent surfaces.57 The effort to define the suitable conditions to load the maximum amount of derivatizing reagent presented so far is something to be dealt with in every concentration range. Despite the amount of PFBHA consumed doing so is enhanced, this operation is necessary to guarantee a complete reaction of the FA, avoiding any mismatch with the effective quantities present. Moreover, as demonstrated in Dugheri et al.,34 the FA blank level of commercial PFBHA is not reducible via further purifications. Thus, a higher mass of derivatizing reagent loaded can maximize the mass of sampled FA, minimizing the impact of the reagent blank. The possibility of limiting the number of tests to be conducted provided by a modelistic approach, as shown so far, represents a powerful tool in terms of cost reduction and effort of compliance with greener approaches. Experimental SR of porous coating SPME fiber completely exposed from the needle Once the SPME system loading was tested and the results confirmed from the adsorption models shown above, experiments were performed to obtain the SR for FA. This evaluation is mandatory in order to predict the best conditions to apply the technique as a passive sampler in different concentration scenarios. Hence, the calibration curve for the airborne concentration of FA (CFAair) in a dynamic system was obtained by permeation tubes, as described in the Experimental section. The experimental SR was obtained by use of Equation 14: 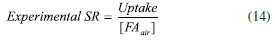 where Uptake (ng s-1) is the slope of the equation of the regression line constructed by correlating the mass of FA chemisorbed on the SPME fiber with the sampling time for a known FA atmosphere (1 mg m-3), as shown in Figure 5 (i.e., 0.29 ng s-1). Every level of the curve was evaluated in five replicates. The absolute quantity of FA was previously calculated as described in the Experimental section. The effect of air velocity on the SPME system was verified using a glass cylinder connected to the exposure chamber characterized by an internal diameter of 2 cm, provided with a plug for the introduction of the SPME fiber, which enables to reach different linear air speeds. The value obtained, about 16 cm s-1, was calculated by dividing the airflow (set at 50 mL s-1) by the cross-sectional area (about 3.14 cm2). In this condition, i.e., above 10 cm s-1, the SR of SPME for FA can be considered constant and independent from the air velocity: the SR obtained experimentally is 17.4 mL min-1, according to the literature data.67
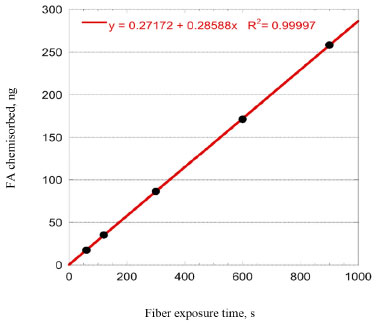 Figure 5. Correlation between chemisorbed FA and SPME exposure time
Whenever a passive sampler is used, similar experiments should be conducted on the SR to set up analytical monitoring to achieve the best standardization possible of the sampling step. The results obtained so far, i.e., the monolayer disposition and the saturation of loaded PFBHA, enable the prediction of the FA theoretical mass range that can be analysed in a single run. Since PFBHA reacts with FA following a 1 to 1 stoichiometric ratio,23 the experimental setup can be adjusted: particularly, the sampling time embodies the most crucial parameter modifiable to optimize the method. Therefore, it can be guaranteed that the analyte amount loaded on the fiber is always representative of the concentration and that no biases are present during the time of exposure, such as loss of FA due to lack of derivatizing reagent. With the inquiries proposed in this work, the tests which need to be conducted to setup an analytical monitoring are reduced to the minimum, starting from maximizing the PFBHA loaded on the fiber, moving to the optimization of FA sampling: a trustworthy approach can then result in higher throughtputs and more efficient monitorings, with the possibility of being extended to a wide range of analytical compounds.
CONCLUSIONS The miniaturization of traditional sample preparation devices fulfills the request of an environmentally friendly analytical chemistry: miniaturized techniques, such as SPME, provide a valuable analytical tool even for the most challenging compounds, such as formaldehyde, reducing the per-analysis time and the cost, while improving analytical productivity. To optimize SPME sampling, a defined knowledge of its sorption kinetic results a crucial information. In this framework, experimental data of loaded PFBHA were fitted using various kinetic adsorption models, observing that PSO was the only model that enabled the prediction of adsorbed derivatizing reagent at equilibrium stage, limiting the tests to be conducted while demonstrating at the same time the complexity of the processes taking place on the fiber. The sampling rate for FA was also determined in our experimental conditions: with these results in hand, it was possible to define the optimal set-up for SPME sampling. In particular, the sampling time represents the most important parameter modifiable, to move towards a trustworthy approach which can be extended to other compounds of environmental interest, reducing pre-analytical uncertainties, such as analyte underestimation.
SUPPLEMENTARY MATERIAL In supplementary material, available on http://quimicanova.sbq.org.br as a PDF file, with free access, are presented the Figure 1S to 15S. In these figures are showed the chromatograms obtained for FA-oxime and PFBHA (Figure 1S), the linearized PSO model, the residual plot of the integrated and the linearized PSO model for PFBHA loading (Figures 2S-4S), the residual plot of Elovich model (Figure 5S), residual plots for IPD and EPD models (Figures 6S and 7S), the linearized PSO model and the residual plots of the integrated and linearized PSO model for PFBHA loading in the unbiased range (Figures 8S-10S), the IPD model alternative formulation (Figure 11S), residual plots of Elovich, IPD and EPD model for PFBHA loading in the unbiased range (Figures 12S-14S), and the residual plot of the Langmuir isotherm model for PFBHA loading in the unbiased range (Figure 15S).
ACKNOWLEDGMENT The study group thanks the Laboratorio per l'Innovazione e per l'applicazione della Robotica nel Monitoraggio degli Ambienti Naturali, di vita e di lavoro (LIROMAN) of PIN - Polo Universitario città di Prato (Prato, Italy) for providing the spaces to carry out the experiments. We would also like to thank the Buzzi Lab (Viale della Repubblica, 9, 59100 Prato, Italy) for providing the additional instruments needed to complete this analytical work.
REFERENCES 1. Songur, A.; Ozen, O. A.; Sarsilmaz, M.; Rev. Environ. Contam. Toxicol. 2010, 203, 105. [Crossref] 2. https://www.grandviewresearch.com/press-release/global-formaldehyde-market, accessed in March 2023. 3. Yang, Z.; Sha, D.; Xu, J.; Niu, N.; Shi, K.; Pan, Y.; Yu, C.; Wei, H.; Wang, B.; Ji, X.; New J. Chem. 2019, 43, 14961. [Crossref] 4. Nikolic, P.; Mudgil P.; Whitenall, J.; MicrobiologyOpen 2020, 9, 1. [Crossref] 5. Reich, H.; Washaw, E.; Dermatitis 2010, 21, 65. [Crossref] 6. Malte, S.; Johansens, J.; Rustemeyer, T.; Elsner, P.; Maibach, H.; Kanerva's Occupational Dermatology, 3rd ed.; Springer: Berlin, 2020. 7. Kandelbauer, A.; Primoz, P.; Medved, S.; Pizzi, A.; Teischinger, A.; Eur. J. Wood Wood Prod. 2010, 68, 63. [Crossref] 8. Zhang, W.; Xiang, Y.; Fan, H.; Wang, L.; Xie, Y.; Zhao, G.; Liu, Y.; J. Agric. FoodChem. 2020, 68, 4595. [Crossref] 9. Pinto, G.; Maaroufi, A.; Polym. Compos. 2012, 33, 2188. [Crossref] 10. Nielsen, G.; Larsen, S.; Wolkoff, P.; Arch. Toxicol. 2017, 91, 35. [Crossref] 11. Bolt, H.; Degen, G.; Hengstler, J.; Arch. Toxicol. 2010, 84, 421. [Crossref] 12. http://www.dguv.de/ifa/gestis/gestis-stoffdatenbank/index-2.jsp, accessed in March 2023. 13. Bianchi, F.; Careri, M.; Musci, M.; Mangia, A.; Food Chem. 2007, 100, 1049. [Crossref] 14. Topiwala, V.; Rivero, R.; J. Cosmet. Sci. 2004, 55, 343. [Link] accessed in March 2023 15. Zhang, J.; Song, F.; Tao, J.; Shi, S.; Int. J. Polym. Sci. 2018, 5, 1. [Crossref] 16. Chigier, N. A. In Energy and Combustion Science Book; Chigier, N. A., ed.; Elsevier: Amsterdam, 1979. 17. Jones, D.; Brischke, C. In Performance of Bio-based Building Materials Book; Jones, D.; Brischke, C., eds.; Elsevier: Amsterdam, 2017. 18. Dugheri, S.; Massi, D.; Mucci, N.; Marrubini, G.; Cappelli, G.; Speltini, A.; Bonferoni, M.; Arcangeli, G.; Trends Environ. Anal. Chem. 2021, 29, e00116. [Crossref] 19. Fabjanowicz, M.; Kalinowska, K.; Namiesnik, J.; Plotka-Wasylka, J.; Curr. Green Chem. 2018, 5, 168. [Crossref] 20. Omena, E.; Oenning, A.; Merib, J.; Richter, P.; Rosero-Moreano, M.; Carasek, E.; Anal. Chim. Acta 2019, 1069, 57. [Crossref] 21. Arthur, C.; Pawliszyn, J.; Anal. Chem. 1990, 62, 2145. [Crossref] 22. Nowak, P.; Wietecha-Posluzny, R.; Pawliszyn, J.; TrAC, Trends Anal. Chem. 2021, 138, 116623. [Crossref] 23. Martos, P.; Pawliszyn, J.; Anal. Chem. 1998, 70, 2311. [Crossref] 24. Filipiak, W.; Bojko, B.; TrAC, Trends Anal. Chem. 2019, 115, 203. [Crossref] 25. Koziel, J.; Jia, M.; Pawliszyn, J.; Anal. Chem. 2000, 72, 5178. [Crossref] 26. Marini, F.; Bellugi, I.; Gambi, D.; Pacenti, M.; Dugheri, S.; Focardi, L.; Tulli, G.; Acta Anaesthesiol. Scand. 2007, 51, 625. [Crossref] 27. Drabińska, N.; Starowicz, M.; Krupa-Kozak, U.; J. Anal. Chem. 2020, 75, 792. [Crossref] 28. Alekseenko, A. N.; Zhurba, O. M.; Efimova, N. V.; Rukavishnikov, V. S.; J. Anal. Chem. 2017, 72, 83. [Crossref] 29. Savelieva, E.; Gavrilova, O.; Gagkaeva, T.; J. Anal. Chem. 2014, 69, 609. [Crossref] 30. Pacenti, M.; Dugheri, S.; Traldi, P.; Esposti, F. D.; Perchiazzi, N.; Franchi, E.; Calamante, M.; Kikic, I.; Alessi, P.; Bonacchi, A.; Salvadori, E.; Arcangeli, G.; Cupelli, V.; J. Autom. Methods Manage. Chem. 2010, 2010, 1. [Crossref] 31. Roux, K. C. P.; Jasinski, E.; Merib, J.; Sartorelli, M.; Carasek, E.; Anal. Methods 2016, 8, 5503. [Crossref] 32. Dugheri, S.; Mucci, N.; Cappelli, G.; Trevisani, L.; Bonari, A.; Bucaletti, E.; Squillaci, D.; Arcangeli, G.; J. Anal. Methods Chem. 2022, 2022, 1. [Crossref] 33. Tuduri, L.; Desauziers, V.; Fanlo, J.; J. Chromatogr. Sci. 2001, 39, 521. [Crossref] 34. Dugheri, S.; Cappelli, G.; Ceccarelli, J.; Fanfani, N.; Trevisani, L.; Squillaci, D.; Bucaletti, E.; Gori, R.; Mucci, N.; Arcangeli, G.; Quim. Nova 2022, 45, 1236. [Crossref] 35. Dugheri, S.; Bonari, A.; Pompilio, I.; Colpo, M.; Mucci, N.; Montalti, M.; Arcangeli, G.; Rasayan J. Chem. 2017, 29, 1. [Crossref] 36. Arnold, J.; Ind. Eng. Chem. 1930, 22, 1091. [Crossref] 37. Gilliland, E.; Ind. Eng. Chem. 1934, 26, 681. [Crossref] 38. Hirschfelder, J.; Bird, R.; Spotz, E.; Chem. Phys. 1949, 44, 205. [Crossref] 39. Wilke, C.; Lee, C.; Ind. Eng. Chem. 1955, 47, 1253. [Crossref] 40. Fuller, E.; Schettler, P.; Giddins, J.; Ind. Eng. Chem. 1966, 58, 19. [Crossref] 41. Brokaw, R. S.; Ind. Eng. Chem. 1966, 8, 240. [Crossref] 42. https://www3.epa.gov/ceampubl/learn2model/part-two/onsite/, accessed in March 2023. 43. Lyman, W.; Reehl, W.; Rosenblatt, D.; Handbook of Chemical Property Estimation Methods: Environmental Behavior of Organic Compounds, 2nd ed.; American Chemical Society: Washington, 1990. 44. Pacenti, M.; Dugheri, S.; Gagliano-Candela, R.; Strisciullo, G.; Franchi, E.; Esposti, F. D.; Perchiazzi, N.; Boccaloni, P.; Arcangeli, G.; Cupelli, V.; Acta Chromatogr. 2009, 21, 379. [Crossref] 45. Vu, D. H.; Koster, R. A.; Wessels, A. M. A.; Greijdanus, B.; Alffenaar, J. W. C.; Uges, D. R. A.; J. Chromatogr. B: Biomed. Sci. Appl. 2013, 917-918, 1. [Crossref] 46. Prokupková, G.; Holadová, K.; Poustka, J.; Hajšlová, J.; Anal. Chim. Acta 2002, 457, 211. [Crossref] 47. Roychowdhury, T.; Patel, D. I.; Shah, D.; Diwan, A.; Kaykhaii, M.; Herringtond, J. S.; Bell, D. S.; Linford, M. R.; J. Chromatogr. A 2020, 1623, 461065. [Crossref] 48. Azenha, M. A.; Nogueira, P. J.; Silva, A. F.; Anal. Chem. 2006, 78, 2071. [Crossref] 49. Diwan, A.; Singh, B.; Roychowdhury, T.; Yan, D.; Tedone, L.; Nesterenko, P. N.; Paull, B.; Sevy, E. T.; Shellie, R. A.; Kaykhaii, M.; Linford, M. R.; Anal. Chem. 2016, 88, 1593. [Crossref] 50. Ho, Y.; Wase, D.; Forster, C.; Water SA 1996, 22, 219. [Link] accessed in March 2023 51. Wang, J.; Guo, X.; J. Hazard. Mater. 2020, 390, 122156. [Crossref] 52. Guo, X.; Wang, J.; J. Mol. Liq. 2019, 288, 111100. [Crossref] 53. Ho, Y.; Pol. J. Environ. Stud. 2006, 15, 81. [Link] accessed in March 2023 54. El-Khaiary, M.; Malash, G.; Ho, Y.; Desalination 2010, 257, 93. [Crossref] 55. Kumar, K.; Sivanesan, S.; J. Hazard. Mater. 2006, 136, 721. [Crossref] 56. Elovich, S.; Larionov, O.; Theory of Adsorption from Nonelectrolyte Solutions on Solid Adsorbents, translated from Izvestiya Akademii Nauk SSSR, Otdelenie Khimicheskikh Nauk 1962, 2, 209. 57. Wu, F. C.; Tseng, R. L.; Juang, R. S.; J. Chem. Eng. 2009, 150, 366. [Crossref] 58. Boyd, G.; Adamson, A.; Myers Junior, J.; J. Am. Chem. Soc. 1947, 69, 2836. [Crossref] 59. Reichenberg, D.; J. Am. Chem. Soc. 1953, 75, 589. [Crossref] 60. Xiaoxia, Y.; Muhammad, T.; Yang, J.; Yasen, A.; Chen, L.; Sens. Actuators, A 2020, 313, 1. [Crossref] 61. Al-Muhtaseba, A.; Ibrahim, K.; Albadarin, A.; Ali-khashman, O.; Walker, G.; Ahmad, M.; J. Chem. Eng. 2011, 168, 691. [Crossref] 62. Semenov, S.; Koziel, J.; Pawliszyn, J.; J. Chromatogr. A 2000, 873, 39. [Crossref] 63. Rana, C.; Pramanik, S.; Martin, M.; De Wit, A.; Mishra, M.; Physical Review Fluids 2019, 4, 104001. [Crossref] 64. Simonin, J.; Chemical Engineering Journal 2016, 300, 254. [Crossref] 65. Tsai, S. W.; Que Hee, S. S.; Appl. Occup. Environ. Hyg. 2002, 17, 551. [Crossref] 66. Azizian, S.; J. Colloid Interface Sci. 2004, 276, 47. [Crossref] 67. Associazione per l'Unificazione nel Settore dell'Industria Chimica, Ambienti di lavoro; Determinazione delle aldeidi aerodisperse: Metodo per microestrazione su fase solida (SPME) ed analisi mediante gascromatografia accoppiata a spettrometria di massa (GC-MS), |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access







