Artigo
|
|
| Efeitos das múltiplas estruturas e da anarmonicidade torcional para as reações de abstração de hidrogênio no butanoato de metila pelo radical H Effects of multiple structures and torsional anharmonicity for the hydrogen abstraction reactions of the thmethyl butanoate by H radical |
|
Joel Leitão Nascimento*; Tiago Vinicius Alves*
Departamento de Físico-Química, Instituto de Química, Universidade Federal da Bahia, 40170-115 Salvador – BA, Brasil Recebido em 03/12/2022 *e-mail: joelnascimento@ufba.br; tiagova@ufba.br Thermal rate constants for the hydrogen abstraction reactions of the methyl butanoate (MB) by H radical were estimated by applying the multistructural canonical variational theory with small-curvature tunneling (CVT/SCT). The conformational search was performed at MPWB1K/6-31+G(d,p) level of theory and 68 distinguishable conformers for MB and transition state located. The multistructural and torsional anharmonicity effects were corrected through the rovibrational partition functions calculated with the multistructural method based on a coupled torsional potential, MS-T(C). The MS-CVT/SCT thermal rate constants are shown in good concordance with previous combustion models. After fitting the rate constants in a four-parameters equation, the activation energy showed a temperature dependence. The product branching ratios indicate a preference for (Rα) until 500 K. Above this temperature, the contribution of other reactions becomes relevant, especially for (Rβ). INTRODUÇÃO A queima de combustíveis fósseis vem sendo a grande causadora da emissão de material particulado e gases, que além de tóxicos, intensificam o efeito estufa.1 Dados recentes apontam que parte desta poluição atmosférica tem sido responsável pelo aumento de hospitalizações e mortes de crianças e adultos por problemas cardiorrespiratórios.2-4 Neste sentido, agendas climáticas têm recomendado o desenvolvimento e uso de fontes energéticas alternativas, como por exemplo os bioderivados, objetivando a redução da emissão de poluentes.5 O biodiesel, um biocombustível renovável constituído por monoésteres alquílicos de ácidos graxos, tem sido amplamente utilizado como substituto ou aditivo ao diesel convencional. Obtido a partir da esterificação de ácidos graxos ou pela transesterificação de óleos e gorduras,6 sua combustão e oxidação, comparativamente ao diesel, gera uma menor quantidade de hidrocarbonetos, CO, CO2 e fuligem. Além disso, estudos experimentais utilizando motores de teste simples, e também similares aos comerciais, indicaram que o uso do biodiesel reduz a emissão de NOx.7-10 Por ser formado por ésteres de cadeia longa, que variam entre 15 a 22 carbonos, o mecanismo de sua combustão e oxidação é complexo, compreendendo milhares de reações elementares. Uma alternativa recente para a construção e validação desse quebra-cabeça mecanístico é o emprego de parâmetros cinéticos envolvendo ésteres de cadeia mais curta, tais como o acetato de metila, propanoato de metila e butanoato de metila.11-13 Neste contexto, faz-se necessário a determinação acurada dos parâmetros cinéticos envolvendo reações elementares de transferência protônica, adição e dissociação envolvendo essas espécies. O butanoato de metila (BM), além de servir de protótipo para o entendimento da oxidação do biodiesel,13-20 tem sido considerado como um potencial substituto ao biodiesel e como aditivos aos combustíveis convencionais.21 Em um primeiro estudo experimental, Fisher et al.20 propuseram um mecanismo de combustão deste éster. Neste trabalho, os parâmetros cinéticos foram estimados a partir do mecanismo desenvolvido por Curran et al.22 para o n-heptano. Em uma outra investigação, Gaïl et al.23 propuseram um mecanismo de oxidação constituído por 1498 reações elementares envolvendo 295 espécies neutras e iônicas. Estudos posteriores, desenvolvidos por Dooley et al.24 e Hakka et al.,25 complementaram e corroboraram com o entendimento deste amplo conjunto de reações químicas. Nestes estudos experimentais envolvendo a combustão e oxidação do BM, as reações de abstração de hidrogênio foram apontadas como as responsáveis por controlar o consumo inicial deste éster. Para as abstrações pelo hidrogênio atômico, foram considerados quatro sítios distintos (Figura 1), resultando em quatro canais reacionais: (Rα'): CH3CH2CH2COOCH3 + H → CH3CH2CH2COOCH2 + H2 (1) (Rα): CH3CH2CH2COOCH3 + H → CH3CH2CHCOOCH3 + H2 (2) (Rβ): CH3CH2CH2COOCH3 + H → CH3CHCH2COOCH3 + H2 (3) (Rγ): CH3CH2CH2COOCH3 + H → CH2CH2CH2COOCH3 + H2 (4)
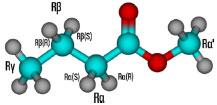 Figura 1. Representação tridimensional dos sítios de abstração de hidrogênio do butanoato de metila (BM)
Dentro deste contexto, inúmeros estudos teóricos buscaram estimar propriedades cinéticas dessas reações elementares. Wang et al.26 investigaram as reações de abstração no carbono metílico α' para ésteres de diferentes tamanhos, baseando-se em reações isodésmicas e, aplicando a teoria do estado de transição de classes de reação (Reaction Class Transition State Theory - RC-TST). Huynh e Violi27 realizaram a determinação dos parâmetros cinéticos para as reações de abstração de hidrogênio butanoato de metila pelo hidrogênio atômico empregando a teoria do estado de transição convencional (Transition State Theory - TST). Os pontos estacionários gerados por essas reações foram caracterizados no nível de teoria BH&HLYP/cc-pVTZ e as contribuições de tunelamento quântico estimadas com a aproximação unidimensional de Eckart.28 Adicionalmente, os autores empregaram a abordagem proposta por Ayala e Schlegel,29 para o tratamento dos modos vibracionais associados às torções internas de reagente e estados de transição. Utilizando uma abordagem cinética semelhante, Zhang e colaboradores30 forneceram as constantes de velocidade para esse conjunto de reações, estimando os parâmetros energéticos com o funcional da densidade B3LYP juntamente com um conjunto de base 6-311++G(d,p). Um refinamento energético com a aproximação QCISD(T), seguido de uma extrapolação para o limite de bases completa, também foi realizado. Em uma investigação similar, Liu et al.31 calcularam os coeficientes de velocidade empregando os modelos de estrutura eletrônica CCSD(T)/CBS//MP2/cc-pVTZ e CCSD(T)/CBS//B3LYP/6-311++G(d,p). Estudos posteriores realizados por Akih-Kumgeh e Bergthorson,32 e Meng et al.,33 dedicaram-se também a essas estimativas cinéticas, embora restritas a aproximações cinéticas menos elaboradas. Muito embora diversos trabalhos teóricos tenham dedicado-se ao estudo da cinética das reações (Rα')-(Rg), efeitos associados a flexibilidade conformacional do butanoato de metila e estados de transição, bem com os da anarmonicidade torcional não foram considerados. Em estudos recentes realizados em nosso grupo de pesquisa, demonstramos a importância e o impacto dessas considerações na estimativa da constante de velocidade térmica envolvendo espécies com potencial energético.34-37 Neste sentido, este trabalho tem como principal objetivo, a determinação das constantes de velocidade para as reações de abstração de hidrogênio do BM pelo átomo de hidrogênio, considerando os efeitos das múltiplas estruturas de reagentes e estados de transição, bem como o da anarmonicidade torcional. Para isso, funções de partição rovibracionais multiestruturais foram determinadas empregando o modelo Multiestrututal Acoplado (Multistructural Torsional Coupled Method – MS-T(C)).38 Por fim, as constantes de velocidade térmica foram determinadas utilizando a Teoria Variacional Canônica Multiestrutural (Multistructural Canonical Variational Theory - MS-CVT)39,40 com tunelamento quântico multidimensional de pequena curvatura (Small Curvature Tunneling - SCT),41 aqui chamada de MS-CVT/SCT.
METODOLOGIA A constante de velocidade térmica, dentro da aproximação MS-CVT/SCT, pode ser escrita como o produto de três termos: 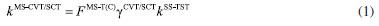 em que FMS-T(C) é o fator multiestrutural que, além de contabilizar a contribuição de todos os confôrmeros de reagente e estados de transição gerados a partir das rotações sobre as suas ligações simples, inclui os desvios da anarmonicidade torcional. Este termo da equação (1) é dado pela razão: 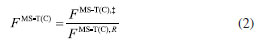 sendo FMS-T(C),X os fatores para reagente e estados de transição (X = R ou ‡), escrito por: 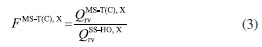 Na equação (3), 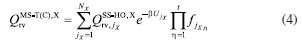 em que NX é o número de confôrmeros (incluindo os enantiômeros torcionais), β = 1/kB T; kB a constante de Boltzmann e T a temperatura, UjX é a energia relativa da jX-ésima estrutura, em relação ao rotâmero mais estável (jX = 1). O termo contabiliza a anarmonicidade torcional para cada h-ésima torção, para um sistema molecular com t-torções. O segundo termo da equação (1), γCVT/SCT, introduz na constante de velocidade térmica os efeitos de recruzamento e quântico de tunelamento para o caminho reacional associado a estrutura de transição mais estável. Mais especificamente, este fator pode ser escrito como o produto do coeficiente de transmissão semiclássico (κCVT/SCT), calculado com modelo de pequena curvatura (Small-Curvature Tunneling - SCT), e pelo termo que contabiliza os efeitos de recruzamento (ΓCVT). Por fim, o terceiro termo da equação (1) estima o coeficiente de velocidade pela teoria do estado de transição convencional, considerando apenas as estruturas mais estáveis de reagente e estado de transição (Single-Structure Transition State Theory - SS-TST),42 ou seja: 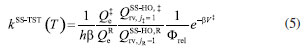 em que h é a constante de Planck, Q‡e e QRe são as funções de partição eletrônicas para o estado de transição e reagente, respectivamente. Φrel é a função de partição que inclui o movimento translacional dos reagentes e é a diferença de energia entre as estruturas de mais baixa energia de reagentes V‡ e estados de transição.
DETALHES COMPUTACIONAIS Numa primeira etapa, realizamos uma busca conformacional sistemática para os pontos estacionários gerados pelas reações (Rα')-(Rγ), no nível de teoria HF/3-21G,43 baseados no conhecimento químico. As torções usadas neste scan estão ilustradas na Figura 2. Os ângulos diedros destacados em vermelho não foram considerados na busca conformacional, uma vez que geram conformações indistinguíveis, entretanto, foram incluídas na estimativa da anarmonicidade torcional. Para as torções envolvendo carbonos sp3 definimos os valores dos ângulos em 60, 180 e 300o, enquanto que para as rotações sobre os carbonos sp2, os valores de 0 e 180o. A seguir, realizamos uma busca estocástica, no mesmo nível de teoria, para localizar outros confôrmeros que estão fora do domínio definido na etapa anterior. Todas as estruturas encontradas nas buscas sistemática e estocástica, foram reotimizadas no nível de teoria MPWB1K/6-31+G(d,p).44,45 Apesar deste nível de cálculo ter sido parametrizado e testado para a obtenção de dados termoquímicos e cinéticos,46 sua acurácia foi verificada frente a abordagens altamente correlacionadas, discutida na próxima seção. As buscas conformacionais, em ambos os níveis, foram realizadas no código TorsiFlex,47,48 em interface com o Gaussian 09.49 As funções de partição rovibracionais foram calculadas com o programa MsTor.50 Para corrigir a inexatidão do método de estrutura eletrônica na estimativa da energia do ponto-zero, utilizamos um fator de escala de 0,951, conforme recomendado por Alecu e colaboradores.51
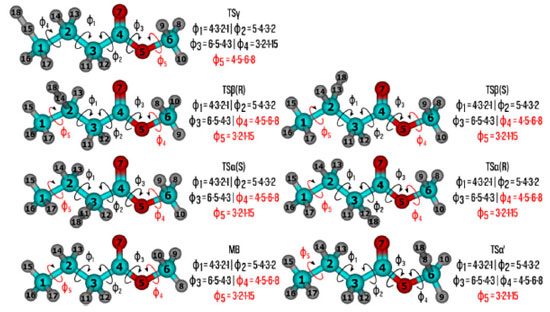 Figura 2. Definição dos ângulos diedros para o butanoato de metila (BM) e estados de transição. Os átomos em ciano, vermelho e cinza representam o carbono, oxigênio e hidrogênio, respectivamente. Os ângulos diedros destacados em vermelhos não foram incluídos na busca conformacional
Para o cálculo das constantes de velocidade MS-CVT/SCT, empregamos o programa Pilgrim,52 escrito em Python 3, que utiliza os arquivos gerados pelo TorsiFlex e MsTor. Nesta etapa, a construção do caminho de energia mínima (Minimum Energy Path - MEP) foi seguido pelo algoritmo de Page-McIver,53 com um passo de 0,005 a0. A matriz Hessiana foi estimada a cada 10 passos. As coordenadas internas redundantes,54 foram automaticamente geradas pelo código Pilgrim e utilizadas para extrair os modos normais ao longo do caminho de energia mínima. Por fim, o MEP foi estendido até que o coeficiente de transmissão semiclássico e o tunelamento de pequena curvatura alcançasse convergência dentro de um erro inferior a 1%.
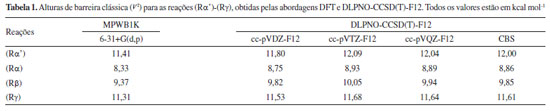
RESULTADOS E DISCUSSÃO Para verificar a acurácia dos parâmetros energéticos estimados no nível de teoria MPWB1K/6-31+G(d,p), realizamos cálculos single point, utilizando as geometrias previamente otimizadas, através da aproximação DLPNO-CCSD(T)-F12,55 com os conjuntos de bases do tipo cc-pVnZ-F12 (n = D, T e Q), e as auxiliares aug-cc-pVnZ/C e cc-pVnZ-F12-CABS, utilizando o programa Orca 5.56 Uma extrapolação das energias obtidas para o limite de base completa (Complete Basis Set - CBS) foi realizada utilizando uma função mista de uma exponencial com uma gaussiana, proposta por Peterson et al.:57 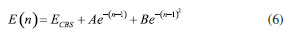 com n = 2, 3, 4... Os valores para as alturas de barreira clássica obtidas com DFT e DLPNO-CCSD(T)-F12, estão listadas na Tabela 1. Como podemos observar, as barreiras energéticas paras as reações em estudo, obtidas no nível MPWB1K/6-31+G(d,p), estão em excelente concordância com as estimadas pela aproximação DLPNO-CCSD(T)-F12/CBSD-Q. Para a reação (Rα'), a diferença entre aos dois métodos de estrutura eletrônica foi de 0,59 kcal mol-1, enquanto que para (Rα) o desvio entre ambas foi de 0,53 kcal mol-1, para as abstrações nos carbonos β e g, essas diferenças foram de 0,48 e 0,30 kcal mol-1. Esses resultados indicam que a as barreiras energéticas estimadas com MPWB1K/6-31+G(d,p) estão dentro do que se pode considerar como precisão química (menor que 1 kcal mol-1).
Na etapa da busca conformacional, foram encontradas 8 conformações para o butanoato de metila e 60 estruturas para todos os estados de transição. As coordenadas cartesianas e frequências vibracionais harmônicas escalonadas estão listadas nas Seções 1S e 2S do Material Suplementar. A Figura 3 ilustra a diferença energética entre a jX-ésima estrutura (X = butanoato de metila ou ‡) e a sua conformação mais estável, bem como as barreiras energeticas listadas na Tabela 1. Para distinguirmos os diferentes confôrmeros encontrados, utilizaremos a nomenclatura definida pela União Internacional de Química Pura e Aplicada (International Union of Pure and Applied Chemistry - IUPAC), com recomendações adicionais de Papajak et al.58
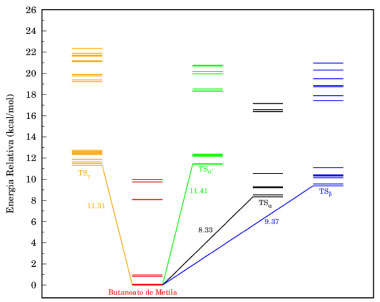 Figura 3. Diferenças de energia entre os jX -ésimos confôrmeros e suas estruturas mais estáveis. As alturas de barreira clássica também são ilustradas.
Para o butanoato de metila (BM), a estrutura mais estável é o BM-G+T-T-, com ângulos diedros no intervalo de [69º, 195º, 182º]. A diferença energética entre BM-G+T-T- e todos os outros 7 rotâmeros é inferior a 10 kcal mol-1. Em um intervalo de 1 kcal mol-1, encontramos 4 estruturas para o butanoato de metila, todas com o diedro Φ3 em aproximadamente 180º. A partir do quinto rotâmero em energia, BM-TTC, todas estruturas possuem o diedro Φ3 em aproximadamente a 0º, com energias relativas em um intervalo de 8-10 kcal mol-1. O aumento energético substancial entre BM-TG-T e BM-TTC, representado na Figura 3, está associado a elevada barreira de rotação em Φ3 e, a instabilidade dos conformeros gerados a partir das demais rotações. Analisando as estruturas do estado de transição TSα', observamos que os rotâmeros TSα'-G-T+T+g- e TSα'-G-T+T+g+, com ângulos diedros no intervalo de [291º,166º,177º,280º] e [291º,167º,179º,80º], respectivamente, apresentam a mesma estabilidade, podendo ser considerados como degenerados. A mudança do ângulo em Φ3, após a estrutura TSα'-G-T+CG-, também geram confôrmeros altamente energéticos, contidos em uma janela energética entre 6 e 10 kcal mol-1. As abstrações de hidrogênio nos carbonos α e β levam a dois estados de transição distinguíveis (R e S). Neste caso, o TSα (S) possui enantiômeros em TSα (R), que não podem se interconverter por rotação interna. As geometrias com um determinado grupo de ângulos em TSα (S), por exemplo, correspondem as geometrias com 360- Φi em TSα (R), em que i indica o número da torção. Para a reação (Rα), a estrutura do estado de transição de mais baixa energia, TSα-G+T-T-, apresenta ângulos diedros no intervalo [72º,195º,183º], enquanto que a estrutura, TSα-G-C+T+, 2,213 kcal mol-1 menos estável que a primeira, apresenta os ângulos no intervalo [286º,14º,179º]. Todos rotâmeros acima de TSα-G-C+T+ apresentam energias superiores a 8 kcal mol-1, também associadas à rotação de 180º em Φ3. Para o estado de transição β, uma diferença de 8,053 kcal mol-1 separa o confôrmero mais estável TSβ-G+T-T- [72º,186º,181º] de TSβ-G+T-C+ [73º,184º,01º]. A partir desta última, todas estruturas apresentam Φ3 em aproximadamente 0º. As três conformações mais energéticas para o TSβ são, TSβ-G-a-C- (10,318 kcal mol-1), TSβ-T-g-C- (10,916 kcal mol-1) e TSβ-G-a+C+ (11,598 kcal mol-1). Na busca conformacional para o estado de transição γ, foram encontradas 22 estruturas, sendo TSγ-G-T+T+G- [292º,170º,179º,299º] a de maior estabilidade. Por se tratar de uma abstração em um grupo metílico, foram localizadas duas estruturas totalmente simétricas, TSγ-TTTT e TSγ-TTCT, 0,564 e 8,589 kcal mol-1 menos estáveis que TSγ-G-T+T+G-, respectivamente. As funções de partição MS-T(C) e SS-HO, usadas para o cálculo dos fatores das equações (2) e (3), estão listados na Tabela 1S do Material Suplementar. A contribuição das múltiplas estruturas e da anarmonicidade torcional para o butanoato de metila e estados de transição, calculados pela equação (3), estão ilustrados na Figura 4. Por terem uma maior quantidade de conformações, os estados de transição α' e γ apresentaram os maiores valores para FMS-T(C),X, comparativamente aos demais pontos estacionários. A 1000 K, por exemplo, este fator é 18,51 e 22,12 para TSα' e TSγ, respectivamente. Nesta mesma temperatura, este parâmetro apresentou os valores de 8,41, 5,94 e 6,41 para BM, TSα, TSβ. É possivel observar também que um valor máximo para FMS-T(C),X é atingido entre 500 e 1200 K. A seguir, este fator decai, uma vez que a densidade de estados da função de partição anarmônica diminuem, enquanto que as harmônicas permanecem constantes.
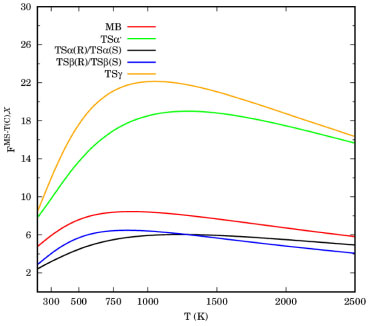 Figura 4. Fator multiestrutural torcional anarmônico (FMS-T(C),X) para o butanoato de metila e estados de transição
Os efeitos multiestruturais e de anarmonicidade torcional nas reações de abstração de hidrogênio do butanoato de metila (Rα'-Rγ), obtidos pela equação (2), estão ilustrados na Figura 5. Como podemos observar, a grande diferença entre as quantidades de conformações do butanoato de metila e dos estados de transição TSα' e TSγ, produzem fatores FMS-T(C) maiores, comparativamente aos demais. Na faixa de temperatura de combustão (1000-1500 K), as reações em (Rα') e (Rγ) são aumentadas por um fator de aproximadamente 2,20 e 2,60, respectivamente. Para as reações de abstração nos carbonos metilênicos, os fatores multiestruturais torcionais anarmônicos são inferiores a unidade, uma vez que FMS-T(C),X para TSα e TSβ, são inferiores ao do butanoato de metila, em toda a faixa de temperaturas.
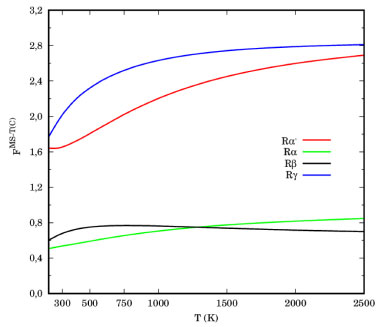 Figura 5. Fator multiestrutural torcional anarmônico para as reações (Rα')-(Rγ)
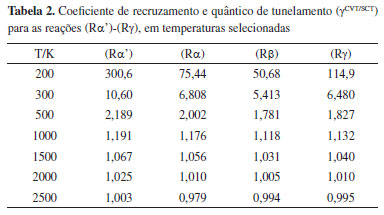
Os caminhos de energia mínima e o potencial adiabático, obtidos apenas para os confôrmeros mais estáveis dos estados de transição, estão ilustrados nas Figuras 1S e 2S do Material Suplementar. Os valores para o coeficiente de recruzamento e quântico de tunelamento, γCVT/SCT, para as reações (Rα')-(Rg) são listados na Tabela 2. Para uma compreensão detalhada da magnitude deste fator, as Tabelas 2S e 3S do Material Suplementar listam os coeficientes de transmissão semiclássico (κCVT/SCT) e os dos efeitos de recruzamento (ΓCVT), em toda faixa de temperaturas deste estudo. A baixas temperaturas, o efeito quântico de tunelamento desempenha um papel importante nas constantes de velocidade térmica, pois dominam a magnitude de γCVT/SCT. A 300 K, por exemplo, os valores de γCVT/SCT são 10,60 (Rα'), 6,808 (Rα), 5,413 (Rβ) e 6,480 (Rγ). Em um potencial unidimensional, a frequência imaginária está diretamente relacionada com a curvatura do potencial no estado de transição, ou seja, uma frequência maior se correlaciona com um potencial mais estreito. Como consequência, espera-se maiores contribuições de tunelamento. Para os estados de transição mais estáveis das abstrações nos carbonos α' e α, a frequência imaginária no nível de teoria deste estudo foram 1431,8i cm-1 e 1443,6i cm-1, respectivamente. Para os confôrmeros mais estáveis de TSβ e TSγ, esses valores foram 1280,9i cm-1 e 1270,3i cm-1, respectivamente. Note que TSα' apresenta frequência vibracional menor comparativamente ao TS. É importante destacar, que o modelo empregado neste trabalho é multidimensional, neste caso a magnitude da frequência imaginária não está diretamente relacionada aos coeficientes de transmissão. Com o aumento da temperatura, os coeficientes γCVT/SCT se aproximam da unidade, devido aos efeitos moderados de recruzamento e a pouca influência do tunelamento quântico.
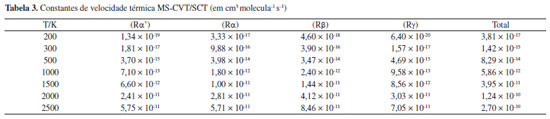
As constantes de velocidade SS-TST para as reações (Rα')-(Rg) na faixa de temperatura de 200-2500 K, calculadas pela equação (5), estão listadas na Tabela 4S do Material Suplementar. As constantes de velocidade MS-CVT/SCT, podem ser facilmente obtidas combinando os dados da Figura 5, Tabela 2 e, as constantes de velocidade SS-TST. Os valores das constantes MS-CVT/SCT são listados na Tabela 3, juntamente com a constante total. Esses resultados foram ajustados pela expressão proposta por Zheng e Trhular:59 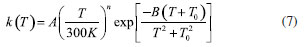
em que A, n, B e T0 são os parâmetros do ajuste. Essa equação fornece bons resultados para reações que apresentam considerável tunelamento quântico, especialmente a baixas temperaturas. A Tabela 3 mostra todos estes parâmetros, para as reações. As energias de ativação (Ea), em uma ampla faixa de temperatura, podem ser obtidas por: 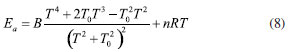 em que R é a constante dos gases ideias. As energias de ativação para as reações de abstração do butanoato de metila, estão disponível na Tabela 5S do Material Suplementar. Analisado os resultados obtidos nesta etapa, nota-se claramente uma dependência da energia de ativação com a temperatura. Numa faixa de 200 a 2500 K, os valores de Ea variaram de 4,58 a 19,98 kcal mol-1 e 3,19 a 16,42 kcal mol-1 para as abstrações em α' e α. Para as reações (Rβ) e (Rγ) a energia de ativação variou de 4,40 a 16,28 kcal mol-1 e 5,35 a 19,12 kcal mol-1, no mesmo intervalo de temperaturas. Complementando esta análise, a Figura 6 apresenta um gráfico de Arrhenius com as estimativas MS-CVT/SCT deste estudo, juntamente com resultados teóricos e experimentais anteriores. Na faixa de temperatura de combustão, nossos resultados subestimam as constantes de velocidades de Gaïl et al.23 e Dooley et al.24 A 1250 K por exemplo a razão kGail/kMS-CVT/SCT e kDooley/kMS-CVT/SCT, são 1,72 e 2,77, respectivamente. Os desvios observados entre os resultados deste estudo e, de ambos os mecanismos, podem estar associados ao fato dos autores terem utilizados propriedades de sistemas análogos para a obtenção dos parâmetrros cinéticos, como destacado por Liu et al.31 Nossos valores MS-CVT/SCT mostraram estar em excelente concordância com os determinados experimentalmente por Hakka et al.25 A 1250 e 1700 K, os resultados encontrados pelos autores são apenas 1,24 e 0,92 vezes os reportados neste estudo. A baixas temperaturas, as constantes apresentadas por Huynh e Violi.27 são superestimadas em aproximadamente dez vezes. Comparativamente aos dados cinéticos obtidos teoricamente por Zhang et al.30 e Liu et al.,31 nossas constantes de velocidade mostram estar em boa concordância. Entretanto, é importante ressaltar que esta coincidência deve estar associada a um possivel cancelamento de erros. Estes autores determinaram seus dados cinéticos utilizando a teoria do estado de transição convencional e modelos unidimensionais para a estimativa das torções internas. Além disso, suas barreiras de reação, mostraram-se superiores às obtidas neste trabalho no nível de teoria MPWB1K/6-31+G(d,p), validadas pela com a aproximação DLPNO-CCSD(T)-F12/CBSD-Q. Observamos também uma divergência entre os dados desta investigação e os apresentados por Akih-Kumgeh e Bergthorson.32 Neste estudo os autores empregaram aproximações de estrutura eletrônica e de cinética química menos elaboradas, tais como CBS-QB3 e teoria do estado de transição convencional. Por fim, destaca-se a boa concordância das constantes de velocidade MS-CVT/SCT obtidas em nossa investigação com as de Meng et al.,33 utilizando o método das correlações de Bell-Evans-Polanyi (BEP) e, barreiras energéticas estimadas no nível de teoria B3LYP/6-311++G(d,p)//QCISD(T)/CBS. Como podemos observar através da análise da Figura 6, nossos valores são superestimados a baixas temperaturas e subestimados a altas temperaturas, comparativamente os dados reportados por esses autores.

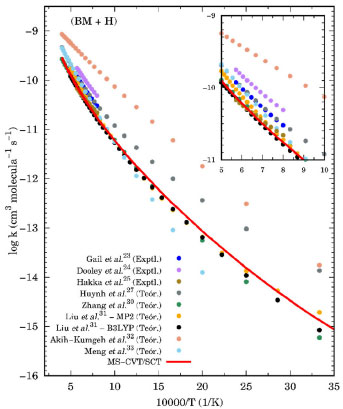 Figura 6. Gráfico de Arrhenius mostrando as constantes de velocidade térmica totais obtidas neste estudo. Resultados teóricos e experimentais anteriores também são ilustrados
Por fim, a Figura 7 ilustra a distribuição percentual dos produtos em função da temperatura, obtidas a partir das razões das constantes de velocidade individuais pela constante de velocidade total. A baixas temperaturas, os produtos da reação (Rα) mostram-se predominante aos demais. A 300 K, por exemplo, a proporção para (Rα'):(Rα):(Rβ):(Rg) é aproximadamente 1:70:28:1. A medida que a temperatura aumenta, a contribuição de outras reações torna-se importante, especialmente a de (Rβ). Acima de 500 K, observa-se uma inversão na formação dos radicais CH3CH2CHCOOCH3 e CH3CHCH2COOCH3. Analisando as funções de partição, na Tabela 1S, notamos que as funções de partição (mesmo que harmônicas) crescem mais rapidamente para TSβ, comparativamente a TSα. Em temperaturas superiores a 1500 K a contribuição dos canais (Rα') e (Rg) tornam-se relevantes. Nossos resultados corroboram os dados obtidos de Huynh e Violi,27 que apontam para uma maior contribuição da reação (Rβ), entre 700-1500 K.
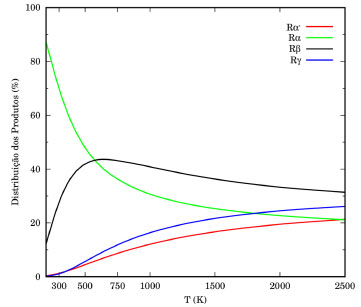 Figura 7. Distribuição percentual dos produtos das (Rα'), (Rα), (Rβ) e (Rγ)
CONCLUSÕES Neste trabalho, empregamos a teoria variacional canônica multiestrutural com tunelamento multidimensional de pequena curvatura (MS-CVT/SCT), para calcular as constantes de velocidade para as reações de abstração de hidrogênio do butanoato de metila pelo radical H. O modelo de estrutura eletrônica empregado para análise conformacional e cinética foi validado através de cálculos single point com a aproximação altamente correlacionada DLPNO-CCSD(T)-F12/CBSD-Q. Os desvios das barreiras obtidas no nível de teoria MPWB1K/6-31+G(d,p), comparativamente a aproximação coupled cluster, mostram-se inferiores a 0,6 kcal mol-1. Na busca conformacional, 68 confôrmeros para o butanoato de metila e estados de transição foram encontrados. Esses rotâmeros foram utilizados para a obtenção de uma função de partição rovibracional multiestrutural, dentro do modelo multiestrutural acoplado, MS-T(C). Efeitos multiestruturais e também associados à anarmonicidade torcional, foram estimados e, seus impactos na estimativa das constantes de velocidade determinados. Estes efeitos mostram-se relevantes para as reações (Rα') e (Rg), em que um maior número de conformações foram observados. As constantes de velocidade deste estudo, mostraram estar em boa concordância com resultados de modelos de combustão descritos previamente. Uma avaliação sobre a distribuição percentual dos produtos, em função da temperatura, indicou a predominância de formação dos radicais gerados partir da reação (Rα). Acima de 500 K a contribuição dos demais canais tornam-se relevantes. Os resultados desta análise mostraram boa concordância o modelo de combustão de Huynh e Violi.
MATERIAL SUPLEMENTAR Coordenadas cartesianas e frequências vibracionais harmônicas. Funções de partição MS-T(C) e SS-HO, caminho mínimo de energia, potencial adiabático, coeficientes variacionais e de tunelamento individuais. Constantes de velocidade térmica TST e energias de ativação. Todos estes dados estão disponíveis em http://quimicanova.sbq.org.br, na forma de arquivo PDF, com acesso livre.
AGRADECIMENTOS T. V. A. agradece a CAPES pelo apoio acadêmico (Código do Financiamento 001), e J. L. N agradece ao CNPq pela bolsa de doutorado.
REFERÊNCIAS 1. Drumm, F. C.; Gerhardt, A. E.; Fernandes, G. D.; Chagas, P.; Sucolotti, M. S.; Kemerich, P. D. D. C.; Revista Eletrônica em Gestão, Educação e Tecnologia Ambiental 2014, 18, 66. [Crossref] 2. Machado, G.; Alves, R.; Senhuk, A.; Fregonesi, B.; Zagui, G.; Nadal, M.; Sierra, J.; Domingo, J.; Segura-Muñoz, S.; Quim. Nova 2018, 42, 28. [Crossref] 3. Nicolussi, F. H.; dos Santos, A. P. M.; André, S. C. S.; Veiga, T. B.; Takayanagui, A. M. M.; Rev. Saude Publica 2014, 48, 326. [Crossref] 4. Amancio, C. T.; Nascimento, L. F.; Sao Paulo Med. J. 2014, 132, 353. [Crossref] 5. Gupta, K. K.; Rehman, A.; Sarviya, R. M.; Renewable Sustainable Energy Rev. 2010, 14, 2946. [Crossref] 6. Meneghetti, S. M. P.; Meneghetti, M. R.; Brito, Y. C.; Rev. Virtual Quim. 2013, 5, 63. [Crossref] 7. Hoekman, S. K.; Robbins, C.; Fuel Process. Technol. 2012, 96, 237. [Crossref] 8. Sahoo, P. K.; Das, L. M.; Babu, M. K. G.; Naik, S. N.; Fuel 2007, 86, 448. [Crossref] 9. Qi, D. H.; Geng, L. M.; Chen, H.; Bian, Y. Z. H.; Liu, J.; Ren, X. C. H.; Renewable Energy 2009, 34, 2706. [Crossref] 10. Koçak, M. S.; Ileri, E.; Utlu, Z.; Energy Fuels 2007, 21, 3622. [Crossref] 11. Tan, T.; Yang, X.; Krauter, C. M.; Ju, Y.; Carter, E. A.; J. Phys. Chem. A 2015, 119, 6377. [Crossref] 12. Tan, T.; Yang, X.; Ju, Y.; Carter, E. A.; Phys. Chem. Chem. Phys. 2016, 18, 4594. [Crossref] 13. Metcalfe, W. K.; Dooley, S.; Curran, H. J.; Simmie, J. M.; El-Nahas, A. M.; Navarro, M. V.; J. Phys. Chem. A 2007, 111, 4001. [Crossref] 14. Lee, S.; Song, S.; Int. J. Hydrogen Energy 2016, 41, 19207. [Crossref] 15. Mendes, J.; Zhou, C.-W.; Curran, H. J.; J. Phys. Chem. A 2014, 118, 4889. [Crossref] 16. Rogers, C. O.; Kaczmarek, D.; Kasper, T.; Labbe, N. J.; Proceedings of the Combustion Institute 2021, 38, 621. [Crossref] 17. Grana, R.; Frassoldati, A.; Cuoci, A.; Faravelli, T.; Ranzi, E.; Energy 2012, 43, 124. [Crossref] 18. Grana, R.; Frassoldati, A.; Saggese, C.; Faravelli, T.; Ranzi, E.; Combust. Flame 2012, 159, 2280. [Crossref] 19. Tao, H.; Lin, K. C.; Combust. Flame 2014, 161, 2270. [Crossref] 20. Fisher, E. M.; Pitz, W. J.; Curran, H. J.; Westbrook, C. K.; Proc. Combust. Inst. 2000, 28, 1579. [Crossref] 21. Dong, X.; Jia, M.; Chang, Y.; Wang, P.; Niu, B.; Energy Fuels 2020, 34, 4882. [Crossref] 22. Curran, H. J.; Gaffuri, P.; Pitz, W. J.; Westbrook, C. K.; Combust. Flame 1998, 114, 149. [Crossref] 23. Gaïl, S.; Thomson, M. J.; Sarathy, S. M.; Syed, S. A.; Dagaut, P.; Diévart, P.; Marchese, A. J.; Dryer, F. L.; Proc. Combust. Inst. 2007, 31, 305. [Crossref] 24. Dooley, S.; Curran, H. J.; Simmie, J. M.; Combust. Flame 2008, 153, 2. [Crossref] 25. Hakka, M. H.; Bennadji, H.; Biet, J.; Yahyaoui, M.; Sirjean, B.; Warth, V.; Coniglio, L.; Herbinet, O.; Glaude, P. A.; Billaud, F.; Battin-Leclerc, F.; Int. J. Chem. Kinet. 2010, 42, 226. [Crossref] 26. Wang, Q.-D.; Wang, X.-J.; Kang, G.-J.; Comput. Theor. Chem. 2014, 1027, 103. [Crossref] 27. Huynh, L. K.; Violi, A.; J. Org. Chem. 2008, 73, 94. [Crossref] 28. Eckart, C.; Phys. Rev. 1930, 35, 1303. [Crossref] 29. Ayala, P. Y.; Schlegel, H. B.; J. Chem. Phys. 1998, 108, 2314. [Crossref] 30. Zhang, L.; Chen, Q.; Zhang, P.; Proc. Combust. Inst. 2015, 35, 481. [Crossref] 31. Liu, W.; Sivaramakrishnan, R.; Davis, M. J.; Som, S.; Longman, D. E.; Lu, T. F.; Proc. Combust. Inst. 2013, 34, 401. [Crossref] 32. Akih-Kumgeh, B.; Bergthorson, J. M.; Combust. Flame 2011, 158, 1037. [Crossref] 33. Meng, Q.; Lin, X.; Zhai, Y.; Zhang, L.; Zhang, P.; Sheng, L.; Combust. Flame 2020, 214, 394. [Crossref] 34. Passos, M. O.; Lins, I. A.; Alves, T. V.; Phys. Chem. Chem. Phys. 2020, 22, 14246. [Crossref] 35. Lins, I. A.; Passos, M. O.; Alves, T. V.; Theor. Chem. Acc. 2020, 139, 85. [Crossref] 36. Nascimento, J. L.; Junior, A. S. L.; Alves, T. V.; J. Phys. Chem. A 2022, 126, 4791. [Crossref] 37. Passos, M. O.; Lins, I. A.; Venâncio, M. F.; Alves, T. V.; Phys. Chem. Chem. Phys. 2021, 23, 25414. [Crossref] 38. Zheng, J.; Truhlar, D. G.; J. Chem. Theory Comput. 2013, 9, 1356. [Crossref] 39. Bao, J. L.; Truhlar, D. G.; Chem. Soc. Rev. 2017, 46, 7548. [Crossref] 40. Yu, T.; Zheng, J.; Truhlar, D. G.; Chem. Sci. 2011, 2, 2199. [Crossref] 41. Hu, W.-P.; Liu, Y.-P.; Truhlar, D. G.; J. Chem. Soc., Faraday Trans. 1994, 90, 1715. [Crossref] 42. Eyring, H.; J. Chem. Phys. 1935, 3, 107. [Crossref] 43. Binkley, J. S.; Pople, J. A.; Hehre, W. J.; J. Am. Chem. Soc. 1980, 102, 939. [Crossref] 44. Zhao, Y.; Truhlar, D. G.; J. Phys. Chem. A 2004, 108, 6908. [Crossref] 45. Hehre, W. J.; Ditchfield, R.; Pople, J. A.; J. Chem. Phys. 1972, 56, 2257. [Crossref] 46. Zhao, Y.; Schultz, N. E.; Truhlar, D. G.; J. Chem. Theory Comput. 2006, 2, 364. [Crossref] 47. Ferro-Costas, D.; Mosquera-Lois, I.; Fernández-Ramos, A.; J. Cheminform. 2021, 13, 100. [Crossref] 48. Ferro-Costas, D.; Fernández-Ramos, A.; Front. Chem. 2020, 8, 16. [Crossref] 49. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Petersson, G. A.; Nakatsuji, H.; Li, X.; Caricato, M.; Marenich, A. v; Bloino, J.; Janesko, B. G.; Gomperts, R.; Mennucci, B.; Hratchian, H. P.; Ortiz, J. v; Izmaylov, A. F.; Sonnenberg, J. L.; Williams-Young, D.; Ding, F.; Lipparini, F.; Egidi, F.; Goings, J.; Peng, B.; Petrone, A.; Henderson, T.; Ranasinghe, D.; Zakrzewski, V. G.; Gao, J.; Rega, N.; Zheng, G.; Liang, W.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Throssell, K.; Montgomery Jr., J. A.; Peralta, J. E.; Ogliaro, F.; Bearpark, M. J.; Heyd, J. J.; Brothers, E. N.; Kudin, K. N.; Staroverov, V. N.; Keith, T. A.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A. P.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Millam, J. M.; Klene, M.; Adamo, C.; Cammi, R.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Farkas, O.; Foresman, J. B.; Fox, D. J.; Gaussian 09; Gaussian, Inc., Wallingford, CT, 2009. 50. Zheng, J.; Mielke, S. L.; Clarkson, K. L.; Truhlar, D. G.; Comput. Phys. Commun. 2012, 183, 1803. [Crossref] 51. Alecu, I. M.; Zheng, J.; Zhao, Y.; Truhlar, D. G.; J. Chem. Theory. Comput. 2010, 6, 2872. [Crossref] 52. Ferro-Costas, D.; Truhlar, D. G.; Fernández-Ramos, A.; Comput. Phys. Commun. 2020, 256, 107457. [Crossref] 53. Page, M.; McIver, J. W.; J. Chem. Phys. 1988, 88, 922. [Crossref] 54. Chuang, Y.-Y.; Truhlar, D. G.; J. Phys. Chem. A 1998, 102, 242. [Crossref] 55. Kumar, A.; Neese, F.; Valeev, E. F.; J. Chem. Phys. 2020, 153, 094105. [Crossref] 56. Neese, F.; WIREs Comput. Mol. Sci. 2022, 12, e1606. [Crossref] 57. Peterson, K. A.; Woon, D. E.; Dunning, T. H.; J. Chem. Phys. 1994, 100, 7410. [Crossref] 58. Papajak, E.; Seal, P.; Xu, X.; Truhlar, D. G.; J. Chem. Phys. 2012, 137, 104314. [Crossref] 59. Zheng, J.; Truhlar, D. G.; Phys. Chem. Chem. Phys. 2010, 12, 7782. [Crossref] |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






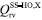 refere-se a função de partição rovibracional calculada para a estrutura mais estável de X, obtida através do produto das funções de partição vibracional e rotacional, dentro das aproximações do oscilador harmônico e do rotor-rígido. é a função de partição multiestrutural, determinada a partir do método multiestrutural acoplado, MS-T(C),38 de acordo com:
refere-se a função de partição rovibracional calculada para a estrutura mais estável de X, obtida através do produto das funções de partição vibracional e rotacional, dentro das aproximações do oscilador harmônico e do rotor-rígido. é a função de partição multiestrutural, determinada a partir do método multiestrutural acoplado, MS-T(C),38 de acordo com: