Revisão
|
|
| Solvatocromismo e as escalas empíricas de polaridade do solvente: uma revisão Solvatochromism and the empirical scales of solvent polarity: a review |
|
Ingrid Maliszewski Paczkowski; Leandra Franciscato Campo*
Departamento de Química Orgânica, Instituto de Química, Universidade Federal do Rio Grande do Sul, 91501-970 Porto Alegre − RS, Brasil Recebido em 22/12/2022 *e-mail: leandra.campo@ufrgs.br The term solvatochromism is used to describe the changes in the optical properties of a dye molecule by influence of the solvent characteristics. Solvatochromic shifts are governed by intermolecular interactions between solute-solvent that can be either electrostatic (non-specific interactions) or chemical (specific interactions). Due to the complexity of these interactions and absence of theoretical models that can explain the specific effects of solvent, different authors have introduced empirical parameters to building more reliable solvent polarity scales. Out of various polarity scales that have arisen from this need, those based on the effect of solvent polarity on the electronic excitation energy of indicator organic dyes are the most prevalent in literature. The use of empirical equations that correlate bathochromic (positive solvatochromism) and hypsochromic (negative solvatochromism) shifts of optical spectra of organic molecules with the polarity of solvent has become essential for understanding solute-solvent interactions. This review article presents main mathematical equations that use linear correlations between macroscopic and/or microscopic polarity functions of solvent with spectroscopic parameters of solute (dye) in construction of solvent polarity scales. In addition, main mathematical models that use solvatochromic shifts to estimate the dipole moment of ground and excited state are discussed. INTRODUÇÃO O termo cromismo é usado para descrever o fenômeno de mudança de cor reversível de uma substância e quando a alteração de cor é provocada pelo solvente denomina-se de solvatocromismo.1-5 De acordo com a IUPAC, solvatocromismo é definido como "uma mudança (pronunciada) na posição e, algumas vezes, na intensidade das bandas de absorção e emissão provocada pela alteração da polaridade do meio. Solvatocromismo negativo (positivo) corresponde a um deslocamento hipsocrômico (batocrômico) com o aumento da polaridade do meio".6 Os efeitos batocrômico (informalmente referido como deslocamento para o vermelho) e hipsocrômico (informalmente referido como deslocamento para o azul) são efeitos opostos. Quando uma banda espectral sofre deslocamento para frequência mais baixa (maior comprimento de onda) devido a uma mudança do solvente diz-se que ouve um deslocamento batocrômico. Por outro lado, no deslocamento hipsocrômico a banda espectral se desloca para frequência mais alta (menor comprimento de onda). O solvatocromismo pode ser explicado pela solvatação diferencial dos estados fundamental e excitado de uma molécula ao absorver luz, mediado por forças intermoleculares específicas e não-específicas que atuam entre uma molécula (soluto) e o solvente.7 Isto significa que, experimentalmente, são observados deslocamentos nas bandas de absorção e/ou emissão de fluorescência, além de mudanças na forma como alargamento ou estreitamento de banda em função da variação do solvente.8-10 Além de alterações espectrais provocadas pela influência do solvente, uma molécula solvatocrômica pode responder também a mudanças na polaridade do microambiente e viscosidade do meio característicos de biomacromoléculas em solução. Isto porque qualquer alteração na organização de uma biomolécula como proteínas, lipídeos ou ácidos nucléicos, resulta na modificação do microambiente local, o que pode ser monitorado por uma sonda solvatocrômica. Por este motivo, diversas sondas solvatocrômicas tem sido utilizadas para monitorar processos biológicos em escala molecular como por exemplo para monitorar domínios de fase de lipídeos em membranas celulares, assimetria de membrana e apoptose, interações proteína-proteína, proteína-membrana, proteína-DNA, etc.11,12 Neste sentido, Taki e colaboradores13 utilizaram uma sonda fluorescente que apresenta solvatocromismo negativo para visualizar a distribuição intracelular de metabólitos de ácidos graxos. Liu e colaboradores14 mostraram que proteínas mudam de polaridade dependendo do estado de agregação a partir de uma sonda solvatocrômica responsiva à viscosidade do meio. Hocek e colaboradores15 sintetizaram nucleosídeos fluorescentes usados como substratos para obter DNA marcado que não fluoresce em solução tampão mas emite luz azul ao interagir com proteínas. De fato, o ambiente químico (polaridade, viscosidade, temperatura, etc.) desempenha um papel fundamental tanto no curso de reações químicas como nos espectros de absorção e emissão molecular, sendo o solvatocromismo um campo de investigação que se ocupa em elucidar as complexas interações intermoleculares entre um soluto e o meio que o circunda. Neste sentido, esforços foram realizados a fim de expressar a polaridade do solvente em função de propriedades macroscópicas tais como constante dielétrica, momento de dipolo, índice de refração, entre outros, porém com algumas falhas, uma vez que o poder de solvatação de um solvente não pode ser medido através de uma única propriedade.8-16 A falta de expressões teóricas contundentes para o cálculo das interações soluto-solvente a partir de parâmetros macroscópicos, bem como a simplificação ao definir a polaridade do solvente em termos de características físicas simples, levou ao desenvolvimento de modelos solvatocrômicos comparativos que utilizam corantes orgânicos indicadores de polaridade do meio (sondas solvatocrômicas).10-18 A primeira escala de polaridade do solvente a utilizar uma sonda solvatocrômica foi proposta por Kosower em 1958 (Z-scale) e baseou-se no deslocamento do comprimento de onda do máximo de absorção do iodeto de 1-etil-4-metoxicarbonilpiridinio em solventes de diferente polaridades.17 Três anos mais tarde, Dimroth, Reichardt e colaboradores utilizaram como sonda solvatocrômica corantes da família das betaínas e propuseram uma nova escala de polaridade do solvente que ficou conhecida como ET(30).6,9 Na metade dos anos 1970, Kamlet e Taft introduziram parâmetros microscópicos do solvente (polarizabilidade, dipolaridade, acidez e basicidade) a fim de minimizar as simplificações dos modelos antecessores.19 No que se refere ao solvatocromismo em moléculas orgânicas fluorescentes (fluorocromos), as interações soluto-solvente são diferentes quando o fluorocromo está no estado eletrônico fundamental e no estado eletrônico excitado, o que se deve a redistribuição de cargas nos dois estados após a absorção de luz.20 Por este motivo, diferentes métodos solvatocrômicos foram desenvolvidos a fim de estimar os valores dos momentos de dipolo nos estados fundamental e excitado, destacando-se entre eles os de Lippert-Mataga, Bakshiev e Kawski-Chamma-Viallet.21,22 As espectroscopias de absorção na região do ultravioleta-visível (UV-Vis) e emissão de fluorescência são as ferramentas analíticas básicas para a realização de estudos solvatocrômicos. As mudanças espectrais que moléculas solvatocrômicas sofrem ao interagir com diferentes solventes são comumente utilizadas como parâmetro tanto para aplicação como novas sondas/sensores como para uma investigação fotofísica mais aprofundada da molécula de interesse. Na prática, nos deparamos com ambientes químicos de natureza complexa como polímeros orgânicos e inorgânicos, materiais híbridos orgânico-inorgânico, proteínas, enzimas, DNA, vírus, polissacarídeos, membranas celulares, entre outros tantos. Por conseguinte, utiliza-se como pressuposto básico para a compreensão de sistemas mais complexos as interações que ocorrem entre soluto (sonda) e solvente, desde que o comportamento espectroscópico do soluto se mostre dependente da natureza do solvente. Com a vasta gama de solventes comercialmente disponíveis, pode-se simular ambientes que sejam mais ou menos ácido, básico, doador/aceptor de ligação de hidrogênio, alterar a viscosidade e a polaridade do meio, etc. Estes parâmetros são então extrapolados na tentativa de elucidar o comportamento espectral da sonda em ambientes químicos complexos, a fim de auxiliar na compreensão de diversos sistemas físico-químico orgânicos tanto em solução como no estado sólido. Assim, as aplicações dos métodos solvatocrômicos incluem, mas não se limitam, a investigação do comportamento solvatocrômico de novas sondas,23-30 na caracterização físico-química de medicamentos,21 na compreensão do metabolismo lipídico em organismos vivos,31 entre outras. Este artigo de revisão tem por objetivo apresentar de forma concisa os modelos matemáticos solvatocrômicos mais recorrentes na literatura. Em todos os modelos, as equações matemáticas se baseiam em correlações lineares entre as funções de polaridade macroscópicas (índice de refração, constante dielétrica, etc.) e/ou microscópicas (polarizabilidade, dipolaridade, etc.) do solvente com os parâmetros espectroscópicos do soluto (absorção e/ou emissão). Para tanto, fazem uso de equações matemáticas que aportam dados espectroscópicos empíricos de UV-Vis e emissão de fluorescência do soluto em análise.
ESCALAS DE POLARIDADE DO SOLVENTE BASEADAS EM CORANTES SOLVATOCRÔMICOS Dimroth-Reichardt A compreensão do efeito local de solvatação é muito importante na química uma vez que tem relação direta com a cinética das reações térmicas de fase líquida e com a estabilização de íons formados em processos de transferência de elétrons. Em geral, as correlações que melhor descrevem o efeito local de solvatação são obtidas a partir da observação do deslocamento do comprimento de onda do máximo de absorção de corantes solvatocrômicos.32,33 Dentre as escalas de polaridade do solvente existentes, destaca-se a escala ET(30) que foi proposta por Dimroth e Reichardt em 1963.34-36 O corante de Reichardt, o 2,6-difenil-4-(2,4,6-trifenilpiridínio)fenolato (Figura 1), foi a base para a construção da popular escala de polaridade ET(30), que se baseia no solvatocromismo negativo desta molécula que ocorre devido às ligações de hidrogênio com solventes como n-butanol, n-propanol, etanol e metanol. A banda de absorção do corante de Reichardt sofre deslocamento hipsocrômico quando se troca o solvente de éter difenílico para água, por exemplo. O parâmetro de polaridade do solvente ET(30) se baseia na energia de transição para os maiores comprimentos de onda da banda de absorção solvatocrômica do corante de Reichardt. Devido ao grande deslocamento da banda de absorção solvacrômica, os valores de ET(30) fornecem uma excelente e sensível caracterização da polaridade do solvente, sendo que quanto maior o valor de ET(30), maior é a polaridade do solvente.32
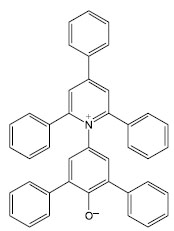 Figura 1. Estrutura do corante de Reichardt utilizado como padrão de polaridade32
Uma solução do corante de Reichardt engloba toda a região visível do espectro eletromagnético, possibilitando uma estimativa visual da polaridade do meio.32,37 A estabilização da betaína da Figura 1 no solvente ocorre devido a mudança de um estado fundamental bastante polarizado para um estado excitado menos polarizado. As principais características desse corante são: (i) altamente polarizável, ideal para registrar as interações do tipo dipolo-dipolo e dipolo-dipolo induzido; (ii) sistema de elétrons π polarizado, adequado para registrar interações de dispersão; (iii) o átomo de oxigênio exibe um forte centro básico doador de par de elétrons, ideal para interações com ácidos de Bronsted (ligações de hidrogênio) e ácidos de Lewis (receptores de par de elétrons).17 Assim, a absorção da transferência de carga intramolecular do corante de Reichardt depende da força de solvatação eletrofílica do solvente como por exemplo, da sua habilidade de doar ligações de hidrogênio e da sua capacidade como doador e receptor de pares de elétrons.32,38,39 Os valores de ET(30) são definidos como as energias de transição eletrônica do corante de Reichardt expressas em kilocalorias por mol (kcal mol-1) à temperatura ambiente (298 K) e pressão de 1 atmosfera.36 Os valores de ET(30) podem ser estimados a partir da Equação 1, em que o número 28.591 é proveniente da multiplicação entre a constante de Planck, velocidade da luz, constante de Avogadro e o número de onda da banda de absorção máxima do corante de Reichardt. A posição da banda de absorção da solução desse corante no espectro do UV-Vis depende da polaridade do solvente (solvatocromismo), da temperatura da solução (termocromismo), da pressão externa aplicada na solução (piezocromismo) e da natureza e concentração de eletrólitos (halocromismo).40 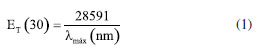 onde λmáx é o valor do comprimento de onda do máximo de absorção da banda de transferência de carga do corante. A escala recebeu o nome ET(30) porque no trabalho original Dimroth, Reichardt e colaboradores sintetizaram uma série de piridínio-N-fenolatos e o corante, que mais tarde receberia o nome de corante de Reichardt, foi o composto de número 30 na sequência montada pelos autores. Os valores de ET(30) foram determinados para mais de 450 solventes e inúmeras misturas binárias.41 A escala de polaridade de Dimroth-Reichardt fornece uma indicação da dipolaridade do solvente bem como da capacidade do solvente de fazer ligações de hidrogênio. Uma limitação desta escala refere-se à suscetibilidade de protonação do corante betaína em meio moderadamente ácido com a consequente protonação do ânion fenolato (Figura 1). Por este motivo, outros corantes têm sido propostos como sondas solvatocrômicas como as estruturas derivadas do N-metilpiridínio-vinil fenolato entre outros corantes zwitteriônicos e também corantes inorgânicos.17 Para evitar o fato de a escala estar em unidades que não condizem com o Sistema Internacional de Unidades, Reichardt propôs em 1983 a escala de polaridade normalizada, conhecida como escala ETN.36 Considerando que a água é o solvente mais polar da escala (ETN = 1) e tetrametilsilano (TMS) o mais apolar (ETN = 0), a escala ETN foi desenvolvida utilizando a Equação 2. 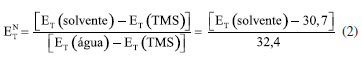 Kamlet-Taft A escala de polaridade de Reichardt possui algumas limitações, tendo em vista que leva em consideração apenas um parâmetro para quantificar a polaridade do meio.41 Em meados dos anos 70, Kamlet e Taft foram os primeiros a desenvolver uma escala de polaridade do solvente com três parâmetros independentes e empíricos, a saber: (i) acidez (relacionada à capacidade do solvente em doar ligações de hidrogênio); (ii) basicidade (relacionada à capacidade do solvente receber ligações de hidrogênio) e (iii) polaridade/polarizabilidade (quantifica a capacidade do solvente de estabilizar uma carga do soluto) (Equação 3).42 A escala de Kamlet-Taft (KAT) baseia-se nos deslocamentos dos máximos de frequência das transições π→π* de diversos corantes induzidos pelo solvente.43-45 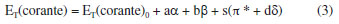 O termo ET(corante) da Equação 3 representa o resultado de um processo químico dependente do solvente e ET(corante)0 é o processo de referência em um meio apolar. Os coeficientes independentes "a", "b", "s" e "d" estão associados ao grau de suscetibilidade do soluto com relação ao solvente/meio; acidez (α); basicidade (β) e dipolaridade/polarizabilidade (π*). O parâmetro (δ) corrige a equação para solventes halogenados e aromáticos.17 Outro conceito de energia de solvatação linear que possui multiparâmetros e vem sendo bastante empregado é aquele representado pela Equação 4, que engloba os parâmetros de Catalán, ou seja, acidez (SA), basicidade (SB), dipolaridade (SdP) e polarizabilidade (SP) do meio. Os coeficientes "a", "b", "c" e "d" são independentes do solvente.46 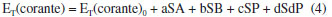 O parâmetro de lipofilicidade do meio de Hansch (log P) também pode ser adicionado às Equações 3 e 4, sendo log P definido como o logaritmo da razão das concentrações de uma molécula isolada do solvente em um sistema saturado de 1-octanol e água a 25 °C.47 O coeficiente P define a sensibilidade da sonda junto ao solvente no que se refere à lipofilicidade do meio. Devido à complexidade dos efeitos do solvente, essa propriedade pode ajudar a refletir bem o conjunto das interações intermoleculares em meios condensados.48 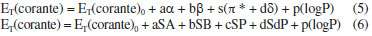 As equações de KAT e Catalán são bem estabelecidas e amplamente utilizadas, já que muitos processos químicos dependentes do solvente podem ser explicados pelas Equações 3 e 4. Entretanto, a metodologia para a determinação dos parâmetros de KAT (α, β e π*) para solventes orgânicos não é tão simples de se rastrear em detalhes para cada solvente, tendo sido corrigidos com mais frequência ao longo do tempo por diferentes autores.45,49-51 Além da determinação dos parâmetros KAT pelo método solvatocrômico, encontramos também aproximações baseadas em métodos teóricos para prever os parâmetros α, β e π*. Sherwood e colaboradores utilizaram uma abordagem in silico para estimar os parâmetros KAT.52 Neste trabalho, os autores aplicaram a teoria COSMO-RS (conductor like screening model for real solvents) na investigação do equilíbrio de tautomerização de compostos 1,3-dicarbonílicos em diferentes solventes. Lethesh e Venkatraman examinaram a eficácia da teoria COSMO-RS em uma coleção de líquidos iônicos.53
DETERMINAÇÃO DO MOMENTO DE DIPOLO DOS ESTADOS FUNDAMENTAL E EXCITADO PELO MÉTODO DO DESLOCAMENTO SOLVATOCRÔMICO Os momentos de dipolo dos estados fundamental e excitado podem ser obtidos teoricamente a partir de cálculos ab initio que descrevem modelos de solvatação contínua como o PCM (polarizable continuum model) e o SMD (solvation model density) que utilizam métodos químico-quânticos do tipo DFT (density functional theory) no programa Gaussian.54 Entretanto, a determinação experimental do momento de dipolo com base no solvatocromismo corresponde ao método mais difundido na literatura, sendo os mais utilizados aqueles que foram desenvolvidos por Lippert-Mataga, Bakshiev e Kawski-Chamma-Viallet.55 Nestes modelos, os momentos de dipolo são estimados a partir de correlações lineares dos máximos de absorção e emissão de fluorescência (deslocamento de Stokes) com relação às funções de polaridade do solvente f(ε,n), onde ε = constante dielétrica e n é o índice de refração do solvente. Estes modelos baseiam-se na teoria de Onsager, a qual assume que o soluto ocupa o centro de uma cavidade esférica, homogênea e isotrópica e que o momento de dipolo dos estados fundamental e excitado são paralelos entre si.56 Modelo de Onsager O modelo de Onsager é o modelo contínuo mais simples, também chamado de campo de reação auto consistente. Nesse modelo o soluto é colocado dentro de uma cavidade esférica de raio a. O solvente (meio envolvente) é descrito como homogêneo e polarizável de constante dielétrica ε.56-58 O momento de dipolo do soluto é disposto como um indutor de momento de dipolo no meio circundante. A polarização resultante do meio leva a uma redistribuição eletrônica do soluto gerando uma polarização mútua que pode ser tratada de forma auto consistente. Esse problema é tratado desta forma na maioria dos programas de modelagem molecular disponíveis como, por exemplo, o Gaussian.56 É importante verificar a proporcionalidade direta do campo de reação () com o momento de dipolo molecular () e a proporcionalidade inversa do campo de reação com a terceira potência do raio da cavidade (a). Isso ocorre porque no modelo de Onsager o campo de reação é descrito como:  A relação existente na Equação 5 sugere que o aumento da cavidade onde a carga está inserida diminui o campo de reação e, com isso, diminui a solvatação. De outro modo, a energia livre de solvatação quase não é afetada com o aumento da constante dielétrica. A falha existente no modelo se deve a interações específicas soluto-solvente, não descrita em modelos contínuos. O problema pode ser contornado adicionando especificidades à interação soluto-solvente ou incluindo solventes explícitos.59 O raio apropriado para a cavidade que envolve o soluto é calculado em fase gasosa. O volume geralmente é definido como o volume dentro de um contorno de densidade de 0,001 elétrons/bohr3. O volume é calculado por uma integração Monte-Carlo, com uma precisão de dois algarismos significativos e, apesar disso, basta para estimar um raio para uso com o modelo de campo de reação de Onsager para o solvente.56 O cálculo do volume de van der Waals pode ser estimado teoricamente utilizando as contribuições atômicas e de ligação das moléculas. O volume de van der Waals pode ser calculado a partir da Equação 8:60  onde NB é o número de ligações, RA é o número de anéis aromáticos e RNA é o número de anéis não aromáticos. Se o número total de átomos na molécula é N, então o número de ligações presentes NB pode ser calculado usando a relação:  o somatório de todas as contribuições atômicas é calculado multiplicando a quantidade do átomo presente na molécula por seu volume de van der Waals tabelado e somando tudo ao final. Considerando que o raio de Onsager "a" (em Å) e assumindo um modelo esférico, então o volume de van der Waals pode ser considerado:  assim, é obtido o valor para o raio de Onsager (a) sem a necessidade de utilizar programas de modelagem molecular. Lippert-Mataga A equação de Lippert-Mataga descreve o deslocamento de Stokes através da variação do momento de dipolo do soluto e de características do solvente como a constante dielétrica (ε) e o índice de refração (n).55 Segundo esse modelo, o soluto é considerado um dipolo em um meio homogêneo e de constante dielétrica uniforme, sem a presença de interações específicas soluto-solvente.9 A diferença de energia entre o estado fundamental e o estado excitado é afetada pelas interações entre o solvente e o fluoróforo. Em uma primeira aproximação, essa diferença de energia está associada ao índice de refração e a constante dielétrica do solvente. O índice de refração está relacionado à movimentação rápida dos elétrons nas moléculas do solvente, já a constante dielétrica é dependente da movimentação eletrônica e molecular do solvente. A dedução da equação de Lippert-Mataga ocorre a partir da definição de energia de um dipolo (Edipolo) num meio dielétrico homogêneo, sendo dada por:  onde R é campo induzido pelo dipolo no meio,55 sendo este paralelo e oposto a direção do dipolo e proporcional ao módulo do momento dipolar,  f é a polarizabilidade do solvente e a é o raio da cavidade do fluoróforo. A polarizabilidade do solvente é definida como um resultado da movimentação de seus elétrons e da movimentação dos momentos dipolares de suas moléculas, que ocorre através da movimentação dos átomos. Cada componente tem um tempo de vida diferente, sendo que a polarizabilidade é muito rápida e depende do índice de refração, dando origem a polarizabilidade de alta frequência f(n),  A orientação dos dipolos depende da constante dielétrica do solvente, sendo calculada através da polarizabilidade de baixa frequência f(ε), dada por:  a diferença entre as Equações 13 e 14 fornece: 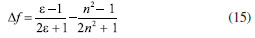 onde Δf é chamado de polarizabilidade de orientação. A interação entre o fluoróforo e o solvente pode ser descrita pelos momentos de dipolo dos estados fundamental (μf) e excitado (μe) e os campos induzidos. Os campos induzidos podem ser divididos entre aqueles que são causados pela movimentação eletrônica ( e ) e aqueles devido a orientação molecular do solvente ( e ). Observando o equilíbrio entre os momentos de dipolo do estado fundamental e excitado esses campos são:7 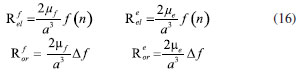 Assim, é possível calcular a energia do estado fundamental e do estado excitado fora do equilíbrio: 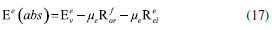 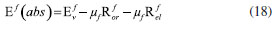 onde e são as energias do fluoróforo sem o efeito do solvente. Usando a fórmula ΔE = hcv e subtraindo a Equação 17 da Equação 14, temos: 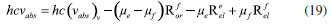 em que o primeiro termo do lado direito é a diferença de energia sem o efeito do solvente. Podemos fazer as mesmas considerações para a emissão e, por analogia: 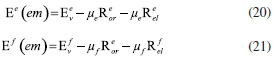 assim, a energia de emissão é dada por: 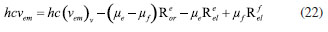 Subtraindo a Equação 22 da Equação 19 e usando a Equação 16, obtêm-se a equação de Lippert-Mataga, em que a diferença (vabs - vem) aparece como função da polarizabilidade de orientação (Δf): 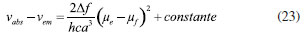 Através da Equação 23, também é possível estimar a variação do momento de dipolo entre os estados fundamental e excitado (μe - μf). Porém, esta medida não é muito precisa, o que pode ser explicado por dois fatores: (1) a imprecisão na medida do deslocamento de Stokes (vabs - vem), uma vez que as bandas de absorção e emissão podem ser muito largas e dificultar a visualização dos comprimentos de onda dos máximos; e (2) imprecisão na definição de raio da cavidade do soluto usado na Equação 23, pois a definição de um raio para uma cavidade esférica é complicada devido à dimensão das moléculas.61 Bakshiev e Kawski-Chamma-Viallet O deslocamento das bandas de absorção e emissão de uma molécula solvatocrômica pode ser usado para a determinação dos momentos de dipolo do estado fundamental e excitado.62 Em geral, o momento de dipolo pode ser estimado usando três equações independentes, sendo elas: a equação de Lippert-Mataga (Equação 24),61 a equação de Bakhshiev (Equação 25) e a equação de Kawski-Chamma-Viallet (Equação 26).63,64 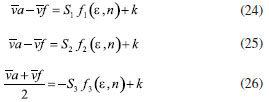 onde e são os números de onda dos máximos de absorção e emissão em cm-1, k é a constante, f1(ε,n) o parâmetro de polaridade do solvente de Lippert-Mataga (Equação 27), f2(ε,n) o parâmetro de polaridade do solvente de Bakshiev (Equação 28), f3(ε,n) o parâmetro de polaridade do solvente Kawski-Chamma-Viallet (Equação 29). Os parâmetros de polaridade do solvente são calculados usando o índice de refração (n) e a constante dielétrica (ε) de solventes reportados na literatura.65 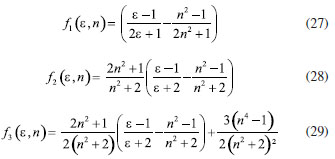 Um gráfico de versus f1(ε,n) sendo linear fornece as inclinações S1 e S2 e um gráfico de versus f3(ε,n) fornece a inclinação S3. As inclinações são dadas por: 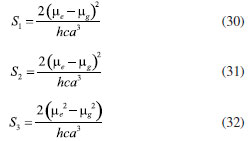 S1, S2 e S3 são os valores das inclinações das retas que, substituídos nas Equações 33 e 34, fornecem os valores dos momentos de dipolo do estado fundamental (μf) e excitado (μe).66,67 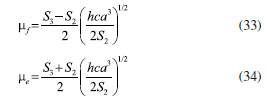 A razão entre μe e μf pode ser expressa como:  obtida pela divisão da Equação 34 pela Equação 33, onde S3 > S2. O método solvatocrômico tem sido utilizado para estimar os valores de μf e μe por diversos grupos de pesquisa para uma grande variedade de compostos orgânicos.68 Na maioria dos trabalhos publicados, os autores aplicam as três equações, Lippert-Mataga, Bakshiev e KCV e comparam os valores encontrados de μf e μe a partir das diferentes abordagens. No entanto, cabe ressaltar que estas equações consideram o soluto em uma cavidade esférica independente do solvente, que a geometria da molécula não muda, e que os momentos dipolares do estado fundamental e excitado são paralelos entre si.21,66 Estas aproximações implicam, em muitos casos, que o deslocamento de Stokes do fluoróforo () não tenha um comportamento linear com relação a função de polaridade do solvente.68 Por exemplo, as sondas biológicas Prodan e Laurdan não obedecem a equação de Lippert-Mataga porque apresentam uma geometria que está mais para um esferoide do que uma esfera.69 Além desta limitação, a equação de Lippert-Mataga também não funciona quando ocorrem interações específicas soluto-solvente como ligações de hidrogênio, presença de grupos aceptores/doadores de pares de elétrons, entre outras. Assim, expressões matemáticas mais aperfeiçoadas foram surgindo ao longo do tempo como os formalismos de Marcus, McRae, Scholte e Abe.3,67,69,70 O modelo proposto por Abe se destaca pois leva em conta a diferença de orientação dos momentos dipolares dos estados fundamental e excitado.71 Mais recentemente, Schmitt e colaboradores utilizaram métodos termocrômicos associados com o volume da cavidade do solvente na determinação dos momentos dipolares.72 Os autores afirmam que ao utilizar o termocromismo no lugar do solvatocromismo e o volume da cavidade do solvente medido experimentalmente lograram um método mais preciso para a determinação dos momentos dipolares.
CONSIDERAÇÕES FINAIS O solvatocromismo tem sido uma ferramenta muito útil na elucidação do comportamento de ambientes químicos de natureza complexa como por exemplo, polímeros orgânicos e inorgânicos, materiais híbridos orgânico-inorgânico, proteínas, enzimas, DNA, vírus, polissacarídeos, membranas celulares, vesículas, micelas, micelas reversas, entre outros tantos. Assim, podemos utilizar como pressuposto básico para a compreensão de sistemas complexos as interações que ocorrem entre uma sonda (soluto) e o solvente, desde que o comportamento espectroscópico da sonda se mostre dependente da natureza do solvente. Com a vasta gama de solventes disponíveis, podemos simular ambientes que sejam mais ou menos ácido, básico, doador/aceptor de ligação de hidrogênio, bem como alterar a polaridade do meio. Estes parâmetros são então extrapolados na tentativa de elucidar o comportamento espectral da sonda em ambientes químicos complexos, a fim de auxiliar na compreensão de diferentes sistemas físico-químico tanto em solução quanto no estado sólido. A ideia de escrever este artigo de revisão surgiu da necessidade de entendermos qual modelo matemático é o mais apropriado para confrontar com os resultados experimentais quando se tem uma nova sonda, bem como para termos uma estimativa dos momentos dipolares dos estados fundamental e excitado da sonda, uma vez que na literatura nos deparamos com diferentes modelos.
AGRADECIMENTOS As autoras agradecem ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) e à Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) pelo suporte financeiro, ao Instituto de Química e ao Programa de Pós-Graduação em Química da UFRGS.
REFERÊNCIAS 1. Kiprianov, A. I.; Russ. Chem. Rev. 1960, 29, 618. [ Crossref] 2. Rauf, M. A.; Hisaindee, S.; J. Mol. Struct. 2013, 1042, 45. [ Crossref] 3. Mallik, T.; Banerjee, D.; Indian J. Chem. 2022, 61, 472. [ Link] acessado em julho 2023 4. Marini, A.; Muñoz-Losa, A.; Biancardi, A.; Mennucci, B.; J. Phys. Chem. B 2010, 114, 17128. [ Crossref] 5. Karmakar, N. K.; Pandey, S.; Pandey, R. K.; Shukla, S. S.; Appl. Spectrosc. Rev. 2021, 56, 513. [ Crossref] 6. Verhoeven, J. W.; Pure Appl. Chem. 1996, 68, 2223. [ Crossref] 7. Reichardt, C.; Solvents and Solvent Effects in Organic Chemistry, 3rd ed.; Wiley-VCH Verlag: Weinheim, 2003. 8. Lakowicz, J. R.; Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, 2006. 9. Spange, S.; Mayerhöfer, T. G.; ChemPhysChem 2022, 23, e202200100. [ Crossref] 10. de Melo, C. E. A.; Domínguez, M.; Rezende, M. C.; Machado, V. G.; Dyes Pigm. 2021, 184, 108757. [ Crossref] 11. Klymchenko, A. S.; Acc. Chem. Res. 2017, 50, 366. [ Crossref] 12. Loving, G. S.; Sainlos, M.; Imperiali, B.; Trends Biotechnol. 2010, 28, 73. [ Crossref] 13. Kajiwara, K.; Osaki, H.; Greßies, S.; Kuwata, K.; Kim, J. H.; Gensch, T.; Sato, Y.; Glorius, F.; Yamaguchi, S.; Taki, M.; Nat. Commun. 2022, 13, 2533. [ Crossref] 14. Wang, W.; Zeng, L.; Jin, W.; Chen, X.; Shen, D.; Huang, Y.; Wang, M.; Bai, Y.; Lyu, H.; Dong, X.; Gao, Z.; Wang, L.; Liu, X.; Liu, Y.; Angew. Chem. 2021, 60, 25865. [ Crossref] 15. Matyasovský, J.; Tack, L.; Palágyi, A.; Kuba, M.; Pohl, R.; Kraus, T.; Gallardo, P. G.; Hocek, M.; Org. Biomol. Chem. 2021, 19, 9966. [ Crossref] 16. Malik, P. K.; Tripathy, M.; Patel, S.; ChemistrySelect 2020, 5, 3551. [ Crossref] 17. Nigam, S.; Rutan, S.; Appl. Spectrosc. 2001, 55, 362A. [ Crossref] 18. Ayachit, N. H.; Rani, G. N.; Phys. Chem. Liq. 2007, 45, 41. [ Crossref] 19. Bozkurt, E.; Gul, H. I.; Mete, E.; J. Photochem. Photobiol., A 2018, 352, 35. [ Crossref] 20. Kawski, A.; Zeitschrift für Naturforschung A 2002, 57a, 255. [ Crossref] 21. Divac, V. M.; Sakić, D.; Weitner, T.; Gabričević, M.; Spectrochim. Acta, Part A 2019, 212, 356. [ Crossref] 22. Pandey, N.; Tewari, N.; Pant, S.; Mehata, M. S.; Spectrochim. Acta, Part A 2022, 267, 120498. [ Crossref] 23. Nagy, M.; Fiser, B.; Szőri, M.; Vanyorek, L.; Viskolcz, B.; Int. J. Mol. Sci. 2022, 23, 1315. [ Crossref] 24. Adamoczky, A.; Nagy, T.; Fehér, P. P.; Pardi-Tóth, V.; Kuki, A.; Nagy, L.; Zsuga, M.; Kéki, S.; Int. J. Mol. Sci. 2022, 23, 7250. [ Crossref] 25. Dorohoi, D. O.; Dimitriu, D. G.; Dulcescu-Oprea, M. M.; Morosanu, A. C.; Puica-Melniciuc, N.; Ardelean, E.; Gritco-Todirascu, A.; Cheptea, C.; Molecules 2021, 26, 3910. [ Crossref] 26. Montoya, A. A.; Trout, G. M.; Williams, B. W.; Basu, S.; J. Lumin. 2020, 228, 117619. [ Crossref] 27. Anandhan, K.; Cerón, M.; Perumal, V.; Ceballos, P.; Gordillo-Guerra, P.; Pérez-Gutiérrez, E.; Castillo, A. E.; Thamotharan, S.; Percino, M. J.; RSC Adv. 2019, 9, 12085. [ Crossref] 28. Torii, Y.; Niioka, Y.; Syundo, K.; Kashiwagi, D.; Iimori, T.; J. Lumin. 2022, 241, 118503. [ Crossref] 29. Paczkowski, I. M.; Coelho, F. L.; Campo, L. F.; J. Mol. Liq. 2020, 319, 114277. [ Crossref] 30. Patil, M. K.; Kotresh, M. G.; Tilakraj, T. S.; Inamdar, S. R.; Eur. J. Chem. 2022, 13, 8. [ Crossref] 31. Kajiwara, K.; Osaki, H.; Greßies, S.; Kuwata, K.; Kim, J. H.; Gensch, T.; Sato, Y.; Glorius, F.; Yamaguchi, S.; Taki, M.; Nat. Commun. 2022, 13, 2533. [ Crossref] 32. Reichardt, C.; Chem. Rev. 1994, 94, 2319. [ Crossref] 33. Weigang, O. E.; Wild, D. D.; J. Chem. Phys. 1962, 37, 1180. [ Crossref] 34. Eyler, G. N.; Cañizo, A. I.; Nesprias, R. K.; Quim. Nova 2002, 25, 364. [ Crossref] 35. Mannrich, K.; Silva, M.; Nandi, L. G.; Nicoleti, C. R.; Machado, V. G.; Quim. Nova 2014, 37, 1707. [ Crossref] 36. Zimmermann-Dimer, L. M.; Machado, V. G.; Quim. Nova 2008, 31, 2134. [ Crossref] 37. Reichardt, C.; Harbusch-Gornert, E.; Liebigs Ann. Chem. 1983, 5, 721. [ Crossref] 38. Harris, D. C.; Bertolucci, M. D.; Symmetry and Spectroscopy: An Introduction to Vibrational and Electronic Spectroscopy, 1st ed.; Dover Publications: New York, 1989. 39. Kamlet, M. J.; Abboud, J. L. M.; Taft, R. W. Em Progress in Physical Organic Chemistry ; Taft, R. W., ed.; John Wiley & Sons: New Jersey, 1981. [ Crossref] 40. Reichardt, C.; Chem. Soc. Rev. 1992, 21, 147. [ Crossref] 41. Machado, V. G.; Stock, R. I.; Reichardt, C.; Chem. Rev. 2014, 114, 10429. [ Crossref] 42. Kamlet, M. J.; Abboud, J. L. M.; Abraham, M. H.; Taft, R. W.; J. Org. Chem. 1983, 48, 2877. [ Crossref] 43. Sousa, C.; Quim. Nova 2008, 31, 1392. [ Crossref] 44. Varela, H.; Huguenin, F.; Malta, M.; Torresi, R. M.; Quim. Nova 2002, 25, 287. [ Crossref] 45. Seoud, O. A.; Quim. Nova 2010, 33, 2187. [ Crossref] 46. Catalán, J.; J. Phys. Chem. B 2009, 113, 5951. [ Crossref] 47. Leo, A.; Hansch, C.; Elkins, D.; Chem. Rev. 1971, 71, 525. [ Crossref] 48. de Melo, C. E. A.; Nandi, L. G.; Domínguez, M.; Rezende, M. C.; Machado, V. G.; J. Phys. Org. Chem. 2015, 28, 250. [ Crossref] 49. Weiß, N.; Schmidt, C. H.; Thielemann, G.; Heid, E.; Schröder, C.; Spange, S.; Phys. Chem. Chem. Phys. 2021, 23, 1616. [ Crossref] 50. Spange, S.; Weiß, N.; Schmidt, C. H.; Schreiter, K.; Chem.: Methods 2021, 1, 42. [ Crossref] 51. Pires, P. A. R.; El Seoud, O.; Machado, V. G.; de Jesus, J. C.; de Melo, C. E. A.; Buske, J. L. O.; J. Chem. Eng. Data 2019, 64, 2213. [ Crossref] 52. Sherwood, J.; Granelli, J.; McElroy, C. R.; Clark, J. H.; Molecules 2019, 24, 2209. [ Crossref] 53. Venkatraman, V.; Lethesh, K. C.; Front. Chem. 2019, 7, 605. [ Crossref] 54. Berrahma, N. B. B.; Springborg, M.; Berrahma, C. A. B.; Sekkal-Rahal, M.; Comput. Theor. Chem. 2018, 1126, 44. [ Crossref] 55. Lippert, V. E.; Zeitschrift für Naturforschung A 1955, 10a, 541. [ Crossref] 56. Onsager, L.; J. Am. Chem. Soc. 1934, 58, 1486. [ Crossref] 57. Oliveira, H. P. M.; Machulek Junior, A.; Legendre, A. O.; Gehlen, M. H.; Quim. Nova 2003, 26, 564. [ Crossref] 58. Correra, T. C.; Frank, A. C.; Quim. Nova 2011, 34, 346. [ Crossref] 59. Pliego, J. R.; Quim. Nova 2006, 29, 535. [ Crossref] 60. Mukhopadhyay, A.; Maka, V. K.; Moorthy, J. N.; Phys. Chem. Chem. Phys. 2017, 19, 4758. [ Crossref] 61. Weber, G.; Farris, F. J.; Biochemistry 1979, 18, 3075. [ Crossref] 62. Kumari, R.; Varghese, A.; George, L.; J. Fluoresc. 2017, 27, 151. [ Crossref] 63. Biradar, D. S.; Siddlingeshwar, B.; Hanagodimath, S. M.; J. Mol. Struct. 2008, 875, 108. [ Crossref] 64. Muddapur, G. V.; Koppal, V.; Patil, N. R.; Melavanki, R. M.; AIP Conf. Proc. 2016, 1728, 020373. [ Crossref] 65. Sadigh, M. K.; Zakerhamidi, M. S.; Shamkhali, A. N.; Babaei, E.; J. Photochem. Photobiol., A 2017, 348, 188. [ Crossref] 66. Akshaya, K. B.; Varghese, A.; Sudhakar, Y. N.; Lobo, P. L.; George, L.; J. Fluoresc. 2017, 27, 1909. [ Crossref] 67. Patil, S.; Desai, V. R.; Basanagouda, M. M.; Hunagund, S. M.; Tuwar, S. M.; Sidarai, A. H.; J. Fluoresc. 2020, 30, 741. [ Crossref] 68. Schmitt, M.; Meerts, L. Em Frontiers and Advances in Molecular Spectroscopy; Laane, J., ed.; Elsevier: Amsterdam, 2018, cap. 5. [ Crossref] 69. Vequi-Suplicy, C. C.; Coutinho, K.; Lamy, M. T.; Biophys. Rev. 2014, 6, 63. [ Crossref] 70. Kirk, W.; J. Phys. Chem. A 2008, 112, 13609. [ Crossref] 71. Abe, T.; Iweibo, I.; Bull. Chem. Soc. Jpn. 1985, 58, 3415. [ Crossref] 72. Lindic, M. M.; Zajonz, M.; Hebestreit, M. L.; Schneider, M.; Meerts, W. L.; Schmitt, M.; MethodsX 2020, 7, 1. [ Crossref] |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access





