Nota Técnica
| Development of a coulometer at the National Metrology Institute of Colombia: determining the amount of substance content of potassium hydrogen phthalate |
|
Jessica Smith-OsorioI; Andrés CastilloII; Henry Torres-QuezadaII; Andrea P. Sandoval-RojasI; Jesús ÁgredaI,*
I. Departamento de Química, Universidad Nacional de Colombia, 111321 Bogotá, Colombia Recebido em: 09/06/2023 *e-mail: jagreda@unal.edu.co Coulometry is a well-established technique for certified reference materials (CRM). However, commercial coulometers are currently expensive and utilize outdated software. The National Metrology Institute of Colombia (INMC) has developed a cheaper and modular coulometer with powerful software capable of controlling the instrument, and acquiring pH, the potential difference between generator electrodes, and the electrical current at any stage of the coulometric titration. The results obtained from this new coulometer align well with the novel method for calculating the amount of substance content of potassium hydrogen phthalate (KHP). This method involves the experimental data fitting with the theoretical titration curve TC(NLR), also developed by the INMC. TC(NLR) replaces the traditional empirical W-function (eWf), which has no chemical basis and does not account for CO2 as an impurity. The KHP content of the CRM KHP 84L from NIST was measured using the developed coulometer, resulting in 4.9069 ± 0.0090 mol kg-1 with a bias of 0.21% for the eWf, and a more accurate result of 4.8983 ± 0.0047 mol kg-1 with a bias of 0.041% for the TC(NLR). The challenges during the development of the coulometer, particularly in terms of instrumentation, as well as their impact on uncertainty, are also discussed. INTRODUCTION Coulometry at constant current, known as coulometric titration, is a technique with great potential in National Metrology Institutes. It allows for quantifying the amount of substance content directly in the International System of Units (SI) for several standards essential in industrial, academic, and research measurements.1-4 Coulometry was officially recognized as a potential primary method by the Consultative Committee for the amount of substance content (CCQM) in 1995.5-7 The coulometric technique directly relates the applied charge (Q) in Coulombs (C) to an electrochemical system with the amount of substance content(v) in mol kg-1of the target analyte by Faraday's law:8 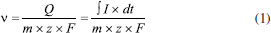 In Equation 1, I represents the electrical current in Amperes (A), t is the duration of the current flow in seconds (s), z is the number of electrons exchanged in the reaction Initially, coulometry has been implemented by some National Metrology Institutes (NMIs) for the quantification of pure substances, such as potassium hydrogen phthalate (KHP),10 as well as other acidimetric standards.11-13 Coulometric titration involves the measurement of physical quantities such as time, mass, potential difference, and electrical resistance. As in any experimental technique, a thorough understanding of its physical and chemical principles is necessary to minimize the impact of variables that could affect the quality of results.11,14 The previously mentioned quantities must be accurately measured, recorded, and analyzed during the coulometric experiment to obtain reliable substance content results. This process is complex because it requires several instruments to obtain the necessary data. Moreover, when the requirements involve a National Metrology Institute, and the production of certified reference materials, the data quality must be as good as possible. Hence, the control and data acquisition software must be well designed, user-friendly, and adaptable to user requirements. The National Metrology Institute of Colombia (INMC) is implementing coulometry as a primary method for certifying KHP as reference material, using its self-built coulometric system. The KHP reference material is required by different institutions, including industries, clinics, and academia, as it ensures their measurements are traceable to SI units. During this process, the INMC has developed a novel mathematical model called "the theoretical titration curve - nonlinear regression, TC(NLR)" to calculate the amount of substance content of KHP based on the data obtained from coulometric titration. This model replaces the conventional empirical W-function (eWf), which has no theoretical chemical support and fails to account for the inevitable CO2 impurity during the KHP coulometric titration. Instead, the TC(NLR) model is grounded in chemical theory and allows the direct determination of KHP content without calculating the endpoint time, eliminating the uncertainty from the endpoint time estimation.15 It is important to note that the accuracy of the nonlinear regression in the model depends on the number of data points used. Consequently, the INMC sought to obtain more data than what could be achieved with a commercial coulometer. Then, a new coulometer was developed, with user-friendly and powerful software to handle and process the KHP coulometric titration data. The data generated by this coulometer aligns well with the previously established TC(NLR). The advantages and limitations of the new INMC coulometric system are discussed in this work.
EXPERIMENTAL SECTION Instrumentation The coulometric system developed in the INMC comprises the instruments shown in Figure 1. A photograph of the coulometer is available in the supplementary material. Although there are no new parts than those in the usual coulometers, it is important to describe them in detail to establish the configuration and then to highlight, in a clear context, how the software was designed and how it works.
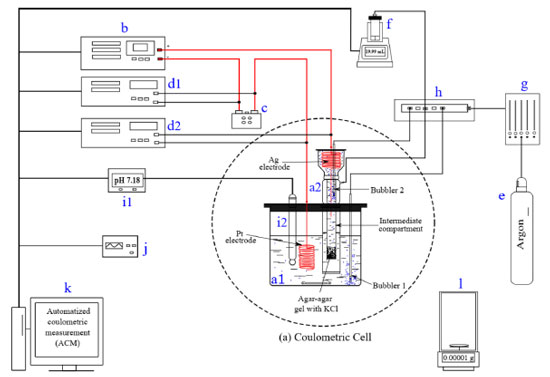 Figure 1. Coulometric constant current measurement system built in the INMC. (a) Coulometric cell, (a1) main compartment, (a2) auxiliar compartment; (b) constant current source; (c) standard resistor; (d1) multimeter 1, (d2) multimeter 2; (e) argon cylinder; (f) burette; (g) pressure regulator; (h) valves unit; (i1) pH-meter, (i2) pH electrode; (j) frequency counter; (k) computer; (l) analytical balance
The coulometric cell (dashed line circle in Figure 1) is composed of a main compartment, the cathode (a1), and the auxiliary compartment, the anode (a2). Both compartments are isolated by an intermediate compartment filled with agar-agar (2.5% w/v) saturated with KCl 1 mol per kilogram of solution, abbreviated as mol kgsoln-1. Separating these compartments diminishes the contamination of the cathode with the anode products and vice versa, preventing the diffusion of the analyte to the auxiliary compartment (anode). The anode consists of a silver electrode, an Ag wire spiral (100 × 3 mm), > 99.9% pure, and the cathode is a platinum (Pt) wire spiral (800 × 1 mm), > 99.95% pure. Pulses of constant current pass through the cathode and the anode using a constant current source Keithley 2200-60-2. The pulses are freely controlled by the experimenter. The current is measured with a 1 Ω standard resistor SRL-1 IET, and a multimeter Keithley 2002. For informative purposes, an additional multimeter Keithley 2700 is used to measure the potential difference between the Pt and Ag electrodes during the KHP coulometric titration. The time is measured using the computer's clock and certified with a calibrated frequency counter Agilent 53220A. A gas system is required to bubble argon (99.999%) to displace oxygen and carbon dioxide from the solution in the coulometric cell. This system is connected to a 20.000 mL burette, Titronic® 500 from SI Analytics, and connected to the coulometric cell by two bubblers at the main and intermediate compartments. The burette maintains the liquid level constant to avoid circuit opening during the measurement. The gas flow is controlled by a pressure regulator with a limit pressure of 100 kPa; the unit valves open and close accordingly to the experimental stage. The electrochemical reaction is monitored using a pH meter, MetrOhm 781 pH/Ion Meter, and a pH electrode, MetrOhm 6.0228.000. The pH electrode is in the cathode compartment. Data are collected on a computer. Sample mass is measured with an analytical balance Mettler Toledo XPE56 with a capacity of 52 g and 0.001 mg of resolution. The coulometric hardware is automatized with a computer program written in LabViewT, a language provided by National Instruments.16 The developed software enables complete control over the current source, multimeters, and burette. Also, it allows the measurement of current in amperes (A), potential difference in volts (V), and time in seconds (s). During the coulometric titration, the current pulses can be adjusted within a range of 2.00 to 200.00 mA, and the time can be set between 3.00000 s to 1200.00000 s. The coulometric system: software commands The electronic devices of the coulometric system are communicated and controlled by the LabViewT coulometric software called Automatized Coulometric Measurement (ACM).17 The description of the commands used to control the instruments is shown in Table 1.
Measurement sequence of the ACM software The ACM software17 consists of two panels: a graphical interface that allows user interaction with the instrument's commands and a functional panel (flux diagram) where the programmer establishes the software algorithm, which can be used to make future modifications. The measurement sequence involves the following steps: (i) configuration of instrument ports for each device, including current source, multimeters, pH meter, frequency counter, and burette; (ii) configuration of the current, potential, time, and volume conditions; (iii) applying constant current pulses to the coulometric cell; (iv) recording the acquired data; (v) ending the experiment; and (vi) saving the recorded data. Coulometric titration: the experiment The experiment is divided into three steps:
The development of the theoretical titration curve - TC(NLR) The theoretical titration curve considers the mass and charge balances at the initial and final coulometric titrations. In the initial titration, the balances depend on the concentration of HCl and the carbonic species present in the solution given as total inorganic carbon, CO2 = CO2(aq) + HCO3- + CO32-, then the reactions involved are:15,18-20 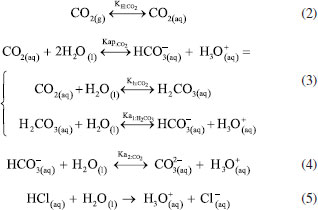 Considering the equilibriums described by Equations 3, 4, and 5, Equation 6 represents the expression as a function of time that allows the construction of the theoretical titration curve (TC) during the initial titration. 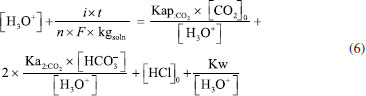 In Equation 6: [H3O+] is the concentration of the hydronium ions in mol kg-1 of solution; [HCl]0 is the initial concentration of hydrochloric acid in mol kg-1 of solution; [CO2]0 is the concentration of the carbonic species in mol kg-1 of solution. [CO2]0 = [CO2](aq) + [HCO3-] + [CO32-]; Kap:CO2 is the apparent dissociation constant of the carbonic acid; Ka2:CO2 is the second dissociation constant of the carbonic acid; KW is the water ionization constant;21 i is the electrical current in amperes (A); t is the time in seconds (s); n is the number of moles of electrons exchanged; F is the Faraday's constant. Since KHP is added to the solution after the initial titration, its equilibrium must be considered in the final titration: 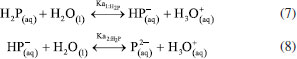 The mass and charge balances established in this stage are obtained by considering the previous equilibriums of KHP, Equations 7 and 8. Therefore, the expression as a function of time for the final titration is given by Equation 9.  In Equation 9: Ka1:H2P is the first dissociation constant of the phthalic acid (H2P); Ka2:H2P is the second dissociation constant of the phthalic acid; [KHP]0 is the total concentration of the phthalic species added to the coulometric cell. Notice that [KHP]0 is the value we are looking for. Equations 6 and 9 are employed to conduct nonlinear regressions that fit the theoretical titration curve to the experimental data. Data treatment Data processing is a decision left to the user because the data provided by the ACM software17 is in plain text format, compatible with free and commercial software. In this study, the data is organized and analyzed using the developed TC(NLR) procedure described elsewhere.15 The TC(NLR) was implemented as an R Script (R version 4.1.2, for Microsoft-WindowsT).22 The R Script utilizes the Levenberg-Marquardt algorithm implemented in the nlsLM R function.23-25 Additionally, for comparison purposes and result verification, the R Script can also perform calculations using the eWf model to fit the experimental data. The mentioned R Script together with some experimental data obtained with the INMC coulometer are available at https://drive.google.com/drive/folders/1LFyulLgu4EdvNPhNJKsNTG8vR1jv_vmt?usp=sharing,26 and also in the supplementary material. Determination of the amount of substance content The R Script performed a nonlinear regression (NLR) of the experimental data obtained from the IT (initial titration) and FT (final titration), using the eWf model,5,26 Equation 10: 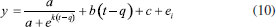 It also uses the TC(NLR) model15 for the IT, Equation 11: 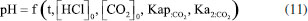 and for the FT, Equation 12: 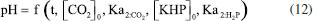 An explicit expression (along with its deduction) for Equations 11 and 12 can be found in reference15 and its supporting information. The eWf model The parameters to be estimated in the nonlinear regression, Equation 10, are a, b, c, k, and q, while ei is the model error. It is worth noting that the parameters in the eWf model do not have any chemical meaning, except for q, which represents the endpoint time in the titration. Therefore, q is the only important parameter, although empirical. Using the q value, the amount of substance content, veWf, is determined with Equation 13: 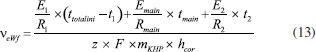 In Equation 13, E1, R1, Emain, Rmain, E2, R2, are the measured potential differences in volts (V) and resistance in ohm (Ω) during the initial, main, and final titrations, respectively; ttotalini is the total time in s of the IT, t1 and t2, are the endpoint times in s in the IT and FT; tmain is the time in s required to titrate the 99.8% of the KHP sample; z, is the number of electrons exchanged in the reaction; F, is the Faraday's constant; mKHP is the KHP sample mass, and hcor is the mass correction factor due to air buoyancy. The TC(NLR) model Equations 11 and 12 uses hydrochloric acid [HCl]0, total inorganic carbon [CO2]0, and KHP concentrations ([KHP]0) in mol kgsoln-1; and Kap:CO2, Ka2:CO2, and Ka2:H2P the dissociation constants of carbonic acid and KHP, respectively. All of them are parameters to be estimated in the NLR. In contrast to the conventional eWf model, all TC(NLR) parameters have chemical meaning and are statistically significant.15 Then, the KHP amount of substance content in mol kg-1, vTC is calculated using Equation 14: 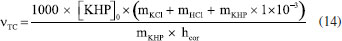 In Equation 14, [KHP]0 corresponds to the concentration in mol kgsoln-1 estimated by the nonlinear regression, mKCl is the mass of the KCl supporting electrolyte in kg, mHCl is the HCl mass added before the IT in kg, mKHP is the mass of the added KHP for the main titration in g, and hcor is the mass correction factor due to air buoyancy. Statistical analysis The normality of the results was evaluated using the Shapiro-Wilk test,27 and the homogeneity of variances was assessed using a Levene test.28 The means were compared using the t-test at the confidence level of α = 0.05.29-31 Uncertainty evaluation Equations 13 and 14 were employed as mathematical models to evaluate the uncertainty following the requirements of the Guide to the Expression of Uncertainty in Measurement.32 The uncertainty was calculated using the R package Propagate.33
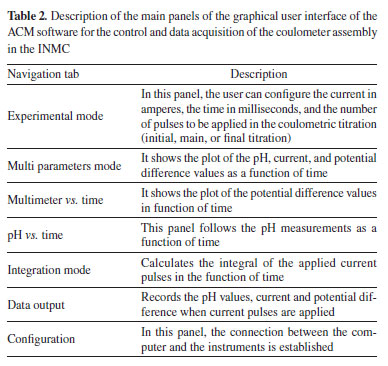
RESULTS AND DISCUSSION The assembly coulometer developed in this work is a homemade device composed of seven replaceable parts. These parts are a current source, a multimeter for voltage measurement across a standard resistor, the standard resistor itself (not an instrument but an essential part), an optional second multimeter for potential difference measurement between Pt and Ag electrodes (or any other potential required by the user), a burette, a frequency counter, and a pH meter. These components work together through the ACM software.17 The seven independent parts in the coulometer design allow users to change each part according to the circumstances. For example, it allows easy replacement of a damaged part. The developed software was designed to control and integrate the six independent instruments into a unified coulometer system. This powerful and modern computer program effectively manages the assembly coulometer and provides users with data in a flexible, convenient, and user-friendly manner. Figure 2 provides an example of the graphical user interface (GUI) tailored explicitly for the coulometric titration, and Table 2 shows the description of each tab within the interface. The GUI offers an easy and visually appealing environment for users to interact with the software and access the functionalities of the coulometer.
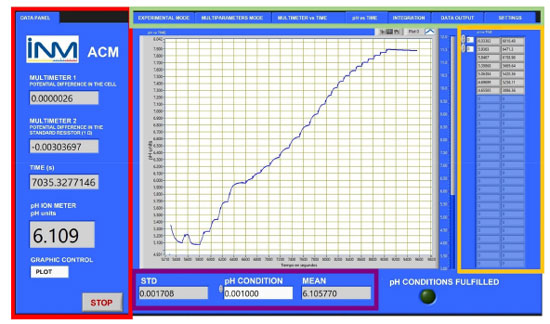 Figure 2. The graphical user interface of the ACM software. The green panel corresponds to the seven navigation tabs: experimental mode, multi parameters mode, multimeter vs. time, pH vs. time, integration mode, data output, and settings. The red panel shows the multimeter 1 (potential difference between Pt and Ag electrodes), multimeter 2 (current measured through a standard resistor 1 Ω), time in seconds, and pH data. The purple panel shows the pH stabilization conditions; a new current pulse will be allowed if the standard deviation is lower than 0.001. The yellow panel shows the pH and the time as soon as the current pulse is applied. The pH vs. time plot is shown in the center of the interface
As evident from Figure 2, the GUI provides real-time data acquisition throughout the entire KHP coulometric titration. Furthermore, the ACM software17 allows the user to set the current, the time, the number of pulses at any experiment stage, and measure the potential between the Pt and Ag electrodes. During the intervals between pulses, the program measures the pH approximately three times per second for a duration of around 30 to 40 s. When the standard deviation of the pH measurements drops below 0.001, a new current pulse is applied according to the user-defined parameters. The number of data points obtained is crucial for accurately calculating the KHP amount of substance content and determining its uncertainty. The capability of the ACM software17 to capture a higher number of data points distinguishes it from other coulometers that rely on the eWf model, which typically record approximately only ten pH values around the endpoint time. Additionally, to achieve better solution homogeneity, the burette fills and empties the internal compartment of the coulometric cell with a setting of 19.9998 mL. The new coulometer was used to obtain the KHP amount of substance content of the KHP NIST certified reference material 84L, vRM = 4.89633 ± 0.00076 mol kg-1 (k = 2.04).34 The nonlinear regression of eWf25 and TC(NLR)15 models were used to compute the KHP amount of substance content, veWf and vTV, respectively. The results are shown in Table 3. Seven replicates were measured for the analysis. In terms of repeatability, the eWf model exhibited a standard deviation (SD) that was 2.875 times greater than that of the TC(NLR) model. Also, the eWf model showed a bias approximately 5.5 times higher than the TC(NLR) value when the percentage of bias (% bias) is computed as 
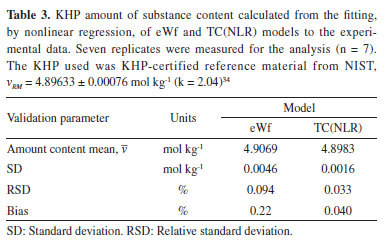
The high SD and, particularly, the high bias observed in the eWf model can be attributed to the solubilization of carbon dioxide into the solution during the coulometric titration.15 The latter fact is unavoidable because the eWf model relies on the endpoint time of the titration, which encompasses the total acidity of the test solution, including the dissolved CO2. On the contrary, the TC(NLR) model directly estimates the KHP amount of substance content from the nonlinear regression without the interference of the dissolved CO2. Another important parameter to evaluate is the uncertainty. As mentioned before, the eWf model determines the endpoint time based on a few points around the end of the coulometric titration. The endpoint time is used to calculate the KHP amount of substance content (veWf) according to Equation 13. The latter equation was used to estimate the standard uncertainty of veWf (called ). Therefore, Table 4 presents the sources of uncertainty from each measurement made during the coulometric titration of KHP that are involved in Equation 13. The uncertainties of Ei, Ri, ttotalini, tmain, and hcor were calculated using the respective calibration certificates of the multimeter (Ei), the standard resistor (Ri), and the frequency counter (ttotalini, and tmain). The uncertainties of t1 and t2 corresponds to the standard error of the estimated parameters in the nonlinear regression of the eWf model.
The final column of Table 4 shows the percentage contribution of each variable to the standard uncertainty, . The most significant source of uncertainty is the potential difference in the main titration (Emain) accounting for 79.58% of the total uncertainty. The high contribution from Emain can be attributed to the non-constant current, which also introduces a spurious signal at the beginning of the pulses, especially during the main titration, as can be seen in Figure 3. Since the parts of the coulometer are independent, it is possible to improve the coulometer performance by changing the actual current source to a more stable one.
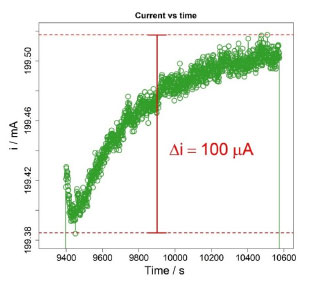 Figure 3. Example of the non-totally constant current with a spurious pulse signal during the main titration of a particular coulometric titration of KHP. δi is the difference between the electrical current's highest and lowest value in this pulse. The current used for computations was the mean value
The second most important contribution to uncertainty is the sample mass, accounting for 18.36%. The sample mass has been identified as one of the main sources of uncertainty in coulometric titrations in previous studies, such as Liandi et al.35 The standard uncertainty 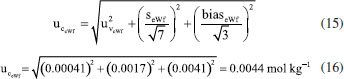 Then, the KHP amount of substance content estimated with the eWf model is 4.9034 ± 0.0090 mol kg-1 (k = 2.04). The relative contributions of the standard uncertainty
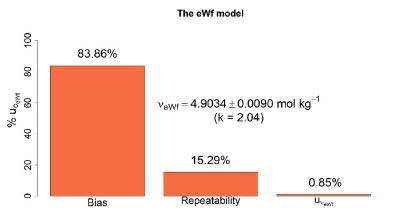 Figure 4. The relative contribution of the standard uncertainty  , bias, and repeatability to the combined uncertainty , bias, and repeatability to the combined uncertainty  for a particular KHP coulometric titration using the eWf model for a particular KHP coulometric titration using the eWf model
In contrast, the repeatability contributes only 15.29% to the combined uncertainty, representing the experimental random errors. The standard uncertainty has a negligible contribution, meaning that the instruments used in assembling the coulometer at the INMC have sufficiently low uncertainties. Therefore, when the eWf model is used to compute the KHP amount of substance content, the main source of uncertainty arises from the bias resulting from the non-selective titration of the KHP, which includes the residual carbon dioxide in the supporting electrolyte. Now, considering the TC(NLR) model, it allows the direct determination of the KHP amount of substance content by calculating the KHP concentration, [KHP]0, as a parameter to estimate during the nonlinear regression. Then, the KHP amount of substance content is calculated using Equation 14. In Table 5, the uncertainty values for each variable in Equation 14 are presented, along with the standard uncertainty
Observe the higher value of standard uncertainty, Now, similar to the eWf model, the combined uncertainty 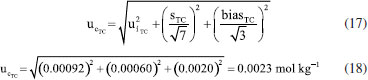 Then, in the sample under study using the TC(NLR) model, the KHP amount of substance content in mol kg-1 is determined to be 4.8999 ± 0.0047 mol kg-1 (k = 2.04). The contributions of the
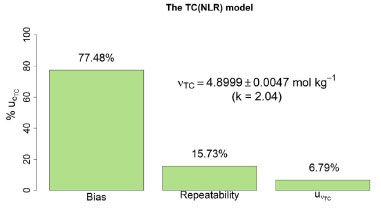 Figure 5. The relative contributions of the standard, repeatability, and bias uncertainties to the combined uncertainty for a particular coulometric titration of KHP when the TC(NLR) model is used to compute the amount of substance content
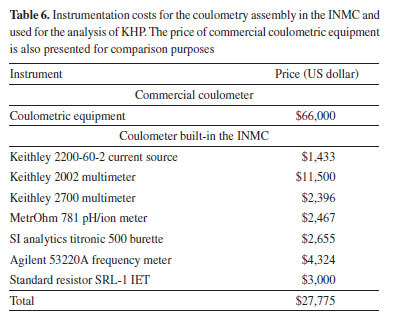
Considering the latter facts, it has been demonstrated that the data obtained from the assembled coulometer can be efficiently used by the TC(NLR) model, surpassing the conventional eWf model. As previously shown, this is mainly because the TC(NLR) model does not rely on calculating the endpoint times for determining the amount of substance content. Moreover, the TC(NLR) model enables the selective determination of the KHP amount of substance content without CO2 interference, reducing the results' uncertainty and bias. Finally, Table 6 shows the costs associated with the individual parts forming the coulometer assembly at the INMC. Remarkably, the total cost for the INMC coulometer is less than half the price of the commercial coulometers used in several NMIs. Therefore, additional investment can be made to upgrade specific components, such as the current source, to improve the performance of the developed coulometer while still maintaining its affordability compared to commercial alternatives.
CONCLUSIONS A coulometric system was developed at the INMC for determining the amount of substance content of KHP. This system utilizes a current source, two multimeters, a standard resistor, an automatic burette, a frequency counter, and a pH potentiometer. These instruments use specialized, user-friendly, powerful, and modern ACM software developed for this work. The ACM software was created using the computer program LabView from National Instruments. The ACM software allows the entire system to be fully controlled, and the data acquisition process becomes user-friendly and flexible. The ACM software allows users to exploit the instrument's capabilities without limitations. The mentioned instrumentation, along with the previously implemented theoretical titration curve - nonlinear regression (for data processing), enables the determination of the amount of substance content of KHP with low bias and acceptable precision and uncertainty. SUPPLEMENTARY MATERIAL The assembly of the coulometric system is shown in Figure 1S. The R Scripts and experimental data for the nonlinear regressions of eWf and TC models are available in a compressed ZIP folder and also in HTML format. Both are available at http://quimicanova.sbq.org.br/, with free access.
ACKNOWLEDGEMENTS The authors thank to Ministerio de Ciencia, Tecnología e Innovación de Colombia for the financing obtained under the project 9932100271370 Plan de Fortalecimiento del Instituto Nacional de Metrología como Centro de Investigación. Project developed by the Universidad Nacional de Colombia and the Instituto Nacional de Metrología de Colombia.
REFERENCES 1. Shlyamina, O. V.; Ziyatdinova, G. K.; Abdullina, S. G.; Budnikov, G. K.; J. Anal. Chem. 2007, 62, 957. [Crossref] 2. Abdullina, S. G.; Petrova, I. K.; Lira, O. A.; Ziyatdinova, G. K.; Budnikov, H. C.; J. Anal. Chem. 2012, 67, 269. [Crossref] 3. Asakai, T.; Murayama, M.; Tanaka, T.; Accredit. Qual. Assur. 2007, 12, 151. [Crossref] 4. Terentiev, G. I.; Sobina, A. V.; Shimolin, A. J.; Zyskin, V. M.; Am. J. Anal. Chem. 2014, 05, 559. [Crossref] 5. Bureau International des poids et Measures; Comité Consultatif Pour La Quantité de Matiére, 1st ed.; BIPM: Pavillon de Breteuil, 1995. 6. Milton, M. J. T.; Quinn, T. J.; Metrologia 2001, 38, 289. [Crossref] 7. JCGM 200:2012; International Vocabulary of Metrology - Basic and General Concepts and Associated Terms (VIM), 2012. [Link] accessed in August 2023 8. Milner, W. C.; Phillips, G.; Coulometry in Analytical Chemistry, 1st ed.; Pergamon Press: Oxford, 1967. 9. NIST, https://physics.nist.gov/cgi-bin/cuu/Value?f, accessed in August 2023. 10. Máriássy, M.; Skutina, A.; Borges, P. P.; Metrologia 2010, 47, 8003. [Crossref] 11. Recknagel, S.; Breitenbach, M.; Pautz, J.; Lück, D.; Anal. Chim. Acta 2007, 599, 256. [Crossref] 12. Asakai, T.; Hioki, A.; Microchem. J. 2013, 108, 24. [Crossref] 13. Yoshimori, T.; Sakaguchi, N.; Talanta 1975, 22, 233. [Crossref] 14. Sobral, S. P.; Borges, P. P.; Serta, I. C.; V Congresso Brasileiro de Metrologia, Bahia, Brasil, 2009. [Link] accessed in August 2023 15. Smith-Osorio, J. L.; Torres-Quezada, H.; Sandoval-Rojas, A. P.; Ágreda, J. A.; ACS Omega 2022, 7, 47851. [Crossref] 16. Vizcaíno, J. R. L.; Sebastiá, J. P.; Labview: Entorno Gráfico de Programación, 2a ed.; Alfa-Omega Grupo Editor: São Paulo, 2011. 17. Castillo-Forero, A. M.; Smith, J.; Ágreda, J.; Sandoval-Rojas, A. P.; Torres-Quezada, H.; Automatized Coulometric Measurement (ACM), Labview software, 2022. 18. Millero, F. J.; Pierrot, D.; Lee, K.; Wanninkhof, R.; Feely, R.; Sabine, C. L.; Key, R. M.; Takahashi, T.; Deep Sea Res., Part I 2002, 49, 1705. [Crossref] 19. Sander, R.; Atmos. Chem. Phys. 2015, 15, 4399. [Crossref] 20. Pines, D.; Ditkovich, J.; Mukra, T.; Miller, Y.; Kiefer, P. M.; Daschakraborty, S.; Hynes, J. T.; Pines, E.; J. Phys. Chem. B 2016, 120, 2440. [Crossref] 21. Brini, E.; Fennell, C. J.; Fernandez-Serra, M.; Hribar-Lee, B.; Luksič, M.; Dill, K. A.; Chem. Rev. 2017, 117, 12385. [Crossref] 22. R Project, https://www.r-project.org/, accessed in August 2023. 23. Elzhov, T. V.; Mullen, K. M.; Spiess, A. N.; Bolker, B.; Minpack.lm: R Interface to the Levenberg-Marquardt Nonlinear Least-Squares Algorithm Found in Minpack, Plus Support for Bounds, 2023. [Link] accessed in August 2023 24. Ritz C.; Carl, J. C.; Nonlinear Regression with R, 1st ed.; Springer: New York, 2008. [Crossref] 25. Villela, R. L. A.; Borges, P. P.; Vyskočil, L.; J. Phys.: Conf. Ser. 2015, 575, 1. [Crossref] 26. Smith, J.; Ágreda, J.; Sandoval-Rojas, A. P.; KHP Amount Content Scripts, R software, 2023. 27. Shapiro, S. S.; Wilk, M. B.; Biometrika 1965, 52, 591. [Crossref] 28. Cowles, J. R.; Daily, S.; Ellison, S. L. R.; Hardcastle, W. A.; Williams, C.; Accredit. Qual. Assur. 2001, 6, 368. [Crossref] 29. King, A. P.; Eckersley, R. J. In Statistics for Biomedical Engineers and Scientists; King, A. P.; Eckersley, R. J., eds.; Academic Press: Cambridge, 2019, p. 119. [Crossref] 30. Miller, J. N.; Miller, J. C.; Statistics and Chemometrics for Analytical Chemistry, 6th ed.; Pearson Education Limited: London, 2010. 31. Mishra, P.; Pandey, C. M.; Singh, U.; Gupta, A.; Sahu, C.; Keshri, A.; Annals of Cardiac Anaesthesia 2019, 22, 67. [Crossref] 32. JCGM 100:2008; Evaluation of Measurement Data - Guide to the Expression of Uncertainty in Measurement, 2008. [Link] accessed in August 2023 33. Spiess, A. N.; Propagate: Propagation of Uncertainty, 2018. [Link] accessed in August 2023 34. National Institute of Standards & Technology; Certificate of Analysis, Standard Reference Material 84L Potassium Hydrogen Phthalate, 2010. [Link] accessed in August 2023 35. Liandi, M.; Bing, W.; Ortiz-Aparicio, J.; Lara, J.; Kozlowski, W.; Dumaska, J.; Pawlina, M.; Pietrzak, A.; Castillo, A.; Torres, H.; España, C.; Cristancho, R.; Peralta, A.; Sobral, S.; Borges, P.; Hatamleh, N.; Puelles, M.; Iglesias, A.; Lozano, H.; Jo, K.; Hwang, E.; Water, J. F.; Mariassy, M.; Shimolin, A.; Sobina, A.; Prokunin, S.; Morozov, I. V.; Dobrovolskiy, V.; Aprelev, A.; Report of the CCQM-K34.2016 Assay of Potassium Hydrogen Phthalate, 2018. [Link] accessed in August 2023 36. Ellison, S. L. R.; Williams, A. In Eurachem/CITAC Guide: Quantifying Uncertainty in Analytical Measurement, 3rd ed.; Ellison, S. L. R.; Williams, A., eds.; 2012. [Link] accessed in August 2023 |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






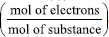 , F is the Faraday's constant (96485.33212 C mol-1),9 and m corresponds to the analyte mass in kilograms (kg).
, F is the Faraday's constant (96485.33212 C mol-1),9 and m corresponds to the analyte mass in kilograms (kg).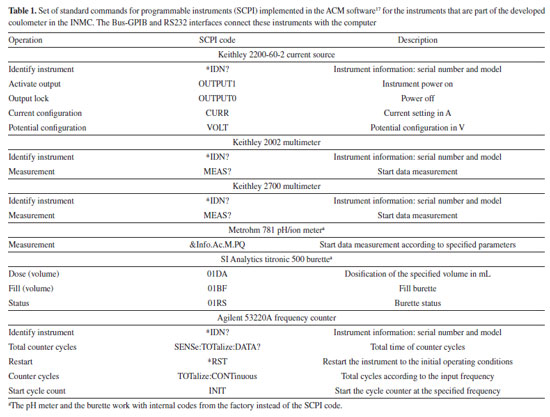
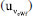 obtained for the specific measurement presented in Table 4 (0.00041 mol kg-1) must be combined with the uncertainties related to repeatability and bias. The uncertainty due to repeatability
obtained for the specific measurement presented in Table 4 (0.00041 mol kg-1) must be combined with the uncertainties related to repeatability and bias. The uncertainty due to repeatability 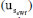 is estimated as
is estimated as 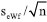 , where
, where 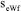 is the standard deviation and n = 7 is the number of replicates. The uncertainty due to
is the standard deviation and n = 7 is the number of replicates. The uncertainty due to 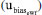 was estimated as
was estimated as 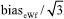 , assuming that has a rectangular distribution.32,36 These uncertainties are combined using Equation (15).
, assuming that has a rectangular distribution.32,36 These uncertainties are combined using Equation (15).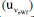 , repeatability
, repeatability 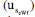 , and bias
, and bias 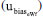 to the combined uncertainty of this result are shown in Figure 4. Notably, the highest contribution is the bias, accounting for 83.86%. This high contribution is explained by the presence of carbon dioxide in the supporting electrolyte, which is unavoidable under standard laboratory conditions (i.e. a non-hermetic coulometric cell).15 The eWf model, Equation 13, estimates the total acidity of the system, including the dissolved carbon dioxide, leading to a significant bias in the result.
to the combined uncertainty of this result are shown in Figure 4. Notably, the highest contribution is the bias, accounting for 83.86%. This high contribution is explained by the presence of carbon dioxide in the supporting electrolyte, which is unavoidable under standard laboratory conditions (i.e. a non-hermetic coulometric cell).15 The eWf model, Equation 13, estimates the total acidity of the system, including the dissolved carbon dioxide, leading to a significant bias in the result.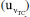 of the measurement.
of the measurement.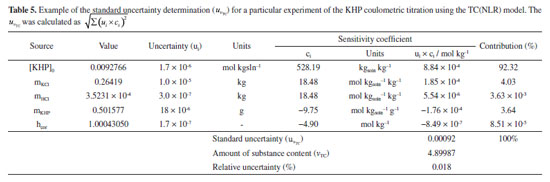
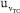 = 0.00092 mol kg-1, for the TC(NLR) model, compared to the equivalent
= 0.00092 mol kg-1, for the TC(NLR) model, compared to the equivalent 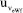 of the eWf model, which is 0.00041 mol kg-1. The increase in
of the eWf model, which is 0.00041 mol kg-1. The increase in 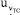 in relation to
in relation to 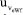 (≈2.2 times higher) is associated with the implicit contribution of the uncertainties of Ei, Ri, ttotalini, and tmain, as well as the significant number of computations involved in the nonlinear regression used to estimate the magnitude of the [KHP]0.15 Consequently, as shown in Table 5, the most significant contribution to the standard uncertainty
(≈2.2 times higher) is associated with the implicit contribution of the uncertainties of Ei, Ri, ttotalini, and tmain, as well as the significant number of computations involved in the nonlinear regression used to estimate the magnitude of the [KHP]0.15 Consequently, as shown in Table 5, the most significant contribution to the standard uncertainty 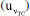 of the KHP amount of substance content, when calculated with the TC(NLR), comes from [KHP]0, accounting for 92.32%. The second most critical source of uncertainty for the TC(NLR) is the mass of the supporting electrolyte, contributing 4.03%. The mass of the supporting electrolyte, which is the highest measured, plays a crucial role in the computation of [KHP]0. The mass of the KHP sample, mHKP, has a similar effect on the final result. The other sources of uncertainty, mHCl, and hcor do not significantly contribute to the standard uncertainty.
of the KHP amount of substance content, when calculated with the TC(NLR), comes from [KHP]0, accounting for 92.32%. The second most critical source of uncertainty for the TC(NLR) is the mass of the supporting electrolyte, contributing 4.03%. The mass of the supporting electrolyte, which is the highest measured, plays a crucial role in the computation of [KHP]0. The mass of the KHP sample, mHKP, has a similar effect on the final result. The other sources of uncertainty, mHCl, and hcor do not significantly contribute to the standard uncertainty.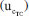 for TC(NLR) model is obtained by the combination of the standard uncertainty
for TC(NLR) model is obtained by the combination of the standard uncertainty 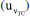 , the repeatability uncertainty
, the repeatability uncertainty 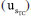 , and the bias uncertainty
, and the bias uncertainty 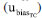 . This combination is presented in Equation 17.
. This combination is presented in Equation 17.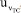 ,
,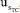 , and
, and 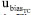 uncertainties to the combined uncertainty
uncertainties to the combined uncertainty 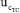 are presented in Figure 5. It shows similar qualitative behavior as Figure 4 for the eWF model. The
are presented in Figure 5. It shows similar qualitative behavior as Figure 4 for the eWF model. The 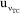 contributes 6,79% to
contributes 6,79% to 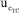 , compared to the 0.85% contribution of the eWf model. The
, compared to the 0.85% contribution of the eWf model. The  contribution (77.48%) decreases compared to the
contribution (77.48%) decreases compared to the  (83.86%). The repeatability contribution,
(83.86%). The repeatability contribution, 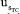 = 15.73% remains nearly unchanged compared to the eWf model,
= 15.73% remains nearly unchanged compared to the eWf model,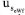 = 15.29%. Nonetheless, the outstanding fact is that the combined uncertainty using the TC(NLR),
= 15.29%. Nonetheless, the outstanding fact is that the combined uncertainty using the TC(NLR), 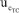 = 0.0023 mol kg-1, is lower than the combined uncertainty using the eWf,
= 0.0023 mol kg-1, is lower than the combined uncertainty using the eWf, 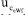 = 0.0044 mol kg-1.
= 0.0044 mol kg-1.