Artigo
| Structural optimization of jet pump based on BP neural network |
|
Bo Liu*
Binnan Oil Production Plant of Shengli Oilfield Co. LTD, 256600 Shandong, China Recebido em: 13/08/2023 *e-mail: liubo202304@126.com With the increasing drilling depth, problems follow, such as the lifting height of the liquid in the well and increased pump operation. Therefore, improving the production efficiency of deep wells is a hot spot in the current oil drilling and production industry. This paper designs a new jet pump that can be mined for high and low-pressure oil layers according to the oil wells' inter-layer contradiction. The FLUENT software is used to simulate the new jet pump, analyze the pump efficiency factors of the jet pump and the physical properties of the fluid, and the BP neural network is used to optimize the structure of the jet pump. The results show that the maximum pump efficiency of spout distance, duct diameter, duct distance, and spread angle is 2.61-5.22 mm, 6.393-8 mm, 42.5-53.2 mm, and 6-9°, respectively. The best spout distance, duct diameter, duct distance, and spread angle are 2.74 mm, 6.80 mm, 46.5 mm, and 7.4°after being optimized by the BP neural network model presented in this paper and the optimized pump efficiency is improved by 9.45%. INTRODUCTION With the continuous increase in drilling depth, well conditions are becoming increasingly complex, and the oil recovery efficiency is significantly reduced. Therefore, the effective cost reduction and efficiency increase is still an urgent problem to be solved in the current oil production project. This article proposes a jet pump that exploits high and low-pressure oil layers simultaneously. Compared with the traditional deep well jet pump, its significant advantage is not only reducing the production cost of injecting high-pressure fluid into the well from the ground equipment but also resolving the contradictions between layers, thus achieving simultaneous exploitation of high and low-pressure oil layers, and highlighting the cost-reducing and efficiency-increasing capabilities of the device. The related research on jet pumps mainly includes theoretical research, simulation research, and basic applications. Jet pump theoretical research: In the 20th century, American scholar Gosline1 conducted multiple systematic experiments and research on jet pumps at the University of California. By organizing and analyzing a large amount of data, he obtained the basic performance equation of jet pumps and published his experimental data and results and derived theories two years later. Between 1953 and 1955, Cunningham2 used the basic performance equation of jet pumps proposed by Gosline to analyze the suction capacity of jet pumps for high-viscosity liquids. In 1970, Cunningham and Dopkin3 began in-depth and comprehensive research on cavitation phenomena in jet pumps. They focused on analyzing cavitation problems in liquid-gas jet pumps in the following years. Choi et al.4 used a time-related N-S equation to analyze the two-dimensional flow field of jet pumps and concluded that the pressure ratio significantly impacts pump efficiency and there is an optimal spout width in jet pumps. Sun et al.5 conducted theoretical analysis and indoor experiments on the efficiency of jet pumps, studying the area ratio between the spout and duct, the impact of different spout cross-sectional shapes on jet pump performance, and ultimately found that jet pumps with circular spouts will have a higher pump efficiency. Jet pump simulation research: Since 1998, many scholars have started simulation studies on jet pumps. They use the RNG k-ε method and isentropic constant pressure mixing method to found the jet pumps model to simulate the internal flow field of the pump.6,7 Li et al.8 designed a range of primary nozzles with same or different area ratio by varying the nozzle's throat and exit diameters, and the impact of nozzle geometries on the critical performance curve is mainly explored. Moreover, it was proposed a linear fractional fitting function of generator temperature to predict the critical entrainment ratio and compression ratio for different nozzles. Shah et al.9 simulated and monitored the working process of a steam jet pump in real time and studied the static pressure, temperature, and liquid flow rate of the pump along the length direction. By comparing with experimental data, they found that the results of the two were in high agreement, thus obtaining the correct working characteristics of the steam jet pump. Aldas and Yapici10 used CFD to simulate jet pumps with different surface roughness and analyzed the influence of absolute and relative roughness changes on pump efficiency. They eventually found that using the SST k-model could improve the simulation accuracy. When the area ratio is 5.92, and the roughness is 0.05, the relative pump rate of the jet pump will decrease by about 60%. Feng et al.11 studied the flow performance and pressure drop of jet pumps in turbulent oscillating flow. They found that when the oscillating flow resistance coefficient is less than 46, the sensitivity of this coefficient to the Womersley number is poor, and the results are in good agreement with those under stable flow conditions. Xu et al.12 used CFD to simulate the annular jet pump numerically. After establishing accurate RBF and NSGA-II models, they optimized the structure and dimensions of the annular jet pump based on the models. Eventually, they concluded that the optimized jet pump had a head ratio about 12% higher than the unoptimized one. Basic jet pump application research: Jet pumps have also shown significant advantages in practical applications. As early as 1987, the United States conducted jet pump gas extraction experiments in a gas well in the south. Although it only lasted a few weeks, it achieved remarkable results, with a gas production rate of about 20 MMSCF D-1.13 Kumar et al.14 applied jet pumps to seawater desalination technology, replacing traditional vacuum pumps with jet pumps to form a new vacuum extraction device. After indoor experiments and field applications, they found that the device had good application effects. Minetto et al.15 applied jet pumps to air conditioning systems. When the evaporator in the air conditioner was always submerged in liquid, the jet pumps could still promote liquid circulation. This device not only greatly improved the operating efficiency of the refrigeration system but also achieved the purpose of energy saving. Han and Li16 proposed installing adjustable jet pumps in the pipeline centralized heating system in northern areas to reduce heating energy consumption. This method saves more energy than traditional centralized heating systems while considering user comfort. Liu et al.17 studied the application of jet pumps in heating systems. Taking the heating pipeline network of a certain city as an example, they studied whether jet pumps had an energy-saving effect on the heating system and finally found that jet pumps could effectively reduce energy consumption. Based on the above theories and research results, this study aims to design a jet pump with a simple structure, easy processing, high oil extraction efficiency, and the ability to extract high and low-pressure oil layers in the well simultaneously. The basic characteristic parameters and characteristic equations were obtained by studying the jet pump's basic structure and working principle. After giving the actual working condition parameters, the main structures were designed, such as spouts and duct pipes in the jet pump. After obtaining the preliminary overall structure of the jet pump, finite element software was used to analyze the factors affecting pump efficiency, explore the structural parameters of the jet pump affecting pump efficiency, and determine the range of various structural parameters with the maximum pump efficiency as the target. Finally, the BP neural network was used to optimize the structure size and obtain the optimal structural parameters where, ρ is the density of the fluid (kg m−3), t is time (s), ux uy uz is the velocity component of the fluid micro element in the X, Y, and Z axes (m s−1).
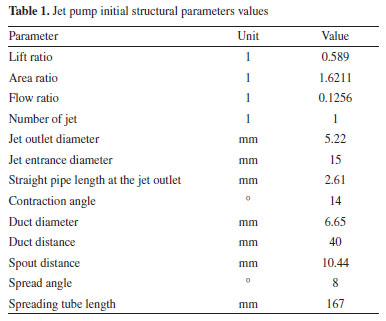
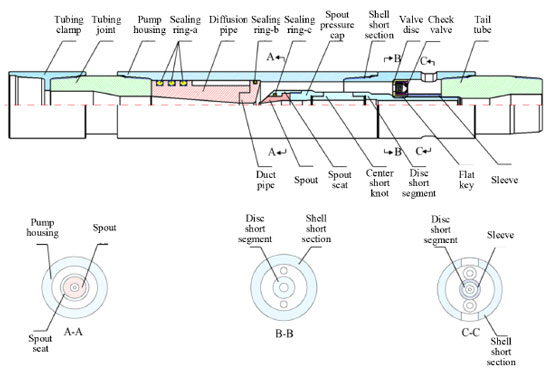
METHODOLOGY Mathematical model For the working process of the jet pump, the fluid is usually described by the following basic control equations. Continuity equation 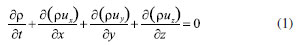 The physical meaning of the equation is that: in unit time, the mass difference of the inflow and the mass change of the outflow are equal to zero when the fluid passes through the unit volume. For an incompressible fluid, due to the density ρ that is constant, the continuity equation can be expressed as follows: 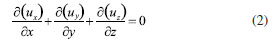 The momentum conservation equation (Navi-Stokes equation): 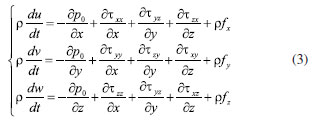 where, p0 is static pressure (Pa), τij (i j can be taken as, x y, and z, respectively) is the tensor of stress (Pa), fk (k can be taken as, x, y, and z, respectively) is volume force of gravity (N m−3). Realizable k-ε model The jet pump in this paper is a typical turbulence model, in which the equations can be expressed as: 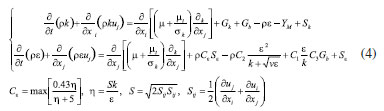 where, Sij is time-averaged strain rate (s−1), S is the tensor modulus of the average strain rate. Physical model The structure of the jet pump is shown in Figure 1 and the initial structural parameters of jet pump are shown in Table 1.
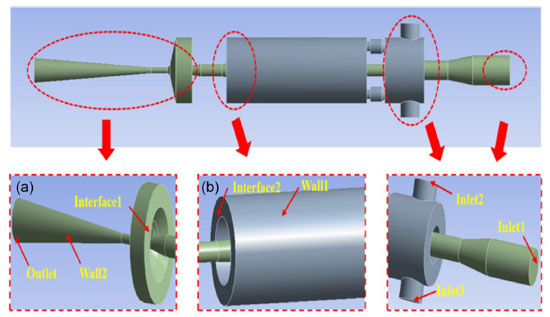
Boundary condition According to the basic condition of the jet pump, the boundary of the geometric model established above is set. As can be seen from Figure 2, there are 8 boundaries on the model, including 3 entrance boundaries (Inlet1, Inlet2, Inlet3), 1 exit boundary (Outlet), 2 interfaces (Interface1, Interface2), and 2 wall boundaries (Wall1, Wall2). In the simulation, the two interfaces are in contact. Wall1 refers to all remaining surfaces in the geometric model not defined in Figure 2b, and Wall2 refers to all remaining surfaces not defined in the geometric model shown in Figure 2a.
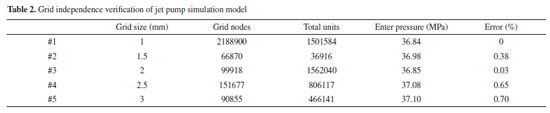
Inlet flow rate of the inhalation fluid is 1.85 kg s−1, and the outlet pressure of the jet pump is 22.45 MPa. Therefore, Inlet1 is finally set as the mass flow inlet boundary of the power fluid, and the value is 4.9 kg s−1. The Inlet2 and Inlet3 are set as the mass flow inlet boundary of the inhalation fluid, and the value is 0.6375 kg s−1. The outlet set as the pressure outlet boundary of the jet pump is 22.45 MPa. Grid-independent validation To further improve the calculation accuracy of CFD and effectively reduce the calculation time of the finite element simulation, the influence of different grid sizes on the simulation results is analyzed by changing the grid size of the geometric model. According to Table 2, five grid sizes are selected in this paper.
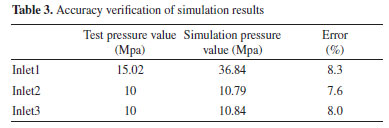
By comparing and analyzing the simulation results of different grid sizes, it is found that when the grid size in the model is 1-2 mm, the pressure value at the dynamic fluid inlet (Inlet1) is almost the same (the error is within 1%). The simulation results well verify the grid independence of the model. To reduce the operation time of the finite element simulation, the #3 grid division method with a grid size of 2 mm is selected for the simulation model of the jet pump. Accurate validation of the simulation results To verify the accuracy of the simulation results, the simulation pressure value of the dynamic fluid inlet (Inlet1) and the suction fluid inlet (Inlet2, Inlet3) are extracted to compare with the test data. As can be seen from Table 3, the difference between the simulation and the theoretical pressure (calculated from the basic characteristic equation of the jet pump)18 value at the dynamic fluid inlet is 2.82 MPa, and the relative error between the two is 8.3%. Moreover, the simulation pressure value at the inlet of the suction liquid is also very close to the theoretical pressure value, and the average relative error between the two is only 7.8%. Therefore, the simulation model has some accuracy within the allowable error limits.
BP neural network A BP neural network model consists of some nodes/neurons, which are set at multiple layers: the input layer, one or more hidden layers and output layer. Each node/neuron has an activation function, which calculates how much neuron is "stimulated". At each layer, the collections of nodes/neurons transform the input parameters, these parameters are distributed to the next layer, which is described as Equations 5, 6 and 7: 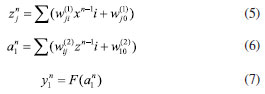 where x represents the input to the first layer, z represents the first layer's output, i and j represent the neural network node index, wji(l) represents the weight between the jth node in the ith layer and the ith node in the (i + 1)th layer, F(ain) represents the output value of ith node in (n + 1)th layer after being activated by the activation function, w and w0 represent the weight and bias between the neurons, which measures the significance of the data passed along the link (synapse). F(a) represents the activation function, which employs the hidden layer's aggregated output to calculates the output y. The initial weights and biases randomly assigned, the training process continues until the desired output is obtained, which is evaluated by the cost function (Equation 8): 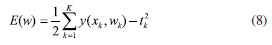 where y represents the output, t represents the desired output. Levenberg-Marquardt (LM) algorithm is utilized in the neural network training process, which is a variation of gradient descent. The weight and bias of the neural network model are changed during the training process to minimize the error, which is described as Equation 9: 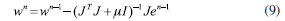 where The Levenberg-Marquardt algorithm starts with a forward computation by Equations 5, 6 and 7. The prediction errors of the output layer and the hidden layer are calculated by Equations 10, 11 and 12:  As shown in Equations 13 and 14, the Jacobian is calculated by a back-propagation process: 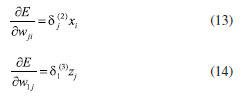 In the training process of the sample, the learning sample should be processed to make it fluctuate in a certain range. The normalization method is adopted in this paper to process the data to ensure that the data is between 0 and 1, which is written as Equation 15:  where x̄i represents the average value, xmax represents the maximum value, xmin represents the minimum value. In this paper, the Levenberg-Marquardt back propagation is employed to enhance the model training rate related to pure error back propagation or steepest descent, and this algorithm maintains the accuracy of the trained model. The neural network regression model is trained with the designed model structure, input parameters, and the number of nodes. The accuracy of both the training and the prediction/estimation is evaluated by mean absolute error (MSE), which is written as Equation 16: 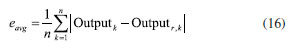 where eavg represents the average absolute error, n represents the number of data points, Outputk represents the kth estimated output parameter, and Outputr,k represents the kth reference output parameter.
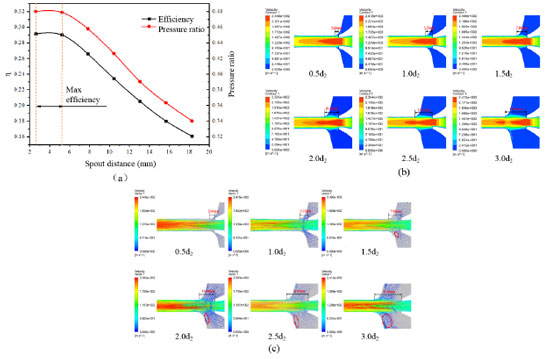
RESULTS AND DISCUSSION Analysis of the influencing factors of the pump efficiency Effect of spout distance on the pump efficiency of jet pump As shown in Figure 3a, the maximum pump efficiency is obtained when the spout distance is between 2.61 and 5.22 mm. As spout distance increases, the pump efficiency decreases gradually, and the decreased amplitude is evident. When the spout distance is 13.05 mm (2.5), the pump efficiency is only about 21%. The results prove that spout distance is one of the main factors affecting pump efficiency. With the gradual increase of spout distance, the pressure ratio curve has the same trend as the pump efficiency (first increases and then decreases).
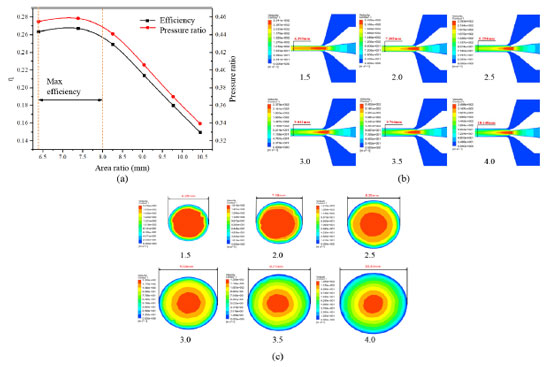
Figure 3b is a velocity cloud view of the spout outlet to the duct inlet in the flux pump. The highest velocity at the spout outlet always fluctuates between 239 and 247 m s-1, and the region of the highest fluid velocity (red region) decreases as the spout distance gradually decreases. When the duct distance is equal to 3 times, it is obvious that only a small part of the high-speed fluid entered the duct. This is because the gradual increase of spout distance makes the effective distance of the suction fluid longer, and the velocity decreases significantly before the fluid enters the duct. Figure 3c shows the flow field diagram from the outlet of the jet pump spout to the inlet of the duct. When the duct distance is 2.61 mm (0.5) and 5.22 mm (1.0), the suction fluid can enter completely into the duct of the jet pump, and the suction fluid forms a wall flow layer at the inlet section of the duct. Furthermore, with the gradual increase of spout distance, the reflux area (red dashed circle) appeared in the inhalation chamber, and the size of the reflux area gradually increased with the increase of spout distance. Finally, the reflux area is very obvious when the duct distance is 15.66 mm (3.0). This is because of the gradual increase of the product distance, the dynamic fluid from the spout jet diverges before entering the duct so that part of the inhalation fluid cannot be carried into the duct, and then the reflux area appears in the inhalation room. Effect of area ratio on the pump efficiency of jet pump As shown in Figure 4a, when the duct diameter ranges from 6.393 (area ratio 1.5) to 7.382 mm (area ratio 2), the pump efficiency gradually increases with the duct diameter increase. However, when the area ratio is greater than 2, the pump efficiency gradually decreases as the duct diameter increases. Therefore, it can be determined that the duct diameter of the maximum pump efficiency is between 6.393 and 8 mm, and the pressure ratio curve has the same trend as the pump efficiency.
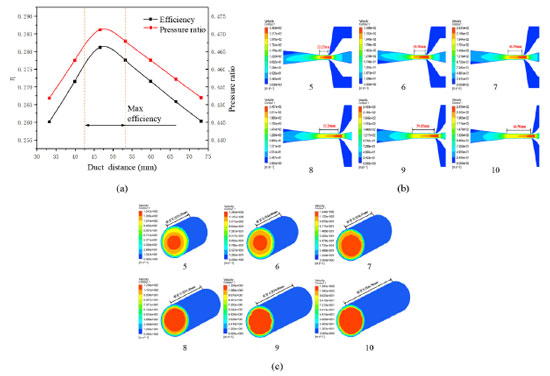
Figure 4b shows a picture of the jet pump's internal velocity cloud at different duct diameters. When the duct diameter is 6.393 mm (area ratio 1.5), the fluid flow rate in the duct is gradually reduced, and the difference between the inlet and the outlet is about 26 m s−1, so the flow rate is low. However, as duct diameter gradually increases (area ratio increases), the decreasing amplitude of the flow velocity in the duct gradually increases. When the duct diameter is 10.440 mm (area ratio 4.0), the difference between the inlet and the outlet flow rate is about 144 m s−1. This is due to the gradual increase in the area ratio. The flow core area of the dynamic fluid decreases, and the contact area between the dynamic fluid and the suction liquid increases so that the flow rate of the mixture is significantly reduced. Figure 4c shows a cloud view of the velocity at the duct outlet at different duct diameters in the jet pump. When the duct diameter is 6.39 mm, the maximum velocity at the outlet is about 204 m s-1, and this velocity region is large. However, with the gradual increase of duct diameter, the maximum velocity at the duct outlet gradually decreases, and when the area ratio gradually increases, the highest velocity area gradually decreases. It can be seen that the maximum velocity at the duct outlet and the area size of the highest velocity gradually decrease with the increase of duct diameter. This is because, with the increase of the area ratio, the section at the duct outlet is larger, so the contact area between the dynamic fluid and the suction fluid in the duct also increases. Thus, the two have sufficient energy transfer in the duct, so the highest speed and maximum speed areas gradually decrease as the area ratio increases. Effect of duct distance on the pump efficiency of jet pump As shown in Figure 5a, when the duct aspect ratio is between 5 and 7, the pump efficiency gradually increases with the increase of the aspect ratio. However, when the aspect ratio is greater than 7, the pump efficiency gradually decreases with the increase of the aspect ratio. Therefore, the duct distance interval can determine the maximum pump efficiency between 42.5 (duct aspect ratio 6.39) and 53.2 mm (duct effect aspect ratio 8). With the increase of the duct distance, the pressure ratio curve shows the same trend as the pump efficiency.
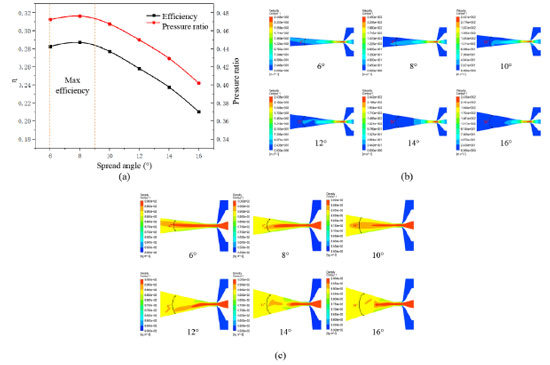
Figure 5b plots the velocity cloud within the duct at different duct distances in the jet pump. With increasing duct distance (aspect ratio), the maximum velocity within the duct always fluctuates between 243 and 246 m s−1, and the region size of the highest velocity is almost the same. Although the duct outlet velocity fluctuates between 194 and 197 m s−1, the region of the export velocity increases with duct distance. This is because the dynamic fluid and the inhalation fluid have been fully mixed in the duct, and the diameter does not change. Even if the duct distance increases again, the flow rate of the mixture does not change much, but the flow rate region will increase with the increase of duct distance. Figure 5c shows a diagram of the velocity cloud at the duct outlet at different duct distances in the jet pump. When the duct distance is 33.25 mm, the maximum velocity at the outlet is about 134 m s−1, and this velocity region is small. However, as the duct distance gradually increases, the maximum velocity at the duct outlet also gradually decreases, and when the aspect ratio gradually increases, the highest velocity area gradually increases. This is due to the increase of the aspect ratio; the contact time between the dynamic fluid and the suction liquid in the product becomes longer so that the dynamic fluid and the suction liquid have full energy transfer, and the maximum velocity area gradually increases with the increase of the aspect ratio. Effect of spread angle on the pump efficiency of jet pump As shown in Figure 6a, when the spread angle is between 6 and 8°, the pump efficiency gradually increases with increasing spread angle. However, when the spread angle is greater than 8°, the pump efficiency decreases gradually with the increase of the spread angle. Thus, it can be determined that the spread angle interval for maximal pump efficacy is between 6 and 9°. Moreover, with the spread angle increase, the pressure ratio curve shows the same trend as the pump efficiency.
Figure 6b shows a cloud plot of the spreading tube's velocity under different spread angles. The highest velocity within the spreading tube fluctuates between 194 and 196 m s−1. When the spread angle is 6°, the mixed liquid can fully develop into the whole section. Because the fluid speed is relatively fast at this time, the friction loss increases and then causes the pump efficiency of the jet pump to decline. However, with the gradual increase of the spread angle, the flow rate of the mixed liquid is significantly less than the increased speed of the spread angle so that the velocity distribution surface in the spreading tube does not fll the entire cross-section of the spreading tube. Consequently, the performance of the jet pump is significantly reduced. Figure 6c shows the density cloud map within the spreading tube at different spread angles. When the spread angle is 6°, a small part of the dynamic fluid (high-pressure fluid) in the spreading tube is not fully mixed with the inhalation fluid (low-pressure fluid), and its density remains at 900 kg m-3. However, with the increase in spread angle, it is obvious that the 900 kg m-3 within the spreading tube is gradually shorter. The reason is that with the gradual increase of the spread angle, the contact area of the dynamic fluid and the suction fluid in the spreading tube is further increased, which promotes the full mixing of the two, and the liquid density after mixing is between the two. Structural size optimization of the jet pump based on the BP neural network To further improve the oil recovery efficiency of the jet pump when exploiting the high and low-pressure oil layer, this paper uses the BP neural network to optimize the structural size of the jet pump based on the optimal numerical interval of spout distance, area ratio, and duct aspect ratio when the medium pump efficiency is maximum. The specific steps are as follows. Training data selection Based on the calculation results of previous section, the optimal value interval of spout distance, duct diameter, duct distance, and spread angle (maximum pump efficiency) is obtained. Thus, the selected range of input variables of the BP neural network is shown in Table 4. In this study, five levels were taken for each parameter, as shown in Table 5.
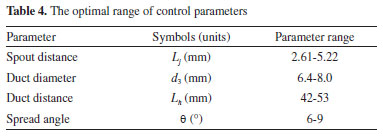
According to the parameter combination and level division of Tables 5 and 6, the 625 (5 × 5 × 5 × 5) groups' training data are obtained. The simulation calculates the pump efficiency of the jet pump according to different parameter combinations. The part of simulation results is shown in Table 6.
Neural network structure determination According to the number of control factors in Table 4, four independent variables including spout distance, duct diameter, duct distance and spread angle are determined. The dependent variable is the pump efficiency under different combinations of structural parameters, and then the number of input layers and output layers of the neural network is determined to be 4 and 1, respectively. For the hidden layer, it is necessary to analyze and judge according to the convergence accuracy, and use the BP neural network to pre-train the data in Table 6 to obtain the convergence accuracy of different hidden layers, as shown in Table 7.
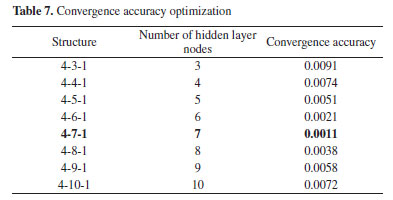
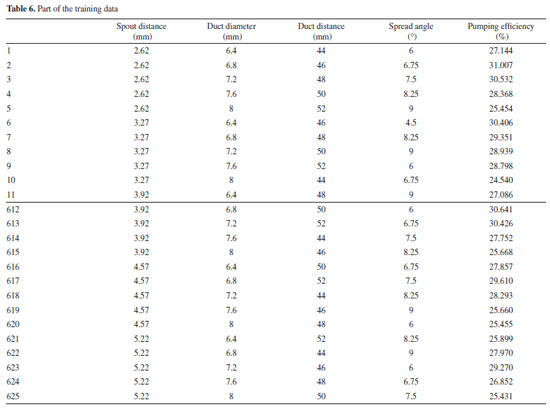
It is obvious from Table 7 that the convergence accuracy of the network is minimal when the number of hidden layers is 7. Therefore, the neural network structure in this paper is set to 4-7-1 (in bold at Table 7). The BP neural network training process In this paper, 625 samples were trained, and the ratio of training sets, validation sets, and test sets was 8:1:1, that is, 499 training sets, 63 validation sets, and 63 test sets. As can be seen from the training curve of Figure 7a, the convergence accuracy of the BP neural network model reaches 0.0011. It does not fall into local minimum points, indicating that the BP network with a 4-7-1 structure can apply the jet pump structure optimization well. Moreover, during training, validation, and testing, the model reaches full convergence at step 35, and the convergence rate is better. As shown in Figure 7b, the model is trained with high fitting accuracy. Specifically, the model in training, verification, testing, and overall accuracy were 97.733, 96.964, 97.160, and 97.541%, respectively. Therefore, the test accuracy of this model is high, and the predicted value of the output parameters is close to the reference value. The error histogram of the model is shown in Figure 7c. The error distribution follows the Gaussian distribution rule, demonstrating the representativeness of the training data.
Structural optimization of the jet pump based on the BP neural network In order to further obtain the optimal structure of the jet pump, more levels of parameters are selected to predict the pump efficiency to determine the optimal structural parameters. The value range of the specific parameters is shown in Table 8.
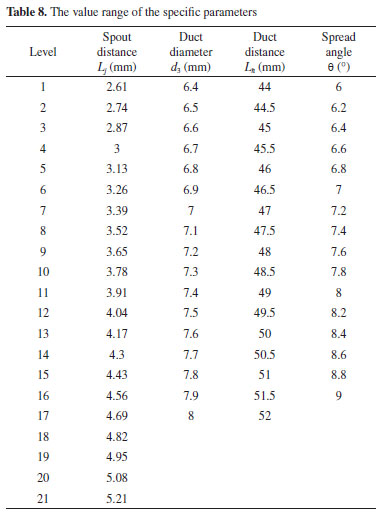
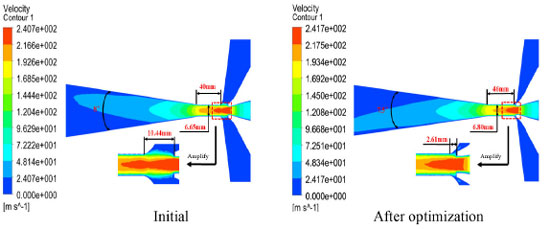
According to Table 8, 97104 (21 × 17 × 17 × 16) data combinations were obtained. The trained BP neural network model was used to predict the pump efficiency on 97104 data sets to complete the structural optimization of the jet pump. Table 9 shows the comparison of pump efficiency before and after size optimization. It can be seen from Table 9 that the calculated pump efficiency is very close to the predicted value of the BP neural network after optimization, which further proves the reliability of the BP neural network model. By comparing the specific structural dimensions of the two, the flow rate and the pump efficiency (obtained by numerical simulation), it can be found that the duct distance in the jet pump before the optimization is much larger than the optimized pump, and the former is about four times that of the latter. Comparing the duct diameter and duct distance in the jet pump before and after optimization shows that the optimized size is larger than before optimization. The difference between duct diameter and duct distance before and after optimization is 0.15 and 6.5 mm, respectively. In contrast, the spread angle is exactly the opposite, the optimized spread angle is smaller than before optimization, and the difference between the two is only 0.6. In addition, the pump efficiency was 21.81% (before optimization) and 31.26% (after optimization), respectively, and the pump efficiency was improved by 9.45%.
Comparison of jet pump performance before and after size optimization As shown in Figure 8, by comparing the cross-section velocity cloud map of the jet pump before and after optimization, it is found that the maximum velocity of the fluid in the optimized jet pump is almost the same. Because the duct distance before the optimization is much larger than after optimization, the effective action distance of the suction fluid carried by the dynamic fluid becomes longer. Only a small part of the high-speed fluid (red area) enters the duct in the jet pump before optimization. Although the spread angle before and after optimization is similar, the mixed liquid can be fully developed for the whole section. By combining the analysis of the data in Table 9 and Figure 8, it proves that the optimized jet pump improves the performance compared with the initial jet pump and further shows that the method in this paper has a good ability to optimize the structural size of the jet pump and improve the pump efficiency.
CONCLUSIONS According to the problems such as the difficulty of reservoir oil exploitation, the low recovery efficiency of deep well jet pump, and the prominent contradiction between layers, this paper analyzes the efficiency of the jet pump and the optimization of the structure and size of a jet pump. The numerical simulation result of the jet pump shows that: spout distance, area ratio, duct aspect ratio, and spread ratio have a great influence on the pump efficiency of the jet pump. According to the numerical simulation results, the spout distance interval of the maximum pump efficiency is between 2.61 and 5.22 mm. The maximum duct diameter interval is between 6.393 mm (area ratio 1.5) and 8 mm (area ratio 2.35), the maximum duct distance interval is between 42.5 mm (effect aspect ratio 6.39) and 53.2 mm (matter aspect ratio 8), of the maximum spread angle interval is between 6 and 9°. The flow ratio interval is between 0.2 and 0.4. The BP neural network optimization results show that: when the spout distance in the jet pump is 2.74 mm, the duct diameter is 6.80 mm, the duct distance is 46.5 mm, and the spread angle is 7.4°, the jet pump has the highest efficiency. After size optimization, the pump efficiency was improved by 9.45%.
REFERÊNCIAS 1. Gosline, J. E.; Transactions of the AIME 1936, 118, 56. [Crossref] 2. Cunningham, R. G.; J. Fluids Eng. 1974, 96, 203. [Crossref] 3. Cunningham, R. G.; Dopkin, R. J.; J. Fluids Eng. 1974, 96, 216. [Crossref] 4. Choi, Y. H.; Soh, W. Y. ; 26th Joint Propulsion Conference, Orlando, United States, 1990. [Crossref] 5. Sun, W.; Li, M.; Fan, Y. ; Zhu, B.; Journal of Power and Energy 2023. [Crossref] 6. Shu, L.; Fan, Y.; Yang, Y.; Song, X.; Guo, H.; Energy Sci. Eng. 2023, 11, 1886. [https://doi.org/10.1002/ese3.1423 Crosssref] 7. Zhang, H.; Zou, D.; Yang, X.; Mou, J.; Zhou, Q.; Xu, M.; Energies 2022, 15, 6978. [Crossref] 8. Li, A.; Chen, J.; Xi, G.; Huang, Z.; Journal of Mechanical Science and Technology 2023, 37, 2139. [Crossref] 9. Shah, A.; Chughtai, I. R.; Inayat, M. H.; Int. J. Multiphase Flow 2011, 37, 1305. [Crossref] 10. Aldas, K.; Yapici, R.; Engineering Applications of Computational Fluid Mechanics 2014, 8, 14. [Crossref] 11. Feng, Y. ; Gao, Y.; Tang, K.; Jin, T.; J. Acoust. Soc. Am. 2019, 145, 1417. [Crossref] 12. Xu, K.; Wang, G.; Zhang, L.; Wang, L.; Yun, F.; Sun, W.; Chen, X.; Journal of Marine Science and Engineering 2021, 9, 236. [Crossref] 13. Green, A. J.; Kevin, A.; Reade, A. T.; SPE Offshore Europe; Aberdeen, United Kingdom, 1993. [Crossref] 14. Kumar, R. S.; Mani, A.; Kumaraswamy, S.; Desalination 2005, 179, 345. [Crossref] 15. Minetto, S.; Brignoli, R.; Zilio, C.; Marinetti, S.; Int. J. Refrig. 2014, 38, 1. [Crossref] 16. Han, J.; Li, D.; Procedia Eng. 2017, 205, 751. [Crossref] 17. Liu, X.; Zhan, Q.; Lia, Y.; Procedia Eng. 2017, 205, 2208. [Crossref] 18. Lu, X.; Wang, D.; Shen, W.; Zhu, C.; Chen, M.; Int. J. Heat Mass Transfer 2015, 88, 379. [Crossref] |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






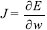 epresents the full-scale Jacobian matrix related to w, I represents the identity matrix, m represents a combination coefficient, e represents the prediction error.
epresents the full-scale Jacobian matrix related to w, I represents the identity matrix, m represents a combination coefficient, e represents the prediction error.