Assuntos Gerais
|
|
| A equação de Nernst: origens e contexto termodinâmico The Nernst equation: origins and thermodynamic context |
|
Douglas C. Silva; Emilio Borges*
Departamento de Química, Universidade Federal de Viçosa, 36570-900 Viçosa - MG, Brasil Recebido: 23/02/2024 *e-mail: emilio.borges@ufv.br In the present article, the scientific journey that led to the development of the Nernst equation, a cornerstone in modern electrochemistry, is discussed. The paper not only explores historical achievements but also traces the evolution of scientific ideas and highlights the key figures who laid the conceptual and experimental groundwork for the seminal contributions of Nernst to the understanding of electrochemical systems. In this exploration, particular attention is paid to the examination of the first three articles published by Nernst between 1888 and 1889. These essential works marked the inception of the engagement of Nernst with the Leipzig Physical Chemistry circle, comprising the distinguished quartet: van't Hoff, Arrhenius, Ostwald, and Nernst himself. Furthermore, the present study examines the intricate relationship between the Nernst equation and the four basic laws of Thermodynamics, all in an approach accessible to undergraduate students. A concise review elucidates the interpretation and significance of these foundational thermodynamic principles and explain how they hold the formulation of the Nernst equation. INTRODUÇÃO No atual mundo tecnológico células eletroquímicas têm um papel de grande destaque principalmente por serem sistemas capazes de converter energia química em elétrica. As baterias recarregáveis, por exemplo, se tornaram indispensáveis na vida cotidiana, pois são fontes de energia para o funcionamento de e , dispositivos eletrônicos sem os quais a sociedade contemporânea não pode mais prescindir para as mais rotineiras tarefas. Em outro exemplo, a tecnologia de células de combustível também se mostra como uma promissora alternativa a motores de combustão interna, o que sugere um grande potencial de redução de emissões de gases poluentes.1,2 Sistemas eletroquímicos também são essenciais para processos industriais como a galvanização, técnica central para a produção de muitos produtos químicos,3 para o tratamento de água,4 para a nanotecnologia e para criação de novos materiais.5,6 Nesse âmbito, o desenvolvimento de células eletroquímicas mais eficientes e seguras e menos poluentes é uma demanda premente e contínua. A compreensão desses sistemas eletroquímicos, indispensáveis para a tecnologia contemporânea, só se tornou viável devido ao trabalho de alguns cientistas do século XIX que, possivelmente, sequer imaginavam o poder de transformação que a eletroquímica teria sobre a sociedade dos séculos XX e XXI. Nesse contexto, "a equação de Nernst" é um dos resultados imprescindíveis da eletroquímica, desempenhando papel essencial na evolução das células eletroquímicas e de suas funcionalidades. Essa equação e suas primeiras implicações foram descritas pelo cientista alemão Walther Nernst entre 1888-1889.7-9 Em seu trabalho, Nernst forneceu uma rigorosa descrição termodinâmica sobre como a pressão osmótica de diferentes soluções iônicas influenciavam a geração de potencial elétrico nas células eletroquímicas. Sua equação permitiu o ajuste e adaptação de concentrações de eletrólitos e diferentes tipos de materiais constituidores de eletrodos para aprimorar o funcionamento desses sistemas. No presente artigo discute-se resumidamente a história por trás do desenvolvimento dessa equação, destacando-se a evolução de algumas ideias científicas sobre sistemas eletroquímicos que culminaram com o trabalho de Nernst. Explora-se também a interconexão entre a equação de Nernst e as quatro leis da termodinâmica, enfatizando-se como esses princípios fundamentais que regem os processos termodinâmicos constituem a base conceitual da equação de Nernst.
AS PRIMEIRAS IDEIAS RELACIONADAS À ELETROQUÍMICA As principais investigações historicamente relevantes sobre a conexão entre fenômenos elétricos e reações químicas, que originaram a eletroquímica moderna, iniciaram-se no século XVIII. Um dos pioneiros nesse campo foi Luigi Galvani (1737-1798), filósofo e médico italiano que, trabalhando em Bologna, realizou estudos elétricos no âmbito da fisiologia e da biologia. Galvani iniciou uma série de experiências em 1780 nas quais o contato de metais diferentes com pernas de rãs promovia a contração dos músculos desses órgãos.10 Galvani inicialmente interpretou tais observações como um evento relacionado à eletricidade produzida dentro dos músculos das rãs, que ele designou "eletricidade animal". Sua proposição era que os músculos continham uma "força elétrica vital"responsável por sua contração. Segundo Galvani, essa força seria inerente aos seres vivos e teria natureza diferente da eletricidade gerada por sistemas não vivos, como reações químicas .11 Essa ideia foi inicialmente aceita pela maioria dos estudiosos da área, mas requeria mais evidências experimentais e, principalmente, uma explicação conceitual. Nesse cenário, surgiram debates e novas experimentações, das quais se destacaram aquelas realizadas pelo físico, também italiano, Alessandro Volta (1745-1827) da Universidade de Pavia.12 Em 1800, Volta sugeriu que a causa da eletricidade verificada por Galvani não seria a hipotética força vital, mas, a interação entre os metais utilizados nos experimentos e os fluidos corporais do animal. Essa conjectura o inspirou a desenvolver em laboratório um primeiro sistema em que corrente elétrica era obtida por meio de reações químicas envolvendo metais e soluções líquidas condutoras de eletricidade. Alessandro Volta imergiu nas soluções, de maneira alternada, placas de diferentes metais, como prata e zinco, cobre e zinco, cobre e prata. Ele catalogou assim uma série de combinações de metais distintos, dois a dois, de acordo com a eficiência de cada combinação para a produção de corrente elétrica. Apoiado nisso, ele percebeu que cada dupla de placas metálicas diferia entre si pela "voltagem" (diferença de potencial) produzida na solução; a corrente elétrica gerada em solução se mostrou proporcional à essa voltagem. Tais sistemas começaram a ser chamados de "pilhas voltaicas" ou "pilhas galvânicas" e evidenciaram definitivamente que a eletricidade obtida a partir de sistemas biológicos não se distinguia daquela obtida por reações químicas em pilhas artificiais.13 O dispositivo inventado por Alessandro Volta foi aperfeiçoado nos anos posteriores e se tornou uma fonte de corrente elétrica que possibilitou a realização de diversos experimentos de "eletrólise" a partir dos quais os cientistas começaram a observar como a eletricidade podia alterar quimicamentecertas substâncias e causar novas reações químicas.14 Por exemplo, em 1800, o britânico Humphry Davy (1778-1829) usou uma pilha voltaica para gerar corrente elétrica e passá-la através de um compartimento contendo água com eletrodos de platina mergulhados. Ele observou a formação de aparentes "bolhas de ar" nos eletrodos e foi capaz de identificar a composição das mesmas: eram os gases hidrogênio e oxigênio.15 Essa foi uma confirmação experimental da proposição anterior de outro britânico, Henry Cavendish, de que a água seria formada por hidrogênio e oxigênio. Humphry Davy também utilizou a eletrólise para isolar elementos químicos como sódio, potássio, cálcio e magnésio a partir de seus compostos, demonstrando como a eletricidade poderia ser útil para isolar elementos químicos de suas combinações químicas. Davy propôs, ademais, a ideia de que as forças que mantinham a agregação estrutural das substâncias químicas seriam de natureza elétrica, um grande avanço conceitual na descrição da estrutura da matéria. Também em 1800, os britânicos William Nicholson (1753-1815) e Anthony Carlisle (1768-1840) demonstraram a eletrólise da água de maneira independente usando uma pilha voltaica. Eles procederam pioneiramente experimentos de eletrólise com sais dissolvidos em água, destacando a capacidade que a eletricidade tinha em "transformar" íons metálicos dissolvidos em água em metais sólidos que se depositavam em um dos eletrodos.16 Um dos gigantes da química do início do século XIX, o sueco Jöns Jacob Berzelius (1779-1848) também realizou experiências de eletrólise na Universidade de Uppsalla. Berzelius utilizou aqueles experimentos para determinar massas de íons envolvidos em reações eletroquímicas, permitindo uma estimativa dos pesos atômicos dos elementos geradores de tais íons. Essa estratégia eletroquímica melhorou bastante a precisão das medidas das massas atômicas conhecidas até então. Em 1807, Berzelius, trabalhando em conjunto com o também sueco (e rico proprietário de minas que continham minerais necessários às experiências) Wilhelm Hisinger (1766-1858) descobriu que, no processo de eletrólise, determinadas espécies químicas eram sempre atraídas para o mesmo "polo" e que tais espécies possuíam algumas características comuns. A partir dessa observação, Berzelius e Hisinger propuseram a ideia de que havia uma relação entre a natureza química e elétrica das substâncias, proposição similar àquela de Humphry Davy.17 Voltando à Inglaterra, no ano de 1812, Humphry Davy proferiu uma série de palestras na e entre seus espectadores estava um jovem, Michael Faraday (1791-1867), que se tornaria, em um primeiro momento, assistente de Davy e em seguida, um dos maiores gênios da Ciência. Faraday criou boa parte da nomenclatura utilizada até hoje em eletroquímica. Ele denominou as substâncias envolvidas no processo de eletrólitos (do grego; aquilo que se decompõe pela eletricidade) e nomeou as placas metálicas de eletrodos (do grego; caminho da eletricidade); ele também designou a parte negativa das substâncias de "ânions" e a positiva de "cátions"e criou as palavras ânodo (eletrodo que atrai o ânion) e cátodo (eletrodo que atrai o cátion).18 Em um artigo publicado em 1833 intitulado , ele enunciou sua primeira lei da eletrólise; "a quantidade de substância liberada ou depositada em um eletrodo durante uma eletrólise é diretamente proporcional à intensidade da corrente elétrica que passa pelo circuito"19Faraday utilizou em seu trabalho a ideia de "equivalentes químicos", uma unidade amplamente adotada na química de seu tempo. Esses equivalentes químicos eram definidos a partir da quantidade de certa substância que participava de uma reação química. O equivalente químico de uma substância seria a massa dessa substância que reagiria totalmente com a massa de outra substância. Esse conceito, popularizado pelo químico francês Auguste Laurent (1807-1853),20 e mais tarde substituído pela ideia de mol e massa molar, ajudou a estabelecer relações quantitativas entre as substâncias participantes de reações químicas, viabilizando um organizado desenvolvimento da estequiometria, a área da química que trata das proporções quantitativas entre substâncias em reações químicas. Faraday elaborou sua segunda lei da eletrólise baseado nos equivalentes químicos; "certa quantidade de eletricidade forma massas de produtos que mantêm uma relação direta com seus respectivos equivalentes químicos."19 Em outras palavras, a segunda lei de Faraday para a eletrólise estabelece que as massas das substâncias liberadas ou depositadas nos eletrodos estão em proporções estequiométricas, obedecendo às proporções das substâncias na reação química envolvida na eletrólise. As leis da eletrólise descobertas por Faraday tiveram uma relação direta com o intenso desenvolvimento tecnológico ocorrido no século XIX pois desempenharam um papel primordial no avanço de métodos eletroquímicos na indústria e no avanço de certas tecnologias.21 Por exemplo, a primeira lei de Faraday propiciou o aprimoramento das técnicas de galvanização, em que metais como cobre, prata e ouro podiam ser depositados, através de eletrólise, sobre outros objetos, com o intuito de produzir moedas, objetos decorativos e instrumentos diversos. A eletrólise fundamentada por Faraday também revolucionou a metalurgia de refino de alumínio em larga escala a partir da bauxita, contribuindo para o progresso da indústria de transportes. Ademais, o conhecimento decorrente dos experimentos de Faraday forneceu uma abordagem nova para a produção de vários produtos químicos, como o cloro e o hidrogênio obtidos da eletrólise da salmoura.22 Após Michael Faraday, o próximo grande nome relacionado à pesquisa em eletroquímica foi o do químico sueco Svante August Arrhenius (1859-1927) que em 1884 elaborou uma teoria segundo a qual os eletrólitos, quando dissolvidos em água, se dissociavam em íons, formando uma solução condutora de eletricidade. No âmbito dessa teoria, Arrhenius definiu ácidos como sendo substâncias que, em solução aquosa, liberavam íons hidrogênio (H+) e bases como substâncias que liberavam íons hidroxila (OH-). A partir de sua teoria ocorreu um novo progresso conceitual na compreensão das reações eletroquímicas em soluções aquosas de distintos fenômenos observados na eletrólise.23,24 Arrhenius foi o terceiro cientista na história a receber o Prêmio Nobel de Química, em 1903, "em reconhecimento aos extraordinários serviços por ele prestados ao avanço da química por sua teoria de dissociação eletrolítica",25 de acordo com o comitê do prêmio. Arrhenius tornou-se amigo de Walther Nernst, que conheceu no sul da Alemanha em 1886, e teve um papel significativo em despertar o interesse de Nernst pela eletroquímica.
QUEM FOI WALTHER NERNST? Walther Nernst nasceu em 25 de junho de 1864 na cidade alemã de Briesen (atualmente Wąbrzeźno na Polônia) e faleceu em 18 de novembro de 1941, em Zurique, Suíça. Ele é, atualmente, amplamente reconhecido por suas contribuições conceituais para a termodinâmica e para a eletroquímica. Nernst foi filho de um advogado e passou sua infância e juventude na cidade de Graudenz (atualmente Grudziadz na Polônia) a 26 km de Briesen para onde seu pai se mudou para ocupar um cargo de juiz de condado. Nessa cidade ele ingressou, em 1874, no Ginásio Real Protestante,uma instituição de ensino que possuía uma excelente biblioteca contendo grandes obras das áreas de humanidades, ciências e matemática.26 Nernst parece ter aproveitado bem essa biblioteca adquirindo uma diversificada formação e demonstrando, inicialmente, forte inclinação para a área de estudos linguísticos, em especial para o latim. Ele também desenvolveu interesse por teatro e literatura chegando mesmo a considerar a possibilidade de se tornar ator ou poeta. Embora não tenha seguido essa vocação inicial, há influências da mesma em seu trabalho posterior. Por exemplo, em 1912 Nernst e sua amiga escritora Charlotte Marie Warburg escreveram uma espécie de "novela de fantasia"sobre a teoria da relatividade, intitulada "Entre o espaço e o tempo", em que narravam uma história de amor eterno entre dois jovens, um físico teórico e uma rainha.No obituário de Nernst em 1941 Einstein comentou: "Ao mesmo tempo ele estava interessado em literatura e tinha um senso de humor que é muito raramente encontrado em homens que carregam uma carga de trabalho tão pesada."26 Também sua amiga Charlotte publicou (sob o pseudônimo de ) um obituário satírico para Nernst em 1941:
No ano de 1883, um jovem Nernst se formou no já citado Ginásio Real com a honra , título dado aos melhores estudantes concluintes, e optou por continuar os estudos em ciências e matemática. Ele ingressou na Universidade de Zurique em abril de 1883, mas obteve uma formação universitária multicêntrica, cursando vários semestres em diferentes instituições da Europa central. Em Zurique, Nernst teve aulas com Heinrich Weber (também professor de Einstein, embora os dois não tenham se dado muito bem) que tinha medido há alguns anos antes as capacidades caloríficas de determinados sólidos a baixas temperaturas, até então incompreendidas pela teoria. Ainda em 1883, Nernst foi para a universidade Friedrich-Wilhelms em Berlim (atualmente Universidade Humboldt).26,28 Lá estava o professor Hermann von Helmholtz, um dos cientistas mais influentes de sua época. Porém, aparentemente, Nernst não assistiu as aulas de Helmholtz, pois havia relatos (inclusive de Max Planck, que fora aluno de Helmholtz) de que as mesmas não eram muito estimulantes.29 Em 1885 Nernst foi para a Universidade de Graz, na Áustria, com esperança de aprender com Boltzmann, segundo suas próprias palavras: "Quando fui para Graz, o fiz com a intenção de assistir as palestras em física teórica, que na época eram ministradas na Universidade de Graz pelos professores Ettingshausen, Heinrich e Franz Streintz, Klemenčič, e outros em número superior ao de qualquer outra universidade alemã (...). Minha esperança em trabalhar também com Boltzmann em física teórica não pôde ser realizada, já que na época Boltzmann oferecia apenas a palestra para iniciantes em física experimental. No entanto, além das excelentes palestras dos professores mencionados anteriormente, fui ricamente compensado pela colaboração experimental diária com o Professor Ettingshausen, em particular, uma vez que Boltzmann mostrou um interesse crescente em nossos resultados. O gênio desse grande físico teórico frequentemente iluminava nosso trabalho experimental durante longas discussões científicas (...)."26 No período 1886-1887 Nernst concluiu sua formação universitária na Universidade Real Julius-Maximilian em Würzburg na Baviera onde trabalhou no laboratório de Friedrich Kohlrausch que em 1886 foi visitado por Arrhenius. Esse encontro com Arrhenius foi o início de uma longa amizade e colocou Nernst em contato pela primeira vez com a teoria de dissociação de eletrólitos, que o deixou bastante inspirado. Arrhenius estivera no Instituto Politécnico de Riga (atual Letônia) com o futuro prêmio Nobel de Química de 1909, Friedrich Wilhelm Ostwald (1853-1932), que era uma referência por seu trabalho em catálise, além de ser grande defensor da teoria de dissociação de eletrólitos. Em 1887 Ostwald assumiu a cátedra de Físico-Química na Universidade de Leipzig (fundada em 1409) e ofereceu a Nernst, por influência de Arrhenius que também se mudara para Leipzig, o cargo de chefe assistente em seu laboratório, o que Nernst prontamente aceitou. A esses três se juntou o primeiro vencedor do prêmio Nobel de Química por seus êxitos em termodinâmica química e determinação da pressão osmótica em soluções, o holandês Jacobus Henricus van't Hoff (1852-1911). Esse "círculo de Físico-Química de Leipzig",com quatro futuros vencedores doPrêmio Nobel em Química, intensificou seus esforços no estudo da termodinâmica, das propriedades coligativas em soluções e na, até então "essencialmente fenomenológica", eletroquímica.26,28-33 Contudo, antes de ir a Leipzig, Nernst obteve seu doutorado em 1887 com uma tese intitulada "Sobre as forças eletromotoras geradas pelo magnetismo dentro de placas metálicas através das quais uma corrente de calor está fluindo".Esse foio trabalho que ele desenvolvera com Albert von Ettingshausen em Graz. Eles haviam estudado a interação entre um campo magnético e um gradiente de temperatura em um material condutor. Descobriram que quando um condutor elétrico era submetido ao mesmo tempo a uma diferença de temperatura entre suas duas extremidades e a um campo magnético externo, ocorria a geração de uma corrente elétrica no material. Esse fenômeno ficou conhecido como "efeito Nernst - Ettingshause" sendo muito relevante no estudo de materiais magnéticos e na compreensão de propriedades termomagnéticas de materiais condutores. Com o quarteto van't Hoff, Arrhenius, Nernst e Ostwald, a Universidade de Leipzig se tornou efetivamente a primeira instituição de ensino e pesquisa em Físico-Química na Europa. Vários outros locais já tinham essa área de ensino em seu programa educacional, mas não possuíam a relevância do grupo estabelecido em Leipzig. Em 1887, o primeiro número do famoso periódico científico (Jornal de Físico-Química, mais tarde chamado apenas de ) foi concebido e editado por Ostwald, Arrhenius e van't Hoff. Essa revista publicaria vários dos principais trabalhos da área de Físico-Química nas primeiras décadas do século XX, incluindo o primeiro estudo de Nernst em eletroquímica.26,31-33
AS CONTRIBUIÇÕES DE NERNST EM ELETROQUÍMICA Em Leipzig, Nernst voltou sua atenção para a teoria de Arrhenius que fornecia uma razoável explanação para o processo de dissociação de eletrólitos e condução de corrente elétrica, mas "precisava" de um melhor desenvolvimento conceitual. Além disso, alguns experimentos da época demonstravam que a diferença de potencial medida em células eletroquímicas variava com diferentes concentrações ou com a mudança dos metais envolvidos, mesmo sem um contato direto entre tais metais; tais verificações experimentais a teoria de Arrhenius não podia explicar. Nernst presumivelmente se indagou: "Qual seria a explicação termodinâmica para essas observações experimentais?" As respostas para essa e outras questões foram apresentadas por ele em três artigos que estabeleceram a base da eletroquímica moderna. O artigo de 1888 sobre a teoria de difusão de eletrólitos Em julho de 1888, Nernst publicou na 7 o artigo "" (Sobre a Cinética dos Corpos Dissolvidos em Solução)apresentando uma teoria para a difusão de substâncias dissolvidas em solução. Neste artigo, ele desenvolveu uma descrição quantitativa para a cinética do mecanismo de difusão de eletrólitos durante a dissolução. Para isso utilizou a lei da difusão proposta em 1855 pelo físico alemão Adolf Fick34 que estabelecia através de uma relação matemática simples, a proporcionalidade entre a taxa de difusão de substâncias e o gradiente da concentração das mesmas. A lei de Fick foi utilizada por Nernst em seu artigo para descrever como os eletrólitos se difundiam através de soluções em resposta a diferenças de concentração. Ao mesmo tempo, Nernst empregou no artigo as ideias de dissociação de Arrhenius, que, por sua vez, adaptara uma abordagem quantitativa desenvolvida por van't Hoff para calcular pressões osmóticas em soluções diluídas.35 Em sua abordagem, Nernst recorreu a uma perspectiva notoriamente "atomística", em uma visão que conflitava com a de seu "chefe"Ostwald que era conhecido por sua defesa do "energetismo", uma abordagem que preconizava a importância da energia, e não dos átomos, na explicação dos processos químicos36 (energia para Ostwald seria uma espécie de "medida quantitativa da interação mútua entre objetos ou sistemas"). Nernst argumentou que os íons em solução deveriam ter taxas individuais de difusão, uma vez que existiam individualmente. A interação entre esses íons não deveria perturbar significativamente essas taxas de difusão. Para uma solução com duas regiões em contato, cada uma contendo o mesmo eletrólito, mas com diferentes concentrações, Nernst sugeriu que surgiria uma força atuando sobre cada íon e essa força seria proporcional ao gradiente da pressão osmótica. Como consequência dessa força seria formada uma dupla camada elétrica na interface entre as duas regiões com diferentes concentrações, provocando uma diferença de potencial chamada "potencial de junção líquida" que afetaria a mobilidade dos íons. A mobilidade de cátions ou ânions seria inversamente proporcional à força atuante sobre eles, ou seja, os íons teriam menor mobilidade na medida em que a força atuante sobre eles se intensificasse em consequência do aumento do potencial de junção líquida. Por outro lado, Nernst explicou que íons se movendo em solução com diferentes velocidades por um curto período de tempo gerariam uma força eletrostática que tenderia a igualar suas velocidades. Nesse cenário, o efeito da força devido ao potencial de junção líquida seria "equilibrado" pela força eletrostática de movimento dos íons. Igualando essas duas forças e utilizando as expressões de van't Hoff para a pressão osmótica e da lei de Fick para a difusão, Nernst chegou a uma expressão que permite o cálculo do potencial de junção líquida. Segundo suas próprias palavras; "(...) encontramos a diferença de potencial E entre duas soluções do mesmo sal, mas de concentrações diferentes." 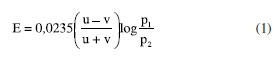 Na Equação 1, u e v são as mobilidades elétricas de cátions e ânions, respectivamente, e p1 e p2 são as pressões osmóticas das soluções 1 e 2 com diferentes concentrações. De acordo com a Equação 1, os potenciais de junção líquida dependem apenas da razão entre as duas pressões osmóticas, p1 e p2, e não de seus valores absolutos. Portanto, duas células eletroquímicas com diferentes valores de p1 e p2, mas com a mesma razão entre p1 e p2, devem fornecer o mesmo potencial de junção líquida. Nernst chamou isso de "princípio da superposição". Esse princípio viabiliza a obtenção de dados experimentais de maneira simples e conveniente em muitos casos, além de fornecer uma evidência experimental para a completa dissociação de eletrólitos em solução, pois a constatação de que a diferença absoluta nas concentrações não afeta o potencial de junção líquida, implica que os eletrólitos estejam completamente dissociados. A Equação 1 é a última do artigo de 18887 e reproduz muito bem os valores experimentais medidos para o potencial de junção líquida. Em outro artigo de 1890,37 Nernst adotaria uma expressão equivalente na qual apareceriam a constante dos gases, R, a temperatura, T, e a constante de Faraday, F: 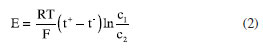 Nessa equação, c1 e c2 são as concentrações das soluções (proporcionais às pressões osmóticas p1 e p2) , t+ e t- são os números de transporte de cátions e de ânions dados por Os artigos de 1889 sobre a teoria do potencial de eletrodo Em janeiro de 1889 Nernst publicou um pequeno artigo ""(Sobre a Teoria dos Elementos Galvânicos Reversíveis)no periódico8(Relatórios das Sessões da Academia de Ciências da Prússia em Berlim), o nome de um periódico da Academia de Ciências da Prússia em Berlim. Em seguida, em maio de 1889, publicou uma versão expandida do mesmo trabalho, (A Eficácia Eletromotriz dos Íons)na .9 Nessas publicações aparece pela primeira vez aquela que ficou conhecida como equação de Nernst. Ele inicia a introdução do artigo de janeiro ressaltando:
Nernst considerou células eletroquímicas em que as duas meias-células eram idênticas, exceto pelas concentrações das duas soluções. O potencial de junção líquida em cada célula poderia ser facilmente calculado a partir da expressão deduzida no artigo de 1888. Contudo, ainda não existia uma equação para a quantificação da capacidade da célula eletroquímica em fornecer energia elétrica a um circuito externo. Para isso seria necessária uma expressão para o cálculo da diferença de potencial elétrico entre os eletrodos, também chamada de força eletromotriz (FEM). Esse tratamento deveria considerar as reações químicas que ocorriam nos eletrodos, além da diferença de potencial em cada interface eletrodo/eletrólito. É precisamente este o notável trabalho desenvolvido por Nernst no segundo artigo de 1889. Utilizando a segunda lei da termodinâmica, Nernst calculou o trabalho elétrico necessário para transportar uma certa quantidade de íons entre soluções com pressão osmótica p1 e p2, obtendo W = K ln(p1/p2), em que K é uma constante dependente das unidades de medidas utilizadas. No entanto, ele enfrentou dificuldade para calcular o trabalho envolvido no transporte de íons do eletrólito para os eletrodos, porque não havia nenhum parâmetro físico que definisse o estado dos íons nos eletrodos. Ele então introduziu o conceito de "pressão de dissolução", representada como P, que se refere à pressão resultante das colisões dos íons dissolvidos com as superfícies dos eletrodos em uma solução. Em outras palavras, P seria uma medida da pressão exercida pelos íons em solução sobre os eletrodos. Esse parâmetro P seria proporcional à concentração dos íons na solução e à temperatura e poderia, assim como a pressão osmótica dos íons em solução, ser calculado utilizando-se a equação de van't Hoff. Seguindo esse raciocínio, Nernst obteve W = K ln(P/p) em que p representava a pressão osmótica da solução em contato com o eletrólito. Para encontrar a diferença de potencial entre a interface eletrodo/eletrólito, Nernst adaptou sua expressão do artigo de 1888 usada no cálculo do potencial de junção líquida. Naquela expressão há as variáveis u e v que representam as mobilidades de cátions e ânions. No entanto, ao considerar a interface entre um catodo e o eletrólito, Nernst argumentou que a contribuição de u se tornaria efetivamente igual a 1 e a contribuição de v seria zero. Isso significa que, na interface catodo-eletrólito, a eletricidade seria transportada exclusivamente pelos cátions. De maneira semelhante, ao considerar a interface entre um anodo e o eletrólito, a contribuição de v seria 1 e a contribuição de u seria zero. Assim, Nernst obteve a seguinte equação para a diferença entre o potencial Em do metal constituinte do catodo e o potencial Ee do eletrólito no catodo: 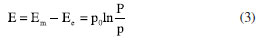 em que p0 é uma constante dependente das unidades. Quando a pressão P na superfície do eletrodo for maior do que a pressão osmótica do eletrólito na solução, p, ocorre a migração de íons do catodo para a solução criando uma diferença de potencial elétrico entre o catodo e a solução, E > 0, que agirá para se opor ao fluxo de íons para a solução. Por outro lado, se P < p, íons se depositam no catodo, deixando-o com excesso de carga positiva e uma carga negativa equivalente na fronteira da solução. Neste caso, E< 0e essa diferença de potencial se oporá à deposição extra de íons na superfície do catodo. Quando as duas pressões se igualarem, P = p, a diferença de potencial entre o eletrodo e o eletrólito será nula alcançando-se um equilíbrio com E = 0. Nesse momento, o trabalho elétrico envolvido no transporte desses íons através da interface, dado por |qE| onde q corresponde à carga envolvida, será nulo, indicando que não há mais movimento líquido de íons na interface eletrodo-eletrólito. Essas conclusões representaram um grande avanço na compreensão de vários aspectos relacionados aos experimentos de eletrodeposição. A partir desse ponto, Nernst conseguiu desenvolver uma expressão para a FEM de uma célula eletroquímica contendo duas soluções com concentrações diferentes. Ele simplesmente somou os potenciais das duas interfaces opostas entre o eletrodo e o eletrólito, resultando em: 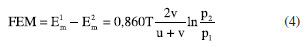 Essa é a primeira versão para a equação de Nernst. Ele a utilizou juntamente com dados experimentais sobre transporte iônico para os íons prata em diferentes eletrólitos (acetato de prata e nitrato de prata) para calcular a FEM dessas células de concentração (como passaram a ser chamadas). Esses cálculos produziram resultados que concordavam com os dados experimentais que existiam na época para esses sistemas. A Equação 4 se tornou possivelmente a mais importante na eletroquímica. Referindo-se a esses três artigos de Nernst de 1888 e 1889, o físico-químico Max Bodenstein38 (1871-1942), um destacado cientista na área da cinética química, fez a seguinte observação:
Nernst finalizou seu trabalho de maio de 1889 declarando que ainda havia muito a ser feito:
Nernst denominou sua abordagem para o cálculo das diferenças de potencial entre duas soluções com concentrações diferentes do mesmo eletrólito como , que significa literalmente "teoria de cadeia de líquidos". É notável destacar que Nernst desenvolveu essa teoria sem o conhecimento direto do elétron, o qual só seria descrito por Joseph John Thomson oito anos mais tarde. No entanto, não há dúvida de que a teoria do potencial de eletrodo que ele criou e a equação derivada nesse contexto representam um marco extraordinário na história da eletroquímica termodinâmica.
A OBTENÇÃO DA EQUAÇÃO DE NERNST A PARTIR DAS LEIS DA TERMODINÂMICA A equação de Nernst pode ser obtida a partir de uma perspectiva alternativa fundamentada nas quatro leis da termodinâmica. A seguir, apresenta-se uma sucinta discussão conceitual sobre cada uma dessas leis, antes de se mostrar sua conexão com a eletroquímica de Nernst. Primeira lei da termodinâmica A primeira lei da termodinâmica está associada à compreensão da variação da energia interna U de um sistema. Esta energia pode ser transferida entre o sistema e sua vizinhança, seja saindo do sistema ou sendo absorvida por ele. Essa transferência ocorre através de dois processos distintos: o processo calor, no qual energia interna é transferida entre sistema e vizinhança devido a uma diferença de temperaturas, e o processo trabalho, em que energia interna é trocada entre sistema e vizinhança devido a uma diferença de pressões, considerando-se exclusivamente o trabalho mecânico. Portanto, tanto o trabalho (W) quanto o calor (Q) são "processos" que requerem a existência de um sistema e suas vizinhanças, manifestando-se ao longo de um gradiente de temperaturas e pressões, "ou um caminho de diminuição de temperatura e pressões"(novamente, considerando exclusivamente o trabalho mecânico). A conexão entre a energia interna, o calor e o trabalho pode ser expressa como:39-41  em que, usualmente, representam-se distintivamente as diferenciais da função de estado (U) e das funções de caminho (W e Q). Se não ocorre troca de energia interna por meio dos processos calor ou trabalho entre o sistema e sua vizinhança, isso indica que o conjunto formado pelo sistema/vizinhança evoluiu para um estado isolado, sendo então chamado de Universo nessa condição. Neste caso:  A Equação 6 fundamenta a afirmação de Rudolf Clausius em relação à primeira lei da termodinâmica, que postula que "a energia total do Universo é constante". Portanto, a primeira lei da termodinâmica estabelece que a criação de energia "a partir do nada" é impossível. Isso implica que um fenômeno só pode ocorrer se a energia do sistema isolado relacionado ao fenômeno permanecer constante. Dessa maneira, a primeira lei define termodinamicamente quais processos são possíveis no Universo: apenas aqueles nos quais a energia se conserva. Mas a primeira lei nada informa sobre o "sentido espontâneo" de ocorrência dos processos possíveis. Para isso existe a segunda lei. Segunda lei da termodinâmica A definição termodinâmica para variação de entropia se baseia na relação  em que agora representa uma diferencial geral, prevalecendo a desigualdade em caso de irreversibilidade e a igualdade para a reversibilidade. Se o sistema se encontrar isolado (se está isolado, não pode realizar ou sofrer calor) tem-se:  A última expressão conduz ao enunciado mais comum da segunda lei da termodinâmica: a variação de entropia para um sistema isolado é nula quando o sistema está em equilíbrio termodinâmico, e positiva para processos fora do equilíbrio, ou seja, espontâneos. Assim, enquanto a primeira lei da termodinâmica indica quais processos são possíveis, baseando-se na conservação de energia para um sistema isolado, a segunda lei da termodinâmica determina quais desses processos são espontâneos, considerando o aumento da entropia do sistema isolado.40 Terceira lei da termodinâmica Enunciados da terceira lei da termodinâmica comuns em livros textos são expressos em termos do teorema do calor de Nernst (outra contribuição de Nernst para a termodinâmica)42,43Esse teorema estabelece que "a diferença na entropia entre dois estados em equilíbrio interno na temperatura T para um sistema, aproxima-se de zero quando a temperatura tende a zero." 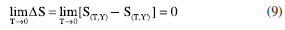 A expressão da terceira lei, em que Y representa o conjunto de propriedades intensivas necessárias além da temperatura para definir o estado do sistema, é simples, porém não é aplicável a sistemas fora do equilíbrio interno, como líquidos, sólidos amorfos e soluções sólidas. Diferentes formulações do teorema de calor de Nernst enfatizam restrições adicionais, como sua validade apenas para sólidos cristalinos perfeitos. Isso tem gerado dúvidas sobre a generalidade da terceira lei. Alguns autores39,40 de obras tradicionais de Físico-Química chegam a sugerir que essa lei não seria "tão universal". Entretanto, a terceira lei não é uma lei restrita. O próprio Nernst propôs uma abordagem mais abrangente em 1912, centrada na inatingibilidade do zero absoluto e expressa como:
A vantagem desta abordagem reside em sua validade abrangente, o que justifica o reconhecimento do terceiro princípio como uma lei. Expressa desta forma, a terceira lei se assemelha aos enunciados da primeira lei, que estabelece a impossibilidade de criar energia, e da segunda lei, que afirma a impossibilidade de reduzir a entropia em processos espontâneos ocorrendo em um sistema isolado. É possível demonstrar a concordância entre o enunciado fornecido pela Equação 9 e a inatingibilidade do zero absoluto.46 Uma maneira de compreender o significado mais profundo da terceira lei da termodinâmica é questionar o que ocorreria em um sistema atômico ou molecular caso o zero absoluto fosse alcançado. Por exemplo, pela teoria cinética molecular, para um sistema gasoso composto por átomos, pode-se demonstrar que Ecinética = constante × T. Portanto, se T = 0, Ecinética = 0. Isso implica que se a temperatura alcançasse o zero absoluto, o sistema não teria energia cinética e os átomos estariam completamente imóveis. A terceira lei da termodinâmica nos adverte: não é viável cessar completamente o movimento de átomos ou moléculas em um sistema gasoso. Exemplos análogos, abrangendo outros tipos de sistemas, podem ser elaborados. A lei zero da termodinâmica Existem várias interpretações para o conceito de temperatura. Por exemplo, como visto anteriormente, a teoria cinética molecular estabelece que para certos sistemas gasosos, Ecinética = constante × T e, consequentemente, T = constante × Ecinética, sendo esse o fundamento para a famosa interpretação da temperatura como diretamente proporcional à energia cinética média de um sistema. Por outro lado, ao combinar a primeira e a segunda lei da termodinâmica para um sistema onde apenas trabalho mecânico está envolvido e o volume permanece constante,  Nesse cenário, a temperatura representa a taxa de variação da energia interna do sistema em relação à entropia. Diante dessas diferentes interpretações para temperatura, surge a questão sobre qual seria a sua "definição". Para abordar essa questão, a lei zero da termodinâmica declara: "Se um corpo (ou sistema) A está em equilíbrio térmico com um corpo (ou sistema) B, e B está em equilíbrio térmico com um corpo (ou sistema) C, então, A estará em equilíbrio térmico com C." Neste contexto, temperatura é conceituada como a propriedade termodinâmica cuja igualdade entre os valores dessa propriedade para dois sistemas estabelece o equilíbrio térmico.39
ENERGIA DE GIBBS - ONDE AS LEIS DA TERMODINÂMICA SE COMBINAM Combinando a primeira e a segunda lei da termodinâmica, de acordo com as relações apresentadas anteriormente:  Nessas relações, o trabalho 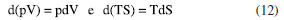 então, 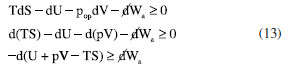 Define-se assim, a função de estado energia de Gibbs:  As duas primeiras leis da termodinâmica foram diretamente empregadas para derivar as relações da Equação 13. No entanto, uma análise minuciosa dessa equação revela também a validade da lei zero e da terceira lei. A definição da temperatura, conforme estabelecida pela lei zero da termodinâmica, é crucial para a Equação 13, já que esse parâmetro é empregado nessa equação. Além disso, a temperatura na Equação 13 não pode ser zerada sem alterar a definição original da energia de Gibbs conforme expressa na Equação 14. Portanto, a terceira lei é sutilmente incorporada nesta definição de G. Finalmente, pode-se escrever dG ≥  Logo, a variação na energia de Gibbs será menor do que o trabalho (que não é de natureza mecânica) em um processo espontâneo. Isso ocorre porque o sinal < resulta do sinal > da segunda lei da termodinâmica, que indica a espontaneidade. E, é claro, a variação na energia de Gibbs será igual a esse trabalho para processos em equilíbrio termodinâmico. Relação entre a energia de Gibbs e o trabalho elétrico Em um processo ocorrendo em um sistema termodinâmico que envolva trabalho elétrico, como em uma célula eletroquímica, a variação na energia de Gibbs molar será igual ao trabalho elétrico máximo realizado pela célula. Isso ocorre porque esse trabalho máximo corresponderia ao estado de equilíbrio, no qual a reação da célula teria atingido seu limite em termos de produção de trabalho. Assim,  esse trabalho elétrico pode ser determinado aplicando-se uma diferença de potencial E entre os eletrodos da célula eletroquímica, o suficiente para interromper a reação da célula. Assim, pode-se expressar o trabalho elétrico máximo da seguinte forma: 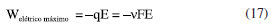 em que n, F e q são a quantidade de elétrons, a constante de Faraday e a carga envolvidos na produção do trabalho elétrico, respectivamente. Relação entre a energia de Gibbs e o quociente reacional Como G = U + pV - TS e dU = TdS - pdV, obtém-se: 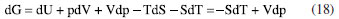 Escrevendo a diferencial total de G como função de T e p: 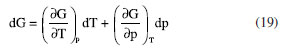 comparando-se as duas expressões anteriores conclui-se que: 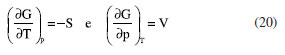 A primeira relação na Equação 20 mostra que a energia de Gibbs a p constante diminui com o aumento da temperatura de maneira proporcional ao aumento da entropia. A segunda relação mostra que a energia de Gibbs a T constante aumenta com o aumento da pressão de maneira proporcional ao volume do sistema. A variação da energia de Gibbs em função da pressão para um sistema constituído por substância pura a T constante pode ser obtida integrando-se,39,40 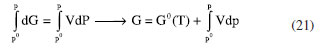 em que G0(T) é a energia de Gibbs padrão da substância, definida para a pressão p0. Se a substância for um gás ideal, 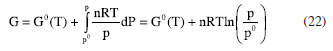 tomando-se p0 como 1 atm, 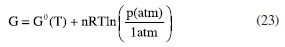 dividindo-se essa equação por n (número de mols) obtém-se outra em termos do potencial químico (tem-se um sistema com um componente e a quantidade de matéria não varia),  nessa equação está implícito que a pressão foi normalizada por 1 atm dentro do logaritmo. Para a reação representada pela equação química 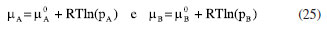 consequentemente, 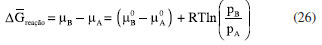 em que é o coeficiente reacional. Assim, 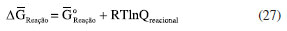 pode-se mostrar, por um tratamento similar, que o quociente reacional pode ser relacionado à razão de concentrações ou atividades em soluções líquidas.39-41
A EQUAÇÃO DE NERNST: RELAÇÃO ENTRE O TRABALHO ELÉTRICO E O QUOCIENTE REACIONAL Finalmente, pode-se igualar as Equações 16 e 27 e utilizar a definição da Equação 17 para obter a equação de Nernst: 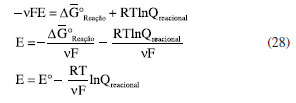 Esta equação possibilita a obtenção do potencial elétrico de uma célula eletroquímica em função das concentrações (ou atividades) das espécies expressas no quociente reacional e é equivalente à Equação 4 obtida por Nernst em 1889. Na equação de Nernst, o potencial padrão E0 é uma propriedade específica para cada célula eletroquímica. Este valor fundamental pode ser determinado por meio da análise dos potenciais de redução e oxidação relacionados às semi-reações que ocorrem nos eletrodos da célula. Para ilustrar esse conceito, pode-se considerar a célula eletroquímica de Daniell como um exemplo clássico. Esta célula é assim denominada em homenagem ao renomado químico britânico John Frederic Daniell, que a desenvolveu e descreveu pela primeira vez em 1839.39-41 A Célula de Daniell é composta por um eletrodo de zinco e um eletrodo de cobre, imersos em soluções de sulfato de zinco e sulfato de cobre, respectivamente. A separação física das soluções por uma ponte salina permite a ocorrência das semi-reações de redução e oxidação em cada eletrodo, gerando uma corrente elétrica contínua. As semi-reações, bem como a reação global da célula, são as seguintes: 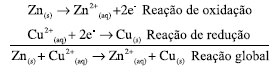 Os potenciais de oxidação do zinco e redução do cobre valem Ered = +0,34 V e Eoxi = +0,76 V de maneira que o potencial padrão para essa célula será de: 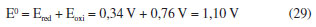 A obtenção da equação de Nernst, conforme descrita nesta abordagem, baseia-se na conexão entre a variação da energia de Gibbs e o trabalho elétrico, como ilustrado pela Equação 16. Esta última equação pressupõe a definição da energia de Gibbs. Notadamente, a energia de Gibbs é uma função de estado que incorpora os princípios das quatro leis da termodinâmica, conforme discutido na seção "Energia de Gibbs - onde as leis da termodinâmica se combinam" do presente artigo. Portanto, a equação de Nernst é um exemplo emblemático da aplicação das quatro leis da termodinâmica na compreensão e descrição dos fenômenos eletroquímicos.
CONCLUSÕES A análise histórica e do contexto termodinâmico envolvendo a equação de Nernst oferece uma visão detalhada e enriquecedora dessa ferramenta essencial, base da eletroquímica contemporânea. O estudo de sua evolução ao longo do tempo e compreensão dos fundamentos termodinâmicos segundo os quais a equação foi desenvolvida, proporcionam uma compreensão mais abrangente e profunda de sua importância e aplicabilidade. Essa abordagem elucida o papel essencial que a equação desempenha na fundamentação teórica e prática da eletroquímica moderna, destacando sua relevância na compreensão e no desenvolvimento de tecnologias voltadas para o armazenamento de energia, eletrólise, corrosão e várias outras aplicações científicas e industriais. A investigação das origens formais da área remonta aos experimentos pioneiros de Alessandro Volta e às primeiras formulações conceituais de uma série de cientistas do século XIX. A partir desses marcos históricos, a evolução do campo foi impulsionada por uma série de contribuições notáveis, entre as quais se destacaram aquelas de Walther Nernst. A análise desse percurso histórico revela a complexidade e a profundidade do desenvolvimento científico que culminou na formulação da equação de Nernst, que representa um marco significativo na compreensão da interação entre eletricidade e química. Ao longo do presente artigo, destacou-se não apenas a evolução histórica, mas também a base termodinâmica que sustenta a equação de Nernst, desde as significações das leis da termodinâmica até sua combinação versátil na forma da função de estado energia de Gibbs, G, enfatizando-se a conexão entre a termodinâmica e os sistemas elétricos, através da igualdade entre a variação dessa função de estado G e o trabalho elétrico. Finalmente, pode-se afirmar que a equação de Nernst não é apenas uma "fórmula matemática", mas sim um reflexo do progresso contínuo da ciência. Sua importância vai além de aspectos puramente técnicos, mas representa um caso exemplar de como a história, a filosofia e a química podem convergir em uma discussão ampla e multidisciplinar sobre temas científicos.
REFERÊNCIAS 1. Sazali, N.; Salleh, W. N. W.; Jamaludin, A. S.; Razali, M. N. M.; 2020, , 99. [Crossref] 2. Selmi, T.; Khadhraoui, A.; Cherif, A.; 2022, , 78121. [Crossref] 3. Kania, H.; Saternus, M.; 2023, , 2003. [Crossref] 4. Zueva, S.; Ferella, F.; Ippolito, N. M.; Ruduka, E.; Michelis, I. D.; 2021, , 01064. [Crossref] 5. Kania, H.; Mendala, J.; Kozuba, J.; Saternus, M.; 2020, , 4168. [Crossref] 6. Reumont, G.; Mathon, M.; Fourmentin, R.; Perrot, P.; 2003, , 411. [Crossref] 7. Nernst, W.; 1888, , 613. [Crossref] 8. Nernst, W.; 1889, , 83. [Link] accessed in June 2024 9. Nernst, W.; 1889, , 129. [Crossref] 10. Haas, L. F.; 1993, , 1084. [Crossref] 11. Piccolino, M.; 1998, , 381. [Crossref] 12. de Santillana, G.; 1965, , 82. [Link] acessado em Junho 2024 13. Volta, A.; 1800, , 403. [Crossref] 14. Szydło, Z. A.; 2021, , 5. [Crossref] 15. Hancock, J. T.; LeBaron, T. W.; 2023, , 102. [Crossref] 16. Smolinka, T.; Bergmann, H.; Garche, J.; Kusnezoff, M. Em ; Smolinka, T.; Garche, J., eds.; Elsevier: Amsterdam, 2022, cap. 4. [Crossref] 17. Russel, C. A.; 1963, , 127. [Crossref] 18. Forbes, N.; Basil, M.; , illustrated ed.; Prometheus Books: New York, 2014. 19. Faraday, M.; , vol. 1, 1st ed.; Richard and John Edward Taylor: London, 1839. 20. Novitski, M. E.; , vol. 1, 1st ed.; Routledge: London, 1992. 21. Stock, J. T.; 1991, , 86. [Link] acessado em Junho 2024 22. Chen, J. P.; Yuh, C. S.; Yung-Tse, H.; , vol. 3, 2005th ed.; Humana Press: Totowa, 2005. 23. Arrhenius, S.; 1912, , 353. [Crossref] 24. De Berg, K. C.; 2003, , 397. [Crossref] 25. The Nobel Prize in Chemistry 1903, https://www.nobelprize.org/prizes/chemistry/1903/summary/, acessado em Junho 2024. 26. Bartel, H. G.; Huebener, R. P.; , 1st ed.; World Scientific Publishing Company: Singapore, 2007. 27. Satirical obituary for Walther Nernst, http://www.nernst.de/satirical-obituary.htm, acessado em Junho 2024. 28. Mendelssohn, K.; , 1st ed.; University of Pittsburgh Press: Pittsburgh, 1973. 29. Planck, M.; Abreu, E. S.; , 1ª ed.; Contraponto Editora: Rio de Janeiro, 2020. 30. Barkan, D. K.; , illustrated ed.; Cambridge University Press: Cambridge, 2011. 31. Laidler, K. J.; 1985, , 43. [Link] acessado em Junho 2024 32. Zott, R.; 2003, , 3990. [Crossref] 33. Dolby, R. G. A.; , , Aldine Publishing Company: USA, 1976. [Link] acessado em Junho 2024 34. Fick, A.; 1855, , 59. [Crossref] 35. van't Hoff, J.; 1888, , 81. [Link] acessado em Junho 2024 36. Pereira, L. D. S.; Freire Junior, O.; Mascarenhas, A. J. S.; Boeck, G.; 2021, , 256. [Crossref] 37. Nernst, W.; 1890, , 65. [Link] acessado em Junho 2024 38. Bodenstein, M.; 1942,, 75. [Link] acessado em Junho 2024 39. Castellan, G. W.; , 1ª ed.; LTC: Rio de Janeiro, 1986. 40. Atkins, P.; de Paula, J.; , vol. 1, 8ª ed.; LTC: Rio de Janeiro, 2008. 41. McQuarrie, D. A.; Simon, J. D.; , 1st ed.; University Science Books: Sausalito, 1997. 42. Nernst, W.; , German Ed.; Dover: New York, 1969. 43. Cropper, W. B.; 1987, , 3. [Crossef] 44. Levy, A.; Alicki, A.; Kosloff, R.; 2012, , 061126. [Crossref] 45. Loebl, E. M.; 1960, , 361. [Crossref] 46. Simon, F.; 1927,, 806. [Crossref]
Associate Editor handled this article: Nyuara A. S. Mesquita |
On-line version ISSN 1678-7064 Printed version ISSN 0100-4042
Qu�mica Nova
Publica��es da Sociedade Brasileira de Qu�mica
Caixa Postal: 26037
05513-970 S�o Paulo - SP
Tel/Fax: +55.11.3032.2299/+55.11.3814.3602
Free access






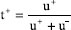 e
e 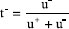 , com u+ e u- sendo as mobilidades elétricas de cátions e ânions.
, com u+ e u- sendo as mobilidades elétricas de cátions e ânions.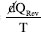 em que
em que 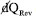 é o processo calor envolvido em uma transformação reversível para o sistema à temperatura fixa T. A reversibilidade aqui corresponde a uma situação termodinâmica de "equilíbrio". A condição para um processo fora de equilíbrio (sinônimo de irreversível ou espontâneo) é a desigualdade, , em que é o processo calor envolvido na transformação irreversível. Essas duas condições, reversibilidade e irreversibilidade termodinâmicas, podem ser agrupadas em:
é o processo calor envolvido em uma transformação reversível para o sistema à temperatura fixa T. A reversibilidade aqui corresponde a uma situação termodinâmica de "equilíbrio". A condição para um processo fora de equilíbrio (sinônimo de irreversível ou espontâneo) é a desigualdade, , em que é o processo calor envolvido na transformação irreversível. Essas duas condições, reversibilidade e irreversibilidade termodinâmicas, podem ser agrupadas em: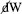 pode ser dividido em
pode ser dividido em 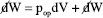 em que diz respeito ao trabalho mecânico (expansão ou compressão) com pop sendo a pressão oposta ao sistema e dV a variação em seu volume; já
em que diz respeito ao trabalho mecânico (expansão ou compressão) com pop sendo a pressão oposta ao sistema e dV a variação em seu volume; já 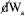 representa um trabalho diferente do mecânico (trabalho elétrico, superficial, etc.). Então,
representa um trabalho diferente do mecânico (trabalho elétrico, superficial, etc.). Então, 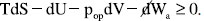 . Se um sistema sofrer uma transformação à pressão e temperatura constantes serão válidas as relações,39
. Se um sistema sofrer uma transformação à pressão e temperatura constantes serão válidas as relações,39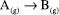 pode-se escrever os potenciais químicos para as espécies como:
pode-se escrever os potenciais químicos para as espécies como: